Abstract
This paper is devoted to the identification of the parameters of discrete fractional systems with errors in variables. Estimates of the parameters of such systems can be obtained using generalized total least squares (GTLS). A GTLS problem can be reduced to a total least squares (TLS) problem. A total least squares problem is often ill-conditioned. To solve a TLS problem, a classical algorithm based on finding the right singular vector or an algorithm based on an augmented system of equations with complex coefficients can be applied. In this paper, a new augmented system of equations with real coefficients is proposed to solve TLS problems. A symmetrical augmented system of equations was applied to the parameter identification of discrete fractional systems. The simulation results showed that the use of the proposed symmetrical augmented system of equations can shorten the time for solving such problems. It was also shown that the proposed system can have a smaller condition number.
1. Introduction
Equations with fractional-order derivatives and differences are widely used to describe various processes and phenomena. Models based on equations with fractional-order derivatives and differences find wide application in hydrology, economics, and forecasts of network data usage [1,2,3].
Most of the research in this field deals with the parameter identification of fractional-order differential equations using the error in an equation or an output error. References [4,5] described time domain identification methods based on the least squares technique. References [6,7,8] presented an overview of different methods for identifying systems with fractional-order derivatives. The use of total least squares for estimating the parameters of fractional-order differential equations was proposed in [9,10].
Autoregressions with fractional differences are widely used in the analysis of time series with long memory [11,12]. There are a large number of different models with generalizations of fractional differences, such as Gegenbauer autoregressive moving average (GARMA) [13,14], fractional ARUMA [15], seasonal autoregressive fractionally integrated moving average (SARFIMA) [16,17], and autoregressive tempered fractionally integrated moving average (ARTFIMA) [18,19]. Various aspects of using fractional differences for time series analysis have been considered [20,21].
In [22], a discrete Kalman filter with fractional differences was proposed. Equations with fractional-order differences were also used to approximate differential equations with Grunwald–Letnikov derivatives [23]. Meanwhile, the modeling of various physical processes based on equations with fractional-order differences was considered in [24,25,26].
All articles cited assumed that the input signal is observed without noise. The problem of identifying integer or fractional-order systems with errors in variables is much more difficult. Reference [27] provided an overview of the contemporary state of this problem.
A small number of articles are devoted to the parameter identification of fractional-order systems with errors-in-variables. The known methods are based on cumulant least squares [28,29], cumulant instrumental variables [30], bias-compensated least squares [31], generalized total least squares [32,33,34], and generalized instrumental variables [35].
The problem of estimating the parameters of fractional systems with error in variables can be solved based on generalized total least squares [32]. A least squares solution is possible based on the SVD approach or based on the secular equation approach. The secular equation approach is more preferable than the SVD approach if [36]:
- The problem is sensitive: The minimum singularities have a small gap;
- The problem is large: The SVD of a large matrix is very expensive. Instead, we can approximate the secular equation in the large-scale problem by Gaussian quadrature rules.
When applying the secular equation approach, it is necessary to solve a biased normal system. A biased normal system has more conditionality than a solution based on the SVD approach.
The problem of estimating the parameters of fractional systems is often ill-conditioned. To reduce the condition number, augmented systems of equations can be used [37,38].
For TLS, [39] proposed an augmented system of equations with complex coefficients equivalent to a biased normal system.
In article [34], an algorithm was proposed for the parameter identification of discrete fractional systems based on an augmented system of equations.
This article proposes a symmetrical augmented system of equations with real coefficients for the parameter identification of discrete fractional systems by generalized total least squares. The proposed symmetrical augmented system of equations has a smaller dimension than the augmented system [39], as well as real coefficients.
2. Materials and Methods
2.1. Problem Statement
The dynamical system is described by linear stochastic equations with fractional differences:
where and are constant coefficients; , , , and are fractional differences [1];
and are generalized binomial coefficients.
The following assumptions are introduced:
A1. The dynamic system (1) is asymptotically stable. Results on the asymptotic stability of discrete time fractional difference systems can be found in [40,41].
A2. The noise sequences , are independent sequences with , , , and , where is the expectation operator.
A3. The input and output sequences are independent of noise sequences . The noise sequences are mutually independent.
A4. The input signal persistently excites the order [42].
A5. The noise variance ratio is known.
It is required to estimate the unknown coefficients of the dynamic system described by Equation (1) from the observed sequences with noise for the known orders and .
If and are unknown, it is necessary to apply algorithms based on global optimization, such as genetic algorithms [43].
2.2. The Objective Function for Parameter Estimation
In [13], the following objective function was proposed for estimating the parameters:
where:
Theorem 1.
Let the dynamic system described by Equation (1) with initial zero conditions and Assumptions A1–A5 be introduced. Then, the estimate of the coefficients determined by expression (2) exists, is unique, and converges to the true value of the coefficients with probability 1, i.e.,
The proof of the theorem is similar to the proof given in [33].
The objective function (2) is a generalized total least squares objective function. In [32], an iterative procedure based on the minimization of the generalized Rayleigh ratio was proposed. The simulation results in [34] showed that for ill-conditioned systems, the algorithm has a low accuracy of parameter estimation.
We transformed the objective function (2) into the following form:
Under Assumptions A1–A5, the matrix is nonsingular. The generalized total least squares problem (3) can be reduced to the total least squares problem [44].
Then objective function (3) can be defined as:
The generalized total least squares algorithm for a nonsingular matrix has this form (Algorithm 1).
| Algorithm 1. Ref. [34]. |
| Step 1. Change variables and |
| Step 2. Calculate the estimate of the vector of parameter by the objective function (5). |
| Step 3. Perform inverse change of variable |
2.3. Numerical Method for the Total Least Squares Problem
There are many algorithms for solving total least squares problems. The classical algorithm for solving the total least squares problem is based on SVD (singular value decomposition) [45]. The solution to a total least squares problem based on augmented systems of the equation was considered in [40]. To solve a large dimension or with a sparse matrix, iterative methods for solving total least squares problems are used, such as Newton’s method [46,47], Rayleigh iterations [48], and Lanschoz iterations [49].
The problem of finding the singular vector is a nonlinear vector problem. Solving this problem numerically involves significant difficulties [50] related to convergence issues, high computational complexity, and the stability of search algorithms. Another approach is based on solving a biased normal system. Reference [51] showed that given the satisfaction of the condition:
where and are minimal singular values of matrices and .
The minimum of function (5) can be found as a solution to the biased normal system of equations
When system (6) is solved, only the scalar problem of finding the minimal singular value remains nonlinear. This problem is always well-conditioned [48]. The vector problem is linear, but the system (6) is often ill-conditioned. The spectral condition number of the biased normal matrix is obtainable from the expression:
The use of Cholesky decomposition can make the solution more stable. As this method applies to systems of linear equations with symmetrical, positively definite matrices, it can also be used for the biased normal system (6). However, Cholesky decomposition for ill-conditioned matrices leads to large errors.
2.3.1. Augmented System of Equations for Total Least Squares
In [39], an approach was proposed for solving normal systems of equations based on equivalent augmented systems of equations. Normal systems of equations corresponding to ordinary least squares:
Can be represented as an equivalent augmented system of equations:
where
The number of conditions (7) is defined as:
where
In [38], a generalization of the augmented system (7) to the case of the biased normal system (6) is proposed. It was proposed to use a complex matrix and vector defined as:
Using notation (8), the biased normal system (6) can be defined as:
Or:
where is an arbitrary positive variable factor:
The number of conditions (9) is defined as [17]:
where and are the maximal and minimal eigenvalues of a matrix , respectively.
The problem of finding the minimum value of the condition number can be considered as a problem of choosing the optimal factor :
Problem (9) has no analytical solution but can be solved by numerical methods. In [38], an estimate was proposed for factor :
Equation (7) can be solved by standard methods for solving systems of equations, such as using LU decomposition [52].
Generalized total least squares with the augmented system of Equation (9) in the second step algorithm were proposed for estimating the parameters of the system (1) [15].
The simulation results in [15,39] showed that the use of the augmented system of equations (7) is superior in accuracy to methods based on minimization of the generalized Rayleigh ratio or Cholesky decomposition for the biased normal system of equations.
The limitations of the augmented system (9) include the following:
- The augmented system of equations has complex coefficients, even if the original system has real coefficients.
- The matrix is non-Hermitian. It is impossible to apply LDLT decomposition for the solution of the system of Equation (9) [52].
- The matrix has the dimensions .
- It is necessary to determine the optimal factor .
2.3.2. Symmetry Augmented System of Equations for Total Least Squares
Let us obtain an alternative augmented system of equations free of these limitations.
We transformed the system of Equation (6):
We combined Equation (13) with the equation :
Let us represent this in matrix form:
Or:
The resulting augmented system has a real symmetric matrix. The dimension of the matrix is .
Theorem 2.
The spectral condition number of the system of Equation (15) is defined as:
Proof of Theorem 2.
We introduced a new variable, , and considered the eigenvalue problem: □
We transformed the system of Equation (17):
From Equation (18), it follows that if , then the eigenvector and are the corresponding eigenvalue of the matrix i.e.,
where the eigenvalues of the matrix by solving the quadratic equation are:
Solving Equation (19), we can obtain .
Then, the spectral condition number is:
3. Results
Test cases were compared to the normalized root mean square error (NRMSE) of parameter estimation, defined as:
The results were based on 50 independent Monte-Carlo simulations. The number of data points N in each simulation was 200. The input signal was a step function. The dynamic system is described by the equation:
Figure 1 shows the step response of the system (20).
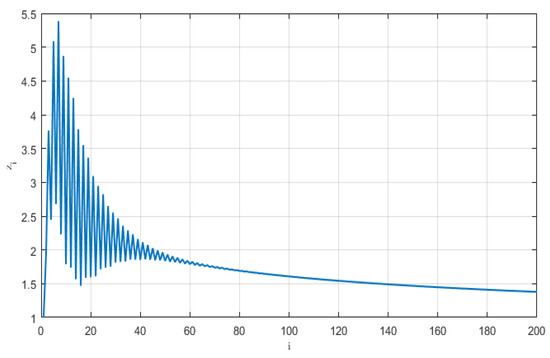
Figure 1.
The step response of the system (20).
Example 1.
The noise-to-signal ratios wereandThe gap between the minimal singular values of the matrixis.
Table 1 shows the mean values of the condition numbers of the matrices and their standard deviations.

Table 1.
The mean values of the condition numbers of the matrices and their standard deviations.
Figure 2 shows the histogram of the decision time.
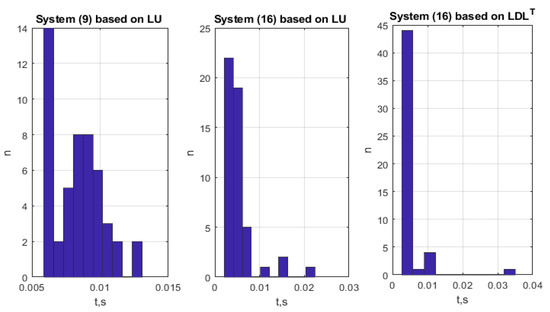
Figure 2.
Histogram of the decision time.
Table 2 shows the mean values of the decision time and their standard deviations.

Table 2.
The mean values of the decision time and their standard deviations.
Figure 3 shows the histogram of the normalized root mean square error of the parameters.
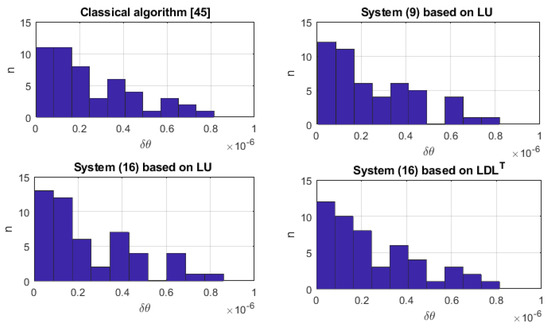
Figure 3.
Normalized root mean square error of the parameters [45].
Table 3 shows the mean values of the normalized root mean square error of the parameter estimation and their standard deviations.

Table 3.
The mean values of the normalized root mean square error of the parameter estimation and their standard deviations.
Example 2.
The noise-to-signal ratios wereand
The gap between the minimal singular values of the matrix is .
Table 4 shows the mean values of the condition numbers of the matrices and their standard deviations.

Table 4.
The mean values of the condition numbers of the matrices and their standard deviations.
Figure 4 shows the histogram of the decision time.
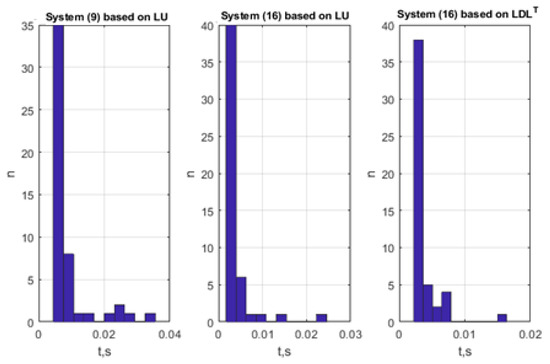
Figure 4.
Histogram of the decision time.
Table 5 shows the mean values of the decision time and their standard deviations.

Table 5.
The mean values of the decision time and their standard deviations.
Figure 5 shows the histogram of the normalized root mean square error of the parameters.
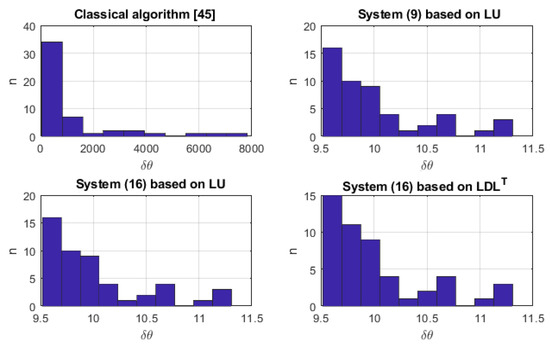
Figure 5.
Normalized root mean square error of the parameters [45].
Table 6 shows the mean values of the normalized root mean square error of parameter estimation and their standard deviations.

Table 6.
The mean values of the normalized root mean square error of parameter estimation and their standard deviations.
In Table 3, the standard deviations and mean values of the normalized root mean square error of the parameters are nearly equal. This is due to the fact that the condition numbers were large enough and the resulting estimates were sensitive to the initial data.
In Table 6, the standard deviations for the classical algorithm significantly exceed the mean values of the normalized root mean square error of the parameters. This indicates that in some experiments the results are very inaccurate, suggesting that the algorithm is numerically unstable and cannot be applied without regularization methods.
As can be seen from Examples 1,2, conditionality is highly dependent on the signal-to-noise ratios upon input and output. Let us investigate how the condition number changes with a change in the signal-to-noise ratio upon input and output. Upon output, there is a signal–noise ratio of , while there is a signal-to-noise ratio upon input of . Figure 2 shows and . As can be seen from Figure 6, the conditionality of the proposed system is lower than the conditionality of the system (8).
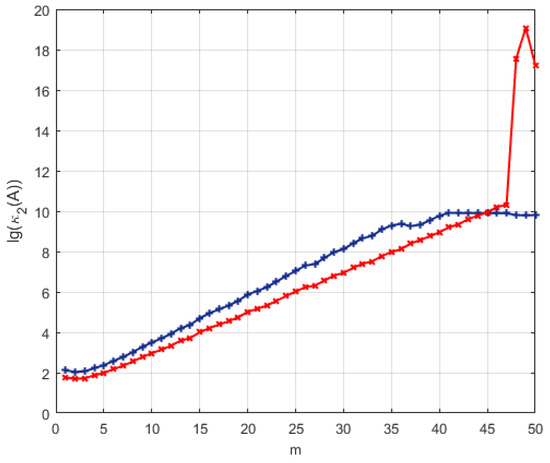
Figure 6.
Condition number logarithms (red line) and (blue line).
4. Discussion
This paper proposed an estimation method of the parameters of discrete fractional systems by generalized total least squares. The simulation results showed that the parameter estimates obtained with the augmented systems of the equation can exceed the accuracy of the SVD-based estimates. This is due to the fact that methods based on augmented systems are less sensitive to the size of the gap between the smallest singular numbers.
In Table 6, showing the standard deviations for the classical algorithm, the mean values of normalized root mean square error of parameters is significantly exceeded. This shows that the method based on the SVD approach in example 2 is numerically unstable.
The solution time for the proposed method is less than that used in [34]. It is also not required to determine the optimal parameter . The LDLT decomposition-based implementation turned out to be faster than the LU decomposition-based implementation.
The application of the proposed augmented system is especially justified in cases when it is necessary to repeatedly estimate the parameters of discrete fractional systems, such as in algorithms that estimate both linear and nonlinear parameters [43]. In the future, it is planned to investigate the use of regularized versions of these systems.
Author Contributions
Conceptualization, D.I.; investigation, D.I. and A.Z. The authors have equally contributed to the writing, editing, and style of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This article was supported by the Federal Agency of Railway Transport (No. 121031500057-3).
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the reviewers for constructive and useful comments, which made it possible to significantly improve the presentation of the results obtained.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Podlubny, I. Fractional differential equations. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198, pp. xxiv, 340. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. In North-Holland Mathematics Studies; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204, pp. xx, 523. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific Publishing Co., Inc.: River Edge, NJ, USA, 2000; ISBN 981-02-3457-0. [Google Scholar] [CrossRef]
- Cois, O.; Oustaloup, A.; Battaglia, E.; Battaglia, J.-L. Non integer model from modal decomposition for time domain system identification. IFAC Proc. Vol. 2000, 33, 989–994. [Google Scholar] [CrossRef]
- Cois, O.; Oustaloup, A.; Poinot, T.; Battaglia, J.-L. Fractional state variable filter for system identification by fractional model. In Proceedings of the 2001 European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 2481–2486. [Google Scholar] [CrossRef]
- Malti, R.; Aoun, M.; Sabatier, J.; Oustaloup, A. Tutorial on system identification using fractional differentiation models. IFAC Proc. Vol. 2006, 39, 606–611. [Google Scholar] [CrossRef]
- Kothari, K.; Mehta, U.; Prasad, R. Fractional-Order System Modeling and its Applications. J. Eng. Sci. Technol. Rev. 2019, 12, 1–10. [Google Scholar] [CrossRef]
- Damarla, S.K.; Kundu, M. Fractional Order Processes: Simulation, Identification, and Control, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Dzielinski, A.; Sierociuk, D.; Sarwas, G.; Petráš, I.; Podlubny, I.; Škovránek, T. Identification of the fractional-order systems: A frequency domain approach. Acta Montan. Slovaca 2011, 16, 26–33. [Google Scholar]
- Dorčák, Ľ.; Gonzalez, E.; Terpák, J.; Valsa, J.; Pivka, L. Identification of fractional-order dynamical systems based on nonlinear function optimization. Int. J. Pure Appl. Math. 2013, 89, 225–250. [Google Scholar] [CrossRef][Green Version]
- Granger, C.W.; Joyeux, R. An introduction to long-memory time series models and fractional differencing. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Woodward, W.A.; Cheng, Q.; Gray, H.L. A k-factor GARMA long-memory model. J. Time Ser. Anal. 1998, 19, 485–504. [Google Scholar] [CrossRef]
- Ivanov, D.V.; Engelgardt, V.V.; Sandler, I.L. Genetic Algorithm of Structural and Parametric Identification of Gegenbauer Autoregressive with Noise on Output. Procedia Comput. Sci. 2018, 131, 619–625. [Google Scholar] [CrossRef]
- Giraitis, L.; Leipus, R. A generalized fractionally differencing approach in long memory modelling. Lith. Math. J. 1995, 35, 53–65. [Google Scholar] [CrossRef]
- Reisen, V.A.; Rodrigues, A.L.; Palma, W. Estimation of Seasonal Fractionally Integrated Processes. Comput. Stat. Data Anal. 2006, 50, 568–582. [Google Scholar] [CrossRef]
- Reisen, V.A.; Rodrigues, A.L.; Palma, W. Estimating seasonal long-memory processes: A Monte Carlo study. J. Stat. Comput. Simul. 2006, 76, 305–316. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Sabzikar, F.; Phanikumar, M.S.; Zeleke, A. Tempered fractional time series model for turbulence in geophysical flows. J. Stat. Mech. Theory Exp. 2014, 2014, P09023. [Google Scholar] [CrossRef]
- Sabzikar, F.; Meerschaert, M.M.; Chen, J. Tempered Fractional Calculus. J. Comput. Phys. 2015, 293, 14–28. [Google Scholar] [CrossRef]
- Ram, M. Recent Advances in Time Series Forecasting, 1st ed.; Bisht, D.C.S., Ed.; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar] [CrossRef]
- Palma, W. Long-memory time series. In Theory and Methods; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Sierociuk, D.; Dzielinski, A. Fractional Kalman filter algorithm for the states parameters and order of fractional system estimation. Int. J. Appl. Math. Comput. Sci. 2006, 16, 129–140. [Google Scholar]
- Čermák, J.; Kisela, T. Note on a discretization of a linear fractional differential equation. Math. Bohem. 2010, 135, 179–188. [Google Scholar] [CrossRef]
- Dzielinski, A.; Sierociuk, D.; Sarwas, G. Some applications of fractional order calculus. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 583–592. [Google Scholar] [CrossRef]
- Oprzędkiewicz, K.; Dziedzic, K. PSO Identification for Discrete Fractional Order Model of Heat Transfer Process. In Advances in Non-Integer Order Calculus and Its Applications; Malinowska, A., Mozyrska, D., Sajewski, Ł., Eds.; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2018; Volume 559, pp. 240–249. [Google Scholar] [CrossRef]
- Martínez-González, R.; Bolea, Y.; Grau, A.; Martínez-García, H. An LPV Fractional Model for Canal Control. Math. Probl. Eng. 2009, 2009, 471540. [Google Scholar] [CrossRef]
- Söderström, T. Errors-in-Variables Methods in System Identification, Communications and Control Engineering; Springer: Cham, Switzerland, 2018; pp. xxvii, 485. [Google Scholar] [CrossRef]
- Chetoui, M.; Malti, R.; Thomassin, M.; Aoun, M.; Najar, S.; Oustaloup, A.; Abdelkrim, M.N. EIV methods for system identification with fractional models. IFAC Proc. Vol. 2012, 45, 1641–1646. [Google Scholar] [CrossRef]
- Chetoui, M.; Thomassin, M.; Malti, R.; Aoun, M.; Najar, S.; Abdelkrim, M.N.; Oustaloup, A. New consistent methods for order and coefficient estimation of continuous-time errors-in-variables fractional models. Comput. Math. Appl. 2013, 66, 860–872. [Google Scholar] [CrossRef]
- Chetoui, M.; Aoun, M. Instrumental variables based methods for linear systems identification with fractional models in the EIV context. In Proceedings of the 16th International Multi-Conference on Systems, Signals & Devices (SSD), Istanbul, Turkey, 21–24 March 2019; IEEE: New York, NY, USA, 2019; pp. 90–95. [Google Scholar] [CrossRef]
- Yakoub, Z.; Aoun, M.; Amairi, M.; Chetoui, M. Identification of Continuous-Time Fractional Models from Noisy Input and Output Signals. In Fractional Order Systems—Control Theory and Applications; Naifar, O., Ben Makhlouf, A., Eds.; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2021; Volume 364, pp. 181–216. [Google Scholar] [CrossRef]
- Ivanov, D.V. Identification discrete fractional order linear dynamic systems with errors-in-variables. In Proceedings of the IEEE East-West Design Test Symposium (EWDTS’2013), Rostov on Don, Russia, 27–30 September 2013; IEEE: Rostov on Don, Russia, 2013; pp. 374–377. [Google Scholar] [CrossRef]
- Ivanov, D.V. Estimation of parameters of linear fractional order ARX systems with noise in the input signal. Tomsk. State Univ. J. Control Comput. Sci. 2014, 2, 30–38. (In Russian) [Google Scholar]
- Ivanov, D.V. Identification of linear dynamic systems of fractional order with errors in variables based on an augmented system of equations. Vestn. Samar. Gos. Tekhnicheskogo Univ. Ser. Fiz.-Mat. Nauk. [J. Samara State Tech. Univ. Ser. Phys. Math. Sci.] 2021, 25, 508–518. [Google Scholar] [CrossRef]
- Ivanov, D.V.; Sandler, I.L.; Kozlov, E.V. Identification of fractional linear dynamical systems with autocorrelated errors in variables by generalized instrumental variables. IFAC-PapersOnLine 2018, 51, 580–584. [Google Scholar] [CrossRef]
- Golub, G.H.; Meurant, G. Matrices, Moments and Quadrature with Applications; Princeton University Press: Princeton, NJ, USA, 2009. [Google Scholar]
- Björck, Å. Iterative refinement of linear least squares solutions I. BIT Numer. Math. 1967, 7, 257–278. [Google Scholar] [CrossRef]
- Zhdanov, A.I.; Gogoleva, S.Y. Solving least squares problems with equality constraints based on augmented regularized normal equations. Appl. Math. E Notes 2016, 15, 218–224. [Google Scholar]
- Zhdanov, A.I.; Shamarov, P.A. A direct projection method in the problem of complete least squares. Autom. Remote Control 2000, 61, 610–620. [Google Scholar]
- Ostalczyk, P. Discrete Fractional Calculus. Applications in Control and Image Processing; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2016; p. 396. [Google Scholar]
- Mozyrska, D.; Wyrwas, M. Stability of discrete fractional linear systems with positive orders. IFAC-PapersOnLine 2017, 50, 8115–8120. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User, 2nd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1999. [Google Scholar]
- Engelgardt, V.V.; Ivanov, D.V.; Katsyuba, O.A. Structural and parametric identification of linear dynamic systems of fractional order with noise on input and output. In Proceedings of the International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017; IEEE: Astana, Kazakhstan, 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Van Huffel, S.; Vandewalle, J. Analysis and properties of the generalized total least squares problem AX ≈ B when some or all columns in A are subject to error. SIAM J. Matrix Anal. Appl. 1989, 10, 294–315. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C. An analysis of the total least squares problem. SIAM J. Matrix Anal. Appl. 1980, 17, 883–893. [Google Scholar] [CrossRef]
- Björk, Å. Newton and Rayleigh quotient methods for total least squares problem. In Proceedings of the Second International Workshop on Total Least Squares and Error-in-Variables 1996, Leuven, Belgium, 21–24 August 1996; Van Huffel, S., Ed.; SIAM: Philadelphia, PA, USA, 1997; pp. 149–160. [Google Scholar]
- Björck, Å.; Heggernes, P.; Matstoms, P. Methods for Large Scale Total Least Squares Problems. SIAM J. Matrix Anal. Appl. 2000, 22, 413–429. [Google Scholar] [CrossRef][Green Version]
- Fasino, D.; Fazzi, A.A. Gauss-Newton iteration for Total Least Squares problems. BIT Numer. Math. 2018, 58, 281–299. [Google Scholar] [CrossRef]
- Abdel-Aziz, M. Rational-Lanczos technique for solving total least squares problems. Kuwait J. Sci. Eng. 2001, 28, 1–12. [Google Scholar]
- Wilkinson, J.H. The Algebraic Eigenvalue Problem; Monographs on Numerical Analysis; Oxford Science Publications; Clarendon Press: Oxford, UK, 1988; pp. xviii, 682. [Google Scholar]
- Zhdanov, A.I. The solution of ill-posed stochastic linear algebraic equations by the maximum likelihood regularization method. USSR Comput. Math. Math. Phys. 1988, 28, 93–96. [Google Scholar] [CrossRef]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Texts in Applied Mathematics; Springer Science& Business Media: Berlin, Germany, 2010; Volume 37. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).