Abstract
This research paper investigates the accuracy of a novel computational scheme (Khater II method) by applying this new technique to the fractional nonlinear Ostrovsky (FNO) equation. The accuracy of the obtained solutions was verified by employing the Adomian decomposition (AD) and El Kalla (EK) methods. The AD and EK methods are considered as two of the most accurate semi-analytical schemes. The FNO model is a modified version of the well-known Korteweg–de Vries (KdV) equation that considers the effects of rotational symmetry in space. However, in the KdV model, solutions to the KdV equations substitute this effect with radiating inertia gravity waves, and thus this impact is ignored. The analytical, semi-analytical, and accuracy between solutions are represented in some distinct plots. Additionally, the paper’s novelty and its contributions are demonstrated by comparing the obtained solutions with previously published results.
Keywords:
fractional nonlinear Ostrovsky equation; novel computational technique; computational and semi-analytical solutions AMS Classification:
35Q60; 78A60; 35C07; 34K28
1. Introduction
Plasma physics is one of the most crucial fields of our time which is attracting a large number of researchers [1,2]. In modern plasma physics, it is essential to work on dense Langmuir turbulence [3,4,5]. This significance stems from their ability to provide a practical solution to Langmuir’s condensation issue [6]. The Langmuir condensation paradox was characterized by an increase in the sum of long-wave disturbances [7]. Landau or radiation cannot damper the vibration; similarly, the Coulomb relation cannot dampen the frequency fluctuations of oscillations at extreme intervals [8,9]. Plasma destruction allows the release of condensing disturbances, resolving the Langmuir turbulence discharge amplitude problem and improving the graphical representation of Langmuir turbulence [10,11,12,13,14].
The increasing interest in creating many theoretical and computational methods for studying these models exemplifies the strength of nonlinear partial differential equations (NLPDEs) such as the Khater method, generalized Khater method, Khater II method, the exp-function method, extended simplest equation method, Riccati expansion method, etc. [15,16,17,18,19,20]. Additionally, many fractional derivatives have been derived to convert the fractional nonlinear partial differential equations into ordinary differential equations with integer-order such as He’s fractional derivative and the two-scale fractal derivative [21,22,23]. These models are used to describe a wide variety of complicated events in various disciplines, including biology, quantum physics, electrochemistry, mechanical engineering, and mechanical sciences [24,25,26,27,28]. When evaluating new features of the research paradigm, the use of specialized schemes is considered a significant advantage [29,30,31]. On the other hand, several researchers failed to examine and provide a cohesive strategy applicable to all NLPDEs [32,33,34].
In this context, we studied the analytical solutions of the FNO equation which is given by [35,36,37,38]
where is a simplified description of the nonlinear ocean wave dynamics that takes Earth rotation into account. represents the in-compressible liquid surfaces. On the other hand, is the Earth’s spinning effect.
Definition 1.
The conformable derivative is defined as follows [39,40,41]:
Suppose a continuous function in the domain and co-domain . Thus, the conformable derivative of with order ε which satisfies , is given by
Additionally, the is defined by
if and only if is ε-differentiable in , and exists.
Lemma 1.
Let and and be ε-differentiable functions Thus, the conformable derivative properties are formulated by [39]:
- (a)
- ;
- (b)
- ;
- (c)
- ;
- (d)
- , provided
- (e)
- , where is a constant.
Lemma 2.
Suppose that is a ε-differentiable and differentiable function, then is formulated by [40]
Theorem 1.
Let be a differentiable and ε-differentiable function. Let be a differentiable function defined in the range of ε [41]. Consequently:
Implementing the following wave transformation (the fractional complex transformation [42,43]) along with the conformable fractional properties where c is an arbitrary constants, then integrating the obtained ODE twice with respect to and zero constants of integration converts Equation (1) into the following ODE:
Balancing the terms in Equation (6) leads to . Applying the Khater II method [44] to Equation (6) leads to the following general solution:
where are arbitrary constants to be subsequently calculated while . Gathering the coefficients of and equating them with zero, leads to a system of algebraic equations.
The rest of the paper’s sections are ordered as following; Section 2 gives the novel analytical solutions of the FNO model with the Khater II method. Section 3 investigates the accuracy of the obtained analytical solutions by employing AD and EK schemes. Furthermore, these solutions are demonstrated in some graphs in two- and three-dimensional as well as contour figures. Section 4 illustrates the paper’s contributions and the solutions’ novelty. Section 5 gives the conclusion of the whole study.
2. Analytical Solutions
Solving the obtained system of algebraic equations by Mathematics 12 leads to the following values of the aforementioned constants.
Case I:
Case II:
Case III:
Thus, the traveling wave solutions of the FNO model is given by
3. Solutions’ Accuracy
Applying the AD and EK methods to the FNO model based on the obtained analytical solutions (8), (10) and (12) when . Thus, the semi-analytical solutions of the FNO model based on the AD method are given by
The semi-analytical solutions of the FNO model based on the EK method are given by
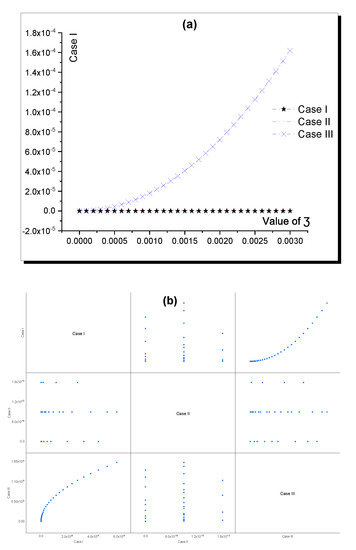
The following Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 show the values of analytical, semi-analytical, and absolute error through .

Table 1.
Accuracy between the analytical solution (8) and the semi-analytical solutions based on (14) (AD method).

Table 2.
Accuracy between the analytical solution (8) and the semi-analytical solutions based on (15) (EK method).

Table 3.
Accuracy between the analytical solution (10) and the semi-analytical solutions based on (14) (AD method).

Table 4.
Accuracy between the analytical solution (10) and the semi-analytical solutions based on (15) (EK method).

Table 5.
Accuracy between the analytical solution (12) and the semi-analytical solutions based on (14) (AD method).

Table 6.
Accuracy between the analytical solution (12) and the semi-analytical solutions based on (15) (EK method).
4. Results and Discussion
This section investigates the constructed wave solutions of the FNO model that has been derived for describing the dynamical behavior of the oceanic waves affected by the Earth’s rotation based on the newly formulated analytical scheme (Khater II method). This method is one of indirect analytical schemes which lead to a difference between its results and the other direct methods’ results. This difference can be demonstrated by comparing our obtained results with those in [36,37,38]. In these published papers [36,37,38], many direct methods have been applied such as the generalized Jacobi elliptical functional method and modified Khater method, the Exp-function method, the hyperbolic tangent method and an exponential function approach. Comparing our results with the constructed solutions in these papers explains the novelty of our solutions where all our solutions are different and new from their solutions.
The dynamical behavior of the oceanic waves affected by the Earth’s rotation is explained through some graphs of the solutions in the contour, three, and two-dimensional Figure 1, Figure 2 and Figure 3 when Additionally, the stability of the obtained solutions can be checked through the Hamiltonian system’s characterizations which lead to demonstrate the stability property of Equation (8) when and where the momentum of Equation (8) is given by
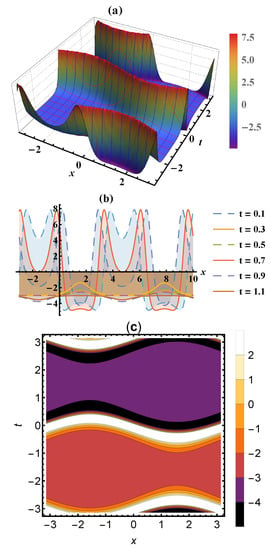
Figure 1.
Periodic solitary wave solutions of the FNO model in (a) 3D, (b) 2D, and (c) contour plots of Equation (8).
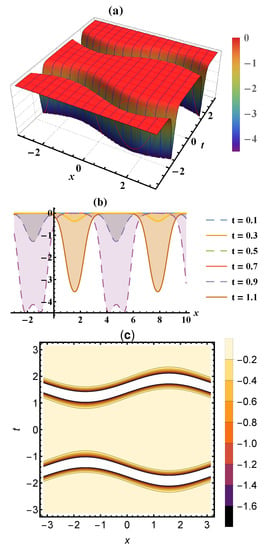
Figure 2.
Periodic solitary wave solutions of the FNO model in (a) 3D, (b) 2D, and (c) contour plots of Equation (10).
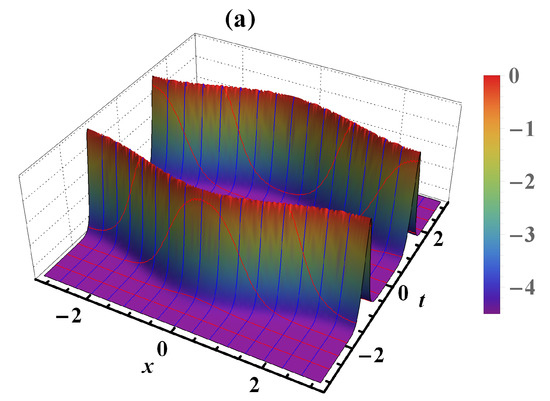
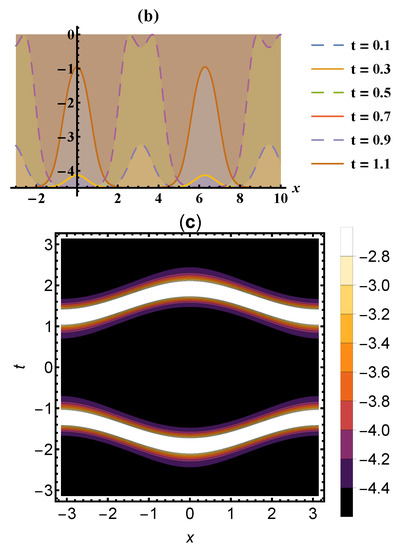
Figure 3.
Periodic solitary wave solutions of the FNO model in (a) 3D, (b) 2D, and (c) contour plots of Equation (12).
Thus, we obtain:
where . Consequently, this solution is a stable one. Handling the other obtained solutions through the same technique can explain their stability property.
Moreover, the accuracy of constructed solutions where the analytical scheme is a new scheme was verified by applying the AD and EK semi-analytical methods based on the constructed analytical solutions to evaluate the initial and boundary conditions of the FNO equation. The accuracy of the analytical and semi-analytical solutions is explained in the above—Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 and is presented in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.
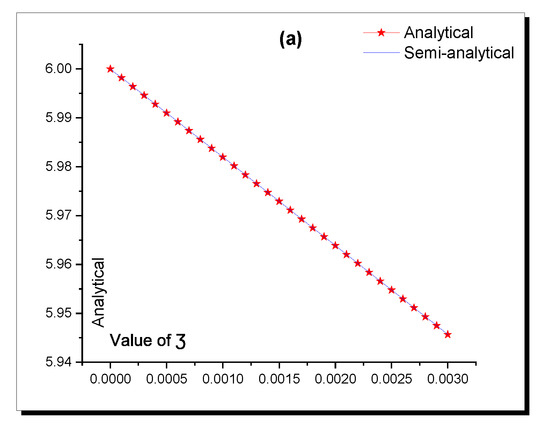
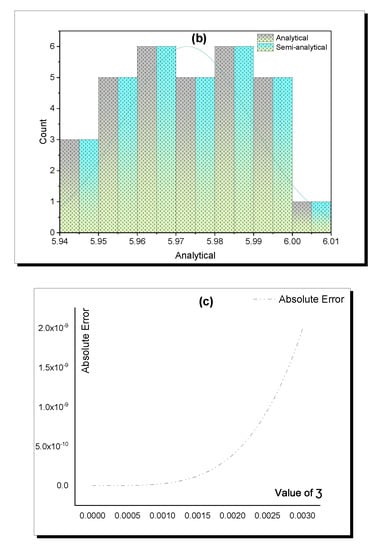
Figure 4.
Accuracy between the analytical (8) and semi-analytical solutions in Table 1. (a) Analytical; (b) Semi-analytical; (c) Absolute Error.
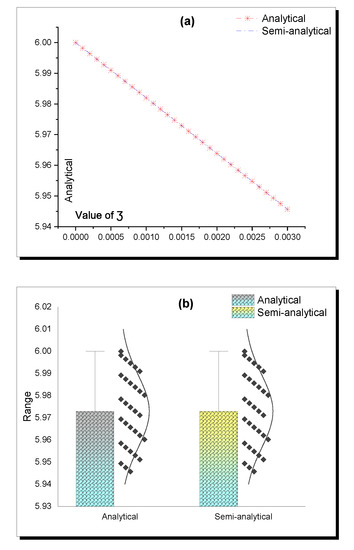
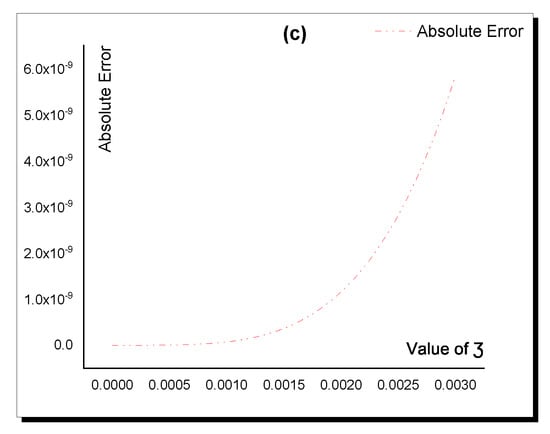
Figure 5.
Accuracy between the analytical (8) and semi-analytical solutions in Table 2. (a) Analytical; (b) Semi-analytical; (c) Absolute Error.
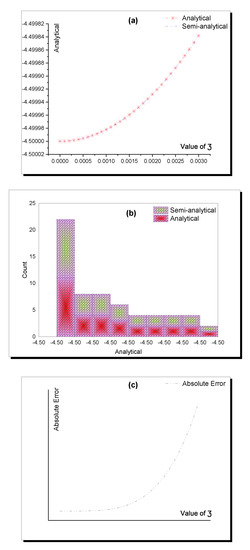
Figure 6.
Accuracy between the analytical (10) and semi-analytical solutions in Table 3. (a) Analytical; (b) Semi-analytical; (c) Absolute Error.
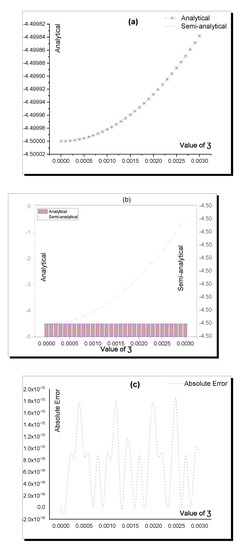
Figure 7.
Accuracy between the analytical (10) and semi-analytical solutions in Table 4. (a) Analytical; (b) Semi-analytical; (c) Absolute Error.
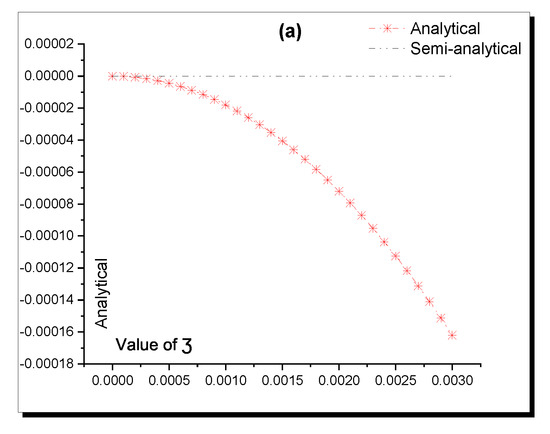
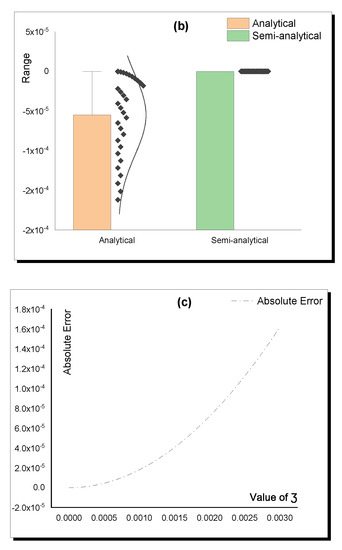
Figure 8.
Accuracy between the analytical (12) and semi-analytical solutions in Table 5. (a) Analytical; (b) Semi-analytical; (c) Absolute Error.
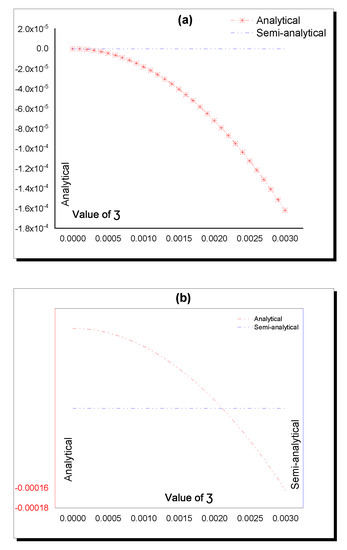
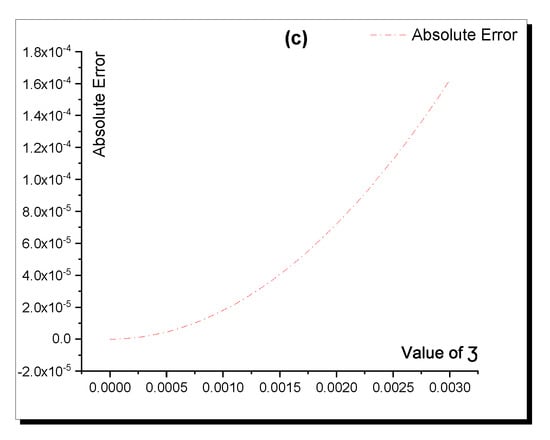
Figure 9.
Accuracy between the analytical (12) and semi-analytical solutions in Table 6. (a) Analytical; (b) Semi-analytical; (c) Absolute Error.
Finally, the superiority of the constructed solutions was verified by comparing the absolute error for each solution to demonstrate which of the obtained solutions is more accurate. Based on the above—Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6—Equation (12) is more accurate than (8), (10). This accuracy is represented through Figure 10 and Figure 11.
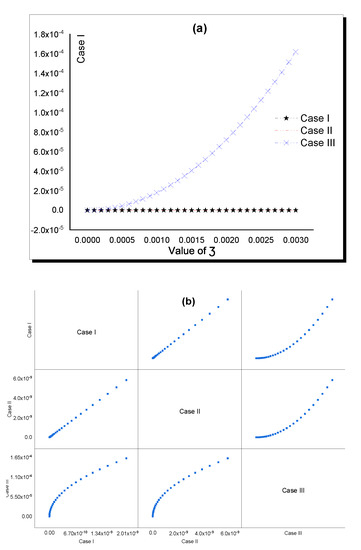
5. Conclusions
This research paper investigated the analytical and semi-analytical solutions of the FNO equation. A new analytical technique (Khater II method) was successfully applied to the investigated model, and many novel solutions were constructed. These solutions are represented by graphs to explain how the ocean wave’s dynamics are affected by the Earth’s rotation. Additionally, the AD and EK semi-analytical schemes were applied to evaluate the FNO model’s semi-analytical solutions and check the accuracy of the obtained analytical solutions.
Author Contributions
M.M.A.K. and A.M.A. have revised the conceptualization, data curation, and Methodology. M.M.A.K. has revised Data curation, Investigation, and Software. A.M.A. has revised the physical meaning of the obtained solutions and raised the given graphs resolutions. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We want to thank the journal’s staff (editors and reviewers) for their support and help.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baskonus, H.M.; Osman, M.; Ramzan, M.; Tahir, M.; Ashraf, S. On pulse propagation of soliton wave solutions related to the perturbed Chen–Lee–Liu equation in an optical fiber. Opt. Quantum Electron. 2021, 53, 1–17. [Google Scholar]
- Sarwar, S. New soliton wave structures of nonlinear (4 + 1)-dimensional Fokas dynamical model by using different methods. Alex. Eng. J. 2021, 60, 795–803. [Google Scholar] [CrossRef]
- Kumar, S.; Almusawa, H.; Hamid, I.; Akbar, M.A.; Abdou, M. Abundant analytical soliton solutions and Evolutionary behaviors of various wave profiles to the Chaffee–Infante equation with gas diffusion in a homogeneous medium. Results Phys. 2021, 30, 104866. [Google Scholar] [CrossRef]
- Zhao, J.; Manafian, J.; Zaya, N.E.; Mohammed, S.A. Multiple rogue wave, lump-periodic, lump-soliton, and interaction between k-lump and k-stripe soliton solutions for the generalized KP equation. Math. Methods Appl. Sci. 2021, 44, 5079–5098. [Google Scholar] [CrossRef]
- Ismael, H.F.; Ma, W.X.; Bulut, H. Dynamics of soliton and mixed lump-soliton waves to a generalized Bogoyavlensky-Konopelchenko equation. Phys. Scr. 2021, 96, 035225. [Google Scholar] [CrossRef]
- Nisar, K.S.; Ilhan, O.A.; Abdulazeez, S.T.; Manafian, J.; Mohammed, S.A.; Osman, M. Novel multiple soliton solutions for some nonlinear PDEs via multiple Exp-function method. Results Phys. 2021, 21, 103769. [Google Scholar] [CrossRef]
- Kumar, S.; Niwas, M.; Osman, M.; Abdou, M. Abundant different types of exact soliton solution to the (4 + 1)-dimensional Fokas and (2 + 1)-dimensional breaking soliton equations. Commun. Theor. Phys. 2021, 73, 105007. [Google Scholar] [CrossRef]
- Raza, N.; Rafiq, M.H.; Kaplan, M.; Kumar, S.; Chu, Y.M. The unified method for abundant soliton solutions of local time fractional nonlinear evolution equations. Results Phys. 2021, 22, 103979. [Google Scholar] [CrossRef]
- Osman, M.; Almusawa, H.; Tariq, K.U.; Anwar, S.; Kumar, S.; Younis, M.; Ma, W.X. On global behavior for complex soliton solutions of the perturbed nonlinear Schrödinger equation in nonlinear optical fibers. J. Ocean. Eng. Sci. 2021, in press. [Google Scholar] [CrossRef]
- Rizvi, S.; Seadawy, A.; Ashraf, M.; Bashir, A.; Younis, M.; Baleanu, D. Multi-wave, homoclinic breather, M-shaped rational and other solitary wave solutions for coupled-Higgs equation. Eur. Phys. J. Spec. Top. 2021, 230, 3519–3532. [Google Scholar] [CrossRef]
- Ismael, H.F.; Bulut, H. Multi soliton solutions, M-lump waves and mixed soliton-lump solutions to the awada-Kotera equation in (2 + 1)-dimensions. Chin. J. Phys. 2021, 71, 54–61. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, X.; Bilige, S. Evolutionary behavior and novel collision of various wave solutions to (3 + 1)-dimensional generalized Camassa–Holm Kadomtsev–Petviashvili equation. Nonlinear Dyn. 2021, 104, 4265–4275. [Google Scholar] [CrossRef]
- Kumar, S.; Jiwari, R.; Mittal, R.; Awrejcewicz, J. Dark and bright soliton solutions and computational modeling of nonlinear regularized long wave model. Nonlinear Dyn. 2021, 104, 661–682. [Google Scholar] [CrossRef]
- Liu, C. The Gaussian soliton in the Fermi–Pasta–Ulam chain. Nonlinear Dyn. 2021, 106, 899–905. [Google Scholar] [CrossRef]
- Ma, W.X.; Osman, M.; Arshed, S.; Raza, N.; Srivastava, H. Practical analytical approaches for finding novel optical solitons in the single-mode fibers. Chin. J. Phys. 2021, 72, 475–486. [Google Scholar] [CrossRef]
- Kuo, C.K.; Chen, Y.C.; Wu, C.W.; Chao, W.N. Novel solitary and resonant multi-soliton solutions to the (3 + 1)-dimensional potential-YTSF equation. Mod. Phys. Lett. B 2021, 35, 2150326. [Google Scholar] [CrossRef]
- Zahran, E.H.; Khater, M.M. Modified extended tanh-function method and its applications to the Bogoyavlenskii equation. Appl. Math. Model. 2016, 40, 1769–1775. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.; Zahran, E.H.; Khater, M.M. The Exp −ϕ(ξ)-expansion method and its application for solving nonlinear evolution equations. Int. J. Mod. Nonlinear Theory Appl. 2015, 4, 37. [Google Scholar] [CrossRef] [Green Version]
- Khater, M.M.; Seadawy, A.R.; Lu, D. Dispersive solitary wave solutions of new coupled Konno-Oono, Higgs field and Maccari equations and their applications. J. King Saud Univ.-Sci. 2018, 30, 417–423. [Google Scholar] [CrossRef]
- Khater, M.M. Extended exp Expansion method for Solving the Generalized Hirota-Satsuma Coupled KdV System. Glob. J. Sci. Front. Res. F Math. Decis. Sci. 2015, 15, 1–15. [Google Scholar]
- Wang, K.L.; Yao, S.W. Numerical method for fractional Zakharov-Kuznetsov equations with He’s fractional derivative. Therm. Sci. 2019, 23, 2163–2170. [Google Scholar] [CrossRef]
- Wang, K.L.; Liu, S.Y. He’s fractional derivative for non-linear fractional heat transfer equation. Therm. Sci. 2016, 20, 793–796. [Google Scholar] [CrossRef]
- Zuo, Y.; Liu, H. A fractal rheological model for sic paste using a fractal derivative. J. Appl. Comput. Mech. 2020, 7, 13–18. [Google Scholar]
- Ma, W.X.; Osman, M.; Arshed, S.; Raza, N.; Srivastava, H. Different analytical approaches for finding novel optical solitons in the single-mode fibers. Chin. J. Phys. 2021, 27, 475–486. [Google Scholar] [CrossRef]
- Khan, Y. A novel type of soliton solutions for the Fokas–Lenells equation arising in the application of optical fibers. Mod. Phys. Lett. B 2021, 35, 2150058. [Google Scholar] [CrossRef]
- Kuo, C.K.; Ghanbari, B. On novel resonant multi-soliton and wave solutions to the (3 + 1)-dimensional GSWE equation via three effective approaches. Results Phys. 2021, 26, 104421. [Google Scholar] [CrossRef]
- Alsaedi, A.; Ahmad, B.; Kirane, M.; Torebek, B.T. Blowing-up solutions of the time-fractional dispersive equations. Adv. Nonlinear Anal. 2021, 10, 952–971. [Google Scholar] [CrossRef]
- Wang, K.J. On new abundant exact traveling wave solutions to the local fractional Gardner equation defined on Cantor sets. Math. Methods Appl. Sci. 2021, 1, 12. [Google Scholar] [CrossRef]
- Fang, Y.; Wu, G.Z.; Wang, Y.Y.; Dai, C.Q. Data-driven femtosecond optical soliton excitations and parameters discovery of the high-order NLSE using the PINN. Nonlinear Dyn. 2021, 105, 603–616. [Google Scholar] [CrossRef]
- Alfalqi, S.H.; Alzaidi, J.F.; Zhang, Y.F.; Salama, S.A.; Khater, M.M. Plenty accurate soliton wave solutions of the prototype of an excitable system. AIP Adv. 2021, 11, 095315. [Google Scholar] [CrossRef]
- Han, C.; Wang, Y.L.; Li, Z.Y. Numerical solutions of space fractional variable-coefficient KdV-modified KdV equation by Fourier spectral method. Fractals 2021, 0, 2150246. [Google Scholar] [CrossRef]
- Manafian, J.; Lakestani, M.; Bekir, A. Comparison between the generalized tanh–coth and the (G′/G)-expansion methods for solving NPDEs and NODEs. Pramana 2016, 87, 1–14. [Google Scholar] [CrossRef]
- Heris, J.M.; Lakestani, M. Solitary wave and periodic wave solutions for variants of the KdV-Burger and the K (n, n)-Burger equations by the generalized tanh-coth method. Commun. Numer. Anal. 2013, 2013, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Dai, D.D.; Ban, T.T.; Wang, Y.L.; Zhang, W. The piecewise reproducing kernel method for the time variable fractional order advection-reaction-diffusion equations. Therm. Sci. 2021, 25, 21. [Google Scholar] [CrossRef]
- Khater, M.M.; Lu, D. Analytical versus numerical solutions of the nonlinear fractional time–space telegraph equation. Mod. Phys. Lett. B 2021, 35, 2150324. [Google Scholar] [CrossRef]
- Khater, M.M. Diverse solitary and Jacobian solutions in a continually laminated fluid with respect to shear flows through the Ostrovsky equation. Mod. Phys. Lett. B 2021, 35, 2150220. [Google Scholar] [CrossRef]
- Köroğlu, C.; Öziş, T. A novel traveling wave solution for Ostrovsky equation using Exp-function method. Comput. Math. Appl. 2009, 58, 2142–2146. [Google Scholar] [CrossRef] [Green Version]
- Yusufoğlu, E.; Bekir, A. A travelling wave solution to the Ostrovsky equation. Appl. Math. Comput. 2007, 186, 256–260. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 3, 000010151520150081. [Google Scholar] [CrossRef]
- Li, Z.B.; He, J.H. Fractional complex transform for fractional differential equations. Math. Comput. Appl. 2010, 15, 970–973. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.B. An extended fractional complex transform. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 335–338. [Google Scholar] [CrossRef]
- Khater, M.M.; Salama, S.A. Novel analytical simulations of the complex nonlinear Davey–Stewartson equations in the gravity–capillarity surface wave packets. J. Ocean. Eng. Sci. 2021, in press. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).