The Basis Invariant of Generalized n-Cube Symmetries Group with Odd Degrees

Abstract

The basis polynomial invariants with even degrees relatively to the symmetries group were described in cited literature. Here, the polynomial invariants with odd degrees are constructed. We give an explicit construction of all the basic polynomial invariants as algebra generators of odd degrees relatively to the symmetries group. All calculations are presented in detail.

1. Introduction

In this paper, we remind the reader of some well-known and some less-well-known terms concerning regular polytopes and their symmetry group. Using [1], we show the terms in Euclid n-dimensional space $E^n$ and picture them considering the symmetries in a three-dimensional cube. The flag definition is mentioned as another point of symmetry view that we found in [2]. We introduce the terms’ generalizations on the complex unitary space and introduce the idea of problems together with their solutions.

The generalized n-cube ${\gamma }_n^m$ in n-dimensional unitary space $U^n$ was first described by Coxeter in [3]. The ${\gamma }_n^m$ symmetries group is generated by reflections relatively to the $(n-1)$-dimensional hyperplanes and it is denoted with $B_n^m$. We studied the properties of the polynomial invariants’ algebra $I^{B_n^m}$ relatively to the generalized n-cube ${\gamma }_n^m$ symmetry group $B_n^m$. In [4], the basis polynomial invariants are given with even exponents but without any proof. The author only mentioned the fact that the polynomials were based on Pogorelov’s polynomials for reflections’ symmetries. We thus try to shed light on the results presented in Rudnitsky’s work ([4]).

We conjectured that it is possible to construct the explicit polynomial invariants with the odd degrees and complete the all-degree generators of the polynomial algebra $I^{B_n^m}$. To this aim, we used a suitable differential operator.

We investigated the available literature searching for other methods giving results considering basic reflections’ algebra invariants. More general unitary reflection groups known as $G(m,p,n)$ were described in [5,6], but no method giving results similar to ours was presented. Accordingly, there is no particular reason for us to mention them. This was also found to be the case by the authors of several other references that we previously mentioned: it was the lack of available literature that prompted us to submit this result together with pictorial representations of the basic concepts.

2. Regular Polytopes and Their Symmetries Groups

Consider $E^n$ with the ordinary orthogonal basis ${\overrightarrow{e}}_1,\dots {\overrightarrow{e}}_n$ such that any point $\overrightarrow{x}\in E^n$ is represented by $\overrightarrow{x}=(x_1,\dots ,x_n)={\sum }_{i=1}^n{x}_i{\overrightarrow{e}}_i$. For the n-cube centered in the coordinates’ origin, there are hyperplanes generating invariant reflections:

$$\begin{array}{ccc}\hfill x_i=0& & i=1,\dots ,n\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill x_i+x_j=0& & 1\le i<j\le n\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill x_i-x_j=0& & 1\le i<j\le n.\hfill \end{array}$$

(3)

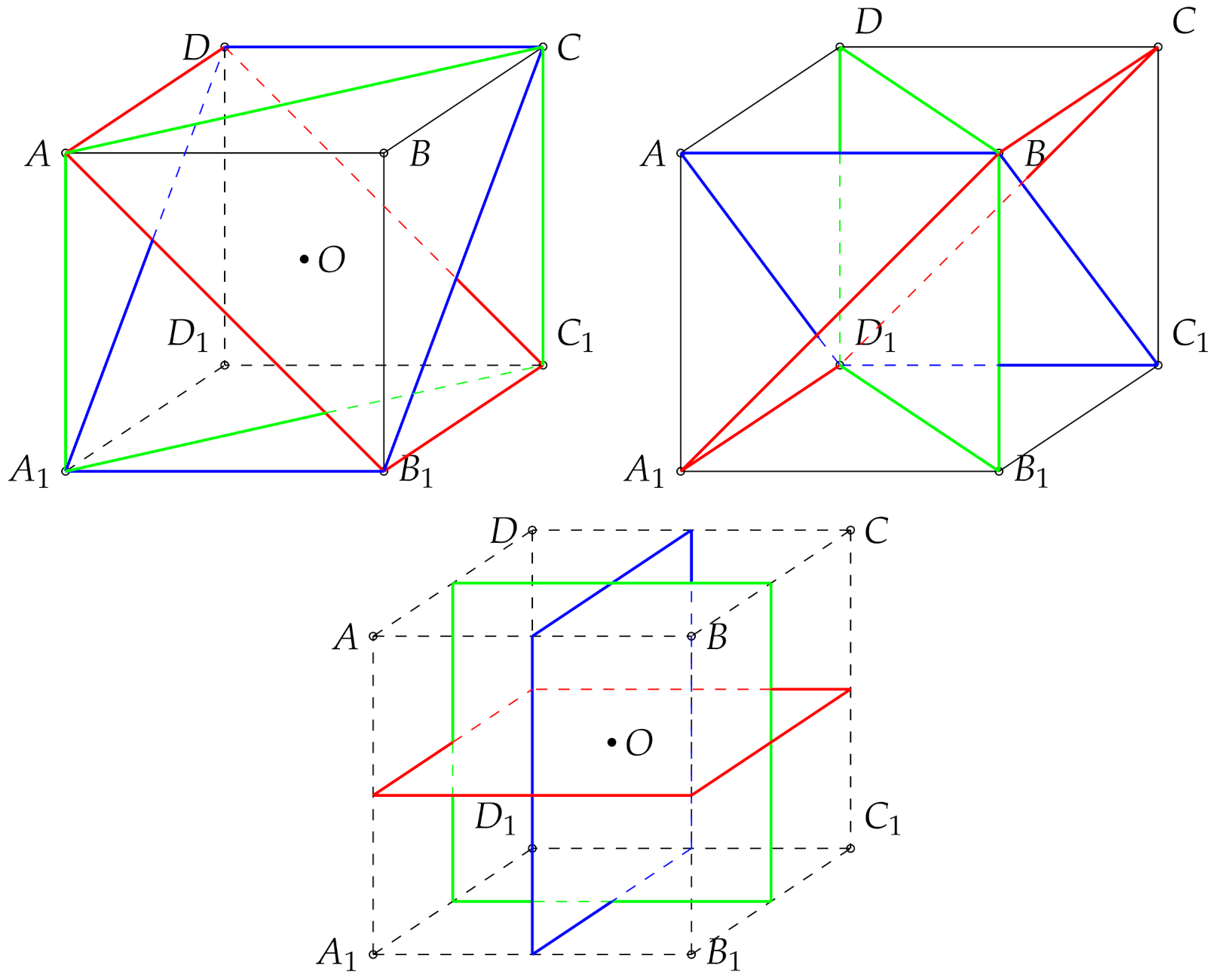
Hyperplanes (1)–(3) are consecutively ordered on Figure 1 with a cube in $E^3$. Reflections’ invariant planes are colored by green, blue and red according the linguistic order of the coordinate appearing within equations.

Every hyperplane in Figure 1 generates the reflection which is a symmetry of the cube of order two. If it is repeatedly applied twice, then all points attend a position identical to that before the application:

Two composited symmetries again provide the symmetry of the cube. The compositing is commutative, associative, and invertible, so the symmetries on a cube form a group. In $E^n$, this group is called the real n-cube symmetry group and it is denoted by $B_n$. The group degree is the number of its elements, denoted by $|B_n|$.

According to (3), a reflection symmetry in $B_n$ was obtained by a sequence of the coordinate transpositions. According to (1), a reflection was obtained by taking the opposite coordinate value while the others remain, and (2) represents the both. Since any symmetry from $B_n$ is a permutation of its coordinates possibly taking the opposites of several of them, then $|B_n|=2^{n}n!$.

Note that in Figure 1, there are nine hyperplanes generating other symmetries as reflections’ compositions within the cube. For a general dimension n, there are $n^2$ such hyperplanes, counting them by (1)–(3):

$$n+\left(\begin{array}{c}n\\ 2\end{array}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)=n^2.$$

(4)

By the hyperplanes in Equations (1)–(3), we rewrite the polynomial invariants constructed in [1,7]:

$$J_{2r}^{B_n}\left(\overrightarrow{x}\right)=\sum _{i=1}^n{x}_i^{2r}+\sum _{1\le i<j\le n}{(x_i+x_j)}^{2r}+\sum _{1\le i<j\le n}{(x_i-x_j)}^{2r}$$

(5)

for natural numbers $r=1,2,\dots$ If only the points coordinate from any of the reflection hyperplanes (1)–(3) and are inserted in (5), then the polynomial value remains.

For natural r, polynomials (5) are within the algebra $I^{B_n}$ consisting of polynomial invariants relatively to the symmetries group $B_n$. In ([8]), it is given that (5) has the following explicit form:

$$J_{2r}^{B_n}\left(\overrightarrow{x}\right)=(n+2^{r-1}-1)\sum _{i=1}^n{x}_i^{2r}+R_{2r}\left(\overrightarrow{x}\right)$$

(6)

with polynomials:

$$R_{2r}\left(\overrightarrow{x}\right)=\sum _{k=1}^{r-1}\sum _{1\le i<j\le n}\left(\begin{array}{c}2r\\ 2k\end{array}\right)x_i^{2(r-k)}{x}_j^{2k}.$$

(7)

The mentioned symmetry group degree calculation was also achieved after Definition 2, considering the flags within the regular polytope in $E^n$.

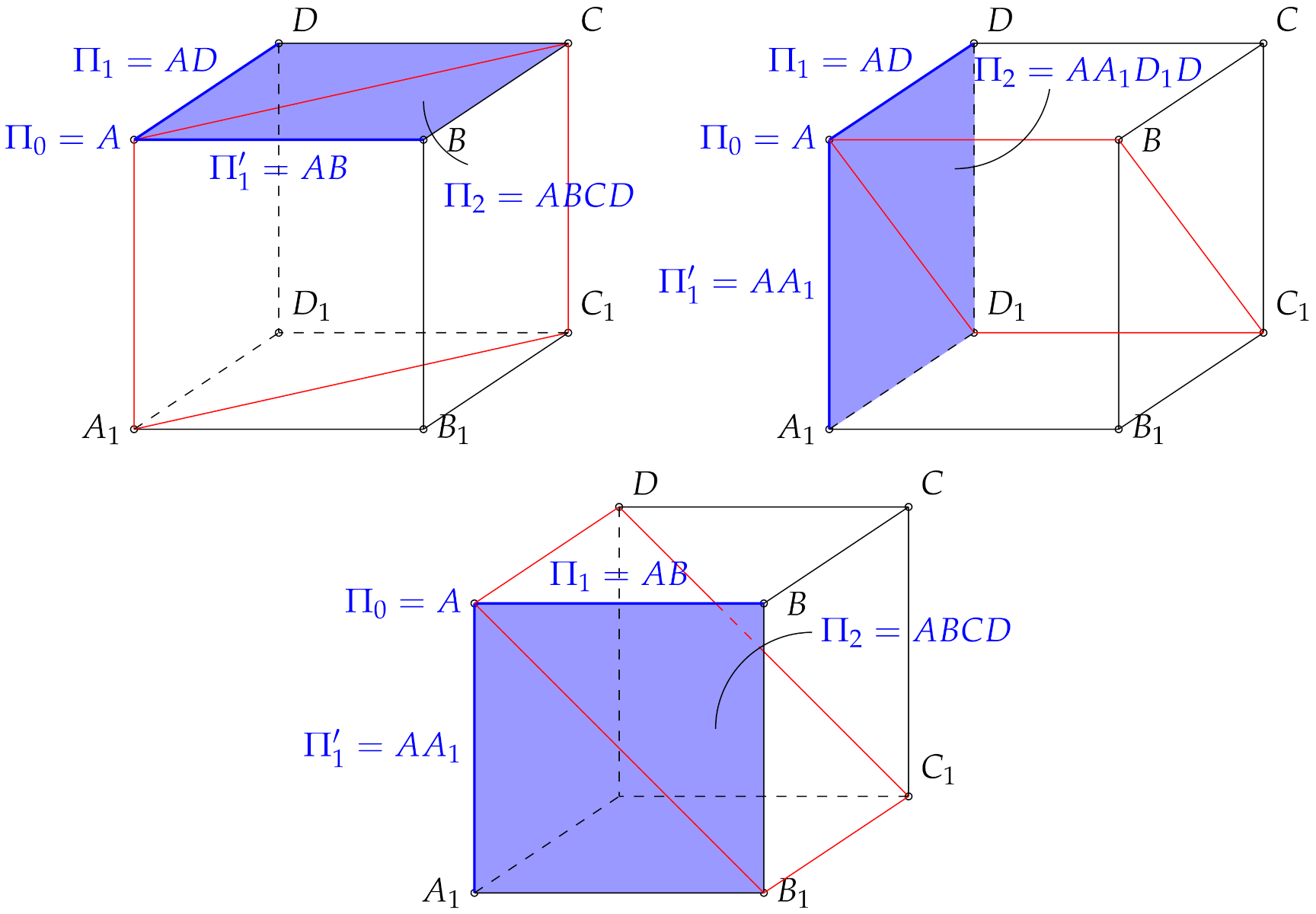
Definition 1

(Incidence and flag). Two subspaces, with dimensions $\mu <\nu$ are incident if one of them is a proper subspace of the other. The flag is a figure consisting of mutually incidental elements with consecutive dimensions $0\le \mu <\mu +1\le n-1$.

Within the cubes $ABCD{A}_1{B}_1{C}_1{D}_1$ in Figure 2, three red colored reflection hyperplanes are transposed on colored pairs of flags $({\mathsf{\Pi }}_0,{\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2)$ and $({\mathsf{\Pi }}_0,{\mathsf{\Pi }}_1^{\prime },{\mathsf{\Pi }}_2)$ from each into another. The next definition from [2] is very natural.

Definition 2

(Regular polytope by [2]). The regular polytope is a polytope whose symmetry group is transiting on flags. This means that every flag is translated into another flag by the symmetry.

Since the symmetry group $B_n$ is strictly transitive on flags, the n-cube is a regular polytope, and the $B_n$ degree is equal to number of flags. There are $2^n$ vertices, and for each of them there are n one-dimensional subspaces called edges. Each such edge belongs to $(n-1)$ two-dimensional subspaces called planes. Any plane is within $n-2$ subspaces with dimension 3, etc. Finally, there is only one hyperplane at the end of the flag. The order of the symmetries group $B_n$ is thus again $2^{n}n!$. See [9] for generalisations.

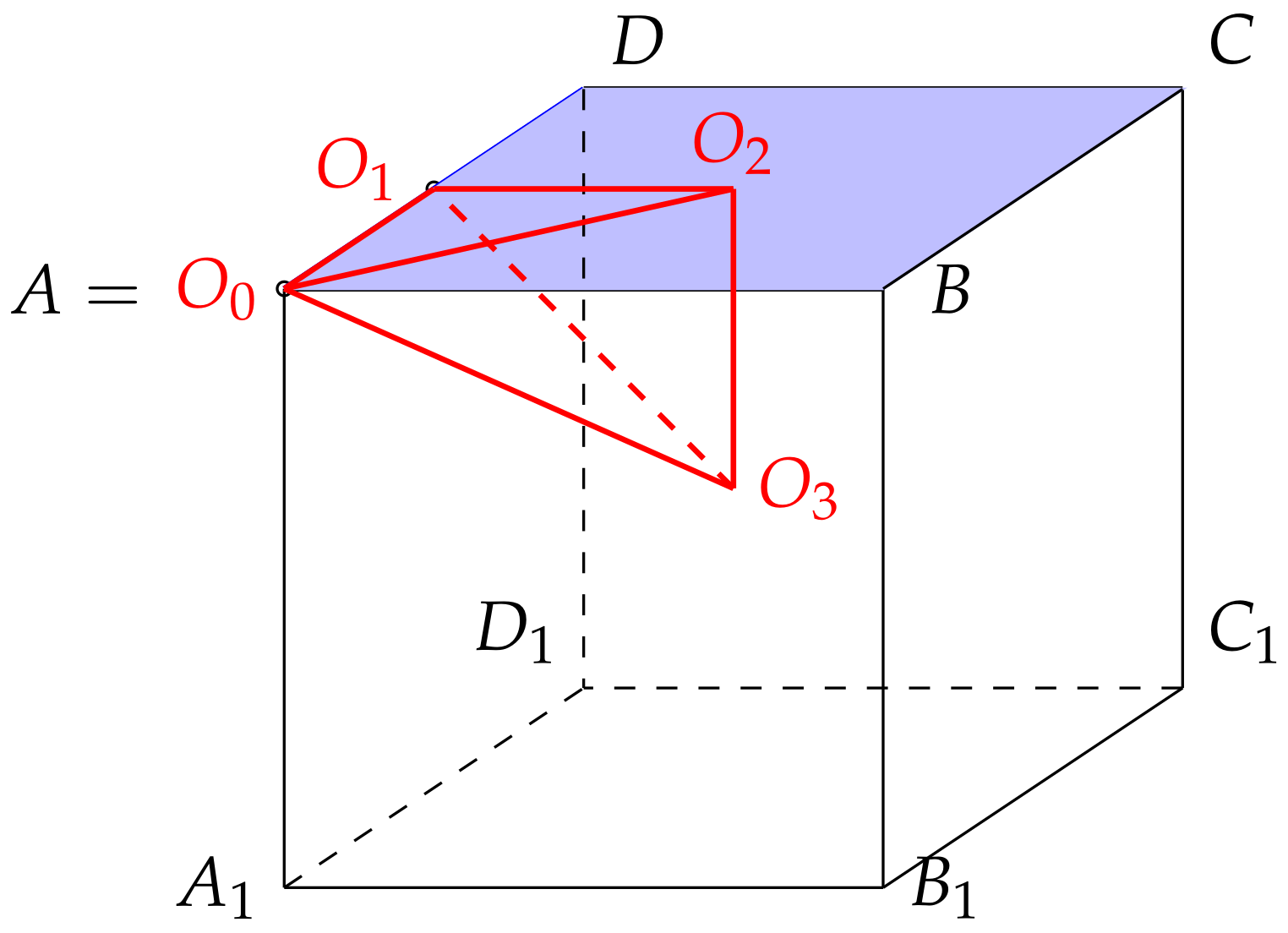
In [2], it was proven by induction that $B_n$ can only be generated by n reflections. On Figure 1, we presented three basis reflection hyperplanes of the group $B_n$ with the flags $({\mathsf{\Pi }}_0,{\mathsf{\Pi }}_1,{\mathsf{\Pi }}_2)$ from the point A on Figure 2. The hyperplanes are determined with triples $O_0{O}_1{O}_2$, $O_0{O}_1{O}_3$, and $O_0{O}_2{O}_3$, and are red colored. In Figure 3, the red points are settled in the centers of each flag element and on the center of the n-cube.

3. Generalized $\mathit{n}$-Cube ${\mathit{\gamma }}_{\mathit{n}}^{\mathit{m}}$ Symmetry Group

In $E^n$, we centered the two-length cube in origin. In the orthogonal basis mentioned above, the vertices of the cube are given with summations

$$\sum _{j=1}^n{(-1)}^{k_j}{\overrightarrow{e}}_j,k_j\in \{1,2\}.$$

Note that different vertices are obtained by choosing $k_i$ so that in each, the summation comes above the prime second root from the unit calculated as $(-1)=e^{\frac{2\pi i}{2}}$ with $i^2=-1$. There are therefore $2^n$ vertices.

The Euclid space $E^n$ over real numbers and the unitary space $U^n$ over complex numbers have the same orthogonal basis: ${\overrightarrow{e}}_1=(1,0,\dots ,0),{\overrightarrow{e}}_2=(0,1,\dots ,0),\dots ,{\overrightarrow{e}}_n=(0,0,\dots ,1)$. We generalize the term of the real n-cube in the n-dimensional complex unitary space. More details are given in [10].

Definition 3.

The generalized n - cube ${\gamma }_n^m$ in ${\mathbb{U}}^n$ is polytope with $m^n$ vertices given by the sums:

$$\sum _{j=1}^n{\theta }^{k_j}{\overrightarrow{e}}_j,k_j\in \{1,2,\dots ,m\}.$$

(8)

Different vertices are created by choosing a different $k_i$ that is coming above the prime m-th root from the unit calculated as ${\displaystyle \theta =e^{\frac{2\pi i}{m}}}$. There are therefore $m^n$ vertices.

Let $B_n^m$ be the cube ${\gamma }_n^m$ symmetries group. Symmetries are generated by reflections that replace the coordinates. They are of order two, since its double returns the cube to its previous position. Other symmetries are related to complex planes that create each unitary space coordinate. For more details see [11].

If we fix $n-1$ coordinates among all coordinates from each vertex of the cube ${\gamma }_n^m$, then we obtain $n·m^{n-1}$ edges ${\gamma }_1^m$ and each ${\gamma }_1^m$ is a part of a one-dimensional complex space ${\mathbb{C}}^1$. In doing so, the polytope ${\gamma }_n^m$ can be represented as a Descartes product of n edges ${\gamma }_1^m$. In each one-dimensional complex edge ${\gamma }_1^m$ within cube ${\gamma }_n^m$, there is a symmetry of order m generated by the regular m-gon determined with m complex roots of unity.

For n dimensions of the space, there are $n!$ coordinate combinations. Within each combination, there are m possible symmetries. Thus, the $B_n^m$ group is of order $|B_n^m|=m^{n}n!$. Analogue to (1)–(3), the symmetries are generated by reflections of order 2 relatively to hyperplanes with equations:

$$x_i-{\theta }^{k_j}{x}_j=0,1\le i<j\le n,k_j\in \{1,\dots ,m\}$$

(9)

and reflections of order m relatively to the coordinate hyperplanes $x_i=0,i=1,\dots ,n$.

In ${\mathbb{U}}^n$, the scalar product is defined with $(\overrightarrow{x},\overrightarrow{y})={\sum }_{j=1}^n{x}_j{\overline{y}}_j$, where ${\overline{y}}_j=a_j-b_{j}i$ for $y_j=a_j+b_{j}i$ with real $a_j,b_j$ and $i^2=-1$. The same bases of $E^n$ and $U^n$ allow us to continue with the notation $\overrightarrow{x}=(x_1,\dots ,x_n)$ for complex coordinates’ vectors.

In [4], the Pogorelov polynomials of degree $2t$ are defined by:

$$J_{2t}^{B_n^m}\left(\overrightarrow{x}\right)=\sum _{\sigma \in B_n^m}{(\overrightarrow{x},\sigma \overrightarrow{s})}^{2t},t\ge 1,$$

(10)

where $\overrightarrow{s}$ are normal unit vectors relatively to hyperplanes generating reflections $\sigma$ from $B_n^m$. Within [4], the normal vectors $\overrightarrow{s}$ are explicitly given by

$${\theta }^h{\overrightarrow{e}}_i,\frac{{\theta }^h}{\sqrt{2}}({\overrightarrow{e}}_i-{\theta }^{k_j}{\overrightarrow{e}}_j),h\in \{1,\dots ,m\}.$$

(11)

Because any reflection relative to the hyperplane with (11) does not move the points within the hyperplane, so polynomial calculations (10) remain if they are calculated by hyperplane points’ coordinates. Thus, Pogorelov polynomials given by (10) belong to the algebra $I^{B_n^m}$ which consists of polynomial invariants relatively to the symmetry group $B_n^m$.

In [4], the author establishes the relations for m and n that allow $I^{B_n^m}$ algebra generators to be represented with (10). If m is even and if $mr=2t,t=1,\dots ,n$, then the polynomials from (10) are given with:

$$J_{mr}^{B_n^m}\left(\overrightarrow{x}\right)=\left(n-1+\frac{2^{\frac{mr}{2}}}{m}\right)\sum _{i=1}^n{x}_i^{mr}+R_{mr}^{\alpha }\left(\overrightarrow{x}\right),$$

(12)

where:

$$R_{mr}^{\alpha }\left(\overrightarrow{x}\right)=\sum _{k=1}^{r-1}\sum _{1\le i<j\le 1}^n{(-1)}^{k\alpha }\left(\begin{array}{c}mr\\ mk\end{array}\right)x_i^{m(r-k)}{x}_j^{mk}.$$

(13)

If m is even within (12) and (13), then $\alpha =0$ and $r=1,\dots n$.

On the contrary, if m is odd, then $\alpha =1$ and $r=2,4,\dots ,n-\rho$ with $\rho =0$ for n being even and $\rho =1$ for odd n. This statement is given in [4] in the form of a Theorem without any explicitly given proof.

Theorem 1.

The polynomials $J_{mr}^{B_n^m}\left(\overrightarrow{x}\right)$ given by (12) are the generators of polynomial invariants algebra $I^{B_n^m}$ with even degree $mr$ and $1\le r\le n$ for 2 cases:

-

For any n which provides $m\ne 2^l,l=1,2,\dots$;

-

For ${\displaystyle n\ne \frac{1}{2}\sum _{k=0}^r\left(\begin{array}{c}mr\\ mk\end{array}\right)-\frac{2^{\frac{mr}{2}-\alpha }}{m}}$, $m=2^l$, here $\alpha =0$ if $l=1$ and $\alpha =1$ if $l=2,3,\dots$.

Together with all the explained above, we noted that for an odd m, the polynomials of type $R_{mr}^{\alpha }$ have $\alpha =1$ and will appear as the basis invariants for algebra $I^{B_n^m}$ in the unitary spaces of any dimension n.

4. Main Result

Naturally, the problem of constructing the polynomial invariants’ algebra bases for $I^{B_n^m}$ with the odd degree that are based on Pogorelov polynomials arises. In the next Theorem, we present invariants relatively to (12) with the odd degree $m(r-1)$.

Theorem 2.

Assume all conditions from Theorem 1. Then, the basis polynomial invariants for the algebra $I^{B_n^m}$ relatively to the group $B_n^m$ are given with:

$$J_{m(r-1)}^{B_n^m}\left(\overrightarrow{x}\right)=\left(n-3+\frac{2^{\frac{mr}{2}}}{m}\right)\frac{\left(mr\right)!}{\left(m\right(r-1\left)\right)!}\sum _{i=1}^n{x}_i^{m(r-1)},$$

(14)

with $r=2,4,\dots ,n-\rho$, where $\rho =0$ for n being even and $\rho =1$ for odd n.

Proof  

We apply a differential operator of m-th degree given by

$$\Delta =\sum _{j=1}^n\frac{{\partial }^m}{\partial x_j^m}.$$

(15)

Applying (15) to the polynomials $J_{mr}^{B_n^m}$ with even degrees $mr$ given by (12) and (13), we obtain polynomial invariants for $I^{B_n^m}$ with odd degrees $m(r-1)$. If (12) and (13) are relatively invariant to the points $\overrightarrow{x}$ that belong to reflections’ hyperplanes that generate symmetries in $B_n^m$, then their m-th partial derivatives are still invariants relatively to the same points $\overrightarrow{x}$.

It is a consequence that polynomials are analytic complex functions and a compositing derivative that don’t change the linear structure of the polynomials’ origin given with (10). Namely, those parts in (10) that equal zero, will equal zero in their derivatives.

The first part of (14) is that of partial derivatives’ consequence that gives:

$$\begin{array}{ccc}\hfill \left(\sum _{j=1}^n\frac{{\partial }^m}{\partial x_j^m}\right)\left(\sum _{i=1}^n{x}_i^{mr}\right)& =& \sum _{i=1}^n\frac{{\partial }^m{x}_i^{mr}}{\partial x_i^m}\hfill \\ \hfill & =& \sum _{i=1}^{n}mr(mr-1)(mr-2)\cdots (mr-m+1)x_i^{mr-m}\hfill \\ \hfill & =& \frac{\left(mr\right)!}{\left(m\right(r-1\left)\right)!}\sum _{i=1}^n{x}_i^{m(r-1)}\hfill \end{array}$$

Together with (12), we obtain the derivative of the first part:

$$\left(\sum _{j=1}^n\frac{{\partial }^m}{\partial x_j^m}\right)\left(n-1+\frac{2^{\frac{mr}{2}}}{m}\right)\sum _{i=1}^n{x}_i^{mr}=\left(n-1+\frac{2^{\frac{mr}{2}}}{m}\right)\frac{\left(mr\right)!}{\left(m\right(r-1\left)\right)!}\sum _{i=1}^n{x}_i^{m(r-1)}$$

(16)

Introducing differential operator:

$$J_{m(r-1)}^{\ast }\left(\overrightarrow{x}\right)=\Delta R_{mr}^1\left(\overrightarrow{x}\right),$$

(17)

we will prove the second part of (14). Since the value m is odd and values r are even, the second part in (14) is the basis polynomial invariants $I_{m(r-1)}^{\ast }\left(\overrightarrow{x}\right)$ with odd degrees $m(r-1)$ relatively to the $B_n^m$ symmetries group.

We analyze the case $n=3$ without losing any generality of the proof, since the further can be analogously obtained. Since potentials are analytic functions, derivative techniques are equivalent as in real variable cases. We analyze the case $r=2$ at the first place:

$$\begin{array}{ccc}\hfill & & \left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\sum _{k=1}^{2-1}\sum _{i<j;i,j=1}^3{(-1)}^k\left(\begin{array}{c}2m\\ km\end{array}\right)x_i^{m(2-k)}{x}_j^{mk}\hfill \\ \hfill & & =\left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\sum _{i<j;i,j=1}^3(-1)\left(\begin{array}{c}2m\\ m\end{array}\right)x_i^m{x}_j^m\hfill \\ \hfill & & =-\left(\begin{array}{c}2m\\ m\end{array}\right)\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\left(x_1^m{x}_2^m+x_1^m{x}_3^m+x_2^m{x}_3^m\right)\hfill \\ \hfill & & =-\left(\begin{array}{c}2m\\ m\end{array}\right)\left(\frac{{\partial }^m}{\partial x_1^m}+\frac{{\partial }^m}{\partial x_2^m}+\frac{{\partial }^m}{\partial x_3^m}\right)\left(x_1^m{x}_2^m+x_1^m{x}_3^m+x_2^m{x}_3^m\right)\hfill \\ \hfill & & =-\left(\begin{array}{c}2m\\ m\end{array}\right)\left[\frac{{\partial }^m}{\partial x_1^m}\left(x_1^m{x}_2^m\right)+\frac{{\partial }^m}{\partial x_1^m}\left(x_1^m{x}_3^m\right)+\frac{{\partial }^m}{\partial x_1^m}\left(x_2^m{x}_3^m\right)+\frac{{\partial }^m}{\partial x_2^m}\left(x_1^m{x}_2^m\right)+\frac{{\partial }^m}{\partial x_2^m}\left(x_1^m{x}_3^m\right)\right.\hfill \\ \hfill & & \left.+\frac{{\partial }^m}{\partial x_2^m}\left(x_2^m{x}_3^m\right)+\frac{{\partial }^m}{\partial x_3^m}\left(x_1^m{x}_2^m\right)+\frac{{\partial }^m}{\partial x_3^m}\left(x_1^m{x}_3^m\right)+\frac{{\partial }^m}{\partial x_3^m}\left(x_2^m{x}_3^m\right)\right]\hfill \\ \hfill & & =-\left(\begin{array}{c}2m\\ m\end{array}\right)(m!x_2^m+m!x_3^m+0+m!x_1^m+0+m!x_3^m+0+m!x_1^m+m!x_2^m)\hfill \\ \hfill & & =-\left(\begin{array}{c}2m\\ m\end{array}\right)(2m!x_1^m+2m!x_2^m+2m!x_3^m)\hfill \\ \hfill & & =-2m!\left(\begin{array}{c}2m\\ m\end{array}\right)\sum _{i=1}^3{x}_i^m=-2\frac{\left(2m\right)!}{m!}\sum _{i=1}^3{x}_i^m\hfill \end{array}$$

If $r=2$, then we have:

$$\left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\sum _{k=1}^{2-1}\sum _{i<j;i,j=1}^3{(-1)}^k\left(\begin{array}{c}2m\\ km\end{array}\right)x_i^{m(2-k)}{x}_j^{mk}=-2\frac{\left(2m\right)!}{m!}\sum _{i=1}^3{x}_i^m$$

For $r=4$, we have the following:

$$\begin{array}{ccc}\hfill & & \left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\sum _{k=1}^{4-1}\sum _{i<j;i,j=1}^3{(-1)}^k\left(\begin{array}{c}4m\\ km\end{array}\right)x_i^{m(4-k)}{x}_j^{mk}\hfill \\ \hfill & & =\left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\left[\sum _{i<j;i,j=1}^3(-1)\left(\begin{array}{c}4m\\ m\end{array}\right)x_i^{3m}{x}_j^m\right.\hfill \\ & & +\left.\sum _{i,j=1}^3{(-1)}^2\left(\begin{array}{c}4m\\ 2m\end{array}\right)x_i^{2m}{x}_j^{2m}+\sum _{i,j=1}^3{(-1)}^3\left(\begin{array}{c}4m\\ 3m\end{array}\right)x_i^m{x}_j^{3m}\right]=\hfill \end{array}$$

The full announcement gives:

$$\begin{array}{ccc}\hfill & & =\left(\frac{{\partial }^m}{\partial x_1^m}+\frac{{\partial }^m}{\partial x_2^m}+\frac{{\partial }^m}{\partial x_3^m}\right)\left[-\left(\begin{array}{c}4m\\ m\end{array}\right)x_1^{3m}{x}_2^m+x_1^{3m}{x}_3^m+x_2^{3m}{x}_3^m\right.\hfill \\ \hfill & & \left.+\left(\begin{array}{c}4m\\ 2m\end{array}\right)x_1^{2m}{x}_2^{2m}+x_1^{3m}{x}_3^{2m}+x_2^{2m}{x}_3^{2m}-\left(\begin{array}{c}4m\\ 3m\end{array}\right)x_1^m{x}_2^{3m}+x_1^m{x}_3^{3m}+x_2^m{x}_3^{3m}\right]=\hfill \end{array}$$

After some algebra, we obtain the odd degree as before:

$$\begin{array}{ccc}\hfill & & =x_1^{3m}m!\left[-\left(\begin{array}{c}4m\\ m\end{array}\right)-\left(\begin{array}{c}4m\\ m\end{array}\right)\right]+x_2^{3m}m!\left[-\left(\begin{array}{c}4m\\ 3m\end{array}\right)-\left(\begin{array}{c}4m\\ m\end{array}\right)\right]\hfill \\ \hfill & & +x_3^{3m}m!\left[-\left(\begin{array}{c}4m\\ 3m\end{array}\right)-\left(\begin{array}{c}4m\\ m\end{array}\right)\right]+x_1^{2m}{x}_2^m\left[-\left(\begin{array}{c}4m\\ m\end{array}\right)\frac{\left(3m\right)!}{\left(2m\right)!}+\left(\begin{array}{c}4m\\ 2m\end{array}\right)\frac{\left(2m\right)!}{\left(m\right)!}\right]\hfill \\ \hfill & & +x_1^{2m}{x}_3^m\left[-\left(\begin{array}{c}4m\\ m\end{array}\right)\frac{\left(3m\right)!}{\left(2m\right)!}+\left(\begin{array}{c}4m\\ 2m\end{array}\right)\frac{\left(2m\right)!}{\left(m\right)!}\right]+x_1^m{x}_2^{2m}\left[\left(\begin{array}{c}4m\\ 2m\end{array}\right)\frac{\left(2m\right)!}{\left(m\right)!}-\left(\begin{array}{c}4m\\ 3m\end{array}\right)\frac{\left(3m\right)!}{\left(2m\right)!}\right]\hfill \\ \hfill & & +x_1^m{x}_3^{2m}\left[\left(\begin{array}{c}4m\\ 2m\end{array}\right)\frac{\left(2m\right)!}{\left(m\right)!}-\left(\begin{array}{c}4m\\ 3m\end{array}\right)\frac{\left(3m\right)!}{\left(2m\right)!}\right]+x_2^m{x}_3^{2m}\left[\left(\begin{array}{c}4m\\ 2m\end{array}\right)\frac{\left(2m\right)!}{\left(m\right)!}-\left(\begin{array}{c}4m\\ 3m\end{array}\right)\frac{\left(3m\right)!}{\left(2m\right)!}\right]\hfill \\ \hfill & & +x_2^{2m}{x}_3^m\left[-\left(\begin{array}{c}4m\\ 3m\end{array}\right)\frac{\left(3m\right)!}{\left(2m\right)!}+\left(\begin{array}{c}4m\\ 2m\end{array}\right)\frac{\left(2m\right)!}{\left(m\right)!}\right]=\cdots \hfill \end{array}$$

Note that:

$${\displaystyle \left(\begin{array}{c}4m\\ m\end{array}\right)=\left(\begin{array}{c}4m\\ 3m\end{array}\right)=\frac{\left(4m\right)!}{\left(3m\right)!m!}.}$$

After that, we obtain:

$$\left(\begin{array}{c}4m\\ 2m\end{array}\right)\frac{\left(2m\right)!}{\left(m\right)!}-\left(\begin{array}{c}4m\\ 3m\end{array}\right)\frac{\left(3m\right)!}{\left(2m\right)!}=\frac{\left(4m\right)!}{\left(2m\right)!\left(2m\right)!}\frac{\left(2m\right)!}{\left(m\right)!}-\frac{\left(4m\right)!}{\left(3m\right)!m!}\frac{\left(3m\right)!}{\left(2m\right)!}=0.$$

As such, every bracket consisted of the four vanished members, which finally results as

$$\cdots =-2m!\left(\begin{array}{c}4m\\ m\end{array}\right)\sum _{i=1}^3{x}_i^{3m}=-2\frac{\left(4m\right)!}{\left(3m\right)!}\sum _{i=1}^3{x}_i^{3m}.$$

Then, if $r=4$, we obtain the odd degree again:

$$\left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\sum _{k=1}^{4-1}\sum _{i<j;i,j=1}^3{(-1)}^k\left(\begin{array}{c}4m\\ km\end{array}\right)x_i^{m(4-k)}{x}_j^{mk}=-2\frac{\left(4m\right)!}{\left(3m\right)!}\sum _{i=1}^3{x}_i^{3m}.$$

The verification will appear with the calculating derivative with $r=6$ as much longer; therefore, we left the majority to the reader. It starts ordinarily, and after some algebra, we have:

$$\begin{array}{ccc}\hfill & & =-\left(\begin{array}{c}6m\\ m\end{array}\right)[5m(5m-1)\cdots (4m+1)x_1^{4m}{x}_2^m+5m\cdots (4m+1)x_1^{4m}{x}_3^m]\hfill \\ \hfill & & +\left(\begin{array}{c}6m\\ 2m\end{array}\right)[4m(4m-1)\cdots (3m+1)(x_1^{3m}{x}_2^{2m}+x_1^{3m}{x}_3^{2m})]\hfill \\ \hfill & & -\left(\begin{array}{c}6m\\ 3m\end{array}\right)3m\cdots (2m+1)(x_1^{2m}{x}_2^{3m}+x_1^{2m}{x}_3^{3m})\hfill \\ \hfill & & +\left(\begin{array}{c}6m\\ 4m\end{array}\right)2m\cdots (m+1)(x_1^m{x}_2^{4m}+x_1^m{x}_3^{4m})-\left(\begin{array}{c}6m\\ 5m\end{array}\right)m!(x_2^{5m}++x_3^{5m})\hfill \\ \hfill & & -\left(\begin{array}{c}6m\\ m\end{array}\right)m!(x_1^{5m}+x_3^{5m})+\left(\begin{array}{c}6m\\ 2m\end{array}\right)2m\cdots (m+1)(x_2^m{x}_1^{4m}+x_2^m{x}_3^{4m})\hfill \\ \hfill & & -\left(\begin{array}{c}6m\\ 3m\end{array}\right)3m\cdots (2m+1)(x_2^{2m}{x}_1^{3m}+x_2^{2m}{x}_3^{3m})\hfill \\ \hfill & & +\left(\begin{array}{c}6m\\ 4m\end{array}\right)4m\cdots (3m+1)(x_2^{3m}{x}_1^{2m}+x_2^{3m}{x}_3^{2m})\hfill \\ \hfill & & -\left(\begin{array}{c}6m\\ 5m\end{array}\right)5m\cdots (4m+1)(x_2^{4m}{x}_1^m+x_2^{4m}{x}_3^m)-\left(\begin{array}{c}6m\\ m\end{array}\right)m!(x_1^{5m}+x_2^{5m})\hfill \\ \hfill & & +\left(\begin{array}{c}6m\\ 2m\end{array}\right)2m\cdots (m+1)(x_3^m{x}_1^{4m}+x_3^m{x}_2^{4m})-\left(\begin{array}{c}6m\\ 3m\end{array}\right)3m\cdots (2m+1)x_3^{2m}(x_1^{3m}+x_2^{3m})\hfill \\ \hfill & & +\left(\begin{array}{c}6m\\ 4m\end{array}\right)4m\cdots (3m+1)(x_3^{3m}{x}_1^{2m}+x_3^{3m}{x}_2^{2m})-\left(\begin{array}{c}6m\\ 5m\end{array}\right)5m\cdots (4m+1)(x_3^{4m}{x}_1^m+x_3^{4m}{x}_2^m)=\cdots \hfill \end{array}$$

Introducing the following notation and knowing that:

$$\left(\begin{array}{c}6m\\ 5m\end{array}\right)=\left(\begin{array}{c}6m\\ m\end{array}\right)\mathrm{and}\left(\begin{array}{c}6m\\ 4m\end{array}\right)=\left(\begin{array}{c}6m\\ 2m\end{array}\right),$$

we have:

$$\begin{array}{ccc}\hfill & & \left(\begin{array}{c}6m\\ m\end{array}\right)5m\cdots (4m+1)=\frac{\left(6m\right)!5m\cdots (4m+1)}{\left(5m\right)!m!}=\frac{\left(6m\right)!}{\left(4m\right)!m!}=k_1\hfill \\ \hfill & & \left(\begin{array}{c}6m\\ 2m\end{array}\right)4m\cdots (3m+1)=\frac{\left(6m\right)!}{\left(3m\right)!\left(2m\right)!}=k_2\hfill \\ \hfill & & \left(\begin{array}{c}6m\\ 3m\end{array}\right)3m\cdots (2m+1)=\frac{\left(6m\right)!3m\cdots (2m+1)}{\left(3m\right)!\left(3m\right)!}=\frac{\left(6m\right)!}{\left(2m\right)!\left(3m\right)!}=k_3\hfill \\ \hfill & & \left(\begin{array}{c}6m\\ 4m\end{array}\right)2m\cdots (m+1)=\frac{\left(6m\right)!2m\cdots (m+1)}{\left(4m\right)!\left(2m\right)!}=\frac{\left(6m\right)!}{\left(4m\right)!m!}=k_4\hfill \\ \hfill & & \left(\begin{array}{c}6m\\ 5m\end{array}\right)m!=\frac{\left(6m\right)!m!)}{\left(5m\right)!m!}=\frac{\left(6m\right)!}{\left(5m\right)!}=k_5\hfill \\ \hfill \end{array}$$

Note that $k_1-k_4=0$ and $k_2-k_3=0$. Using the notations defined above, we proceed with the calculations as follows:

$$\begin{array}{ccc}\hfill & & =-2k_5{x}_1^{5m}-2k_5{x}_2^{5m}-2k_5{x}_3^{5m}+x_1^{4m}{x}_2^m(k_4-k_1)+x_1^{4m}{x}_3^m(k_4-k_1)-x_1^{3m}{x}_2^{2m}(k_2-k_3)\hfill \\ \hfill & & +x_1^{3m}{x}_3^{2m}(k_2-k_3)+x_1^{2m}{x}_2^{3m}(k_2-k_3)+x_1^{2m}{x}_3^{3m}(k_2-k_3)+x_1^m{x}_2^{4m}(k_4-k_1)\hfill \\ \hfill & & +x_1^m{x}_3^{4m}(k_4-k_1)+x_2^m{x}_3^{4m}(k_4-k_1)+\hfill \\ \hfill & & x_2^{2m}{x}_3^{2m}(k_2+k_3)+x_2^{3m}{x}_3^{2m}(k_2-k_3)-x_2^{4m}{x}_3^m(k_1+k_4)=-2k_5\sum _{i=1}^3{x}_i^{5m}\hfill \end{array}$$

Finally, with $r=6$, we have an odd degree basis invariant:

$$\left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\sum _{k=1}^{6-1}\sum _{i<j;i,j=1}^3{(-1)}^k\left(\begin{array}{c}6m\\ km\end{array}\right)x_i^{m(6-k)}{x}_j^{mk}=-2\frac{\left(6m\right)!}{\left(5m\right)!}\sum _{i=1}^3{x}_i^{5m}$$

After all above, we set $r=p+1$, and obtaining the following:

$$\begin{array}{ccc}\hfill & & \left(\frac{{\partial }^m}{\partial x_1^m}+\frac{{\partial }^m}{\partial x_2^m}+\frac{{\partial }^m}{\partial x_3^m}\right)\left[-\left(\begin{array}{c}m(p+1)\\ m\end{array}\right)\left(x_1^{mp}{x}_2^m+x_1^{mp}{x}_3^m+x_2^{mp}{x}_3^m\right)\right.\hfill \\ \hfill & & +\left(\begin{array}{c}m(p+1)\\ 2m\end{array}\right)\left(x_1^{m(p-1)}{x}_2^{2m}+x_1^{m(p-1)}{x}_3^{2m}+x_2^{m(p-1)}{x}_3^{2m}\right)\hfill \\ \hfill & & -\left(\begin{array}{c}m(p+1)\\ 3m\end{array}\right)\left(x_1^{m(p-2)}{x}_2^{3m}+x_1^{m(p-2)}{x}_3^{3m}+x_2^{m(p-2)}{x}_3^{3m}\right)+\cdots \hfill \\ \hfill & & +{(-1)}^k\left(\begin{array}{c}m(p+1)\\ km\end{array}\right)x_i^{m(p+1-k)}{x}_j^{mk}+\cdots -\hfill \\ \hfill & & -\left(\begin{array}{c}m(p+1)\\ m(p-2)\end{array}\right)\left(x_1^{3m}{x}_2^{m(p-2)}+x_1^{3m}{x}_3^{m(p-2)}+x_2^{3m}{x}_3^{m(p-2)}\right)+\hfill \\ \hfill & & +\left(\begin{array}{c}m(p+1)\\ m(p-1)\end{array}\right)\left(x_1^{2m}{x}_2^{m(p-1)}+x_1^{2m}{x}_3^{m(p-1)}+x_2^{2m}{x}_3^{m(p-1)}\right)-\hfill \\ \hfill & & \left(\begin{array}{c}m(p+1)\\ mp\end{array}\right)\left(x_1^m{x}_2^{mp}+x_1^m{x}_3^{mp}+x_2^m{x}_3^{mp}\right).\hfill \end{array}$$

After the pretty long and exhausted calculus, we have:

$$\left(\sum _{i=1}^3\frac{{\partial }^m}{\partial x_i^m}\right)\sum _{k=1}^p\sum _{i<j;i,j=1}^3{(-1)}^k\left(\begin{array}{c}m(p+1)\\ km\end{array}\right)x_i^{m(p+1-k)}{x}_j^{mk}=-2\frac{\left(m\right(p+1\left)\right)!}{\left(mp\right)!}\sum _{i=1}^3{x}_i^{mp}.$$

By this way, we proved:

$${\displaystyle J_{m(r-1)}^{\ast }=-2\frac{\left(mr\right)!}{\left(m\right(r-1\left)\right)!}\sum _{i=1}^n{x}_i^{m(r-1)}.}$$

(18)

Formulas (16) and (18) together form basis invariants (14) with odd degrees $m(r-1)$ for the polynomial invariants’ algebra $I^{B_n^m}$ relatively to group $B_n^m$ and based on the Pogorelov polynomials. All the algebra $I^{B_n^m}$ generators are now explicitly obtained regardless of degree parity. □

5. Conclusions

In this article, we constructed odd-degree polynomial invariants algebra $I^{B_n^m}$ generators. As such, we used the suitable differential operator (15) acting on polynomial invariants ${\displaystyle J_{mr}^{B_n^m}}$ in (12) and (13) with $\alpha =1$.

In doing so, we introduced the polynomial invariants of the symmetry group generated by reflections we pictured in the 3-dimensional real space. We also introduced the term of flag as a possibility for the symmetry group investigation.

The original article [4] presented several results without exact proof. However, it was not entirely clear why the polynomial invariants’ exponents in (10) were of even $2t$ and consequently must be $mr=2t$. If the author in [1,7] simply found even exponents $2t$ since n-cube was settled in the origin and symmetry degree, then accordingly (1) is two, and we conjecture that the exponent in (10) might be $mt$ instead of $2t$. Our result can confirm the conjecture.

Further investigation may yield the answer. It will be interesting to generalize the flag term into generalized n-cube investigations. After all, unfinished articles are motivating further research studies.