A Variant Cubic Exponential B-Spline Scheme with Shape Control

Abstract

This paper presents a variant scheme of the cubic exponential B-spline scheme, which, with two parameters, can generate curves with different shapes. This variant scheme is obtained based on the iteration from the generation of exponentials and a suitably chosen function. For such a scheme, we show its $C^2$-convergence and analyze the effect of the parameters on the shape of the generated curves and also discuss its convexity preservation. In addition, a non-uniform version of this variant scheme is derived in order to locally control the shape of the generated curves. Numerical examples are given to illustrate the performance of the new schemes in this paper.

1. Introduction

Subdivision can be used as an effetive tool to generate smooth curves/surfaces starting from a given set of initial control points. Due to their advantages such as numerical stability and refinability, subdivision schemes have been widely used in fields such as geometric modeling [1], wavelets and framelets [2], isogeometric analysis [3], and multigrid [4]. Generally speaking, subdivision can be classified into stationary and non-stationary schemes. Compared with stationary schemes, non-stationary subdivision depend on the recursion level and thus have more flexibility to generate different curves. Recall that the stationary subdivision are the schemes whose subdivision rules are independent of the recursion level while the non-stationary subdivision are the ones whose subdivision rules depend on the recursion level. This means that, in the subdivision process, as the recursion level changes, the subdivision rules of the stationary schemes keep the same while the subdivision rules of the non-stationary schemes change.

Therefore, there have been amounts of works on the construction of non-stationary subdivision. Beccari. et al. [5] derived the non-stationary 4-pt interpolatory scheme reproducing conics. Dyn et al. [6] investigated the non-stationary interpolatory schemes reproducing exponential polynomials. Fang [7] gave a family of generalized curve subdivision generating different kinds of curves. All of these schemes can be seen as obtained from the view of generating exponentials and thus can produce curves such as conics and helix. For other references on this kind of non-stationary schemes, please refer to [8,9,10,11,12,13] and the references therein. For such schemes, the interpolatory ones are usually more powerful than the approximating ones in controlling the shape of the limit curves while the approximating ones can have higher smoothness order than the interpolatory ones.

In fact, besides such non-stationary subdivision, there is another kind of non-stationary schemes, which can be seen as obtained based on some fixed point iteration. For this kind of schemes, Beccari [14] constructed a ternary interpolatory non-stationary scheme generating various kinds of curves. Tan et al. [15] presented a binary approximating non-stationary scheme with a similar property. Compared with the ones obtained in the view of generating exponentials, the approximating ones based on iterations can be as powerful as the interpolatory ones in controlling the shape of the limit curves without reducing the smoothness order. In fact, similar to [14,15], Zhang et al. [9] also proposed a modified cubic exponential B-spline scheme and a non-stationary Catmull–Clark scheme controlling the shape of the curves and surfaces freely. Yet, the analysis of the parameters on the shape of the generated curves/surfaces and the convexity preservation is absent. Note that the analysis of these properties is also important in applications, since it is better that we know how to adjust the parameters to generate the curves with the needed shape. In fact, for the convexity preservation of non-stationary schemes, Akram et al. [16] analyzed the shape preservation of the non-stationary 4-pt interpolatory scheme [5].

Therefore, in this paper, continuing our work in [9], we base on the iteration from the generation of exponentials and a suitable function of this iteration, and give a variant scheme of the cubic exponential B-spline scheme, which can generate different kinds of curves, including the conics. For this scheme, we analyze its $C^l$-convergence and show that it has the same smoothness order as the cubic exponential B-spline scheme. Then, we give the limit position of the initial control points and analyze the convexity preservation. This analysis can show us how to control the shape of the limit curves and preserve the convexity of the initial control polygon by adjusting the parameters. Furthermore, a non-uniform version of this variant scheme is also given to locally control the shape of the limit curves. Numerous examples are given to illustrate the performance of the new schemes.

The rest of this paper is organized as follows. Section 2 gives a brief review of non-stationary subdivision. In Section 3, we present the variant cubic exponential B-spline scheme and show that it can indeed generate curves with different shapes. Section 4 is devoted to the analysis of this variant cubic exponential B-spline scheme, including the smoothness analysis, the limit position of the initial control points and the convexity preservation. In Section 5, we move a further step and give a discussion on the local control of the shape of the limit curves to generate more kinds of curves. Section 6 concludes this paper.

2. Preliminaries

In this section, we present some basic knowledge about the non-stationary subdivision schemes, which is needed in the rest of this paper.

Let $l\left(\mathbb{Z}\right)$ denote the linear space of real sequences indexed by $\mathbb{Z}$ and $l_0\left(\mathbb{Z}\right)$ denote the linear space of real sequences with finite support. Given an initial data sequence ${\mathit{q}}^0=\{q_i^0,i\in \mathbb{Z}\}$, we consider the following binary non-stationary subdivision

$${\left(S_{{\mathit{a}}^k}{\mathit{q}}^k\right)}_i=q_i^{k+1}=\sum _{j\in \mathbb{Z}}{a}_{i-2j}^k{q}_j^k,j\in \mathbb{Z},$$

where $S_{{\mathit{a}}^k}$ is the k-level subdivision operator, the sequence ${\mathit{a}}^k=\{a_i^k,i\in \mathbb{Z}\}$ is the k-level mask with finite support, and the k-level symbol is the Laurent polynomial $a^k\left(\mathit{z}\right)={\displaystyle \sum _{i\in \mathbb{Z}}}{a}_i^k{z}^i$. We denote this non-stationary subdivision by ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$.

By attaching $q_i^k$, $i\in \mathbb{Z}$ to the parameter values $\frac{i}{2^k}$, $k\ge 0$, we say the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ is $C^0$-convergent if, for the initial data sequence ${\mathit{q}}^0\in l_0\left(\mathbb{Z}\right)$, there exists a function $f_{{\mathit{q}}^0}\in C^0\left(\mathbb{R}\right)$ satisfying

$$\underset{k\to \infty }{lim}\underset{i\in \mathbb{Z}\cap K}{max}|f_{{\mathit{q}}^0}\left(\frac{i}{2^k}\right)-{\left(S_{{\mathit{a}}^k}{\mathit{q}}^k\right)}_i|=0,$$

with K being any compact set in $\mathbb{R}$, and $f_{{\mathit{q}}^0}\ne 0$ for at least some initial data sequence ${\mathit{q}}^0$. If $f_{{\mathit{q}}^0}\in C^l\left(\mathbb{R}\right)$, the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ is $C^l$-convergent.

For the convergence and smoothness of the non-stationary subdivision in this paper, we recall the following definitions.

Definition 1 ([17]).

A non-stationary scheme ${\left\{S_{{\mathit{u}}^k}\right\}}_{k\ge 0}$ with the k-level mask ${\mathit{u}}^k$ is said to be asymptotically similar to the stationary scheme $S_{\mathit{u}}$ with the mask $\mathit{u}$, if the k-level mask ${\mathit{u}}^k$ and the mask $\mathit{u}$ have the same support U and satisfy

$$\underset{k\to \infty }{lim}{u}_{\mathit{\alpha }}^k=u_{\mathit{\alpha }},\mathit{\alpha }\in U.$$

Definition 2 ([18]).

A non-stationary scheme ${\left\{S_{{\mathit{u}}^k}\right\}}_{k\ge 0}$ with the k-level symbol $u^k\left(\mathit{z}\right)$ is said to satisfy the approximate sum rules of order $r+1$ if

$${\mu }^k=|u^k\left(1\right)-2|,{\delta }^k=\underset{\left|\eta \right|\le r}{max}\left|2^{-k\left|\eta \right|}{D}^{\eta }{u}^k(-1)\right|$$

with $\eta \in {\mathbb{N}}_0$ satisfy

$$\sum _k{\mu }^k<\infty ,\sum _k{2}^{kr}{\delta }^k<\infty .$$

Now we cite the result on the smoothness of non-stationary subdivision for the $C^l$-convergence of the variant cubic exponential B-spline scheme in this paper as follows.

Theorem 1 ([17]).

Assume that the non-stationary scheme ${\left\{S_{{\mathit{u}}^k}\right\}}_{k\ge 0}$ satisfies the approximate sum rules of order $r+1$, and is asymptotically similar to a convergent stationary scheme $S_{\mathit{u}}$, which is $C^r$-convergent. Then the non-stationary scheme ${\left\{S_{{\mathit{u}}^k}\right\}}_{k\ge 0}$ is $C^r$-convergent.

3. The Variant Cubic Exponential B-Spline Scheme

The main purpose of this section is to derive the variant cubic exponential B-spline scheme in this paper. To this purpose, we start from reviewing the cubic exponential B-spline [19] and the non-stationary 4-pt interpolatory scheme [5].

As is known, the cubic exponential B-spline scheme [19] and the non-stationary 4-point interpolatory scheme [5] can be characterized by their k-level masks

$${\tilde{\mathit{a}}}^k=\{\frac{1}{4(v^{k+1}+1)},\frac{1}{2},\frac{2v^{k+1}+1}{2(v^{k+1}+1)},\frac{1}{2},\frac{1}{4(v^{k+1}+1)}\},$$

(1)

and

$${\tilde{\mathit{b}}}^k=\{\frac{-1}{8v^{k+1}(v^{k+1}+1)},0,\frac{{(2v^{k+1}+1)}^2}{8v^{k+1}(v^{k+1}+1)},1,\frac{{(2v^{k+1}+1)}^2}{8v^{k+1}(v^{k+1}+1)},0,\frac{-1}{8v^{k+1}(v^{k+1}+1)}\},$$

(2)

respectively, where

$$v^{k+1}=\frac{e^{\frac{t}{2^{k+1}}}+e^{-\frac{t}{2^{k+1}}}}{2}.$$

It can be seen that, $v^k$ and $v^{k+1}$ satisfies the iteration

$$v^{k+1}=\sqrt{\frac{1+v^k}{2}},$$

(3)

with $v^0\in$$(-1,\infty )$. Now let

$$h_0\left(x\right)=\frac{1}{1+x},h_1\left(x\right)=\frac{1}{x(1+x)},$$

then, the k-level masks in (1) and (2) can be rewritten as

$${\tilde{\mathit{a}}}^k=\{\frac{h_0\left(v^{k+1}\right)}{4},\frac{1}{2},1-\frac{h_0\left(v^{k+1}\right)}{2},\frac{1}{2},\frac{h_0\left(v^{k+1}\right)}{4}\},$$

and

$${\tilde{\mathit{b}}}^k=\{-\frac{h_1\left(v^{k+1}\right)}{8},0,\frac{1}{2}+\frac{h_1\left(v^{k+1}\right)}{8},1,\frac{1}{2}+\frac{h_1\left(v^{k+1}\right)}{8},0,-\frac{h_1\left(v^{k+1}\right)}{8}\},$$

respectively.

Both schemes generate conics but the cubic exponential B-spline scheme is $C^2$ convergent while the non-stationary 4-pt interpolatory scheme is $C^1$ convergent. In addition, as seen in [9], for $h_0\left(x\right)$ and $h_1\left(x\right)$, combining with the iteration in (3), we have

$$\underset{x\to 0^{+}}{lim}{h}_0\left(x\right)=1,\underset{x\to 0^{+}}{lim}{h}_1\left(x\right)=\infty ,\underset{x\to 1}{lim}{h}_i\left(x\right)=\frac{1}{2},i=0,1.$$

(4)

and

$$\underset{v^0\to -1^{+}}{lim}{h}_0\left(v^0\right)=1,\underset{v^0\to -1^{+}}{lim}{h}_1\left(v^0\right)=\infty ,\underset{k\to \infty }{lim}{h}_i\left(v^k\right)=\frac{1}{2},i=0,1.$$

(5)

It follows that, with the functions $h_0\left(x\right)$ and $h_1\left(x\right)$ behaving differently as shown in (4) and (5), the non-stationary 4-pt interpolatory scheme can generate curves with more kinds of shapes than the exponential cubic B-spline scheme [9].

In this way, similar to [9], based on the iteration in (3), we choose a function such that it satisfies (4) and (5) with $i=1$. Here, we can choose $h\left(x\right)$ as the following one

$$h\left(x\right)=\frac{1}{4x^{\beta }(1+x)},\beta \in [0,\infty ).$$

(6)

Now with the iteration in (3) and the function $h\left(x\right)$, we can derive the following k-level mask

$${\mathit{a}}^k=\{h\left(v^{k+1}\right),\frac{1}{2},1-2h\left(v^{k+1}\right),\frac{1}{2},h\left(v^{k+1}\right)\}.$$

We denote the corresponding scheme by ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$, which is just the desired variant cubic exponential B-spline scheme.

It can be seen that, when $\beta =0$, $h\left(x\right)$ reduces to $h_0\left(x\right)$ and the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ reduces to the cubic exponential B-spline and, when $\beta >0$, $h\left(x\right)$ behaves like $h_1\left(x\right)$ as in (4) and (5), and thus the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ can generate curves with different shapes.

Figure 1 and Figure 2 show the curves generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with different choices of $v^0$ and $\beta$. It can be seen from these two figures that, with different choices of the parameters $v^0$ and $\beta$, the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ can indeed generate curves with different shapes. In particular, when $\beta =0$, the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ reduces to the cubic exponential B-spline scheme and Figure 1 and Figure 2 show the generation of circles with $v^0=cos(\pi /3)$ and $\beta =0$.

Figure 1. Curves generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with $(v^0,\beta )=(-0.6,2.1),(-0.4,1.9)$, $\left(cos\right(\pi /3),0),(3,4),(5,6)$ (from left to right).

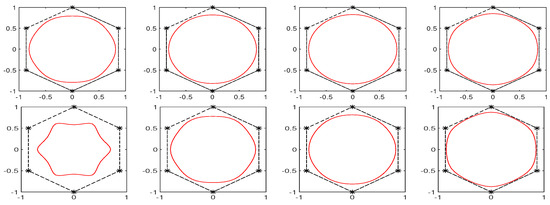
Figure 2. Curves generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with $v^0=-0.75$,$-0.3$, $cos(\pi /3)$, 3 (from left to right) and $\beta =0$ (top row), $1.5$ (bottom row).

4. Analysis of the Variant Cubic Exponential B-Spline Scheme

This section is devoted to the analysis of the properties of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$, including the $C^l$-convergence, the limit position of the initial control points and the convexity preservation.

4.1. Smoothness Analysis

We now analyze the $C^l$-convergence of the variant scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$. In fact, this can be done similar to [9]. Yet, for completeness, we prove the following result.

Theorem 2.

The non-stationary scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ is $C^2$-convergent.

Proof. 

The k-level symbol of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ can be written as

$$a^k\left(z\right)=\frac{{(1+z)}^2}{4}\left(4h\left(v^{k+1}\right)+(2-8h\left(v^{k+1}\right))z+4h\left(v^{k+1}\right)z^2\right)z^{-2}.$$

(7)

Recall that for the sequence ${\left\{v^k\right\}}_{k\ge 0}$, we have $\underset{k\to \infty }{lim}{v}^k=1$, for $v^0\in (-1,\infty )$. Therefore, $\underset{k\to \infty }{lim}h\left(v^{k+1}\right)=\frac{1}{8}$ and the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ is, by Definition 1, asymptotically similar to the cubic B-spline scheme, which is $C^2$-convergent. If we can show that the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ satisfies the approximate sum rules of order 3, then by Theorem 1, the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ is $C^2$-convergent.

In fact, from (7), it can be computed that $a^k\left(1\right)=2$ and $a^k(-1)=D^1{a}^k(-1)=0$, $D^2{a}^k(-1)=8h\left(v^{k+1}\right)-1$. Thus, for ${\mu }^k$ and ${\delta }^k$ in Definition 2, it follows that, for $\eta \in {\mathbb{N}}_0$,

$${\mu }^k=|a^k\left(1\right)-2|=0,{\delta }^k=\underset{0\le \eta \le 2}{max}{2}^{-k\eta }|D^{\eta }{a}^k(-1)|=2^{3-2k}|h^k\left(v^{k+1}\right)-\frac{1}{8}|.$$

In this way, following [9], by Definition 2 and the function $h\left(x\right)$ in (6), there exists a constant $c_1$ independent of k, such that

$$\sum _{k=0}^{\infty }{2}^{2k}{\delta }^k=\sum _{k=0}^{\infty }8|h^k\left(v^{k+1}\right)-\frac{1}{8}|\le c_1\sum _{k=0}^{\infty }|v^{k+1}-1|.$$

Therefore, according to Definition 2, we only have to show ${\displaystyle \sum _{k=0}^{\infty }}|v^{k+1}-1|<\infty$.

Let $v^{k+1}=\phi \left(v^k\right)=\sqrt{\frac{v^k}{2}+\frac{1}{2}}$ with $\phi \left(x\right)=\sqrt{\frac{x}{2}+\frac{1}{2}}$, then $\phi \left(1\right)=1$ and thus 1 is the fixed point of the iteration $v^{k+1}=\phi \left(v^k\right)$. Then, as shown in [9], for $v^0\in (-1,\infty )$,

$$|v^k-1|=|\phi \left(v^{k-1}\right)-\phi \left(1\right)|\le L|v^{k-1}-1|\le \cdots \le c_2{L}^k|v^0-1|,$$

with $0<L<1$ and $c_2$ is a constant independent of k. Thus,

$$\sum _{k=0}^{\infty }|v^{k+1}-1|\le \sum _{k=0}^{\infty }{c}_3{L}^{k+1}|v^0-1|<\infty ,$$

where $c_3$ is a constant independent of k. Therefore, we can conclude that the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ satisfies the approximate sum rules of order 3 and, thus, is $C^2$-convergent. □

4.2. The Limit Position of the Initial Control Points

Now we give the limit position of the initial control points, by which we can discuss the effect of the parameters on the shape of the limit curves. To this purpose, we give the following result.

Theorem 3.

In the subdivision process of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$, the limit position of the initial control point $P_i^0$ is

$$P_i^{\infty }=P_i^0+\Delta P_i^0\sum _{l=0}^{\infty }h\left(v^{l+1}\right)\prod _{s=0}^{l-1}(\frac{1}{2}-2h\left(v^{s+1}\right))).$$

(8)

Proof. 

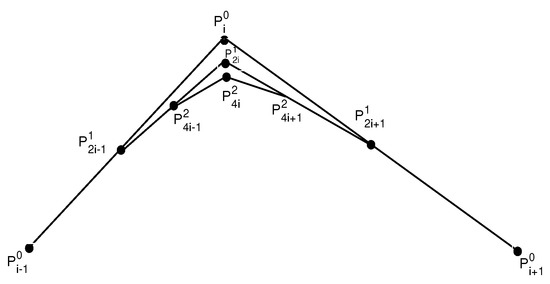
For the point $P_i^0$, according to the subdivision rules of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$, after one step of subdivision, it is moved to

$$\begin{array}{cc}\hfill P_{2i}^1& =h\left(v^1\right)(P_{i-1}^0+P_{i+1}^0)+(1-2h\left(v^1\right))P_i^0\hfill \\ \hfill & =P_i^0+h\left(v^1\right)\Delta P_i^0,\hfill \end{array}$$

where $\Delta P_i^0$ is the displacement $\Delta P_i^0=P_{i-1}^0-2P_i^0+P_{i+1}^0$. Similarly, after another step of subdivision, the point $P_{2i}^1$ is moved to

$$P_{4i}^2=P_{2i}^1+h\left(v^2\right)\Delta P_{2i}^1.$$

This can be seen in Figure 3. Generally, we can show that after $k+1$ steps of subdivision using the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$, we actually have

$$P_{2^{k+1}i}^{k+1}=P_{2^{k}i}^k+h\left(v^{k+1}\right)\Delta P_{2^{k}i}^k.$$

Figure 3. Location of the point $P_i^0$ in the first two steps of subdivision.

For the displacement $\Delta P_{2^{k}i}^k$, note that combining with the subdivision rules of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$, it follows that

$$\begin{array}{cc}\hfill \Delta P_{2^{k}i}^k& =P_{2^{k}i-1}^k-2P_{2^{k}i}^k+P_{2^{k}i+1}^k\hfill \\ \hfill & =\frac{1}{2}(P_{2^{k-1}i-1}^{k-1}+P_{2^{k-1}i}^{k-1})-2(h\left(v^k\right)(P_{2^{k-1}i-1}^{k-1}+P_{2^{k-1}i+1}^{k-1})+(1-2h\left(v^k\right))P_{2^{k-1}i}^{k-1})\hfill \\ \hfill & +\frac{1}{2}(P_{2^{k-1}i}^{k-1}+P_{2^{k-1}i+1}^{k-1})\hfill \\ \hfill & =(\frac{1}{2}-2h\left(v^k\right))(P_{2^{k-1}i-1}^{k-1}+P_{2^{k-1}i+1}^{k-1})+(4h\left(v^{k+1}\right)-1)P_{2^{k-1}i}^{k-1}\hfill \\ \hfill & =(\frac{1}{2}-2h\left(v^k\right))(P_{2^{k-1}i-1}^{k-1}-2P_{2^{k-1}i}^{k-1}+P_{2^{k-1}i+1}^{k-1})\hfill \\ \hfill & =(\frac{1}{2}-2h\left(v^k\right))\Delta P_{2^{k-1}i}^{k-1}.\hfill \end{array}$$

Generally, we have, for $k\in \mathbb{N}$,

$$\Delta P_{2^{k+1}i}^{k+1}=(\frac{1}{2}-2h\left(v^{k+1}\right))\Delta P_{2^{k}i}^k=\cdots =\prod _{s=0}^k(\frac{1}{2}-2h\left(v^{s+1}\right))\Delta P_i^0.$$

Therefore, after $k+1$ steps of subdivision, the initial control point $P_i^0$ is moved to

$$\begin{array}{cc}\hfill P_{2^{k+1}i}^{k+1}& =P_{2^{k}i}^k+h\left(v^{k+1}\right)\Delta P_{2^{k}i}^k\hfill \\ \hfill & =P_{2^{k-1}i}^{k-1}+h\left(v^k\right)\Delta P_{2^{k-1}i}^{k-1}+h\left(v^{k+1}\right)\Delta P_{2^{k}i}^k\hfill \\ \hfill & =P_i^0+\sum _{l=0}^{k}h\left(v^{l+1}\right)\Delta P_{2^{l}i}^l\hfill \\ \hfill & =P_i^0+\sum _{l=0}^{k}h\left(v^{l+1}\right)\prod _{s=0}^{l-1}(\frac{1}{2}-2h\left(v^{s+1}\right))\Delta P_i^0.\hfill \end{array}$$

Recall that as k tends to ∞, $v^k$ tends to 1. Thus $h\left(v^k\right)$ tends to $\frac{1}{8}$, $\frac{1}{2}-2h\left(v^k\right)$ tends to $\frac{1}{4}$. Together with $h\left(x\right)$ in (6), it can be shown that the term ${\displaystyle \prod _{s=0}^{l-1}}(\frac{1}{2}-2h\left(v^{s+1}\right))$ is actually bounded. Then it can seen that ${\displaystyle \sum _{l=0}^k}h\left(v^{l+1}\right){\displaystyle \prod _{s=0}^l}(\frac{1}{2}-2h\left(v^{s+1}\right))$ converges as $k\to \infty$. Therefore, the limit position of $P_i^0$, which can be denoted by $P_i^{\infty }$, is

$$P_i^{\infty }=P_i^0+\sum _{l=0}^{\infty }h\left(v^{l+1}\right)\prod _{s=0}^{l-1}(\frac{1}{2}-2h\left(v^{s+1}\right))\Delta P_i^0,$$

which is just (8). □

Now, denote the displacement between the initial control point $P_i^0$ and its limit position by

$$\Delta =P_i^{\infty }-P_i^0=\Delta P_i^0\sum _{l=0}^{\infty }h\left(v^{l+1}\right)\prod _{s=0}^{l-1}(\frac{1}{2}-2h\left(v^{s+1}\right)).$$

Then Theorem 3 actually implies the effect of the parameters $v^0$ and $\beta$ on the shape of the limit curve. In fact, from Theorem 3, it can be seen that, for given $\beta$, with a larger $v^0$, each term of $\Delta$ gets smaller and thus the limit point $P_i^{\infty }$ gets closer to $P_i^0$, which makes the limit curve shrinks to the initial control polygon. Similarly, for given $v^0>1$, with a larger $\beta$, the limit point $P_i^{\infty }$ also gets closer to $P_i^0$ and, thus, the limit curve shrinks to the initial control polygon. For $v^0=1$, (8) actually becomes

$$\begin{array}{cc}\hfill P_i^{\infty }& =P_i^0+\Delta P_i^0(\frac{1}{8}+\frac{1}{8}·\frac{1}{4}+\frac{1}{8}·\frac{1}{4^2}+\cdots )\hfill \\ \hfill & =P_i^0+\frac{1}{6}\Delta P_i^0,\hfill \end{array}$$

which actually implies the limit position of the initial control points using the cubic B-spline scheme. In addition, for given $-1<v^0<1$, when $\beta$ increases, the limit point $P_i^{\infty }$ gets far away from $P_i^0$, which implies the big change of the shape of the limit curve.

The above analysis can be seen in Figure 4, which shows the curves generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with different choices of the parameters $v^0$ and $\beta$.

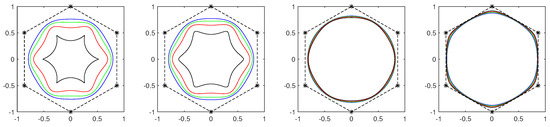
Figure 4. Limit curves generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with $v^0=-0.5,-0.4,cos(pi/3),5$ (from left to right) and $\beta =0.5$ (blue), 1 (green), $1.6$ (red), $2.5$ (black).

4.3. Convexity Preservation

Now we analyze the convexity preservation of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ and show how to choose the parameters to preserve the convexity of the initial control polygon.

Given a set of control points ${\left\{p_i^k\right\}}_{i\in \mathbb{Z}}$, $p_i^k=(x_i^k,f_i^k)$. Suppose $x_{i+1}^0-x_i^0=1$, i.e., these points are equally spaced, and suppose they are strictly convex, which means that the second divided difference $d_i^0=\frac{1}{2}(f_{i-1}^0-2f_i^0+f_{i+1}^0)>0$ [20]. Then for the k level control points, they are also equally spaced, meaning that $x_{i+1}^k-x_i^k=\frac{1}{2^k}$. Now let $d_i^k=2^{2k-1}(f_{i-1}^k-2f_i^k+f_{i+1}^k)$ be the second order divided differences and let $r_i^k=\frac{d_{i+1}^k}{d_i^k}$, $R^k={max}_i\{r_i^k,\frac{1}{r_i^k}\}$. Then, we have the following result.

Theorem 4.

Suppose the initial control points ${\left\{p_i^0\right\}}_{i\in \mathbb{Z}}$, $p_i^0=(x_i^0,f_i^0)$, are strictly convex, i.e., $d_i^0>0$, and $R^0<\lambda$ with $\lambda >1$. Then, if $\frac{1}{\lambda }<\frac{1}{2h\left(v^k\right)}-3<\lambda$, $k\in {\mathbb{Z}}_{+}$, we have $d_i^k>0$, $R^k<\lambda$.

Proof. 

We first show $d_i^k>0$. In fact, according to the subdivision rules of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$, it follows that

$$\begin{array}{cc}\hfill d_{2i}^{k+1}& =2^{2k+1}(f_{2i-1}^{k+1}-2f_{2i}^{k+1}+f_{2i+1}^{k+1})\hfill \\ \hfill & =2^{2k+1}\{\frac{1}{2}(f_{i-1}^k+f_i^k)-2h\left(v^{k+1}\right)(f_{i-1}^k+f_{i+1}^k)-2(1-2h\left(v^{k+1}\right))f_i^k+\frac{1}{2}(f_{i+1}^k+f_i^k)\}\hfill \\ \hfill & =2^{2k+1}(\frac{1}{2}-2h\left(v^{k+1}\right))(f_{i-1}^k-2f_i^k+f_{i+1}^k)\hfill \\ \hfill & =4(\frac{1}{2}-2h\left(v^{k+1}\right))d_i^k.\hfill \end{array}$$

(9)

Similarly, we have

$$\begin{array}{cc}\hfill d_{2i+1}^{k+1}& =2^{2k+1}(f_{2i}^{k+1}-2f_{2i+1}^{k+1}+f_{2i+2}^{k+1})\hfill \\ \hfill & =2^{2k+1}\left\{h\left(v^{k+1}\right)(f_{i-1}^k+f_{i+1}^k)\right)+(1-2h\left(v^{k+1}\right))f_i^k-f_i^k-f_{i+1}^k\hfill \\ \hfill & +h\left(v^{k+1}\right)(f_i^k+f_{i+2}^k)+(1-2h\left(v^{k+1}\right))f_{i+1}^k\}\hfill \\ \hfill & =2^{2k+1}h\left(v^{k+1}\right)((f_{i-1}^k-2f_i^k+f_{i+1}^k)+(f_i^k-2f_{i+1}^k+f_{i+2}^k))\hfill \\ \hfill & =4h\left(v^{k+1}\right)(d_i^k+d_{i+1}^k).\hfill \end{array}$$

(10)

Therefore, since $d_i^0>0$ and $h\left(v^k\right)>0$, by induction, it follows that $d_i^k>0$.

Now we show $R^k<\lambda$ by showing $r_i^k,\frac{1}{r_i^k}<\lambda$. In fact, when $k=0$, $R^0<\lambda$ is valid. Now we show if $r_i^k,\frac{1}{r_i^k}<\lambda$, then $r_i^{k+1},\frac{1}{r_i^{k+1}}<\lambda$. In fact, from (9) and (10), we have

$$\begin{array}{cc}\hfill r_{2i}^{k+1}& =\frac{d_{2i+1}^{k+1}}{d_{2i}^{k+1}}=\frac{4h\left(v^{k+1}\right)(d_i^k+d_{i+1}^k)}{4(\frac{1}{2}-2h\left(v^{k+1}\right))d_i^k}=\frac{h\left(v^{k+1}\right)}{\frac{1}{2}-2h\left(v^{k+1}\right)}(1+\frac{d_{i+1}^k}{d_i^k})\hfill \\ \hfill & =\frac{h\left(v^{k+1}\right)}{\frac{1}{2}-2h\left(v^{k+1}\right)}(1+r_i^k),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill r_{2i+1}^{k+1}& =\frac{d_{2i+2}^{k+1}}{d_{2i+1}^{k+1}}=\frac{4(\frac{1}{2}-2h\left(v^{k+1}\right))d_{i+1}^k}{4h\left(v^{k+1}\right)(d_i^k+d_{i+1}^k)}=\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}\frac{1}{1+\frac{d_i^k}{d_{i+1}^k}}\hfill \\ \hfill & =\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}\frac{r_i^k}{1+r_i^k}.\hfill \end{array}$$

Therefore, it follows that

$$\frac{r_{2i}^{k+1}}{\lambda }=\frac{h\left(v^{k+1}\right)}{\frac{1}{2}-2h\left(v^{k+1}\right)}\frac{1+r_i^k}{\lambda }<\frac{h\left(v^{k+1}\right)}{\frac{1}{2}-2h\left(v^{k+1}\right)}\frac{1+\lambda }{\lambda },$$

(11)

and

$$\frac{r_{2i+1}^{k+1}}{\lambda }=\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}\frac{r_i^k}{\lambda (1+r_i^k)}<\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}\frac{1}{\lambda (1+\frac{1}{\lambda })}=\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}\frac{1}{1+\lambda }.$$

(12)

Let ${\mu }^k=\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}=\frac{1}{2h\left(v^{k+1}\right)}-2$. Then if

$$\frac{1}{\lambda }<{\mu }^k-1<\lambda ,$$

(13)

from (11) and (12), we have

$$\frac{r_{2i}^{k+1}}{\lambda }<1,\frac{r_{2i+1}^{k+1}}{\lambda }<1.$$

Note that $r_i^k,\frac{1}{r_i^k}<\lambda$ also implies $\frac{1}{\lambda }<r_i^k$. Then, similar to (11) and (12), if (13) is valid, we have

$$\begin{array}{cc}\hfill \frac{\frac{1}{r_{2i}^{k+1}}}{\lambda }& =\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}\frac{1}{\lambda (1+r_i^k)}<\frac{\frac{1}{2}-2h\left(v^{k+1}\right)}{h\left(v^{k+1}\right)}\frac{1}{1+\lambda }<1,\hfill \\ \hfill \frac{\frac{1}{r_{2i+1}^{k+1}}}{\lambda }& =\frac{h\left(v^{k+1}\right)}{\frac{1}{2}-2h\left(v^{k+1}\right)}\frac{1+\frac{1}{r_i^k}}{\lambda }<\frac{h\left(v^{k+1}\right)}{\frac{1}{2}-2h\left(v^{k+1}\right)}(1+\frac{1}{\lambda })<1.\hfill \end{array}$$

Therefore, for $\lambda >1$, if $\frac{1}{\lambda }<{\mu }^k-1=\frac{1}{2h\left(v^{k+1}\right)}-3<\lambda$, since $R^0<\lambda$, the variant scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ preserves convexity. □

Figure 5 shows the curves generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with $v^0=-0.35$ and $\beta =1.2,0.8,0.1,0$. From Figure 5, it can be seen that, although the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ can generate curves with different shapes, with certain choice of $v^0$ and $\beta$ (see Figure 5 with $v^0=-0.35$ and $\beta =2$ ), the curve generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ may not be convex. However, Theorem 4 implies that we can rechoose $\beta$ to guarantee that the limit curve is convex. This can be seen in Figure 5 with $v^0=-0.35$ and $\beta =1.2,0.8,0.1,0$.

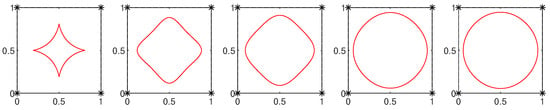
Figure 5. Curves generated by the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with $v^0=-0.35$ and $\beta =2,1.2,0.8,0.1,0$ (from left to right).

5. Discussion on the Local Control

Now we move a further step and give a non-uniform version of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ to locally control the shape of the limit curves.

In fact, there have been works [5,21,22] on the local control, which assigned a parameter to each edge of the initial control polygon. Different from these schemes, the work in [9] assigned a parameter to each initial control point, which can also locally control the limit curves.

Here, following [9], we also assign each initial control point a parameter ${\beta }_i$ and then we can derive a non-uniform version of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$. Following the work in [9], we can also show the $C^2$-convergence of this non-uniform scheme.

Figure 6 shows the curves generated by the non-uniform version of the variant scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with $v^0=-0.8$ and different choices of ${\beta }_i$ assigned to the i-th point. From Figure 6, it can be seen that by suitably adjusting the parameters assigned to the initial control points, we can indeed locally control the shape of the limit curve.

Figure 6. Curves generated by the non-uniform version of the scheme ${\left\{S_{{\mathit{a}}^k}\right\}}_{k\ge 0}$ with $v^0=-0.8$ and $({\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4)=(0,0,0,0),(0.6,0,0,0),(0,0.6,0,0),(0,0,0.6,0),(0,0,0,0.6),(0.6,0.6,0.6,0.6)$ (from left to right).

We point out that, similar to the above non-uniform scheme, we can also assign a parameter $v_i^0$ to each initial control point to derive another non-uniform scheme in order to locally control the shape of the limit curves.

6. Conclusions

This paper presented a variant cubic exponential B-spline scheme, which can generate curves with different shapes, including the conics. Such a scheme is obtained based on the iteration from the generation of exponential polynomials and a suitable function. For such a scheme, we verified its $C^2$-convergence and gave the limit position of the initial control points to show the effect of the parameters on the shape of the limit curves. Apart from these properties, we also discussed the convexity preservation of this variant scheme and showed how to preserve the convexity of the initial control polygon by adjusting the parameters. In addition, a non-uniform generalization of this variant scheme is also given, which can locally control the shape of the limit curves.