The Generalized DUS Transformed Log-Normal Distribution and Its Applications to Cancer and Heart Transplant Datasets
Abstract
:1. Introduction
2. Construction of the New Distribution
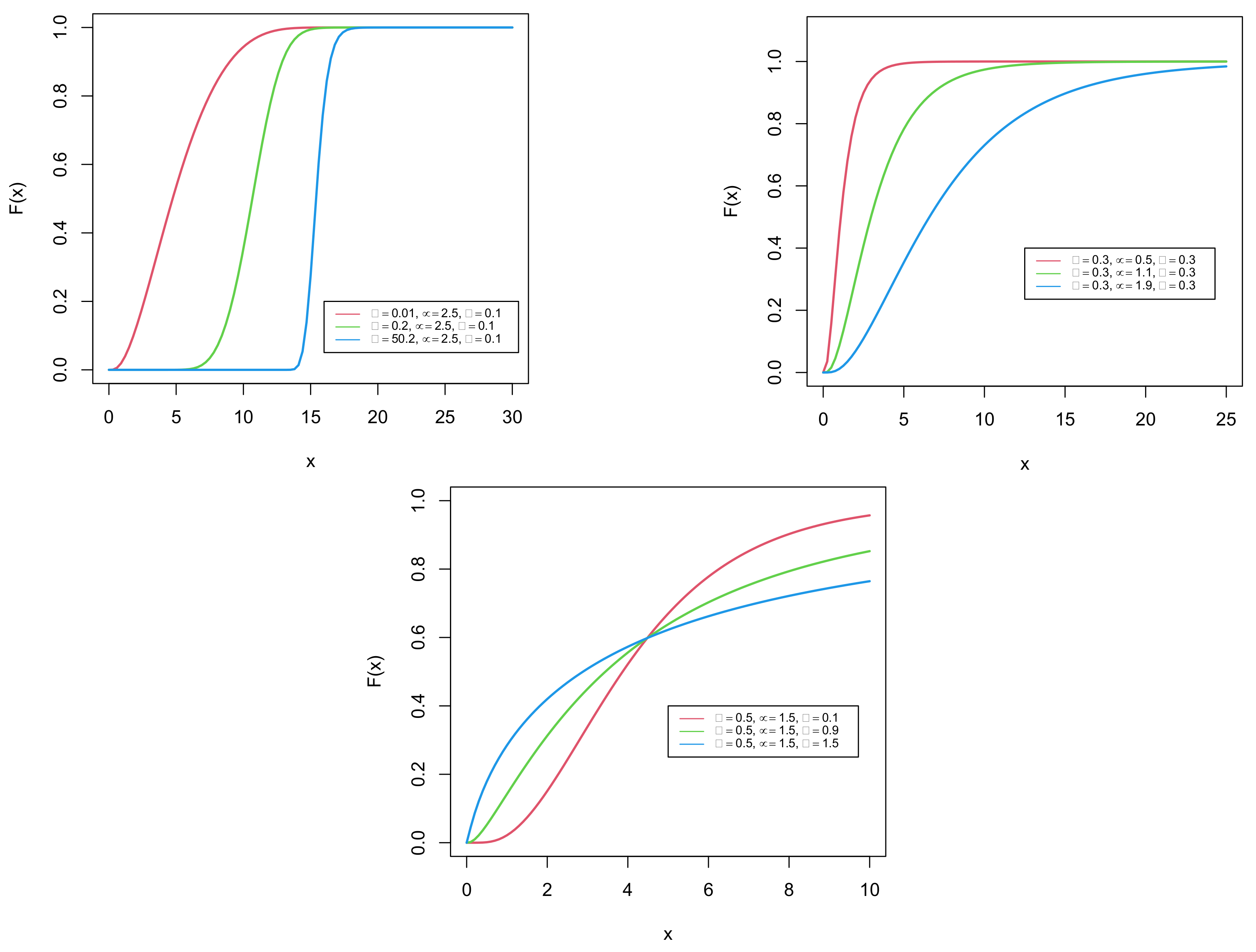
3. Definition of the Distribution
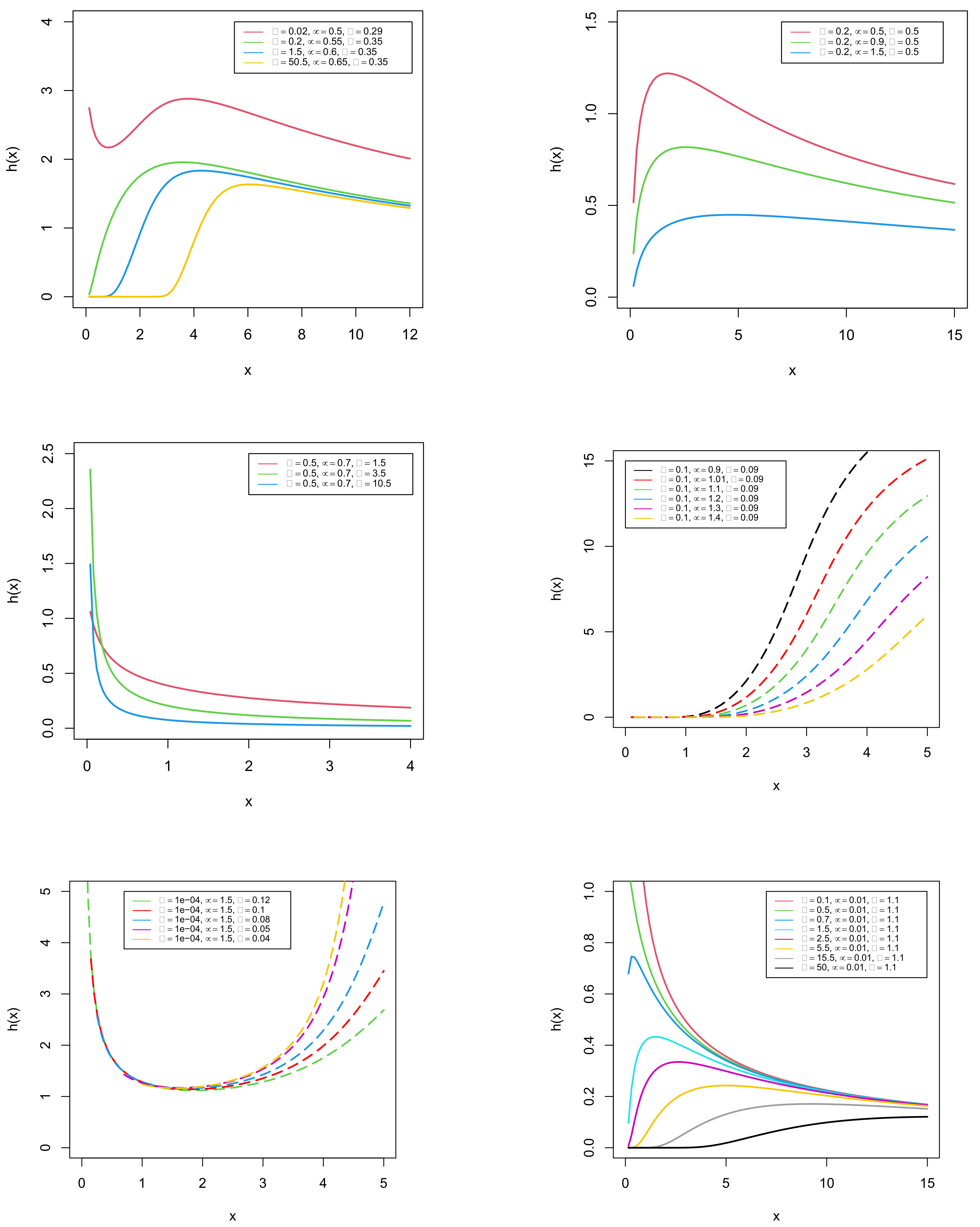
Hazard Rate Function
4. Quantile Function and Associated Measures
5. Estimation of Parameters
5.1. ML Estimation
5.2. Bayesian Estimation
6. Bootstrap Confidence Intervals
7. GDUSLN Regression Model
8. Bayesian Regression Model
9. Performance of the Estimates Using Simulation Study
9.1. Simulation Study for the MLE
- Average bias = , and
- Average MSE = ,
9.2. Simulation Study for Bayesian Estimates
10. Applications and Empirical Study
10.1. Cancer Survival Data
- A plot around the diagonal indicates a constant hazard rate, that is, the failure times can be considered exponentially distributed.
- A concave plot (above the diagonal) indicates an increasing hazard rate function.
- A convex plot (under the diagonal) indicates a decreasing hazard rate function.
- A plot which first is convex, and then concave indicates a bathtub shaped hazard rate function.
- A plot which first is concave, and then convex indicates an upside-down bathtub shaped hazard rate function.
- The two-parameter LN distribution.
- The exponentiated LN (ELN) distribution or otherwise, the log-power-normal distribution (see [17]) with pdf
- Generalized half-normal (GHN) distribution (see [18]) with pdf
- The new generalized Lindley distribution (NGLD) (see [19]) with pdfwhere .
- The modified Weibull (MoW) distribution (see [20]) with pdf
- The Weibull distribution with pdf
10.1.1. Results on Bootstrap Confidence Intervals
10.1.2. Likelihood Ratio Test
10.2. Stanford Heart Transplant Data
10.2.1. Results Using the GDUSLN Regression Model
10.2.2. Results Using the GDUSLN Bayesian Regression
11. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sinnott, E.W. The Relation of Gene to Character in Quantitative Inheritance. Proc. Natl. Acad. Sci. USA 1937, 23, 224–227. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kermack, K.A.; Haldane, J.B.S. Organic correlation and allometry. Biometrika 1950, 37, 30–41. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, L.; Weatherall, M. Statistics for Medical and Other Biological Students. Q. Rev. Biol. 1954, 29, 303. [Google Scholar]
- Beal, J. Biochemical complexity drives log-normal variation in genetic expression. Eng. Biol. 2017, 1, 55–60. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, J.; Piaggio, G.; Wojdyla, D.; Widmer, M.; Gülmezoglu, A. Distribution of postpartum blood loss: Modeling, estimation and application to clinical trials. Reprod. Health 2018, 15, 199. [Google Scholar] [CrossRef] [PubMed]
- Aitchison, J.; Brown, J.A.C. The Lognormal Distribution with Special Reference to Its Uses in Economics; Cambridge University Press: Cambridge, UK, 1957. [Google Scholar]
- Jobe, J.; Crow, E.; Shimizu, K. Lognormal Distributions: Theory and Applications. Technometrics 1989, 31, 392. [Google Scholar] [CrossRef]
- Pham, A.; Lai, C.D. On Recent Generalizations of the Weibull Distribution. Reliab. IEEE Trans. 2007, 56, 454–458. [Google Scholar] [CrossRef]
- Dinesh, K.; Umesh, S.; Sanjay Kumar, S. A Method of Proposing New Distribution and its Application to Bladder Cancer Patients Data. J. Stat. Appl. Probab. Lett. 2015, 3, 235–245. [Google Scholar]
- Maurya, S.K.; Kaushik, A.; Singh, S.K.; Singh, U. A new class of distribution having decreasing, increasing, and bathtub-shaped failure rate. Commun. Stat. Theory Methods 2017, 46, 10359–10372. [Google Scholar] [CrossRef]
- Irshad, M.R.; Maya, R.; Krishna, A. Exponentiated Power Muth Distribution and Associated Inference. J. Indian Soc. Probab. Stat. 2021, 1–38. [Google Scholar] [CrossRef]
- MacDonald, I.L. Does Newton-Raphson really fail? Stat. Methods Med. Res. 2014, 23, 308–311. [Google Scholar] [CrossRef] [PubMed]
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Analytical Methods for Social Research; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Wasserman, L. All of Nonparametric Statistics; Springer Texts in Statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Lee, E.; Wang, J. Statistical Methods for Survival Data Analysis; Wiley Series in Probability and Statistics; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Aarset, M.V. How to Identify a Bathtub Hazard Rate. IEEE Trans. Reliab. 1987, R-36, 106–108. [Google Scholar] [CrossRef]
- Martínez-Flórez, G.; Bolfarine, H.; Gómez, H.W. The log-power-normal distribution with application to air pollution. Environmetrics 2014, 25, 44–56. [Google Scholar] [CrossRef]
- Cooray, K.; Ananda, M.M.A. A Generalization of the Half-Normal Distribution with Applications to Lifetime Data. Commun. Stat. Theory Methods 2008, 37, 1323–1337. [Google Scholar] [CrossRef]
- Elbatal, I.; Merovci, F.; Elgarhy, M. A new generalized Lindley distribution. Math. Theory Model. 2013, 3, 30–47. [Google Scholar]
- Xie, M.; Tang, Y.; Goh, T. A modified Weibull extension with bathtub-shaped failure rate function. Reliab. Eng. Syst. Saf. 2002, 76, 279–285. [Google Scholar] [CrossRef]
- Crowley, J.; Hu, M. Covariance Analysis of Heart Transplant Survival Data. J. Am. Stat. Assoc. 1977, 72, 27–36. [Google Scholar] [CrossRef]



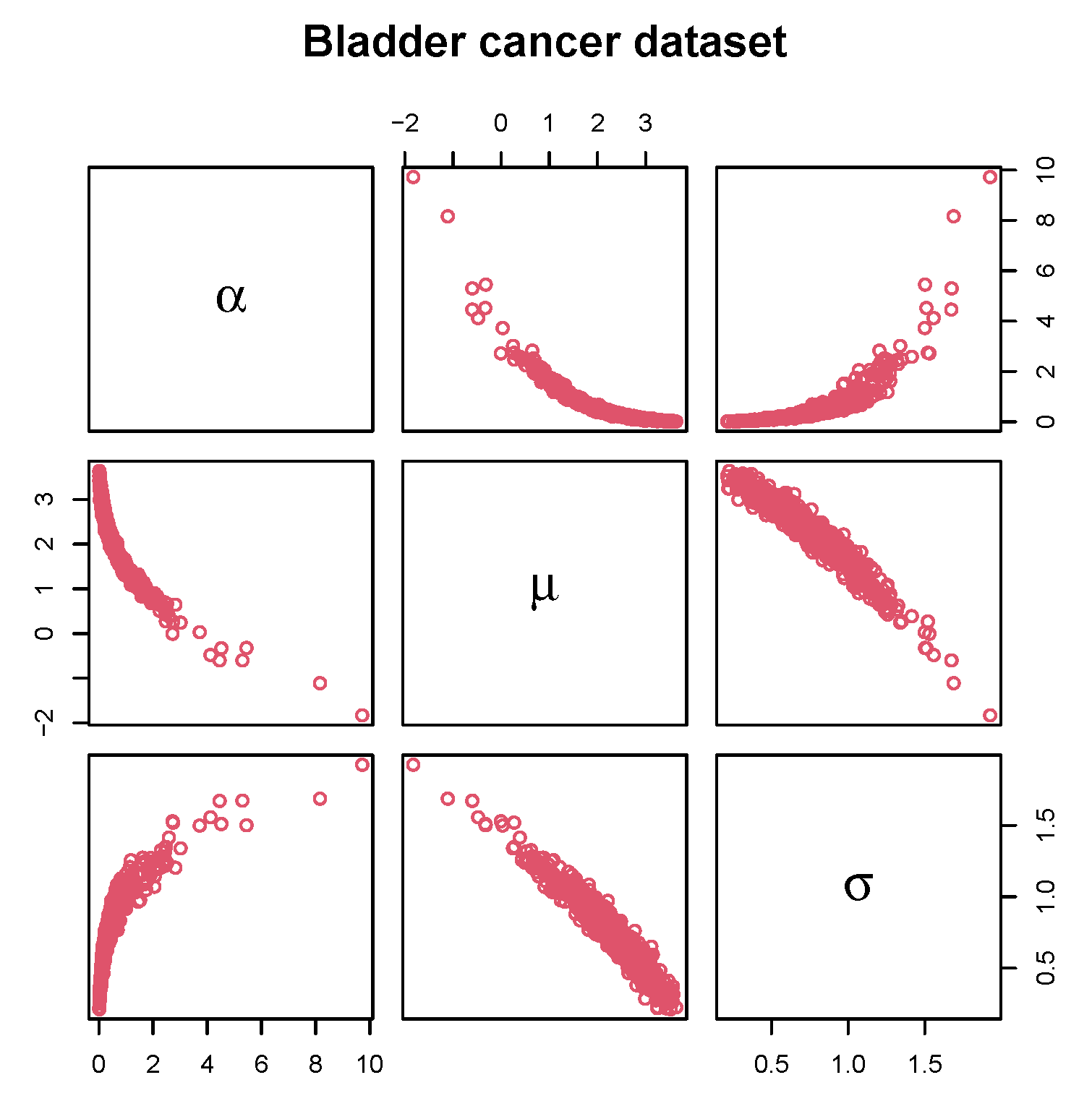
| Parameters | n | MLE | Bias | MSE | CP | AL |
|---|---|---|---|---|---|---|
| 50 | 0.0265 | 0.0165 | 0.0117 | 0.9860 | 0.1884 | |
| 100 | 0.0171 | 0.0071 | 0.0029 | 0.9900 | 0.0703 | |
| 250 | 0.0128 | 0.0028 | 0.000062 | 0.9980 | 0.0285 | |
| 500 | 0.0118 | 0.0018 | 0.000025 | 0.9999 | 0.0170 | |
| 750 | 0.0118 | 0.0018 | 0.000011 | 0.9999 | 0.0138 | |
| 1000 | 0.0117 | 0.0017 | 0.9999 | 0.0118 | ||
| 50 | −0.2877 | −0.2877 | 2.0349 | 0.9999 | 6.5780 | |
| 100 | −0.1107 | −0.1107 | 0.8001 | 0.9990 | 3.9497 | |
| 250 | −0.0636 | −0.0636 | 0.1924 | 0.9980 | 2.2907 | |
| 500 | −0.0306 | −0.0306 | 0.0821 | 0.9910 | 1.5273 | |
| 750 | −0.0809 | −0.0809 | 0.0398 | 0.9880 | 1.2473 | |
| 1000 | −0.0774 | −0.0774 | 0.0310 | 0.9860 | 1.0726 | |
| 50 | 1.2084 | 0.2084 | 0.4160 | 0.9880 | 3.0793 | |
| 100 | 1.1361 | 0.1361 | 0.1808 | 0.9910 | 1.8328 | |
| 250 | 1.0964 | 0.0964 | 0.0519 | 0.9950 | 1.0693 | |
| 500 | 1.0685 | 0.0685 | 0.0238 | 0.9970 | 0.7011 | |
| 750 | 1.0737 | 0.0737 | 0.0160 | 0.9950 | 0.5817 | |
| 1000 | 1.0699 | 0.0699 | 0.0131 | 0.9950 | 0.4989 |
| Parameters | n | MLE | Bias | MSE | CP | AL |
|---|---|---|---|---|---|---|
| 50 | 3.4450 | 1.9450 | 17.9693 | 0.8212 | 29.7384 | |
| 100 | 2.8944 | 1.3944 | 11.9153 | 0.8352 | 17.3465 | |
| 250 | 2.3789 | 0.8789 | 7.2803 | 0.8851 | 9.2240 | |
| 500 | 1.8799 | 0.3799 | 2.2217 | 0.8981 | 4.5803 | |
| 750 | 1.7522 | 0.2522 | 0.7747 | 0.9341 | 3.3028 | |
| 1000 | 1.6936 | 0.1936 | 0.5628 | 0.9281 | 2.7298 | |
| 50 | −0.1516 | −0.1516 | 1.5050 | 0.9211 | 6.7687 | |
| 100 | −0.1322 | −0.1322 | 1.0738 | 0.9221 | 4.7298 | |
| 250 | −0.1360 | −0.1360 | 0.6004 | 0.9471 | 3.0166 | |
| 500 | −0.0557 | −0.0557 | 0.3029 | 0.9461 | 2.0178 | |
| 750 | −0.0638 | −0.0638 | 0.1646 | 0.9610 | 1.6335 | |
| 1000 | −0.0495 | −0.0495 | 0.1298 | 0.9491 | 1.4036 | |
| 50 | 0.9850 | −0.0151 | 0.1354 | 0.9351 | 1.9180 | |
| 100 | 0.9993 | −0.00076 | 0.0946 | 0.9261 | 1.3519 | |
| 250 | 1.0217 | 0.0217 | 0.0486 | 0.9590 | 0.8666 | |
| 500 | 1.0080 | 0.0080 | 0.0253 | 0.9421 | 0.5928 | |
| 750 | 1.0136 | 0.0136 | 0.0139 | 0.9640 | 0.4816 | |
| 1000 | 1.0110 | 0.0110 | 0.0112 | 0.9511 | 0.4152 |
| Parameters | n | MLE | Bias | MSE | CP | AL |
|---|---|---|---|---|---|---|
| 50 | 3.3691 | −0.1309 | 7.3639 | 0.7602 | 26.7792 | |
| 100 | 3.7652 | 0.2652 | 6.7212 | 0.8092 | 20.8407 | |
| 250 | 4.0625 | 0.5625 | 5.5040 | 0.8681 | 14.4071 | |
| 500 | 3.9641 | 0.4641 | 4.1423 | 0.8931 | 10.1917 | |
| 750 | 4.0522 | 0.5523 | 3.3380 | 0.9271 | 8.6438 | |
| 1000 | 3.8094 | 0.3094 | 2.5673 | 0.9261 | 6.9700 | |
| 50 | 0.3772 | 0.3772 | 0.9082 | 0.8841 | 5.7295 | |
| 100 | 0.1891 | 0.1891 | 0.5807 | 0.9081 | 4.2434 | |
| 250 | 0.0229 | 0.0229 | 0.3165 | 0.9431 | 2.8635 | |
| 500 | −0.00075 | −0.00075 | 0.2164 | 0.9461 | 2.0896 | |
| 750 | −0.0493 | −0.0493 | 0.1510 | 0.9650 | 1.7545 | |
| 1000 | −0.0105 | −0.0105 | 0.1240 | 0.9610 | 1.5016 | |
| 50 | 0.8607 | −0.1393 | 0.0962 | 0.9051 | 1.5967 | |
| 100 | 0.9266 | −0.0734 | 0.0551 | 0.9211 | 1.1520 | |
| 250 | 0.9831 | −0.0169 | 0.0250 | 0.9560 | 0.7596 | |
| 500 | 0.9943 | −0.0057 | 0.0160 | 0.9541 | 0.5523 | |
| 750 | 1.0085 | 0.0085 | 0.0106 | 0.9750 | 0.4605 | |
| 1000 | 0.9992 | −0.00078 | 0.0089 | 0.9630 | 0.3970 |
| Parameters | n | MLE | Bias | MSE | CP | AL |
|---|---|---|---|---|---|---|
| 50 | 0.8120 | 0.8020 | 99.3306 | 0.9990 | 17.2775 | |
| 100 | 0.0597 | 0.0497 | 0.0180 | 0.9960 | 0.3258 | |
| 250 | 0.0278 | 0.01780 | 0.0009 | 0.9950 | 0.0855 | |
| 500 | 0.0120 | 0.010 | 0.00023 | 0.9970 | 0.0393 | |
| 750 | 0.0172 | 0.0072 | 0.00012 | 0.9990 | 0.0260 | |
| 1000 | 0.0160 | 0.0060 | 0.9970 | 0.0201 | ||
| 50 | −0.5673 | −2.0673 | 10.6468 | 0.9950 | 9.7789 | |
| 100 | 0.6150 | −0.8850 | 1.6948 | 0.9920 | 4.0846 | |
| 250 | 1.0235 | −0.4765 | 0.4590 | 0.9690 | 1.9015 | |
| 500 | 1.1998 | −0.3002 | 0.1834 | 0.9421 | 1.1122 | |
| 750 | 1.2758 | −0.2242 | 0.1068 | 0.9091 | 0.8285 | |
| 1000 | 1.3111 | −0.1889 | 0.0784 | 0.8711 | 0.6806 | |
| 50 | 1.3170 | 0.8170 | 1.3831 | 0.9980 | 3.7459 | |
| 100 | 0.9005 | 0.4005 | 0.3222 | 0.9880 | 1.8729 | |
| 250 | 0.7345 | 0.2344 | 0.1043 | 0.9860 | 0.9233 | |
| 500 | 0.6570 | 0.1570 | 0.0474 | 0.9600 | 0.5459 | |
| 750 | 0.6234 | 0.1234 | 0.0293 | 0.9481 | 0.4065 | |
| 1000 | 0.6059 | 0.1059 | 0.0219 | 0.9031 | 0.3325 |
| Parameters | n | Mean | SD | MCE | 95% CI | Median |
|---|---|---|---|---|---|---|
| 50 | 0.1442 | 0.1824 | 0.0519 | (0.0042, 0.6596) | 0.0570 | |
| 100 | 0.0334 | 0.1207 | 0.0132 | (0.0063, 0.0611) | 0.0167 | |
| 250 | 0.0220 | 0.0212 | 0.0081 | (0.0141, 0.0898) | 0.0150 | |
| 500 | 0.0185 | 0.0076 | 0.0024 | (0.0118, 0.0466) | 0.0172 | |
| 750 | 0.0231 | 0.0052 | 0.0011 | (0.0208, 0.0262) | 0.0208 | |
| 1000 | 0.0149 | 0.0009 | 0.00058 | (0.0135, 0.0156) | 0.0154 | |
| 50 | −3.4733 | 3.0723 | 0.8754 | (−9.6826, 0.8414) | −2.7271 | |
| 100 | −0.3452 | 1.2663 | 0.5454 | (−2.4443, 1.5253) | −0.1428 | |
| 250 | −0.4035 | 0.5696 | 0.2240 | (−2.3547, −0.0708) | −0.1831 | |
| 500 | −0.5347 | 0.4115 | 0.1992 | (−0.8684, 0.8708) | −0.6868 | |
| 750 | −0.7501 | 0.4026 | 0.1564 | (−1.2204, 0.1082) | −0.6910 | |
| 1000 | −0.7085 | 0.3481 | 0.1240 | (−0.8361, 0.6058) | −0.8361 | |
| 50 | 2.3915 | 1.2560 | 0.3398 | (0.6745, 5.0700) | 2.1073 | |
| 100 | 1.3575 | 0.8723 | 0.2097 | (0.7271, 2.4231) | 1.1131 | |
| 250 | 1.3106 | 0.5267 | 0.1905 | (1.1652, 2.6330) | 1.1652 | |
| 500 | 1.2938 | 0.2787 | 0.0835 | (1.0247, 2.0993) | 1.2751 | |
| 750 | 1.4881 | 0.2525 | 0.0783 | (1.4131, 1.7219) | 1.4131 | |
| 1000 | 1.1867 | 0.0506 | 0.03160 | (1.1108, 1.2723) | 1.2102 |
| Parameters | n | Mean | SD | MCE | 95% CI | Median |
|---|---|---|---|---|---|---|
| 50 | 4.1662 | 7.3244 | 2.0432 | (0.0093, 20.6094) | 0.9974 | |
| 100 | 4.2131 | 5.2494 | 1.5542 | (0.0717, 22.7491) | 2.2271 | |
| 250 | 2.2417 | 2.1410 | 0.6711 | (0.0846, 9.0499) | 1.6914 | |
| 500 | 1.5378 | 1.6005 | 0.2416 | (0.4581, 4.3854) | 1.3377 | |
| 750 | 1.6211 | 0.4696 | 0.1316 | (0.7095, 2.7769) | 1.5799 | |
| 1000 | 1.4906 | 0.2316 | 0.0615 | (1.4512, 2.0980) | 1.4514 | |
| 50 | 0.0369 | 1.2995 | 0.3834 | (−2.5848, 2.0525) | 0.3404 | |
| 100 | −0.4092 | 1.0441 | 0.3193 | (−2.6677, 1.8552) | −0.1807 | |
| 250 | 0.1550 | 0.7931 | 0.2581 | (−1.3816, 1.7138) | 0.0570 | |
| 500 | 0.1253 | 0.4695 | 0.0839 | (−1.0430, 0.9718) | 0.1231 | |
| 750 | −0.1065 | 0.2889 | 0.0811 | (−0.7150, 0.5232) | −0.0650 | |
| 1000 | −0.0170 | 0.1420 | 0.0331 | (−0.4267, 0.0236) | 0.0226 | |
| 50 | 0.8448 | 0.3702 | 0.1073 | (0.1403, 1.5976) | 0.8392 | |
| 100 | 1.0815 | 0.2833 | 0.0866 | (0.3392, 1.5447) | 1.0771 | |
| 250 | 0.8506 | 0.2329 | 0.0747 | (0.3265, 1.2604) | 0.8995 | |
| 500 | 0.9565 | 0.1442 | 0.0291 | (0.6713, 1.2297) | 0.9641 | |
| 750 | 1.0589 | 0.0986 | 0.0277 | (0.8357, 1.2506) | 1.0656 | |
| 1000 | 1.0097 | 0.0521 | 0.0142 | (0.9907, 1.1366) | 0.9907 |
| Parameters | n | Mean | SD | MCE | 95% CI | Median |
|---|---|---|---|---|---|---|
| 50 | 8.4499 | 7.6768 | 2.1079 | (0.1380, 24.5375) | 6.2095 | |
| 100 | 5.3500 | 9.4171 | 1.7008 | (0.3285, 13.5378) | 3.2753 | |
| 250 | 2.3796 | 2.7053 | 0.8287 | (0.3081, 10.1427) | 1.3011 | |
| 500 | 2.8784 | 2.2901 | 0.8092 | (1.0101, 10.4748) | 1.9153 | |
| 750 | 4.4209 | 2.0585 | 0.6653 | (2.6587, 6.5986) | 4.0738 | |
| 1000 | 2.8436 | 1.4592 | 0.3074 | (1.6108, 6.7540) | 2.8355 | |
| 50 | 0.2228 | 0.9573 | 0.2940 | (−1.0484, 2.0049) | −0.0019 | |
| 100 | 0.0332 | 0.7769 | 0.2336 | (−1.3759, 1.4283) | 0.0934 | |
| 250 | 0.5618 | 0.6370 | 0.1979 | (−0.7925, 1.4505) | 0.6533 | |
| 500 | 0.2950 | 0.4991 | 0.1552 | (−0.8614, 0.9619) | 0.4101 | |
| 750 | −0.1969 | 0.4249 | 0.1302 | (−0.7398, 0.2054) | −0.1912 | |
| 1000 | 0.2197 | 0.3472 | 0.1082 | (−0.6779, 0.5688) | 0.1770 | |
| 50 | 0.8080 | 0.2633 | 0.0797 | (0.2915, 1.1814) | 0.9090 | |
| 100 | 0.8718 | 0.2162 | 0.0649 | (0.4689, 1.1968) | 0.8866 | |
| 250 | 0.7443 | 0.1800 | 0.0582 | (0.4790, 1.0736) | 0.7109 | |
| 500 | 0.9343 | 0.1354 | 0.0390 | (0.7414, 1.2237) | 0.9326 | |
| 750 | 1.0692 | 0.1295 | 0.0371 | (0.9619, 1.2253) | 1.0566 | |
| 1000 | 0.9466 | 0.1004 | 0.0306 | (0.8628, 1.2225) | 0.9323 |
| Parameters | n | Mean | SD | MCE | 95% CI | Median |
|---|---|---|---|---|---|---|
| 50 | 0.1779 | 0.2908 | 0.0794 | (0.0041, 1.3728) | 0.0583 | |
| 100 | 0.0734 | 0.0987 | 0.0260 | (0.0060, 0.3889) | 0.0330 | |
| 250 | 0.0300 | 0.0488 | 0.0124 | (0.0075, 0.1611) | 0.0160 | |
| 500 | 0.0160 | 0.0364 | 0.0062 | (0.0110, 0.0843) | 0.0110 | |
| 750 | 0.0159 | 0.0090 | 0.0021 | (0.0061, 0.0240) | 0.0147 | |
| 1000 | 0.0092 | 0.0069 | 0.0012 | (0.0068, 0.0202) | 0.0076 | |
| 50 | −0.1424 | 1.4196 | 0.3924 | (−4.0866, 1.5825) | 0.3360 | |
| 100 | 0.6450 | 0.9748 | 0.2626 | (−1.6869, 1.8166) | 0.9622 | |
| 250 | 0.9545 | 0.6301 | 0.1960 | (−0.9009, 1.4706) | 1.1956 | |
| 500 | 1.1691 | 0.3183 | 0.0822 | (−0.1112, 1.2343) | 1.2343 | |
| 750 | 1.3269 | 0.2115 | 0.0573 | (1.0271, 1.7025) | 1.3379 | |
| 1000 | 1.6181 | 0.1493 | 0.0226 | (1.2482, 1.7385) | 1.6251 | |
| 50 | 0.9612 | 0.5966 | 0.1678 | (0.2695, 2.6994) | 0.8186 | |
| 100 | 0.9495 | 0.5012 | 0.1325 | (0.3651, 2.0675) | 0.8613 | |
| 250 | 0.6918 | 0.3148 | 0.0984 | (0.4297, 1.5184) | 0.6134 | |
| 500 | 0.5719 | 0.1891 | 0.0508 | (0.5299, 1.4506) | 0.5300 | |
| 750 | 0.5760 | 0.1087 | 0.0281 | (0.3929, 0.7253) | 0.5727 | |
| 1000 | 0.4504 | 0.1012 | 0.0194 | (0.4045, 0.7358) | 0.4185 |
| Statistic | n | IQR | |||||
|---|---|---|---|---|---|---|---|
| Values | 128 | 0.08 | 3.348 | 6.280 | 11.678 | 79.05 | 8.330 |
| Distribution | MLE |
|---|---|
| GDUSLN() | = 0.2330, = 2.5675, = 0.6660 |
| LN() ine ELN() | = 1.7423, = 1.0647 = 0.1514, = 3.0502, = 0.5401 |
| GHN() | = 0.7593, = 11.4510 |
| NGLD() | = 1.1848, = 0.1287, = 1.1851 |
| MoW() | = , = 0.1378, = 123.976 |
| Weibull() | = 1.0546, = 9.4371 |
| Distribution | AIC | BIC | KS | |||
|---|---|---|---|---|---|---|
| GDUSLN | 409.0979 | 824.1958 | 832.7519 | 0.0551 | 0.0646 | 0.4318 |
| LN | 412.6565 | 829.3131 | 835.0171 | 0.0644 | 0.1313 | 0.8708 |
| ELN | 410.0441 | 826.0883 | 834.6444 | 0.0562 | 0.0846 | 0.5590 |
| GHN | 418.7864 | 841.5727 | 847.2768 | 0.1018 | 0.3815 | 2.4201 |
| NGLD | 411.0846 | 828.1691 | 836.7252 | 0.0751 | 0.1415 | 0.8233 |
| MoW | 419.3804 | 844.7608 | 853.3169 | 0.0949 | 0.3632 | 2.3184 |
| Weibull | 411.8936 | 827.7873 | 833.4913 | 0.0731 | 0.1670 | 1.0441 |
| Parameter | Lower | Upper |
|---|---|---|
| −0.1241 | 0.5901 | |
| 1.6222 | 3.5128 | |
| 0.2978 | 1.0341 |
| Parameter | ML | Bayes |
|---|---|---|
| 0.2330 | 0.2058 | |
| 2.5675 | 2.6519 | |
| 0.6660 | 0.6395 |
| Parameter | Median | Bootstrap CI | |
|---|---|---|---|
| Bladder cancer dataset | 0.2599 | (0.0336, 2.2893) | |
| 2.4878 | (0.6703, 3.3436) | ||
| 0.6813 | (0.3100, 1.2527) |
| LR | p-Value | |
|---|---|---|
| GDUSLN versus LN | 7.1173 | 0.00763 |
| Parameter | AIC | |||||||
|---|---|---|---|---|---|---|---|---|
| LN | 8.058 | −0.024 | −0.022 | 1.131 | - | 1.317 | 487.873 | 985.747 |
| GDUSLN | 10.039 | −0.016 | −0.032 | 0.499 | 0.0104 | 0.207 | 485.526 | 983.051 |
| Parameter | Mean | SD | MCSE | ESS | 95% CI | Median |
|---|---|---|---|---|---|---|
| 12.319 | 0.125 | 0.059 | 6.657 | (11.865, 12.419) | 12.312 | |
| −0.064 | 0.009 | 0.007 | 1.296 | (−0.078, −0.052) | −0.067 | |
| −0.018 | 0.0122 | 0.009 | 1.785 | (−0.037, 0.002) | −0.016 | |
| 0.750 | 0.309 | 0.061 | 32.293 | (0.161, 1.309) | 0.740 | |
| 0.069 | 0.052 | 0.028 | 6.064 | (0.022, 0.258) | 0.055 | |
| 0.460 | 0.133 | 0.076 | 5.967 | (0.308, 0.795) | 0.421 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irshad, M.R.; Chesneau, C.; Nitin, S.L.; Shibu, D.S.; Maya, R. The Generalized DUS Transformed Log-Normal Distribution and Its Applications to Cancer and Heart Transplant Datasets. Mathematics 2021, 9, 3113. https://doi.org/10.3390/math9233113
Irshad MR, Chesneau C, Nitin SL, Shibu DS, Maya R. The Generalized DUS Transformed Log-Normal Distribution and Its Applications to Cancer and Heart Transplant Datasets. Mathematics. 2021; 9(23):3113. https://doi.org/10.3390/math9233113
Chicago/Turabian StyleIrshad, Muhammed Rasheed, Christophe Chesneau, Soman Latha Nitin, Damodaran Santhamani Shibu, and Radhakumari Maya. 2021. "The Generalized DUS Transformed Log-Normal Distribution and Its Applications to Cancer and Heart Transplant Datasets" Mathematics 9, no. 23: 3113. https://doi.org/10.3390/math9233113
APA StyleIrshad, M. R., Chesneau, C., Nitin, S. L., Shibu, D. S., & Maya, R. (2021). The Generalized DUS Transformed Log-Normal Distribution and Its Applications to Cancer and Heart Transplant Datasets. Mathematics, 9(23), 3113. https://doi.org/10.3390/math9233113








