On the Geometrical Properties of the Lightlike Rectifying Curves and the Centrodes

Abstract

This paper mainly focuses on some notions of the lightlike rectifying curves and the centrodes in Minkowski 3-space. Some geometrical characteristics of the three types of lightlike curves are obtained. In addition, we obtain the conditions of the centrodes of the lightlike curves are the lightlike rectifying curves. Meanwhile, a detailed analysis between the N-type lightlike slant helices and the centrodes of lightlike curves is provided in this paper. We give the projections of the lightlike rectifying curves to the timelike planes.

1. Introduction

Despite its long history, curve theory is still one of the most important interesting topics in differential geometry [1,2,3,4,5,6,7,8,9,10,11]. The rectifying curves and the centrodes, which were introduced by B.Y. Chen in [3] and played important roles in mechanics, engineering, joint kinematics, as well as in differential geometry, had been given attention in various applications [3,4,5,8,9,11,12]. Thus far, many mathematicians have researched the characterizations of the non-lightlike rectifying curves in Euclidean space [3,4,5,11] and Lorentz–Minkowski space [9,12,13,14,15,16]. The relationship between a non-lightlike rectifying curve and the centrode of a non-lightlike curve was given in [5,12]. A necessary and sufficient condition for the centrodes in Euclidean 3-space was researched in [5].

Motivated from [6,7,9,17,18,19,20,21,22,23], there are many new geometrical properties of the lightlike curves compared with the spacelike curves and the timelike curves. In physics, the most important property of a lightlike curve is clear from the following fact: a classical relativistic string is a single lightlike curve [19,20]. Penrose indicated that null curves were null geodesics [22]. Hiscock revealed that the null hypersurfaces were a part of horizon [23].

However, until recently, to the best of our knowledge, there has been little information available in the literature concerning the lightlike rectifying curves. In the present paper, we pursue and describe the geometrical characteristics of lightlike rectifying curves in Minkowski 3-space. In addition, we obtain the relationship between centrodes of the lightlike curves and the N-type lightlike slant helices.

We organize the present manuscript as follows: the second section contains the basic notions of Minkowski 3-space and the Frenet frame of a lightlike curve in ${\mathbb{R}}_1^3.$ We focus on geometrical characteristics of the three types of lightlike curves (lightlike rectifying curves, lightlike normal curves, and lightlike osculating curves) in Section 3. The main conclusions (Theorems 1 and 4) describe the geometrical properties of the lightlike rectifying curves. For the remainder of this article, we show the relationship between the N-type lightlike slant helices and the centrodes of the lightlike curves in Section 4. In Section 5, we deal with the projection equations of the lightlike rectifying curves to the timelike planes. Finally, two examples and graphs are used to certify our main conclusions.

2. Preliminaries

Let ${\mathbb{R}}^3=\left\{(x_1,x_2,x_3)\right|x_i\in \mathbb{R}(i=1,2,3)\}$ be a three-dimensional vector space. For any vectors $\mathit{x}=(x_1,x_2,x_3)$ and $\mathit{y}=(y_1,y_2,y_3)$ in ${\mathbb{R}}^3,$ the pseudo scalar product of $\mathit{x}$ and $\mathit{y}$ is defined to be $\langle \mathit{x},\mathit{y}\rangle =-x_1{y}_1+x_2{y}_2+x_3{y}_3$. $({\mathbb{R}}^3,\langle ,\rangle )$ is called Minkowski 3-space and written by ${\mathbb{R}}_1^3.$

A vector $\mathit{x}$ in ${\mathbb{R}}_1^3\backslash \left\{\mathbf{0}\right\}$ is called a spacelike vector, a lightlike vector or a timelike vector if $\langle \mathit{x},\mathit{x}\rangle$ is positive, zero, or negative, respectively. The norm of a vector $\mathit{x}\in {\mathbb{R}}_1^3$ is defined by $\parallel \mathit{x}\parallel =\sqrt{|\langle \mathit{x},\mathit{x}\rangle |}.$ For any two vectors $\mathit{x}$ and $\mathit{y}$ in ${\mathbb{R}}_1^3,$ we call $\mathit{x}$ pseudo-perpendicular to $\mathit{y}$ if $\langle \mathit{x},\mathit{y}\rangle =0.$ The pseudo vector product of vectors $\mathit{x}$ and $\mathit{y}$ is defined by

$$\mathit{x}\wedge \mathit{y}=\left|\begin{array}{ccc}-{\mathit{e}}_1& {\mathit{e}}_2& {\mathit{e}}_3\\ x_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right|,$$

where $\{{\mathit{e}}_1,{\mathit{e}}_2,{\mathit{e}}_3\}$ is the canonical basis of ${\mathbb{R}}_1^3$. One can easily show that $\langle \mathit{a},\mathit{x}\wedge \mathit{y}\rangle =\det (\mathit{a},\mathit{x},\mathit{y})$. For a real number $c,$ we define the hyperplane with pseudo normal vector $\mathit{n}$ by $HP(\mathit{n},c)=\{\mathit{x}\in {\mathbb{R}}_1^3\mid \langle \mathit{x},\mathit{n}\rangle =c\}.$ We call $HP(\mathit{n},c)$ a spacelike hyperplane, a timelike hyperplane or a lightlike hyperplane if $\mathit{n}$ is a timelike, spacelike or lightlike vector, respectively.

Definition 1.

Let $\mathbf{\alpha }:I\to {\mathbb{R}}_1^3$ be a curve with the Frenet frame $\left\{\mathit{t}\right(s),\mathit{n}(s),\mathit{b}(s\left)\right\}$, where $\mathit{t}\left(s\right)$ is the tangent vector, $\mathit{n}\left(s\right)$ is the normal vector, and $\mathit{b}\left(s\right)$ is the binormal vector. $\mathbf{\alpha }\left(s\right)$ is called a lightlike curve, a spacelike curve or a timelike curve if its tangent vector $\mathit{t}\left(s\right)$ is a lightlike vector, spacelike vector, or timelike vector for $s\in I$, respectively.

Definition 2.

Let $\mathbf{\alpha }:I\to {\mathbb{R}}_1^3$ be a curve with the Frenet frame $\left\{\mathit{t}\right(s),\mathit{n}(s),\mathit{b}(s\left)\right\}$. Then, $\mathbf{\alpha }\left(s\right)$ is said to be a rectifying curve if it satisfies $\langle \mathbf{\alpha }\left(s\right),\mathit{n}\left(s\right)\rangle =0,s\in I$; in other words, the position vector $\mathbf{\alpha }\left(s\right)$ always lies in its rectifying plane. As the same method, $\mathbf{\alpha }\left(s\right)$ is said to be a normal curve or an osculating curve if $\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle =0$ or $\langle \mathbf{\alpha }\left(s\right),\mathit{b}\left(s\right)\rangle =0$, respectively.

A lightlike curve $\mathbf{\alpha }:I\to {\mathbb{R}}_1^3$ with the Frenet frame $\left\{\mathit{t}\right(s),\mathit{n}(s),\mathit{b}(s\left)\right\}$, satisfies

$$\langle \mathit{t}\left(s\right),\mathit{t}\left(s\right)\rangle =\langle \mathit{b}\left(s\right),\mathit{b}\left(s\right)\rangle =0,$$

$$\langle \mathit{t}\left(s\right),\mathit{b}\left(s\right)\rangle =1,\langle \mathit{n}\left(s\right),\mathit{n}\left(s\right)\rangle =1,$$

$$\langle \mathit{t}\left(s\right),\mathit{n}\left(s\right)\rangle =\langle \mathit{n}\left(s\right),\mathit{b}\left(s\right)\rangle =0.$$

The Frenet Equations of $\mathbf{\alpha }\left(s\right)$ are given as follows [18]:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathit{t}}^{\prime }\left(s\right)=\mathit{t}\left(s\right)-{\kappa }_1\left(s\right)\mathit{n}\left(s\right)\hfill \\ {\mathit{n}}^{\prime }\left(s\right)={\kappa }_1\left(s\right)\mathit{b}\left(s\right)+{\kappa }_2\left(s\right)\mathit{t}\left(s\right)\hfill \\ {\mathit{b}}^{\prime }\left(s\right)=-\mathit{b}\left(s\right)-{\kappa }_2\left(s\right)\mathit{n}\left(s\right)\hfill \end{array}\right.,\end{array}$$

(1)

where ${\kappa }_1\left(s\right)=\langle \mathit{t}\left(s\right),{\mathit{n}}^{\prime }\left(s\right)\rangle$ and ${\kappa }_2\left(s\right)=\langle \mathit{b}\left(s\right),{\mathit{n}}^{\prime }\left(s\right)\rangle$ are called the curvature function and torsion function of $\mathbf{\alpha }\left(s\right)$, respectively.

3. Three Types of the Lightlike Curves

In this section, we consider some geometrical properties of the three types of lightlike curves (lightlike rectifying curves, lightlike normal curves, and lightlike osculating curves). Meanwhile, a necessary and sufficient condition of the lightlike rectifying curves is given in Theorem 4.

Theorem 1.

Let $\mathbf{\alpha }:I\to {\mathbb{R}}_1^3$ be a lightlike curve with the Frenet frame $\{\mathit{t}\left(s\right),\mathit{n}\left(s\right),\mathit{b}\left(s\right),{\kappa }_1\left(s\right),{\kappa }_2\left(s\right)\}$, ${\kappa }_1\left(s\right)\ne 0$, and the following statements are equivalent:

(1): $\mathbf{\alpha }\left(s\right)$ is a lightlike rectifying curve in ${\mathbb{R}}_1^3$.

(2): The tangential component of the position vector of the curve is given by $\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle =C_1{e}^s$ and $\langle \mathbf{\alpha }\left(s\right),\mathit{b}\left(s\right)\rangle =C_2{e}^{-s}+1$, where $C_1,C_2$ are constants. When ${\kappa }_2>0$, $C_1{C}_2<\frac{{\kappa }_1}{4{\kappa }_2}$; when ${\kappa }_2<0$, $C_1{C}_2>\frac{{\kappa }_1}{4{\kappa }_2}$.

(3): The distance function $\rho =\left|\mathbf{\alpha }\right|$ satisfies ${\rho }^2=C_1+C_2{e}^s$ for constants $C_1,C_2$.

(4): The curvatures satisfy one of the following conditions: ${\kappa }_1\left(s\right)=-{\kappa }_2\left(s\right)$ or ${\kappa }_1\left(s\right){\kappa }_2^{\prime }\left(s\right)-{\kappa }_1^{\prime }\left(s\right){\kappa }_2\left(s\right)={\kappa }_1\left(s\right)({\kappa }_1\left(s\right)-{\kappa }_2\left(s\right))$.

Proof. 

A lightlike rectifying curve $\mathbf{\alpha }\left(s\right)$ can be shown that

$$\mathbf{\alpha }\left(s\right)=\lambda \left(s\right)\mathit{t}\left(s\right)+\mu \left(s\right)\mathit{b}\left(s\right).$$

(2)

Differentiating the above equation

$$\begin{array}{cc}\hfill {\mathbf{\alpha }}^{\prime }\left(s\right)& =\mathit{t}\left(s\right)={\lambda }^{\prime }\left(s\right)\mathit{t}\left(s\right)+\lambda \left(s\right){\mathit{t}}^{\prime }\left(s\right)+{\mu }^{\prime }\left(s\right)\mathit{b}\left(s\right)+\mu \left(s\right){\mathit{b}}^{\prime }\left(s\right)\hfill \\ \hfill & =({\lambda }^{\prime }\left(s\right)+\lambda \left(s\right))\mathit{t}\left(s\right)-({\kappa }_1\left(s\right)\lambda \left(s\right)+{\kappa }_2\left(s\right)\mu \left(s\right))\mathit{n}\left(s\right)+({\mu }^{\prime }\left(s\right)-\mu \left(s\right))\mathit{b}\left(s\right),\hfill \end{array}$$

implies that

$$\left\{\begin{array}{c}{\lambda }^{\prime }\left(s\right)+\lambda \left(s\right)=1\hfill \\ {\kappa }_1\left(s\right)\lambda \left(s\right)+{\kappa }_2\left(s\right)\mu \left(s\right)=0\hfill \\ {\mu }^{\prime }\left(s\right)-\mu \left(s\right)=0\hfill \end{array}\right..$$

(3)

Solving the equations, $\lambda \left(s\right)=C_1{e}^{-s}+1$ and $\mu \left(s\right)=C_2{e}^s$ imply that $\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle =C_1{e}^s$ and $\langle \mathbf{\alpha }\left(s\right),\mathit{b}\left(s\right)\rangle =C_2{e}^{-s}+1$.

Substitute the $\lambda \left(s\right),\mu \left(s\right)$ to the middle equation of Equations (3), ${\kappa }_2\left(s\right)C_2{e}^{2s}+{\kappa }_1\left(s\right)e^s+{\kappa }_1\left(s\right)C_1=0,$ $▵={\kappa }_1^2\left(s\right)-4C_1{C}_2{\kappa }_1\left(s\right){\kappa }_2\left(s\right)>0.$ Hence, statement (2) is established.

Conversely, from statement (2), we obtain

$$\langle \mathbf{\alpha }\left(s\right),{\mathit{t}}^{\prime }\left(s\right)\rangle =C_1{e}^s.$$

(4)

By the Frenet Equations (1), $\langle \mathbf{\alpha }\left(s\right),\mathit{n}\left(s\right)\rangle =0$ is obvious for ${\kappa }_1\left(s\right)\ne 0$. The curve $\mathbf{\alpha }\left(s\right)$ is a lightlike rectifying curve. For the other case, by the same method, statement (1) and statement (2) are equivalent.

Since ${\left({\rho }^2\right)}^{\prime }={\langle \mathbf{\alpha }\left(s\right),\mathbf{\alpha }\left(s\right)\rangle }^{\prime }=2\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle =C_1{e}^s$, ${\rho }^2=C_1{e}^s+C_2$, where $C_1,C_2$ are constants. It is obvious that statement (2) and statement (3) are equivalent.

From Equations (3), $\lambda \left(s\right)=C_1{e}^{-s}+1$, $\mu \left(s\right)=C_2{e}^s$ and $\frac{{\kappa }_1\left(s\right)}{{\kappa }_2\left(s\right)}=-\frac{\mu \left(s\right)}{\lambda \left(s\right)}$. Hence,

$${\kappa }_1\left(s\right)({\kappa }_1\left(s\right)-{\kappa }_2\left(s\right))={\kappa }_1^{\prime }\left(s\right)({\kappa }_1\left(s\right)-{\kappa }_2\left(s\right))-{\kappa }_1\left(s\right){({\kappa }_1\left(s\right)-{\kappa }_2\left(s\right))}^{\prime },$$

which indicates statement (4).

Conversely, supposing ${\kappa }_1\left(s\right)=-{\kappa }_2\left(s\right)$, $\lambda \left(s\right)=\mu \left(s\right)$ and $\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle =\langle \mathbf{\alpha }\left(s\right),\mathit{b}\left(s\right)\rangle$, it shows that

$$\langle \mathbf{\alpha }\left(s\right),\mathbf{\alpha }\left(s\right)\rangle ={\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle }^2+{\langle \mathbf{\alpha }\left(s\right),\mathit{b}\left(s\right)\rangle }^2.$$

Differentiating the above equation,

$$\begin{array}{cc}2\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle \hfill & =2\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle (\langle \mathit{t}\left(s\right),\mathit{t}\left(s\right)\rangle +\langle \mathbf{\alpha }\left(s\right),{\mathit{t}}^{\prime }\left(s\right)\rangle )\hfill \\ \hfill & +2\langle \mathbf{\alpha }\left(s\right),\mathit{b}\left(s\right)\rangle (\langle \mathit{t}\left(s\right),\mathit{b}\left(s\right)\rangle +\langle \mathbf{\alpha }\left(s\right),{\mathit{b}}^{\prime }\left(s\right)\rangle ).\hfill \end{array}$$

(5)

The equation $\langle \mathbf{\alpha }\left(s\right),\mathit{n}\left(s\right)\rangle =0$ is obvious by $\langle \mathbf{\alpha }\left(s\right),\mathit{t}\left(s\right)\rangle =\langle \mathbf{\alpha }\left(s\right),\mathit{b}\left(s\right)\rangle$ and Equation (1). Hence, the curve $\mathbf{\alpha }\left(s\right)$ is a lightlike rectifying curve.

When ${\kappa }_1\left(s\right){\kappa }_2^{\prime }\left(s\right)-{\kappa }_1^{\prime }\left(s\right){\kappa }_2\left(s\right)={\kappa }_1\left(s\right)({\kappa }_1\left(s\right)-{\kappa }_2\left(s\right))$, $\lambda \left(s\right)=\mu \left(s\right)$ is obtained by Equation (3). The curve $\mathbf{\alpha }\left(s\right)$ is a lightlike rectifying curve. Hence, statement (1) and statement (4) are equivalent. we complete the proof. □

In the following, we would like to obtain the geometrical properties of the other two types of lightlike curves in ${\mathbb{R}}_1^3$.

Theorem 2.

If the curve $\mathbf{\alpha }\left(s\right)$ is a lightlike normal curve with ${\kappa }_2\left(s\right)\ne 0$ in ${\mathbb{R}}_1^3$, the curvatures should satisfy $m{\kappa }_1\left(s\right)+m^{\prime }+m^{\prime 2}{\kappa }_2\left(s\right)-m^{″}=0$, where $m=\frac{1}{{\kappa }_2\left(s\right)}$.

Proof. 

Let $\mathbf{\alpha }\left(s\right)$ be a lightlike curve with the Frenet frame $\{\mathit{t}\left(s\right),\mathit{n}\left(s\right),\mathit{b}\left(s\right),{\kappa }_1\left(s\right),{\kappa }_2\left(s\right)\}$, if it is a normal curve, we can write

$$\mathbf{\alpha }\left(s\right)=\lambda \left(s\right)\mathit{n}\left(s\right)+\mu \left(s\right)\mathit{b}\left(s\right).$$

Differentiate the equation

$$\begin{array}{cc}{\mathbf{\alpha }}^{\prime }\left(s\right)\hfill & =\mathit{t}\left(s\right)=\left(\lambda \left(s\right){\kappa }_2\left(s\right)\right)\mathit{t}\left(s\right)-({\lambda }^{\prime }\left(s\right)-{\kappa }_2\left(s\right)\mu \left(s\right))\mathit{n}\left(s\right)\hfill \\ \hfill & +(\lambda \left(s\right){\kappa }_1\left(s\right)+{\mu }^{\prime }\left(s\right)-\mu \left(s\right))\mathit{b}\left(s\right).\hfill \end{array}$$

(6)

and

$$\left\{\begin{array}{c}\lambda \left(s\right){\kappa }_2\left(s\right)=1\hfill \\ {\lambda }^{\prime }\left(s\right)-{\kappa }_2\left(s\right)\mu \left(s\right)=0\hfill \\ \lambda \left(s\right){\kappa }_1\left(s\right)+{\mu }^{\prime }\left(s\right)-\mu \left(s\right)=0\hfill \end{array}\right..$$

(7)

Note that $\lambda =\frac{1}{{\kappa }_2\left(s\right)}$ and $\mu ={\left(\frac{1}{{\kappa }_2\left(s\right)}\right)}^{\prime }{\kappa }_2\left(s\right)$. Substitute the $\lambda ,\mu$ to the third equation of Equation (7), one can obtain $\frac{1}{{\kappa }_2\left(s\right)}{\kappa }_1\left(s\right)+{\left(\frac{1}{{\kappa }_2\left(s\right)}\right)}^{\prime }+{\left(\frac{1}{{\kappa }_2\left(s\right)}\right)}^{\prime 2}{\kappa }_2\left(s\right)-{\left(\frac{1}{{\kappa }_2\left(s\right)}\right)}^{″}=0$. We complete the proof. □

Theorem 3.

There is no any lightlike osculating curve with ${\kappa }_1\left(s\right)\ne 0$ in ${\mathbb{R}}_1^3.$

Proof. 

If $\mathbf{\alpha }\left(s\right)$ be a lightlike osculating curve with ${\kappa }_1\left(s\right)\ne 0$ in ${\mathbb{R}}_1^3,$

$$\mathbf{\alpha }\left(s\right)=\lambda \left(s\right)\mathit{t}\left(s\right)+\mu \left(s\right)\mathit{n}\left(s\right).$$

Differentiate the equation

$$\begin{array}{c}\hfill {\mathbf{\alpha }}^{\prime }\left(s\right)=\mathit{t}\left(s\right)=({\lambda }^{\prime }\left(s\right)+\lambda \left(s\right)+\mu \left(s\right){\kappa }_2\left(s\right))\mathit{t}\left(s\right)+({\mu }^{\prime }\left(s\right)-\lambda \left(s\right){\kappa }_1\left(s\right))\mathit{n}\left(s\right)+\left(\mu \left(s\right){\kappa }_1\left(s\right)\right)\mathit{b}\left(s\right),\end{array}$$

there is no any s satisfying the equation.

□

It is worth mentioning that the important applications of the rectifying curves used in mathematic and physics [4,9,11,12] in ${\mathbb{R}}_1^3$.

Theorem 4.

Let $\mathbf{\alpha }\left(s\right)$ be a lightlike curve with ${\kappa }_1\left(s\right)\ne 0$ in ${\mathbb{R}}_1^3$, then $\mathbf{\alpha }\left(s\right)$ is a lightlike rectifying curve if and only if $\mathbf{\alpha }\left(s\right)=e^s\mathbf{\beta }\left(s\right)$ when $\mathbf{\beta }\left(s\right)$ is a unit speed curve in ${\mathbb{S}}_1^2$; or $\mathbf{\alpha }\left(s\right)=e^{-s}\mathbf{\beta }\left(s\right)$ when $\mathbf{\beta }\left(s\right)$ is a unit speed curve in ${\mathbb{H}}_0^2$.

Proof. 

Let $\mathbf{\alpha }\left(t\right)$ be a lightlike rectifying curve with ${\kappa }_1\left(t\right)\ne 0$. According to Theorem 1, the distance function $\rho$ of the curve satisfies ${\rho }^2=C_1+C_2{e}^t$ for some constants $C_1,C_2$. Making a suitable parameter t, we have ${\rho }^2=C+e^t$ for constant C.

Define a curve in ${\mathbb{S}}_1^2$ by

$$\mathbf{\beta }\left(t\right)=\frac{\mathbf{\alpha }\left(t\right)}{\rho }$$

and

$$\mathbf{\alpha }\left(t\right)=\sqrt{C+e^t}\mathbf{\beta }\left(t\right).$$

(8)

Differentiate the equation with respect to t,

$$\mathit{t}\left(t\right)={\mathbf{\alpha }}^{\prime }\left(t\right)=\frac{e^t}{2\sqrt{C+e^t}}\mathbf{\beta }\left(t\right)+\sqrt{C+e^t}{\mathbf{\beta }}^{\prime }\left(t\right)$$

and

$$\mid {\mathbf{\beta }}^{\prime }\left(t\right){\mid }^2=\langle {\mathbf{\beta }}^{\prime }\left(t\right),{\mathbf{\beta }}^{\prime }\left(t\right)\rangle =\frac{e^{2t}}{{(C+e^t)}^2},$$

where $v=\mid {\mathbf{\beta }}^{\prime }\left(t\right)\mid$ is the pseudo unit speed function of the spherical curve $\mathbf{\beta }\left(t\right)$.

Let us put

$$s^{\prime }={\int }_0^t\frac{e^u}{C+e^u}du=ln(C+e^t)-ln(C+1),$$

for some translation, substituting $t=ln(e^s-C)$ in to Equation (8), $\mathbf{\alpha }\left(s\right)=e^s\mathbf{\beta }\left(s\right)$ is obtained.

When $\mathbf{\beta }\left(t\right)=\frac{\mathbf{\alpha }\left(t\right)}{\rho }\in {\mathbb{H}}_0^2$, choosing $t=ln(e^{-s}-C)$ implies that

$$\mathbf{\alpha }\left(s\right)=e^{-s}\mathbf{\beta }\left(s\right).$$

Conversely, supposing $\mathbf{\alpha }\left(s\right)$ is a lightlike curve defined by $\mathbf{\alpha }\left(s\right)=e^{-s}\mathbf{\beta }\left(s\right)$, $\mathbf{\beta }\left(s\right)\in {\mathbb{H}}_0^2$.

Then,

$${\mathbf{\alpha }}^{\prime }\left(s\right)=e^{-s}(\mathbf{\beta }\left(s\right)+{\mathbf{\beta }}^{\prime }\left(s\right)).$$

Since $\mathbf{\beta }\left(s\right)$ and ${\mathbf{\beta }}^{\prime }\left(s\right)$ are orthonormal vector fields, we can obtain that $\mathbf{\alpha }\left(s\right)$ is lightlike curve and $\mathbf{\beta }\left(s\right)$ is a timelike unit curve in ${\mathbb{H}}_0^2$.

Suppose $\mathbf{\alpha }\left(s\right)=\lambda \left(s\right)\mathit{t}\left(s\right)+\mu \left(s\right)\mathit{n}\left(s\right)+\nu \left(s\right)\mathit{b}\left(s\right)$, $\mathbf{\beta }\left(s\right)=e^s\mathbf{\alpha }\left(s\right)$, and ${\mathbf{\beta }}^{\prime }\left(s\right)=e^s(\mathbf{\alpha }\left(s\right)+{\mathbf{\alpha }}^{\prime }\left(s\right))$, by the fact

$$\langle \mathbf{\alpha }\left(s\right),\mathbf{\alpha }\left(s\right)\rangle +\langle \mathbf{\alpha }\left(s\right),{\mathbf{\alpha }}^{\prime }\left(s\right)\rangle =0,$$

(9)

we can obtain

$$\langle {\mathbf{\alpha }}^{\prime }\left(s\right),{\mathbf{\alpha }}^{\prime }\left(s\right)\rangle =0.$$

(10)

Hence, $\mu =0$ by Equations (1), (9) and (10), $\mathbf{\alpha }\left(s\right)$ is a lightlike rectifying curve.

As the same method as $\mathbf{\beta }\left(s\right)\in {\mathbb{H}}_0^2$, we finish the proof. □

Remark 1.

By the same method as [8], if $\mathbf{\beta }\left(s\right)$ is a unit speed curve in ${\mathbb{S}}_1^2$ or ${\mathbb{H}}_0^2$, for any constants C and $s_0$, we have that $\mathbf{\alpha }\left(s\right)=C{e}^{s+s_0}\mathbf{\beta }\left(s\right)$ is a lightlike rectifying curve in ${\mathbb{R}}_1^3$.

4. The Centrodes of Lightlike Curves

In this section, the centrodes of lightlike curves and the N-type lightlike slant helices in ${\mathbb{R}}_1^3$ are given. Meanwhile, we obtain the relationship between the centrodes of lightlike curves and the N-type lightlike slant helices.

Definition 3.

For a curve $\mathbf{\alpha }\left(s\right)\subset {\mathbb{R}}_1^3$ with ${\kappa }_1\left(s\right){\kappa }_2\left(s\right)\ne 0$, the curve given by the Darboux vector $\mathit{d}\left(s\right)={\kappa }_2\left(s\right)\mathit{t}\left(s\right)+{\kappa }_1\left(s\right)\mathit{b}\left(s\right)$ is called the centrode of the curve $\mathbf{\alpha }\left(s\right)$.

Theorem 5.

The centrode of a lightlike curve $\mathbf{\alpha }\left(s\right)$ is a lightlike rectifying curve, when the curvature ${\kappa }_1\left(s\right)=C{e}^{-s}$ and the torsion ${\kappa }_2\left(s\right)\ne {\kappa }_1\left(s\right)$. As the same, when the centrode of a lightlike curve $\mathbf{\alpha }\left(s\right)$ satisfies the torsion ${\kappa }_2\left(s\right)=C{e}^{-s}$ and the curvature ${\kappa }_1\left(s\right)\ne {\kappa }_2\left(s\right)$, the lightlike curve $\mathbf{\alpha }\left(s\right)$ is also a lightlike rectifying curve, where C is a constant.

Proof. 

Supposing that $\mathbf{\alpha }\left(s\right)$ is a lightlike curve with ${\kappa }_1\left(s\right)=e^{-s}\ne {\kappa }_2\left(s\right)$, we consider the centrode

$$\mathit{d}\left(s\right)={\kappa }_2\left(s\right)\mathit{t}\left(s\right)+{\kappa }_1\left(s\right)\mathit{b}\left(s\right).$$

(11)

Differentiate the equation above and use the Frenet Equations (1),

$$\begin{array}{cc}\hfill {\mathit{d}}^{\prime }\left(s\right)& ={\kappa }_2^{\prime }\left(s\right)\mathit{t}\left(s\right)+{\kappa }_2\left(s\right){\mathit{t}}^{\prime }\left(s\right)+{\kappa }_1^{\prime }\left(s\right)\mathit{b}\left(s\right)+{\kappa }_1\left(s\right){\mathit{b}}^{\prime }\left(s\right)\hfill \\ \hfill & =({\kappa }_2\left(s\right)+{\kappa }_2^{\prime }\left(s\right))\mathit{t}\left(s\right)+({\kappa }_1\left(s\right)+{\kappa }_1^{\prime }\left(s\right))\mathit{b}\left(s\right),\hfill \end{array}$$

Case 1: when ${\kappa }_1\left(s\right)=e^{-s}$, we know ${\kappa }_1\left(s\right)+{\kappa }_1^{\prime }\left(s\right)=0$ and ${\kappa }_2\left(s\right)+{\kappa }_2^{\prime }\left(s\right)\ne 0$. Then, the tangent vector of $\mathit{d}\left(s\right)$ and $\mathit{d}\left(s\right)$ at the corresponding point are parallel. The position vector $\mathit{d}\left(s\right)$ always lies in its rectifying plane. The centrode of $\mathbf{\alpha }\left(s\right)$ is a lightlike curve. By Definition 2, the centrode $\mathit{d}\left(s\right)$ is a lightlike rectifying curve.

Case 2: when ${\kappa }_2\left(s\right)=e^{-s}$, we know ${\mathit{d}}^{\prime }\left(s\right)=({\kappa }_1\left(s\right)+{\kappa }_1^{\prime }\left(s\right))\mathit{b}\left(s\right).$ In addition, the tangent vector of $\mathit{d}\left(s\right)$ is parallel to the binormal vector of $\mathbf{\alpha }\left(s\right)$. For the binormal vector $\mathit{b}\left(s\right)$ is a lightlike vector, the centrode $\mathit{d}\left(s\right)$ is a lightlike curve. The tangent vector field of $\mathit{d}\left(s\right)$ and the binormal vector field of $\mathbf{\alpha }\left(s\right)$ are parallel. The same as case 1, the centrode of the lightlike curve $\mathbf{\alpha }\left(s\right)$ is also a rectifying curve. □

Definition 4.

Let $\mathbf{\alpha }\left(s\right)$ be a lightlike curve with the Frenet frame $\left\{\mathit{t}\right(s),\mathit{n}(s),\mathit{b}(s\left)\right\}$. For a constant vector field $\mathit{U}$ satisfying $\langle \mathit{U},\mathit{n}\left(s\right)\rangle =C$, where C is constant, we call the curve $\mathbf{\alpha }\left(s\right)$ be an N-type lightlike slant helix.

Theorem 6.

Let $\mathbf{\alpha }\left(s\right)$ be an N-type lightlike slant helix in ${\mathbb{R}}_1^3$ with ${\kappa }_1\left(s\right){\kappa }_2\left(s\right)\ne 0$ if and only if the equation $\frac{{\eta }^{\prime }-1}{\eta }=\frac{{\kappa }_1^{\prime }\left(s\right)+{\kappa }_2\left(s\right)}{2{\kappa }_1\left(s\right)}$ is established, where $\eta ={\left(\frac{{\kappa }_1}{{\kappa }_2}\right)}^{\prime }$.

Proof. 

Supposing a vector field $\mathit{U}=\lambda \left(s\right)\mathit{t}\left(s\right)+\xi \left(s\right)\mathit{n}\left(s\right)+\mu \left(s\right)\mathit{b}\left(s\right)$, we obtain $\xi \left(s\right)=C$ by Definition 4.

Differentiate the constant vector $\mathit{U}$,

$$({\lambda }^{\prime }\left(s\right)+\lambda \left(s\right)+C{\kappa }_2\left(s\right))\mathit{t}\left(s\right)+(\lambda \left(s\right){\kappa }_1\left(s\right)+{\kappa }_2\left(s\right)\mu \left(s\right))\mathit{n}\left(s\right)+(C{\kappa }_1\left(s\right)+{\mu }^{\prime }\left(s\right)-\mu \left(s\right))\mathit{b}\left(s\right)=\mathbf{0},$$

and

$$\left\{\begin{array}{c}{\lambda }^{\prime }\left(s\right)+\lambda \left(s\right)+C{\kappa }_2\left(s\right)=0,\hfill \\ {\kappa }_1\left(s\right)\lambda \left(s\right)+{\kappa }_2\left(s\right)\mu \left(s\right)=0,\hfill \\ C{\kappa }_1\left(s\right)+{\mu }^{\prime }\left(s\right)-\mu \left(s\right)=0.\hfill \end{array}\right.$$

(12)

Differentiate the second equation of Equations (12) and substitute the ${\lambda }^{\prime }\left(s\right)$ and ${\mu }^{\prime }\left(s\right)$ to the first and third equation of Equation (12),

$${\kappa }_1^{\prime }\left(s\right)\lambda \left(s\right)+({\kappa }_2^{\prime }\left(s\right)+{\kappa }_2\left(s\right))\mu \left(s\right)=2C{\kappa }_1\left(s\right){\kappa }_2\left(s\right).$$

(13)

We obtain

$$\mu \left(s\right)=\frac{2C{\kappa }_1^2\left(s\right){\kappa }_2\left(s\right)}{{\kappa }_2^{\prime }\left(s\right){\kappa }_1\left(s\right)+2{\kappa }_1\left(s\right){\kappa }_2\left(s\right)-{\kappa }_1^{\prime }\left(s\right){\kappa }_2\left(s\right)}.$$

(14)

Substituting Formula (14) to the third equation of Equation (12), we have $\frac{{\left(\frac{{\kappa }_1}{{\kappa }_2}\right)}^{″}-1}{{\left(\frac{{\kappa }_1}{{\kappa }_2}\right)}^{\prime }}=\frac{{\kappa }_1^{\prime }\left(s\right)+{\kappa }_2\left(s\right)}{2{\kappa }_1\left(s\right)}.$ The proof is completed. □

Theorem 7.

Let $\mathbf{\alpha }\left(s\right)$ be a lightlike curve in ${\mathbb{R}}_1^3$ with ${\kappa }_1\left(s\right){\kappa }_2\left(s\right)\ne 0$. Then, the centrode $\mathit{d}\left(s\right)={\kappa }_2\left(s\right)\mathit{t}\left(s\right)+{\kappa }_1\left(s\right)\mathit{b}\left(s\right)$ is a rectifying curve and the curve $\mathbf{\alpha }\left(s\right)$ is an N-type lightlike slant helix.

Proof. 

Letting $\mathbf{\alpha }\left(s\right)$ be a lightlike curve, the centrode curve of $\mathbf{\alpha }\left(s\right)$ can be written as

$$\mathit{d}\left(s\right)={\kappa }_2\left(s\right)\mathit{t}\left(s\right)+{\kappa }_1\left(s\right)\mathit{b}\left(s\right).$$

(15)

${\mathit{d}}^{\prime }\left(s\right)={\kappa }_2^{\prime }\left(s\right)\mathit{t}\left(s\right)+{\kappa }_1^{\prime }\left(s\right)\mathit{b}\left(s\right)$ and $v_d=\sqrt{{\kappa }_1^{\prime 2}\left(s\right)+{\kappa }_2^{\prime 2}\left(s\right)}$. Then,

$${\mathit{t}}_d\left(s\right)=\frac{{\kappa }_2^{\prime }\left(s\right)}{v_d}\mathit{t}\left(s\right)+\frac{{\kappa }_1^{\prime }\left(s\right)}{v_d}\mathit{b}\left(s\right).$$

(16)

Differentiate Equation (16),

$$v_d({\mathit{t}}_d\left(s\right)-{\kappa }_{1d}\left(s\right){\mathit{n}}_d\left(s\right))={\left(\frac{{\kappa }_2^{\prime }\left(s\right)}{v_d}\right)}^{\prime }\mathit{t}\left(s\right)+\frac{{\kappa }_2^{\prime }\left(s\right)}{v_d}{\mathit{t}}^{\prime }\left(s\right)+{\left(\frac{{\kappa }_1^{\prime }\left(s\right)}{v_d}\right)}^{\prime }\mathit{b}\left(s\right)+\frac{{\kappa }_1^{\prime }\left(s\right)}{v_d}{\mathit{b}}^{\prime }\left(s\right),$$

and $v_d{\kappa }_{1d}\left(s\right){\mathit{n}}_d\left(s\right)=v_d{\mathit{t}}_d\left(s\right)-[{\left(\frac{{\kappa }_2^{\prime }\left(s\right)}{v_d}\right)}^{\prime }\mathit{t}\left(s\right)+\frac{{\kappa }_2^{\prime }\left(s\right)}{v_d}{\mathit{t}}^{\prime }\left(s\right)+{\left(\frac{{\kappa }_1^{\prime }\left(s\right)}{v_d}\right)}^{\prime }\mathit{b}\left(s\right)+\frac{{\kappa }_1^{\prime }\left(s\right)}{v_d}{\mathit{b}}^{\prime }\left(s\right)].$

Using the Frenet Equations (1) and (16),

$$v_d{\kappa }_{1d}\left(s\right)\langle {\mathit{n}}_d\left(s\right),\mathit{d}\left(s\right)\rangle ={\kappa }_1^{\prime }\left(s\right){\kappa }_2\left(s\right)({\left(\frac{{\kappa }_1^{\prime }\left(s\right)}{v_d}\right)}^{\prime }-\frac{{\kappa }_1^{\prime }\left(s\right)}{v_d})+{\kappa }_1\left(s\right){\kappa }_2^{\prime }\left(s\right)({\left(\frac{{\kappa }_2^{\prime }\left(s\right)}{v_d}\right)}^{\prime }+\frac{{\kappa }_2^{\prime }\left(s\right)}{v_d}).$$

Substitute $v_d$,

$$2{\kappa }_1\left(s\right){\kappa }_2^2\left(s\right)(\frac{\phi \left(s\right)}{{\kappa }_2^4\left(s\right)}-1)=({\kappa }_2\left(s\right)+{\kappa }_1^{\prime }\left(s\right))({\kappa }_1^{\prime }\left(s\right){\kappa }_2\left(s\right)-{\kappa }_1\left(s\right){\kappa }_2^{″}\left(s\right)),$$

where $\phi \left(s\right)={\kappa }_1{\kappa }_1^{″}{\kappa }_2{\kappa }_2^{\prime }+{\kappa }_1{\kappa }_1^{\prime }{\kappa }_2^{\prime 2}-{\kappa }_1^{\prime 2}{\kappa }_2{\kappa }_2^{\prime }-{\kappa }_1{\kappa }_2{\kappa }_1^{\prime }{\kappa }_2^{″}$.

We obtain

$$\frac{{\left(\frac{{\kappa }_1}{{\kappa }_2}\right)}^{\prime \prime }-1}{{\left(\frac{{\kappa }_1}{{\kappa }_2}\right)}^{\prime }}=\frac{{\kappa }_1^{\prime }\left(s\right)+{\kappa }_2\left(s\right)}{2{\kappa }_1\left(s\right)}.$$

Hence, by Theorem 6, the curve $\mathbf{\alpha }\left(s\right)$ is an N-type lightlike slant helix. □

5. The Projections of the Lightlike Rectifying Curves

The projections of the non-lightlike curves onto the lightlike planes in ${\mathbb{R}}_1^3$ were given in [9]. The lightlike curves belong to one of the lightlike planes in ${\mathbb{R}}_1^3$. In this section, we study the projections of the lightlike rectifying curves onto the timelike planes.

Theorem 8.

Let $\mathbf{\alpha }\left(s\right)$ be a lightlike rectifying curve in ${\mathbb{R}}_1^3$ and an orthogonal projection $\mathbf{\beta }\left(s\right)$ on the timelike plane. Then, we can obtain the parametrical $\mathbf{\alpha }\left(s\right)$ as

$$\mathbf{\alpha }\left(s\right)=\{tan(\sqrt{ϵe^{2ϵs}-1}-C),sec(\sqrt{ϵe^{2ϵs}-1}-C),\sqrt{ϵe^{2ϵs}-1}\},$$

where C is a constant.

Proof. 

Let $\mathbf{\beta }\left(t\right)$ be an orthogonal projection of $\mathbf{\alpha }\left(s\right)$ onto the timelike plane. Then, $\mathbf{\alpha }\left(s\right)$ is given by

$$\mathbf{\alpha }\left(s\right)=\mathbf{\beta }\left(t\right(s\left)\right)+\mu \left(s\right)\mathbf{\nu },$$

where $\mathbf{\nu }$ is a spacelike vector; supposing $\mathbf{\nu }=\{0,0,1\}$ for any another spacelike vector, we have the same method, and $\mu \left(s\right)$ is a non-constant differentiable function. Assuming $\mathbf{\beta }\left(s\right)$ is a osculating curve on the timelike plane satisfying

$$\langle {\mathbf{\beta }}^{\prime }\left(t\right),{\mathbf{\beta }}^{\prime }\left(t\right)\rangle =1.$$

Then, ${\mathbf{\alpha }}^{\prime }\left(s\right)={\mathbf{\beta }}^{\prime }\left(t\right)t^{\prime }\left(s\right)+{\mu }^{\prime }\left(s\right)\mathbf{\nu }$ for $\langle {\mathbf{\alpha }}^{\prime }\left(s\right),{\mathbf{\alpha }}^{\prime }\left(s\right)\rangle =0$. We know

$$\langle {\mathbf{\alpha }}^{\prime }\left(s\right),{\mathbf{\alpha }}^{\prime }\left(s\right)\rangle =\langle {\mathbf{\beta }}^{\prime }\left(t\right)t^{\prime }\left(s\right)+{\mu }^{\prime }\left(s\right)\mathbf{\nu },{\mathbf{\beta }}^{\prime }\left(t\right)t^{\prime }\left(s\right)+{\mu }^{\prime }\left(s\right)\mathbf{\nu }\rangle =-t^{\prime 2}\left(s\right)+{\mu }^{\prime 2}\left(s\right)=0.$$

(17)

By $\langle \mathbf{\alpha }\left(s\right),{\mathbf{\alpha }}^{″}\left(s\right)\rangle =0$, one obtains

$${\mathbf{\alpha }}^{″}\left(s\right)={\mathbf{\beta }}^{″}{t}^{\prime 2}+{\mathbf{\beta }}^{\prime }{t}^{″}+{\mu }^{″}\mathbf{\nu }.$$

The equation

$$\langle \mathbf{\beta },{\mathbf{\beta }}^{″}\rangle t^{\prime 2}+\mu {\mu }^{″}=-\mu {\mu }^{″}{t}^{\prime 2}+\mu {\mu }^{″}=0$$

(18)

is obvious. From Formulas (17) and (18), we obtain

$$-\mu {\mu }^{″}(t^{\prime 2}-1)=-\mu {\mu }^{″}({\mu }^{\prime 2}-1)=0.$$

Case 1: when ${\mu }^{\prime 2}=1$, $\mu =\pm s+C,$ where C is constant;

Case 2: when ${\mu }^{″}=0$, $\mu =C_{1}s+C_2,$ where $C_1,C_2$ are constants;

Case 3: when $\mu =0$, the curve $\mathbf{\alpha }\left(s\right)$ is on the timelike plane, we omit it here.

In the following text, we only consider case 2, case 1 is a special case of case 2. When $\mu =C_{1}s+C_2,$ the arclength parameter of $\mathbf{\beta }$ is

$$t\left(s\right)={\int }_0^s\mid {\mathbf{\beta }}^{\prime }\left(u\right)\mid du,$$

and

$$\mid {\mathbf{\beta }}^{\prime }\left(u\right)\mid =\sqrt{\langle {\alpha }^{\prime }+{\mu }^{\prime }\mathbf{\nu },{\alpha }^{\prime }+{\mu }^{\prime }\mathbf{\nu }\rangle }=\sqrt{2\langle {\alpha }^{\prime },{\mu }^{\prime }\mathbf{\nu }\rangle +{\mu }^{\prime 2}}=\mid {\mu }^{\prime }\mid =C_1;$$

therefore, $t\left(s\right)=\mid C_1\mid s.$

We obtain

$$\mathbf{\beta }\left(s\right)=\{tan\mid C_1\mid s,sec\mid C_1\mid s,0\}$$

and

$$\mathbf{\alpha }\left(s\right)=\{tan\mid C_1\mid s,sec\mid C_1\mid s,C_{1}s+C_2\}.$$

When $ϵ=1$ or $ϵ=-1$, the lightlike rectifying curve $\mathbf{\alpha }\left(s\right)=e^{ϵs}\mathbf{\gamma }\left(s\right)$ belongs to ${\mathbb{S}}_1^2$ or ${\mathbb{H}}_0^2$, respectively.

In addition,

$$\mathbf{\gamma }\left(s\right)=e^{-ϵs}\{tan\mid C_1\mid s,sec\mid C_1\mid s,C_{1}s+C_2\}.$$

By the conditions $\langle \mathbf{\gamma }\left(s\right),\mathbf{\gamma }\left(s\right)\rangle =ϵ$ and $\langle {\mathbf{\gamma }}^{\prime }\left(s\right),\mathbf{\gamma }\left(s\right)\rangle =0,$ we have

$$ϵe^{2ϵs}=1+{(\mid C_1\mid s+C_2)}^2.$$

Hence, $\mid C_1\mid s=\sqrt{ϵe^{2ϵs}-1}-C_2$,

$$\mathbf{\alpha }\left(s\right)=\{tan(\sqrt{ϵe^{2ϵs}-1}-C),sec(\sqrt{ϵe^{2ϵs}-1}-C),\sqrt{ϵe^{2ϵs}-1}\}.$$

□

6. Some Examples

In this section, we give some examples about the lightlike rectifying curves to certify our main conclusions. The graphics of the lightlike rectifying curves and the centrodes are described in the following graphs. In addition, we give the projection graph of a lightlike rectifying curve to the timelike plane in Example 1.

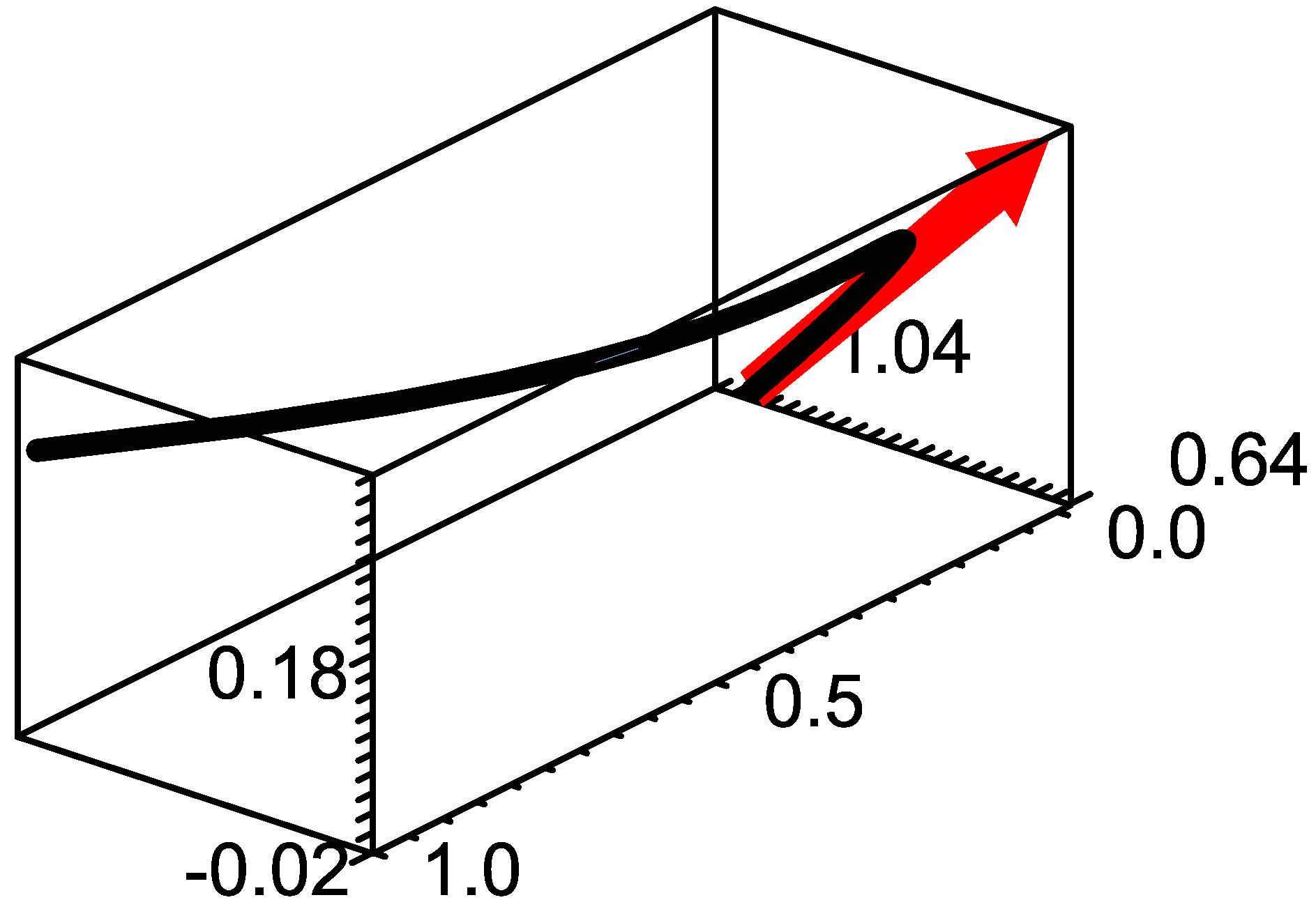
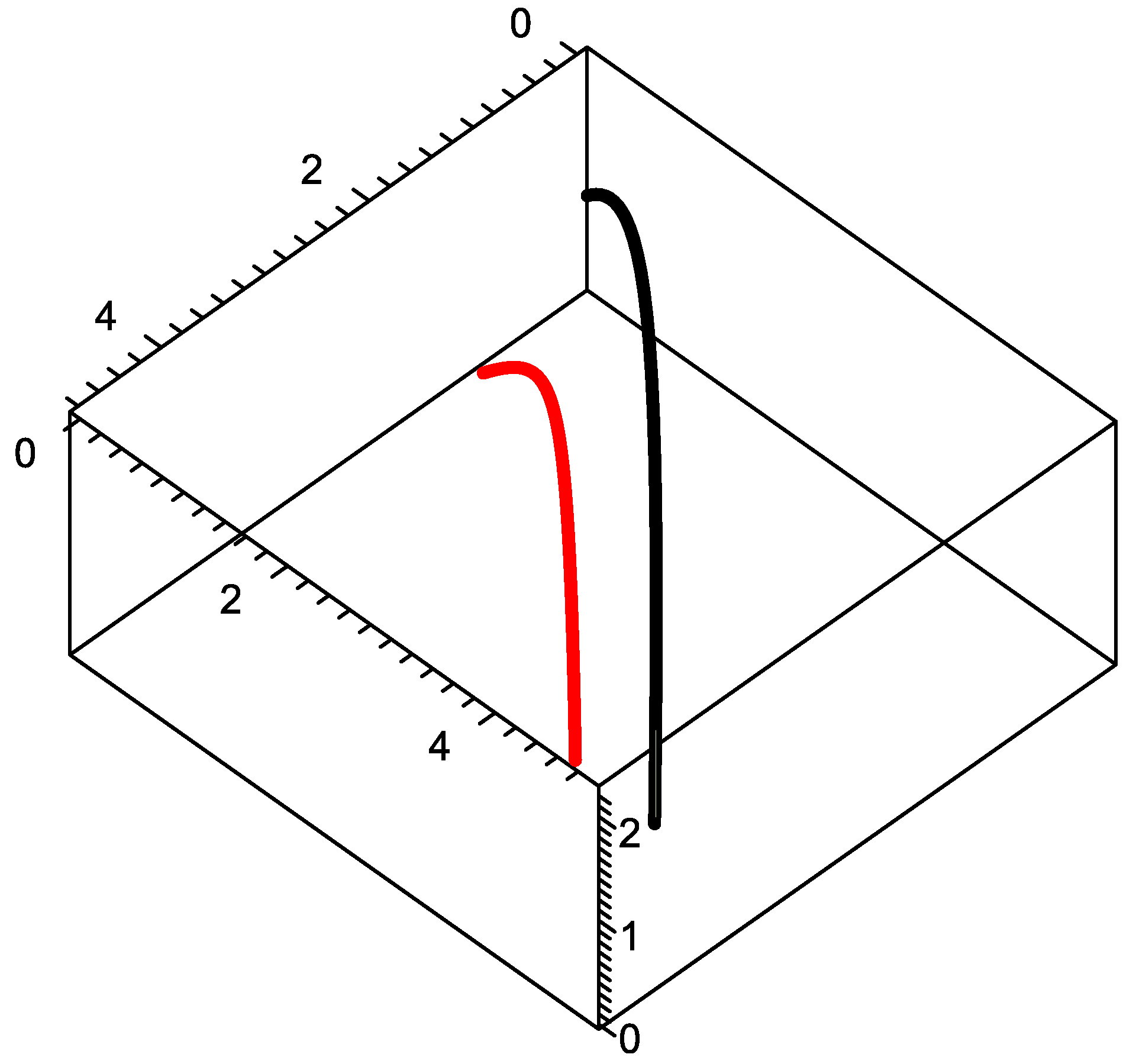
Example 1.

For a lightlike curve $\mathbf{\alpha }:I\to {\mathbb{R}}_1^3$ with the Frenet frame $\left\{\mathit{t}\right(s),\mathit{n}(s),\mathit{b}(s\left)\right\}$, where

$$\mathbf{\alpha }\left(s\right)=e^s\left\{sinstans,sinssecs,coss\right\},$$

the projection equation of the lightlike rectifying curve $\mathbf{\alpha }\left(s\right)$ to the timelike plane as

$$\mathbf{\beta }\left(s\right)=\left\{sinstans,sinssecs,coss\right\}\subset {\mathbb{S}}_1^2$$

and the graph of the projection curve is in Figure 1.

$$\mathit{t}\left(s\right)=\left\{(coss+sins)tans+secstans,1+tans+{tan}^{2}s,coss-sins\right\},$$

where the graph of the lightlike curve $\mathbf{\alpha }\left(s\right)$ and the tangent vector $\mathit{t}\left(s\right)$ are in Figure 2.

$$\mathit{b}\left(s\right)=\frac{1}{2e^s{(coss-sins)}^2}\left\{-(coss+sins)tans-secstans,-1-tans-{tan}^{2}s,coss-sins\right\}.$$

The curvatures are

$${\kappa }_1\left(s\right)=e^s(coss-sins),{\kappa }_2\left(s\right)=2e^{-s}.$$

The centrode of the lightlike curve is

$$\begin{array}{cc}\hfill \mathit{d}\left(s\right)& ={\kappa }_2\left(s\right)\mathit{t}\left(s\right)+{\kappa }_1\left(s\right)\mathit{b}\left(s\right)=\{(2-\frac{1}{2(coss-sins)})((coss+sins)tans+secstans),\hfill \\ \hfill & (2-\frac{1}{2(coss-sins)})(1+tans+{tan}^{2}s),(2+\frac{1}{2(coss-sins)})(coss-sins)\}.\hfill \end{array}$$

the centrode $\mathit{d}\left(s\right)$ of the lightlike curve $\mathbf{\alpha }\left(s\right)$ is in Figure 3.

Example 2.

For a lightlike curve $\mathbf{\alpha }:I\to {\mathbb{R}}_1^3$ with the Frenet frame $\left\{\mathit{t}\right(s),\mathit{n}(s),\mathit{b}(s\left)\right\}$,

$$\mathbf{\alpha }\left(s\right)=e^{-s}\left\{secs,sinstans,cosstans\right\},$$

$$\mathbf{\beta }\left(s\right)=\left\{secs,sinstans,cosstans\right\}\subset {\mathbb{H}}_0^2,$$

the graph of the centrode $\mathit{d}\left(s\right)$ of the lightlike curve $\mathbf{\alpha }\left(s\right)$ is drawn in Figure 4.

7. Conclusions

This paper considered the geometrical properties of three types of lightlike curves in Minkowski 3-space (lightlike rectifying curves, lightlike normal curves, and lightlike osculating curves). The lightlike rectifying curves are mainly studied. In addition, the conditions that the centrodes of the lightlike curves are the lightlike rectifying curves are obtained. Furthermore, we obtain the relationship between the N-type lightlike slant helices and the centrodes of lightlike curves. In addition, the projections of the lightlike rectifying curves to the timelike planes are researched.

In the following research, we will continue study the geometric properties of the lightlike rectifying curves in high dimensional spaces, such as in 4-space. Some unique geometric properties of curves in high dimensional space are desired to be obtained in the future.