A Modern Industrial Policy for the Czech Republic: Optimizing the Structure of Production

Abstract

The decreased demand for new vehicles will put pressure on the economy of the Czech Republic, a country deeply integrated into global value chains, as part of global vehicle production. The aim of this research was to define an appropriate industrial policy for the Czech Republic that will ensure that the country maintains its competitive position in the global market. A constrained optimization model was built, based on input–output analysis, to determine the optimal value-added structure and the intersectoral structure of the Czech economy for the country to retain its exporting character. The optimization problem was solved by using a particle swarm optimization algorithm. The results suggest that the optimal industrial policy plan for the country is the structural transformation of production, mainly targeting the development of technologically advanced sectors of manufacturing (such as: chemicals and chemical products; basic pharmaceutical products; computer, electronic, and optical products; electrical equipment; and machinery and equipment). The suggested restructuring process increased the domestic value-added in gross exports as a share of total exports by 6.77%, creating optimal production capabilities for the economy. The Czech Republic appears to have the potential for the implementation of an industrial policy, avoiding the increasingly vulnerable motor-vehicle sector.

1. Introduction

The Czech Republic is among Europe’s most industrialized countries. The share of manufacturing in the non-financial-business sector of the economy was, in terms of value-added and employment, in 2016, 39.2% (ranking second in the EU27) and 35.3% (the highest rate in the EU27), respectively. The automotive industry’s share was 8.5% in the non-financial-business economy value-added, making the Czech Republic the most specialized country among the EU27. The Czech Republic showed a high ratio of exports of goods and services in its GDP, which was 79.6% in 2016, while the EU27 countries’ average was 46.7%. The motor vehicle industry and its performance substantially contribute to the export strength of the Czech economy. The participation of the automotive industry in the export of goods was 23% in 2016, with more than 1.4 million vehicles manufactured in the country [1]. Furthermore, the Czech Republic is deeply integrated into global value chains, as part of global vehicle production [2].

This currently strong feature of the Czech industry brings considerable risks for future economic development. Changes in the production technology and consumption patterns are expected to challenge the motor-vehicle sector worldwide. On the one hand, technological development is expected to improve the efficiency of electro-mobility and self-steering cars [3], while, on the other hand, the shift towards collaborative consumption (for example, car-sharing, bicycling, and public transport) will decrease the demand for new vehicles [4]. Both the technological transformation and the new consumption patterns raise the question of the country’s long-term viability with regard to its motor-vehicle-related export-based character. Complementary to the technological and social risks, the instability of the global economic environment could lead to unexpected consequences [5] affecting the motor vehicle industry. In addition, the growing number of automobile manufacturers worldwide increased international competition, putting pressure on traditional manufacturers [6,7]. Moreover, in the case of the Czech Republic, the low population growth rate will further reduce the demand for new vehicles due to the subsequent reduction in domestic sales. It should be stressed that the trend towards consumption patterns compatible with sustainable development led to increased demand for electric vehicles in several countries, but this is not the case for the Czech Republic, where sales of electric cars are relatively low [8].

A decline in the demand for cars will affect the Czech industry and the exports of the country, given the high shares the automotive industry holds in production and exports, with an essential social and economic cost. Furthermore, the automotive industry is a high-value sector using high-skilled employment. Thus, the shrinkage of the sector will lead to a reduction in the demand for highly qualified labor in the economy. Therefore, the production specialization of the country should be replaced by efforts to strengthen other productive sectors towards the productive transformation of the economy.

The recent debate on the contribution of industrial policy to economic growth underlines the importance of interventions aimed at improving the productive structure of an economy [9], where the productive structure is defined at the sectoral level and is captured by the contribution of the different sectors to the economy’s output. Following this line of research, the objective of this research was to provide a methodological framework for determining the optimal productive structure of an economy. The proposed methodology was applied to the Czech economy, addressing the question: “In which areas should the Czech Republic’s industrial policy focus for not losing the export orientation, given the expected reduction in demand for motor vehicles?”.

This article is structured as follows. After the introduction in the first section, the second section discusses the industrial policy in a modern economy. A detailed description of the proposed methodology is given in the third section. Reports on the empirical results obtained from implementing the proposed methodology in the Czech economy are included in the fourth section. The final section contains conclusions of the research and discussions as to the directions of further ongoing research.

2. Industrial Policy in Modern Economies

In recent years, several studies have referred to the rejuvenation [10] or renaissance [11] of industrial policy, which has emerged as a strategic priority on the political agenda. Moreover, the attention of researchers and decision-makers in industrial policy strategies reappeared after the 2008 economic crisis and the prolonged recession in some countries or the stagnation of development in other ones that followed [12]. Moreover, given the growth and expansion of global value chains (GVCs) in recent years, attention has focused on the contribution of industrial policy to the process of a country’s upgrading within the GVCs, bringing the approach to the core of the contemporary literature [13].

2.1. Defining Industrial Policy

Based on Chang [14], industrial policy aims “at particular industries (and firms as their components) to achieve the outcomes that are perceived by the state to be efficient for the economy as a whole”. This approach emphasizes the importance of interventions in specific economic sectors, but, at the same time, the impact of the interventions should disseminate in the whole economy rather than appearing only in particular sectors. Pack and Saggi [15] are stressing that industrial policy, promoting sectors that can offer significant growth prospects, concentrates on altering the sectoral structure of production. Various definitions of the term “industrial policy” have been debated in the literature [13]. In this research, industrial policy was defined as sector-specific interventions with a strategic target: the structural transformation of the entire economic system to accelerate economic development and optimize specific macroeconomic targets. Therefore, industrial policy has a strategic role in the economic development process that sets it apart from other government policies with short-term impact. Furthermore, the sectors on which industrial policy should focus are subsumed under the term “strategic sectors”.

An issue of critical importance is the inter-sectoral impact of industrial policy or the improvement in the economy’s connectedness. Focusing on the strategic nature of industrial policy, Günther and Alcorta [16] conclude that industrial policy targeting strategic sectors also manages to improve the inter- and intra-sectoral structure of production. The inter-sectoral structure improvement refers to the shift of production to more sophisticated and technologically advanced industries. The intra-sectoral structure improvement refers to the increase in the economy’s interconnectedness and complementarity [17].

Another significant aspect of industrial policy is its strictly country-specific character. As analytically discussed by Chang and Andreoni [18], “industrial policy strategies should always be accompanied by a country-specific mapping of inherited production capabilities and existing structures”. Thus, government interventions should align with the economy’s productive potential at the specific conjuncture; otherwise, there is a significant failure risk.

Together, these studies indicate two preconditions as critical for determining the optimal industrial policy: Firstly, the detection of the strategic sectors where the intervention will be directed. Secondly, the ex-ante evaluation of the socioeconomic impact of the intervention to ensure their alignment with the original targets. Furthermore, decision-makers should simultaneously address these two preconditions, i.e., to optimize specific socioeconomic measurements with targeted interventions in strategic sectors. Such a methodology approaching industrial policy planning as a constrained optimization problem will provide a comprehensive and robust framework for identifying the optimal industrial policy.

2.2. Locating Strategic Sectors

Prior researchers agree that the first step to an effective industrial policy is the determination of the strategic sectors. However, there is no general agreement on the methodology for that process. Different viewpoints about the methodological approaches for locating the strategic sectors are widely discussed in the literature. The majority of them are based on the theoretical background of the comparative advantage theory and the input–output analysis (IOA), while the use of composite indicators is also proposed in several studies [19,20]. Moreover, IOA has been used in the recent literature to underline the empirical aspects of GVCs research [21].

In the literature, the notion of comparative advantage is used in connection with two district theoretical approaches to international trade. The first approach is the Ricardian international trade model, where the comparative advantage of a country is derived from different technologies between the countries. The second approach is the Heckscher–Ohlin–Samuelson theory, where the comparative advantage is specified by the differences in the endowments of the production factors across the countries. Several studies [22,23] conclude that a country’s comparative advantages result from the long-term economic development process; thus, the idea of the initial endowment of factors has limited usefulness in understanding economic development. Focusing on the feasibility of industrial policy, which is defined by the level of development and the production capabilities of the sectors, Lin and Monga [24] proposed the notion of a latent comparative advantage as a roadmap for a successful industrial policy that prevents the economy from the vicious cycle of stagnation. It should be noted that targeting sectors with latent comparative advantage ensure that policy interventions will not occur in too-advanced or deprived sectors; however, the lack of a method for determining these sectors has been limiting the potential applications. In general, even if the comparative-advantage-based approaches manage to identify the strategic sectors, they fail in facing the second precondition of industrial policy, the estimation of the industrial policy impact. Moreover, these approaches do not provide a comprehensive methodology to address the constrained optimization problem.

Trying to define strategic sectors beyond strictly economic criteria, Di Tommaso et al. [19] introduced a composite indicator with seven criteria to determine the strategic sectors of an economy. The applied criteria combine the share and the growth of a sector in terms of value-added and employment, the productivity level and its trend, the capital intensity, and the exporting performance. Composite indicators are aggregate measures calculated as weighted combinations of selected criteria via the underlying policy domains of interest [25]. Composite indicators are widely used in various policy fields, but they lack a robust theoretical background in criteria choice and weighting, making them unreliable [26]. This lack of methodological rigor raises questions on the results of the composite indicator method and makes the optimization of industrial policy impossible.

The process of locating strategic sectors should go beyond a strictly sectoral approach, according to the industrial policy definition. An important feature of identifying the strategic sectors is the level of their interdependencies with the remaining sectors of the economy empowering them to generate significant results for the economy as a whole. Hence, it is necessary to formulate an integrated methodological framework that represents the functioning of the economic system. An input–output analysis supports the capture of these interdependencies in forecasting the effectiveness of the industrial policy on the whole economy and the estimation of policy trade-offs [27,28].

The determination of strategic sectors is based on the contribution of Hirschman [29], who maintains that the sectors with strong backward linkages (sectors with relatively large intermediate purchases) are of high importance for the overall economic activity because an expansion of the sector stimulates all the associated sectors. From another point of view, Rasmussen [30] advocates that the sectors with strong forward linkages (sectors with relatively large intermediate sales) are also crucial, given that their expansion promotes the intermediate consumption. For the estimation of both backward and forward linkages, the techniques of input–output analysis are employed. In this line of research, several authors proposed measures of various complexity levels to define the most important of economic sectors [31,32,33]. IOA is the only approach capable of simultaneously addressing the preconditions of the optimal industrial policy: IOA provides techniques to identify strategic sectors and can be used to assess the impact of industrial policy implementation.

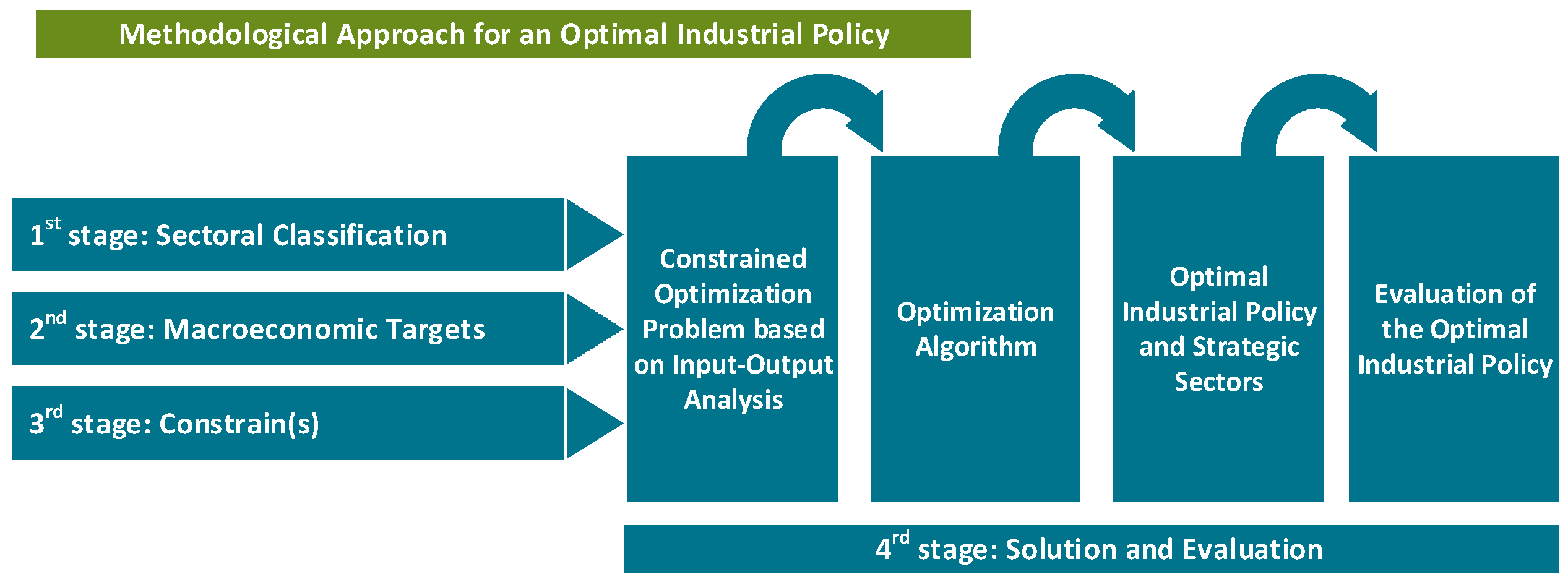
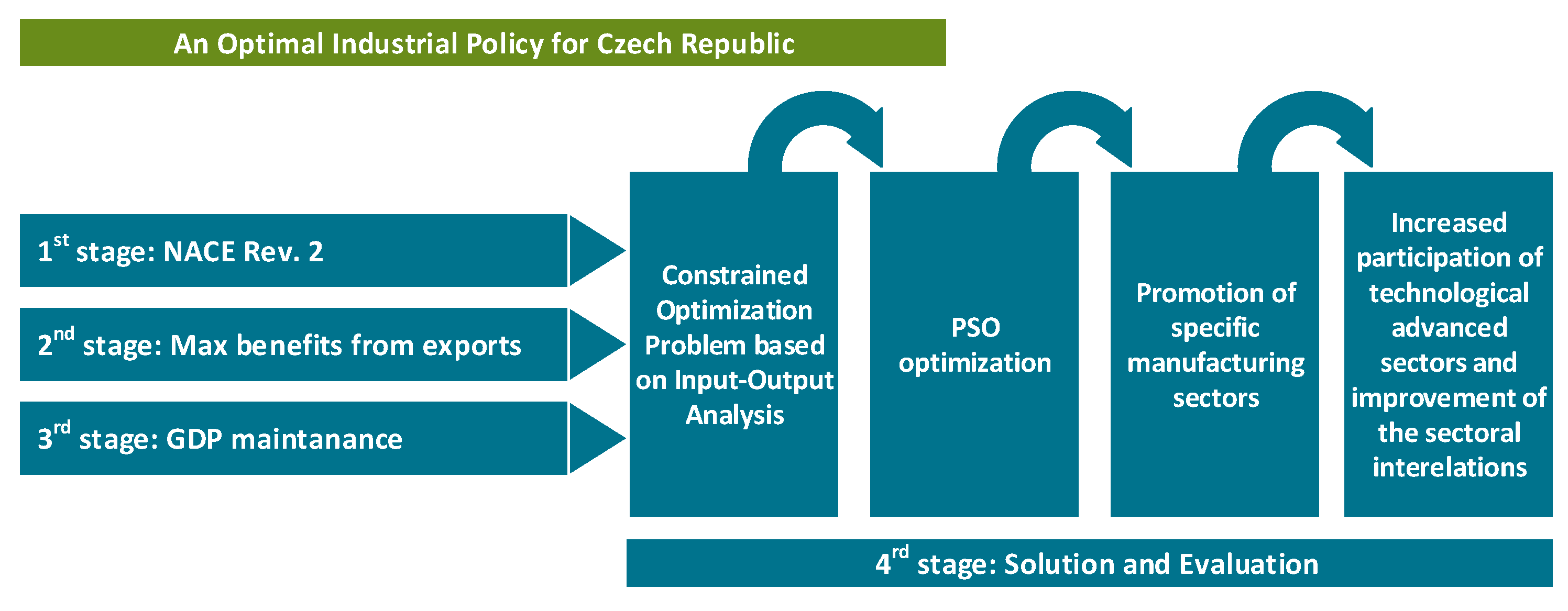
2.3. Optimizing the Impact Industrial Policy: A Methodological Approach

Although the identification of the strategic sectors itself provides the bases for the construction of the industrial policy, there is no certainty about the impact of the policy plan implementation. Nevertheless, the industrial policy can contribute on solving the so-called “co-ordination problem” between the government and the private sector, thus, contributing to removing obstacles in adopting new technologies, upgrading skills, and improving productivity and facilitating positive externalities [23,34].

The majority of the relevant literature involves studies on China’s [35,36,37,38,39,40] or Beijing’s [41,42] optimal productive structure. The target of industrial policy varies among the studies. For instance, in Chang [35], Wang et al. [38] and Xu et al. [40], the target is maximizing the gross domestic product and minimizing the $C{O}_2$ emissions. In Tian et al. [36] and Lin [43], the maximization of GDP with the minimum possible energy consumption was considered. In Yu et al. [37], the maximization of GDP and the employment rate jointly with the minimization of energy consumption was attempted. In Su et al. [39], the optimization target was to maximize the overall social welfare expressed by per capita consumption. In the regional studies for Beijing, Mi et al. [41] simultaneously maximized GDP and minimized energy intensity, carbon intensity, energy consumption, and $C{O}_2$ emissions, while, for Zhu and Shan [42], the target was the minimization of $C{O}_2$ emissions and energy consumption and the maximization of GDP.

Other studies provide evidence of the structural transformation for Spain, Brazil, Australia, Vietnam, and Greece. San Cristóbal et al. [44] studied the economy of Spain in order to find the optimal structure through maximizing GDP and minimizing greenhouse gas emissions. De Carvalho et al. [45] optimized the productive structure for Brazil for four separate targets: maximization of GDP, minimization of the greenhouse gas emissions, minimization of the energy consumption, and maximization of employment. Sánchez et al. [46] defined the optimal structure of the Australian economy by maximizing GDP and employment and minimizing greenhouse gas emissions. Nguyen et al. [47] determined the ideal structure of Vietnam with the minimization of the carbon emissions and the energy consumption and the maximization of GDP. In the case of Greece, three different studies provide evidence for its optimal structure: Hristu-Varsakelis et al. [48] explored different scenarios based on GDP maximization and energy conservation to determine the optimal structure of the country. Papadakis and Markaki [49] optimized the economic structure of the country by minimizing greenhouse gas emissions intensity. Notably, all studies emphasized the vital importance of industrial policy due to the important difference between the observed and the optimal productive structure.

Although the existing research managed to provide a solution to case-study problems, it does not give a robust methodological framework for exploring different aspects of industrial policy. The diversity of the set targets and the different types of constraints usually make it difficult to recognize even the common denominator among the different approaches, that is, the modelling of the optimization problem using the IOA. Thus, a robust methodological approach was necessary to support various empirical applications, providing the tools to classify, compare, and evaluate different industrial policy plans.

This research addressed a generalized question: Which are the strategic sectors that an industrial policy should focus on for achieving the optimization of the economy’s productive structure, meeting specific macroeconomic targets? This study applied the proposed methodology to identify the strategic sectors based on the optimal exploitation of the development potential of the Czech economy.

The proposed methodology is structured into four stages (Figure 1):

• At the first stage, the productive structure of the examined economy is expressed by the selected sectoral classification. The applied classification should be in line with the corresponding classification of the available input–output tables.
• The second stage involves the determination of industrial policy target(s) and their mathematical modelling based on input–output analysis. Given that the proposed methodology has a strictly country-specific nature, the target(s) of different countries could be highly diverse, from macroeconomic to social or to environmental, or to any combination of them. At this stage, taking advantage of the IOA to provide a mathematical model for the real-world economic system [50], the target(s) of the industrial policy is expressed in connection with the productive structure of the examined economy at the sectoral level.
• Potential constraints are considered at the third stage. The possible constraints could guide the transformation process to inhibit the effectiveness of industrial policy measures. They are determined based on the economic and social features (such as technology, resources, and skills level) of the examined economy.
• Finally, the fourth stage includes the solution of the constrained optimization problem and the evaluation of the optimal economic structure.

Before proceeding with the examination of the mathematical formulation of the industrial policy’s optimization problem, the description of the aims of an industrial policy plan for the Czech Republic is necessary. The Czech Republic is an export-oriented economy. Currently, the automobile sector has the leading share in total exports. A slow-down in the motor-vehicle sector will herald a significant decline in the performance of the Czech economy. An industrial policy plan is necessary for the country to remedy this negative impact. In particular, policymakers in the Czech Republic should address the question of productive transformation without dropping the export-oriented character of the country.

At the first stage of the methodology, the sectoral classification of the economic system is determined. In this research, the NACE Rev. 2 classification was used, as it is also followed in the compilation of the input–output table for the Czech Republic [51]. At the second stage, the improvement in the performance of exports of the Czech Republic is set as the macroeconomic target. A measure of the impact of exports in an economy is the domestic value-added content of exports (DCX), a measure widely used to quantify a country’s position in the GVCs [52,53]. DCX represents the impact of exports in a country’s value-added generation. Carrasco and Tovar-Garcia [54] found that the DCX is positively associated with economic growth. Thus, the maximization of DCX also means the maximization of the trade benefits for the country. Finally, at the third stage, the current level of GDP is set as the constraint to the optimization model. The choice of this constraint is due to the economic instability of the international trade, which could create a bulwark against economic growth (Figure 2).

The principal peculiarity of the optimization model for the Czech industry is the use of both the value-added structure and the structure of sectoral interdependencies as the decision variables. Thus, the reallocation of production concerns not only sectoral shifts in production but also changes in the economic interdependencies of the sectors. This type of productive transformation, focusing on the interdependencies, is usually connected with the import substitution policies [49]. The recent GVCs literature draws attention to the “quality” participation in GVCs, resulting from an improved productive structure (i.e., in the GVCs terminology, this improvement is connected with higher value-added activities). Furthermore, in the process of GVCs integration, the intermediate structure of the economy, as expressed through IOA, should not be ignored. López González et al. [55] maintain that the limited gaining from GVCs participation in some counties is connected with overlooking the effort to build capabilities by developing the backward linkages. Thus, a decline in a country’s dependence on imported intermediate inputs and the subsequent limitation of the economic leakages will improve its export performance, as expressed in DCX [56]. In this research, a coherent methodological approach connecting the exports performance, the reallocation of production, and the improvement in the sectoral interdependencies is proposed for the optimization of the productive structure of the Czech economy.

3. The Optimization Model

This section provides the required mathematical background for formulating the productive transformation of the economy as a constraint optimization problem. The objective function, expressing the domestic value-added content of exports (DCX) and the constraint (GDP level), is given as a function of the decision variables (sectoral structure of the value-added and the distribution coefficients of the economy), based on input–output analysis. A full description of the IOA analysis for the formulation of the optimization problem can be found in [49].

3.1. The Decision Variables

The decision variables of the optimization model are the sectoral structure of the value-added and the domestic distribution coefficients. Given an economy with $n\in \mathbb{Z}$ sectors, the first decision variable is the vector $\mathit{v} \in {ℝ}^{n\times 1}$, a specific element of which represents the value-added of the respective sector. The second decision variable is a matrix ${\mathit{B}}_d\in {ℝ}^{n\times n}$, whose elements represent the distribution coefficients. A specific element $b\left[i,j\right]$ of ${\mathit{B}}_d$ expresses the share of sector $i^{th}$ production used as intermediate input for the production of sector $j^{th}$. The domain of $\mathit{v}$ is defined by a lower and an upper vector ${\mathit{n}}_1,{\mathit{n}}_2\in {ℝ}^{n\times 1}$, respectively, according to Equation (1), where the symbol $\preccurlyeq$ denotes an element-wise comparison for all the elements of the respective vectors.

$${\mathit{n}}_1\preccurlyeq \mathit{v}\preccurlyeq {\mathit{n}}_2$$

(1)

The domain of ${\mathit{B}}_d$ depends on the share of imported intermediate demand, which can be covered by domestic production. It is defined based on the estimated economic capacities of each sector. The domain of ${\mathit{B}}_d$ is defined by a lower and by an upper matrix ${\mathit{B}}_{\mathbf{1}},{\mathit{B}}_{\mathbf{2}}\in {ℝ}^{n\times n}$, respectively, described by Equation (2).

$${\mathit{B}}_1\preccurlyeq {\mathit{B}}_d\preccurlyeq {\mathit{B}}_2$$

(2)

The determination of the vectors ${\mathit{n}}_1,{\mathit{n}}_2$ and the matrices ${\mathit{B}}_1,{\mathit{B}}_2$ is discussed in Section 3.5.

3.2. The Optimization Model

The domestic value-added content of exports ($DCX \in {ℝ}^{1\times 1})$ is defined as:

$$DCX={\mathit{v}}_{\mathit{I}}^T·{\left({\mathit{I}}_n-{\mathit{A}}_d\right)}^{-\mathbf{1}}·\mathit{e}$$

(3)

where $\mathit{e}\in {ℝ}^{n\times 1}$ is a vector whose specific element represents the exports of a particular sector, ${\left({\mathit{I}}_n-{\mathit{A}}_d\right)}^{-\mathbf{1}}\in {ℝ}^{n\times n}$ is the Leontief inverse matrix, ${\mathit{I}}_n\in {ℝ}^{n\times n}$ is the unity matrix of dimension $n$, and ${\mathit{v}}_{\mathit{I}}\in {ℝ}^{n\times 1}$ is the value-added intensity per sector.

The matrix of technological coefficients ${\mathit{A}}_d \in {ℝ}^{n\times n}$ (or the matrix of direct requirements) is defined by Equation (4) for determining the Leontief inverse matrix.

$${\mathit{A}}_d={\mathit{Z}}_d·{\widehat{\mathit{X}}}^{-1}$$

(4)

where ${\mathit{Z}}_d\in {ℝ}^{n\times n}$ represents the matrix of domestically produced intermediate demand, and $\widehat{\mathit{X}}\in {ℝ}^{n\times n}$ is a diagonal matrix, whose diagonal elements are the elements of vector $\mathit{x} \in {ℝ}^{n\times 1}$. A specific element of $\mathit{x}$ represents the gross output of a particular sector. A specific element $z_d\left[i,j\right]$ of ${\mathit{Z}}_d$ represents the production of sector $i$, which is used as an intermediate input by sector $j$. Dividing $z_d\left[i,j\right]$ by the total output of sector $j$, the domestic technological coefficient $a_d\left[i,j\right]=z_d\left[i,j\right]/x\left[j\right]$ is computed. The domestic technological coefficient $a_d\left[i,j\right]$ represents the direct domestic requirement of sector $i^{th}$ output needed to produce one unit of sector $j^{th}$ output.

Following Leontief [50], the gross output per sector of economic activity $\mathit{x}$, can be expressed as follows:

$$\mathit{x}={\mathit{A}}_d·\mathit{x}+{\mathit{f}}_d \Rightarrow \mathit{x}={\left({\mathit{I}}_n-{\mathit{A}}_d\right)}^{-1}·{\mathit{f}}_d$$

(5)

where ${\mathit{1}}_n\in {ℝ}^{n\times 1}$ is an $n$-dimensional vector, each element of which equals one, and ${\mathit{f}}_d\in {ℝ}^{n\times 1}$ is the vector of the final demand components (exports, public and private consumption, gross capital formation, and change in inventories) that are domestically produced.

A typical element $i,j\in \left[1,n\right]$ of the Leontief inverse matrix [27] shows the sector’s-$i$ product, which is required for the production of one unit of the final demand of the sector’s-$j$ output.

The value-added intensity is defined as the ratio of value-added over to gross output [57], and it is computed by Equation (6).

$${\mathit{v}}_I={\widehat{\mathit{X}}}^{-\mathbf{1}}·\mathit{v}$$

(6)

Following Ghosh [58], the gross output per sector of economic activity $\mathit{x}$, can be expressed as follows:

$$\mathit{x}={({\left({\mathit{I}}_n-\mathit{B}\right)}^{-\mathbf{1}})}^{\mathit{T}}·\mathit{v}$$

(7)

where $\mathit{B}\in {ℝ}^{n\times n}$ is the matrix of total distribution coefficients, defined as follows:

$$\mathit{B}={\widehat{\mathit{X}}}^{-\mathbf{1}}·\mathit{Z}$$

(8)

In Equation (8), Z $\in {ℝ}^{n\times n}$ is the matrix of the total intermediate demand, both domestic and foreign. A particular element $z\left[i,j\right]$ of $\mathit{Z}$ represents the production of sector $i$ (domestic and imported), which is used as intermediate input by the sector $j$.

Let ${\mathit{Z}}_m\in {ℝ}^{n\times n}$ be the matrix of imported intermediate demand. A particular element $z_m\left[i,j\right]$ of ${\mathit{Z}}_m$ expresses the imports of sector $i$ that is used as intermediate input by the sector $j$. Then, Equation (9) is followed by the definition of $\mathit{Z},{\mathit{Z}}_m,{\mathit{Z}}_d$.

$$\mathit{Z}={\mathit{Z}}_{\mathit{d}}+{\mathit{Z}}_{\mathit{m}}$$

(9)

In line with Equation (4), the matrices ${\mathit{B}}_d\in {ℝ}^{n\times n}$ and ${\mathit{B}}_m\in {ℝ}^{n\times n}$ are defined as follows:

$${\mathit{B}}_d={\widehat{\mathit{X}}}^{-\mathbf{1}}·{\mathit{Z}}_d$$

(10)

$${\mathit{B}}_m={\widehat{\mathit{X}}}^{-\mathbf{1}}·{\mathit{Z}}_m$$

(11)

The matrix $\mathit{B}$ is defined from Equations (9)–(11) as:

$$\mathit{Z}={\mathit{Z}}_d+{\mathit{Z}}_m\Rightarrow \widehat{\mathit{X}}·\mathit{B}=\widehat{\mathit{X}}·{\mathit{B}}_d+\widehat{\mathit{X}}·{\mathit{B}}_m\Rightarrow \mathit{B}={\mathit{B}}_d+{\mathit{B}}_m$$

(12)

As shown in Miller and Blair [27], the matrices ${\mathit{A}}_d$ and ${\mathit{B}}_d$ are similar; hence:

$${\mathit{A}}_d=\widehat{\mathit{X}}·{\mathit{B}}_d·{\widehat{\mathit{X}}}^{-1}$$

(13)

Finally, exports are part of the final demand. If $\mathit{e}\in {ℝ}^{n\times 1}$ is a vector expressing the share of exports in the final demand per sector and $\widehat{\mathit{E}} \in {ℝ}^{n\times n}$ is a diagonal matrix with diagonal elements equal to the elements of vector $\mathit{e}$, then:

$$\mathit{e}=\widehat{\mathit{E}}·{\mathit{f}}_d=\widehat{\mathit{E}}·\left({\mathit{I}}_n-{\mathit{A}}_d\right)·\mathit{x}$$

(14)

Based on Equations (3), (4), (6) and (13), the objective function $DCX$ can be expressed by using the decision variables ${\mathit{B}}_d,\mathit{v}$, when ${\mathit{e}}_s$ and $\mathit{B}$ are given.

The constraint of the optimization model is that the $GDP$ of the economy should remain at a specific level $GD{P}_0\in {ℝ}^{1\times 1}$. The mathematical formulation of $GDP\in {ℝ}^{1\times 1}$ is:

$$gdp\left(\mathit{v}\right)={\mathbf{1}}_{\mathit{n}}^{\mathit{T}}·\mathit{v}$$

(15)

In summary, the productive restructuring model can be formulated as a constraint optimization problem, as it is defined by Equation (16):

$$\begin{array}{cc}Maximize& DCX\left({\mathit{B}}_d,\mathit{v}\right)\\ {\mathit{B}}_1\preccurlyeq {\mathit{B}}_d\preccurlyeq {\mathit{B}}_2& \\ {\mathit{n}}_1\preccurlyeq \mathit{v}\preccurlyeq {\mathit{n}}_2& \\ & \\ subject to:& \\ & \\ GDP\left(\mathit{v}\right)=GD{P}_0& \\ & \end{array}$$

(16)

A matrix ${\mathit{B}}_d^{*}$ and a vector ${\mathit{v}}^{*}$ that maximize the $DCX$ describe the optimal structure of the economic system.

It should be underlined that the matrix $\mathit{B}$ (Equation (8)) is considered constant since there is not a technical change in the economy. Thus, ${\mathit{B}}_d^{*}$ reflects an optimal level of import substitution in the intermediate demand, which also defines an optimal matrix ${\mathit{B}}_m^{*}$ so that the equation ${\mathit{B}}_d^{*}+{\mathit{B}}_m^{*}=\mathit{B}$ is satisfied.

The constraint optimization problem of Equation (16) could be converted into an equivalent unconstraint optimization problem by penalizing the solutions that violate the constraints by using a penalty function given by Equation (17).

$$p\left(\mathit{v},GD{P}_0\right)=\lambda ·\left|gdp\left(\mathit{v}\right)-GD{P}_0\right|$$

(17)

where $\lambda$ is a positive arbitrarily large real number. Consequently, the unconstraint objective function, equivalent to Equation (16), is given by Equation (18).

$$Q\left({\mathit{B}}_d,\mathit{v}\right)=\frac{DCX\left({\mathit{B}}_d,\mathit{v}\right)}{1+p\left(\mathit{v},GD{P}_0\right)}$$

(18)

3.3. Evaluating the Results

Based on Miller and Blair [27], the backward linkages of an economy are represented by the row vector ${\mathit{b}}_l\in {ℝ}^{n\times 1}$, computed by Equation (19), while the forward linkages are the row vector ${\mathit{f}}_l\in {ℝ}^{n\times 1}$ computed by Equation (20).

$${\mathit{b}}_{\mathit{l}}={\mathbf{1}}_n^T·{\left({\mathit{I}}_{\mathit{n}}-{\mathit{A}}_{\mathit{d}}\right)}^{-\mathbf{1}}$$

(19)

$${\mathit{f}}_{\mathit{l}}={\left({\mathit{I}}_{\mathit{n}}-{\mathit{B}}_{\mathit{d}}\right)}^{-1}·{\mathbf{1}}_{\mathit{n}}$$

(20)

A specific element $b_l\left[j\right], j=1,2,\dots ,n$ of ${\mathit{b}}_l$ measures the direct and indirect product due to one unit increasing the $j^{th}$ sector final demand. A specific element $f_l\left[j\right], j=1,2,\dots ,n$ of ${\mathit{f}}_l$ measures the direct and indirect product due to one unit increasing the $j^{th}$ sector’s value-added. Thus, the backward linkages of a sector quantify its dependency upon the production of other sectors, while forward linkages quantify its dependency upon the purchases of other sectors.

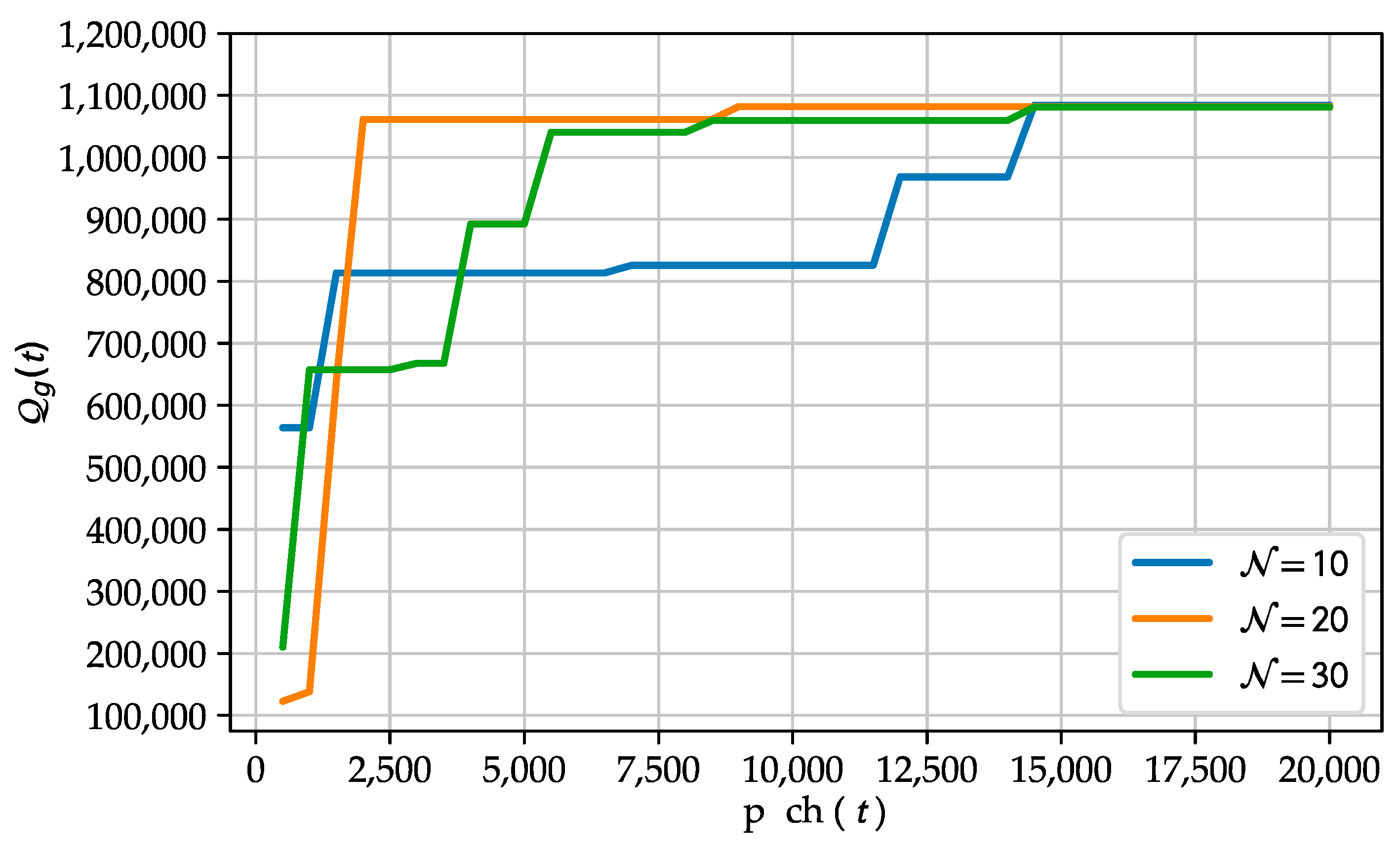
3.4. Particle Swarm Optimization

The function given by Equation (18) is a non-linear function in the parameter vectors $\mathit{v},{\mathit{B}}_d$ because of the fraction in Equation (18) and the inverse Leontief used for computing DCX. Therefore, a nonlinear optimization algorithm should be applied for solving it. The nonlinear optimization algorithms can be roughly divided into two major classes: (a) derivative-based optimization methods, where the derivatives of the objective function in the depended variables are required, and (b) evolutionary, bio-inspired optimization algorithms that belong to the computational intelligence paradigm [59,60] and which are derivative-free non-linear optimization techniques (e.g., genetic algorithms, particle swarm optimization, etc.).

The second class of algorithms has many advantages over the first one such that: (a) the derivatives of the objective function are not required. It is an essential advantage because the objective function is optimizable even in the case that it is non-differentiable and non-continuous. In addition, the application of the algorithm is simpler because the theoretical computation of derivatives, which is hard in some cases, is not required. (b) They are by design able to escape from local optima by in parallel evaluating the search space using a population of solutions, in contrast to the derivative-based methods that use a single solution and that are prone to be trapped at local optima.

The common architecture of those (bio-nature inspired) algorithms is that they consist of a predefined population of individuals, each encoding a particular solution to the problem. The solution of each individual is evaluated through a function (quality function). The quality function is usually the objective function, which is going to be optimized (function optimization). At the initialization step of the algorithm, the individuals represents random solutions. These solutions are evaluated through the objective function, and a new population is generated according to an evolution mechanism (e.g., reproduction, motion, etc.) with the expectation that the new population will include better solutions than the previous one. The way the new generation is produced is the foremost noticeable difference between the algorithms. Moreover, the performance of each algorithm is affected by some operational parameters, namely, hyperparameters (e.g., population size, maximum numbers of epochs, etc.).

The particle swarm optimization (PSO for short) introduced by [61] is one of the most competitive choices from the wide list [59] of algorithms for two reasons. (A) It has a relatively easy configuration (i.e., decision of hyper parameter values) and (B) the tuning of the balance between exploration-exploitation capacity, which is a key concept in optimization, is quite comprehensive. Especially, for a particular variation of the original PSO algorithm, namely, constriction factor PSO, ref. [62], theoretical analysis of their operation and convergence exists [63]. Moreover, the optimal values for the majority of the hyperparameters are suggested ensuring fast convergence and minimizing the risk of being trapped in local optima. The constriction factor PSO, employed in this work, is briefly described in the following paragraphs.

The PSO algorithm imitates the moving behavior of flocks [61]. It consists of a population of $\mathcal{N}\in \mathbb{N}$ number of particles. Each particle ${𝓅}_i , i=1,\dots ,\mathcal{N}$ is an entity consisted of a position vector ${\mathit{𝔁}}_i=\left[{𝔁}_{i,1},\dots ,{𝔁}_{i,j},\dots ,{𝔁}_{i,m}\right]\in {ℝ}^{𝓂}$ representing a candidate solution in the $𝓂-$ dimensional real value space and a real value ${𝓆}_i=\mathcal{Q}\left({\mathit{𝔁}}_i\right)\in ℝ$ (quality), where $\mathcal{Q}:𝔁\mapsto ℝ$ is the quality function (objective function for function-optimization problems). The position of each particle is randomly initialized at the beginning of evolution (step or epoch $𝓉=0$). The quality of each particle is computed through $\mathcal{Q}(.)$, and its position ${\mathit{𝔁}}_{i,\ell }\left(𝓉\right)$ (particle local best) is memorized. The position ${\mathit{𝔁}}_g\left(𝓉\right)$ of the best particle of the population is also memorized. The position of particles is modified in the next epoch $\left(𝓉=1\right)$ according to the motion equations given by Equations (21) and (22).

$$\begin{gathered} {𝓋}_{i,j}\left(𝓉+1\right)={𝓋}_{i,j}\left(𝓉\right)+{𝒸}_1·{𝓇}_{1,i,j}·\left[{𝓍}_{\ell ,i,j}\left(𝓉\right)-{𝓍}_{i,j}\left(𝓉\right)\right]+{𝒸}_2·{𝓇}_{2,i,j} \\ ·\left[{𝓍}_{\mathrm{g},j}\left(𝓉\right)-{𝓍}_{i,j}\left(𝓉\right)\right] \end{gathered}$$

(21)

$$\begin{array}{cc}\hfill {𝓍}_{i,j}\left(𝓉+1\right)& ={𝓍}_{i,j}\left(𝓉\right)+\mathcal{K}·{𝓋}_{i,j}\left(𝓉+1\right)\hfill \\ \hfill i& =1,\dots ,\mathcal{N}\hfill \\ \hfill j& =1,\dots ,𝓂\hfill \end{array}$$

(22)

where $𝓉$ denotes the current epoch; ${𝓋}_{ij}$ denotes the velocity of ${𝓅}_i, i=1,\dots ,\mathcal{N}$ in dimension $j=1,\dots ,𝓂$; ${𝒸}_1,{𝒸}_2$ are constants, namely, the self and social learning factors, respectively; ${𝓇}_{1,i,j},{𝓇}_{2,i,j}$ are random numbers uniformly distributed in the interval $\left[0,1\right]$. $\mathcal{K}\in ℝ$ is a factor named the constriction factor, introduced in [63] and given by Equation (23). In the same theoretical analysis, Clerc and Kenedy showed that if $\varphi ={𝒸}_1+{𝒸}_2>4$, then the convergence of the algorithm is guaranteed, and its capacity for avoiding local optima is reinforced. The proposed ${𝒸}_1={𝒸}_2=2.1$, is a rational choice for the majority of applications.

$$\mathcal{K}=\frac{2}{\left|2-\varphi -\sqrt{{\varphi }^2-4·\varphi }\right|}$$

(23)

The particles change their positions according to Equations (21) and (22), and the new positions are evaluated according to the quality function $\mathcal{Q}(.)$. In addition, the particle’s local best ${\mathit{𝔁}}_{i,\ell }\left(𝓉\right)$ (i.e., the best position the particle achieved until epoch $𝓉$) and the global best position ${\mathit{𝔁}}_g\left(𝓉\right)$(i.e., the best position achieved over all particles until epoch $𝓉$) are also updated and memorized. The evolution proceeds for a predefined number $\mathcal{T}\in \mathbb{N}$ of epochs, and the vector ${\mathit{𝔁}}_g\left(\mathcal{T}\right)$ is the final solution to the problem.

In order to apply the PSO algorithm for optimizing the function given by Equation (18), we seek the values ${\mathit{B}}_d^{*},{\mathit{v}}^{*}$ of ${\mathit{B}}_d,\mathit{v}$ that maximize the value of $Q\left({\mathit{B}}_d,\mathit{v}\right)$. To this end, the elements of matrix ${\mathit{B}}_d$ as well as the elements of vector $\mathit{v}$ should be encoded as position vectors of particles. Given the $n$ sectors of the economy ${\mathit{B}}_d$ has $n\times n=n^2$ elements, which are mapped row-wise into the first $n^2$ elements of the position vector. Additionally, the last $n$ elements of the position vector represent the $n$ elements of vector $\mathit{v}$. Conclusively, the length of position vector equals $n^2+n$. The quality function, according to which the positions (solutions to the problem) are evaluated, is given by Equation (18), that is $\mathcal{Q}\equiv Q$. Finally, there exists two hyperparameters: (a) the number $\mathcal{N}$ of particles and (b) the maximum number of epochs $\mathcal{T}$, since the rest of the hyperparameters (${𝒸}_1,{𝒸}_2,\mathcal{K}$) are theoretically suggested. The parameters $\mathcal{N},\mathcal{T}$ are experimentally decided by monitoring the best quality ${\mathcal{Q}}_g\left(𝓉\right)$ in the number of epochs for several values of $\mathcal{N},\mathcal{T}$. We observed (Figure 3) that by using $\mathcal{N}=10$ or $\mathcal{N}=30$ particles, the convergence of PSO was slower than using $\mathcal{N}=20$ particles. Moreover, the best quality landscape showed no improvement after $\mathcal{T}=10,000$ epochs for $\mathcal{N}=20$ particles. Hence, we decided $\mathcal{N}=20,$ $\mathcal{T}=20,000$ as an empirical “near optimal” value for the number of particles and the maximum number of epochs, respectively.

3.5. Data Collection and Preparation

The formulation of the optimization model is based on the 2015 input–output table for the Czech Republic [8], according to the NACE Rev. 2 classification [64], listed in

Table 1. Sectoral classification and substitution rate.

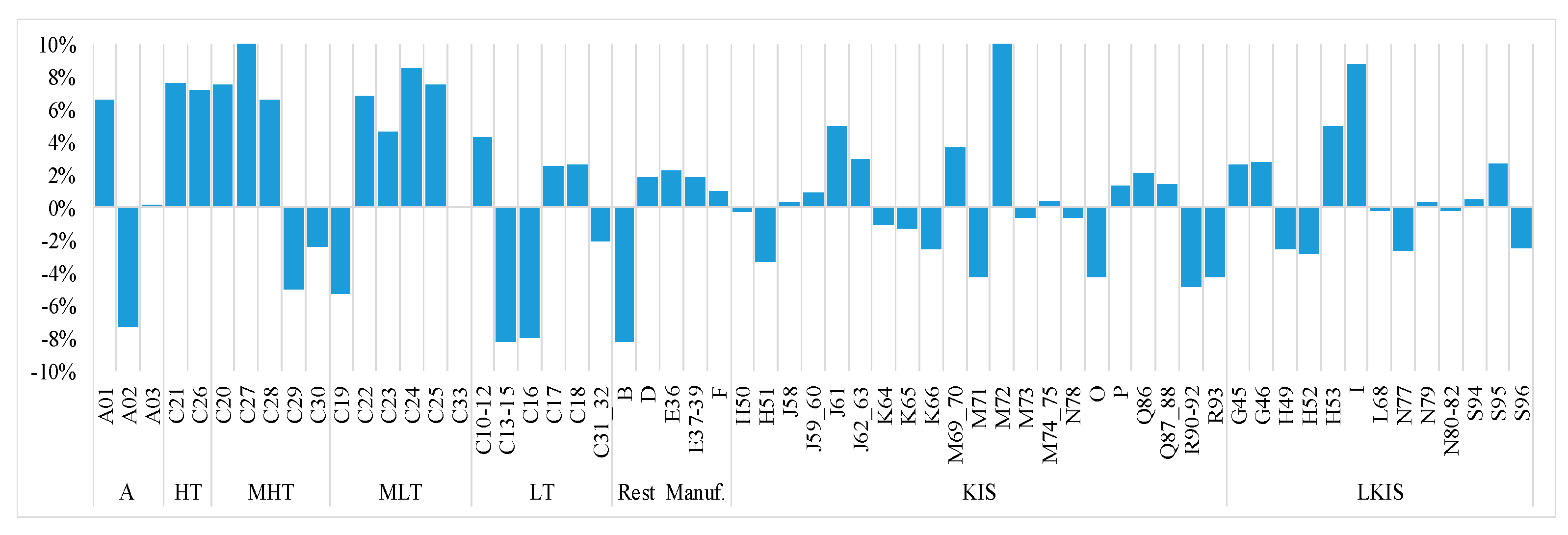
Sectors		Value-Added Change (%)		${\mathit{s}}_{\mathit{i}} (\%)$
		Minimum	Maximum
A01, products of agriculture, hunting, and related services	A	−5	15	5
A02, products of forestry, logging, and related services	A	−15	10	20
A03, fish and other fishing products	A	−1	1	15
B, Mining and quarrying	B	−10	0	2
C10–12, Food, beverages, and tobacco products	LT	2	7	25
C13–15, Textiles, wearing apparel, etc.	LT	−10	2	25
C16, Wood and products of wood and cork	LT	−8	8	25
C17, Paper and paper products	LT	−1	8	25
C18, Printing and recording services	LT	−10	1	15
C19, Coke and refined petroleum products	MLT	−15	5	5
C20, Chemicals and chemical products	MHT	−20	10	25
C21, Basic pharmaceutical products	HT	−10	15	25
C22, Rubber and plastic products	MLT	−10	2	25
C23, Other non-metallic mineral products	MLT	−5	5	25
C24, Basic metals	MLT	−15	10	25
C25, Fabricated metal products	MLT	−2	15	30
C26, Computers, electronic, and optical products	HT	−5	20	30
C27, Electrical equipment	MHT	−5	20	30
C28, Machinery and equipment n.e.c.	MHT	−5	0	30
C29—Motor vehicles, trailers, and semi-trailers	MHT	−5	−5	0
C30, Other transport equipment	MHT	−5	0	30
C31–32, Furniture and other manufactured goods	LT	−10	15	25
C33, Repair and installation services of machinery and equipment	MLT	0	5	50
D, Electricity, gas, steam, and air conditioning	D&E	−5	20	5
E36, Natural water; water treatment and supply services	D&E	−5	20	20
E37–39, Sewerage services; waste collection, etc.	D&E	0	15	20
F, Construction	F	−10	1	15
G45, Wholesale and retail trade and repair services of motor vehicles and motorcycles	LKIS	−8	3	40
G46–47, Wholesale and retail trade services	LKIS	−3	3	40
H49, Land transport and transport services via pipelines	LKIS	−10	0	5
H50, Water transport services	KIS	0	0	2
H51, Air transport services	KIS	−15	5	0
H52, Warehousing and support transportation services	LKIS	−5	5	2
H53, Postal and courier services	LKIS	−5	5	15
I, Accommodation and food services	LKIS	−15	5	5
J58, Publishing services	KIS	−2	2	5
J59–60, Motion picture, video, television program, etc.	KIS	−5	8	3
J61, Telecommunication services	KIS	−2	9	10
J62–63, Computer programming, consultancy etc.	KIS	−5	20	10
K64, Financial services	KIS	−2	7	25
K65, Insurance, pension funding services	KIS	−2	7	10
K66, Services auxiliary to financial and insurance services	KIS	−3	3	10
L68, Real estate services	LKIS	−8	9	5
M69–70, Legal and accounting services, etc.	KIS	−10	10	10
M71, Architectural and engineering services, etc.	KIS	−8	15	10
M72, Scientific research and development services	KIS	0	20	15
M73, Advertising and market research services	KIS	−20	10	20
M74–75, Other professional and veterinary services	KIS	−1	5	10
N77—Rental and leasing services	LKIS	−5	10	5
N78—Employment Services	KIS	−15	0	10
N79—Travel agency, etc.	LKIS	−20	5	0
N80–82—Security and investigation services, etc.	LKIS	−10	5	5
O—Public administration and defense services, etc.	KIS	−10	20	5
P—Educational services	KIS	−5	20	20
Q86—Human health services	KIS	−8	15	20
Q87–88—Residential care services; social work, etc.	KIS	−5	5	15
R90–92—Creative, arts, entertainment, libraries, etc.	KIS	−5	5	5
R93—Sporting, amusement, and recreation services	KIS	−5	5	5
S94—Services furnished by membership organizations	LKIS	−5	5	5
S95—Repair services of computers and personal goods	LKIS	−5	5	5
S96 T—Other personal services, etc.	LKIS	−5	5	5

Note: The technological intensity of the manufacturing sectors and the knowledge intensity of the services sectors follow Eurostat [65]. Sectors not listed in Eurostat [65] (i.e., A01–A03, B, E36–E39, and F) are referred to with the 1-digit NACE Rev. 2 classification. HT: high technology; MHT: medium-high technology; MLT: medium-low technology; LT: low-technology; KIS: knowledge-intensive services; LKIS: less-knowledge-intensive services; A: agriculture, forestry, and fishing; B: mining and quarrying; D&E: electricity, gas, steam, air-conditioning supply, water supply, sewerage, waste management, and remediation; F: construction.

. Furthermore, in the second column of Table 1, we also provide the aggregation of the manufacturing sectors according to the technology and the knowledge intensity [65], respectively.

Finally, the process for the determination of the decision variable’s domain is described. The determination of the value-added domain ${\mathit{n}}_1$ and ${\mathit{n}}_2$ was based on estimations of the minimum and maximum percentage change of the value-added, respectively, as depicted in the third and fourth columns of Table 1. Note that a decline of sector C29 was set to 5%. The minimum change ranged between −20% and 2% for the rest of the sectors, while the maximum change ranged between 0% and 20%.

The lower limit (${\mathit{B}}_1$) of ${\mathit{B}}_d$ was set equal to the matrix of distribution coefficients for the year 2015. The upper limit of ${\mathit{B}}_d$ was set to ${\mathit{B}}_2={\mathit{B}}_d+S·{\mathit{B}}_m$ where $\mathit{S}\in {ℝ}^{n\times n}$ is a diagonal matrix whose diagonal elements $s_i\in$ [0,1] are depicted in the last column of Table 1. The coefficients $s_i$ represent the maximum rate of intermediate input substitution. If $s_i=0\%$, then there is no possibility for intermediate import substitution for sector $i$, while if $s_i=100\%$, then the substitution of intermediates imports is full. For the Czech Republic, the minimum level of $s_i$ was set to 0% and the maximum to 50%. Owing to a lack of space, this section does not include a detailed description of the determination of ${\mathit{n}}_1, {\mathit{n}}_2, {\mathit{B}}_1$, and ${\mathit{B}}_2$.

4. Results and Discussions

The results indicate that the optimization of the production structure will increase the domestic content of exports for the Czech Republic. In monetary values, the optimal structure will increase the DCX from CZK 1661.9 billion to CZK 1721.5 billion. Nevertheless, the expected decline in the country’s exports due to the decrease in the demand for motor vehicles can be partly addressed by an improvement in the production structure. The optimal structure is accompanied by a decline in total exports by 1.03%. Notably, the DCX as a share of total exports will increase from 52.40% to 56.95% of gross exports, which equals a percentage increase of 6.77%. The rise of the DCX as a percentage of total exports is the result of the improved internal structure of the economic system. The reallocation of production and the densification of sectoral linkages increase DCX, even when total exports are decreasing.

Table 2. Impact of restructuring in the basic economic measures of the Czech Economy.

		Distribution of Value-Added		% Change of Value-Added between Base and Optimal Structure	Domestic Content of Exports per Unit of Gross Exports
		Current Structure	Optimal Structure		Current Structure	Optimal Structure	% Change
Primary	A	2.52%	2.57%	2.049%	0.017	0.018	6.73%
Secondary	HT	1.88%	2.02%	7.28%	0.018	0.020	9.01%
	MHT	11.31%	11.53%	1.87%	0.128	0.140	9.41%
	MLT	8.38%	8.88%	5.93%	0.088	0.096	9.67%
	LT	5.01%	4.98%	−0.63%	0.041	0.044	7.90%
	Rest Secondary (B, D, E, & F)	12.48%	12.66%	0.44%	0.037	0.039	3.64%
Tertiary	KIS	30.28%	29.94%	−1.14%	0.077	0.082	6.27%
	LKIS	29.75%	29.18%	−1.91%	0.117	0.126	7.48%
Total		100%	100%	-	0.524	0.566	7.93%

summarizes the impact of the optimal structure concerning the technological level of the sectors. As shown in Table 2, in 2015, 39.70% of the Czech economy’s total value-added was concentrated in manufacturing sectors, while some 60.04% was found in services sectors and only 2.52% in primary sectors. The optimal economic structure will increase production in the manufacturing and primary sectors up to 40.07% and 2.57%, respectively, along with a decline in the services sector to 59.12%. From the technological level point of view, the higher expansion of production was detected in the HT sectors (7.28%), followed by the MLT sectors (5.93%), and the MHT sectors (1.87%), while the LT sectors showed a slight decrease (−0.63%). Primary sectors showed an increase in their participation in the value-added creation (2.05%), and both the KIS and LKIS tertiary sectors showed a decline in their participation in value-added creation (−1.14% and −1.91%, respectively). Thus, the transition of the economy to the optimal structure requires increased participation of primary and secondary sectors and a slight decrease in the services sector. Notably, the outcome of the optimization was not homogenous if the results were analyzed in the two-digit NACE Rev. 2 classification. For example, the motor vehicle industry showed a decreased participation in the total value-added.

Nevertheless, the optimal structure suggests an increased share in total value-added even in MHT sectors, where the motor vehicle industry is included. Accordingly, a few manufacturing sectors showed a decreased participation in the value-added creation, even when they participated in a technological category with increased participation. This finding is analyzed in the following section.

Furthermore, Table 2 compares the domestic contents of sectors for the current and the optimal structure. The results reveal that the DCX per unit of gross exports will significantly improve for all technological levels. The increase was higher in the MLT, MHT, and HT sectors (9.67%, 9.41%, and 9.01%, respectively).

The findings presented in Table 2 reveal that the optimal productive structure of the Czech economy will significantly increase the participation of primary and manufacturing sectors to the creation of value-added and will decline the participation of services sectors. Simultaneously, the optimal productive structure is connected with increased DCX in all the economic sectors, even those with decreased value-added shares. For the interpretation of this unanticipated finding, the components of DCX should be carefully examined. As described in Equation (3), three components consist of the DCX: the value-added per sectoral output, the interlinkages of the sector, and the participation of each sector to the gross exports. Thus, the improved DCX in sectors that show a decline in value-added and exports was the result of the increased strength of the interlinkages of the economic system, expressed by the Leontief inverse matrix.

Moreover, the accumulative increase in DCX for the whole economy by 7.93% results from the restructuring process. The restructuring process creates superior production capabilities in the economy due to the reallocation of production towards higher value-added sectors and the stronger articulation of the economy resulting from the increased levels of the intermediate inputs. Specifically, the higher involvement of manufacturing and, particularly, of the advanced technology sectors improves the capabilities of the economic system. The industry is the main driver of productivity growth, generating forward and backward linkages, a spillover effect, and technological externalities; thus, manufacturing plays a special role in the economic development in connection with the rest of the economy [66,67]. In parallel, import substitution policies generate a more-complete and articulated economic structure contributing to production expansion and value-added generation [68].

The investigation of the results at an analytical sectoral level, as presented in Figure 4, revealed several sectors showing a significant increase (more than 7%) in value-added participation. Those sectors mainly belong to manufacturing, except for the services sector M72. In manufacturing, the HT sectors C21 & C26; the MHT sectors C20, C27, & C28; and the MLT sector C25 demonstrated higher levels of participation. The aforementioned sectors arise as the strategic sectors of the Czech Republic.

Furthermore, the primary sector A01 and the MLT manufacturing sectors C22, C23, & C24 also show increased value-added participation. Nevertheless, the participation of the sectors A02, B, C13–15, C16, and C19 in the value-added generation was significantly decreased (more than 5%) between the current and the optimal economic structure. The decline in these sectors was even higher than the motor-vehicle-sector decline. In addition, the sectors H50, H51, K64, K65, K66, M71, M73, N78, O, R90–92, R93, H49, H52, L68, N77, N80–82, and S96 of services and the sectors C31–32 of manufacturing showed a small or average decrease in their value-added ratio.

The technological structure of manufacturing is seen as an indicator of the development level of an economy [69]; thus, as Petralia et al. [70] observe, more developed, “high-income” countries tend to specialize in more complex, more valuable, and less concentrated technologies”. Thus, the increased participation of HT and MHT sectors in the Czech economy will lead to a productive structure oriented towards the production of more sophisticated goods and higher value-added goods. Accordingly, the domestic content of the country’s exports will be increased.

The investigation of the impact of restructuring on the level of interconnectedness of the economic system is an important aspect of the optimization. To this end, the percentage changes of the backward and the forward linkages are presented in Figure 4. As shown in Figure 4, all sectors demonstrated an improvement in their backward and forward linkages, with a more significant impact on manufacturing. Analytically, the manufacturing sectors C27, C30, C24, C25, and C18 and the manufacturing sectors C13–15, C17, C20, C21, C22, C24, C25, C26, C27, C28, and C33 showed a more than 5% increase in their backward and forward linkages, respectively. The corresponding increase in primary and services sectors was smaller, with an average rise of 1.84% and 1.15% of their backward and forward linkages, respectively.

Notably, all the strategic manufacturing sectors (C20, C21, C25, C26, C27, & C28) significantly expanded their forward linkages, and C25 also developed its backward linkages. These results are consistent with Savona (2018), who argues that interventions in processing industries (such as C25) would stimulate upstream supply via backward linked industries, while interventions in technologically advanced sectors rejuvenated demand coming from more mature manufacturing.

Furthermore, Figure 4 and Figure 5 show that no pattern of change exists. For instance, a relatively high increase in the value-added participation of a sector was not linked to a corresponding change in the backward and/or forward linkages, and vice versa. However, in manufacturing, the growth of value-added generation was accompanied by an improvement in forward linkages to a degree higher than backward linkages. This asymmetry between the improvement in forward and backward linkages is associated with the ability of forward linkages to express the level of import substitution of a sector in a straightforward manner. On the contrary, the improvement in backward linkages represents the level of import substitution of a sector’s suppliers.

Three main findings arise from the optimization model. The first one is the importance of manufacturing in the restructuring process. The central role of manufacturing in both value-added generation and the enhancement of the economy’s articulation is highlighted in this research. The second finding supports the notion of technologically advanced sectors as the drivers of economic growth and, in the case of the Czech Republic, as the ones that can also increase the value-added creation of exports. The majority of strategic sectors were defined as HT and MHT. Finally, the third finding is the relation between value-added creation and the forward linkage in the manufacturing sectors. As a sector grows, it increases the connection with other sectors, as a supplier of their intermediate inputs, and can respond to the import substitution policies more effectively.

5. Conclusions and Implementation Issues

The return of industrial policy in the academic debate and the political agenda of modern countries shows that sector-specific policy interventions should be undertaken to achieve the structural transformation of the economies. This research introduced a methodological framework based on input–output analysis to determine the optimal productive structure of an economy and, thus, the strategic sectors on which policy interventions should focus. A quantitative methodological framework was established to optimize the productive structure of an economic system with specific macroeconomic targets. The adopted methodological approach contributes to the growing body of research on industrial policy, ensuring that country-specific industrial policy is not just a wish-list of objectives. The policymakers could use the strategic sectors positioned by our approach for advocating specific policy interventions. The methodology was applied to the case of the Czech Republic, where manufacturing industries will face a production output cut-down due to the decreased demand for vehicles worldwide. The findings show that industrial policy in the Czech Republic should bring technologically advanced manufacturing to the forefront of restructuring policies for the country to retain its exporting performance.

The implementation of industrial policy is a critical issue that cannot be ignored. The restructuring methodology proposed in this research can be designed to address different economic and social objectives under a diverse range of constraints. Although the model can be applied in any country using country-specific objectives and constraints, the appropriate selection of policy instruments depends on its socioeconomic, institutional, and political conditions. Thus, the feasibility and practicality of the suggested productive restructuring should be evaluated [71]. Besides protectionism, policy measures such as increased research and development (R&D) funding, public procurement policies, encouraging foreign direct investment, export promotion, and GVCs integration policies are essential. The aforementioned measures are sector-oriented and can be designed to lead the economy to the optimal productive structure. However, policy measures such as skills and education policies, entrepreneurship programs, and infrastructure improvement might also be necessary.

The status of the Czech Republic could provide a first estimation of the feasibility of the industrial policy. The Czech Republic has relatively large shares of R&D-intensive technology-driven manufacturing industries, owing to which the country ranks 6th among the EU27 countries in the R&D index [72]. Analytically, the R&D spending amounted to 1.68% of GDP in 2018, whereas 32% of the R&D investment were sourced from third countries, indicating that the Czech Republic has attracted important and high-quality foreign-direct investments. In conclusion, the Czech Republic appears to have the potential to implement an industrial policy, avoiding the increasingly vulnerable motor-vehicle sector. Finally, the implementation of industrial policy is a long-term dynamic process that requires a monitoring mechanism to integrate and coordinate different types of policy measures.

Two possible directions for future research will be suggested here. The first direction concerns assessing the impact on the Czech economy of the recent EU proposal to ban all internal-combustion engines in new vehicles by 2035 [73]. As a result, Czech automobile manufacturers will be forced to redesign their production lines, significantly diversifying the industry’s interconnection with the rest of the economy. The mathematical modelling of this diversification through input–output analysis can provide important insights into the macroeconomic impact of the internal combustion engine ban and the diversified industrial policy perspectives of the country. The second direction of future research relates to central industrial policy issues that emerged for economic recovery in the post-COVID era. Such an issue identifies the optimal industrial policy that will ensure a degree of autarky so that countries can cope with global production and trade disruptions. Another important issue is the association between these policies and aspects of sustainable development, such as sustainable development and poverty reduction. Identifying optimal policies that can ensure a degree of autarky and sustainability provides an integrated macroeconomic framework for an economy. The input–output analysis offers the methodological framework for the mathematical modelling of that complex optimization problem.