Abstract
The purpose of this paper is to develop a numerical scheme for the two-dimensional fourth-order fractional subdiffusion equation with variable coefficients and delay. Using the approximation of the time Caputo derivative, a finite difference method with second-order accuracy in the temporal direction is achieved. The novelty of this paper is to introduce a numerical scheme for the problem under consideration with variable coefficients, nonlinear source term, and delay time constant. The numerical results show that the global convergence orders for spatial and time dimensions are approximately fourth order in space and second-order in time.
1. Introduction
The theory of fractional integrals and derivatives of arbitrary real or complex orders dates back approximately three centuries. In recent years, researchers have shown that differential equations with non-integer order derivatives can better model real-world physical phenomena than integer-order derivatives. Because of their importance in science and engineering, chemistry, physics, finance, and other fields [1], fractional differential equations have received increasing attention in recent years. In some cases, the analytical solution to fractional differential equations can be obtained using Laplace and Fourier transforms, as well as the Green function [2,3]. Due to the presence of a singular kernel in fractional derivatives, it is difficult to find an analytical solution for the majority of fractional differential equations.
In this paper, we implement a difference analog of the Caputo fractional derivative known as the [4] formula, which provides second-order global convergence in the time direction. Abbaszadeh and Dehghan [5] developed an accurate and robust numerical solution for solving neutral delay time-space distributed-order fractional damped diffusion-wave equation based on the Galerkin meshless method. They also obtained a meshless numerical simulation for a fractional damped diffusion-wave equation with delay [6]. Abbaszadeh et al. [7] introduced an interpolating stabilized element-free Galerkin method for neutral delay fractional damped diffusion-wave equations. In some important applications, the fourth-order derivative term plays a crucial role. Nikan et al. [8] proposed an efficient numerical procedure, the local radial basis function created by the finite difference method, for computing the approximation solution of the time-fractional fourth-order reaction-diffusion equation in terms of the Riemann–Liouville derivative. The time-fractional derivative was estimated using the second-order accurate formulation, while the spatial terms were discretized using the local radial basis function generated by the finite difference method. Huang and Stynes [9] studied -robust error analysis of a mixed -finite element method for a time-fractional fourth-order diffusion equation. For a two-dimensional distributed-order time-fractional fourth-order partial differential equation, Fakhar-Izadi [10] investigated the space-time Petrov–Galerkin spectral approach. The problem is converted to a multi-term time-fractional equation by using an appropriate Gauss-quadrature rule to discretize the distributed integral operator. Liu et al. [11] presented and discussed a finite difference/finite element algorithm for casting about for numerical solutions to a time-fractional fourth-order reaction–diffusion problem with a nonlinear reaction term, which is based on a finite difference approximation in time and a finite element method in spatial direction. Moreover, many numerical methods have been developed for solving different classes of fractional differential equations such as spectral methods [12,13,14,15,16,17,18,19], finite difference methods [20,21,22,23,24,25], finite element methods [26,27], finite volume method [28,29], and matrix transfer technique [30,31]. The study of delay differential equations with fractional derivatives is rapidly expanding these days since they are frequently employed in modeling of elastic media and stress–strain behavior for the torsional model, control difficulties, high-speed machining communications, and so on [1].
The multidimensional fourth order nonlinear fractional subdiffusion model with time delay is obtained from the standard problem by replacing the first-order time derivative by fractional derivatives in the Caputo sense. The analytical solution of this problem is only gained for the linear case when the coefficients constants. Recently, the authors of [32,33,34] constructed numerical techniques for this problem with fourth-order fractional diffusion wave equations and some modifications have been considered in [35]. In [36], a Newton-linearized compact ADI scheme for Riesz space fractional nonlinear reaction-diffusion equations was constructed and analyzed. The numerical computation for a class of fourth-order linear fractional subdiffusion equations with spatially variable coefficient under the first Dirichlet boundary conditions were considered in [37]. Two finite difference schemes with second-order accuracy were derived by applying formula and formula, respectively, to approximate the time Caputo derivative. Liu et al. [38] studied and analyzed a Galerkin mixed finite element method combined with time second-order discrete scheme for solving nonlinear time fractional diffusion equation with fourth-order derivative term. Most of the numerical techniques opted in the articles are based upon approximation of Caputo time derivative which gives first-order convergence for fractional order , where is the fractional order (present in time-fractional derivative). Recently, articles based on orthogonal spline collocation method are published [39] which focus on weakly singular solutions and constructing a high-order numerical scheme for fourth-order subdiffusion equations.
In the real world, parameters such as the coefficients in the problem under consideration are spatially or temporally variable. Therefore, presenting a numerical scheme and finding numerical solution becomes a tedious task. There are many difficulties to build numerical schemes for fourth-order fractional differential equations with delay due to non-locality of the problem, variable coefficients, nonlinearity, and error depends upon the history of considered problem. Therefore, the main issue we address in this paper is introducing an effective numerical approach for multi-dimensional fourth-order fractional subdiffusion equations with delay. In the studies discussed above and mainly in literature, there is a lack of studies available on delay differential equations.
In this paper, our target is to present high ordered difference scheme to solve the following two-dimensional time-fractional subdiffusion equation of fourth-order with variable coefficients and nonlinear source term having a delay constant.
with the initial and the boundary conditions:
where and is its boundary. Here, is the temporal Caputo fractional operator of order , is the constant delay parameter and is the nonlinear source function with delay. , , , , , , , , and are all given sufficiently smooth functions. Now, we present the definitions of fractional integral, and fractional derivatives which would be used later.
Definition 1.
The Caputo fractional derivative [40] of order is defined by
Next, for discretization, we partition the mesh , where , , . Introducing the positive integers , , and N, let , , ( is a positive constant) are the spatial and temporal steps respectively. Define , , , , , .
1.1. The Discretization of the Time Fractional Operator
Alikhanov [4] constructed a discrete approximation for Caputo fractional derivative which will be mentioned firstly. Next, some Lemmas important in the later context are introduced to aid in constructing the numerical scheme for the system (1).
Definition 1
([4]). Let , the approximated formula for at the fixed point , , is called formula of second order temporal convergence for , given as follows:
Let , , ,
, ,
For , , and
further when ,
Defining
Below given Lemma estimates the error of the formula.
Lemma 1
([4]). For any and , it holds that
The next lemmas are giving some technical properties for Alikhanov formula.
Lemma 2
([41,42]). Let function , , and , then
Define
For any , , , we introduce the following notations:
Now, we define inner products and discrete norms useful in the analysis section of the described numerical scheme (for any ):
1.2. Numerical Scheme Construction
A numerical scheme is constructed by employing the linear operator for the spatial dimensions and the approximation of Caputo time-fractional derivative.
First, consider
Substituting (7) into (1a), yields
The numerical scheme for (1) is ready after that order reduction. Considering Equations (8)–(10) at yields
Using Lemma 1, we can write
Using the Taylor’s expansion we can write the following equalities:
Similarly, acting the operator on (17) gives
Employing Taylor’s expansion for the source term (linearization) gives
, , , ,
, , , , and there exists a positive constant C such that , , , .
Noticing the initial and boundary conditions at
2. Numerical Simulations
Two examples are presented here to show the efficiency of numerical scheme (29) for the problem defined in (1). Let be the solution of proposed numerical scheme.
Denote . , , .
Example 1.
Consider the following two-dimensional fourth-order subdiffusion equation:
where the initial and boundary conditions are defined specially so that the exact solution of above problem is
Problem (1) is solved using our proposed method. The numerical results are listed in Table 1 and Table 2. It can be monitored from the results that our proposed method gives order of convergences. The numerical results are obtained for different values of fractional order with varying values of time and spatial step sizes. Figure 1 gives surface plot for different values of time . The variation in numerical values can be observed from the varying range in with respect to change in the value of time variable. The obtained convergence orders are approximately 4, 4, 2 for spatial directions and time direction, respectively, and same is validated in Stability and Convergence section discussed above.

Table 1.
The maximum error and convergence order in time-dimension for example 1.

Table 2.
The maximum error and average convergence order in spatial-dimensions for Example 1.
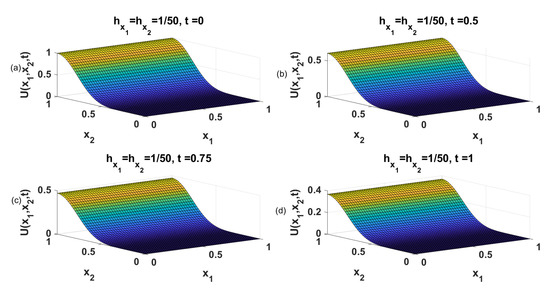
Figure 1.
The numerical solutions for Example 1 for different time values (a: , b: , c: , d: ).
We present a second problem solved with described numerical scheme. Maximum error was being computed for varying step sizes in space and time dimensions as given in Table 3 and Table 4. The decrease in error can be observed from these tables with decrease in step size. Moreover, we can observe that approximate convergence orders for space and time are 4 and 2, respectively. Figure 2 depicts the numerical solution for different values of time variable with spatial step sizes . Moreover, the convergence orders for spatial and time dimensions are authenticated in Stability and convergence section as well.

Table 3.
The maximum error and average convergence order in spatial dimensions for Example 2.

Table 4.
The maximum error and convergence order in time-dimension for Example 2.
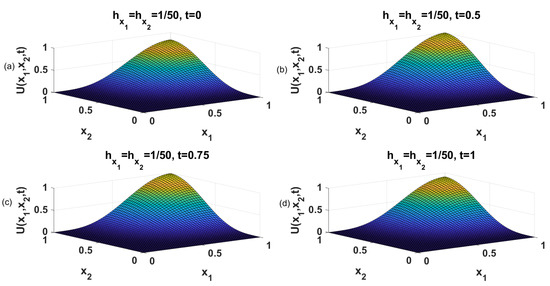
Figure 2.
The numerical solutions for Example 2 for different time values (a: , b: , c: , d: ).
Example 2.
Consider the two dimensional fourth order subdiffusion equation in the following form:
The exact solution of above example is
2.1. A Final Example
Finally, we consider a problem whose exact solution is not known to us.
Similar to above problems, we find the numerical results using the numerical scheme given in Equation (29). The above problem has variable coefficients and the exact solution is not known to us; therefore, we check the accuracy of proposed numerical scheme by means of absolute residual error function, which is a measure of how well the approximation satisfies the original nonlinear fractional differential problem given in Example Section 2.1. The absolute residual error is defined as
The numerical results are shown in Figure 3 with different time variable values. Table 5 and Table 6 show the numerical results of residual error , . From our numerical results, we can conclude that numerical and theoretical results are in agreement. The numerical scheme gives the global second-order time convergence and fourth-order convergence in spatial dimensions. The accuracy of getting convergence order becomes more pronounced when step sizes are decreased. In all the calculations MATLAB is used.
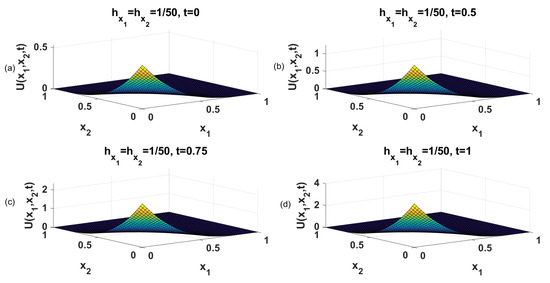
Figure 3.
The numerical solutions for Example Section 2.1 for different time values (a: , b: , c: , d: ).

Table 5.
The absolute residual error and average convergence order in spatial dimensions for Example Section 2.1 with .

Table 6.
The absolute residual error and average convergence order in time-dimension for Example Section 2.1 with .
3. Conclusions
The major contribution of this works lies in the construction of the numerical scheme and numerical results for two-dimensional fourth-order fractional subdiffusion equation with delay, nonlinear source term, and variable coefficients in case of smooth solutions. The numerical scheme presented in this paper incorporates the formula for Caputo’s time-fractional derivative. By invoking the works in [37,43] and due to the nonlocality of time Caputo fractional derivatives which need high computational cost and storage, we can improve our approach in the near future by presenting a high-order scheme based on the sum of exponential functions technique to speed up the evaluation. Furthermore, recalling the methodologies in [37,44] side by side to the numerical analysis in [35] and the appropriate discrete Grönwall inequality in [35,45], the unconditional convergence and stability estimates with out any constraints on time and space steps can be deduced. Assuming that and such that and are positive constants, is essential to prove the stability and convergence estimates which will be devoted to a new study in the near future. The numerical results indicate the efficiency of the numerical scheme. We obtained the fourth-order convergence in spatial dimensions and second-order convergence in the time dimension. Our numerical results validate the obtained theoretical results. The proposed numerical scheme can easily be extended and implemented for higher dimension problems.
Author Contributions
Conceptualization, all authors; methodology, all authors; software, S.N.; validation, M.A.Z. and A.S.H.; formal analysis, all authors; writing—original draft preparation, S.N., A.S.H., and M.A.Z.; writing—review and editing, A.S.H. and R.H.D.S.; visualization, S.N.; supervision and publication costs, R.H.D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by Woosong University Academic Research in 2021 and Nazarbayev University Program 091019CRP2120 and the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan (Grant “Dynamical Analysis and Synchronization of Complex Neural Networks with Its Applications”) and the National Research Centre of Egypt (NRC).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
M.A.Z. wishes to acknowledge the support of Nazarbayev University Program 091019CRP2120 and the partial support of the Science Committee of the Ministry of Education and Science of the Republic of Kazakhstan (Grant “Dynamical Analysis and Synchronization of Complex Neural Networks with Its Applications”). M.A.Z. wishes also to acknowledge the financial support of the National Research Centre of Egypt (NRC).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Anh, V.V. The analytical solution and numerical solutions for a two-dimensional multi-term time fractional diffusion and diffusion-wave equation. J. Comput. Appl. Math. 2019, 345, 515–534. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Liu, F.; Lin, Z.; Anh, V. Analytical and numerical solutions of a multi-term time-fractional Burgers’ fluid model. Appl. Math. Comput. 2019, 356, 1–12. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef] [Green Version]
- Abbaszadeh, M.; Dehghan, M. A Galerkin meshless reproducing kernel particle method for numerical solution of neutral delay time-space distributed-order fractional damped diffusion-wave equation. Appl. Numer. Math. 2021, 169, 44–63. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. Numerical and analytical investigations for neutral delay fractional damped diffusion-wave equation based on the stabilized interpolating element free Galerkin (IEFG) method. Appl. Numer. Math. 2019, 145, 488–506. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M.; Zaky, M.A.; Hendy, A.S. Numerical and analytical investigations for neutral delay fractional damped diffusion-wave equation based on the stabilized interpolating element free Galerkin (IEFG) method. J. Funct. Spaces 2021, 2021, 6665420. [Google Scholar] [CrossRef]
- Nikan, O.; Machado, J.T.; Golbabai, A. Numerical solution of time-fractional fourth-order reaction-diffusion model arising in composite environments. Appl. Math. Model. 2021, 89, 819–836. [Google Scholar] [CrossRef]
- Huang, C.; Stynes, M. α-robust error analysis of a mixed finite element method for a time-fractional biharmonic equation. Numer. Algorithms 2021, 87, 1749–1766. [Google Scholar] [CrossRef]
- Fakhar-Izadi, F. Fully petrov–galerkin spectral method for the distributed-order time-fractional fourth-order partial differential equation. Eng. Comput. 2021, 37, 2707–2716. [Google Scholar] [CrossRef]
- Liu, Y.; Du, Y.; Li, H.; He, S.; Gao, W. Finite difference/finite element method for a nonlinear time-fractional fourth-order reaction–diffusion problem. Comput. Math. Appl. 2015, 70, 573–591. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. A method based on the Jacobi tau approximation for solving multi-term time–space fractional partial differential equations. J. Comput. Phys. 2015, 281, 876–895. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K.M.; Baleanu, D.; Kumar, S. A spectral collocation method for fractional chemical clock reactions. Comput. Appl. Math. 2020, 39, 1–12. [Google Scholar] [CrossRef]
- Ameen, I.G.; Zaky, M.A.; Doha, E.H. Singularity preserving spectral collocation method for nonlinear systems of fractional differential equations with the right-sided Caputo fractional derivative. J. Comput. Appl. Math. 2021, 392, 113468. [Google Scholar] [CrossRef]
- Hafez, R.M.; Zaky, M.A.; Hendy, A.S. A novel spectral Galerkin/Petrov–Galerkin algorithm for the multi-dimensional space–time fractional advection–diffusion–reaction equations with nonsmooth solutions. Math. Comput. Simul. 2021, 190, 678–690. [Google Scholar] [CrossRef]
- Kumar, S.; Ghosh, S.; Kumar, R.; Jleli, M. A fractional model for population dynamics of two interacting species by using spectral and Hermite wavelets methods. Numer. Methods Partial. Differ. Equ. 2021, 37, 1652–1672. [Google Scholar] [CrossRef]
- Ameen, I.; Elkot, N.; Zaky, M.; Hendy, A.; Doha, E. A pseudo-spectral scheme for systems of two-point boundary value problems with left and right sided fractional derivatives and related integral equations. Comput. Model. Eng. Sci. 2021, 128, 21–41. [Google Scholar]
- Abo-Gabal, H.; Zaky, M.A.; Hendy, A.S.; Doha, E.H. Computational aspects of fractional Romanovski–Bessel functions. Comput. Appl. Math. 2021, 40, 1–16. [Google Scholar] [CrossRef]
- Ghosh, S.; Kundu, S.; Kumar, S.; Mahmoud, E.E. Spectral approximation methods for non equilibrium transport in turbulent channel flows using fADE. Appl. Numer. Math. 2021, 162, 53–66. [Google Scholar] [CrossRef]
- Hendy, A.S.; Zaky, M.A.; De Staelen, R.H. A general framework for the numerical analysis of high-order finite difference solvers for nonlinear multi-term time-space fractional partial differential equations with time delay. Appl. Numer. Math. 2021, 169, 108–121. [Google Scholar] [CrossRef]
- Hendy, A.S.; Zaky, M.A.; Abbaszadeh, M. Long time behavior of Robin boundary sub-diffusion equation with fractional partial derivatives of Caputo type in differential and difference settings. Math. Comput. Simul. 2021, 190, 1370–1378. [Google Scholar] [CrossRef]
- Hendy, A.S.; Zaky, M.A.; Suragan, D. Discrete fractional stochastic Grönwall inequalities arising in the numerical analysis of multi-term fractional order stochastic differential equations. Math. Comput. Simul. 2022, 193, 269–279. [Google Scholar] [CrossRef]
- Hendy, A.S.; Zaky, M.A.; Doha, E.H. On a discrete fractional stochastic Grönwall inequality and its application in the numerical analysis of stochastic FDEs involving a martingale. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Hendy, A.; Zaky, M.A.; Macías-Díaz, J. On the dissipativity of some Caputo time-fractional subdiffusion models in multiple dimensions: Theoretical and numerical investigations. J. Comput. Appl. Math. 2022, 400, 113748. [Google Scholar] [CrossRef]
- Hendy, A.S.; Zaky, M.A. Graded mesh discretization for coupled system of nonlinear multi-term time-space fractional diffusion equations. Eng. Comput. 2020, 1–13. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, Y.; Wang, F.; Liu, F. Novel superconvergence analysis of anisotropic triangular FEM for a multi-term time-fractional mixed sub-diffusion and diffusion-wave equation with variable coefficients. Numer. Methods Partial. Differ. Equ. 2021. [Google Scholar] [CrossRef]
- Yin, B.; Liu, Y.; Li, H.; Zhang, Z. Finite element methods based on two families of second-order numerical formulas for the fractional Cable model with smooth solutions. J. Sci. Comput. 2020, 84, 1–22. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, F.; Turner, I.W.; Anh, V.V.; Feng, L. A finite volume method for the two-dimensional time and space variable-order fractional Bloch-Torrey equation with variable coefficients on irregular domains. Comput. Math. Appl. 2021, 98, 81–98. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. The fourth-order time-discrete scheme and split-step direct meshless finite volume method for solving cubic–quintic complex Ginzburg–Landau equations on complicated geometries. Eng. Comput. 2020, 1–15. [Google Scholar] [CrossRef]
- Zheng, M.; Jin, Z.; Liu, F.; Anh, V. Matrix transfer technique for anomalous diffusion equation involving fractional Laplacian. Appl. Numer. Math. 2022, 172, 242–258. [Google Scholar] [CrossRef]
- Xu, T.; Liu, F.; Lü, S.; Anh, V.V. Numerical approximation of 2D multi-term time and space fractional Bloch–Torrey equations involving the fractional Laplacian. J. Comput. Appl. Math. 2021, 393, 113519. [Google Scholar] [CrossRef]
- Nandal, S.; Pandey, D.N. Numerical treatment of non-linear fourth-order distributed fractional sub-diffusion equation with time-delay. Commun. Nonlinear Sci. Numer. Simul. 2020, 83, 105146. [Google Scholar] [CrossRef]
- Nandal, S.; Pandey, D.N. Numerical solution of non-linear fourth order fractional sub-diffusion wave equation with time delay. Appl. Math. Comput. 2020, 369, 124900. [Google Scholar] [CrossRef]
- Nandal, S.; Pandey, D.N. Numerical technique for fractional variable-order differential equation of fourth-order with delay. Appl. Numer. Math. 2021, 161, 391–407. [Google Scholar] [CrossRef]
- Zaky, M.A.; Hendy, A.S.; Alikhanov, A.A.; Pimenov, V.G. Numerical analysis of multi-term time-fractional nonlinear subdiffusion equations with time delay: What could possibly go wrong? Commun. Nonlinear Sci. Numer. Simul. 2021, 96, 105672. [Google Scholar] [CrossRef]
- Cheng, X.; Duan, J.; Li, D. A novel compact ADI scheme for two-dimensional Riesz space fractional nonlinear reaction–diffusion equations. Appl. Math. Comput. 2019, 346, 452–464. [Google Scholar] [CrossRef]
- Pu, Z.; Ran, M.; Luo, H. Fast and high-order difference schemes for the fourth-order fractional sub-diffusion equations with spatially variable coefficient under the first Dirichlet boundary conditions. Math. Comput. Simul. 2021, 187, 110–133. [Google Scholar] [CrossRef]
- Liu, N.; Liu, Y.; Li, H.; Wang, J. Time second-order finite difference/finite element algorithm for nonlinear time-fractional diffusion problem with fourth-order derivative term. Comput. Math. Appl. 2018, 75, 3521–3536. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Tang, J. The OSC solver for the fourth-order sub-diffusion equation with weakly singular solutions. Comput. Math. Appl. 2021, 82, 1–12. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Sun, Z.Z. An unconditionally stable and O(τ2 + h4) order L∞ convergent difference scheme for linear parabolic equations with variable coefficients. Numer. Methods Partial. Differ. Equ. 2001, 17, 619–631. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Zhang, Z.B. A linearized compact difference scheme for a class of nonlinear delay partial differential equations. Appl. Math. Model. 2013, 37, 742–752. [Google Scholar] [CrossRef]
- Yan, Y.; Sun, Z.Z.; Zhang, J. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: A second-order scheme. Commun. Comput. Phys. 2017, 22, 1028–1048. [Google Scholar] [CrossRef]
- Zhong, J.; Liao, H.l.; Ji, B.; Zhang, L. A fourth-order compact solver for fractional-in-time fourth-order diffusion equations. arXiv 2019, arXiv:1907.01708. [Google Scholar]
- Hendy, A.S.; Pimenov, V.G.; Macías-Díaz, J.E. Convergence and stability estimates in difference setting for time-fractional parabolic equations with functional delay. Numer. Methods Partial. Differ. Equ. 2020, 36, 118–132. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).