Shearing Effects on the Phase Coarsening of Binary Mixtures Using the Active Model B
Abstract
1. Introduction
2. The Model
3. Results
3.1. Planar Interface
3.2. Phase Separation under Weak and Strong Shear
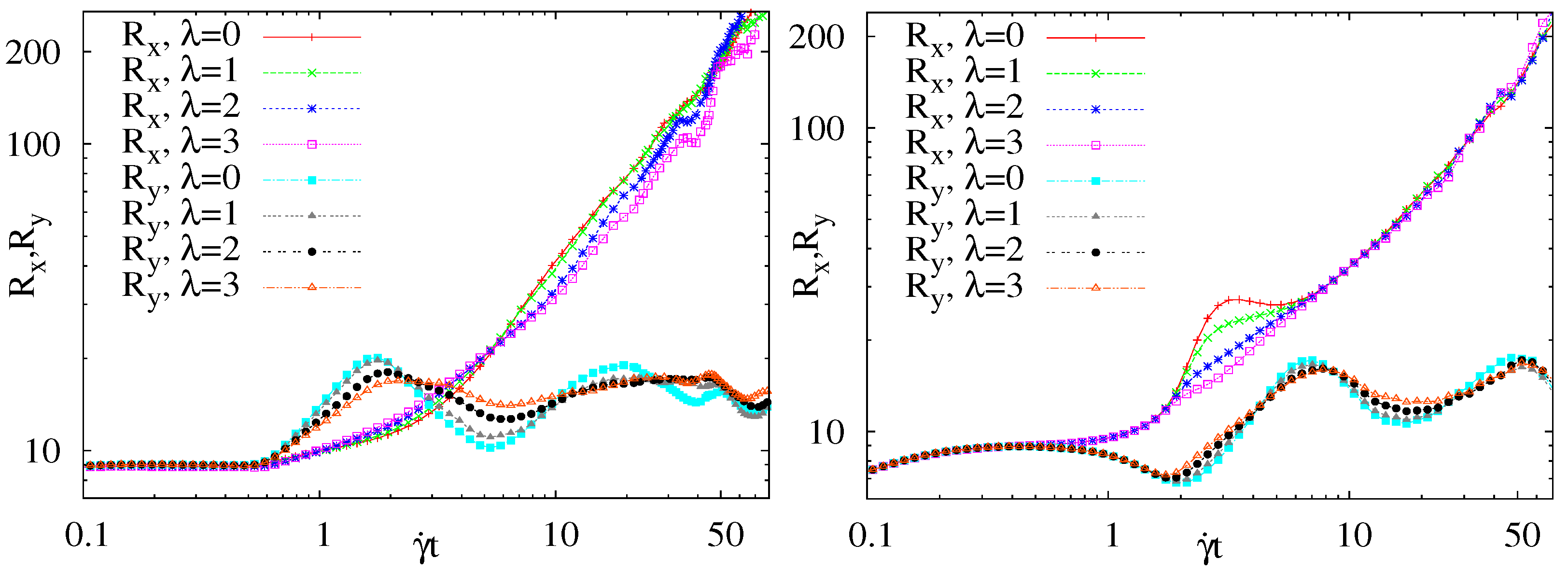
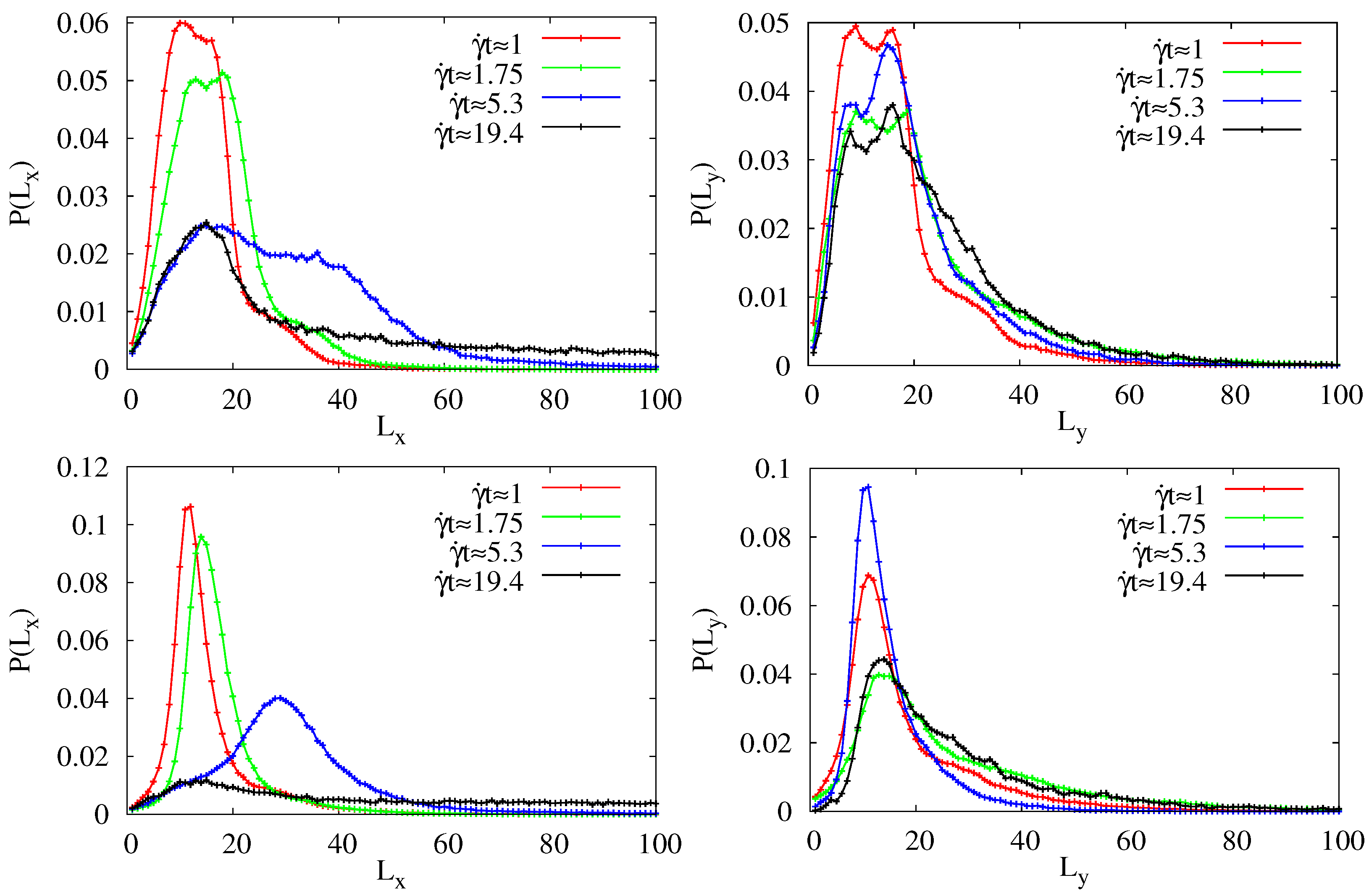
3.3. Domain Size
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ramaswamy, S. The Mechanics and Statistics of Active Matter. Annu. Rev. Condens. Mat. Phys. 2010, 1, 323–345. [Google Scholar] [CrossRef]
- Romanczuk, P.; Bär, M.; Ebeling, W.; Lindner, B.; Schimansky-Geier, L. Active Brownian particles. Eur. Phys. J. Spec. Top. 2012, 202, 1–62. [Google Scholar] [CrossRef]
- Marchetti, M.C.; Joanny, J.F.; Ramaswamy, S.; Liverpool, T.B.; Prost, J.; Rao, M.; Sima, R.A. Hydrodynamics of soft active matter. Rev. Mod. Phys. 2013, 85, 1143. [Google Scholar] [CrossRef]
- Bechinger, C.; Leonardo, R.D.; Löwen, H.; Reichhardt, C.; Volpe, G.; Volpe, G. Active particles in complex and crowded environments. Rev. Mod. Phys. 2016, 88, 045006. [Google Scholar] [CrossRef]
- Ramaswamy, S. Active fluids. Nat. Rev. Phys. 2019, 1, 640. [Google Scholar] [CrossRef]
- Leonardo, R.D.; Angelani, L.; Dell’Arciprete, D.; Ruocco, G.; Iebba, V.; Schippa, S.; Conte, M.P.; Mecarini, F.; Angelis, F.D.; Fabrizio, E.D. Bacterial ratchet motors. Proc. Nat. Acad. Sci. USA 2010, 107, 9541. [Google Scholar] [CrossRef]
- Sanchez, T.; Chen, D.T.N.; DeCamp, S.J.; Heymann, M.; Dogic, Z. Spontaneous motion in hierarchically assembled active matter. Nature 2012, 491, 431. [Google Scholar] [CrossRef]
- López, H.M.; Gachelin, J.; Douarche, C.; Auradou, H.; Clément, E. Turning Bacteria Suspensions into Superfluids. Phys. Rev. Lett. 2015, 115, 028301. [Google Scholar] [CrossRef]
- Dell’Arciprete, D.; Blow, M.L.; Brown, A.T.; Farrell, F.D.C.; Lintuvuori, J.S.; McVey, A.S.; Marenduzzo, D.; Poon, W.C.K. A growing bacterial colony in two dimensions as an active nematic. Nat. Commun. 2018, 9, 1. [Google Scholar] [CrossRef]
- Theurkauff, I.; Cottin-Bizonne, C.; Palacci, J.; Ybert, C.; Bocquet, L. Dynamic Clustering in Active Colloidal Suspensions with Chemical Signaling. Phys. Rev. Lett. 2012, 108, 268303. [Google Scholar] [CrossRef]
- Buttinoni, I.; Bialké, J.; Kümmel, F.; Löwen, H.; Bechinger, C.; Speck, T. Dynamical Clustering and Phase Separation in Suspensions of Self-Propelled Colloidal Particles. Phys. Rev. Lett. 2013, 110, 238301. [Google Scholar] [CrossRef]
- Palacci, J.; Sacanna, S.; Steinberg, A.P.; Pine, D.J.; Chaikin, P.M. Living crystals of light-activated colloidal surfers. Science 2013, 339, 936. [Google Scholar] [CrossRef] [PubMed]
- Needleman, D.; Dogic, Z. Active particles induce large shape deformations in giant lipid vesicles. Nat. Rev. Mater. 2017, 2, 17048. [Google Scholar] [CrossRef]
- Saw, T.B.; Doostmohammadi, A.; Nier, V.; Kocgozlu, L.; Thampi, S.; Toyama, Y.; Marcq, P.; Lim, C.T.; Yeomans, J.M.; Ladoux, B. Topological defects in epithelia govern cell death and extrusion. Nature 2017, 544, 212. [Google Scholar] [CrossRef] [PubMed]
- Shaebani, M.R.; Wysocki, A.; Winkler, R.G.; Gompper, G.; Rieger, H. Computational models for active matter. Nat. Rev. Phys. 2020, 2, 181. [Google Scholar] [CrossRef]
- Tailleur, J.; Cates, M.E. Statistical Mechanics of Interacting Run-and-Tumble Bacteria. Phys. Rev. Lett. 2008, 100, 218103. [Google Scholar] [CrossRef] [PubMed]
- Cates, M.E.; Tailleur, J. Motility-Induced Phase Separation. Annu. Rev. Cond. Matt. Phys. 2015, 6, 219–244. [Google Scholar] [CrossRef]
- Gonnella, G.; Marenduzzo, D.; Suma, A.; Tiribocchi, A. Motility-induced phase separation and coarsening in active matter. Compt. Ren. Phys. 2015, 16, 316. [Google Scholar] [CrossRef]
- Fily, Y.; Marchetti, M.C. Athermal Phase Separation of Self-Propelled Particles with No Alignment. Phys. Rev. Lett. 2012, 108, 235702. [Google Scholar] [CrossRef]
- Stenhammar, J.; Tiribocchi, A.; Allen, R.J.; Marenduzzo, D.; Cates, M.E. Continuum Theory of Phase Separation Kinetics for Active Brownian Particles. Phys. Rev. Lett. 2013, 111, 145702. [Google Scholar] [CrossRef]
- Stenhammar, J.; Allen, R.J.; Marenduzzo, D.; Cates, M.E. Phase behaviour of active Brownian particles: The role of dimensionality. Soft Matter 2014, 10, 1489. [Google Scholar] [CrossRef]
- Speck, T.; Bialké, J.; Menzel, A.M.; Löwen, H. Effective Cahn-Hilliard Equation for the Phase Separation of Active Brownian Particles. Phys. Rev. Lett. 2014, 112, 218304. [Google Scholar] [CrossRef]
- Fodor, E.; Nardini, C.; Cates, M.E.; Tailleur, J.; Visco, P.; van Wijland, F. How Far from Equilibrium Is Active Matter? Phys. Rev. Lett. 2016, 117, 038103. [Google Scholar] [CrossRef] [PubMed]
- Nardini, C.; Fodor, E.; Tjhung, E.; van Wijland, F.; Tailleur, J.; Cates, M.E. Entropy Production in Field Theories without Time-Reversal Symmetry: Quantifying the Non-Equilibrium Character of Active Matter. Phys. Rev. X 2017, 7, 021007. [Google Scholar] [CrossRef]
- Takatori, S.C.; Yan, W.; Brady, J.F. Swim Pressure: Stress Generation in Active Matter. Phys. Rev. Lett. 2014, 113, 028103. [Google Scholar] [CrossRef]
- Solon, A.P.; Chaté, H.; Tailleur, J. From Phase to Microphase Separation in Flocking Models. Phys. Rev. Lett. 2015, 114, 068101. [Google Scholar] [CrossRef] [PubMed]
- Ginot, F.; Theuekauff, I.; Levis, D.; Ybert, C.; Bocquet, L.; Berthier, L.; Cottin-Bizonne, C. Nonequilibrium Equation of State in Suspensions of Active Colloids. Phys. Rev. X 2015, 5, 011004. [Google Scholar] [CrossRef]
- Tjhung, E.; Nardini, C.; Cates, M.E. Cluster Phases and Bubbly Phase Separation in Active Fluids: Reversal of the Ostwald Process. Phys. Rev. X 2018, 8, 031080. [Google Scholar] [CrossRef]
- Caporusso, C.B.; Digregorio, P.; Levis, D.; Cugliandolo, L.F.; Gonnella, G. Motility-Induced Microphase and Macrophase Separation in a Two-Dimensional Active Brownian Particle System. Phys. Rev. Lett. 2020, 125, 178004. [Google Scholar] [CrossRef]
- Shi, X.-Q.; Fausti, G.; Chaté, H.; Nardini, C.; Solon, A. Self-Organized Critical Coexistence Phase in Repulsive Active Particles. Phys. Rev. Lett. 2020, 125, 168001. [Google Scholar] [CrossRef]
- Cates, M.E. Active Field Theories. arXiv 2019, arXiv:1904.01330. [Google Scholar]
- Wittkowski, R.; Tiribocchi, A.; Stenhammar, J.; Allen, R.J.; Marenduzzo, D.; Cates, M.E. Scalar φ4 field theory for active-particle phase separation. Nat. Comm. 2014, 5, 4351. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. III. Nucleation in a Two-Component Incompressible Fluid. J. Chem. Phys. 1959, 31, 688. [Google Scholar] [CrossRef]
- Bray, J. Theory of phase-ordering kinetics. Adv. Phys. 1994, 43, 357. [Google Scholar] [CrossRef]
- Otha, T.; Nozaki, H.; Doi, M. Computer simulations of domain growth under steady shear flow. J. Chem. Phys. 1990, 93, 2664. [Google Scholar]
- Corberi, F.; Gonnella, G.; Lamura, A. Spinodal Decomposition of Binary Mixtures in Uniform Shear Flow. Phys. Rev. Lett. 1998, 81, 3852. [Google Scholar] [CrossRef]
- Corberi, F.; Gonnella, G.; Lamura, A. Structure and Rheology of Binary Mixtures in Shear Flow. Phys. Rev. E 2000, 61, 6621. [Google Scholar] [CrossRef]
- Berthier, L. Phase separation in a homogeneous shear flow: Morphology, growth laws, and dynamic scaling. Phys. Rev. E 2001, 63, 051503. [Google Scholar] [CrossRef]
- Corberi, F.; Gonnella, G.; Lamura, A. Two-Scale Competition in Phase Separation with Shear. Phys. Rev. Lett. 1999, 83, 4057. [Google Scholar] [CrossRef]
- Corberi, F.; Gonnella, G.; Lamura, A. Phase Separation of Binary Mixtures in Shear Flow: A Numerical Study. Phys. Rev. E 2000, 62, 8064. [Google Scholar] [CrossRef] [PubMed]
- Gonnella, G.; Lamura, A. Long-time behavior and different shear regimes in quenched binary mixtures. Phys. Rev. E 2007, 75, 011501. [Google Scholar] [CrossRef] [PubMed]
- Rothman, D.H. Complex rheology in a model of a phase-separating fluid. Europhys. Lett. 1991, 14, 337. [Google Scholar] [CrossRef]
- Hashimoto, T.; Matsuzaka, K.; Moses, E.; Onuki, A. String Phase in Phase-Separating Fluids under Shear Flow. Phys. Rev. Lett. 1995, 74, 126. [Google Scholar] [CrossRef]
- Nakano, H.; Minami, Y.; Sasa, S. Long-Range Phase Order in Two Dimensions under Shear Flow. Phys. Rev. Lett. 2021, 126, 160604. [Google Scholar] [CrossRef]
- Saracco, G.P.; Gonnella, G. Critical behavior of the Ising model under strong shear: The conserved case. Phys. A 2021, 576, 126038. [Google Scholar] [CrossRef]
- Stenhammar, J.; Wittkowski, R.; Marenduzzo, D.; Cates, M.E. Activity-Induced Phase Separation and Self-Assembly in Mixtures of Active and Passive Particles. Phys. Rev. Lett. 2015, 114, 018301. [Google Scholar] [CrossRef]
- Cates, M.E.; Tjhung, E. Theories of binary fluid mixtures: From phase-separation kinetics to active emulsions. J. Fluid Mech. 2018, 836, P1. [Google Scholar] [CrossRef]
- Caballero, F.; Nardini, C.; Cates, M.E. From bulk to microphase separation in scalar active matter: A perturbative renormalization group analysis. J. Stat. Mech. 2018, 2018, 123208. [Google Scholar] [CrossRef]
- Solon, A.P.; Stenhammar, J.; Cates, M.E.; Kafri, Y.; Tailleur, J. Generalized thermodynamics of phase equilibria in scalar active matter. Phys. Rev. E 2018, 97, 020602R. [Google Scholar] [CrossRef]
- Pattanayak, S.; Mishra, S.; Puri, S. Ordering kinetics in the active model B. Phys. Rev. E 2021, 104, 014606. [Google Scholar] [CrossRef] [PubMed]
- Pattanayak, S.; Mishra, S.; Puri, S. Domain Growth in the Active Model B: Critical and Off-critical Composition. Soft Mater. 2021, 19, 286. [Google Scholar] [CrossRef]
- Redner, G.S.; Hagan, M.F.; Baskaran, A. Structure and Dynamics of a Phase-Separating Active Colloidal Fluid. Phys. Rev. Lett. 2013, 110, 055701. [Google Scholar] [CrossRef]
- Tiribocchi, A.; Wittkowski, R.; Marenduzzo, D.; Cates, M.E. Scalar Active Matter in a Momentum-Conserving Fluid. Phys. Rev. Lett. 2015, 115, 188302. [Google Scholar] [CrossRef]
- Kardar, M.; Parisi, G.; Zhang, Y.-C. Dynamic Scaling of Growing Interfaces. Phys. Rev. Lett. 1986, 56, 889. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.K.; Saxton, R. Dynamics of Director Fields. Siam J. Appl. Math. 1991, 51, 1498. [Google Scholar] [CrossRef]
- Kuramoto, Y. Diffusion-Induced Chaos in Reaction Systems. Prog. Theor. Phys. Suppl. 1978, 64, 346. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. On Flame Propagation Under Conditions of Stoichiometry. Siam J. Appl. Math. 1980, 39, 67. [Google Scholar] [CrossRef]
- Rogers, T.M.; Elder, K.R.; Desai, R.C. Numerical study of the late stages of spinodal decomposition. Phys. Rev. B 1988, 37, 9638. [Google Scholar] [CrossRef]
- Strikwerda, J.C. Finite Difference Schemes and Partial Differential Equations; Chapman and Hall: New York, NY, USA, 1989. [Google Scholar]
- Lees, A.W.; Edwards, S.F. The computer study of transport processes under extreme conditions. J. Phys. C 1972, 5, 1921. [Google Scholar] [CrossRef]
- Frischknecht, A. Effect of shear flow on the stability of domains in two-dimensional phase-separating binary fluids. Phys. Rev. E 1997, 56, 6970. [Google Scholar] [CrossRef]
- Gonnella, G.; Lamura, A. Sheared phase-separating binary mixtures with surface diffusion. J. Phys. A 2020, 53, 305002. [Google Scholar] [CrossRef]
- Lamura, A.; Gonnella, G. Computer simulations of domain growth in off-critical quenches of two-dimensional binary mixtures. Comput. Mater. 2002, 25, 531. [Google Scholar] [CrossRef][Green Version]






| A | |
|---|---|
| 0 | 4.40 |
| 1 | 2.75 |
| 2 | 0.99 |
| 3 | 0.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamura, A.; Tiribocchi, A. Shearing Effects on the Phase Coarsening of Binary Mixtures Using the Active Model B. Mathematics 2021, 9, 3008. https://doi.org/10.3390/math9233008
Lamura A, Tiribocchi A. Shearing Effects on the Phase Coarsening of Binary Mixtures Using the Active Model B. Mathematics. 2021; 9(23):3008. https://doi.org/10.3390/math9233008
Chicago/Turabian StyleLamura, Antonio, and Adriano Tiribocchi. 2021. "Shearing Effects on the Phase Coarsening of Binary Mixtures Using the Active Model B" Mathematics 9, no. 23: 3008. https://doi.org/10.3390/math9233008
APA StyleLamura, A., & Tiribocchi, A. (2021). Shearing Effects on the Phase Coarsening of Binary Mixtures Using the Active Model B. Mathematics, 9(23), 3008. https://doi.org/10.3390/math9233008






