Abstract
The purpose of this paper is to investigate the linear stability analysis for the laminar-turbulent transition region of the high-Reynolds-number instabilities for the boundary layer flow on a rotating disk. This investigation considers axial flow along the surface-normal direction, by studying analytical expressions for the steady solution, laminar, incompressible and inviscid fluid of the boundary layer flow due to a rotating disk in the presence of a uniform injection and suction. Essentially, the physical problem represents flow entrainment into the boundary layer from the axial flow, which is transferred by the spinning disk surface into flow in the azimuthal and radial directions. In addition, through the formation of spiral vortices, the boundary layer instability is visualised which develops along the surface in spiral nature. To this end, this study illustrates that combining axial flow and suction together may act to stabilize the boundary layer flow for inviscid modes.
1. Introduction
The fluid mechanics governing turbulent flow are not fully understood, it will also take decades to disentangle the myriad routes to turbulence to provide a development of the next generation of silent, ultra-efficient aircraft engines and turbofans. Hydrodynamic stability theory in generating precise and cost-effective predictions compared with experimental studies, reveals flow control and drag reduction strategies, including potential environmental and economic benefits that would result from reduced noise and CO2 emissions due to significant fuel consumption. According to Helmholtz, Kelvin, Rayleigh and Reynolds, the fundamental basics of hydrodynamic stability were known, formulated and recognised in the 19th century. For instance, the instabilities of Kelvin-Helmholtz [1,2], Taylor-Couette [3] and Rayleigh-Bénard [4] have been analysed, evaluated and examined by linear stability analysis (LSA) with a referral to the Navier–Stokes equations. After that, many more numerical analysis methods and nonlinear stability approaches were launched and developed to investigate and evaluate the stability of a complicated fluid flows [5,6]. However, the main examination and analysis of hydrodynamic stability are still a challenging problem in the applied mathematics communities and engineering [7,8,9].
It is known that hydrodynamic instability is linked and related to the critical values of dimensionless parameters in fluid systems, such as the Rayleigh, Mach and Reynolds numbers, etc. [5,9]. Studies that have used linear stability analysis are not completely accurate, while nonlinear stability analysis is usually complicated to implement after formulation. However, analysis of the linear stability for laminar flow considers fluid particles following paths in layers, where every layer is smoothly moving past adjacent layers with little or no mixing. Laminar to turbulent flow studies have been reviewed considering the effect of parameters, such as roughness, on the transition process [10]. Tremendous interest has been drafted towards the mechanisms governing laminar-turbulent transition and analysing the instability of flow in three-dimensional boundary layers in detail. (see, for example, Reed et al. [11], Hall and Malik [12], Lakin and Hussaini [13]). Recently machine learning (ML) algorithms have started to pave an alternative way to identify and spot the location where the hydrodynamic instability starts to take place, differentiate the transition to turbulence process, predict the critical parameters and the influences of these parameters on hydrodynamic flows. These algorithms are automatic, reliable and accurate and will always be ready for generating new conditions to be applied on highly chaotic systems such as turbulent flow. However, it is currently still a challenge to introduce these issues more clearly and consistently [14].
During the classical series of experiments on the instability of flow in a pipe by Reynolds [16], he investigated high speed flow in parallel channels. Meanwhile, the definition of the boundary layer was firstly described by Prandtl [17] as a thin layer along a solid boundary where the viscosity of the fluid/gas has an impact. His model is used to show how the airflow around an airfoil wing would behave. Consequently, there was great attention towards the governing mechanisms of three-dimensional (3D) boundary-layer flow stability as well as application to the design of aerofoils. Importantly, it is required to clearly understand the instability mechanisms that govern the breaking down of the boundary layer (Reed et al. [11], Reshotko [18] and Saric et al. [19]). This understanding is driven by the rotating disk’s fundamental importance as a model for cross-flow dominated flows such as those that appear over swept wings and in other applications. Since the 1950s, there was a great interest by many researchers towards the disk, however, in recent decades, the study of boundary-layer flows has developed to consider more complex axisymmetric rotating bodies (Kobayashi [20], Hussain [21] and [22])
Moreover, problems concerning the effect of Magneto-Hydrodynamics (MHD) on boundary layer flow have recently undergone further investigation in order to understand a range of geophysical, astrophysical, and engineering phenomena. For instance, the geophysical flow process that occurs at the core-mantle interface of the earth (see Berker [23], Coirier [24] and Mohanty [25]).
In addition, several engineering applications include the non-Newtonian behaviour of fluids, for instance, remediation, hydraulic fracturing and other industrial operations. It is considered that non-Newtonian fluid motion equations are extremely nonlinear compared to linear models of the Navier-Stokes equations. These non-Newtonian fluids models are divided into three groups; integral, rate and differential type fluids. In addition, a Maxwell fluid is a sub-category of a fluid rate type that forecasts the effects of time of relaxation. However, other fluid types cannot project these effects [26]. In the study of Mabood et al. [27], they scrutinized the thermal radiation impact on this Maxwell fluid flow while convective boundary constraints are considered. Ijaz and Ayub [28] also tried to explore the activation energy influence on Maxwell fluid flow stratified with the suspended nanoparticle. Ahmed et al. [29] examined the Maxwell fluid flow driven through gyrating disks considering a mix between convection and swirling flow. In other studies, Maxwell fluid flow was investigated over a vertically rotating disk moving with the impact of a magnetic effect and radiation, Khan et al. [30].
Despite several studies in this field, many gaps are still not filled such as the instability for a rotating disk within axial flow and varying parameters suction/ injection (see Hussain et al. [31] and Turkyilmazoglu [32] for the respective separate studies). In particular, this study addresses the lack of positive and negative strengths of axial flow when and (18), and analytic high Reynolds number asymptotic solutions of rotating disk boundary layer flow subject to a varying suction/injection within a fixed axial flow.
This study investigates the laminar-turbulent transition of incompressible boundary layer flow on a rotating disk. For this purpose, the linear stability regimes will be analysed, both for positive and negative axial flow strengths and various injections or suction for a given positive fixed axial flow. In Section 2, the formulation of the rotating disk and boundary layer approximation of the problem is analysed and discussed by deriving the governing linear disturbance equations. In Section 3, the inviscid model is obtained based on the asymptotic expansions of a small parameter. In Section 4, conclusions about the stability parameters for a rotating disk in axial flow and corresponding to suction and injection velocities are analysed.
1.1. The Problem Definition
This study is designed based on the theoretical investigations of Garrett and Peake [33], and Garrett et al. [34], who considered the absolute instability over a family of cones rotating within imposed axial flows. More specifically, we follow and extend the analysis and evaluation of Hussain et al. [31] for a rotating disk, creating and formulating the linear disturbances equations before reaching the stage of identifying the upper branch inviscid modes. Thus, the rotating disk is considered to be a special case of a cone with half-angle 90 degrees. However, in those studies, the initiation of absolute instability is affected by the rate of imposed axial flow, and the initiation location is importantly delayed with axial flow increase.
1.2. The Importance of the Problem
In order to investigate the fluid flow stability in a complex model of rotating disk flow, an asymptotic analysis revealing the best parameters for stable flow is conducted. This includes varying the suction/ injection and axial flow. Since these parameters interact in a complex way, consequently the aim is uncovering how they affect flow stability and lead to turbulent flow. Suction and axial flow are observed in natural flows (tornadoes and typhoons) and have been used on a wide scale, for decades, in applications such as heat exchange, aeronautics, spray drying, chemical mixing, separation, combustion, etc. More generally, this problem requires consideration of the link between the engineering input parameters used in experiments and industry as well as the physical processes involved in these complicated fluid flows.
2. Formulation of the Problem and Boundary Layer Approximation
We applied a high Reynolds number asymptotic formulation, with numerical solutions used in certain parts of the analysis, which are outlined at the pertinent points.
Here, the boundary-layer flow governing equations over a rotating disk are the incompressible Navier–Stokes as well as continuity equation in the cylindrical coordinates in the rotating frame of reference:
Here, the total velocity vector is , time is , the pressure is , also is the position vector in space, the constant angular velocity vector is , is the dimensional density and is the dimensional kinematic viscosity. Due to the rotating coordinate frame, we have noted the appearance of the Coriolis forcing term, . In addition, the frequently used coordinate system is the Cartesian. It is composed of three constant unit vectors orthogonal to each other in 3D (r, y and z directions). This system is simple and not complicated to understand that a rotating-disk flow could be suitably identified. This is because of the axisymmetry of the flow which is making the cylindrical unit vectors corresponding to the three characterizing directions of the flow, the azimuthal, radial, and vertical direction (see Appelquist [35]). However, by using the cylindrical operator, the equations in each and , in orthogonal curvilinear coordinates, will lead us to the full Navier-Stokes equations (for the case of the rotating cone see also Garrett [33] considered with a fixed frame of reference) the equations in each and component are
and
along with the equation of continuity
where
Laplacian operator for the coordinate set is the dimensional (). Moreover, the boundary conditions considering the rotating reference frame (no-slip conditions) are,
We put into consideration an infinite extent of a rigid disk rotating about the -axis that goes through the disk’s centre. The azimuthal and radial coordinates are and , respectively, with the rotating disk surface. However, in an incompressible fluid, at upstream infinity the disk will be placed with axial flow coming parallel to the -axis. In addition, the dimensional surface velocity distribution along the disk at the edge of the boundary layer is provided by the well-recognised potential-flow solution , (for example see [36,37]). Through the free-stream axial flow (scale factor) is determined on the disk. Taking into account here the asterisks indicate dimensional quantities. Figure 1 illustrates a diagram of the formulation of [33]. According to [38], the non-dimensionalization of the analysis will lead us to the Reynolds number
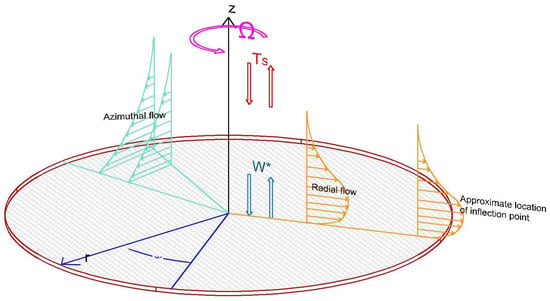
Figure 1.
Rotating disk diagram is showing model setup in axial flow within suction and injection.
The angular speed of the rotation disk is , the kinematic viscosity of the fluid is , and is a length scale of the disk surface. The distances in the direction are scaled based on thickness of the boundary-layer leading to which is a non-dimensional variable (see Hussain [31]). However, we observed is the boundary-layer thickness. Taking into account this scaling is different from the one used in [39]. In addition, over the disk the basic steady flow has the form in the radial, azimuthal and normal directions and respectively.
The basic flow of velocity scales are given by
While pressure of the basic flow is
with
is representing the inviscid Bernoulli pressure by matching between the pressure inside the boundary layer and outside coming from the free-stream flow. We observed these basic flows are determined by the non-dimensional N-S and continuity equations as following:
with boundary conditions
Here a prime denotes differentiation with respect to . The ratio of the local slip velocity is the parameter considered at a radial position in relation to the rotational speed of the disk surface:
Here is independent of , simplifying the analysis for the rotating disk, which differs from the rotating cone in axial flow. Given von Kármán equations [40], represents the disk rotating in still fluid. Depending on conditions (16) the Equations (13)–(15) are solved using a Runge-Kutta integration method (fourth-order) via MATLAB software by extending codes from Hussain et al. [31] in order to obtain large and small , in coincidence with a two-dimensional Newton-Raphson searching routine to iterate on the outer boundary conditions for different values of . Since these codes have a stability function, we tested that stability by changing the location of the edge of the boundary layer to confirm convergent solutions, which are represented in Figure 2, Figure 3 and Figure 4.
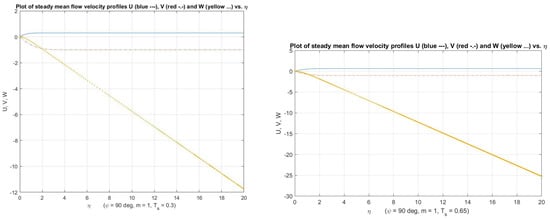
Figure 2.
Plot showing the mean flow profile U, V and W for , (left) and (right).
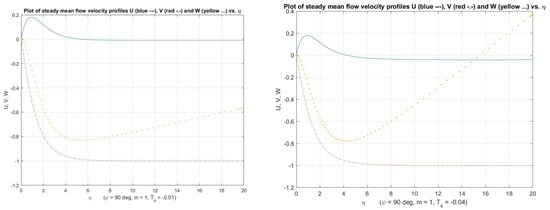
Figure 3.
Plot showing the mean flow profile U, V and W for , (left) and (right).
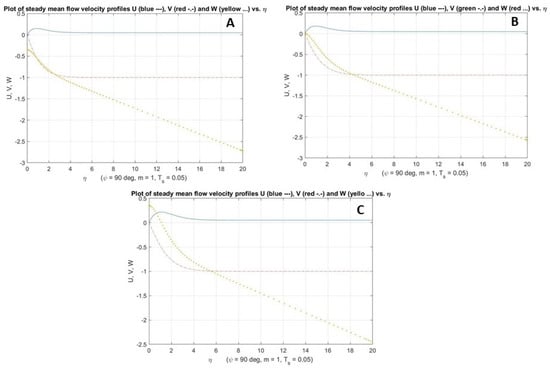
Figure 4.
Plot showing the mean flow profile U, V and W, with = −0.35 (A), 0 (B) and 0.35 (C).
Following Hussain [15] for rotating disk boundary layer flow within an axial flow, we derive a similarity solution of the laminar, axially symmetric, steady, and viscous flow induced by an infinite porous of the disk rotating. We take into account the impact of applying various suction/injection strengths to the fixed axial direction and the boundary conditions with inserted into the N-S equation. Hence, extending the previous work of Hussain [15] of the rotating disk by using the same mean flow boundary layer Equations (13)–(15), and the boundary conditions (16) within the changed parameters of and . Here the parameter in (14) is the axial flow for , and , the same for the boundary condition parameter in (16) is suction for and injection if . In the absence of the uniform axial velocity fixed at the disk these equations reduce to the well-known classical equations for fluid flow above a rotating disk.
2.1. Positive and Negative Strength of Axial Flow ()
Firstly, we consider the equations of mean the flow to extend the results of Hussain [15] representing when . Likewise, when . For these cases, the rotating disk is placed and located in an oncoming axial flow. Although, with the boundary conditions (16), the Equations (13)–(15) are solved by using the integration methods of Runge-Kutta (fourth-order), through the boundary conditions at infinity, we are applying a two-dimensional Newton-Raphson search routine to iterate. In addition, the azimuthal, radial, and normal to the wall components of the steady mean flow velocity of the disk in the boundary layer for as well as for are shown in Figure 2 and Figure 3.
2.2. Various Suction/Injection () within a Positive Fixed Axial Flow
In this case, we consider the results of Hussain [15] for a rotating disk in axial flow at while applying various suction/injection parameters () for the boundary condition. Once more, the Equations (13)–(15) with the boundary conditions and are mainly solved using the integration methods of Runge-Kutta (fourth-order), through the boundary conditions at infinity, we are applying a two-dimensional Newton-Raphson search routine to iterate. By applying the different values of , the azimuthal, radial, and normal to the wall components of the steady mean flow velocity of the disk in the boundary layer for varying suction/injection at are shown in Figure 4.
2.3. Linear Disturbance Equations
For theses cases of the rotating disk with ( and ) and applied to varying suction / injection for the boundary condition, by introducing small basic perturbation quantities and , we linearise (3)–(6) about the basic pressure (11) and steady mean flow profile (10) which leads us to governing equations independent of according to
where
Upon non-dimensionalising and ignoring the left-hand side of the nonlinear terms to keep the basic flow with the convective cross-terms only and retaining the right-hand side of the perturbation terms, will lead us to equations of the linearised perturbation.
Here are the operator of the non-dimensional Laplacian is and .
3. Inviscid Model
To analyse the inviscid type of the rotating disk in axial flow, we have to follow the same track of the analysis of Hall [12,41] and Hussain [15] who studied the stationary spiral modes of oscillation on a rotating disk. We extended the analysis for varying rotating disks with axial flow and suction/injection with fixed axial flow, respectively. Precisely, on the boundary layer thickness, we scale the inviscid mode wavelengths of order , in the and r. Then is a small parameter given by
As a function of the wall-normal coordinate z, we will define the perturbation velocities in the form
using similar expressions for the perturbation , and . We started expanding the azimuthal and radial wavenumbers and as
Importantly, to see that perturbations with these associated disturbances are neutrally stable, we explain the conditions . Hence, by following the arguments of Hall, that demonstrated the presence of two layers, firstly a viscous layer with thickness which incorporates the non-slip condition at the wall. Secondly, an inviscid layer with thickness , by balancing diffusion terms and convection in the disturbance equations.
However, in the inviscid layer of thickness the velocity and pressure perturbations are expanded to
where the parameter . Also, and are replaced to and , respectively.
3.1. Leading Order Eigenmodes
For the rotating disk in axial flow and suction/injection situations, we equate the terms in the expansions of (21)–(24) to lead us to
Here . From the above equation we will eliminate and to lead us to an equation for given by
So from the cross-stream and radial directions, the acts as the effective wavenumber, in a similar form to the rotating disk as discussed by Hall [41], here is explained as the effective velocity profile. Hence, on a rotating disk is in the direction of the spiral vortices. Likewise, by using a similar approach and solving the Rayleigh equation of regarding , we obtained as an eigenvalue of the boundary condition at infinity and the wall,
However, by applying central finite differences and choosing (), both and disappeared at this point, the location of the critical layer away from the wall, while the effective velocity profile has to have a point of inflexion and a root at the same point [15], as shown in Figure 5, Figure 6 and Figure 7.
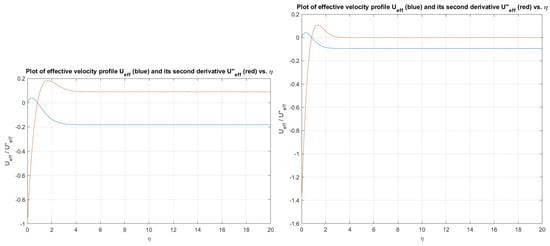
Figure 5.
Plot showing the velocity effectiveness (lower curve at ) and its second derivative (upper curve at ) for (left) and (right).
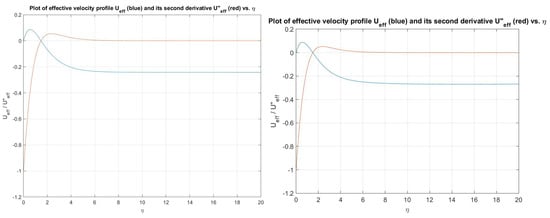
Figure 6.
Plot showing the velocity effectiveness (below graph at ) and its second derivative (above graph at ) for (left) and (right).
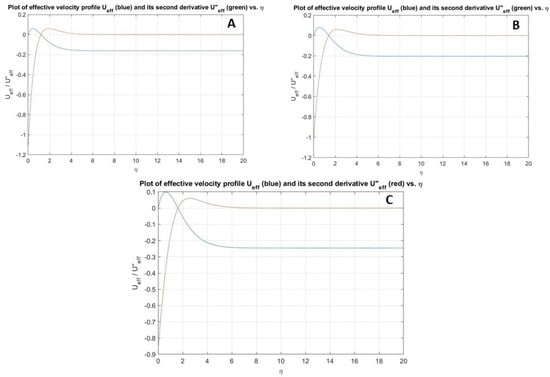
Figure 7.
Plot showing the velocity effectiveness (below graph at ) and its second derivative (above graph at ) for , with = −0.35 (A), 0 (B) and 0.35 (C).
Furthermore, we found that as , and behave like , hence the singularity in their combined profiles, , is removable. To conclude, investigating separately each profile’s critical layer structure is not needed. However, it is necessary to find a solution only for .
As a result, we obtained by following Hussain [15] for the stationary instability of rotating disk. The results that we obtained when the that we choose are.
Additionally, when such that we choose
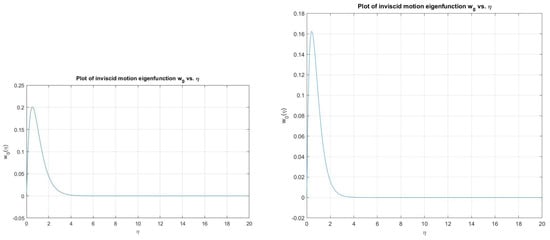
Figure 8.
Plot showing the inviscid motion eigenfunction against for , (left) and (right).
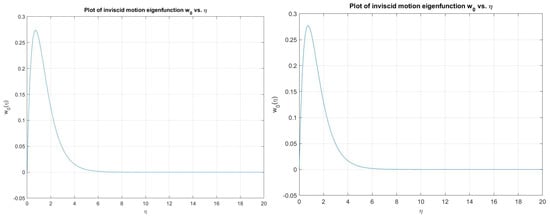
Figure 9.
Plot showing the inviscid motion eigenfunction against for , (left) and (right).
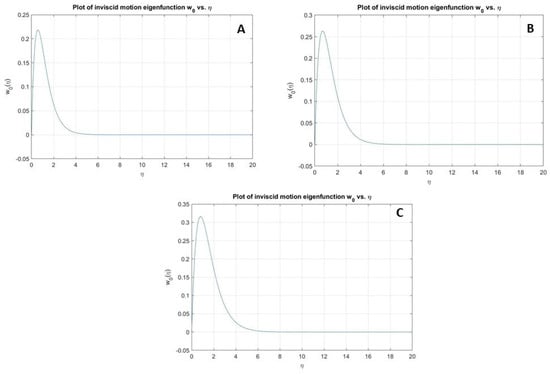
Figure 10.
Plot showing the inviscid motion eigenfunction against for , with = −0.35 (A), 0 (B) and 0.35 (C).
Now we focus our attention on the solution to lead us to the order of inviscid mode type I within the wall layer. Thus, the proper normal to the wall coordinate can be taken as
that is related to the surface-normal coordinate by (see Hussain [15]). However, from the wall of a disk, the no-slip conditions must be satisfied with the basic flow and its derivatives being linear in . It is represented by the following form
which is zero from continuity, also and then we expand the pressure and velocity perturbation inside the wall layer as
noting dependence on the small parameter , we see the surface-normal and pressure exist at first order, within the wall layer. Therefor, when substituting these expansions into the disturbance Equations (21)–(24), and equating terms of , , , , respectively we find
Balancing terms of and leads to , = const in the surface-normal disturbance equation respectively. However, we have to carry out the manipulation (51)’+(52)’, which along with (50), leads to
We observe the solution of Equation (50) satisfies at . Now, when we make the substitution
and if we let , where , then (54) becomes
indicating the eigenfunction behaviour of the wall layer is characterized by an Airy function decay for . Using the condition at and (50) yields
The required exponentially decaying solution of Airy’s Equation (56) is Ai(). To simplify the resulting integrand, we use integration by parts, substituting the Airy Equation (56) applying . However, the large case of the wall layer at the outer edge, which matches to the inner edge of the inviscid layer as leads to
Consequently, we apply the Prandtl criterion in the form
As a result, at the outer edge of the wall layer, we match the normal perturbation to the corresponding value at the inner edge of the inviscid layer and use to output the expression for the order inviscid zone normal to the wall velocity component, that is given by
3.2. First Order Eigenmodes
For the next-order problem in the inviscid zone the perturbation Equations (21)–(24) will expand to to yield
In terms of the disturbance quantities that we found from the previous Equations (32)–(35), the system of Equations (61)–(64) is comparable to those for . We noticed inhomogeneous cross-terms. Hence, the disturbance quantities and are similarly eliminated as the above leading order problem. Additionally, we used Equation (32) of leading order continuity to eliminate and Equation (61) of next order continuity to eliminate . Consequently, all these helped us to obtain the below equation that governs of the next order inviscid mode eigenfunction.
Notably, at the point , the right-hand side of the second part of Equation (65) results in acquiring a logarithmic singularity. This is removable for type I via including at this location a critical layer. Moreover, the left-hand side of the Rayleigh differential operator in Equation (65) is observed to be the same as the operator acting on in Equation (36) which will lead us to the solution for . Therefore, is the complementary function solution. To produce the second solution, we must exert the reduction of order method.
Following Hall [41], in order to achieve the solution of the particular integration of , with consideration of the Equation (65) of the right-hand side in the inhomogenous part, we utilised the method of variation of parameters of one of the quantities of the complementary function solution for , named as in the form [], this yields
and to obtain the solution of the particular integration, we replaced the expression for , in order to give
Here . We observed that the expression which we obtained is similar to the one obtained for rotating disk by Hall [41]. The solution that we noticed is only valid when . Consequently, by expanding as a Taylor series for close to zero, we obtained the same eigenrelation that Hall [41] obtained, taking into account that at the wall.
where
In Equation (70) we computed the value through a numerical integration approximation of a fixed-step Simpson’s rule. However, we found that Equation (71) is singular at for . To be consistent with a viscous critical layer calculation, deforming the integration path above the singularity is required. The integrated path of deformation is above the singularity as long as (below if we have a positive value), will help us to obtain correctly. Consequently, the integration of can be expressed by using the original definition for in the form
3.2.1. Rotating Disk in Axial Flow When and
In this case, we focus and analyse the rotating disk with oncoming axial flow . We found the singularity appearance at . When applying a fixed step Simpson’s rule numerical integration approximation, we anticipate this integral again, taking into our consideration the singularity by integration from to just below the singularity, , also from the above the singularity, to infinity. For the imaginary part calculation, we must evaluate half of the complex residue, whilst for the real part of , we use , importantly the integration of at the point has a simple pole. Therefore, parts of the Taylor series were expanded. Then criteria were used at the singularity in order to obtain
On one hand when the case of the rotating disk in axial flow is , we evaluated both integrals to obtain
We observed a significant difference between the values we obtained and the ones obtained by Hussain [15] for the type I case of rotating disk in axial flow. Hussain obtained the axial flow to , while we obtained to . On the other hand, when the axial flow is , we obtained
Therefore, proceeding to follow the analysis, we used our previous computed values for each , and to match with the solution in the wall layer of Equation (60), consequently the eigenrelation result is
By using the results of and , we have
We observed the above expressions would help us to compute both the first-order corrections and leading order estimates of the effective wavenumber
Since the spiral waveangle has the following expansion
Following Hall [41] and Hussain [15], we re-scaled these obtained results, writing both the waveangle and wavenumber using the Reynolds number based on boundary layer thickness
given by
This will result in expressing the inviscid model local (wavenumber)
and the inviscid mode waveangle expansion as following:
Therefore, we expression of the waveangle and wavenumber using displacement thickness Reynolds number would eliminate their reliance on the radial coordinate, r. Figure 11 and Figure 12 show the type I branches of the asymptotic waveangle and wavenumber predictions, where scales of semi-log and log-log were used for the waveangle and wavenumber plots.
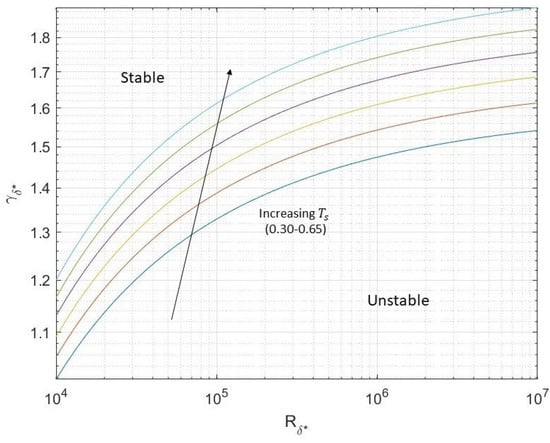
Figure 11.
Plot illustrating predictions of asymptotic neutral wavenumber against for type I modes for . Larger values move the plots up as shown by the arrow.
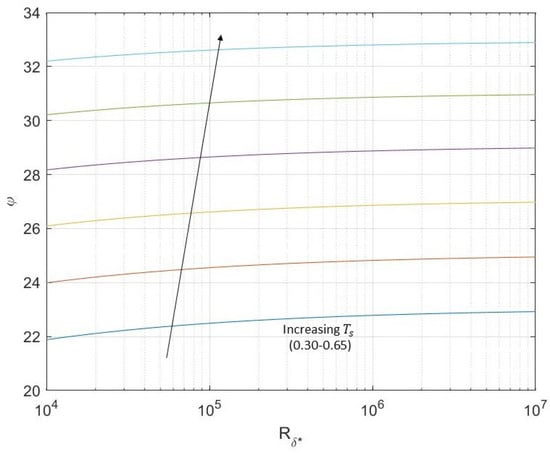
Figure 12.
Plot illustrating predictions of asymptotic neutral waveangle against for type I modes for . Larger values move the plots up as shown by the arrow.
The acquired data for the case of the rotating disk in axial flow type I spiral modes are illustrated in Table 1 and Table 2 showing the significant parameter values for and . At the wall these are the parameters of the azimuthal and radial velocity gradients, are representing values of the profile of effective velocity and the location of the critical layer. The integrals and are defined in Equations (70) and (71).

Table 1.
Values of stability parameter for a rotating disk in axial flow .

Table 2.
Values of stability parameter for a rotating disk in axial flow .
As a consequence, we observed the effective velocity profile -values elevate with increasing the axial flow , via the perpendicular geometry of the rotating disk, the greater streamwise forced flow is diverted and swept along the disk surface. The more the flow is naturally swept around along the disk’s surface, the higher the ratio of azimuthal to radial wavenumbers. We also observed that effective velocity direction wavenumbers, , increases and the critical layer location for the type I mode disturbances is moving closer to the wall. Accordingly, the boundary layer of the disk is experiencing a larger oncoming axial flow (). By using those computations of the type I mode waveangles and wavenumber, we proceed with the evaluation of asymptotic estimates at large Reynolds number for various cases of the axial flow, . These are shown in Figure 11 and Figure 12, respectively. On the other hand for the case we observed the results are opposite to the case , then we decided to evaluate estimates which are asymptotic for the inviscid mode both waveangles and wavenumbers at large Reynolds number for different cases of the axial flow . Figure 13 and Figure 14 illustrate these results.
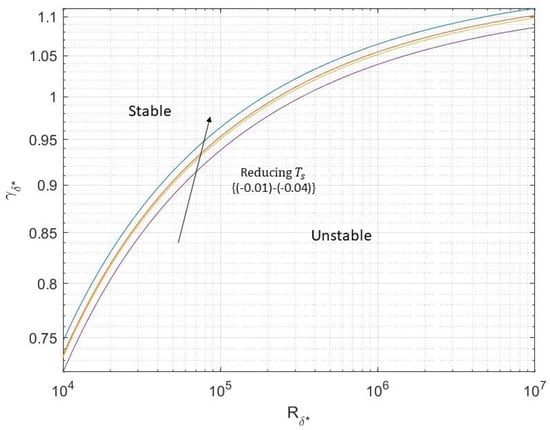
Figure 13.
Plot illustrating predictions of asymptotic neutral wavenumber against for type I modes for . Smaller values move the plots up as shown by the arrow.
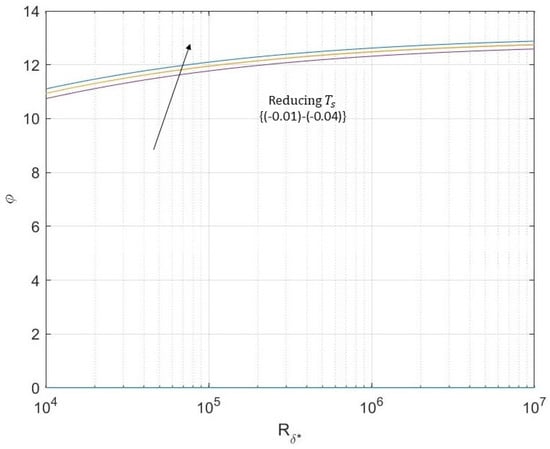
Figure 14.
Plot illustrating predictions of asymptotic neutral waveangle against for type I modes for . Smaller values move the plots up as shown by the arrow.
In conclusion, the efficiency has degraded substantially, and also, we could not get the convergence for parameters approximately less than . Whereas, at it was easier to obtain the convergence.
3.2.2. Rotating Disk with a Varying Suction/Injection Parameter
We combined the rotating disk case where axial flow is fixed with varying suction/injection parameters. To this end, we used the same approach from the previous case as shown in Table 3, which includes the values of the most critical parameters for varying suction and injection within fixed axial flow . Additionally, we chose the fixed axial flow that was given by Hussain [15] and applied various suction and injection parameters . Figure 7 demonstrates the mean flow profile as acquired from the previous case. We can see in Table 3 the most important parameter values for various suction and injection with fixed axial flow .

Table 3.
Values of stability parameter corresponding to several suction and injection velocities.
Despite the injection parameters better exhibiting convergence, the required iterations number for the maintenance of the convergence enormously increased while using the injection parameter. Moreover, the necessary number of terms to attain convergence were considered for solutions for . However, we observed the -values increasing with increasing , while, the effective velocity direction wavenumbers reduced with increasing , and the critical layer location for the type I mode disturbances moved away from the wall. We also observed that the injection situation would be more obvious to obtain the convergence when increasing at fixed axial flow . Figure 10 shows the normalised eigenfunction with gradient at as well as the effective velocity profile. Figure 15 and Figure 16 demonstrates inviscid branches of the asymptotic predictions of waveangles and wavenumbers where semi-log and log-log scales were used for the plots.
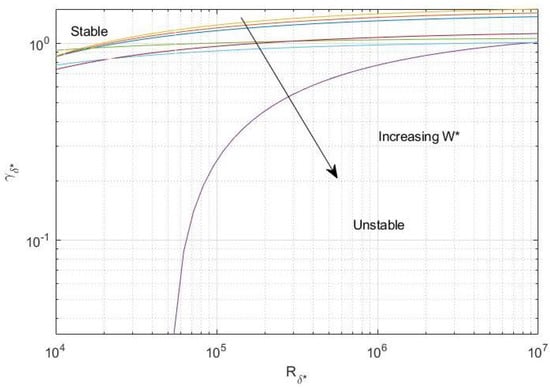
Figure 15.
Plot illustrating predictions of asymptotic neutral wavenumber against for type I modes for with to . Increasing shifts the curves vertically downwards.
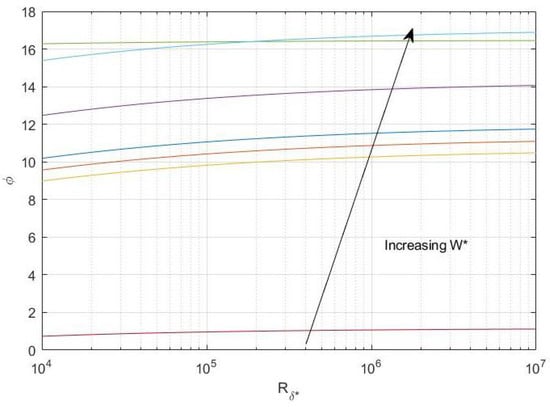
Figure 16.
Plot illustrating predictions of asymptotic neutral waveangle predictions against for type I modes for with to . Increasing shifts the curves vertically upwards.
4. Conclusions
Through this study, we were able to identify the respective modes of type I with regards to primary instability on a rotating disk surface. By applying asymptotic analyses in the linear regime we showed their existence. In addition, we investigated the effect on essential physical parameters such as the local waveangle, local wavenumber as well as the large Reynolds number asymptotic behaviour. Collectively, the results of this study are as follows:
4.1. Positive and Negative Strength of Axial Flow
- For the rotating disk within axial flow between (0.30–0.65), the stability parameter values for a rotating disk are gradually increased by increasing axial flow.
- For negative axial flow, the efficiency is degraded substantially and using parameters less than could not achieve convergence compared to which is consistent with the physical interpretation of positive axial flow stabilising according to Hussain [15], Hussain et al. [31], and Al Malki [42].
- Positive and negative shifts the curves vertically upwards. In general, our results are consistent with Hussain et al. [31] in that axial flow causes a stabilisation of the type I cross flow instability mode.
4.2. Rotating Disk with a Suction/Injection Parameter
- Injection at the boundary is easier to obtain convergence of stability when increasing , for example when compared with a negative axial flow in the bulk fluid.
- The required number of iterations for the maintenance of convergence for the injection parameter is comparatively better than for suction parameters.
- For injection, the efficiency is degraded substantially. Convergence was also not achieved for injection parameters less than .
- Increasing shifts the curves vertically downwards. In general, our results are consistent with Al-Malki [43] for Blasius flow, in that suction causes a stabilisation of the type I cross flow instability mode.
Based on these results the future direction could consider the type II instability of stationary viscous modes for the cases increasing /reducing the strength of the axial flow () for the rotating disk when and , as well as applying suction/injection (). This work is currently under development following Hall [41] and Hussain [15], and we hope to report on the results in due course.
Author Contributions
Conceptualization, B.A.S.; Methodology, B.A.S.; Project administration, Z.H.; Supervision, Z.H.; Writing original draft, B.A.S.; Writing review and editing, B.A.S. and Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
B.A.S. would like to express his sincere thanks to Moataz Badawi for his help in improving this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thompson, W.S. Hydrokinetic solutions and observations. Phil. Mag. 1871, 4, 374. [Google Scholar]
- Helmholtz, H.L.F. On Discontinuous Movements of Fluids; Academy of Sciences: Berlin, Germany, 1868; Volume 36, pp. 215–228. [Google Scholar]
- Taylor, G.I., VIII. Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. A 1923, 223, 289–343. [Google Scholar]
- Getling, A.V. Rayleigh—Bénard Convection: Structures and Dynamics, 1st ed.; Scientific: London, UK, 1998; Volume 11. [Google Scholar]
- Lin, C.C. The Theory of Hydrodynamic Stability, 1st ed.; Cambridge University Press: Cambridge, UK, 1955. [Google Scholar]
- Holm, D.D.; Marsden, J.E.; Ratiu, T.; Weinstein, A. Nonlinear stability of fluid and plasma equilibria. Phys. Rep. 1985, 123, 1–116. [Google Scholar] [CrossRef]
- Criminale, W.O.; Jackson, T.L.; Joslin, R.D. Theory and Computation in Hydrodynamic Stability, 1st ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Swaters, G.E. Introduction to Hamiltonian Fluid Dynamics and Stability Theory; CRC Press: London, UK, 2010. [Google Scholar]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability, 1st ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Dryden, H.L. Review of published data on the effect of roughness on transition from laminar to turbulent flow. J. Aero. Sci. 1953, 20, 477–482. [Google Scholar] [CrossRef]
- Reed, H.L.; Saric, W.S. Stability of three-dimensional boundary layers. Ann. Rev. Fluid Mech. 1989, 21, 235–284. [Google Scholar] [CrossRef]
- Hall, P.; Malik, M.R. On the stability of a three-dimensionalattachment-line boundary layer: Weakly non-linear theory and a numerical approach. J. Fluid Mech. 1986, 163, 257–282. [Google Scholar] [CrossRef]
- Lakin, W.; Hussaini, Y. Stability of the laminar boundary layer in a streamwise corner. Proc. R. Soc. Lond. 1984, A 393, 101–116. [Google Scholar]
- Duraisamy, K. Perspectives on machine learning-augmented Reynolds-averaged and large eddy simulation models of turbulence. Phys. Rev. Fluids. 2021, 6, 050504. [Google Scholar] [CrossRef]
- Hussain, Z. Stability and Transition of Three-Dimensional Rotating Boundary Layers. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2010. [Google Scholar]
- Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Philos. Trans. R. Soc. 1883, 174, 935–982. [Google Scholar]
- Prandtl, L. Verhandlungen des dritten internationalen Mathematiker-Kongresses in Heidelberg. Teubner Leipz. Ger. 1905, 8, 485–491. [Google Scholar]
- Reshotko, E. Boundary-layer instability, transition and control. AIAA J. 1994, 94, 0001. [Google Scholar]
- Saric, W.S.; Reed, H.L.; White, E.B. Stability and transition of three-dimensional boundary layers. Ann. Rev. Fluid Mech. 2003, 35, 413–440. [Google Scholar] [CrossRef]
- Kobayashi, R.; Izumi, H. Boundary-layer transition on a rotating cone in still fluid. J. Fluid Mech. 1983, 127, 353–364. [Google Scholar] [CrossRef]
- Hussain, Z.; Garrett, S.J.; Stephen, S.O.; Griffiths, P.T. The centrifugal instability of the boundary-layer flow over a slender rotating cone in an enforced axial free stream. J. Fluid Mech. 2016, 788, 70–94. [Google Scholar] [CrossRef]
- Hussain, Z.; Garrett, S.J.; Stephen, S.O. The centrifugal instability of the boundary-layer flow over slender rotating cones. J. Fluid Mech. 2014, 755, 274–293. [Google Scholar] [CrossRef][Green Version]
- Berker, R. Integration des Equations du Movement d’un Fluid Visquent Incompressible. In Hand Book of Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1963; Volume 3. [Google Scholar]
- Coirier, J. Rotations non coaxials d’un disque et d’un fluide a I’infini. J. Mec. 1972, 11, 317–340. [Google Scholar]
- Mohanty, H.K. Hydromagnetic flow between two rotating disks with noncoincident parallel axes of rotation. Phys. Fluids 1972, 15, 1456–1458. [Google Scholar] [CrossRef]
- Mabood, F.; Rauf, A.; Prasannakumara, B.C.; Izadi, M.; Shehzad, S.A. Impacts of Stefan blowing and mass convention on flow of Maxwell nanofluid of variable thermal conductivity about a rotating disk. Chin. J. Phys. 2021, 71, 260–272. [Google Scholar] [CrossRef]
- Mabood, F.; Imtiaz, M.; Hayat, T.; Alsaedi, A. Unsteady convective boundary layer flow of Maxwell fluid with nonlinear thermal radiation: A numerical study. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 221–229. [Google Scholar] [CrossRef]
- Ijaz, M.; Ayub, M. Nonlinear convective stratified flow of Maxwell nanofluid with activation energy. Heliyon 2019, 5, e01121. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Khan, M.; Ahmed, J. Mixed convective flow of Maxwell nanofluid induced by vertically rotating cylinder. Appl. Nanosci. 2020, 2, 01320. [Google Scholar] [CrossRef]
- Khan, M.; Ahmed, J. Ali, Thermal analysis for radiative flow of magnetized Maxwell fluid over a vertically moving rotating disk. J. Therm. Anal. Calorim. 2021, 143, 4081–4094. [Google Scholar] [CrossRef]
- Hussain, Z.; Garrett, S.J.; Stephen, S.O. The instability of the boundary layer over a disk rotating in an enforced axial flow. Phys. Fluids 2011, 23, 114108. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Analytic approximate solutions of rotating disk boundary layer flow subject to a uniform suction or injection. Int. J. Mech. Sci. 2010, 52, 1735–1744. [Google Scholar] [CrossRef]
- Garrett, S.J.; Peake, N. The absolute instability of the boundary layer on a rotating cone. Eur. J. Mech. B 2007, 26, 344–353. [Google Scholar] [CrossRef]
- Garrett, S.J.; Hussain, Z.; Stephen, S.O. Boundary-layer transition on broad cones rotating in an imposed axial flow. IAA J. 2010, 48, 1184–1194. [Google Scholar] [CrossRef]
- Appelquist, E. Direct Numerical Simulations of the Rotating-Disk Boundary-Layer Flow; Royal Institute of Technology KTH Mechanics: Stockholm, Sweden, 2014. [Google Scholar]
- Rosenhead, L. Laminar Boundary Layers, 1st ed.; Oxford University Press: Oxford, UK, 1963. [Google Scholar]
- Evans, H. Laminer Boundary Layer Theory; Addison Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Garrett, S.J.; Hussain, Z.; Stephen, S.O. The crossflow instability of the boundary layer on a rotating cone. J. Fluid Mech. 2009, 622, 209–232. [Google Scholar] [CrossRef]
- Chen, K.; Mortazavi, A.R. An analytic study of the chemical vapor deposition (CVD) processes in a rotating pedestal reacto. R. J. Cryst. Growth 1986, 77, 199–208. [Google Scholar] [CrossRef]
- von Kármán, T. Uber laminare und turbulente Reiburg. Z. Agnew. Math. 1921, 1, 233–252. [Google Scholar]
- Hall, P. An asymptotic investigation of the stationary modes of instability of the boundary layer on a rotating disk. Proc. R. Soc. Lond. A 1986, 406, 93–106. [Google Scholar]
- Al-Malki, M.; Garrett, S.J.; Camarri, S.; Hussain, Z. The effects of roughness levels on the instability of the boundary-layer flow over a rotating disk with an enforced axial flow. Phys. Fluids 2021, 33, 104109. [Google Scholar] [CrossRef]
- Al-Malki, M.; Hussain, Z.; Garrett, S.J.; Calabretto, S.A. The effects of parietal suction and injection on the stability of the Blasius boundary-layer flow over a permeable, heated plate. Phys. Rev. Fluids 2021, 6, 113902. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).