A Space-Time Fully Decoupled Wavelet Integral Collocation Method with High-Order Accuracy for a Class of Nonlinear Wave Equations
Abstract
:1. Introduction
2. Wavelet Approximation of Multiple Integrals in a Bounded Domain
3. Solution Procedure
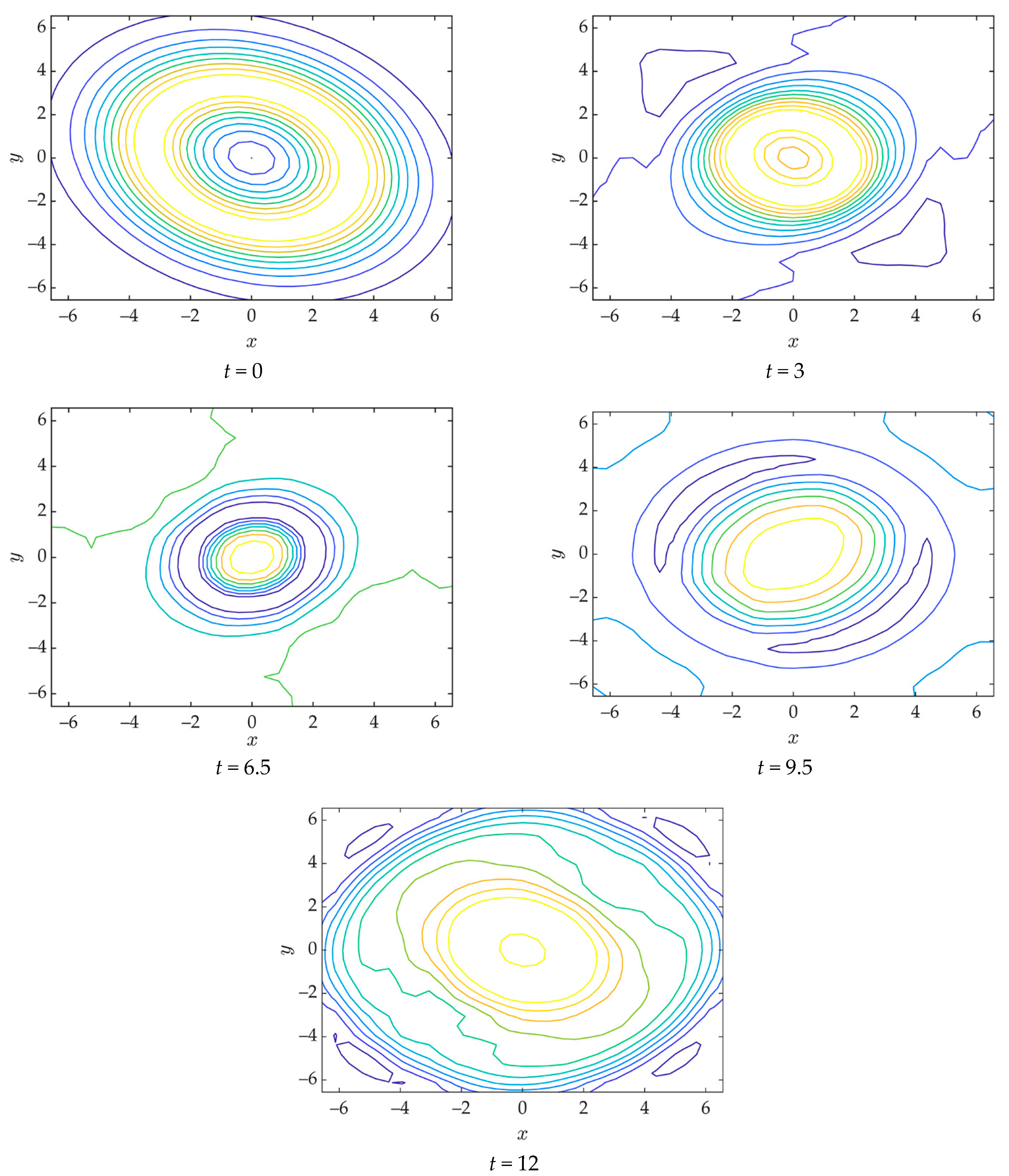
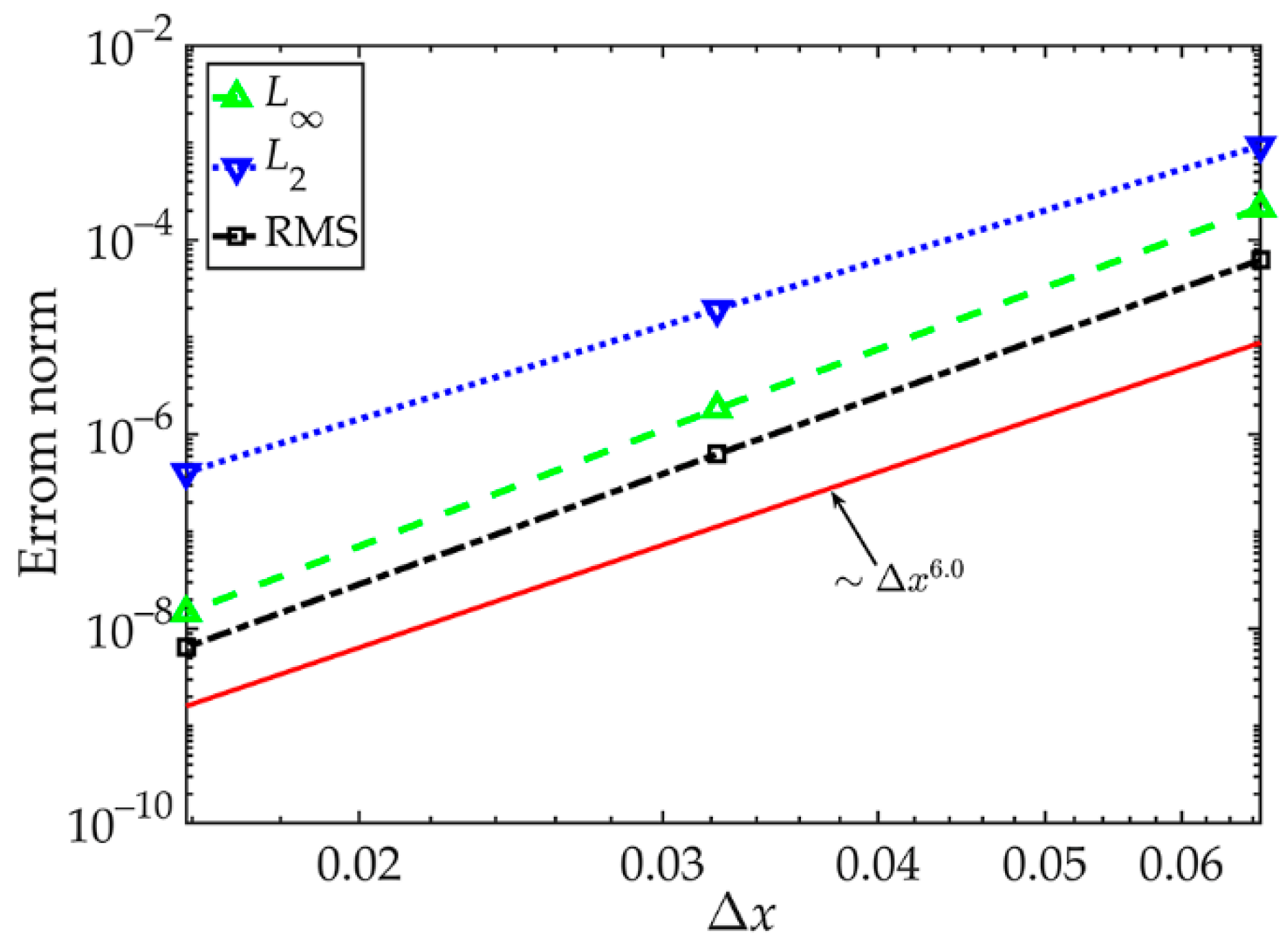
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- Dehghan, M.; Mirzaei, D. The dual reciprocity boundary element method (DRBEM) for two-dimensional sine–Gordon equation. Comput. Methods Appl. Mech. Eng. 2008, 197, 476–486. [Google Scholar] [CrossRef]
- Dehghan, M.; Shokri, A. A numerical method for solution of the two-dimensional sine–Gordon equation using the radial basis functions. Math. Comput. Simul. 2008, 79, 700–715. [Google Scholar] [CrossRef]
- Biazar, J.; Islam, R. Solution of wave equation by Adomian decomposition method and the restrictions of the method. Appl. Math. Comput. 2004, 149, 807–814. [Google Scholar] [CrossRef]
- Jafari, H.; Daftardar-Gejji, V. Solving linear and nonlinear fractional diffusion and wave equations by Adomian decomposition. Appl. Math. Comput. 2006, 180, 488–497. [Google Scholar] [CrossRef]
- Malfliet, W. The tanh method: A tool for solving certain classes of nonlinear evolution and wave equations. J. Comput. Appl. Math. 2004, 164, 529–541. [Google Scholar] [CrossRef] [Green Version]
- Wang, C. Lump solution and integrability for the associated Hirota bilinear equation. Nonlinear Dyn. 2017, 87, 2635–2642. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Shao, W.T.; Wu, X.H. The numerical solution of the nonlinear Klein–Gordon and sine–Gordon equations using the Chebyshev tau meshless method. Comput. Phys. Commun. 2014, 185, 1399–1409. [Google Scholar] [CrossRef]
- Pekmen, B.; Tezer-Sezgin, M. Differential quadrature solution of nonlinear Klein–Gordon and sine–Gordon equations. Comput. Phys. Commun. 2012, 183, 1702–1713. [Google Scholar] [CrossRef]
- Bulbul, B.; Sezer, M. A new approach to numerical solution of nonlinear Klein–Gordon equation. Math. Probl. Eng. 2013, 2013, 869749. [Google Scholar] [CrossRef]
- Hulbert, G.M.; Hughes, T.J.R. Space-time finite element methods for second-order hyperbolic equations. Comput. Methods Appl. Mech. Eng. 1990, 84, 327–348. [Google Scholar] [CrossRef] [Green Version]
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef] [Green Version]
- Kuo, P.Y.; Luis, V. Numerical solution of a nonlinear wave equation in polar coordinates. Appl. Math. Comput. 1984, 14, 313–329. [Google Scholar]
- Argyris, J.; Haase, M. An engineer’s guide to soliton phenomena: Application of the finite element method. Comput. Methods Appl. Mech. Eng. 1987, 61, 71–122. [Google Scholar] [CrossRef]
- Lakestani, M.; Dehghan, M. Collocation and finite difference-collocation methods for the solution of nonlinear Klein–Gordon equation. Comput. Phys. Commun. 2010, 181, 1392–1401. [Google Scholar] [CrossRef]
- Aziz, I.; Šarler, B. Wavelets collocation methods for the numerical solution of elliptic BV problems. Appl. Math. Model. 2013, 37, 676–694. [Google Scholar] [CrossRef]
- Mohanty, R.K. New unconditionally stable difference schemes for the solution of multi-dimensional telegraphic equations. Int. J. Comput. Math. 2009, 86, 2061–2071. [Google Scholar] [CrossRef]
- Liao, H.L.; Sun, Z.Z. Maximum norm error estimates of efficient difference schemes for second-order wave equations. J. Comput. Appl. Math. 2011, 235, 2217–2233. [Google Scholar] [CrossRef] [Green Version]
- Bratsos, A.G.; Twizell, E.H. A family of parametric finite-difference methods for the solution of the sine–Gordon equation. Appl. Math. Comput. 1998, 93, 117–137. [Google Scholar] [CrossRef]
- Dehghan, M.; Mohebbi, A.; Asgari, Z. Fourth-order compact solution of the nonlinear Klein–Gordon equation. Numer. Algorithms 2009, 52, 523–540. [Google Scholar] [CrossRef]
- Mohebbi, A.; Dehghan, M. High-order solution of one-dimensional sine–Gordon equation using compact finite difference and DIRKN methods. Math. Comput. Model. 2010, 51, 537–549. [Google Scholar] [CrossRef]
- Guo, P.F.; Liew, K.M.; Zhu, P. Numerical solution of nonlinear Klein–Gordon equation using the element-free kp-Ritz method. Appl. Math. Model. 2015, 39, 2917–2928. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J.Z.; Zhou, Y.H. A space-time fully decoupled wavelet Galerkin method for solving two-dimensional Burgers’ equations. Comput. Math. Appl. 2016, 72, 2908–2919. [Google Scholar] [CrossRef]
- Liu, X.J.; Wang, J.Z.; Zhou, Y.H. A space-time fully decoupled wavelet Galerkin method for solving a class of nonlinear wave problems. Nonlinear Dyn. 2017, 90, 599–616. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.Z.; Zhou, Y.H. Wavelet solution for large deflection bending problems of thin rectangular plates. Arch. Appl. Mech. 2015, 85, 355–365. [Google Scholar] [CrossRef]
- Jiwari, R. Lagrange interpolation and modified cubic B-spline differential quadrature methods for solving hyperbolic partial differential equations with Dirichlet and Neumann boundary conditions. Comput. Phys. Commun. 2015, 193, 55–65. [Google Scholar] [CrossRef]
- Yin, F.K.; Tian, T.; Song, J.Q.; Zhu, M. Spectral methods using Legendre wavelets for nonlinear Klein∖Sine-Gordon equations. J. Comput. Appl. Math. 2015, 275, 321–334. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Mohebbi, A. The numerical solution of nonlinear high dimensional generalized Benjamin–Bona–Mahony–Burgers equation via the meshless method of radial basis functions. Comput. Math. Appl. 2014, 68, 212–237. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Mohebbi, A. The use of interpolating element-free Galerkin technique for solving 2D generalized Benjamin–Bona–Mahony–Burgers and regularized long-wave equations on non-rectangular domains with error estimate. J. Comput. Appl. Math. 2015, 286, 211–231. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, J.Z.; Liu, X.J.; Zhou, Y.H. A wavelet integral collocation method for nonlinear boundary value problems in physics. Comput. Phys. Commun. 2017, 215, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.Z.; Zhang, L.; Zhou, Y.H. A simultaneous space-time wavelet method for nonlinear initial boundary value problems. Appl. Math. Mech.-Engl. Ed. 2018, 39, 1547–1566. [Google Scholar] [CrossRef]
- Zhou, Y.H. Wavelet Numerical Method and Its Applications in Nonlinear Problems; Springer: Berlin, Germany, 2021. [Google Scholar]
- Wang, J.Z. Generalized Theory and Arithmetic of Orthogonal Wavelets and Applications to Researches of Mechanics Including Piezoelectric Smart Structures. Ph.D. Thesis, Lanzhou Univeristy, Lanzhou, China, 2001. (In Chinese). [Google Scholar]
- Dehghan, M.; Shokri, A. Numerical solution of the nonlinear Klein–Gordon equation using radial basis functions. J. Comput. Appl. Math. 2009, 230, 400–410. [Google Scholar] [CrossRef] [Green Version]
- Bratsos, A.G. The solution of the two-dimensional sine–Gordon equation using the method of lines. J. Comput. Appl. Math. 2007, 206, 251–277. [Google Scholar] [CrossRef] [Green Version]
- Bratsos, A.G. An improved numerical scheme for the sine–Gordon equation in 2+1 dimensions. Int. J. Numer. Methods Eng. 2008, 75, 787–799. [Google Scholar] [CrossRef]
- Dehghan, M.; Ghesmati, A. Numerical simulation of two-dimensional sine–Gordon solitons via a local weak meshless technique based on the radial point interpolation method (RPIM). Comput. Phys. Commun. 2010, 181, 772–786. [Google Scholar] [CrossRef]
- Jiang, C.L.; Sun, J.Q.; Li, H.C.; Wang, Y.F. A fourth-order AVF method for the numerical integration of sine–Gordon equation. Appl. Math. Comput. 2017, 313, 144–158. [Google Scholar] [CrossRef]
- Jiwari, R.; Pandit, S.; Mittal, R.C. Numerical simulation of two-dimensional sine–Gordon solitons by differential quadrature method. Comput. Phys. Commun. 2012, 183, 600–616. [Google Scholar] [CrossRef]
- Liu, C.Y.; Wu, X.Y. Arbitrarily high-order time-stepping schemes based on the operator spectrum theory for high-dimensional nonlinear Klein–Gordon equations. J. Comput. Phys. 2017, 340, 243–275. [Google Scholar] [CrossRef]
- Liu, X.J.; Liu, G.R.; Wang, J.Z.; Zhou, Y.H. A wavelet multiresolution interpolation Galerkin method for targeted local solution enrichment. Comput. Mech. 2019, 64, 989–1016. [Google Scholar] [CrossRef]
- Liu, X.J.; Liu, G.R.; Wang, J.Z.; Zhou, Y.H. A wavelet multi-resolution enabled interpolation Galerkin method for two-dimensional solids. Eng. Anal. Bound. Elem. 2020, 117, 251–268. [Google Scholar] [CrossRef]

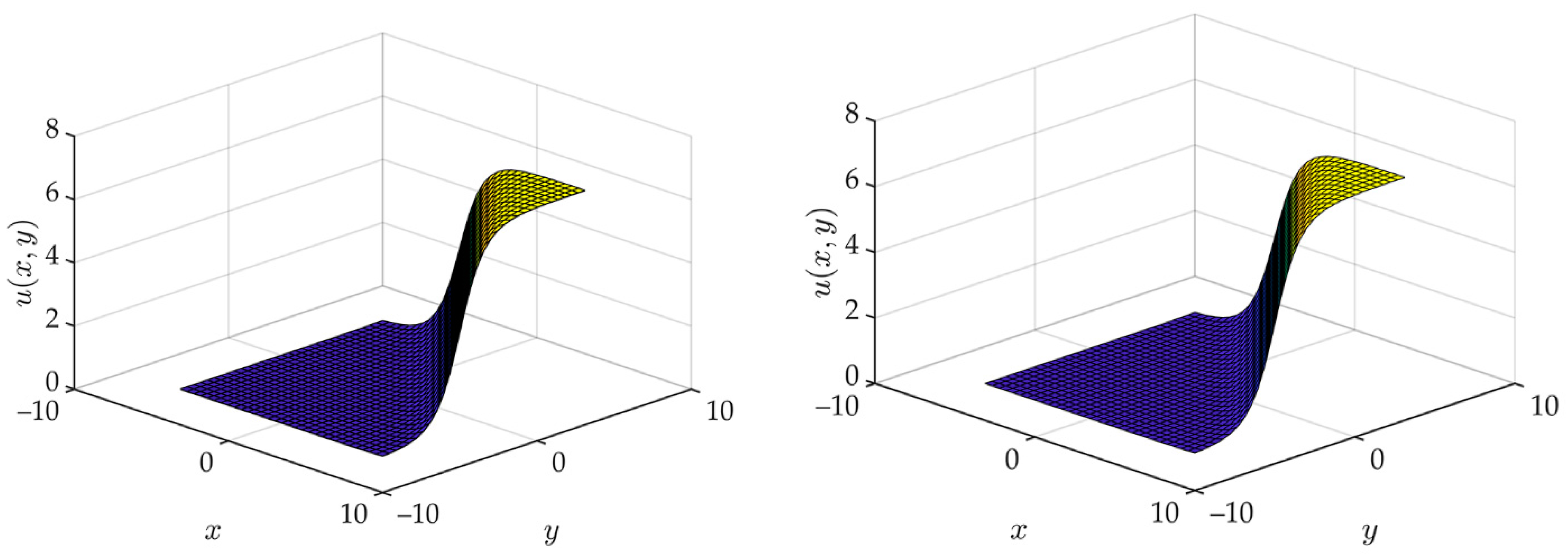
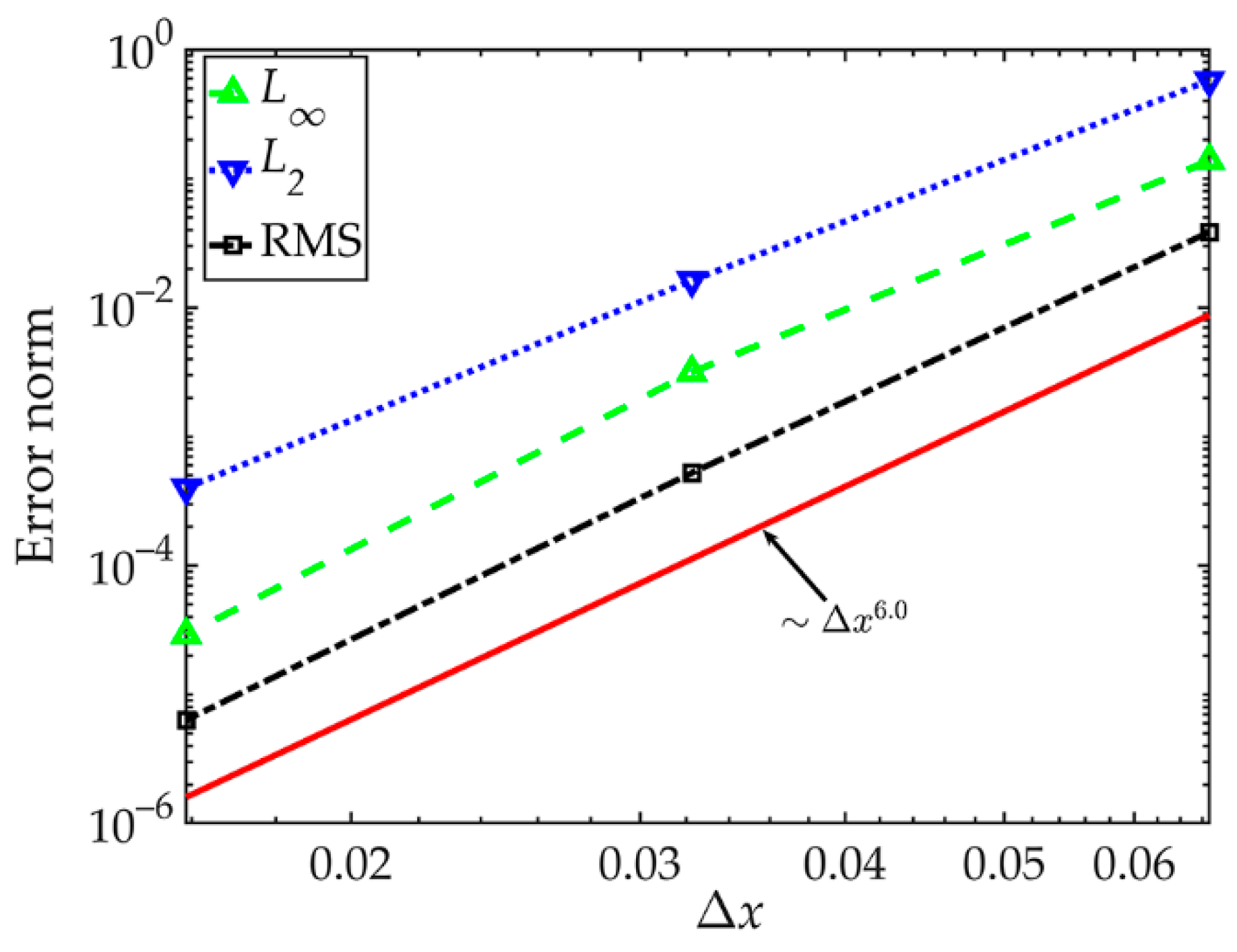

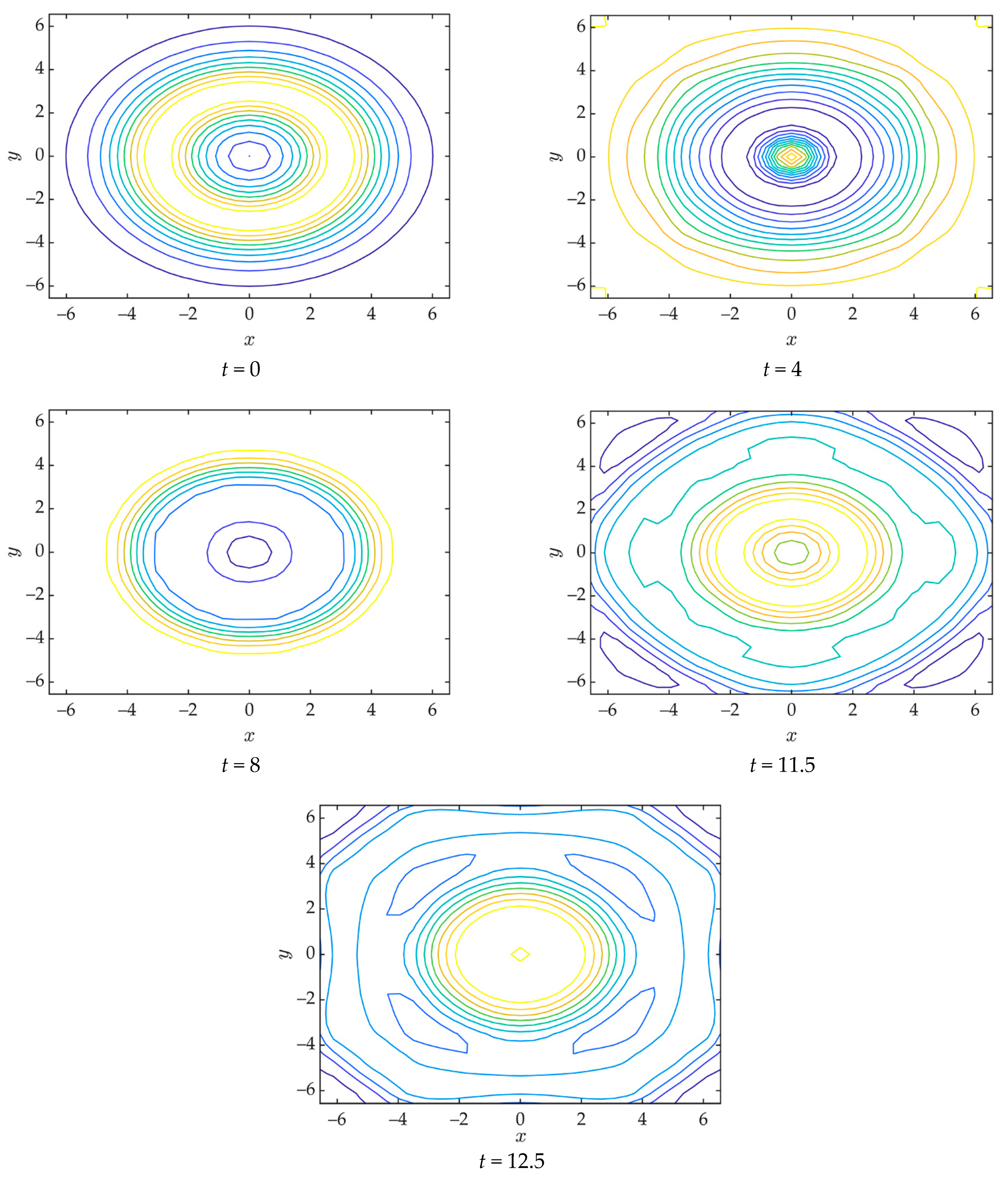
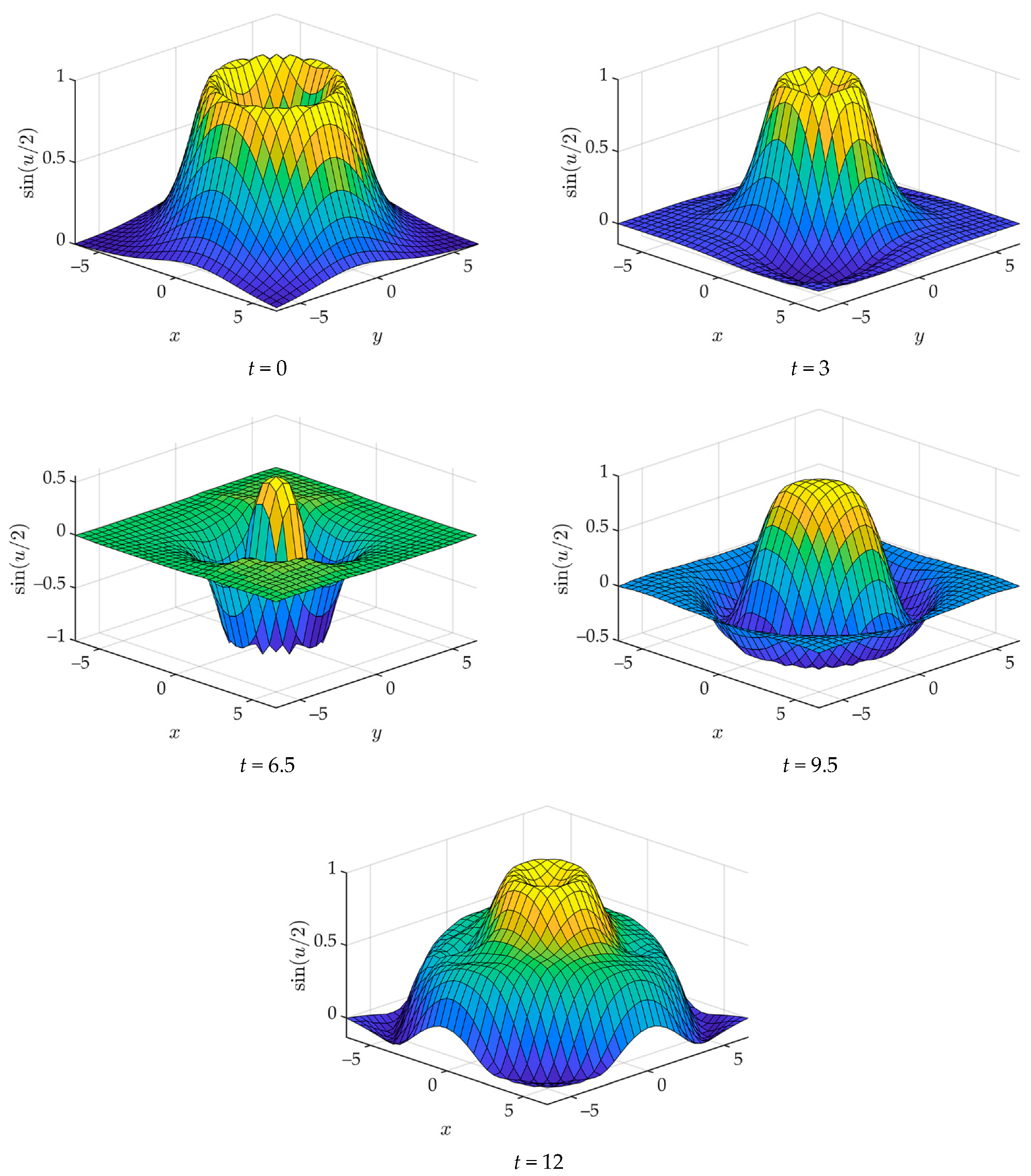

| K | ωK | K | ωK | K | ωK |
|---|---|---|---|---|---|
| −1 | 0.328691834525214 | 3 | −0.149711341365277 | 7 | 2.30481019094508 × 10−5 |
| 0 | 0.998606741614628 | 4 | 0.0345899116285495 | 8 | 2.08826733683054 × 10−10 |
| 1 | −0.57539605262846 | 5 | −0.00453827543632113 | 9 | −9.43911615536308 × 10−13 |
| 2 | 0.367253112532719 | 6 | 0.000481043784287261 |
| t | RBFCM (M = 50) [35] | LWSCM (M = 24) [28] | WICM (M = 15) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| L∞ | L2 | RMS | L∞ | L2 | RMS | L∞ | L2 | RMS | |
| 1 | 6.0 × 10−6 | 4.1 × 10−5 | 4.1 × 10−6 | 6.1 × 10−6 | 1.1 × 10−5 | 3.6 × 10−6 | 1.2 × 10−10 | 2.0 × 10−10 | 5.1 × 10−11 |
| 2 | 2.2 × 10−5 | 1.6 × 10−4 | 1.6 × 10−5 | 2.2 × 10−5 | 4.1 × 10−5 | 1.4 × 10−5 | 1.7 × 10−9 | 2.6 × 10−9 | 6.7 × 10−10 |
| 3 | 9.1 × 10−5 | 6.5 × 10−4 | 6.4 × 10−5 | 9.1 × 10−5 | 1.6 × 10−4 | 5.4 × 10−5 | 6.7 × 10−8 | 9.4 × 10−8 | 2.4 × 10−8 |
| t | RBFCM (M = 50) [35] | LWSCM (M = 24) [28] | WICM (M = 15) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| L∞ | L2 | RMS | L∞ | L2 | RMS | L∞ | L2 | RMS | |
| 1 | 3.6 × 10−7 | 1.8 × 10−6 | 1.8 × 10−7 | 1.1 × 10−7 | 1.7 × 10−7 | 5.6 × 10−8 | 1.0 × 10−11 | 2.0 × 10−11 | 5.3 × 10−12 |
| 2 | 3.9 × 10−7 | 1.5 × 10−6 | 1.5 × 10−7 | 2.0 × 10−7 | 3.6 × 10−7 | 1.2 × 10−7 | 1.2 × 10−11 | 2.2 × 10−11 | 5.8 × 10−12 |
| 3 | 4.2 × 10−7 | 1.7 × 10−6 | 1.7 × 10−7 | 2.4 × 10−7 | 4.2 × 10−7 | 1.4 × 10−7 | 1.6 × 10−11 | 2.9 × 10−11 | 7.5 × 10−12 |
| t | PDQM (M = 21, Δt = 0.001) [27] | MCB-DQM (M = 21, Δt = 0.001 [27] | WICM (M = 15, Δt = 1/210) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| L∞ | L2 | RMS | L∞ | L2 | RMS | L∞ | L2 | RMS | |
| 0.5 | 2.2 × 10−5 | 5.1 × 10−6 | 1.1 × 10−6 | 1.8 × 10−5 | 8.9 × 10−5 | 1.4 × 10−5 | 6.6 × 10−11 | 2.0 × 10−10 | 5.3 × 10−11 |
| 1 | 2.5 × 10−5 | 6.6 × 10−6 | 1.4 × 10−5 | 5.1 × 10−5 | 2.6 × 10−4 | 4.0 × 10−5 | 1.2 × 10−10 | 2.0 × 10−10 | 5.1 × 10−11 |
| 1.5 | 5.2 × 10−5 | 1.4 × 10−4 | 2.9 × 10−5 | 6.7 × 10−5 | 2.8 × 10−4 | 4.4 × 10−5 | 4.3 × 10−10 | 8.0 × 10−10 | 2.1 × 10−10 |
| 2 | 4.9 × 10−5 | 1.3 × 10−4 | 2.8 × 10−5 | 3.0 × 10−5 | 1.2 × 10−4 | 1.8 × 10−5 | 1.7 × 10−9 | 2.6 × 10−9 | 6.7 × 10−10 |
| 3 | 3.3 × 10−4 | 8.6 × 10−5 | 1.8 × 10−5 | 4.9 × 10−5 | 2.2 × 10−4 | 3.4 × 10−5 | 6.7 × 10−8 | 9.4 × 10−8 | 2.4 × 10−8 |
| t | FDM [3] (M = 56 × 56, Δt = 0.001) | RBFCM [3] (M = 56 × 56, Δt = 0.001) | WICM (M = 31 × 31, Δt = 1/210 ≈ 0.001) | |||
|---|---|---|---|---|---|---|
| L2 | L∝ | L2 | L∝ | L2 | L∝ | |
| 1 | 0.7221 | 0.0350 | 0.2860 | 0.0670 | 0.0162 | 0.0032 |
| 3 | 0.7877 | 0.0431 | 0.5872 | 0.0834 | 0.0216 | 0.0086 |
| 5 | 0.5167 | 0.0404 | 0.8288 | 0.1015 | 0.0279 | 0.0104 |
| h | RBF [29] | EFG [30] | Present Method | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMS | L∝ | C | RMS | L∝ | C | RMS | L∝ | C | |
| 1/4 | 2.3 × 10−3 | 8.9 × 10−3 | - | 4.1 × 10−4 | 1.5 × 10−3 | - | 2.1 × 10−4 | 2.9 × 10−4 | - |
| 1/8 | 8.9 × 10−4 | 4.1 × 10−3 | 1.1 | 2.1 × 10−4 | 6.5 × 10−4 | 1.2 | 2.9 × 10−6 | 2.6 × 10−6 | 5.9 |
| 1/16 | 4.5 × 10−4 | 1.2 × 10−3 | 1.8 | 1.1 × 10−4 | 7.4 × 10−4 | 0.2 | 3.0 × 10−8 | 2.2 × 10−8 | 6.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, J.; Liu, X.; Zhou, Y.; Wang, J. A Space-Time Fully Decoupled Wavelet Integral Collocation Method with High-Order Accuracy for a Class of Nonlinear Wave Equations. Mathematics 2021, 9, 2957. https://doi.org/10.3390/math9222957
Weng J, Liu X, Zhou Y, Wang J. A Space-Time Fully Decoupled Wavelet Integral Collocation Method with High-Order Accuracy for a Class of Nonlinear Wave Equations. Mathematics. 2021; 9(22):2957. https://doi.org/10.3390/math9222957
Chicago/Turabian StyleWeng, Jiong, Xiaojing Liu, Youhe Zhou, and Jizeng Wang. 2021. "A Space-Time Fully Decoupled Wavelet Integral Collocation Method with High-Order Accuracy for a Class of Nonlinear Wave Equations" Mathematics 9, no. 22: 2957. https://doi.org/10.3390/math9222957
APA StyleWeng, J., Liu, X., Zhou, Y., & Wang, J. (2021). A Space-Time Fully Decoupled Wavelet Integral Collocation Method with High-Order Accuracy for a Class of Nonlinear Wave Equations. Mathematics, 9(22), 2957. https://doi.org/10.3390/math9222957







