Abstract
Stepped hydrostatic thrust bearings used in metal-cutting machines are characterized by high load capacity and damping, which ensure the stable operation of structures. However, in comparison with throttle thrust bearings, they have a high compliance. It is preferable that, in addition to the main bearing function, a modern hydrostatic bearing has the ability to provide low (including negative) compliance for the implementation of an adaptive function in order to actively compensate for the deformation of the machine resilient system, thereby increasing the accuracy of metalworking. This paper considers the design of a stepped hydrostatic thrust bearing, which, in order to reduce the compliance to negative values, features a technical improvement consisting of the use of an active displacement compensator on an elastic suspension. In this paper, the results of mathematical modeling and theoretical research of stationary and non-stationary modes of operation of the adaptive thrust bearing are presented. The possibility of a significant reduction in the static compliance of the structure, including the negative compliance values, is shown. It was found that negative compliance is provided in a wide range of loads, which can be up to 80% of the range of permissible bearing loads. The study of the dynamic characteristics showed that with a targeted selection of parameters that ensure optimal performance, the adaptive thrust bearing is able to operate stably in the entire range of permissible loads. It has been established that an adaptive stepped hydrostatic thrust bearing with a displacement compensator has a high stability margin, sufficient to ensure its operability when implementing the adaptive function.
1. Introduction
Stepped hydrostatic bearings are used in metal-cutting machines and, when compared with similar throttle bearings, are characterized by their increased load capacity [1,2,3]. In addition, they are structurally and technologically simpler [4,5,6] and they are characterized by high quality indicators of dynamics [7,8,9]. At the same time, such bearings have disadvantages, among which the main one is the high pliability of the bearing lubricant layer [10,11,12]. In the past, hydrostatic bearings were required to provide a high load capacity and low compliance, which was ensured by feeding throttle systems. At the present time, this is no longer enough. It is preferable that the hydrostatic bearings of machine tools, in addition to the main bearing function, also have adaptive properties. During metalworking, cutting forces act on the spindle assembly and cause the spindle to move. This is due to a change in the thickness of the lubricant layer in the bearing, which is the cause of machining inaccuracy. To compensate for such an inaccuracy, an adaptive system is needed [13,14]. Thus, the best technical solution would be a hydrostatic bearing, which is not only a bearing but also an adaptive system, because a decrease in compliance by itself is not able to provide the bearing with an adaptive function.
An adaptive function is required for precise positioning; the compensation for tool wear or elastic deformations of a machine tool, fixture, or part; and to compensate for temperature deformations [15,16,17,18]. To implement the adaptive function, it is necessary to create an additional control movement of the bearing, or to ensure the negative compliance of its load-bearing layer. Usually, additional movements in adaptive systems are carried out with the help of special complex devices [19]. It is known that the use of aerostatic supports, controlled by the position of the movable element, make it possible to increase the load capacity, reduce the compliance, and also obtain an additional function—the drive of the micro-displacements of the shaft [20,21,22]. Similar systems with hydrostatic supports are known [23], but it should be noted that all of these structures that provide the necessary adaptive displacement are complex.
Simpler designs include hydrostatic and aerostatic bearings with negative compliance. To reduce the compliance in non-contact sliding bearings, an active compensation of the lubricant flow rate is used, in which membrane regulators of the nozzle-flap type [24,25] or Laub elastic washers are used as inlet flow compensators [26,27]. The use of membrane or elastic regulators make it possible to reduce the static compliance to negative values (in the latter case, the increments of the load and the gap in the load-bearing fluid layer have the same signs), which ensures the adaptive function of such bearings. However, such designs are too energy intensive as a result of the need to significantly increase the lubricant flow rate using the input regulators to reduce compliance. In addition, negative compliance is usually provided only in a narrow range of loads [26,28]. The use of such regulators creates a large pressure flow rate gain, which has a negative effect on the bearing dynamics, so that it is very difficult to obtain negative compliance [26].
The preferred means of reducing the compliance of the bearings is the use of compensators for the movement of the movable element (shaft) [29,30,31]. Such designs allow for a decrease in compliance to negative values, which also allows them to be used not only as supporting systems, but also as automatic strain relief compensators of the technological system of machine tools, in order to reduce the time and increase the accuracy of metalworking, thereby realizing the mentioned adaptive function.
The present paper discusses the results of a theoretical study of the static and dynamic characteristics of an adaptive stepped hydrostatic thrust bearing with an active displacement compensator.
Figure 1 shows a schematic diagram of an improved circular stepped hydrostatic thrust bearing with a displacement compensator.
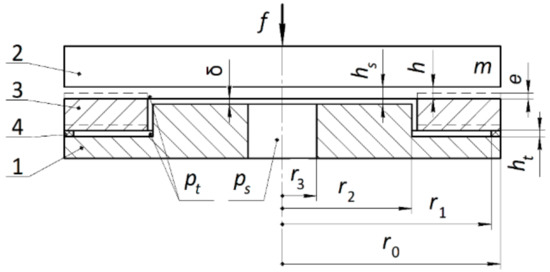
Figure 1.
Design diagram of an adaptive stepped thrust bearing.
The structure has an abutment (shaft) 2 and a base 1, which is hermetically connected to rigid ring 3 of the inner radius r2 and the outer radius r0 by means of elastic ring 4 of the inner radius r1. The thrust bearing is supplied from a source of liquid injection under pressure ps through a hole of radius r3. In the absence of pressure, a step of height δ is formed between the surfaces of base 1 and ring 3. In working conditions, a lubricant film of thickness h is created between the surfaces of ring 3 and shaft 2. Between base 1 and ring 3, there is a blind annular gap of thickness ht, into which the lubricant is supplied without resistance under pressure pt < ps, which is formed as a result of overcoming the hydraulic resistance to the lubricant flow in the gap of thickness hs on the ring r3 < r < r2. The size of this gap is determined by the following sum:
where e is the axial deformation of elastic ring 4, caused by the action of the difference in the hydrostatic forces on the working surfaces of ring 3.
With the rigid ring, 4, the bearing works like a conventional thrust bearing. If the ring is elastic and has axial compliance ke > 0, then under the influence of hydrostatic forces on the surfaces of ring 3, ring 4 is deformed, and at certain values of the structure’s radii, the displacement of ring 3 in the direction opposite to the action of the external force f is ensured. As a result, the gap hs increases, which entails a decrease in the compliance of the thrust bearing.
This paper considers a mathematical model of the unsteady state of the thrust bearing and calculates and studies its static and dynamic characteristics.
2. Mathematical Modeling
The study of the characteristics of the thrust bearing was carried out in a dimensionless form. The following scales of values are accepted: ps—for pressures; r0—for radii; t0—for current time; h0—for gaps; step size and deformation e of ring 4; —for volumetric lubricant flow rates; and —for axial forces, where h0 corresponds to gap h in the thrust bearing receiving the design load f0, where μ is the lubricant viscosity. Dimensionless quantities are designated by capitalized Latin and Greek letters.
The pressure function P(R,τ) in thin gaps satisfies the unsteady Reynolds equation for an incompressible fluid [32]:
where Hi(τ) is the function of the flat gap, R is the current radius, is the so-called “compression number” of the liquid film in the gap, and τ is the dimensionless time.
On the circle , the pressure function is constant and equal to the following:
On the ring , in the region of the gap Hs, the boundary value problem for Equation (2) satisfies the boundary conditions:
The solution to the boundary value problem in (2) and (4) is the following function:
On the ring , in the region of the gap H, the boundary value problem for Equation (2) satisfies the following boundary conditions:
The solution to the boundary value problem in (2) and (6) is the following function:
On the ring , in the region of the gap Ht, the boundary value problem for Equation (2) satisfies the following boundary conditions:
The solution to the boundary value problem in (2) and (8) is the following function:
The reactions of the pressure forces in the specified areas are determined by the general formula:
Substituting (3), (5), (7) and (9) in (10), we obtain the following expressions for force reactions:
where
The lubricant flow rate at the junction of the step and the ledge and at the entrance to the blind gap is determined by the general formula [32]
Formula (15) gives the flow rate at the outlet of the gap Hs:
where
At the entrance to the gap H, the flow rate is
where
At the entrance to the gap Ht the flow rate is
where
The formulas for hydrostatic forces and flow rates, derived from the analytical solution of boundary value problems for the Reynolds equation, are verified by an alternative numerical finite difference method [33].
In addition to the listed forces, the inertial force of the shaft acts in the dynamic system
where m is the mass of the shaft.
The load capacity of the thrust bearing is
where
A hydrostatic force acts on the surface of ring 3
where
The mathematical model of the thrust bearing dynamics includes two equations of the force balance of shaft 2 and ring 3, one equation for the balance of the lubricant flow rate, and formulas for determining the gap Ht and the total gap Hs
where ε is the dimensionless axial deformation of ring 4 and Ht0 is the thickness of the blind gap in the absence of a load on ring 3. Formula (23) is obtained on the basis of Hooke’s law [34] for small axial deformations of elastic ring 4, where Ke is the axial compliance (elasticity) coefficient of this ring.
Substituting (16)–(21) into (22)–(24) and taking into account (26), we write (22)–(24) in the following form:
A closed system of 4 nonlinear differential Equations (26)–(29) is a mathematical model of the thrust bearing dynamics, which can be considered as a continuous automatic control system (controlled object) [35] containing an input disturbing function of the external load F and 4 output controlled functions: H, Hs, ε, and Pt.
Studying the characteristics of the thrust bearing is divided into two parts. In the first part, a study of its stationary state is carried out in order to detect the modes of negative compliance that provide an adaptive function. In the second part, the stability criteria and stability margin of the dynamic system are studied and the optimal dynamic modes are determined, which are important from the point of view of its speed, and which have a decisive effect on the quality and accuracy of metalworking.
3. Static Characteristics of the Thrust Bearing
The mathematical model of the stationary state of the thrust bearing is a special case of the dynamics model (26)–(29) in the absence of oscillations. The model can be represented as the following system of four nonlinear equations:
To study the characteristics of the resulting system, it is necessary to adjust the parameters of the so-called stationary “calculated point” mode. To do this, we need to select a point on the load curve Hs(F), setting one part of the parameters and calculating the other part of them.
3.1. Setting the Parameters of the “Calculated Point” Mode
Under the “calculated point” mode we assumed a set of values of quantities corresponding to a dimensionless unit gap H = 1, when the dimensional gap in the region of the ledge was equal to the calculated gap h = h0. It was convenient to adjust the thrust bearing to this mode by setting the pressure at the junction of the step and the ledge using the normalized pressure adjustment factor , according to the formula The input values also included the radii R1, R2, R3, and the elasticity coefficient Ke. Using (30)–(33), we calculated the deformation ε0, gap Hs0, step height Δ, bearing load capacity W0, and lubricant flow rate Q0.
A necessary condition for ensuring the adaptive function is the positiveness of the hydraulic force We. It follows from (21) that this takes place when An analysis of this condition shows that the radius R1 should be set proceeding from the condition
When adjusting the parameters of the “calculated point”, it is advisable to find the value of the elasticity coefficient Ke = Ke0, at which point the thrust bearing will have zero compliance K = 0.
To derive the compliance formula K, it is convenient to use the formula
Taking into account (31) and (32), we performed differentiation in (30) and (33) and substituted the results in (36). In this case, we obtained the required formula for calculating the compliance
Using (37), one can find the elasticity coefficient Ke, at which the thrust bearing will have zero compliance K = 0 at the “calculated point”. By substituting H = 1 and Pt = χ in (37), and equating the numerator of the expression to zero, and after simple transformations, we get
Formula (38) can be conveniently used to calculate the static characteristics of the load capacity, compliance, and lubricant flow rate, setting the elasticity coefficient Ke in proportion to the value of Ke0. So, for Ke = Ke0, the thrust bearing at the “calculated point” will have zero compliance K = 0, for 0 ≤ Ke < Ke0 it will have positive compliance, and for Ke > Ke0 it will be negative.
3.2. Static Characteristics and their Discussion
After determining the parameters of the “calculated point”, we can start calculating the static characteristics of the thrust bearing. It is convenient to carry out calculations in parametric form, taking the pressure Pt as a parameter. For the current pressure, using the Formulas (20) and (21), one can find the bearing load capacity W and the hydraulic force We. Furthermore, from Equation (31), it is possible to determine the deformation ε. Using (32), we can calculate the gap
where
Next, we can determine the gap Hs and flow rate Q.
When calculating these characteristics, it is necessary to take into account that the denominator (39) can become zero. This takes place at the minimum permissible operating pressure Therefore, when calculating the characteristics, the pressure Pt as a parameter should vary within the range
Figure 2 shows the graph of the load characteristics for various values of the coefficient of elasticity Ke. Radii R2 = 0.85 and R3 = 0.1 are accepted. For these values The value of the radius R1 = 0.95 is taken, at which condition (35) is fulfilled and, therefore, the adaptive function of the thrust bearing should be provided. The pressure was adjusted according to the formula for the average permissible pressure value Subsequently, using (38), the elasticity coefficient of ring 4 was found at which the thrust bearing at the “calculated point” had 0 compliance, and, finally, the values (34) were determined The listed values are the same for all curves in Figure 2. The values depend on the coefficient Ke; therefore, for each curve in Figure 2, they were calculated using Formula (34), separately.
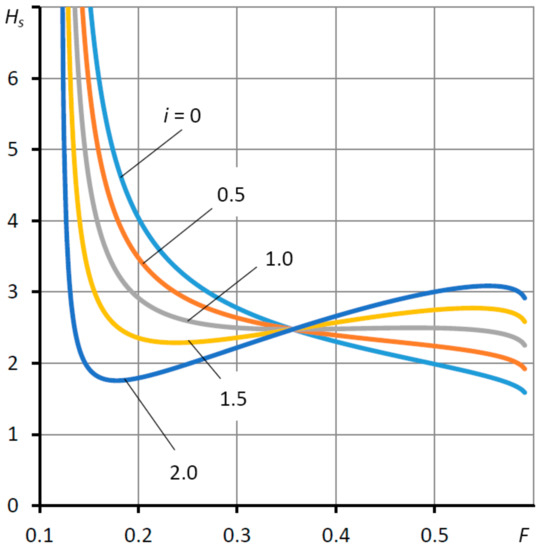
Figure 2.
Load characteristics Hs(F) of the thrust bearing at different values of the elasticity coefficient Ke = i Ke0.
The common point of the curves corresponds to the “calculated point” mode. The curve for i = 0 corresponds to the load characteristic of a conventional thrust bearing, for which the coefficient of elasticity Ke = 0. The graph shows that with an increase in i and, consequently, the coefficient Ke, the nature of the curves changes. In this case, in the region of low and moderate loads, the compliance K of the thrust bearing decreased, which can be judged by the change in the slope of the curves.
At Ke = Ke0 (i = 1), at the «calculated point», the thrust bearing will acquire zero compliance. A further increase in the coefficient for Ke > Ke0 (i > 1) promotes the formation of negative compliance. This mode is characterized by the presence of areas of simultaneous increase in load and gap. In such areas, the thrust bearing acquires an adaptive function, since it is able to perform not only the bearing function, but also actively compensate for the deformations of the elastic system of the machine tool, due to the counter-directional force deformation of the load-bearing layer of the thrust bearing.
In a more visual form, the discovered effect is illustrated by the curves of the dependence of the compliance K on the external force F, which are shown in Figure 3. It is observable that, with an increase in Ke, the compliance K decreases in the range of working loads. At Ke = Ke0, the thrust bearing reaches zero compliance at the “calculated point”. In this case, a small area of negative compliance appears on the curve. At Ke > Ke0, the areas of negative compliance become wider. In the range of loads F, corresponding to negative compliance K, the thrust bearing is capable of carrying loads and compensating for the elastic deformations of the machine, that is, performing an adaptive function.
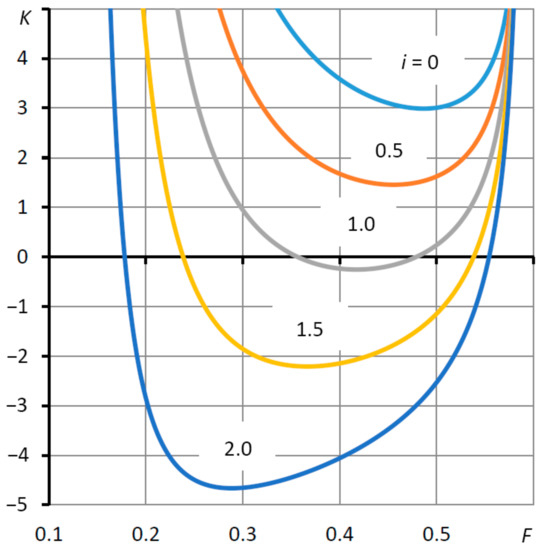
Figure 3.
Dependences of compliance K on external force F at different values of the elasticity coefficient Ke = i Ke0.
Figure 4 shows the flow characteristics Q(F) of the thrust bearing. With an increase in the coefficient of elasticity Ke for loads F, preceding the “calculated point”, the flow rate Q decreases and, for subsequent values of F, it increases.
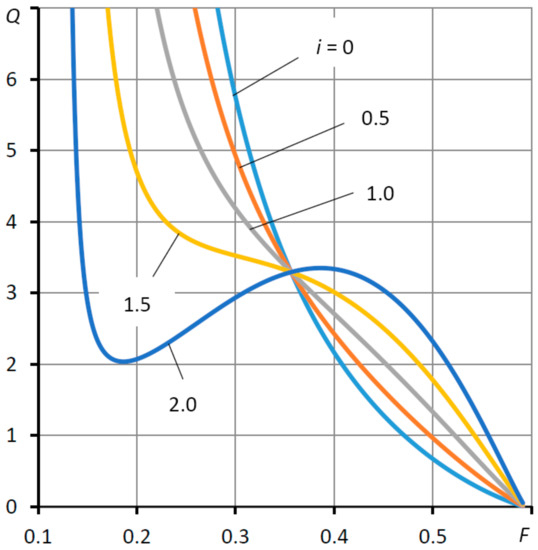
Figure 4.
Flow characteristics Q(F) of the thrust bearing at different values of the elasticity coefficient Ke = i Ke0.
As follows from Formula (17), the gap H affects the flow rate Q to the third degree; therefore, the curves shown in Figure 4 are largely determined by the dependence H(F). The graph of this dependence is shown in Figure 5. It can be observed that with an increase in the Ke coefficient, the noted pattern appears, albeit in a less pronounced form. This pattern has a decisive influence on the dependence Q(F).
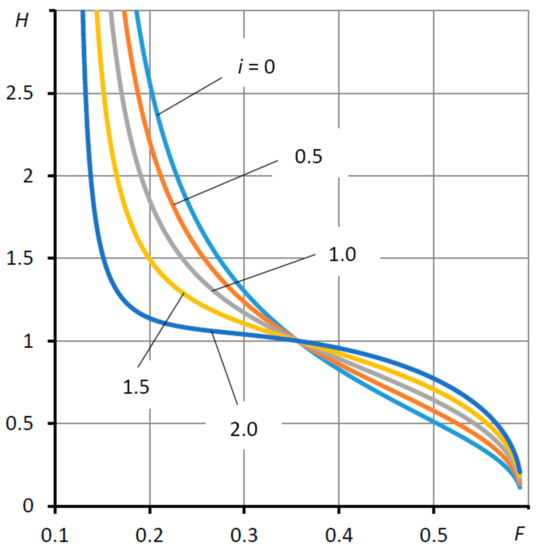
Figure 5.
Dependences of the gap H on the external force F of the thrust bearing at various values of the elasticity coefficient Ke = i Ke0.
As can be observed in Figure 4, the lubricant flow rate in the region of low and moderate loads is several times less than in a conventional thrust bearing. At the same time, in the area of loads exceeding the one that has been calculated, the flow rate in the active thrust bearing is higher, but not to a significant extent. By analyzing the flow rate dependences, it can be concluded that the thrust bearing with negative compliance in the range of operating loads is generally more economical in comparison with the conventional thrust bearing (Ke = 0).
The graph in Figure 6 presents the dependences ε (F) of the deformation of elastic ring 4 on the external load on the bearing. These dependences are linear. It can be seen that, in order to achieve negative compliance, the deformation of elastic ring 4 must be 1–2 times greater than the thickness of the working gap H. At the “calculated point”, the deformation exceeded this gap by only 1.5 times. However, with a different combination of input parameter values, this indicator can change. At lower χ, these indicators are lower, at higher χ they get higher.
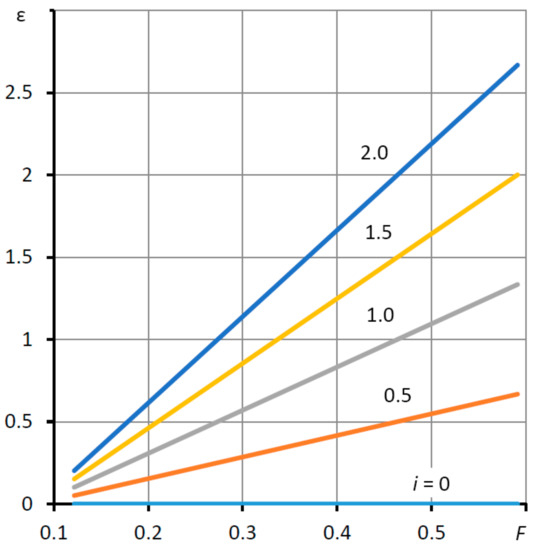
Figure 6.
Characteristics of deformation ε(F) of elastic ring 4 at different values of the elasticity coefficient Ke = i Ke0.
A formal analysis of the static characteristics of an active stepped thrust bearing shows that the use of a displacement compensator makes it possible to realize an adaptive function by providing a negative compliance mode. At the same time, as can be seen, from Figure 3, the range of loads in which this mode is maintained can reach 80% or more of the operating range of loads on the thrust bearing.
However, the conclusion about the performance of such a thrust bearing can be given only on the basis of an analysis of its dynamic characteristics, because the structure can turn out to be unstable, or stable but with insufficient dynamics.
4. Dynamic Characteristics of the Thrust Bearing
Let us consider the dynamics of a thrust bearing whose output values, under the influence of small perturbations of the external load, make small fluctuations relative to their values in a steady (stationary) state.
4.1. Linear Model of Thrust Bearing Dynamics
We represented dynamic quantities in the following form:
where, in each expression, the first term represents the value of the quantity in a steady state, and the second term is equal to the small deviation of the corresponding quantity from this state. Substituting (40) into the nonlinear system of differential Equations (26)–(29), performing linearization [35] and applying the integral Laplace transform [35] to the resulting linear system of equations, we obtained a linear model of the dynamics of the studied thrust bearing. In the matrix form, the system can be represented as
where is the Laplace transform of a small deviation of the disturbing external force; are the transformants of the deviations of the corresponding output quantities; and s is the Laplace transform variable:
By applying Cramer’s rule [36] and the algorithm for the symbolic expansion of the determinants of polynomial matrices to the solution of the system of linear Equation (41), we found the transfer function of the thrust bearing dynamic compliance, which is a rational function of the variable s
where
The denominator of the transfer function (42) is the characteristic polynomial of the system, from which it is possible to judge the stability and quality of transients in a linear dynamic system, describing the “in small” dynamics of a stepped hydrostatic thrust bearing with a displacement compensator.
4.2. Quality Criteria of the Linear Dynamic System
To assess the quality of the linear system describing the dynamics of the thrust bearing, we used the root criteria [35]:
- -
- The degree of stability where si are the zeros of the characteristic polynomial of the dynamical system, which is the polynomial of the denominator of the transfer function (42).
- -
- The damping of oscillations for a period where β is the imaginary part of the root of the characteristic equation with the largest real part.
The degree of stability η characterizes the speed of the system, that is, the speed of damping of its free oscillations. This criterion can be used to judge the stability of the system. For η < 0, the system is unstable; for η > 0, it is stable; and for η = 0, the system is on the stability boundary.
The criterion ξ of oscillation damping over a period can be used to assess the stability margin of the system. The smaller ξ, the more oscillations the transient response will have, and the system will have a smaller stability margin. It is believed that a dynamic system is well damped if ξ ≥ 90% [35].
4.3. Dynamic Characteristics of the Thrust Bearing and their Discussion
The calculation of the dynamic criteria was carried out for the same values of the parameters that affected the static characteristics and for which the graphs of these characteristics were plotted. Three new parameters have been added to the dynamics—the shaft mass M, the static gap Ht and the “compression number” σ (2). In the calculations, we assumed M = 1, which made it possible to determine the scale of the current time t0. It was found that the parameter Ht had a weak effect on the dynamics of the thrust bearing; therefore, it was assumed that Ht = 1.
Of greatest interest was the study of stability modes that provided negative static compliance and, consequently, the adaptive function of the thrust bearing. The dynamic system (41) contained the “compression number” σ, which had a decisive effect on the dynamics of the thrust bearing. Figure 6 shows the curves of the dependence of the stability degree η on the parameter σ for different values of the elasticity coefficient Ke, including those that give the thrust bearing negative static compliance in the “calculated point” mode.
By comparing the graphs in Figure 3 and Figure 7, we find that with positive static compliance (i < 1, K > 0), the thrust bearing is stable (η > 0) for any values of the parameter σ. However, even at zero compliance (i = 1, K = 0), stability takes place only at σ > σmin, where σmin is the value of the parameter σ at which the bearing reaches the stability boundary (η = 0). Therefore, for a bearing of zero compliance, σmin = 39. At 0 < σ < σmin, it is unstable (η < 0).
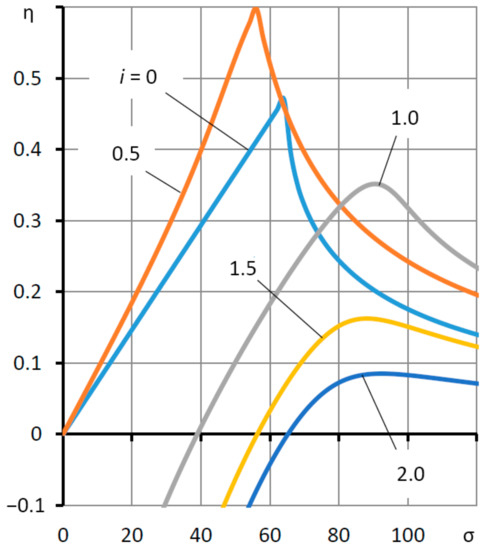
Figure 7.
Dependences of the degree of stability η on the “compression number” σ for different values of the coefficient of elasticity Ke = i Ke0.
With a further increase in the values of the elasticity coefficient Ke (i > 1) in the area of negative compliance, the stability boundary shifts to the right. Thus, at Ke = 1.5 Ke0, the stability limit is σmin = 54. Nevertheless, there is a region σ > σmin, in which the bearing remains stable, even with greater compliance.
It is noteworthy that the dependences η(σ) have a pronounced extreme character, which indicates the existence of an optimal value of the parameter σ = σopt, at which point this dependence reaches a maximum, providing the thrust bearing with the best response rate during the damping of the dynamic transient processes. For Ke ≥ Ke0, the optimal performance takes place at σopt = 90.
A comparison of the curves of the dependence of the decay criterion ξ, for the period on the parameter σ presented in Figure 8 with the curves in Figure 7, shows that the maximum response rate corresponds to the transition of the nature of oscillatory transient processes (ξ < 100%) to aperiodic (ξ = 100%). The latter are preferable because they are characterized by the maximum margin of the stability of the structure against vibrations that reduce the quality of its dynamics. However, at large values of the elasticity coefficient, the aperiodicity of the transient processes cannot be ensured. Nevertheless, even in these cases, the values of the ξ criterion remain significant (ξ ≥ 90%), providing the structure with a sufficient margin of stability to vibrations. Based on the analysis performed, it can be concluded that, when designing the thrust bearing, it is preferable to choose the value of the parameter σ as slightly more than σ = σopt, in order to provide a sufficient margin of stability and not to lose speed. From this point of view, σ = 90–95 can be considered optimal for the given graphs.
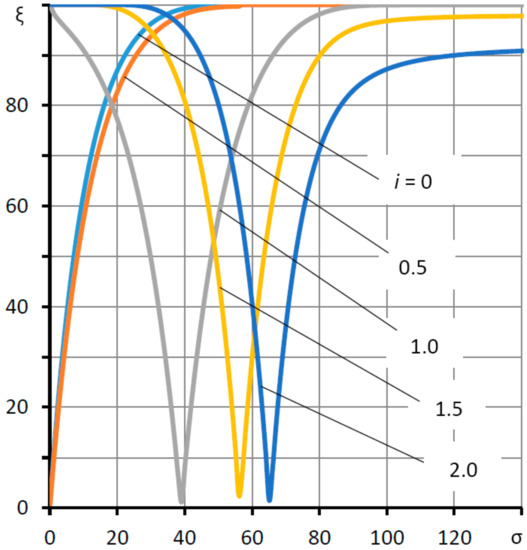
Figure 8.
Dependences of the oscillation damping criterion for the period ξ on the “compression number” σ for different values of the elasticity coefficient Ke = i Ke0.
From the optimal value of the dimensionless parameter σ, it is possible to determine the dynamic scale h0 of the gaps, the step height, and the deformation of ring 4. Since the dimensionless mass of the shaft M = 1 is accepted in the calculations, from the expression for the mass scale, we can obtain the formula for the current time scale
By substituting (43) into the formula for the “compression number” σ and performing the transformations, we obtained the following formula for calculating the scale h0:
For example, let us take By substituting these data in (44), we find h0 = 20 μm. At the “calculated point”, the dimensionless gap H = 1, and hence the gap on the ledge, which is optimal from the point of view of dynamics, is h = h0 = 20 μm. In this case, the external load at the “calculated point” will be f = 90 N. Using (43), we can now calculate the scale of the current time and, using the well-known formula [35], find the decay time of the transient process
which determines the speed of the thrust bearing at the “calculated point”. Let us calculate the shortest decay time of the transient process for the curve Ke = 1.5 Ke0 in Figure 7. The maximum of the function η(σ) = 0.16 at σ = 90. Using Formula (45), we find tp = 0.009 s.
Of interest is the quality of the thrust bearing dynamics at various values of the load in the entire range of its variation. Graphs 9 and 10 show the curves of the stability degree η and damping of the oscillations during the period ξ from load F for various values of the coefficient Ke at σ = 90.
The graph in Figure 9 shows that the thrust bearing remains stable at all values of the Ke coefficient over the entire range of the load variation. On this basis, an important conclusion can be made that the adaptive bearing is operable not only in the “calculated point” mode, but also in the entire range of permissible loads.
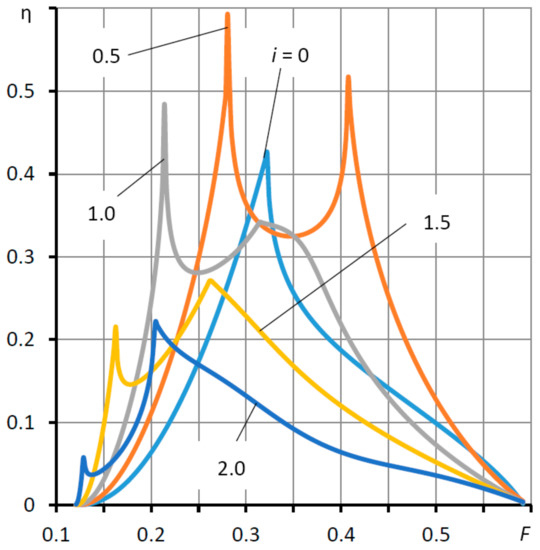
Figure 9.
Dependences of the degree of stability η on load F for different values of the elasticity coefficient Ke = i Ke0.
The stability margin of the thrust bearing in the range of permissible loads makes it possible to evaluate the graph in Figure 10. It can be seen that at moderate loads the structure has a sufficiently high stability margin, since the criterion ξ > 90%. A decrease in the values of the criterion is observed only at very low or extremely high loads, when the criterion gives lower indicators. But even with such loads, the thrust bearing has a sufficient stability margin, which does not fall below 80%.
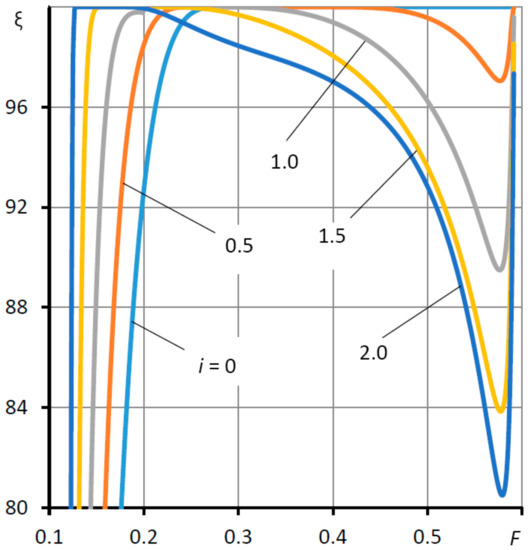
Figure 10.
Dependences of the oscillation damping criterion for the period ξ on the load F at different values of the elasticity coefficient Ke = i Ke0.
The quality of the structure dynamics can be judged not only by the criteria of free oscillations, but also by the amplitude–frequency characteristics of forced oscillations of the transfer function of dynamic compliance (42), the graph for which is shown in Figure 11.
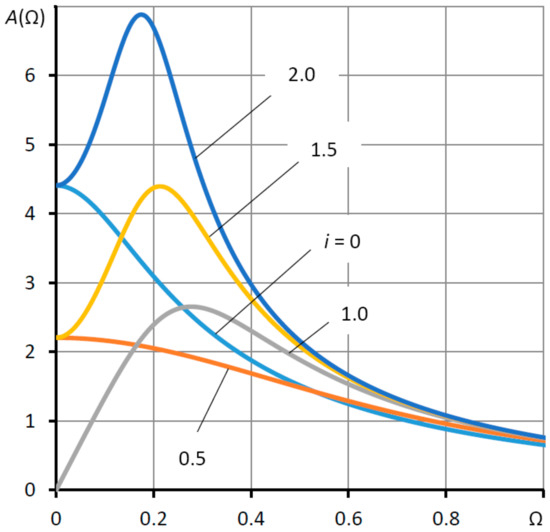
Figure 11.
Amplitude–frequency characteristics of the thrust bearing at the “calculated point” for different values of the elasticity coefficient Ke = i Ke0.
It can be observed that in the modes of positive compliance, the frequency response does not have resonance points, since A(0) ≥ A(Ω), which is evidence of the absolute margin of stability for such structures. The curve corresponding to zero static compliance formally has a resonance point Ωr = 0.28. However, the amplitude of such a resonance does not exceed the compliance of a conventional thrust bearing.
The greatest resonance occurs in the thrust bearing with low negative compliance at Ke = 2 Ke0. The resonance amplitude is A(Ωr) = 6.87. In this case, the initial amplitude is A(0) = 4.4. The frequency response oscillation index Π = A(Ωr)/A(0) = 1.56. It is believed that the dynamic system is well damped if Π < 2.5 [35]. Thus, even with a very small negative static compliance, the system has a very large stability margin at the “calculated point”.
The results obtained for the particular case of a conventional stepped bearing were compared with the experimental data given in [2]. The comparison showed a complete qualitative and satisfactory quantitative agreement between theoretical and experimental data.
5. Conclusions
This paper considers the design and carries out a theoretical study of the static and dynamic characteristics of an adaptive stepped hydrostatic thrust bearing with an active displacement compensator on an elastic suspension. In the present study, the results of the mathematical modeling and theoretical research of stationary and non-stationary modes of operation of the adaptive thrust bearing are presented. Moreover, the possibility of a significant reduction in the static compliance of the structure, including to negative values, in order to implement the adaptive function and using the thrust bearing not only as a support, but also as an active compensator for the deformation of the elastic system of a metal-cutting machine, in order to improve the quality of metalwork, is presented in this study. It was found that negative compliance is provided in a wide range of loads, which can be up to 80% of the range of permissible thrust bearing loads. The study of dynamic characteristics shows that, with a targeted selection of parameters that ensure optimal performance, the thrust bearing is able to operate stably in the entire range of permissible loads. It has also been established that an adaptive stepped hydrostatic thrust bearing with a displacement compensator has a high stability margin sufficient enough to ensure its operability.
Author Contributions
Conceptualization, V.K.; formal analysis, A.K.; investigation, S.B., A.S. and L.G.; data curation, O.G., M.B. and L.S.; writing—original draft preparation, V.K.; writing—review and editing, A.K.; project administration, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| H, h | dimensionless thickness, thickness of the gap |
| Ht | dimensionless thickness of the step gap |
| Hs | dimensionless thickness of the total gap |
| ε | dimensionless deformation of elastic ring 4 |
| K, Ke | dimensionless compliance of bearing and elastic ring 4 |
| P (R,τ) | dimensionless dynamic pressure in the bearing gap |
| pt | lubricant pressure at the junction of the step and the ledge |
| ps | supply pressure |
| Qh | dimensionless flow rate through the gap |
| Qt | dimensionless flow rate at the entrance to the gap Ht |
| Qs | dimensionless flow rate at the outlet of the gap Hs |
| r0, r1, r2, r3 | bearing radii (Figure 1) |
| R | dimensionless radius |
| t0 | current time scale |
| W | dimensionless load capacity |
| δ | step height |
| μ | coefficient of dynamic viscosity of the lubricant |
| χ | normalized adjustment coefficient of the external throttling system |
| σ | “compression number” |
| τ | dimensionless time |
References
- Stachowiak, G.W.; Batchelor, A.W. (Eds.) 6—Hydrostatic Lubrication. In Engineering Tribology, 3rd ed.; Butterworth-Heinemann: Burlington, VT, USA, 2006; pp. 261–285. [Google Scholar]
- Shatokhin, S.; Tyurikov, A.; Petrov, A. Calculation of the static characteristics of the step hydrostatic thrust bearing. In Quality, Reliability and Durability in Mechanical Engineering; Krasnoyarsk Polytechnic Institute Publishing House: Krasnoyarsk, Russia, 1970; pp. 23–27. [Google Scholar]
- Shatokhin, S.; Tyurikov, A.S.; Tsaregorodtsev, M. Increasing the stiffness of the step hydrostatic thrust bearing. In New Equipment and Methods of Its Application in the National Economy; Krasnoyarsk Polytechnic Institute Publishing House: Krasnoyarsk, Russia, 1972; pp. 11–17. [Google Scholar]
- Berthe, D.; Dowson, D.; Godet, M.; Taylor, C.M. Fluid Film Lubrication—Osborne Reynolds Centenary; Elsevier: Leeds, UK, 1986; Volume 11, 706p. [Google Scholar]
- Tyurikov, A.; Borisov, V. Study of the static characteristics of the step hydrostatic thrust bearing. In Improving the Accuracy and Productivity of Machining on Machine Tools; Krasnoyarsk Polytechnic Institute Publishing House: Krasnoyarsk, Russia, 1973; pp. 31–39. [Google Scholar]
- Scharrer, J.; Hibbs, R.; San Andres, L. The asymmetrically stepped, orifice compensated hydrostatic bearing. In Proceedings of the 28th Joint Propulsion Conference and Exhibit, Nashville, TN, USA, 6–8 July 1992. [Google Scholar] [CrossRef]
- Rowe, W.B. (Ed.) Ten—hydrostatic and hybrid plain journal bearings. In Hydrostatic and Hybrid Bearing Design; Butterworth-Heinemann: Burlington, VT, USA, 1983; pp. 154–166. [Google Scholar]
- Tyurikov, A.; Shatokhin, S. Dynamic characteristics of a thrust stepped hydrostatic bearing. In Sliding Bearings with an External Pressure Source; Krasnoyarsk Polytechnic Institute Publishing House: Krasnoyarsk, Russia, 1974; pp. 8–16. [Google Scholar]
- Hemingway, E. A performance investigation into the elastically stepped and shrouded thrust bearing. Proc. Inst. Mech. Eng. 1967, 182, 769–782. [Google Scholar] [CrossRef]
- Mikula, A. Further test results of the leading-edge-groove (leg) tilting pad thrust bearing. J. Tribol. 1988, 110, 174–179. [Google Scholar] [CrossRef]
- Rao, P.S.; Agarwal, S. Theoretical Study of Couple Stress Fluid Film in Rough Step Slider Bearing with Assorted Porous Structures. J. Nanofluids 2018, 7, 92–99. [Google Scholar] [CrossRef]
- Hossain, M.Z.; Razzaque, M.M. Load capacity of a grooved circular step thrust bearing. J. Tribol. 2014, 136, 011705. [Google Scholar] [CrossRef]
- Johnstone, R.; Kirkham, E. Adaptive Control System for Machine Tool or the Like. US4514123A, 30 April 1985. [Google Scholar]
- Lee, J.; Dixon, W.E.; Ziegert, J.C. Adaptive nonlinear contour coupling control for a machine tool system. Int. J. Adv. Manuf. Technol. 2012, 61, 1057–1065. [Google Scholar] [CrossRef] [Green Version]
- Dullo, B. Precise determination of machine positioning. Precis. Eng. 1994, 16, 76. [Google Scholar] [CrossRef]
- Wada, T.; Sakurai, M.; Ogura, A. Tool wear in cutting of sintered iron material. J. Jpn. Soc. Powder Powder Metall. 2001, 48, 386–391. [Google Scholar] [CrossRef]
- Budak, E. Analytical models for high performance milling. Part I: Cutting forces, structural deformations and tolerance integrity. Int. J. Mach. Tools Manuf. 2006, 46, 1478–1488. [Google Scholar] [CrossRef] [Green Version]
- Adamczak, S.; Zmarzły, P.; Janecki, D. Theoretical and practical investigations of v-block waviness measurement of cylindrical parts. Metrol. Meas. Syst. 2015, 22, 181–192. [Google Scholar] [CrossRef]
- Watanabe, T.; Iwai, S. Designs of an adaptive control constraint system of a milling machine tool. In Computer Aided Design of Multivariable Technological Systems; Elsevier: Amsterdam, The Netherlands, 1983; pp. 553–564. [Google Scholar]
- Legaev, V. Analysis of the influence of the design parameters of a controlled-type aerostatic support on stability. Proc. Universities. Mech. Eng. 2005, 3, 16–28. [Google Scholar]
- Legaev, V. Mathematical model of a gas-static support with built-in adjustable nozzles. Sov. J. Vestn. Mashinostroyeniya 2005, 7, 8–12. [Google Scholar]
- Cowley, A.; Kher, A. The dynamic characteristics of a hydrostatically supported spindle bearing system. In Advances in Machine Tool Design and Research 1969; Tobias, S.A., Koenigsberger, F., Eds.; Pergamon: Oxford, UK, 1970; pp. 437–451. [Google Scholar]
- Chen, K.; Yang, H.; Yang, G.; Wang, X. A system approach to the dynamic characteristics of hydrostatic bearings used on machine tools. Int. J. Mach. Tool Des. Res. 1980, 20, 287–297. [Google Scholar] [CrossRef]
- Shatokhin, S.; Kodnyanko, V. Load and Flow Rate Characteristics of an Axial Pressurized Gas Bearing with an Active Compensation of Gas Flow; Springer: Berlin, Germany, 2017; pp. 110–115. [Google Scholar]
- Shatokhin, S.; Kodnyanko, V. Radial gasostatic bearing-seal with opposite internal gas flow compensation. Sov. J. Frict. Wear 1984, 5, 32–35. [Google Scholar]
- Kodnyanko, V.; Shatokhin, S.; Kurzakov, A.; Pikalov, Y. Mathematical modeling on statics and dynamics of aerostatic thrust bearing with external combined throttling and elastic orifice fluid flow regulation. Lubricants 2020, 8, 57. [Google Scholar] [CrossRef]
- Newgard, P.; Kiang, R. Elastic orifices for pressurized gas bearings. ASLE Trans. 1966, 9, 311–317. [Google Scholar] [CrossRef]
- Kodnyanko, V.; Pikalov, Y.; Shatokhin, S. Investigation of the characteristics of a gas-static bearing with active flow rate compensation. Bull. Mech. Eng. 1979, 4, 9–12. [Google Scholar]
- Kodnyanko, V.; Shatokhin, S.; Kurzakov, A.; Pikalov, Y.; Brungardt, M.; Strok, L.; Pikalov, I. Theoretical investigation on performance characteristics of aerostatic journal bearings with active displacement compensator. Appl. Sci. 2021, 11, 2623. [Google Scholar] [CrossRef]
- Kodnyanko, V. Method for calculating the static characteristics of radial hydrostatic compensator of machine tool bearings deformation. Period. Polytech. Transp. Eng. 2021, 49, 114–119. [Google Scholar] [CrossRef] [Green Version]
- Kodnyanko, V.; Belyakova, S.; Grigorieva, O.; Gogol, L.; Surovtsev, A.; Strok, L. The use of a displacement compensator for improve the static characteristics of a step hydrostatic thrust bearing. J. Res. Mech. Eng. 2021, 7, 11–16. [Google Scholar]
- Cameron, A.; Ettles, C.M.M. Basic Lubrication Theory, 3rd ed.; Horwood, E., Ed.; Ellis Horwood Series in Engineering Science; Halsted Press: Chichester, NY, USA, 1981; 256p. [Google Scholar]
- Demidovich, B.; Maron, I.; Shuvalova, E. Numerical Methods of Analysis. Approximation of Functions, Differential and Integral Equations, 5th ed.; Lan: Moscow, Russia, 2010; 400p. [Google Scholar]
- Ugural, A.C.; Fenster, S.K. Advanced Strength and Applied Elasticity; Pearson Education: London, UK, 2003; 471p. [Google Scholar]
- Besekersky, V.; Popov, E. Theory of Automatic Control Systems; Profession: Saint Petersburg, Russia, 2003; 752p. [Google Scholar]
- Ricardo, H. A Modern Introduction to Linear Algebra; CRC Press: New York, NY, USA, 2009; 670p. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).