Adaptive Active Disturbance Rejection Control of Solar Tracking Systems with Partially Known Model
Abstract
:1. Introduction
- 1.
- In contrast with the disturbance estimation approach proposed in [49], in this article, the disturbance is estimated in terms of both states and an additional constant term used to compensate possible offset errors and external components that are independent of the states.
- 2.
- The stability and robustness of the controller is mathematically tested by means of the second method of Lyapunov, and its effectiveness is experimentally tested in a robotic test bed.
- 3.
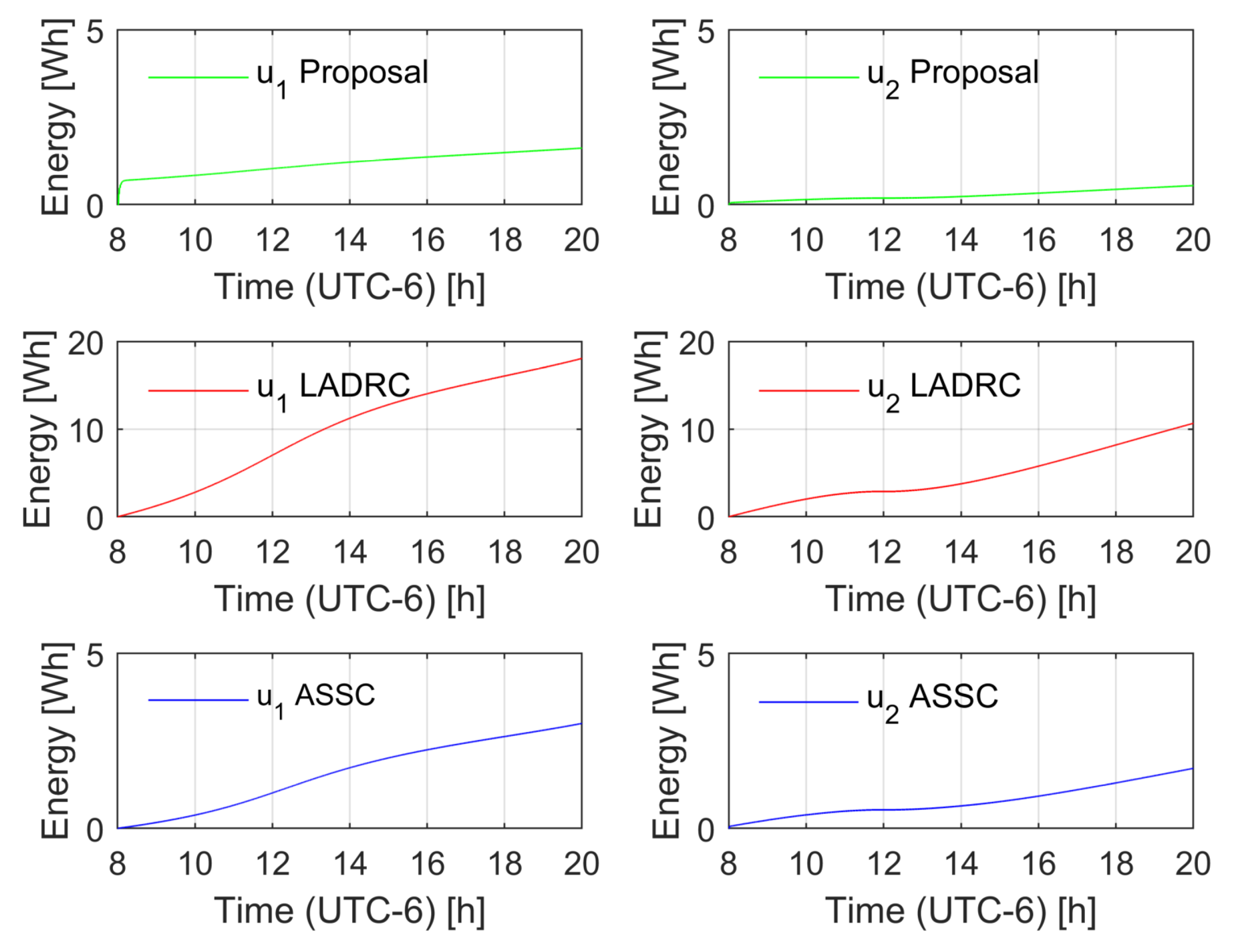
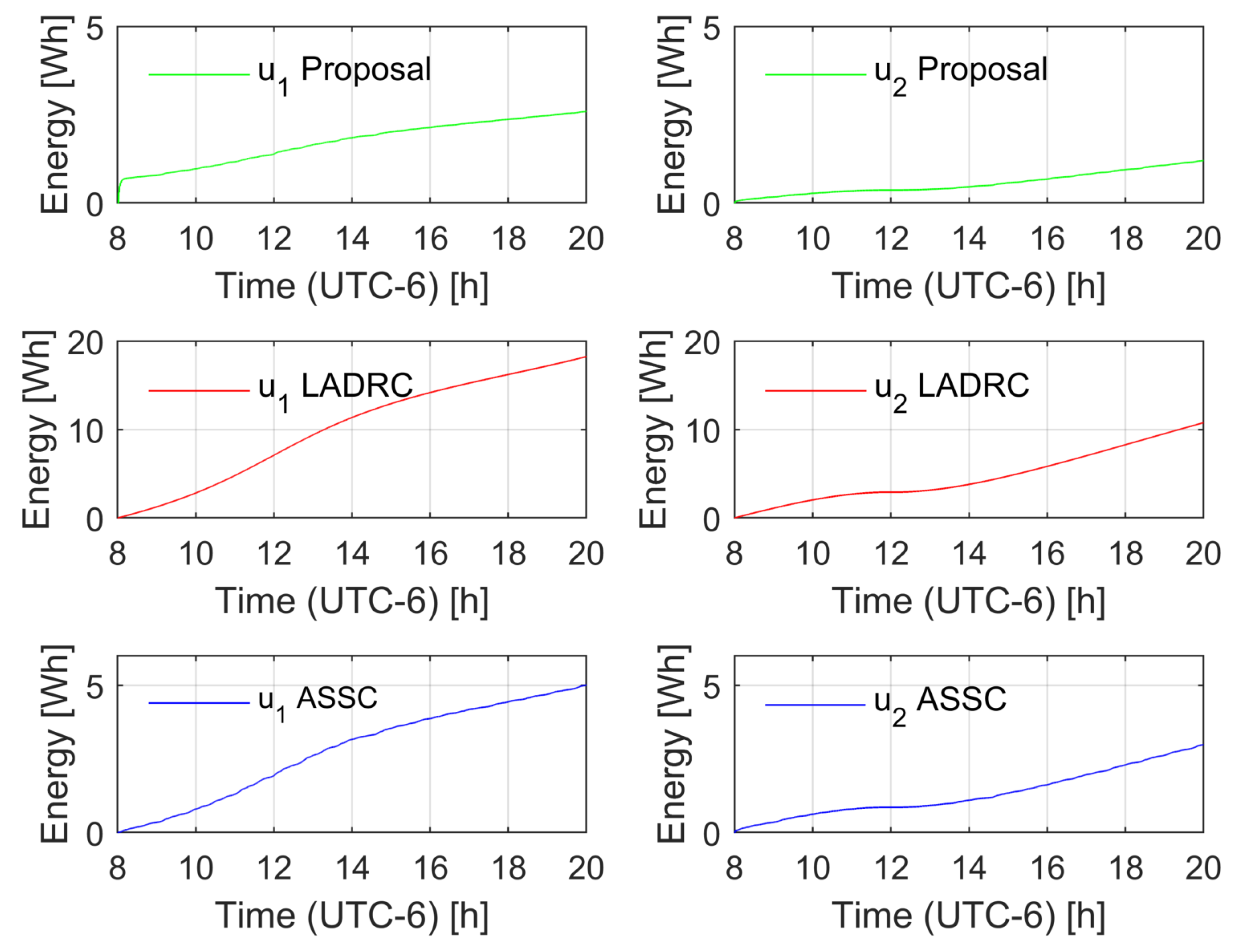
- Some numerical and experimental tests show that the proposed controller demands a low energy consumption, in contrast to a classic ADRC scheme, while keeping appropriate estimation and tracking results for the solar tracking application.
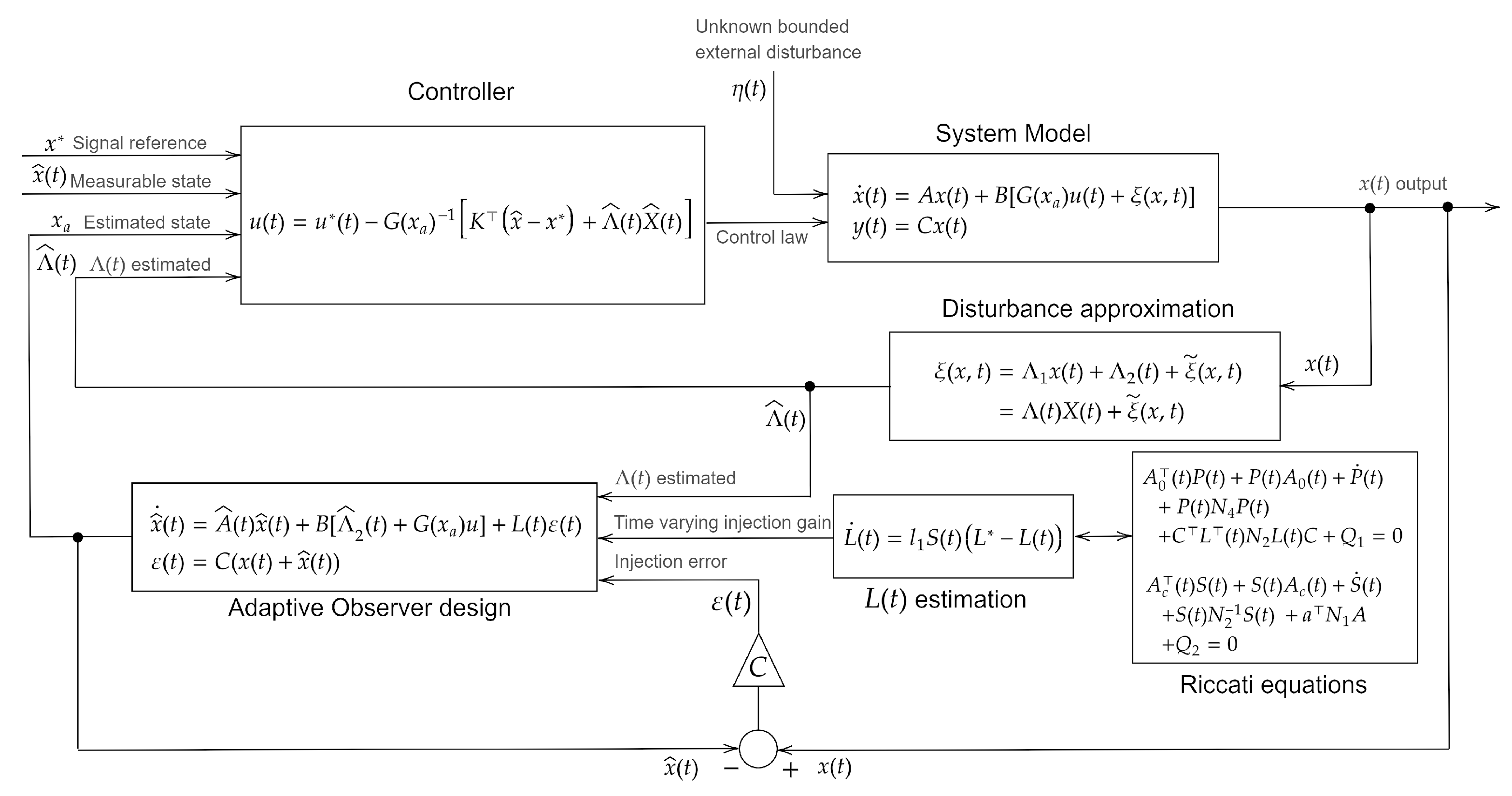
2. Controller Design
3. Observer Design
Control Law
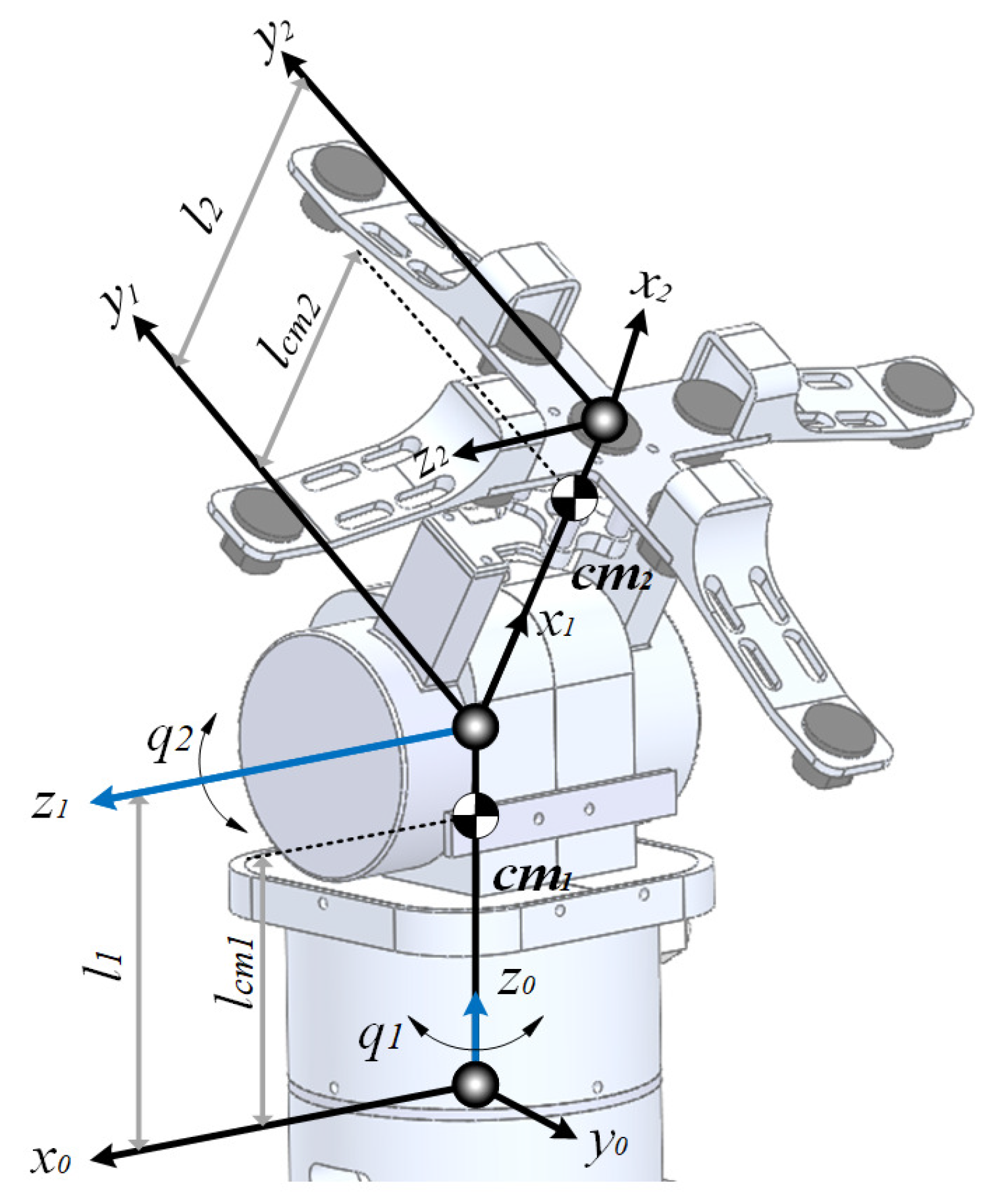
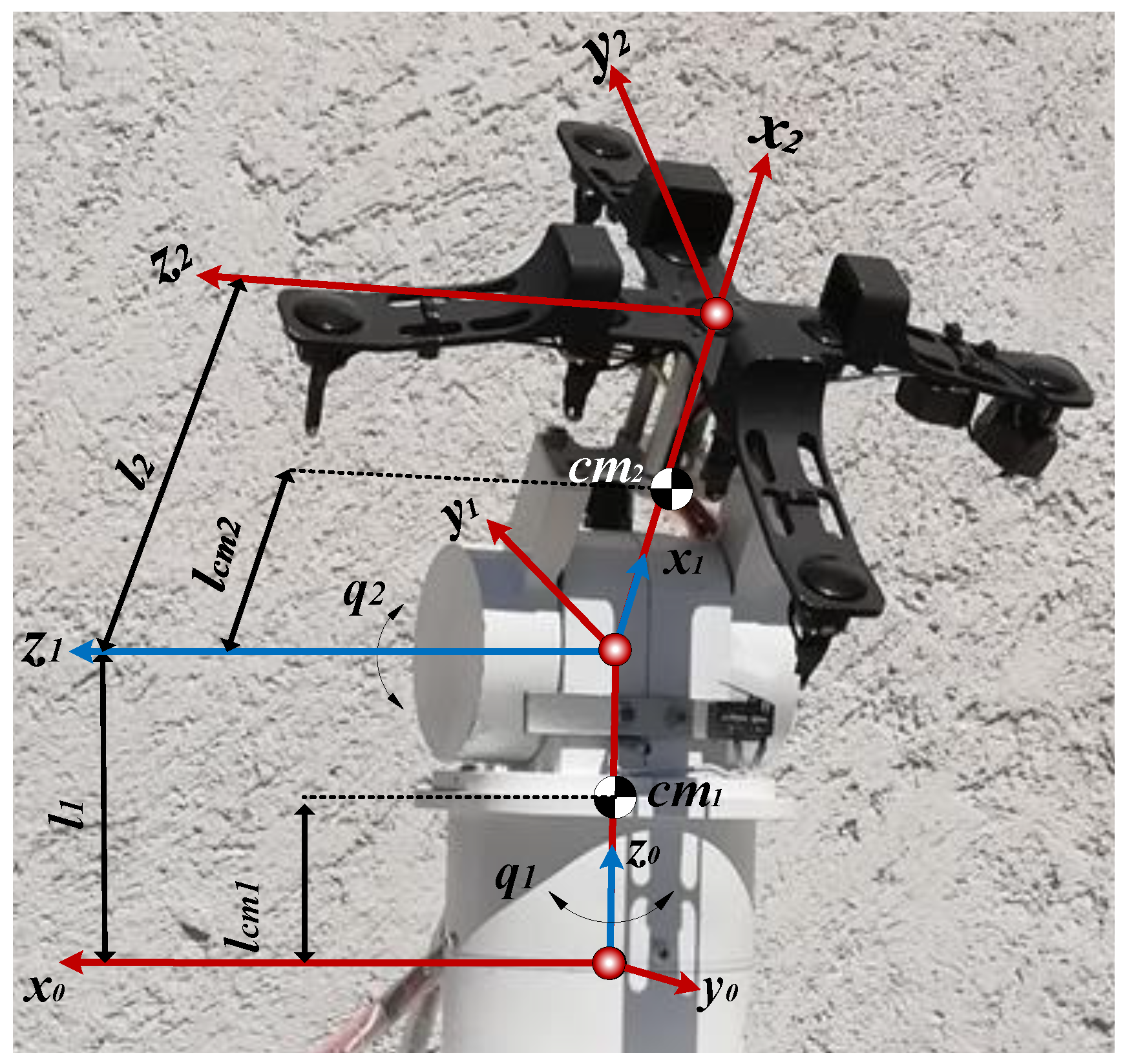
4. Case Study: A Two Degrees of Freedom Solar Tracker
4.1. System and Control Parameters
- The parameters of the robotic system are provided in Table 1.
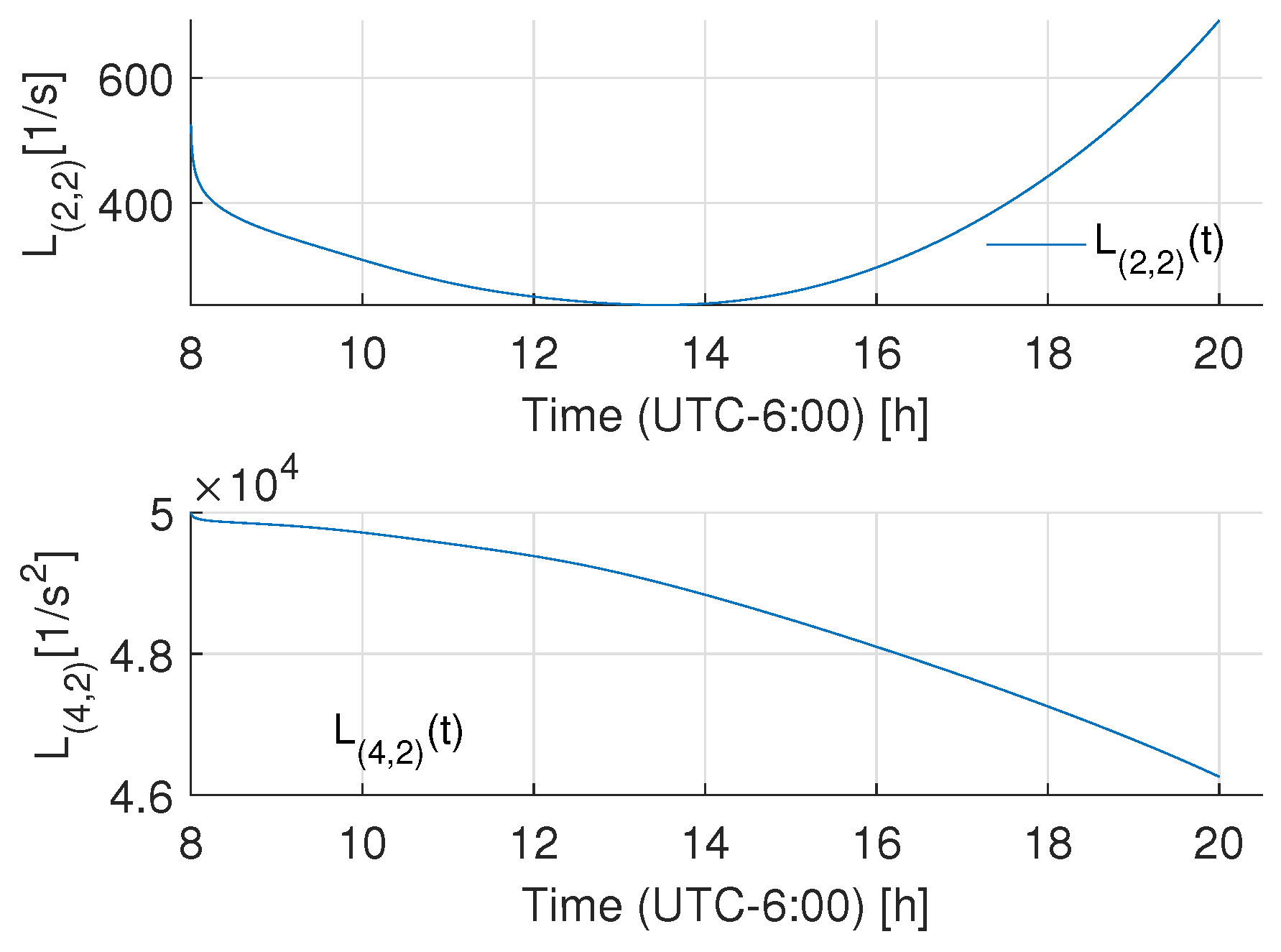
- The reference trajectory is defined by the Cooper’s algorithm [56], given bywhere , is the solar declination, are the longitude and latitude coordinates of the robot, n is the day number (), and denotes the hour angle. In this case, , , . The time interval, t, was set to be from 8 a.m. to 8 p.m.
- The controller gain parameters were set to beThe choice of , , was in the context of a set of a model matching with two decoupled, stable, second-order linear model references of the form , , . That is,where , , , . This choice can be enhanced by optimization procedures [57], but this aspect is out of the scope of this work and will be considered in future research.
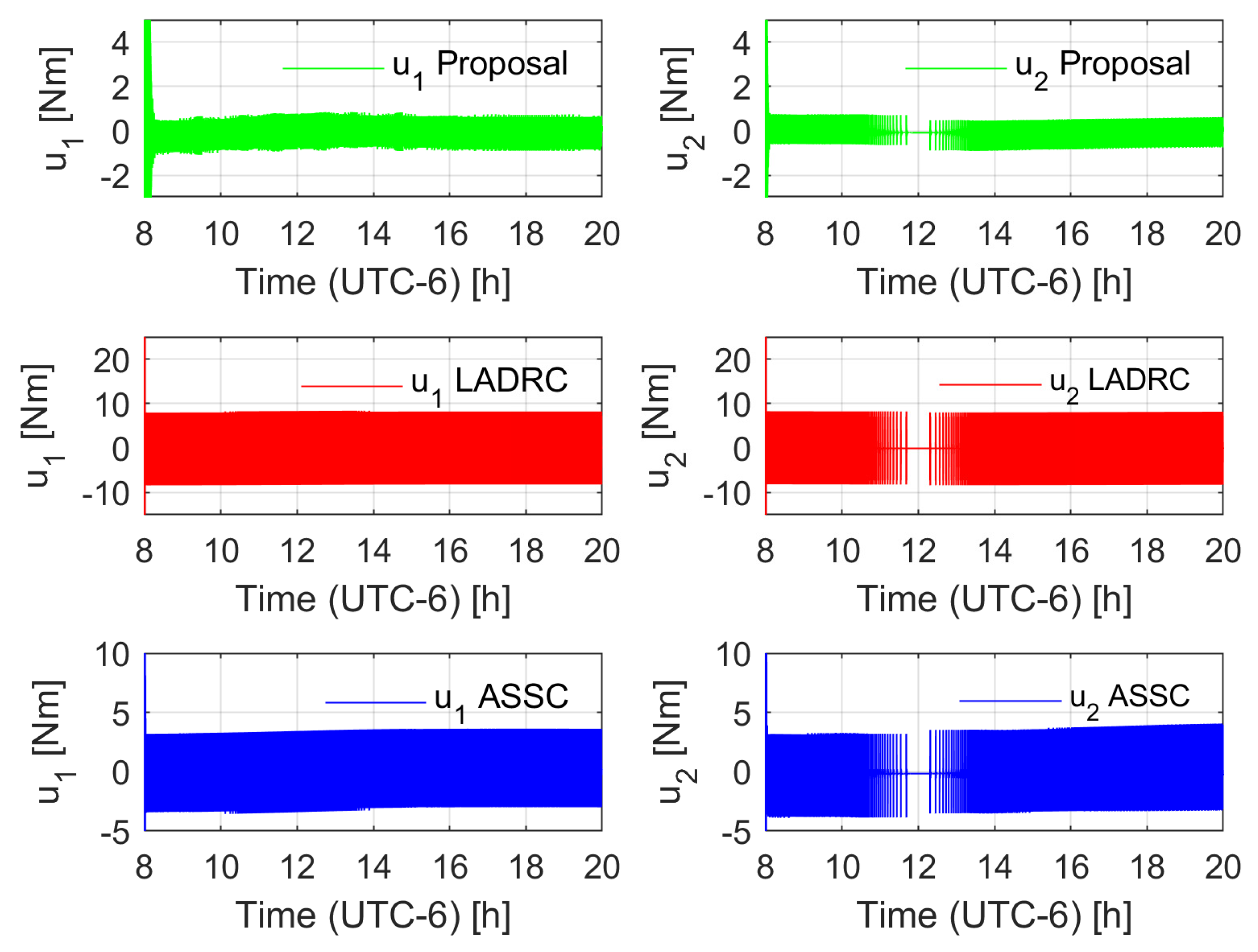
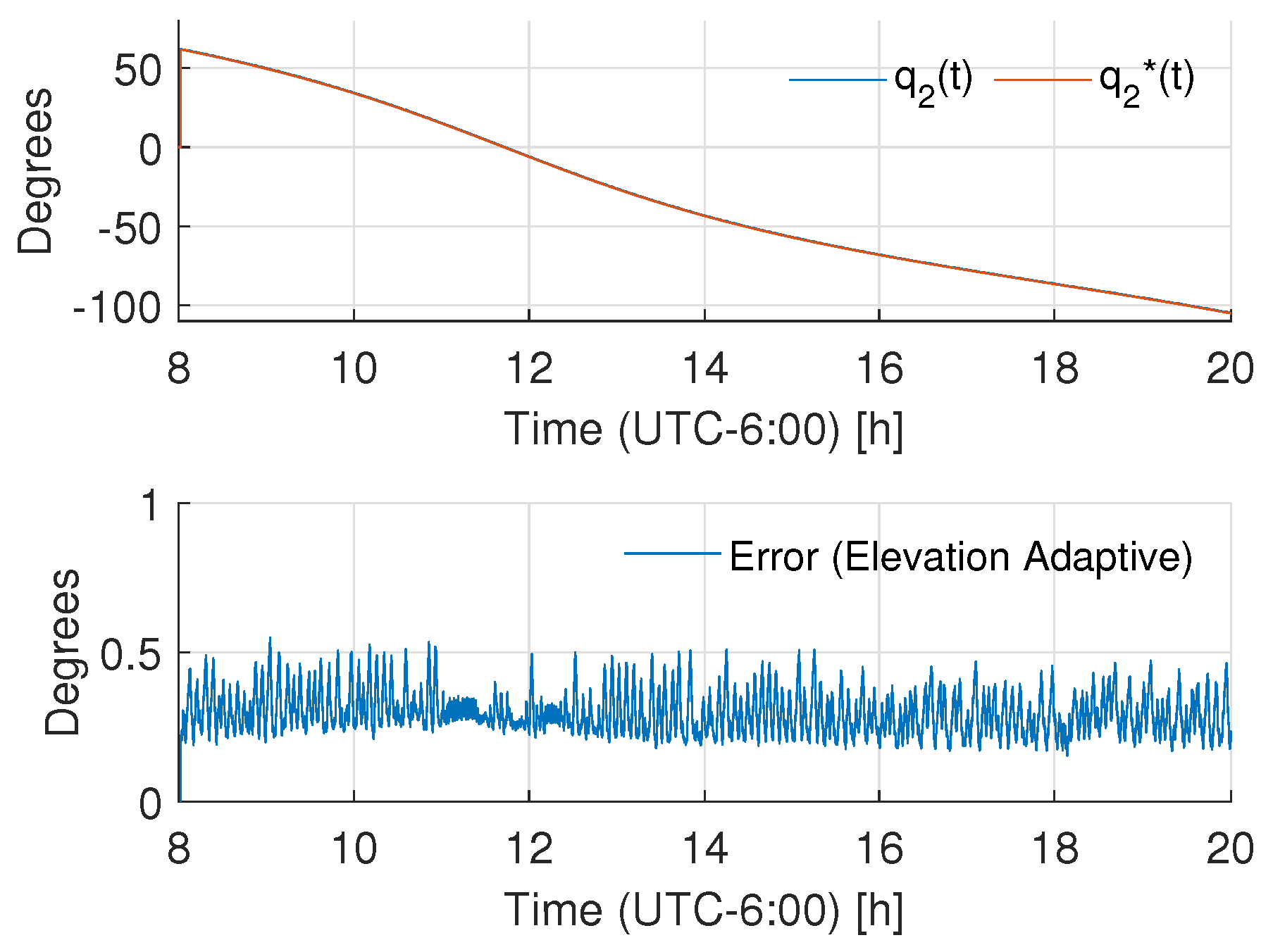
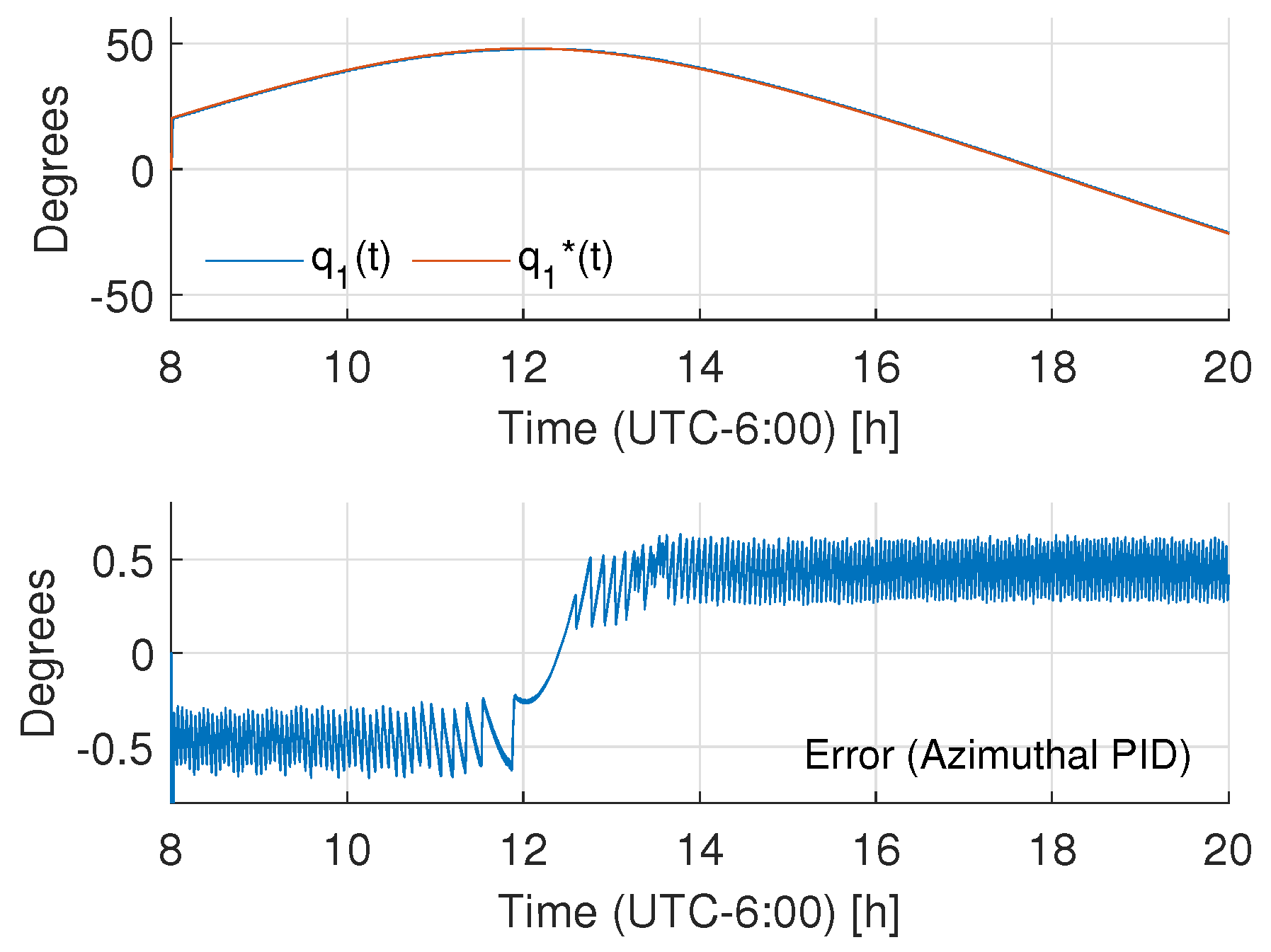
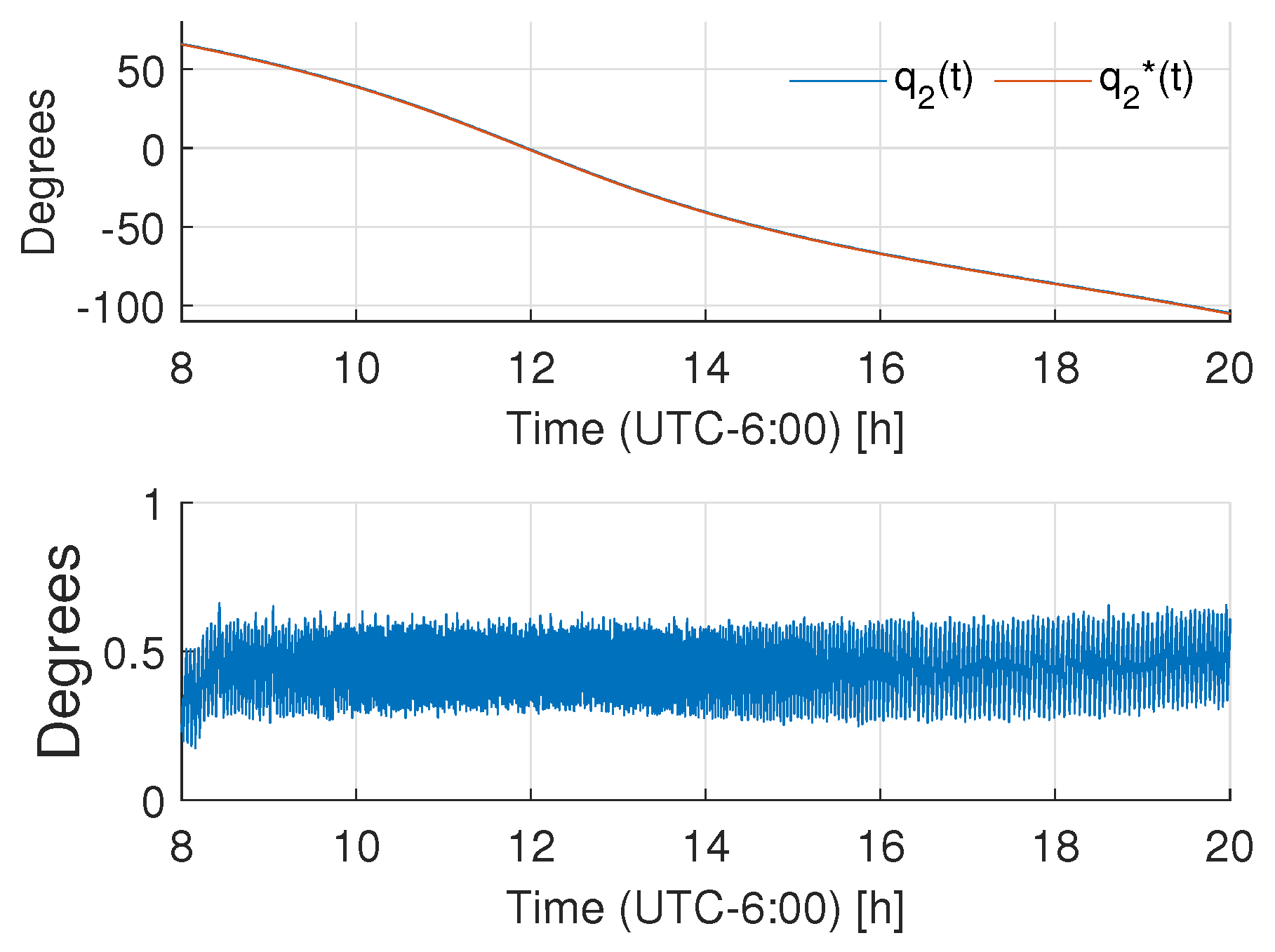
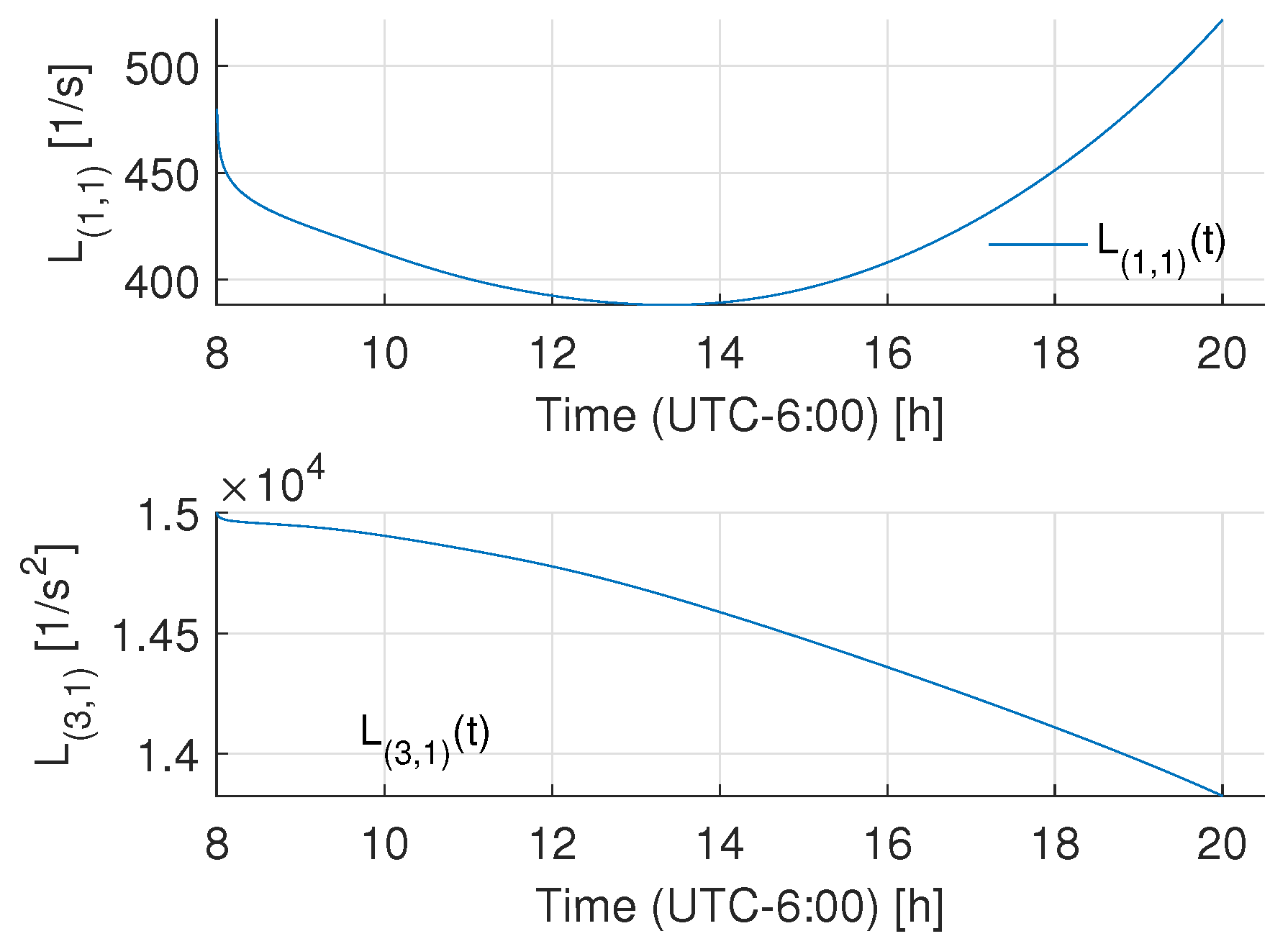
4.2. Numerical Results
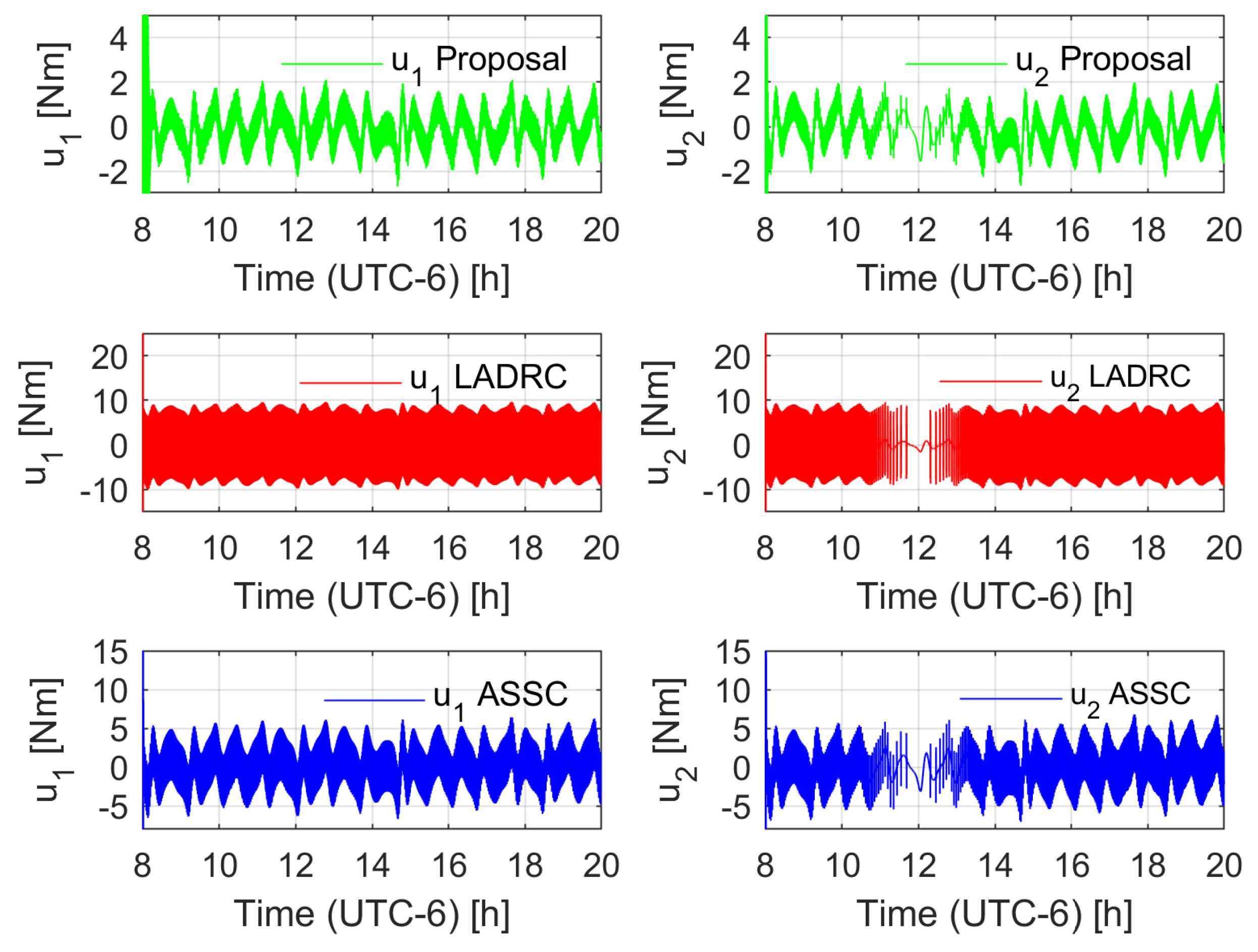
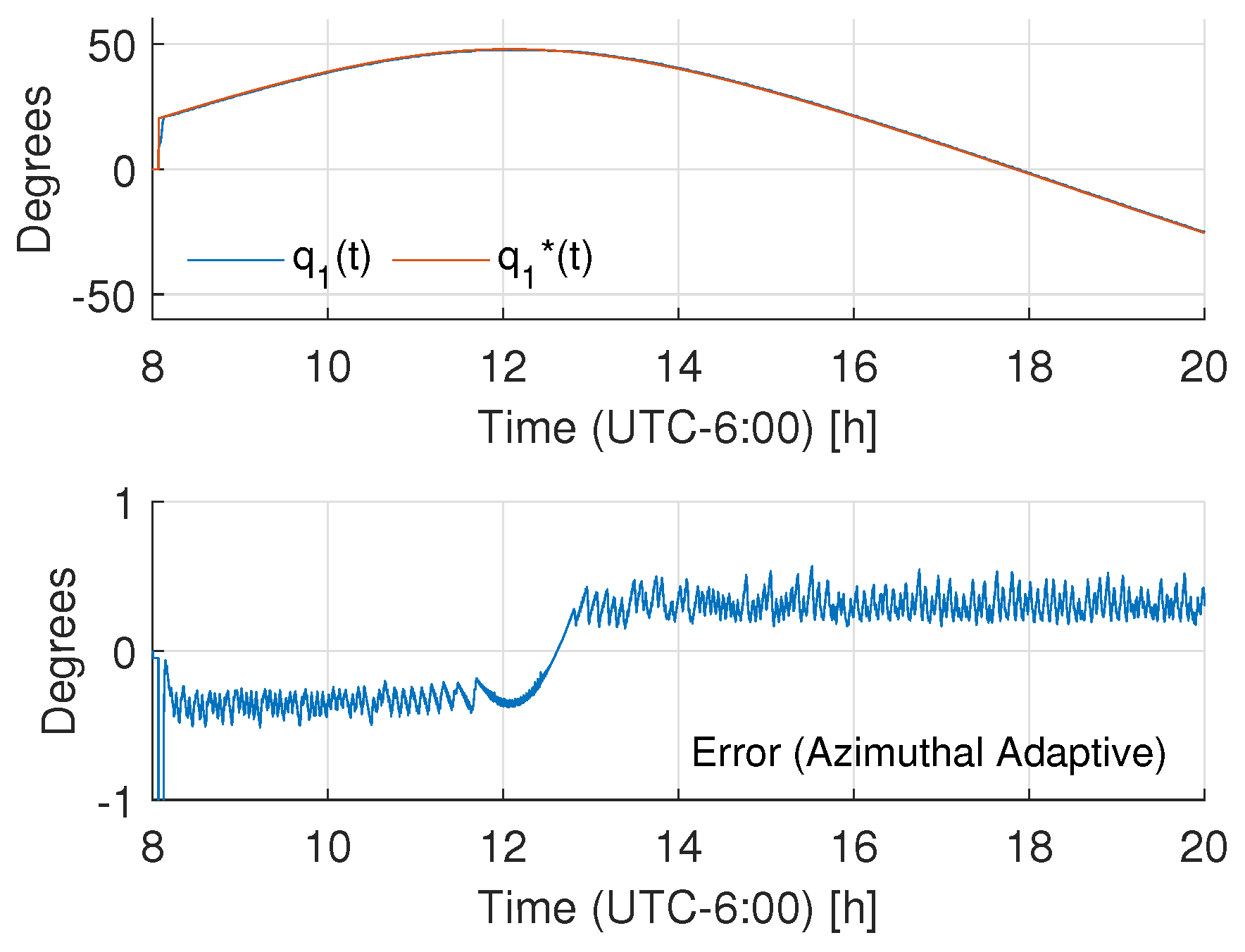
4.3. Experimental Results
- As advantages, the proposal provides low energy consumption, achieving acceptable results in trajectory tracking for solar tracking. It showed low energy consumption with respect to both classic PID control and robust control of the LADRC nature. The adaptation rule is suitable for an implementation in embedded systems, which ensures low energy consumption in contrast with other strategies that are tested in a PC-based controller. The adaptive nature of the system may be suitable for noisy measurements with respect to high-gain state estimators.
- As possible drawbacks, even when the proposed tuning process is of the same nature as the classic PID and LADRC controllers, the process is not as natural as the former controllers. The robustness of the scheme is lower than that shown by the LADRC, but in the case of solar trackers, the mechanism design can contribute to avoiding aggressive robust actions. Besides, even when the system was successfully implemented in an embedded processor, the computational cost of the scheme was larger in comparison to classic schemes.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ohkubo, T.; Yabe, T.; Yoshida, K.; Uchida, S.; Funatsu, T.; Bagheri, B.; Oishi, T.; Daito, K.; Ishioka, M.; Nakayama, Y.; et al. Solar-pumped 80 W laser irradiated by a Fresnel lens. Opt. Lett. 2009, 34, 175–177. [Google Scholar] [CrossRef] [PubMed]
- Allil, R.C.; Manchego, A.; Allil, A.; Rodrigues, I.; Werneck, A.; Diaz, G.C.; Dino, F.T.; Reyes, Y.; Werneck, M. Solar tracker development based on a POF bundle and Fresnel lens applied to environment illumination and microalgae cultivation. Sol. Energy 2018, 174, 648–659. [Google Scholar] [CrossRef]
- Hidayanti, F.; Rahmah, F.; Agusto, J. Design of Solar Tracker on Solar Panel with Fresnel Concentrator. Int. J. Adv. Sci. Technol. 2020, 29, 1014–1025. [Google Scholar]
- Bentaher, H.; Kaich, H.; Ayadi, N.; Hmouda, M.B.; Maalej, A.; Lemmer, U. A simple tracking system to monitor solar PV panels. Energy Convers. Manag. 2014, 78, 872–875. [Google Scholar] [CrossRef]
- Camacho, E.; Berenguel, M.; Rubio, F.; Martínez, D. Control of Solar Energy Systems; Advances in Industrial Control b; Springer: London, UK, 2012. [Google Scholar]
- Fernández-Ahumada, L.; Ramírez-Faz, J.; López-Luque, R.; Varo-Martínez, M.; Moreno-García, I.; de la Torre, F.C. Influence of the design variables of photovoltaic plants with two-axis solar tracking on the optimization of the tracking and backtracking trajectory. Sol. Energy 2020, 208, 89–100. [Google Scholar] [CrossRef]
- Alexandru, C.; Irina Tatu, N. Optimal design of the solar tracker used for a photovoltaic string. J. Renew. Sustain. Energy 2013, 5, 023133. [Google Scholar] [CrossRef]
- Alexandru, C. Optimal design of the dual-axis tracking system used for a PV string platform. J. Renew. Sustain. Energy 2019, 11, 043501. [Google Scholar] [CrossRef]
- Al Garni, H.Z.; Awasthi, A.; Ramli, M.A. Optimal design and analysis of grid-connected photovoltaic under different tracking systems using HOMER. Energy Convers. Manag. 2018, 155, 42–57. [Google Scholar] [CrossRef]
- Alexandru, C.; Pozna, C. Simulation of a dual-axis solar tracker for improving the performance of a photovoltaic panel. Proc. Inst. Mech. Eng. Part J. Power Energy 2010, 224, 797–811. [Google Scholar] [CrossRef]
- Ahmed, R.; Oh, S.J.; Mehmood, M.U.; Kim, Y.; Jeon, G.; Han, H.J.; Lim, S.H. Computer vision and photosensor based hybrid control strategy for a two-axis solar tracker-Daylighting application. Sol. Energy 2021, 224, 175–183. [Google Scholar] [CrossRef]
- Diaz, A.; Garrido, R.; Soto-Bernal, J. A filtered sun sensor for solar tracking in HCPV and CSP systems. IEEE Sens. J. 2018, 19, 917–925. [Google Scholar] [CrossRef]
- Ortega, P.; López-Rodríguez, G.; Ricart, J.; Domínguez, M.; Castañer, L.M.; Quero, J.M.; Tarrida, C.L.; García, J.; Reina, M.; Gras, A.; et al. A miniaturized two axis sun sensor for attitude control of nano-satellites. IEEE Sens. J. 2010, 10, 1623–1632. [Google Scholar] [CrossRef] [Green Version]
- Saymbetov, A.; Mekhilef, S.; Kuttybay, N.; Nurgaliyev, M.; Tukymbekov, D.; Meiirkhanov, A.; Dosymbetova, G.; Svanbayev, Y. Dual-axis schedule tracker with an adaptive algorithm for a strong scattering of sunbeam. Sol. Energy 2021, 224, 285–297. [Google Scholar] [CrossRef]
- Urbano, J.A.; Matsumoto, Y.; Asomoza, R.; Aceves, F.; Sotelo, A.; Jacome, A. 5 Wp PV module-based stand-alone solar tracking system. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; Volume 3, pp. 2463–2465. [Google Scholar]
- Lee, C.Y.; Chou, P.C.; Chiang, C.M.; Lin, C.F. Sun tracking systems: A review. Sensors 2009, 9, 3875–3890. [Google Scholar] [CrossRef]
- Nsengiyumva, W.; Chen, S.G.; Hu, L.; Chen, X. Recent advancements and challenges in Solar Tracking Systems (STS): A review. Renew. Sustain. Energy Rev. 2018, 81, 250–279. [Google Scholar] [CrossRef]
- Hafez, A.; Yousef, A.; Harag, N. Solar tracking systems: Technologies and trackers drive types—A review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Sumathi, V.; Jayapragash, R.; Bakshi, A.; Akella, P.K. Solar tracking methods to maximize PV system output—A review of the methods adopted in recent decade. Renew. Sustain. Energy Rev. 2017, 74, 130–138. [Google Scholar] [CrossRef]
- Barbón, A.; Bayón-Cueli, C.; Bayón, L.; Ayuso, P.F. Influence of solar tracking error on the performance of a small-scale linear Fresnel reflector. Renew. Energy 2020, 162, 43–54. [Google Scholar] [CrossRef]
- Fuentes-Morales, R.F.; Diaz-Ponce, A.; Peña-Cruz, M.I.; Rodrigo, P.M.; Valentín-Coronado, L.M.; Martell-Chavez, F.; Pineda-Arellano, C.A. Control algorithms applied to active solar tracking systems: A review. Sol. Energy 2020, 212, 203–219. [Google Scholar] [CrossRef]
- Sidek, M.; Azis, N.; Hasan, W.; Ab Kadir, M.; Shafie, S.; Radzi, M. Automated positioning dual-axis solar tracking system with precision elevation and azimuth angle control. Energy 2017, 124, 160–170. [Google Scholar] [CrossRef]
- Sabir, M.M.; Ali, T. Optimal PID controller design through swarm intelligence algorithms for sun tracking system. Appl. Math. Comput. 2016, 274, 690–699. [Google Scholar] [CrossRef]
- Spong, M.; Hutchinson, S.; Vidyasagar, M. Robot Modeling and Control; John Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Visioli, A. Practical PID Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shamsuzzoha, M.; Skogestad, S. The setpoint overshoot method: A simple and fast closed-loop approach for PID tuning. J. Process. Control 2010, 20, 1220–1234. [Google Scholar] [CrossRef]
- Ali, A.; Majhi, S. PI/PID controller design based on IMC and percentage overshoot specification to controller setpoint change. ISA Trans. 2009, 48, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Boonto, S.; Nuchkrua, T. On-line self tuning of contouring control for high accuracy robot manipulators under various operations. Int. J. Control Autom. Syst. 2020, 18, 1818–1828. [Google Scholar] [CrossRef]
- Nuchkrua, T.; Leephakpreeda, T. Fuzzy self-tuning PID control of hydrogen-driven pneumatic artificial muscle actuator. J. Bionic Eng. 2013, 10, 329–340. [Google Scholar] [CrossRef]
- Roman, R.C.; Precup, R.E.; Petriu, E.M. Hybrid data-driven fuzzy active disturbance rejection control for tower crane systems. Eur. J. Control 2021, 58, 373–387. [Google Scholar] [CrossRef]
- Hou, Z.; Xiong, S. On model-free adaptive control and its stability analysis. IEEE Trans. Autom. Control 2019, 64, 4555–4569. [Google Scholar] [CrossRef]
- Safan, Y.M.; Shaaban, S.; El-Sebah, M.I.A. Performance evaluation of a multi-degree of freedom hybrid controlled dual axis solar tracking system. Sol. Energy 2018, 170, 576–585. [Google Scholar] [CrossRef]
- Lashab, A.; Sera, D.; Guerrero, J.M.; Máthé, L.; Bouzid, A. Discrete model-predictive-control-based maximum power point tracking for PV systems: Overview and evaluation. IEEE Trans. Power Electron. 2017, 33, 7273–7287. [Google Scholar] [CrossRef]
- Rubio, F.; Ortega, M.; Gordillo, F.; Lopez-Martinez, M. Application of new control strategy for sun tracking. Energy Convers. Manag. 2007, 48, 2174–2184. [Google Scholar] [CrossRef]
- Kim, I.S. Robust maximum power point tracker using sliding mode controller for the three-phase grid-connected photovoltaic system. Sol. Energy 2007, 81, 405–414. [Google Scholar] [CrossRef]
- Chu, C.C.; Chen, C.L. Robust maximum power point tracking method for photovoltaic cells: A sliding mode control approach. Sol. Energy 2009, 83, 1370–1378. [Google Scholar] [CrossRef]
- Alata, M.; Al-Nimr, M.; Qaroush, Y. Developing a multipurpose sun tracking system using fuzzy control. Energy Convers. Manag. 2005, 46, 1229–1245. [Google Scholar] [CrossRef]
- Al Nabulsi, A.; Dhaouadi, R. Efficiency optimization of a DSP-based standalone PV system using fuzzy logic and dual-MPPT control. IEEE Trans. Ind. Inform. 2012, 8, 573–584. [Google Scholar] [CrossRef]
- Bahgat, A.; Helwa, N.; Ahmad, G.; El Shenawy, E. Maximum power point traking controller for PV systems using neural networks. Renew. Energy 2005, 30, 1257–1268. [Google Scholar] [CrossRef]
- AL-Rousan, N.A.; Isa, N.A.M.; Desa, M.K.M. Efficient Single and Dual Axis Solar Tracking System Controllers Based on Adaptive Neural Fuzzy Inference System. J. King Saud-Univ.-Eng. Sci. 2020, 32, 459–469. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Active disturbance rejection control: A paradigm shift in feedback control system design. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; IEEE: New York, NY, USA, 2006; pp. 2399–2405. [Google Scholar]
- Chu, Z.; Wu, C.; Sepehri, N. Active disturbance rejection control applied to high-order systems with parametric uncertainties. Int. J. Control. Autom. Syst. 2019, 17, 1483–1493. [Google Scholar] [CrossRef]
- Liu, F.; Li, H.; Liu, L.; Zou, R.; Liu, K. A Control Method for IPMSM Based on Active Disturbance Rejection Control and Model Predictive Control. Mathematics 2021, 9, 760. [Google Scholar] [CrossRef]
- Patelski, R.; Dutkiewicz, P. On the stability of ADRC for manipulators with modelling uncertainties. ISA Trans. 2020, 102, 295–303. [Google Scholar] [CrossRef]
- Madoński, R.; Herman, P. Survey on methods of increasing the efficiency of extended state disturbance observers. ISA Trans. 2015, 56, 18–27. [Google Scholar] [CrossRef]
- Sira-Ramírez, H.; Luviano-Juárez, A.; Ramírez-Neria, M.; Zurita-Bustamante, E.W. Active Disturbance Rejection Control of Dynamic Systems: A Flatness Based Approach; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Ahi, B.; Haeri, M. Linear active disturbance rejection control from the practical aspects. IEEE/ASME Trans. Mechatron. 2018, 23, 2909–2919. [Google Scholar] [CrossRef]
- Lozada-Castillo, N.; Luviano-Juárez, A.; Chairez, I. Robust control of uncertain feedback linearizable systems based on adaptive disturbance estimation. ISA Trans. 2019, 87, 1–9. [Google Scholar] [CrossRef]
- Nuchkrua, T.; Leephakpreeda, T. Novel Compliant Control of Pneumatic Artificial Muscle Driven by Hydrogen Pressure under Varying Environment. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Escobar, J.; Poznyak, A. Time-varying matrix estimation in stochastic continuous-time models under coloured noise using LSM with forgetting factor. Int. J. Syst. Sci. 2011, 42, 2009–2020. [Google Scholar] [CrossRef]
- Poznyak, A. Advanced Mathematical Tools for Control Engineers: Volume 1: Deterministic Systems; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Khalil, H. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Flores-Hernandez, D.; Palomino-Resendiz, S.; Luviano-Juárez, A.; Lozada-Castillo, N.; Gutierrez-Frias, O. A heuristic approach for tracking error and energy consumption minimization in solar tracking systems. IEEE Access 2019, 7, 52755–52768. [Google Scholar] [CrossRef]
- Cooper, P. The absorption of radiation in solar stills. Sol. Energy 1969, 12, 333–346. [Google Scholar] [CrossRef]
- da Silva Campos, V.C.; Nguyen, A.T.; Palhares, R.M. Adaptive gain-scheduling control for continuous-time systems with polytopic uncertainties: An LMI-based approach. Automatica 2021, 133, 109856. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Fliess, M. An algebraic state estimation approach for the recovery of chaotically encrypted messages. Int. J. Bifurc. Chaos 2006, 16, 295–309. [Google Scholar] [CrossRef]
- Hmidet, A.; Hasnaoui, O. Waijung blockset-STM32F4 environment for real time induction motor speed control. In Proceedings of the 2018 IEEE 5th International Congress on Information Science and Technology (CiSt), Marrakech, Morocco, 21–27 October 2018; IEEE: New York, NY, USA, 2018; pp. 600–605. [Google Scholar]




| Parameter | Value |
|---|---|
| 100 mm | |
| 120 mm | |
| 61 mm | |
| 104 mm | |
| Kg | |
| Kg | |
| g·mm | |
| g·mm | |
| g·mm | |
| g·mm | |
| Kg·m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palomino-Resendiz, S.I.; Lozada-Castillo, N.B.; Flores-Hernández, D.A.; Gutiérrez-Frías, O.O.; Luviano-Juárez, A. Adaptive Active Disturbance Rejection Control of Solar Tracking Systems with Partially Known Model. Mathematics 2021, 9, 2871. https://doi.org/10.3390/math9222871
Palomino-Resendiz SI, Lozada-Castillo NB, Flores-Hernández DA, Gutiérrez-Frías OO, Luviano-Juárez A. Adaptive Active Disturbance Rejection Control of Solar Tracking Systems with Partially Known Model. Mathematics. 2021; 9(22):2871. https://doi.org/10.3390/math9222871
Chicago/Turabian StylePalomino-Resendiz, Sergio Isai, Norma Beatriz Lozada-Castillo, Diego Alonso Flores-Hernández, Oscar Octavio Gutiérrez-Frías, and Alberto Luviano-Juárez. 2021. "Adaptive Active Disturbance Rejection Control of Solar Tracking Systems with Partially Known Model" Mathematics 9, no. 22: 2871. https://doi.org/10.3390/math9222871
APA StylePalomino-Resendiz, S. I., Lozada-Castillo, N. B., Flores-Hernández, D. A., Gutiérrez-Frías, O. O., & Luviano-Juárez, A. (2021). Adaptive Active Disturbance Rejection Control of Solar Tracking Systems with Partially Known Model. Mathematics, 9(22), 2871. https://doi.org/10.3390/math9222871






