Assessing Methods for Evaluating the Number of Components in Non-Negative Matrix Factorization
Abstract
:1. Introduction
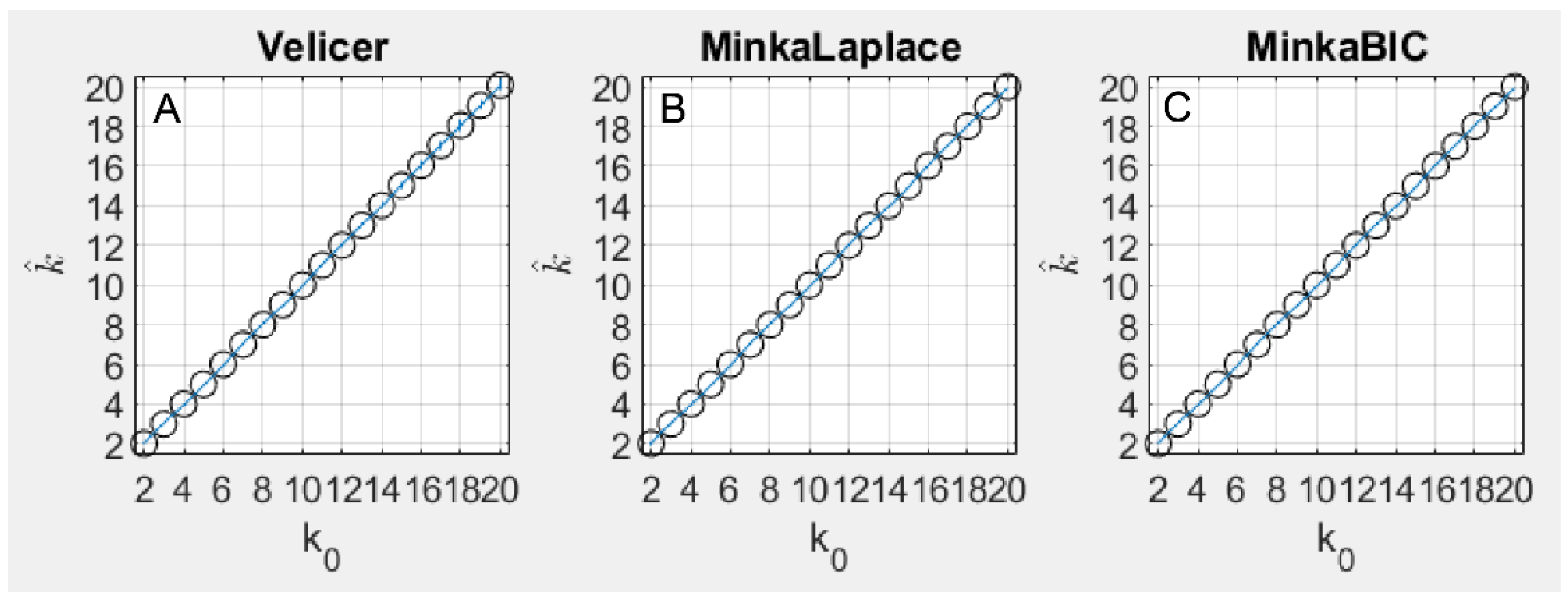
- Velicer’s Minimum Average Partial (MAP) method [31,32]. In this method, a complete PCA is performed. Then, a stepwise assessment of a series of matrices of partial correlations is performed, where is the number of principal components. In the pth such matrix, the first principal components are partialed out of the correlations. Then, the average squared coefficient in the off-diagonals of the resulting partial correlation matrix is computed. Components are retained if the variance in the matrix of partial correlations is judged to represent systematic variance. For a full description of this method, see the original papers [31,32], as well as O’Connor [35]).
- Minka’s BIC-PCA method [33]. This is a variant of Minka’s Laplace-PCA method in which a second approximation is made that further simplifies the computation. See Equation (82) of Minka’s technical report for details.
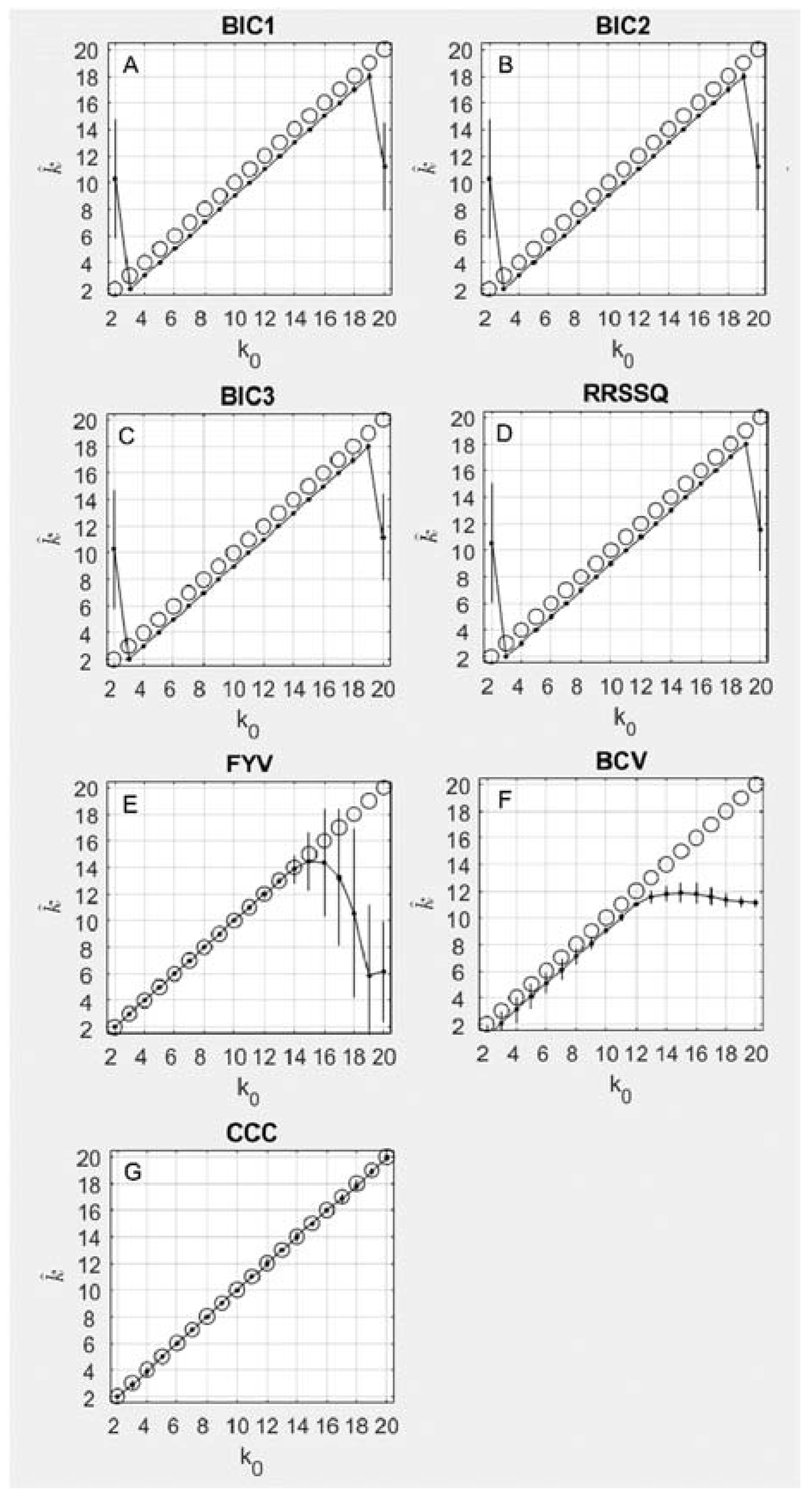
- Three Bayesian Information Criterion (BIC) methods. Let and be the result of computing the NMF as per Equation (1), where is some possible number of underlying components, i.e., is and is . Further, let . Then three model selection criteria similar to the Bayesian Information Criterion ([37]; see [38] for review) are [39,40]:where and [39,40].
- Shao’s relative root of sum of square differences (RRSSQ). With as defined above, Shao et al. suggest the following optimization criterion [41]:
- Fogel and Young’s volume-based method (FYV). Let be reshaped into a column vector, with defined as above. The vectors are computed, and are each normalized. A -column matrix is then constructed from the vectors , and the determinant of this matrix is used as the optimization criterion. An abrupt decrease in the value of this determinant (plotted as a function of ) indicates the best estimate of the underlying components ; Fogel and Young use the algorithm of Zhu and Ghodsi [42], originally developed to automate Cattell’s scree test [29], to detect this abrupt decrease. This volume-based method is based on the geometric interpretation of the determinant of an matrix as the volume of a -dimensional parallelepiped ([43], p. 154).
- Brunet’s cophenetic correlation coefficient method (CCC) [23]. This method uses the cophenetic correlation coefficient to measure dispersion for the calculated consensus matrix , computed specifically as the Pearson correlation between two matrices measuring distance:
- , the distance between samples measured by the distance matrix; and
- the distance between samples measured by the linkage used to reorder .
The value of where begins to decrease is selected as the best estimate of . - Owen and Perry’s bi-cross-validation method (BCV) [40]. This method is based on the Frobenius norm criterion given in Equation (7) (see step 8 in the algorithm on page 11 of Owen and Perry’s technical report), uses a truncated SVD, and performs cross-validation across both columns and rows (hence bi-cross-validation).
2. Materials and Methods
- Compute the CCC for a range of values for . Let the CCC value corresponding to a value be .
- Find the maximum value of across the range of values for ; call this .
- Compute the CCC threshold, , where is a tuning parameter, . For example, if you want to allow for peaks that are at least 99.9% of the maximum value , set .
- Find the largest index such that .
- No normalization
- Set mean = 0, standard deviation = 1 by rows.
- Set mean = 0, standard deviation = 1 by columns.
- Set mean = 0, standard deviation = 1 globally. (This method was not listed by Pascual-Montano et al. [45], but was included for completeness.)
- Subtract the mean by the rows.
- Subtract the mean by the columns.
- Subtract the mean by the rows and then by the columns.
3. Results
3.1. Methods for Estimating
3.1.1. Methods Based on PCA
3.1.2. Iterative Methods
3.1.3. NMF Methods
3.2. Effects of Normalization
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2013. [Google Scholar]
- Tatsuoka, M.M.; Healy, M.J.R. Matrices for Statistics. J. Am. Stat. Assoc. 1988, 83, 566. [Google Scholar] [CrossRef]
- Schott, J.R.; Stewart, G.W. Matrix Algorithms, Volume 1: Basic Decompositions. J. Am. Stat. Assoc. 1999, 94, 1388. [Google Scholar] [CrossRef]
- Jiang, X.; Langille, M.G.I.; Neches, R.; Elliot, M.; Levin, S.; Eisen, J.A.; Weitz, J.S.; Dushoff, J. Functional Biogeography of Ocean Microbes Revealed through Non-Negative Matrix Factorization. PLoS ONE 2012, 7, e43866. [Google Scholar] [CrossRef] [PubMed]
- Sutherland-Stacey, L.; Dexter, R. On the use of non-negative matrix factorisation to characterise wastewater from dairy processing plants. Water Sci. Technol. 2011, 64, 1096–1101. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, A.; Pullum, L.L.; Hobson, T.C.; Stahl, C.; Steed, C.A.; Quinn, S.P.; Chennubhotla, C.S.; Valkova, S. Discovering Multi-Scale Co-Occurrence Patterns of Asthma and Influenza with Oak Ridge Bio-Surveillance Toolkit. Front. Public Health 2015, 3, 182. [Google Scholar] [CrossRef] [Green Version]
- Stein-O’Brien, G.L.; Arora, R.; Culhane, A.C.; Favorov, A.V.; Garmire, L.X.; Greene, C.S.; Goff, L.A.; Li, Y.; Ngom, A.; Ochs, M.F.; et al. Enter the Matrix: Factorization Uncovers Knowledge from Omics. Trends Genet. 2018, 34, 790–805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.; Wang, S.-L.; Zhang, J.-F. Prediction of Microbe–Disease Associations by Graph Regularized Non-Negative Matrix Factorization. J. Comput. Biol. 2018, 25, 1385–1394. [Google Scholar] [CrossRef]
- Luo, J.; Du, J.; Tao, C.; Xu, H.; Zhang, Y. Exploring temporal suicidal behavior patterns on social media: Insight from Twitter analytics. Health Inform. J. 2019, 26, 738–752. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Raychaudhuri, S.; Stuart, J.M.; Altman, R.B. Principal components analysis to summarize microarray experiments: Application to sporulation time series. In Biocomputing 2000; World Scientific: Singapore, 1999; pp. 455–466. [Google Scholar]
- Kong, W.; Vanderburg, C.; Gunshin, H.; Rogers, J.; Huang, X. A review of independent component analysis application to microarray gene expression data. Biotechniques 2008, 45, 501–520. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKeown, M.J.; Makeig, S.; Brown, G.G.; Jung, T.P.; Kindermann, S.S.; Bell, A.J.; Sejnowski, T.J. Analysis of fMRI data by blind separation into independent spatial components. Hum. Brain Mapp. 1998, 6, 160–188. [Google Scholar] [CrossRef]
- Cichocki, A.; Zdunek, R.; Phan, A.H.; Amari, S. Nonnegative Matrix and Tensor Factorizations: Applications to Exploratory Multi-Way Data Analysis and Blind. Source Separation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Devarajan, K. Nonnegative Matrix Factorization: An Analytical and Interpretive Tool in Computational Biology. PLoS Comput. Biol. 2008, 4, e1000029. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Song, H.A.; Lee, S.-Y. Hierarchical Representation Using NMF. In Neural Information Processing; Springer: Berlin/Heidelberg, Germany, 2013; pp. 466–473. [Google Scholar]
- Guess, M.J.; Wilson, S.B. Introduction to Hierarchical Clustering. J. Clin. Neurophysiol. 2002, 19, 144–151. [Google Scholar] [CrossRef] [PubMed]
- Boutsidis, C.; Gallopoulos, E. SVD based initialization: A head start for nonnegative matrix factorization. Pattern Recognit. 2008, 41, 1350–1362. [Google Scholar] [CrossRef] [Green Version]
- Langville, A.N.; Meyer, C.D. Initializations for Nonnegative Matrix Factorization. Citeseer 2006, 23–26. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.131.4302 (accessed on 4 November 2021).
- Okun, O.; Priisalu, H. Fast Nonnegative Matrix Factorization and Its Application for Protein Fold Recognition. EURASIP J. Adv. Signal. Process. 2006, 2006, 71817. [Google Scholar] [CrossRef] [Green Version]
- Wild, S.; Curry, J.; Dougherty, A. Improving non-negative matrix factorizations through structured initialization. Pattern Recognit. 2004, 37, 2217–2232. [Google Scholar] [CrossRef]
- Brunet, J.-P.; Tamayo, P.; Golub, T.R.; Mesirov, J.P. Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl. Acad. Sci. USA 2004, 101, 4164–4169. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.-J. Projected Gradient Methods for Nonnegative Matrix Factorization. Neural Comput. 2007, 19, 2756–2779. [Google Scholar] [CrossRef] [Green Version]
- Cichocki, A.; Phan, A.H.; Caiafa, C. Flexible HALS algorithms for sparse non-negative matrix/tensor factorization. In Proceedings of the 2008 IEEE Workshop on Machine Learning for Signal Processing, Cancun, Mexico, 16–19 October 2008; pp. 73–78. [Google Scholar] [CrossRef]
- Kim, J.; Park, H. Toward Faster Nonnegative Matrix Factorization: A New Algorithm and Comparisons. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 353–362. [Google Scholar] [CrossRef] [Green Version]
- Ding, C.; He, X.; Simon, H.D. On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering. In Proceedings of the 2005 SIAM International Conference on Data Mining, Newport Beach, CA, USA, 21–23 April 2005; pp. 606–610. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Park, H. Sparse Nonnegative Matrix Factorization for Clustering; Georgia Institute of Technology: Atlanta, GA, USA, 2008; p. 15. [Google Scholar]
- Cattell, R.B. The Scree Test for The Number of Factors. Multivar. Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef]
- Kaiser, H.F. The Application of Electronic Computers to Factor Analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Velicer, W.F. Determining the number of components from the matrix of partial correlations. Psychometrika 1976, 41, 321–327. [Google Scholar] [CrossRef]
- Velicer, W.F.; Eaton, C.A.; Fava, J.L. Construct explication through factor or component analysis: A review and evaluation of alternative procedures for determining the number of factors or components. In Problems and Solutions in Human Assessment; Douglas, N., Goffin, R.D., Helmes, E., Eds.; Springer: Boston, MA, USA, 2000; pp. 41–71. [Google Scholar] [CrossRef]
- Minka, T.P. Automatic Choice of Dimensionality for PCA. In Advances in Neural Information Processing Systems 13; The MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Li, Y.-O.; Adalı, T.; Calhoun, V.D. Estimating the number of independent components for functional magnetic resonance imaging data. Hum. Brain Mapp. 2007, 28, 1251–1266. [Google Scholar] [CrossRef]
- O’Connor, B.P. SPSS and SAS programs for determining the number of components using parallel analysis and Velicer’s MAP test. Behav. Res. Methods Instrum. Comput. 2000, 32, 396–402. [Google Scholar] [CrossRef] [Green Version]
- Kass, R.E.; Raftery, A.E. Bayes Factors and Model Uncertainty. J. Am. Stat. Assoc. 1995, 90, 73. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Stoica, P.; Selen, Y. A Review of Information Criterion Rules. 2004. Available online: http://www.sal.ufl.edu/eel6935/2008/01311138_ModelOrderSelection_Stoica.pdf (accessed on 25 November 2019).
- Bai, J.; Ng, S. Determining the Number of Factors in Approximate Factor Models. Econometrica 2002, 70, 191–221. [Google Scholar] [CrossRef] [Green Version]
- Owen, A.B.; Perry, P.O. Bi-cross-validation of the SVD and the nonnegative matrix factorization. Ann. Appl. Stat. 2009, 3, 564–594. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Wang, G.; Wang, S.; Su, Q. Extraction of Mass Spectra and Chromatographic Profiles from Overlapping GC/MS Signal with Background. Anal. Chem. 2004, 76, 5143–5148. [Google Scholar] [CrossRef]
- Zhu, M.; Ghodsi, A. Automatic dimensionality selection from the scree plot via the use of profile likelihood. Comput. Stat. Data Anal. 2006, 51, 918–930. [Google Scholar] [CrossRef]
- Strang, G. Linear Algebra and Its Applications, 2nd ed.; Academic Press: New York, NY, USA, 1980; Available online: https://www.worldcat.org/title/linear-algebra-and-its-applications/oclc/299409644 (accessed on 25 November 2019).
- Fogel, P.; Young, S.S.; Hawkins, D.M.; Ledirac, N. Inferential, robust non-negative matrix factorization analysis of microarray data. Bioinformatics 2006, 23, 44–49. [Google Scholar] [CrossRef] [Green Version]
- Pascual-Montano, A.; Carmona-Saez, P.; Chagoyen, M.; Tirado, F.; Carazo, J.M.; Pascual-Marqui, R.D. bioNMF: A versatile tool for non-negative matrix factorization in biology. BMC Bioinform. 2006, 7, 366. [Google Scholar] [CrossRef] [Green Version]
- Golub, T.R.; Slonim, D.K.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P.; Coller, H.; Loh, M.L.; Downing, J.R.; Caligiuri, M.A.; et al. Molecular Classification of Cancer: Class Discovery and Class Prediction by Gene Expression Monitoring. Science 1999, 286, 531–537. [Google Scholar] [CrossRef] [Green Version]
- Maisog, J.M.; Devarajan, K.; Young, S.; Fogel, P.; Luta, G. Non-Negative Matrix Factorization: Estimation of the Number of Components and the Effect of Normalization. In Proceedings of the Joint Statistical Meetings, Washington DC, USA, 5–10 August 2009. [Google Scholar]
- Cichocki, A.; Zdunek, R.; Amari, S.-I. Csiszár’s Divergences for Non-negative Matrix Factorization: Family of New Algorithms. In Independent Component Analysis and Blind Signal Separation; Springer: Berlin/Heidelberg, Germany, 2006; pp. 32–39. [Google Scholar] [CrossRef]
- Lin, L.I.-K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255. [Google Scholar] [CrossRef]
- Getz, G.; Levine, E.; Domany, E. Coupled two-way clustering analysis of gene microarray data. Proc. Natl. Acad. Sci. USA 2000, 97, 12079–12084. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eggert, J.; Korner, E. Sparse coding and NMF. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 4, pp. 2529–2533. [Google Scholar] [CrossRef]
- Cichocki, A.; Lee, H.; Kim, Y.-D.; Choi, S. Non-negative matrix factorization with α-divergence. Pattern Recognit. Lett. 2008, 29, 1433–1440. [Google Scholar] [CrossRef]
- Févotte, C.; Idier, J. Algorithms for Nonnegative Matrix Factorization with the β-Divergence. Neural Comput. 2011, 23, 2421–2456. [Google Scholar] [CrossRef]
- Kompass, R. A Generalized Divergence Measure for Nonnegative Matrix Factorization. Neural Comput. 2007, 19, 780–791. [Google Scholar] [CrossRef] [PubMed]
- Devarajan, K.; Cheung, V.C.-K. On Nonnegative Matrix Factorization Algorithms for Signal-Dependent Noise with Application to Electromyography Data. Neural Comput. 2014, 26, 1128–1168. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Wang, S.; Li, H.; Li, Z. SAC-NMF-Driven Graphical Feature Analysis and Applications. Mach. Learn. Knowl. Extr. 2020, 2, 630–646. [Google Scholar] [CrossRef]
- Kutlimuratov, A.; Abdusalomov, A.; Whangbo, T.K. Evolving Hierarchical and Tag Information via the Deeply Enhanced Weighted Non-Negative Matrix Factorization of Rating Predictions. Symmetry 2020, 12, 1930. [Google Scholar] [CrossRef]
- Ren, Z.; Zhang, W.; Zhang, Z. A Deep Nonnegative Matrix Factorization Approach via Autoencoder for Nonlinear Fault Detection. IEEE Trans. Ind. Inform. 2019, 16, 5042–5052. [Google Scholar] [CrossRef]
- Trigeorgis, G.; Bousmalis, K.; Zafeiriou, S.; Schuller, B. A Deep Matrix Factorization Method for Learning Attribute Representations. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 417–429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vu, T.T.; Bigot, B.; Chng, E.-S. Combining non-negative matrix factorization and deep neural networks for speech enhancement and automatic speech recognition. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 499–503. [Google Scholar] [CrossRef]
- Bolboaca, S.D.; Jäntschi, L. Comparison of Quantitative Structure-Activity Relationship Model Performances on Carboquinone Derivatives. Sci. World J. 2009, 9, 1148–1166. [Google Scholar] [CrossRef] [Green Version]
| k Estimation Method | Normalization Method | |||||||
|---|---|---|---|---|---|---|---|---|
| None | Scale Cols Then Norm Rows | Subtract Mean by Rows Then Std to 1 | Subtract Mean by Columns Then Std to 1 | Subtract Global Mean Then Std to 1 | Subtract Means by Rows | Subtract Mean by Columns | Subtract Mean by Rows Then by Columns | |
| Velicer | 20 | 9 | 10 | 20 | 20 | 15 | 20 | 15 |
| Minka-Laplace | 27 | 17 | 15 | 25 | 27 | 27 | 27 | 27 |
| Minka-BIC | 70 | 70 | 70 | 70 | 70 | 70 | 70 | 70 |
| FYV | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| BIC1 | 4 | 4 | 4 | 4 | 4 | 4 | 10 | 4 |
| BIC2 | 4 | 4 | 4 | 4 | 4 | 4 | 10 | 4 |
| BIC3 | 4 | 4 | 4 | 4 | 4 | 4 | 10 | 4 |
| RRSSQ | 4 | 8 | 4 | 4 | 4 | 4 | 10 | 12 |
| BCV | 18 | 10 | 24 | 20 | 14 | 16 | 12 | 16 |
| CCC | 18 | 10 | 24 | 20 | 14 | 16 | 12 | 16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maisog, J.M.; DeMarco, A.T.; Devarajan, K.; Young, S.; Fogel, P.; Luta, G. Assessing Methods for Evaluating the Number of Components in Non-Negative Matrix Factorization. Mathematics 2021, 9, 2840. https://doi.org/10.3390/math9222840
Maisog JM, DeMarco AT, Devarajan K, Young S, Fogel P, Luta G. Assessing Methods for Evaluating the Number of Components in Non-Negative Matrix Factorization. Mathematics. 2021; 9(22):2840. https://doi.org/10.3390/math9222840
Chicago/Turabian StyleMaisog, José M., Andrew T. DeMarco, Karthik Devarajan, Stanley Young, Paul Fogel, and George Luta. 2021. "Assessing Methods for Evaluating the Number of Components in Non-Negative Matrix Factorization" Mathematics 9, no. 22: 2840. https://doi.org/10.3390/math9222840







