Abstract
Previous studies aimed at determining hedging strategies commonly used daily closing spot and futures prices for the analysis and strategy building. However, the daily closing price might not be the appropriate for price in some or all trading days. This is because the intraday data at various minute intervals, in our view, are likely to better reflect the information about the concrete behavior of the market returns and reactions of the market participants. Therefore, in this study, we propose using high-frequency data along with daily data in an attempt to determine hedging strategies, using five major international currencies against the American dollar. Specifically, in our study we used the 5-min, 30-min, 60-min, and daily closing prices of the USD/CAD (Canadian Dollar), USD/CNY (Chinese Yuan), USD/EUR (Euro), USD/GBP (British Pound), and USD/JPY (Japanese Yen) pairs over the 2018–2019 period. Using data at 5-min, 30-min, and 60-min intervals or high-frequency data, however, means the use of a relatively large number of observations for information extractions in general and econometric model estimations, making data processing and analysis a rather time-consuming and complicated task. To deal with such drawbacks, this study collected the high-frequency data in the form of a histogram and selected the representative daily price, which does not have to be the daily closing value. Then, these histogram-valued data are used for investigating the linear and nonlinear relationships and the volatility of the interested variables by various single- and two-regime bivariate GARCH models. Our results indicate that the Markov Switching Dynamic Copula-Generalized autoregressive conditional heteroskedasticity (GARCH) model performs the best with the lowest BIC and gives the highest overall value of hedging effectiveness (HE) compared with the other models considered in the present endeavor. Consequently, we can conclude that the foreign exchange market for both spot and futures trading has a nonlinear structure. Furthermore, based on the HE results, the best derivatives instrument is CAD using one-day frequency data, while GBP using 30-min frequency data is the best considering the highest hedge ratio. We note that the derivative with the highest hedging effectiveness might not be the one with the highest hedge ratio.
1. Introduction
Big data are understood as data in a gigantic size having a large volume of many varieties of information, compiled continuingly and in general at a relatively high frequency. However, the data collected can be either structured or non-structured, making it unable to be managed in the general database systems [1,2]. Presently, big data are utilized in many fields such as medicine, sciences, computer science, and business, in addition to as a financial investment. At present, global stock markets such as the New York Stock Exchange (NYSE) and the Nasdaq Stock Market (NASDAQ) commissioned IBM Netezza to collect and process big data from various sources, while some companies in different financial markets have started to use big data technologies as a tool for extracting, processing, and analyzing relevant information for the purpose of risk reduction, business control, and trading strategy determination [3].
However, it remains uncommon for small-scale investors in financial markets to utilize big data for risk management or investment decision-making, particularly those in the international currency market, which is one of the financial markets characterized by high liquidity and high risk at the same time. Risk, here, is the risk from investment in the securities market defined as the likelihood of occurrence of losses relative to the expected return on a particular investment, which is unpredictable for the future [4]. Therefore, risk management needs to be considered in the process of making investment decisions. One of the alternative methods for risk management is buying derivatives in the futures market, which is quite effective and is commonly preferred by investors. Nevertheless, an interesting issue is how an investor manages his/her investment portfolio with the inclusion of futures. In other words, questions remain, such as what is the share of futures to be purchased for an optimal portfolio? In addition, how much risk can be reduced by the inclusion of futures in the portfolio? To address these questions, we are interested in examining the performance of hedging—a strategic method for risk management—using futures in the international Forex market, which has received enormous attention from investors, institutions, transnational corporates, exporters, importers, etc., which is exposed to foreign currencies that are highly fluctuating in values due to the dynamic global economic conditions and the speculative currency trading.
Previous studies on currency hedging strategies are quite limited. Chang, González-Serrano, and Jimenez-Martin [5] conducted a study on currency hedging strategies using the dynamic multivariate generalized autoregressive conditional heteroscedastic (GARCH) model for USD/EUR, USD/GBP, and USD/JPY pairs. Gagnon, Lypny, and McCurdy [6] constructed efficient hedging foreign currency portfolios with futures, considering Deutsche Mark (USD/DEM), Swiss Franc (USD/CHF), and Japanese Yen (USD/JPY), and using the multivariate GARCH model. Meanwhile, Kotkatvuori-Örnberg [7] used the DCC-EGARCH model to determine the optimal hedge ratios for the Australian dollar (USD/AUD), Canadian dollar (USD/CAD), European Euro (USD/EUR), British pound (USD/GBP), and Japanese Yen (USD/JPY).
However, all of the previous studies briefly described above relied on daily closing prices, which might not reflect the actual behavior of the price movements [8,9]. Furthermore, low frequency data (daily, weekly, and monthly data) are known for not being able to reveal the actual behavior of stock prices comprehensively during the trading day. To take into account the actual behavior of the currency returns, this study used big data for the analysis and construction of currency hedging strategies. Therefore, the big data to be used were those released every 5 min, 30 min, and 60 min.
In building the currency hedging strategies, we considered the hedge ratio and hedging effectiveness to determine the optimal number of spot and futures contracts in an investment portfolio, as well as the risk that can be reduced. To calculate the hedge ratio (HR) and the hedging effectiveness (HE), we need to know the variance and covariance values of two variables: spot price and futures price [10]. Therefore, finding the best model for the estimation to get the correct variance and covariance is another important task in this endeavor. There are many models for estimating the correlation between the time-series variables and for obtaining the variance and covariance values, such as the constant conditional correlation (CCC)-GARCH model of Bollerslev [11], the dynamic conditional correlation (DCC) GARCH model of Engle [12], and the dynamic copula GARCH model of Patton [13]. Nonetheless, these models might not be appropriate for the analysis in order to understand the real behavior of the data as they assume no structural change in the time series. In reality, there are always ups and downs of a market, particularly the securities markets and stock exchanges. Dueker [14], consequently, proposed using the Markov switching-GARCH model to capture the economic fluctuations that are different between the upturn and the downturn periods. However, the MS-GARCH model is still not suitable for the estimation to obtain the HR and the optimal portfolio containing spot and futures contracts because it cannot provide the variance and covariance of the returns of the hedging instruments, which are key variables in the hedging equation for risk management.
The present study takes into consideration the probable existence of structural change, which demarcates the upturns and downturns episodes in the currency market. It, thus, employs the Markov switching CCC-GARCH model of Pelletier [15]; the Markov switching DCC-GARCH model of Billio and Caporin [16]; and the recent Markov switching dynamic copula GARCH models of Pastpipatkul, Yamaka, and Sriboonchitta [17] as a means to obtain the variance and covariance of spot and future returns of the international currency for calculating the hedge ratio and hedging effectiveness.
This study uses, for its analysis, the spot and future returns of the top five international currencies against the American dollar released at 5-min, 30-min, 60-min, and daily intervals for the one-year time period of 2018 to 2019. As the data used were of a high frequency, we reduced the series into the daily histogram-valued form following the concepts of González-Rivera and Arroyo [8] so as to simplify and quicken data processing. The histogram is particularly useful for dealing with large data sets when big data are more meaningful in some instances. In our case, conceptually, the optimal hedging strategies should be built on the basis of the best representative of the intraday trading prices rather than the daily closing price. In the conventional method, the solution to analyzing the daily high-frequency data is to reduce the collection of records (in the form of histogram-valued data) associated with each observation (taken every 5 min, 30 min or 60 min of the day) to one value, which may be represented by either the mean, mode, maximum, or minimum of all observations, called the histogram-valued data. However, with these representations, the variability across the records in the histogram is lost [18]. Thus, Dias and Brito [18] suggested finding the representative of the data by considering the quantile of the cumulative distribution of the histogram-valued data. González-Rivera and Arroyo [8] and Rakpho et al. [9] mentioned that by recording the high-frequency data as a histogram, all information of the data during the day is collected, and It is possible to choose reference points that better represent the histogram in each day. In this study, we aimed at finding currency hedging strategies using histogram-valued data and Markov switching CCC-GARCH, Markov switching DCC-GARCH, and Markov switching dynamic copula GARCH. More specifically, we aimed at calculating the HR from the conditional covariance matrices to achieve the hedging strategy and compared the performance of HR by considering HE. One of the main contributions of this paper is that it allows for a comparison for whether the results are different depending on the model, currency, and futures contract of the currency selected. In addition, to the best of our knowledge, this was the first attempt ever to investigate and determine currency hedging strategies using histogram-valued data and the Markov switching dynamic copula GARCH model.
The remainder of this paper is organized as follows. Section 2 introduces the methodologies considered in this study. Section 3 describes the data and discusses the related statistics in this study. Section 4 provides the model comparison results and compares the hedge performance across the currency markets. Finally, Section 5 is the conclusion.
2. Model
In this section, we first explain the histogram-valued data concept and the way to obtain the representative data from the histogram. Various econometric models used to forecast the dynamic volatility and dynamic correlation are briefly presented. Finally, we explain the procedure to compute the hedge ratio and hedging effectiveness for the currency markets.
2.1. Histogram-Valued Data
In this study, we consider high-frequency data, i.e., 5 min, 30 min, and 60 min and these data can be recorded in the form of a histogram [18]. Let be the vector of the histogram-valued variable and , be the histogram-valued data at time which can be represented by the histogram
where and are the lower and upper bounds of the sub-interval , respectively, with . being the number of sub-intervals for the observation, being the probability or frequency associated with the sub-interval at time and . Note that within sub-interval , the values of for each unit are uniformly distributed.
To find the reference point that best represents , the cumulative empirical distribution function is used to derive the and its inverse or quantile function [19,20]
where .
2.2. Markov Switching(MS)-CCC-GARCH and Markov Switching(MS)-DCC-GARCH
Billio and Caporin [16] and Chodchuangnirun, Yamaka, and Khiewngamdee [21] introduced the extension of the CCC-GARCH and DCC-GARCH of Engle [12] to the Markov switching model of Hamilton [22]. These two models have similar structures, with the only difference being that MS-CCC-GARCH assumes the regime-dependent correlation matrix to be constant in each regime, while the regime-dependent correlation matrix is considered to be varying over time in each regime, , for MS-DCC-GARCH. Note that is a state variable, which follows a first-order Markov process and can assume only integer values of 0,1.., ; thus, the correlation matrix at time t, , can be split in regimes, and we have for , ,…, .
In this section, only MS-DCC-GARCH is explained. Following Billio and Caporin [16], the model takes the following form
where is vector of the reference points that best represent the histogram at time t for spot and futures returns, respectively. is an independent and identically distributed process with zero mean and variance-covariance matrix . is the time-varying variance-covariance matrix presented as
where is the diagonal matrix of conditional variances and . We note that the univariate GARCH(1,1) model is also used to compute the conditional variances and , thus
where and are the error terms following Student’s-t distributions with degrees of freedom of and for spot and futures, respectively. and are the constant terms.
Thus, becomes a matrix of the regime-dependent time-varying correlation between spot and futures. We would like to note that if MS-CCC-GARCH is estimated, is assumed to be constant for each regime. However, in the case of MS-DCC-GARCH, is the time-varying conditional correlation matrix that can be predicted by the following process
where represents the regime-dependent unconditional correlation and is the vector of standardized residuals, It is worth noting that DCC just imposes a GARCH(1,1) on the conditional correlation and uses only and to add a dynamic behavior according to Billio and Caporin (2005). This model allows parameters and to be governed by , where is the latent and unobservable market state variable at time , and is a positive integer representing the total number of market states. In this study, we considered only upturn and downturn market regimes, thus was assumed. The state variable evolves according to the following transition probabilities:
where is the probability of switching from state i to state j.
2.3. Markov Switching Dynamic Copula GARCH
In this subsection, the Markov switching dynamic copula (MSDC) GARCH model is explained. The Student’s-t copula function is assumed for this model as it has been commonly and successfully used for fitting financial data [17]. This model is different from the MS-CCC-GARCH and MS-DCC-GARCH in two aspects. First, the joint distribution assumption of this model is a Student’s-t copula, while multivariate Gaussian distribution or normal joint distribution is assumed for the MS-CCC-GARCH and MS-DCC-GARCH models. Second, the dynamic copula GARCH is extended to the Markov switching model; thus the dynamic conditional correlation is predicted by restricted ARMA (1,10) [13], which can be written as
where , , and are parameters. is the transformation function to ensure that the regime-dependent dynamic correlation always remains in [−1,1]. This transformation function is represented by the following equation
and is the forcing variable, which is defined as follows
where is the quantile function of Student’s-t distribution. and are student-t cumulative distribution functions (CDFs) of and , respectively.
Formally, the copula function is used to join different univariate distributions to form a valid multivariate distribution. According to the theorem of Sklar [23], the conditional bivariate joint distribution function of and can be defined as
where is the time-varying Student’s-t copula function and denotes the vector of the regime-dependent parameters in ARMA(1,10) in Equation (11). Assuming all CDFs are differentiable, the conditional bivariate joint density is then given by
where is the vector of parameters to be estimated in the GARCH models in Equations (5) and (6), and , and are the density functions corresponding to the marginal distribution of and , respectively, constructed by the GARCH models. Thus, the full conditional likelihood function can be expressed as:
where , and is the filtered probabilities [24], where is all past information at time . Note that getting the filtered probabilities is a recursive process and the probabilities of staying in regimes 1 and 2 are predicted by
In the estimation perspective, it is difficult to optimize and maximize the likelihood function in Equation (15); thus, we followed the two-step estimation or inference for the margins (IFM) of Joe and Xu [25] to partially resolve this problem, where the marginal densities and the copula density were estimated separately. This is to say, the GARCH process was firstly estimated to obtain the GARCH parameters. The obtained parameters are treated as a fixed parameter in the likelihood function in Equation (15), and then MSDC is estimated to obtain and forecasts the regime-dependent dynamic correlation .
2.4. Hedge Ratio and Hedging Effectiveness
To secure positions in a spot market, investors employ futures as hedging assets. For each spot contract, the hedge ratio tells us how many futures contracts should be purchased or sold [26]. Once , and are obtained, the regime-dependent hedge ratio can be defined as
After obtaining the optimal hedge ratio, we consider the reduction in the hedged portfolio’s variance as the hedging effectiveness. The corresponding regime-dependent hedging effectiveness (HE) can be calculated by
where and are the regime-dependent variance of the unhedged portfolio (only spot) and the hedged portfolio at time t, respectively.
To compare the performance of HR obtained from different correlation and volatility models, Chang, González-Serrano, and Jimenez-Martin [5] suggested considering the HE values, because a higher HE indicates a larger risk reduction, meaning that the hedging method with a higher HE is regarded as a superior hedging strategy. Therefore, this study also uses HE to compare the performance of our bivariate conditional correlation models, namely Markov switching (MS) CCC-GARCH, Markov switching (MS) DCC-GARCH and the Markov switching dynamic copula (MSDC) GARCH. In addition, we also consider the classical models consisting of CCC-GARCH, DCC-GARCH, copula-GARCH, and dynamic copula (DC)-GARCH as other competing models.
3. Data
The data used in the present study are the futures and spot closing prices of the top five most traded currency pairs, namely USD/CAD, USD/CNY, USD/EU, USD/GBP, and USD/JPY at 5 min, 30 min, 60 min, and one day’s intervals—thus considered as high-frequency data. The study period is from January 2018 to May 2019, which coincides with the time the UK is pursuing its withdrawal from the European Union (EU). Brexit is considered one of the major events bringing about shocks and high volatility in financial markets in UK, Europe, and the world, as well as the concern and interest of people worldwide. The futures prices here refer to the prices of futures contracts with an expiry date in June 2019. All historical time series were collected from the Bloomberg database for transformation into a logarithm of the change in price or return as
The descriptive statistics of the variables for the investigation are provided in Table 1 and Table 2.

Table 1.
Descriptive statistics of the currency returns with the American dollar as the base currency (Spot).

Table 2.
Descriptive statistics of the currency returns with the American dollar as the base currency (Futures).
Table 1 and Table 2 present the descriptive statistics of the spot and future prices of the variables at different frequencies. Most currency spot and futures prices have negative means. The standard deviation (Std) of both the spot and future series is close to zero, indicating the low dispersal of data points or return levels. The largest Std for both the spot and futures belongs to the daily returns of JPY at 0.0073 and 0.0071, respectively, suggesting the high dispersal of return levels, with some distance away from the mean. Meanwhile, the smallest Std for both the spot and futures is found in the daily returns of CAD and CNY at 0.0002 and 0.0005, respectively. The skewness of some variables is less than 0, meaning that the returns are distributed skewed to the left, and if it is greater than 0, it is said to be negatively skewed. The largest skewness was presented in the 30-min spot returns of CAD. As a measure of the tailedness of the data distribution, the kurtosis of both spot and future returns at 5-min and 30-min intervals, including that of future returns at 60-min intervals, had values indicating that the distributions had heavier tails than a normal distribution. The kurtosis of 5-min JPY future returns, in particular, had a value as high as 15.3740, much higher than the highest point of the bell-shaped curve of a normal distribution. The remaining data series had kurtosis values lower than that of the normal distribution (=3), meaning that their distributions were lightly tailed. Figure 1 reveals the high-frequency data of the spot and future returns of five currencies to exhibit a high fluctuation over the whole sample period. The spot currencies seemed to be more fluctuating than the futures. Figure 2 presents the histogram-valued data in the first ten sample periods. We can see that the variation of the 5-min spot returns is not greater compared with the futures counterpart.
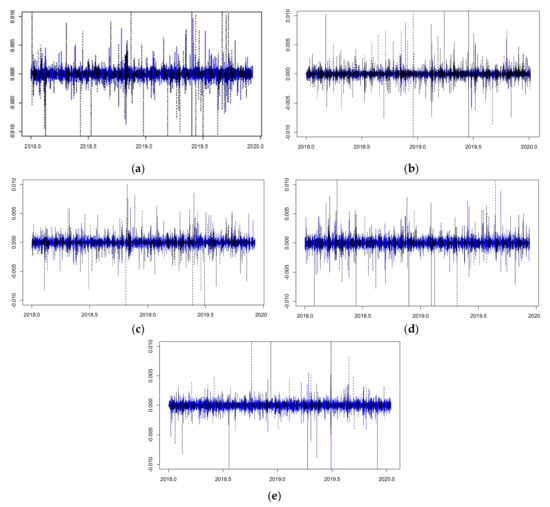
Figure 1.
Spot (blue line) and future (black dotted line) 5-min return plots: (a) CAD-5 min, (b) CNY-5 min, (c) EUR-5 min, (d) GBP-5 min, and (e) JPY-5 min.
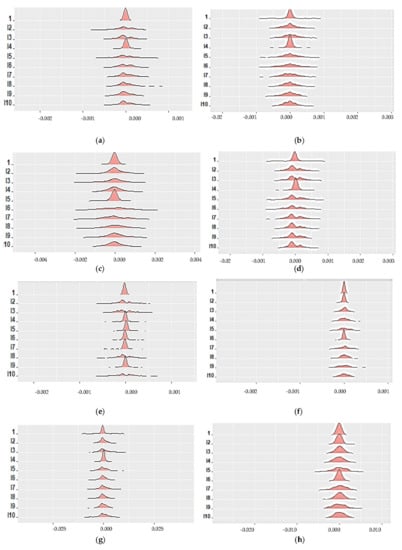
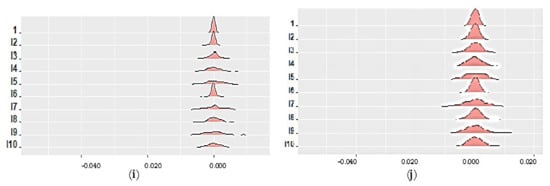
Figure 2.
The 5-min spot returns in the first ten days of the sample period in the form of a histogram. (a) CAD spot-histogram, (b) CAD futures-histogram, (c) CNY spot-histogram, (d) CNY futures-histogram, (e) EUR spot-histogram, (f) EUR futures-histogram, (g) GBP spot-histogram, (h) GBP futures-histogram, (i) JPY spot-histogram, and (j) JPY futures-histogram.
4. Results
In this section, we provide the results of the study. The estimation results of the GARCH models are firstly reported, then the obtained standardized residual of spot and futures are further used as the input of single-regime bivariate GARCH and two-regime bivariate GARCH models. Finally, all volatility models are compared using various criteria.
4.1. The GARCH Model Estimation Results
Table 3, Table 4, Table 5 and Table 6 report the results from the estimation using the GARCH(1,1) model for spot and future returns at various frequencies, which will be used to determine the standardized residuals for further analysis of the relationship among the variables. The results tell us that only the parameter estimates of are statistically significant for all currencies in terms of spot and futures, as well as data frequencies, except for future returns of CNY. The coefficients of the intercept term are also statistically significant for the returns of EUR futures and CNY futures.

Table 3.
Results from the GARCH (1,1) model estimation for 5-min spot and future returns.

Table 4.
Results from the GARCH(1,1) model estimation for 30-min spot and future returns.

Table 5.
Results from the GARCH(1,1) model estimation for 60-min spot and futures returns.

Table 6.
Results from the GARCH(1,1) model estimation for one-day spot and future returns.
To validate the estimation model, we performed a test of autocorrelation and heteroscedasticity using the Ljung−Box Q-Statistic and the ARCH(1,1)-LM tests, respectively [27,28]. Evidently, these two econometric problems were not present in the spot and future returns of all currencies at all data frequencies. This means that the standardized residuals derived from the GARCH(1,1) model estimation were reliable and thus could be used for further estimation using the correlation models.
As this study took into consideration the probable structural change causing the occurrence of upturn and downturn episodes in the currency market, we proposed using the Markov switching CCC-GARCH, Markov switching DCC-GARCH, and Markov switching dynamic copula GARCH models as the mechanisms to find out the covariance of the spot and future returns of all currencies that were used for calculating the hedge ratio and the hedging effectiveness. However, we had to test the reliability of our proposed models to ensure achieving an accurate HR and HE by comparing them with the other five competing models commonly found in previous research works, namely the CCC-GARCH, DCC-GARCH, COPULA-GARCH, DC-GARCH, and MS-COPULA-GARCH. Therefore, we had eight models to estimate in order to get the optimal hedge ratio and hedging effectiveness.
4.2. Optimal Model Selection
In this sub-section, we compared the performance of the volatility models for all of the data frequencies. The results of the model performance comparison are shown in Table 7, Table 8, Table 9 and Table 10, and the selection of the optimal model was based on the Bayesian information criterion (BIC) and Log-likelihood (LL). The model with the lowest BIC was preferred because the lower BIC corresponded to the lower variation in the error term. As evident in Table 7, Table 8, Table 9 and Table 10, the MSDC-GARCH model had the lowest BIC for all cases. Thus, we will used its estimates to compute HR and HE.

Table 7.
BIC and Log-likelihood (LL) values for different models fitted to the 5-min returns of five currencies.

Table 8.
BIC and Log-likelihood (LL) values for different models fitted to the 30-min returns of five currencies.

Table 9.
BIC and Log-likelihood (LL) values for different models fitted to the 60-min returns of five currencies.

Table 10.
BIC and Log-likelihood (LL) values for different models fitted to the one-day returns of five currencies.
4.3. Parameter Estimates of the Optimal Model
The parameter estimates from all models are presented in Table 11. This result implies that a structural change exists in currency spot and futures. Our finding is in line with Korley and Giouvris [29].

Table 11.
Parameter estimates of the MSDC-GARCH model.
4.4. Testing the Efficiency of Hedge Ratios Obtained from Different Estimation Models
After getting the optimal model, we used its estimation results for calculating the hedging effectiveness: HE for the hedge ratio and HR for hedging with futures for international currencies. Furthermore, we assessed the extent of risk reduction by the hedging strategy using HE. To confirm that the selected MSDC-GARCH model could produce unquestionably reliable results, we calculated HE for comparison using the estimation results of the other seven competing models, and the overall results are presented in Table 12.

Table 12.
The estimated hedging effectiveness (HE) and hedge ratios (HR) through different models.
Table 12 shows the averages of the HE and HR values derived from the eight models considered in this study for all currencies and four data frequencies, which were at 5-min, 30-min, 60-min, and 1-day intervals. Our MSDC-GARCH model was indeed the best hedging model for all currencies and all frequencies as it provided higher HE values than other the models. From this model, the hedging effectiveness lay between a maximum of 8.99 % for CAD 30 min data and a minimum of 1.60% for JPY 60 min data. In contrast, we found that the average of HE was smaller for the CCC-GARCH in most cases and in particular, ranging from a maximum of 7.22% for EUR daily data to a minimum of 0.003% for CAD 5-min data. We also observed that with the use of CAD 30-min data, the HR of the MSDC-GARCH model was 0.301; indicating that in order to minimize risk, a long position of one dollar in CAD should be hedged by a short position of $0.301 in CAD futures contracts. Meanwhile, the HR of the CCC-GARCH model for EUR daily data and CAD 5-min data were 0.530 and 0.271, respectively. By comparing the HE across data frequencies, we found that the highest HE values for CNY, EUR, and GBP were from using 1-day future returns, while CAD had the highest HE using the 30-min returns, and JPY did so from using the 5-min returns.
To obtain a better picture of time-varying evolution, we illustrated the evolution of the time-varying hedge ratio between the spot and futures returns over the full sample period. These time-varying hedge ratios were computed from the MSDC-GARCH model with 5-min data (presented by the blue dotted line), 30-min data (presented by the black dashed line), 60-min data (presented by the red dashed line), and daily data (presented by the green dashed line) and are shown in Figure 3. We can observe that there was a substantial time-variation in the optimal hedge ratio for all currencies in most frequencies, arguably only for 5-min data, as there was some stability in the HR. Nevertheless, all time-varying hedge ratios exhibited a mean-reverting pattern and were stationary.
Figure 3.
Time-varying hedge ratio measurements. Note: the hedge ratio measure plotted is the weighted average with weights given by the smoothed probability of two regimes, i.e., and : (a) CAD, (b) CNY, (c) EUR, (d) GBP, and (e) JPY.
5. Conclusions and Recommendations
This study introduces various bivariate MS-GARCH models for histogram-valued data to quantify HR and HE for five major international currencies. This study finds that the MSDC-GARCH model outperforms the others because it provides the highest HE values for all currencies and data frequencies. In addition, BIC also indicates that the MSDC-GARCH model outperforms other hedging methods. Therefore, with a more precise specification of the joint distribution of assets, we can effectively manage the risk exposure of portfolios. This result also confirms that the behavior of spot and future returns in the currency market can be explained appropriately by a nonlinear model.
MSDC-GARCH provides the best-performed hedge ratios and hedge effectiveness for risk reduction for all currencies, implying that MSDC-GARCH hedge strategies are suitable for those currency markets. Among the five currencies, the most efficient hedging currency is CAD with an HE of 0.889, while the least efficient hedging currency is JPY with an HE of 0.160.
Considering that the highest HE values estimated from the MSDC-GARCH model for JPY and CAD are from the 5-min and 30-min data, respectively, we can state that the data series for a particular variable (or currency in our case) and different frequencies will lead to a difference in the estimated values of HR and HE. Therefore, risk managers that commonly prefer using daily closing price or return for investment analysis and risk prevention have to be careful about using such data. With the use of big data in this study, we can conclude that daily data may not provide the best HE, and thus we should estimate HE using different frequencies of data.
The data used in this study are regarded as big data because of its enormous size and being collected at a high frequency—sometimes described as high-frequency data. The sizable data points result in the time-consuming and complicated nature of data management. This study uses the histogram-valued data as a solution for data management, but this approach has a drawback in that we cannot determine which data frequency will lead to the highest hedging effectiveness. In essence and to the best of our understanding, daily closing prices should be used carefully along with data at a wide range of frequencies [30].
For further study, we suggest applying the Smooth transition dynamic copula model of Yamaka and Maneejuk [31] to fit histogram-valued data and to quantify the HR and HE. Moreover, the copula approach is quite flexible for modeling the dependence between spot and futures; thus, we suggest considering different copula functions to capture the dependence structure of spot and futures and to improve the hedging strategy.
Author Contributions
Conceptualization, W.Y. and P.M.; data curation, N.P. and S.S.; methodology, W.Y. and N.P.; visualization, and writing—original draft, W.Y. and N.P.; writing—review and editing, W.Y. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by Center of Excellence in Econometrics, Chiang Mai University, Thailand.
Data Availability Statement
The data used in the empirical analyses are available online at Thomson Reuter database. The data are available upon request.
Acknowledgments
The authors would like to express their gratitude to Laxmi Worachai for her help and constant support. This work was supported by the Center of Excellence in Econometrics, Faculty of Economics, Chiang Mai University, Thailand.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sagiroglu, S.; Sinanc, D. Big data: A review. In Proceedings of the 2013 International Conference on Collaboration Technologies and Systems (CTS), San Diego, CA, USA, 20–24 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 42–47. [Google Scholar]
- Fan, J.; Han, F.; Liu, H. Challenges of big data analysis. Natl. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef] [PubMed]
- Jothimani, D.; Shankar, R.; Yadav, S.S. A big data analytical framework for portfolio optimization. arXiv 2018, arXiv:1811.07188. [Google Scholar]
- Markowitz, H.M. Portfolio Selection; Yale University Press: London, UK, 1968. [Google Scholar]
- Chang, C.L.; González-Serrano, L.; Jimenez-Martin, J.A. Currency hedging strategies using dynamic multivariate GARCH. Math. Comput. Simul. 2013, 94, 164–182. [Google Scholar] [CrossRef]
- Gagnon, L.; Lypny, G.J.; McCurdy, T.H. Hedging foreign currency portfolios. J. Empir. Financ. 1998, 5, 197–220. [Google Scholar] [CrossRef]
- Kotkatvuori-Örnberg, J. Dynamic conditional copula correlation and optimal hedge ratios with currency futures. Int. Rev. Financ. Anal. 2016, 47, 60–69. [Google Scholar] [CrossRef]
- Gonzalez-Rivera, G.; Arroyo, J. Time series modeling of histogram-valued data: The daily histogram time series of S&P500 intradaily returns. Int. J. Forecast. 2012, 28, 20–33. [Google Scholar]
- Rakpho, P.; Yamaka, W.; Sriboonchitta, S. Markov Switching Dynamic Multivariate GARCH Models for Hedging on Foreign Exchange Market. In Proceedings of the International Econometric Conference of Vietnam, Ho Chi Minh City, Vietnam, 14–16 January 2019; Springer: Cham, Switzerland, 2019; pp. 806–817. [Google Scholar]
- Metzger, N.; Shenai, V. Hedge Fund Performance during and after the Crisis: A Comparative Analysis of Strategies 2007–2017. Int. J. Financ. Stud. 2019, 7, 15. [Google Scholar] [CrossRef]
- Bollerslev, T. Generalized autoregressive conditional heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Engle, R. Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. J. Bus. Econ. Stat. 2002, 20, 339–350. [Google Scholar] [CrossRef]
- Patton, A.J. Modelling asymmetric exchange rate dependence. Int. Econ. Rev. 2006, 47, 527–556. [Google Scholar] [CrossRef]
- Dueker, M.J. Markov switching in GARCH processes and mean-reverting stock-market volatility. J. Bus. Econ. Stat. 1997, 15, 26–34. [Google Scholar]
- Pelletier, D. Regime switching for dynamic correlations. J. Econom. 2006, 131, 445–473. [Google Scholar] [CrossRef]
- Billio, M.; Caporin, M. Multivariate Markov switching dynamic conditional correlation GARCH representations for contagion analysis. Stat. Methods Appl. 2005, 14, 145–161. [Google Scholar] [CrossRef]
- Pastpipatkul, P.; Yamaka, W.; Sriboonchitta, S. Dependence structure of and co-movement between Thai currency and international currencies after introduction of quantitative easing. In Causal Inference in Econometrics; Springer: Cham, Switzerland, 2016; pp. 545–564. [Google Scholar]
- Dias, S.; Brito, P. Linear regression model with histogram-valued variables. Stat. Anal. Data Min. ASA Data Sci. J. 2015, 8, 75–113. [Google Scholar] [CrossRef]
- Irpino, A.; Verde, R. A new Wasserstein based distance for the hierarchical clustering of histogram symbolic data. In Data Science and Classification; Springer: Berlin/Heidelberg, Germany, 2006; pp. 185–192. [Google Scholar]
- Irpino, A.; Verde, R.; De Carvalho, F.D.A. Dynamic clustering of histogram data based on adaptive squared Wasserstein distances. Expert Syst. Appl. 2014, 41, 3351–3366. [Google Scholar] [CrossRef][Green Version]
- Chodchuangnirun, B.; Yamaka, W.; Khiewngamdee, C. A regime switching for dynamic conditional correlation and GARCH: Application to agricultural commodity prices and market risks. In Proceedings of the International Symposium on Integrated Uncertainty in Knowledge Modelling and Decision Making, Hanoi, Vietnam, 15–17 March 2018; Springer: Cham, Switzerland, 2018; pp. 289–301. [Google Scholar]
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econom. J. Econom. Soc. 1989, 57, 357–384. [Google Scholar] [CrossRef]
- Sklar, A. Random variables, distribution functions, and copulas: A personal look backward and forward. Lect. Notes-Monogr. Ser. 1996, 28, 1–14. [Google Scholar]
- Hamilton, J.D.; Susmel, R. Autoregressive conditional heteroskedasticity and changes in regime. J. Econom. 1994, 64, 307–333. [Google Scholar] [CrossRef]
- Joe, H.; Xu, J.J. The Estimation Method of Inference Functions for Margins for Multivariate Models; University of British Columbia: Vancouver, BC, Canada, 1996. [Google Scholar]
- Liu, S.D.; Jian, J.B.; Wang, Y.Y. Optimal dynamic hedging of electricity futures based on copula-GARCH models. In Proceedings of the 2010 IEEE International Conference on Industrial Engineering and Engineering, Macau, China, 7–10 December 2010. [Google Scholar]
- La Torre-Torres, D.; Oscar, V.; Galeana-Figueroa, E.; Álvarez-García, J. A test of using Markov-switching GARCH models in oil and natural gas trading. Energies 2020, 13, 129. [Google Scholar] [CrossRef]
- Rakpho, P.; Yamaka, W.; Tansuchat, R. Risk Valuation of Precious Metal Returns by Histogram Valued Time Series. In Proceedings of the International Conference of the Thailand Econometrics Society, Chiang Mai, Thailand, 10–12 January 2018; Springer: Cham, Switzerland, 2018; pp. 549–562. [Google Scholar]
- Korley, M.; Giouvris, E. The Regime-Switching Behaviour of Exchange Rates and Frontier Stock Market Prices in Sub-Saharan Africa. J. Risk Financ. Manag. 2021, 14, 122. [Google Scholar] [CrossRef]
- Toque, C.; Terraza, V. Histogram-valued data on value at risk measures: A symbolic approach for risk attribution. Appl. Econ. Lett. 2014, 21, 1243–1251. [Google Scholar] [CrossRef]
- Yamaka, W.; Maneejuk, P. Analyzing the Causality and Dependence between Gold Shocks and Asian Emerging Stock Markets: A Smooth Transition Copula Approach. Mathematics 2020, 8, 120. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).