A Fast-Tracking Hybrid MPPT Based on Surface-Based Polynomial Fitting and P&O Methods for Solar PV under Partial Shaded Conditions
Abstract
:1. Introduction
- A hybrid SPF-P&O GMPPT algorithm is proposed to determine the GMPP of the PV system. This method can operate under uniform or nonuniform irradiance conditions.
- The proposed SPF-P&O MPPT method is compared with the GMPPT P&O [13], obtaining results that prove a fast convergence and minimum steady-state oscillations for the PV system under 133 different cases of shading patterns.
- For the validation of the proposed GMPPT algorithm, six scenarios with different transient of shading patterns are presented: (i) system start-up, (ii) uniform irradiance variations, (iii) sharp change of the (PSCs), (iv) multiple peaks in the P-V characteristic, (v) dark cloud passing, and vi) light cloud passing.
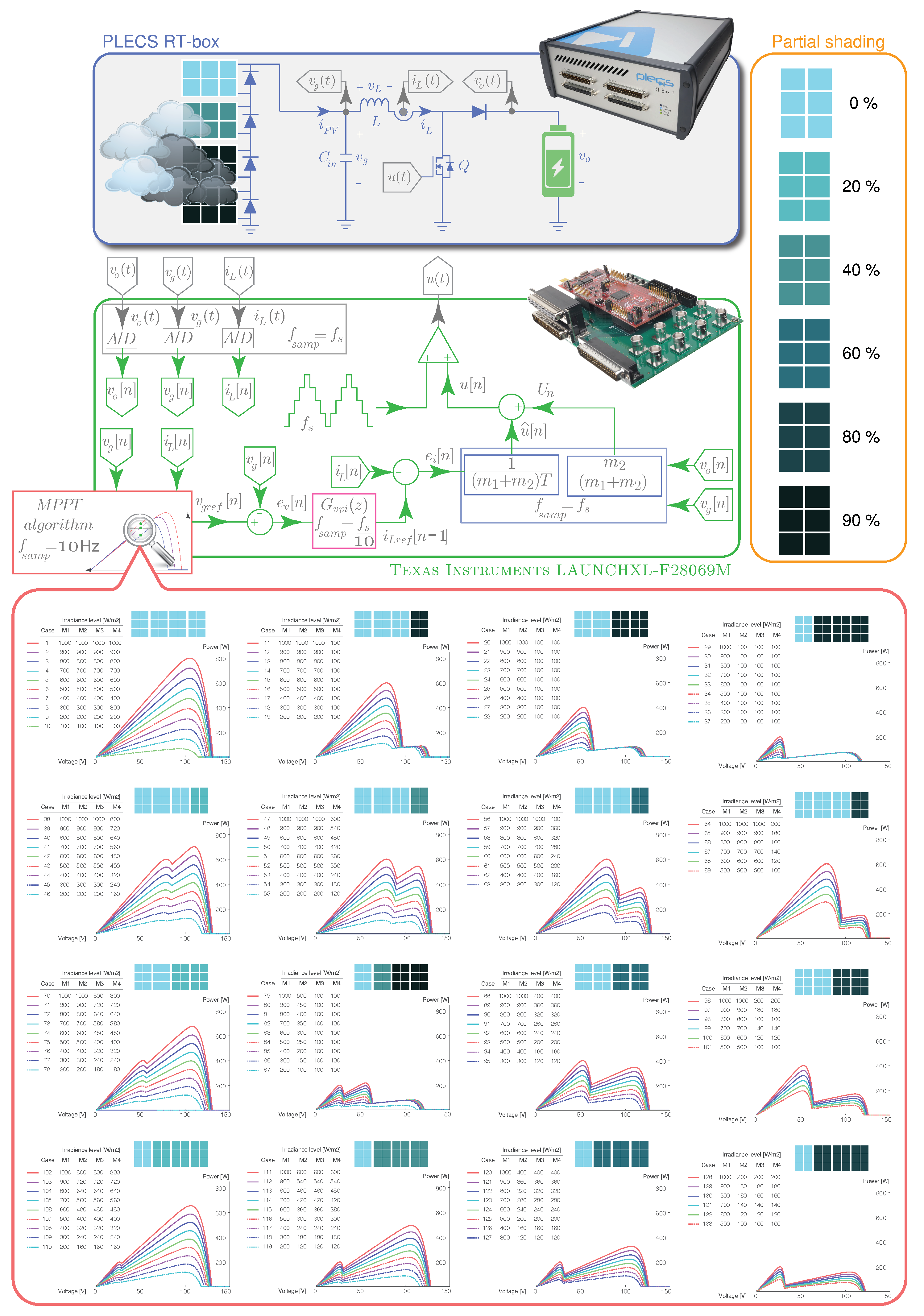
- A two-stage strategy for the experimental PV system is proposed: (i) Modeling the PV array with the DC-DC boost converter using a real-time and high-speed simulator (PLECS RT Box), (ii) Implementing the proposed GMPPT algorithm and the double-loop controller of the DC-DC boost converter in a commercial low-priced digital signal controller (DSC).
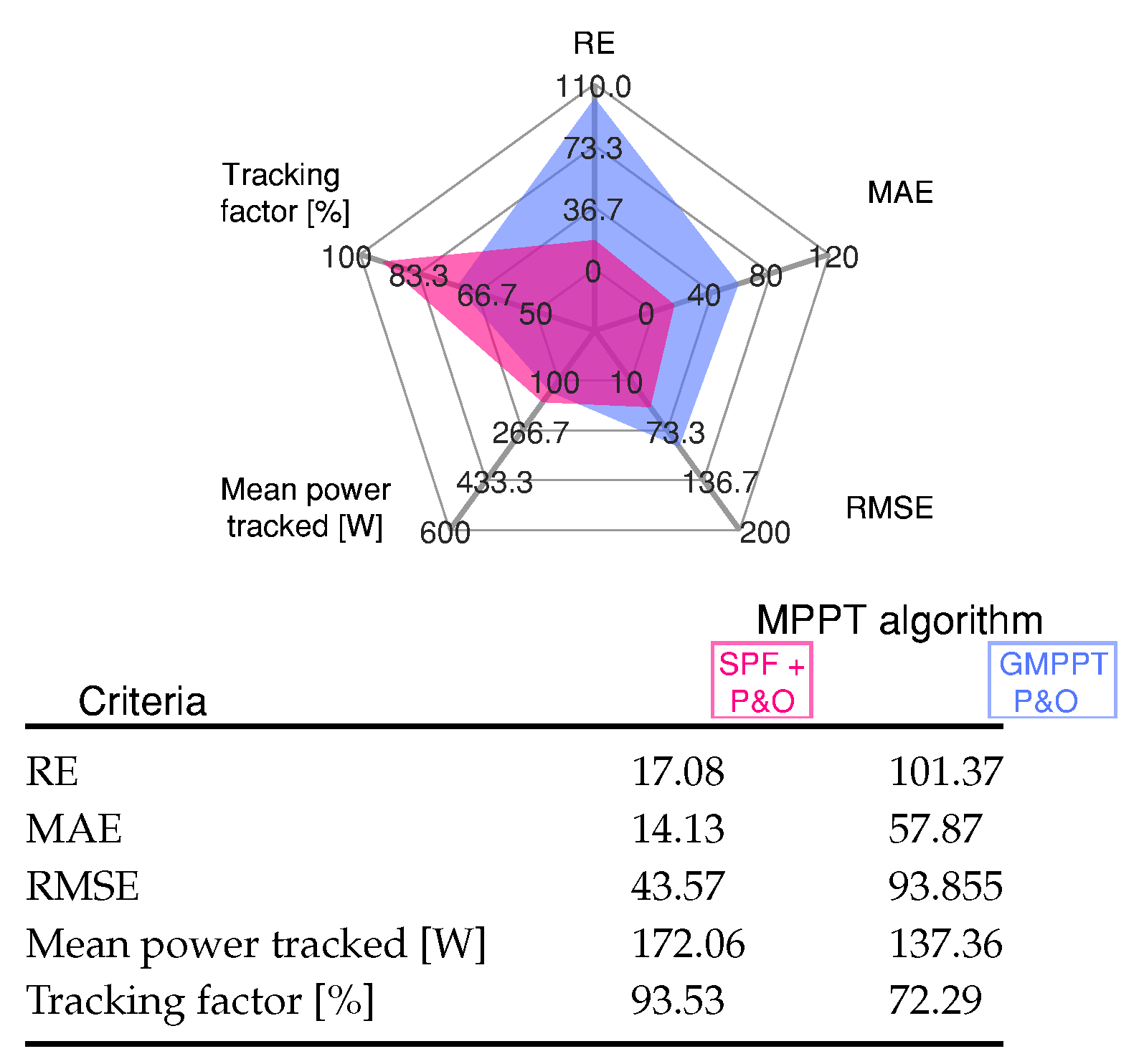
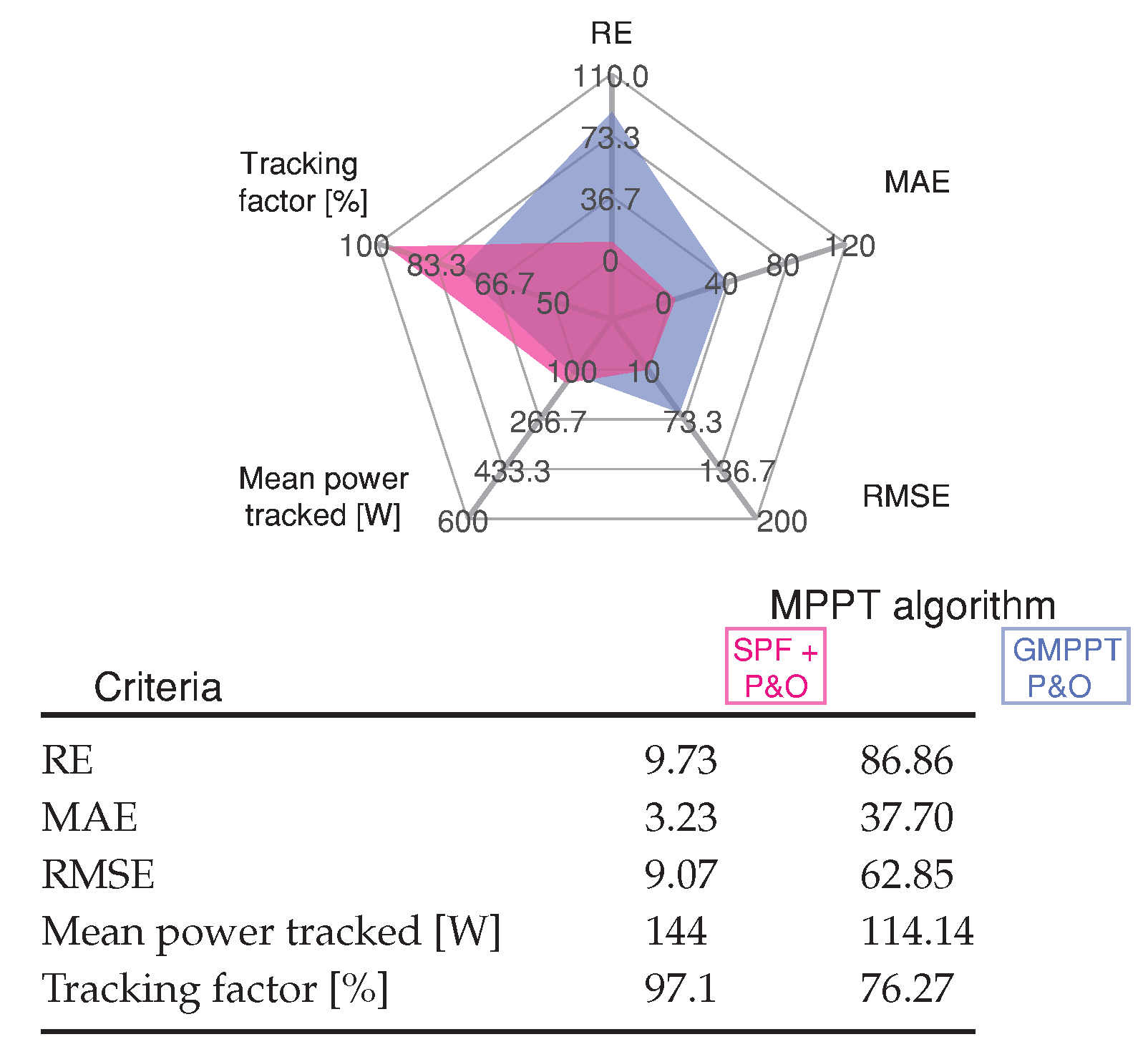
- The simulated and hardware-in-the-loop results of the six scenarios are evaluated using the standard errors, and the mean power tracked and tracking factor scores.
- A nested control loop design is proposed to regulate—along with the SPF-P&O MPPT algorithm—the output voltage of the PV system under challenging environmental conditions. The double-loop control scheme consists of a current (inner-loop) controller and a voltage (outer loop) controller. Low steady-state error under demanding tests including irradiance variations, dynamic partial shading changes and system start-up, and the fast-tracking of control set points, are ensured by each proposed controller. In addition, the implementation of these loops guarantees an independent and fast dynamic response from the system.
2. PV Modeling
2.1. Discrete-Time Sliding-Mode Current Control
2.2. Discrete-Time PI Voltage Control
3. SPF-P&O MPPT
3.1. Maximum Power Point Tracking (MPPT) Algorithm
3.2. Conventional “Perturb and Observe” Method
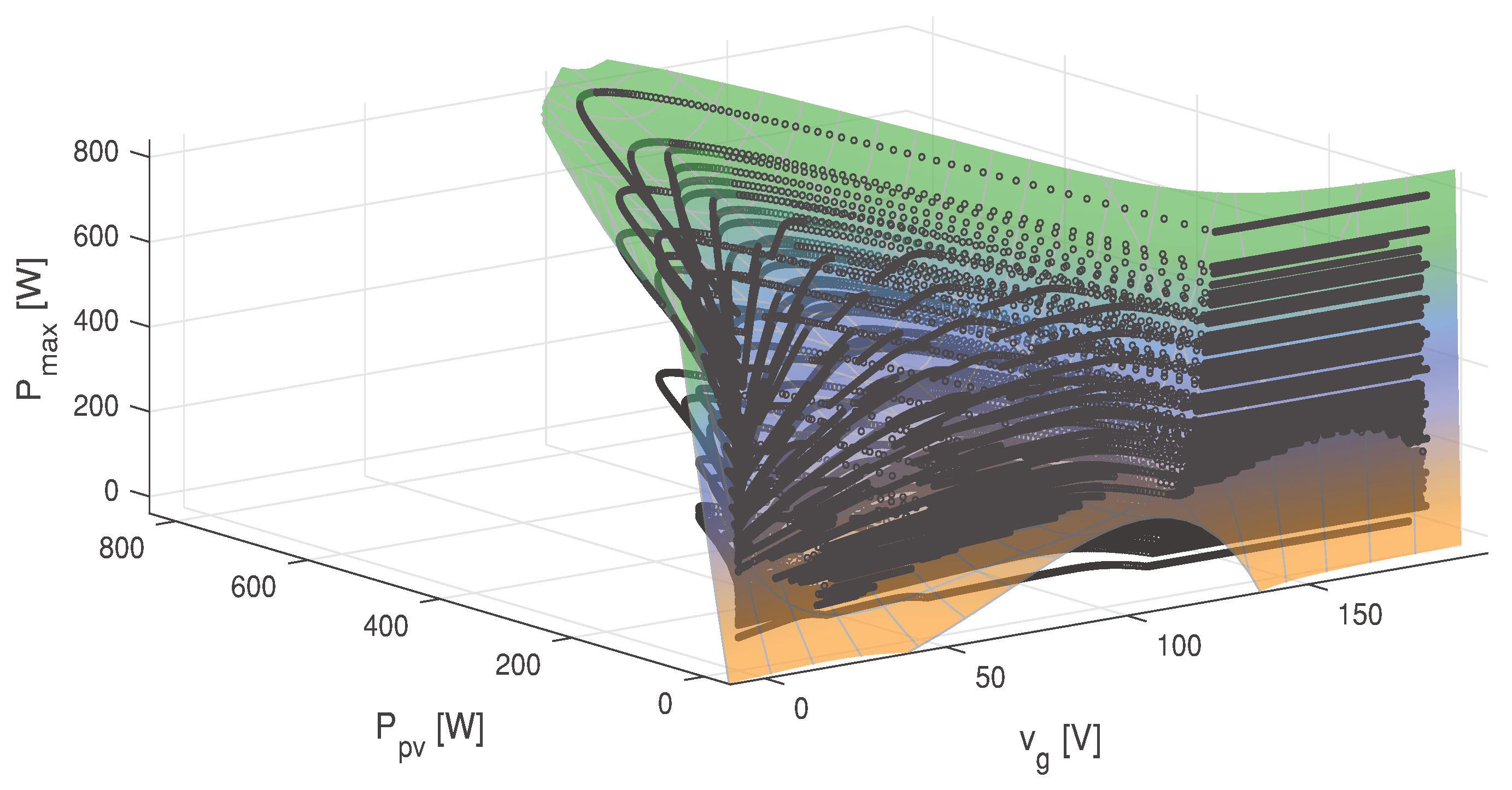
3.3. Proposed MPPT Method
3.3.1. Curve-Based Fitting
3.3.2. Surface-Based Fitting
- z: maximum power estimation for PV module current and voltage measurements (),
- x: current ,
- y: power measurement from the PV module .
3.4. SPF-P&O Algorithm
| Algorithm 1: SPF-P&O GMPPT algorithm running at the microcontroller (see Figure 1). |
 |
4. Simulation and Real-Time HIL Results
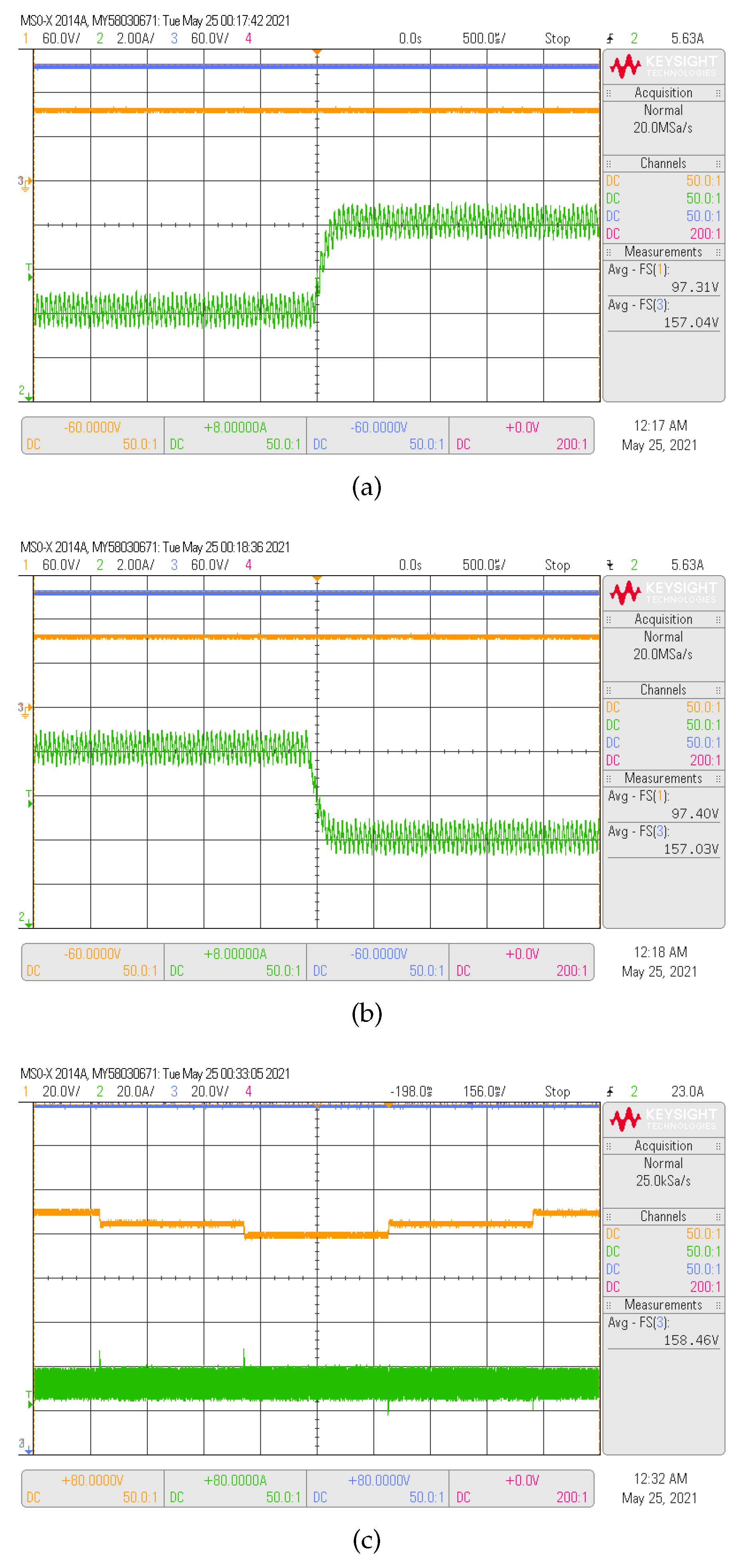
4.1. Inner-Loop Current Control Results
4.2. Double-Loop Results
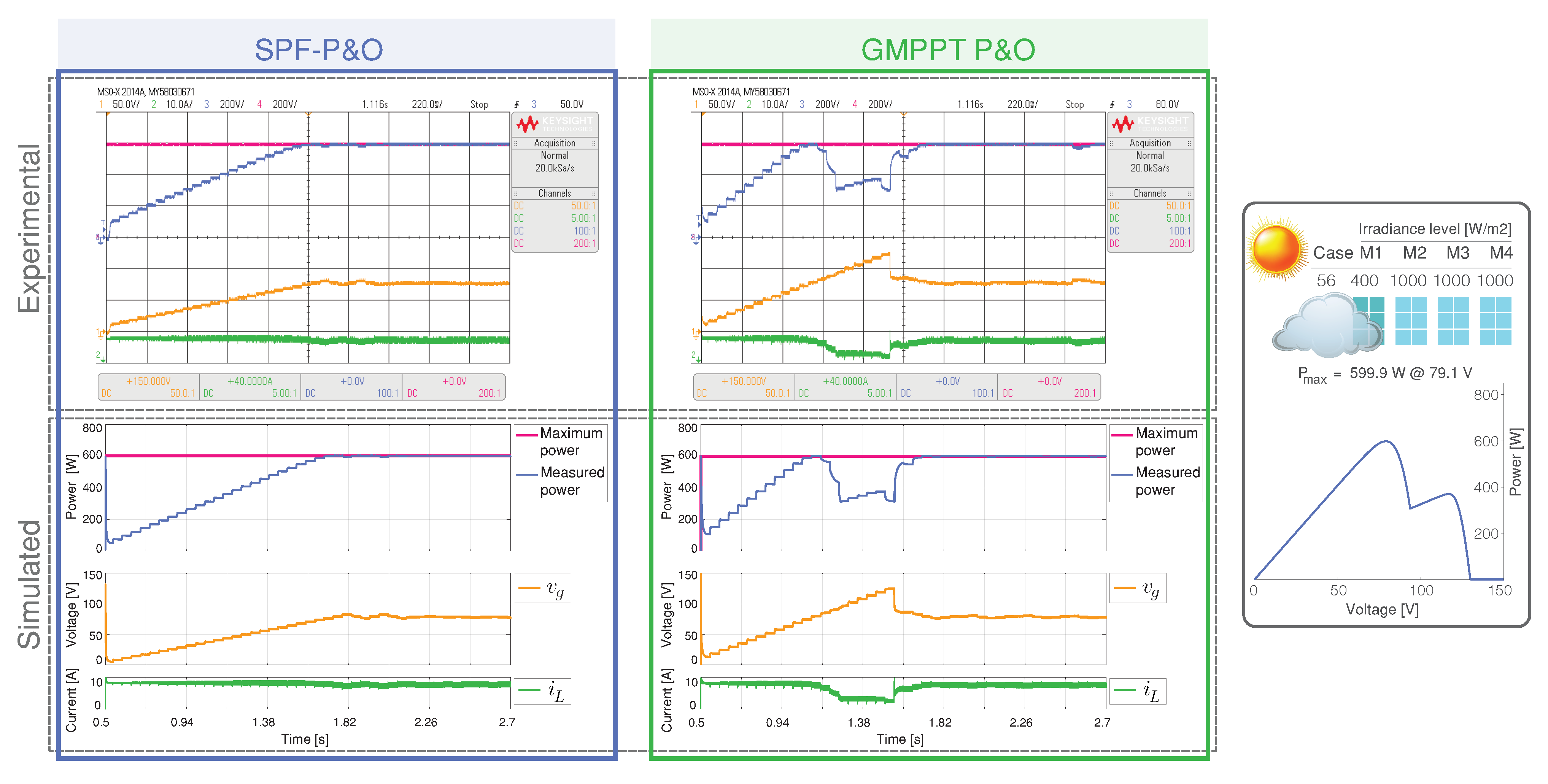
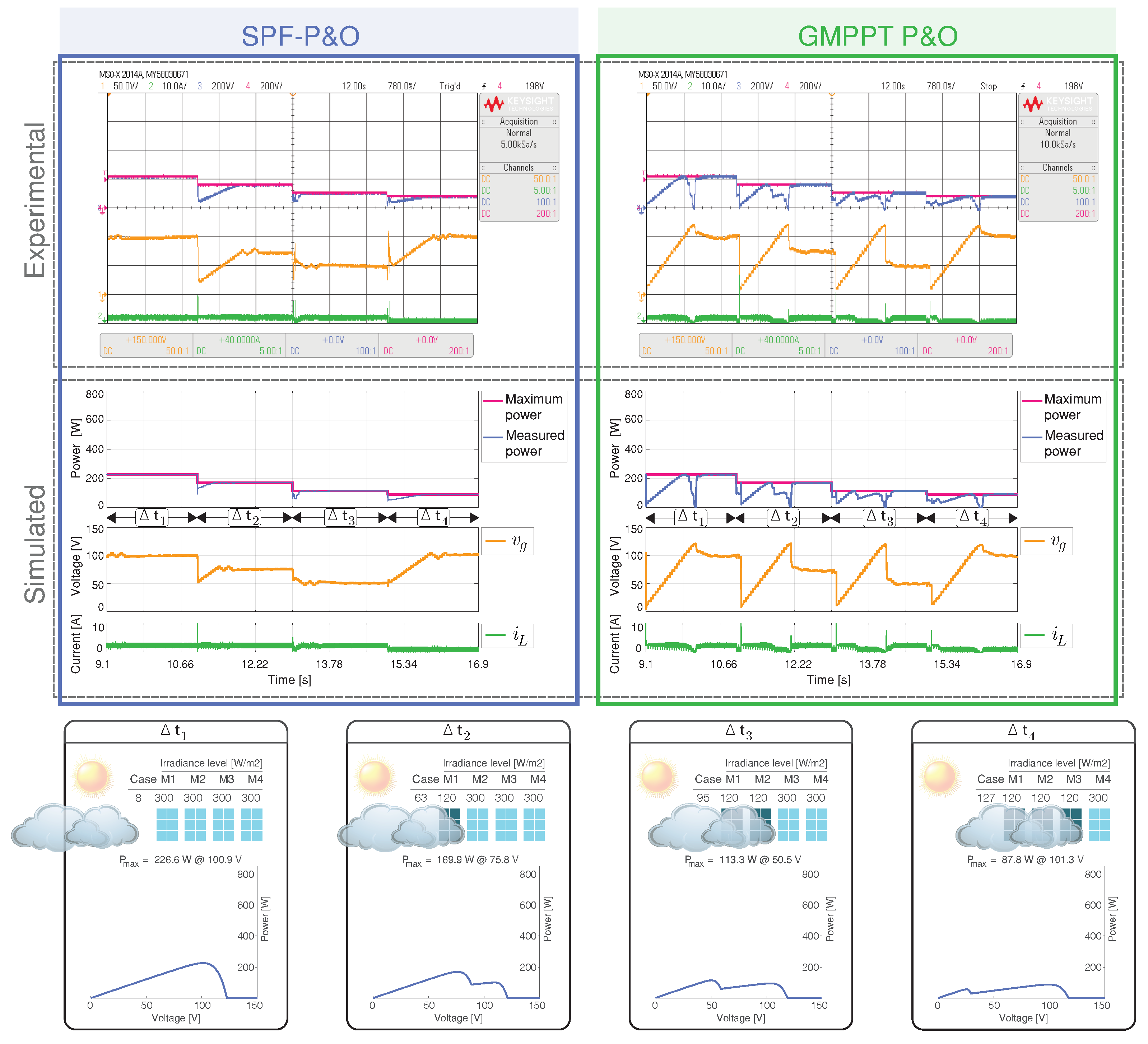
4.3. GMPPT P&O and Proposed SPF-P&O Method Comparison
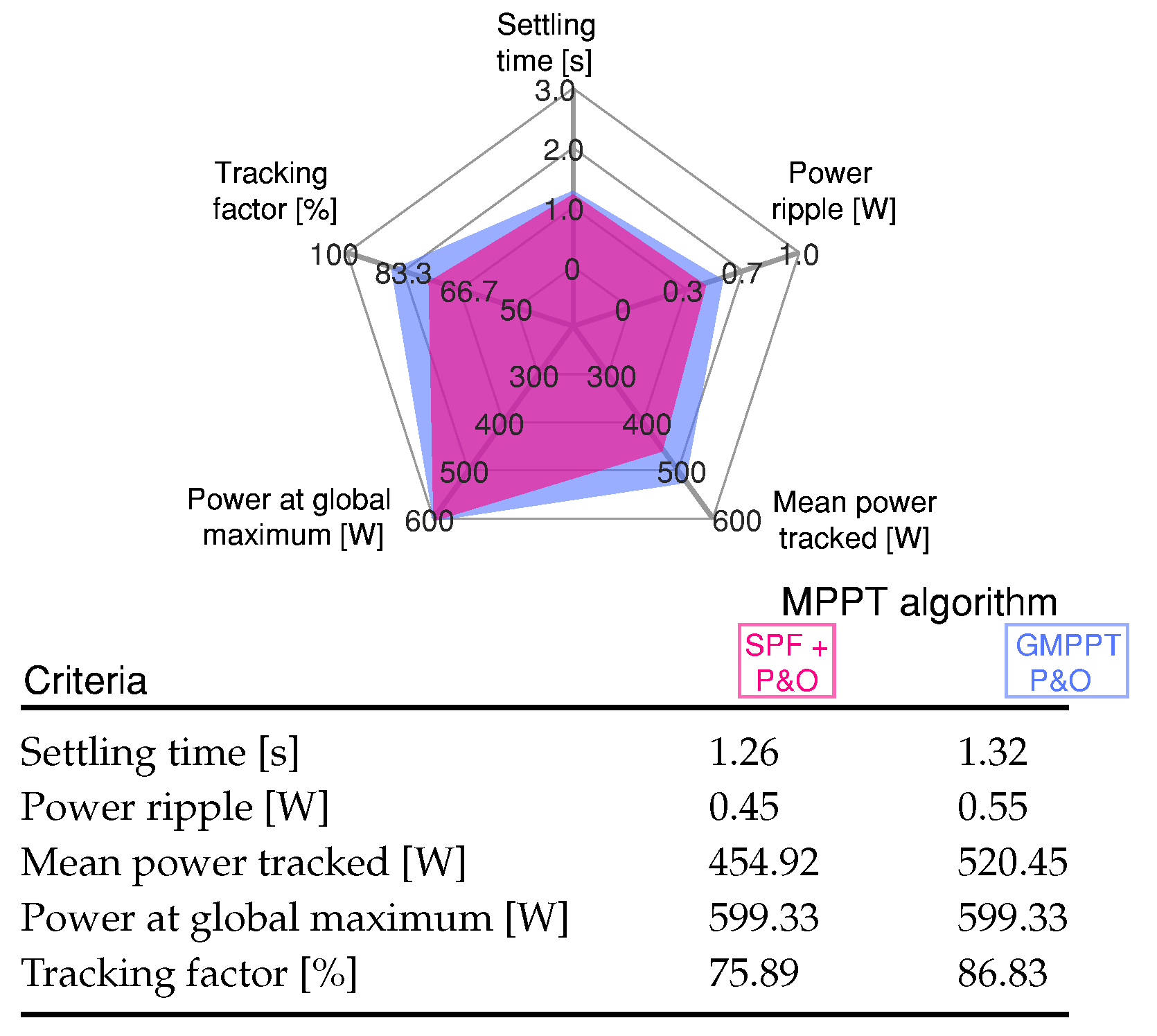
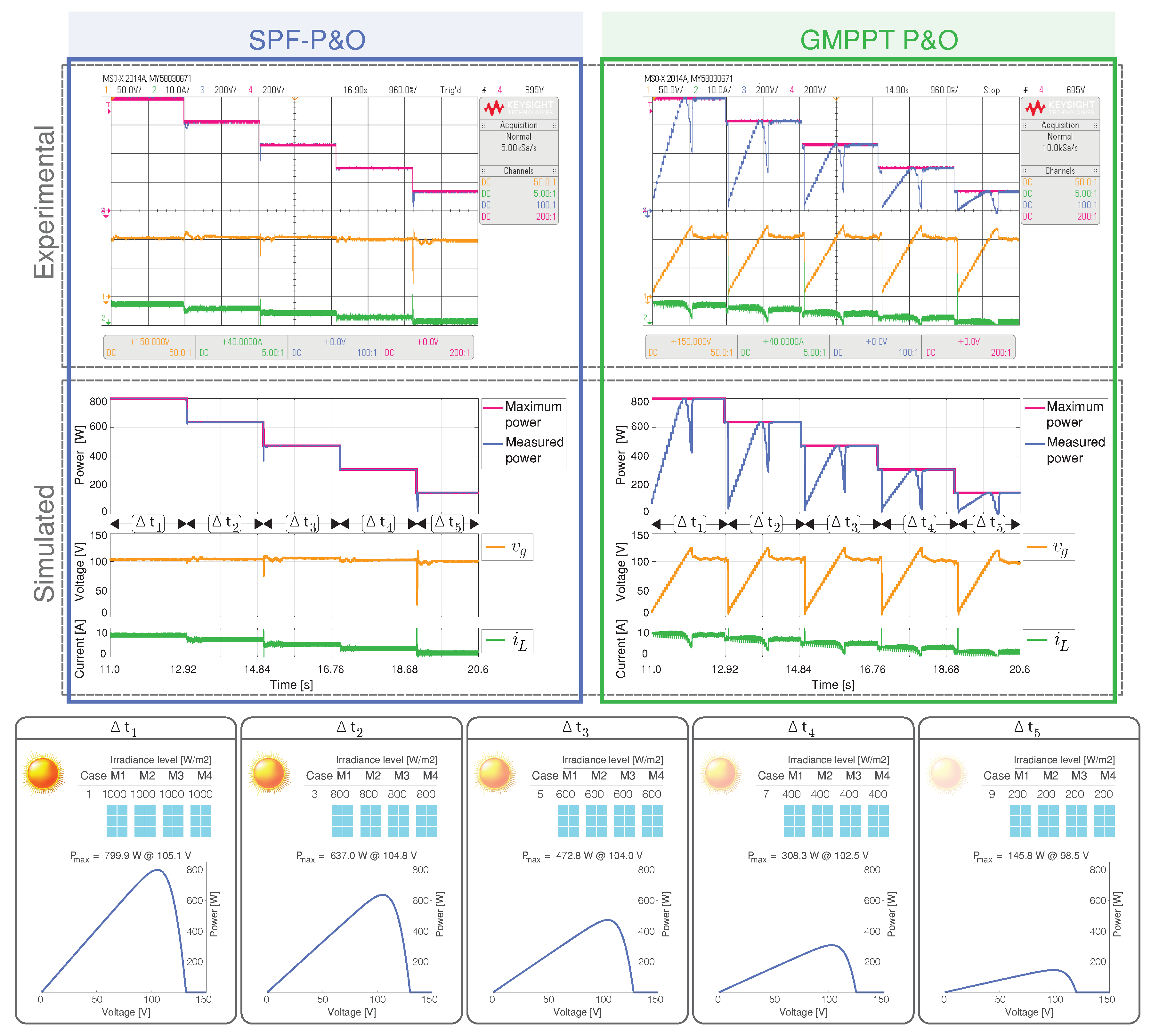
4.3.1. Scenario 1: System Start-Up
4.3.2. Scenario 2: Uniform Irradiance Variations
4.3.3. Scenario 3: Sharp Change of the PSCs
4.3.4. Scenario 4: Multiple Peaks in the P-V Characteristic
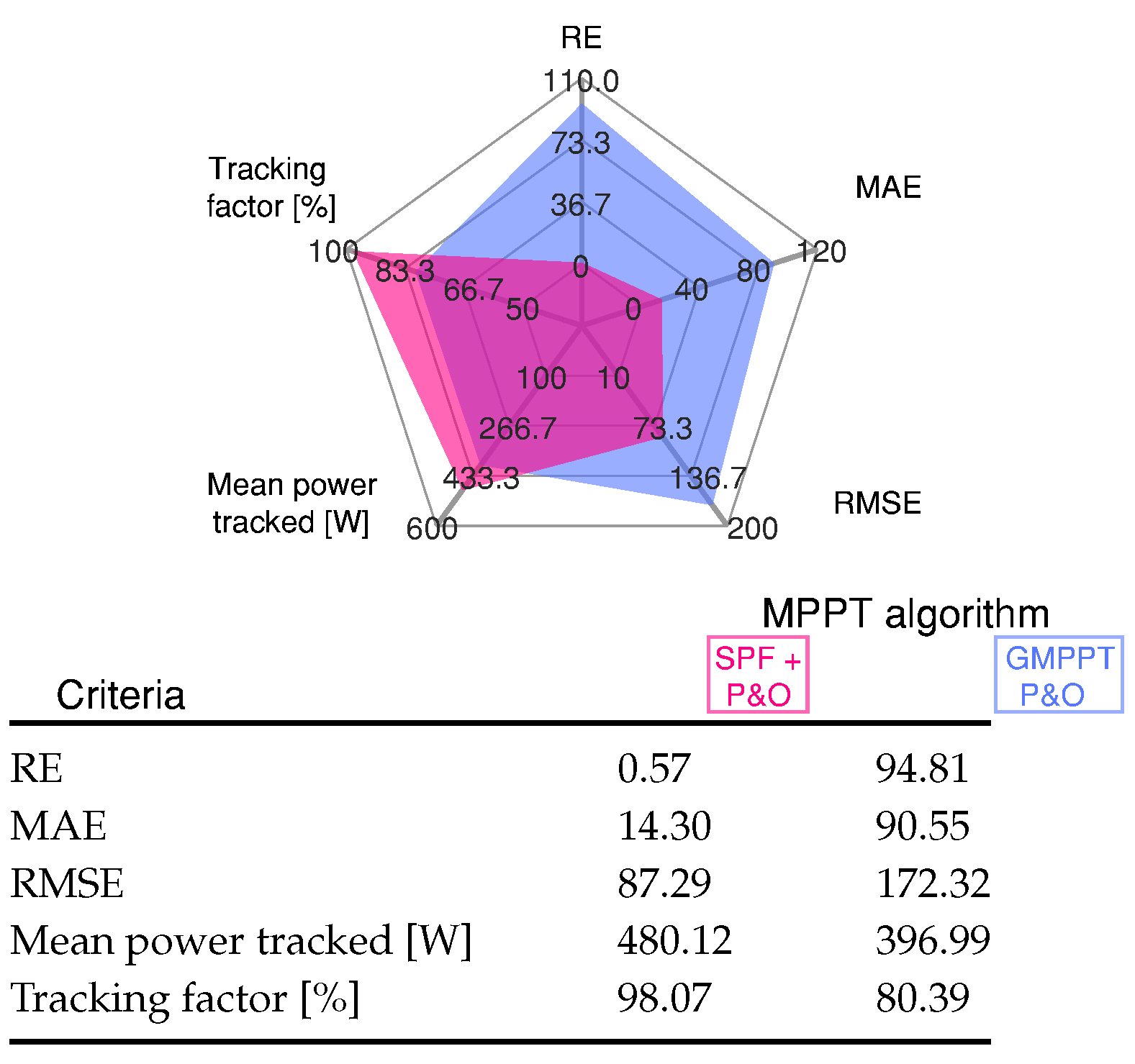
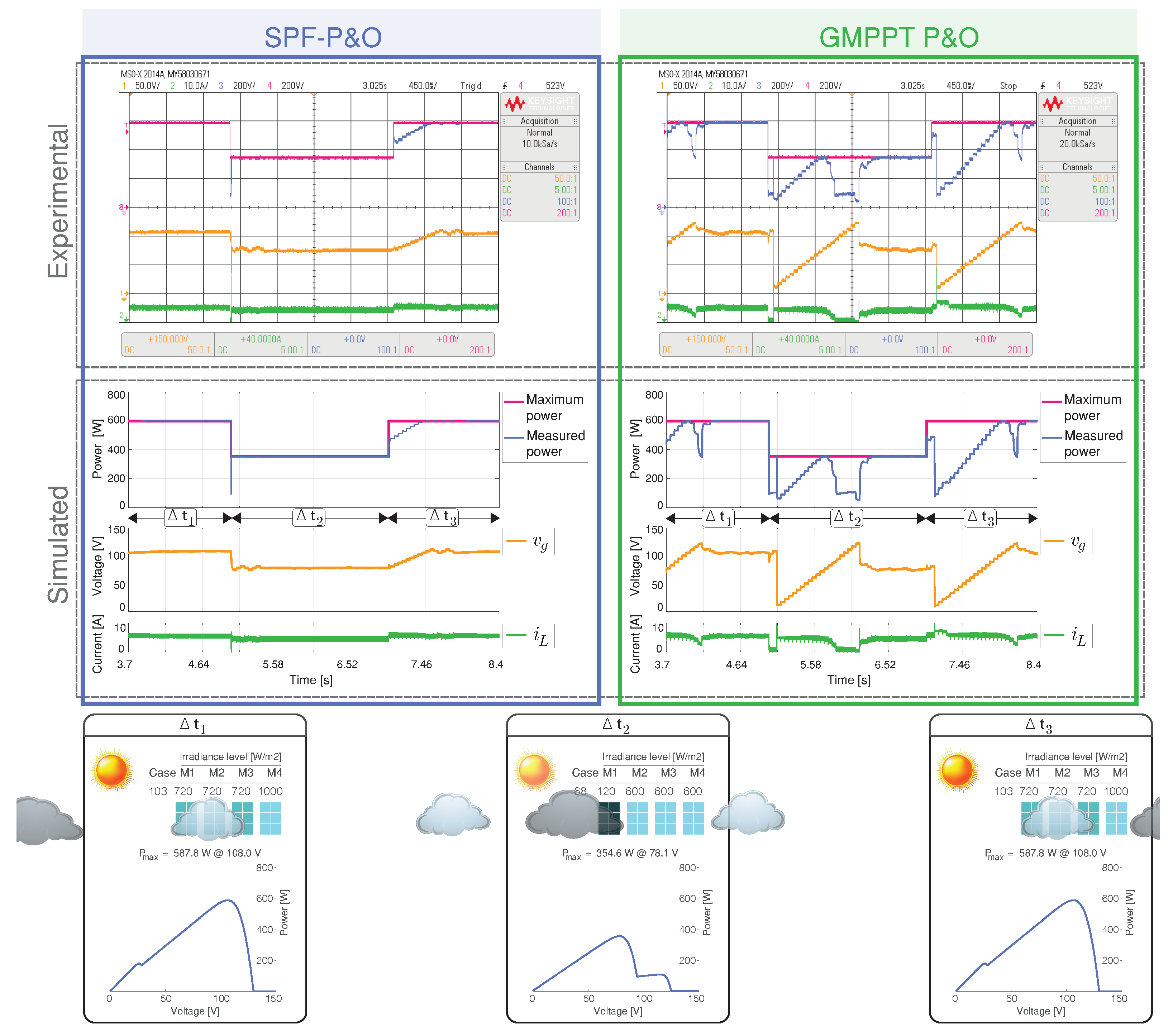
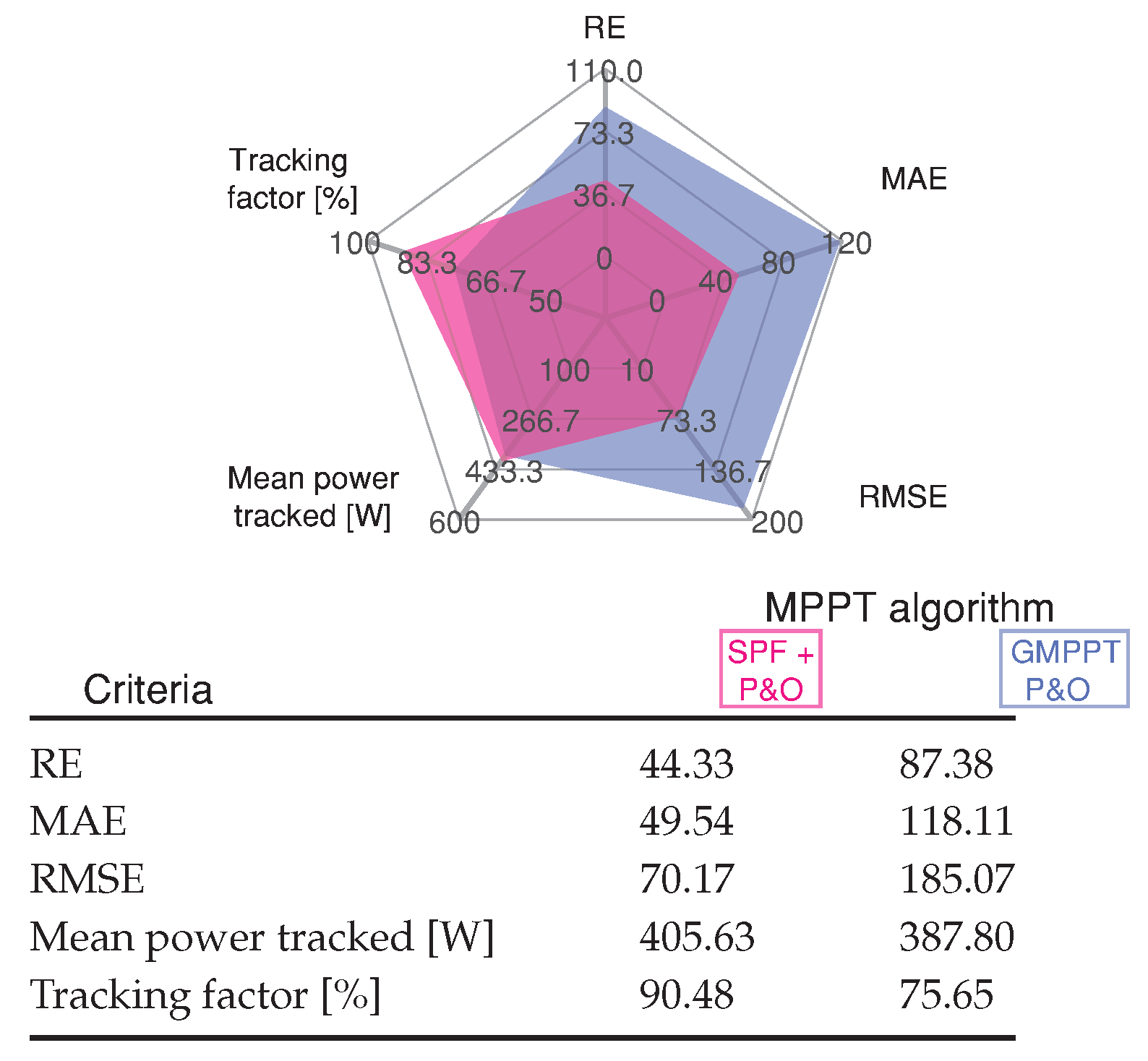
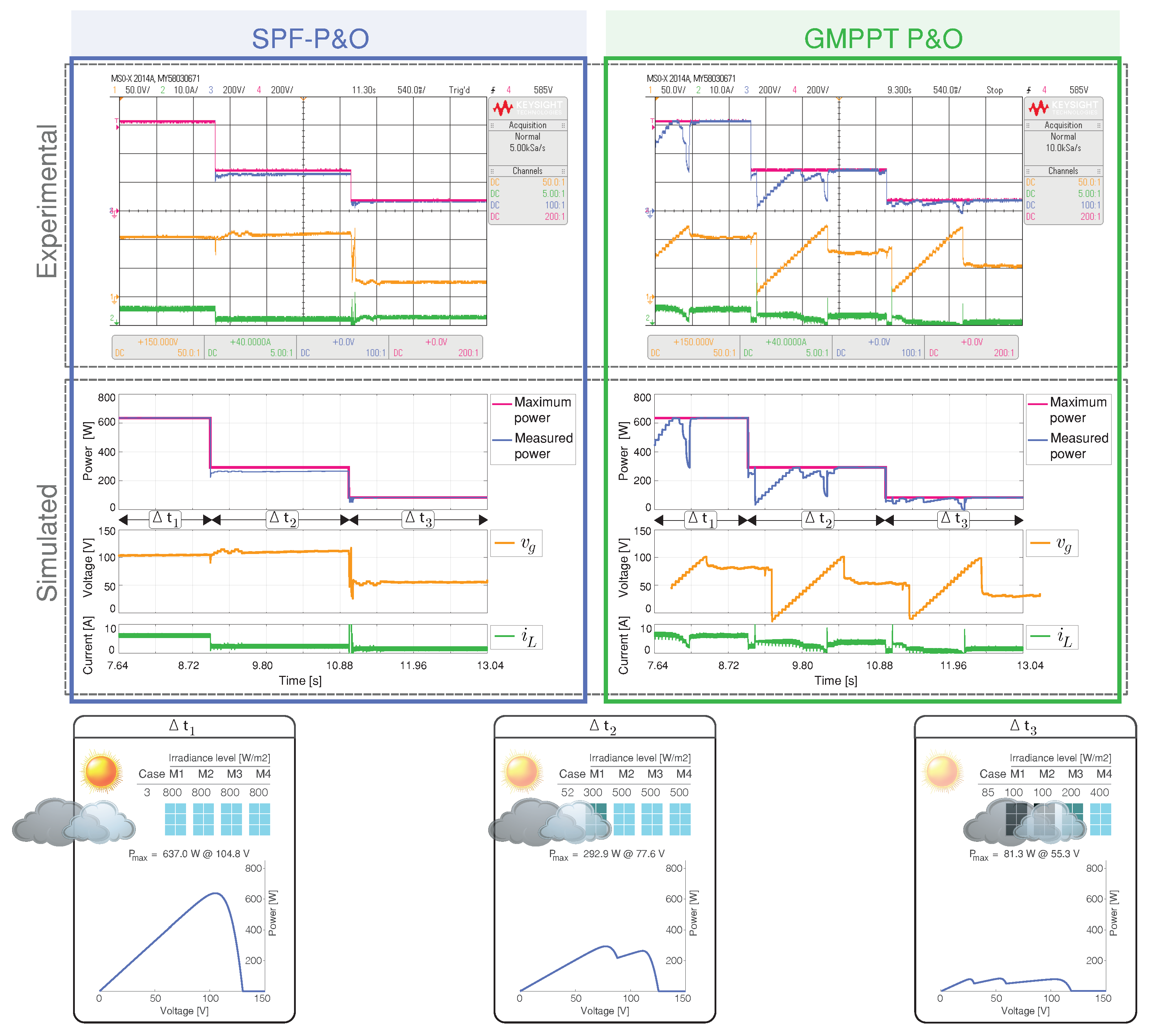
4.3.5. Scenario 5: Dark Cloud Passing
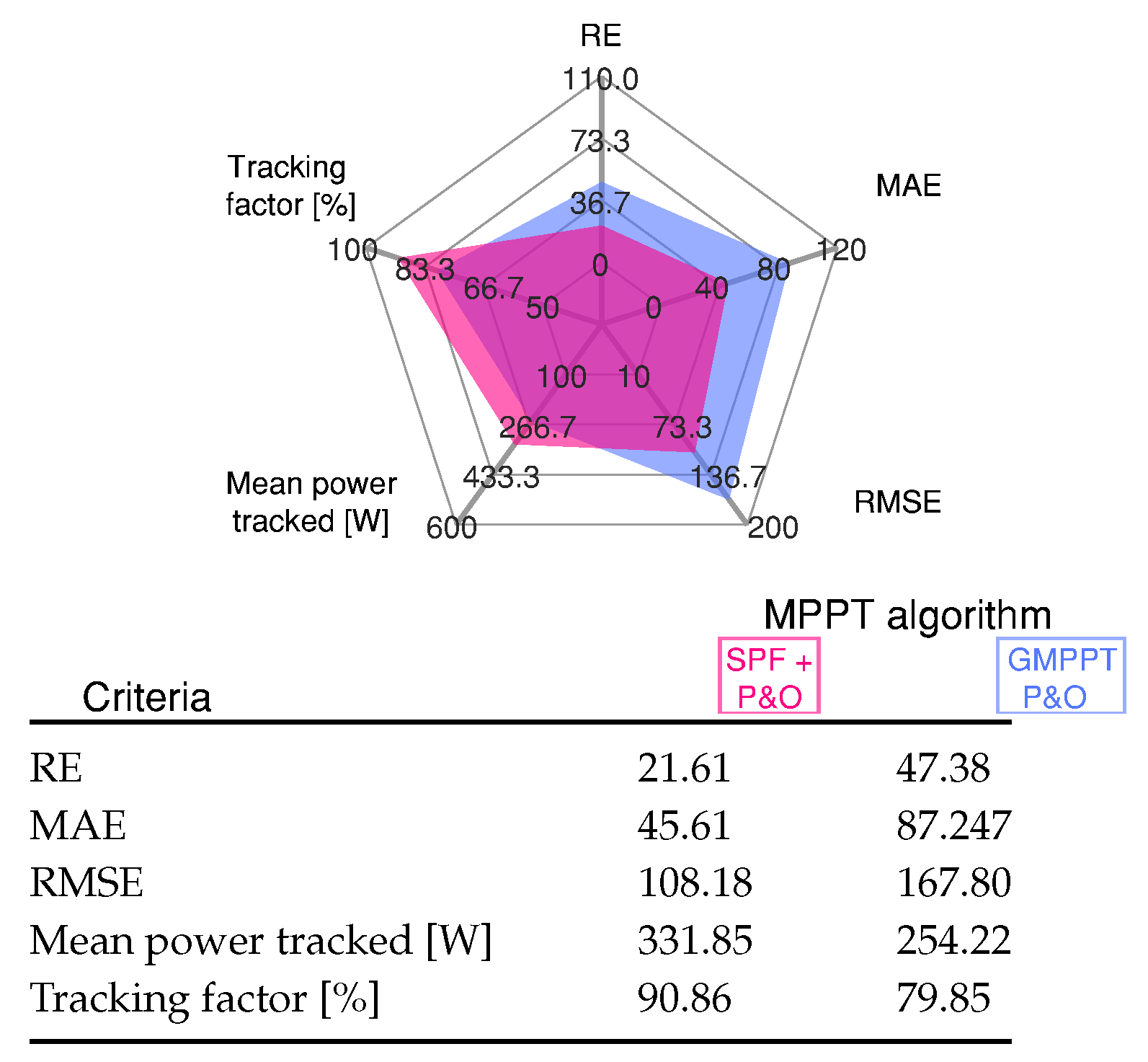
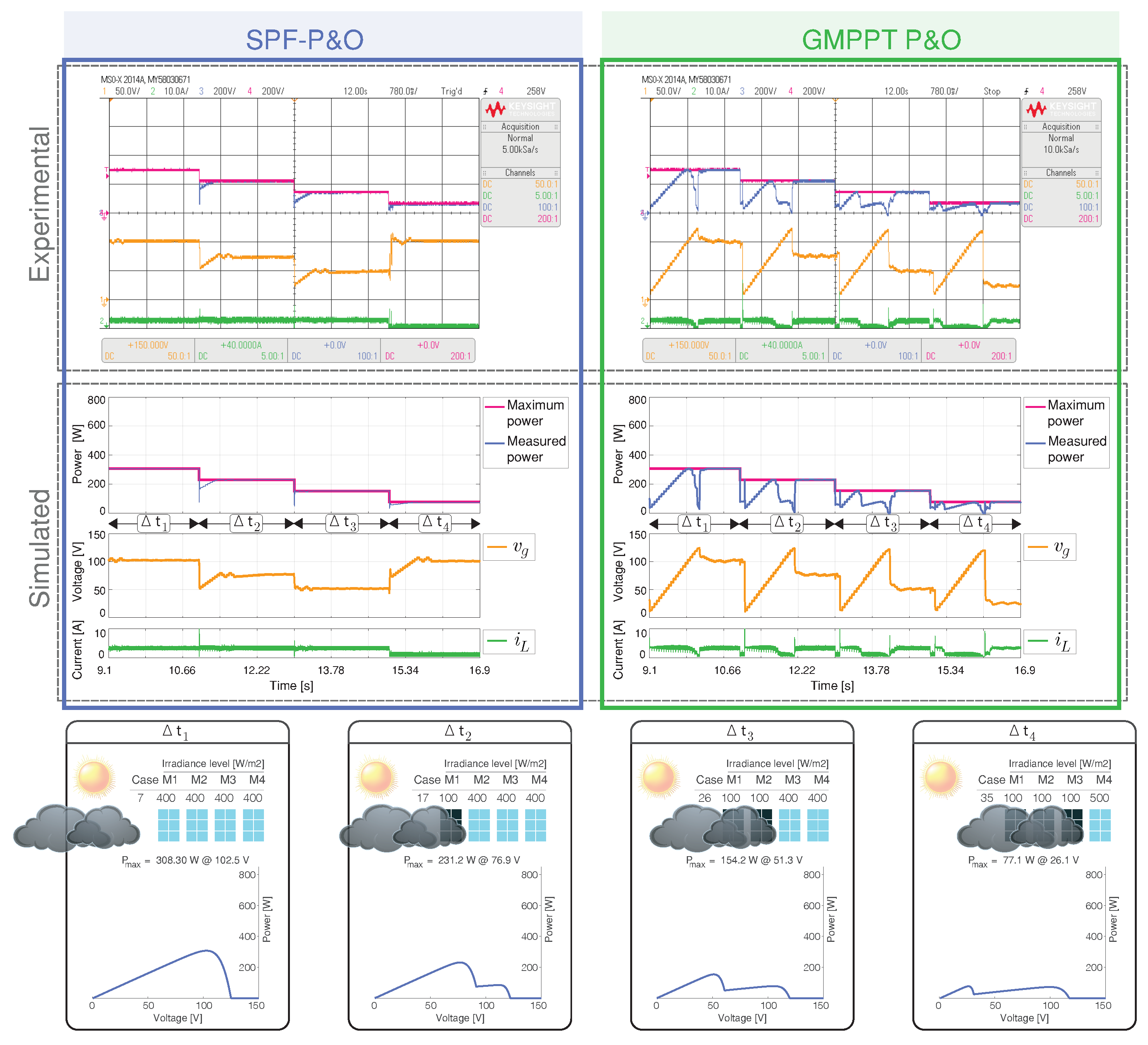
4.3.6. Scenario 6: Light Cloud Passing
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Murdock, H.E.; Gibb, D.; Andre, T.; Sawin, J.L.; Brown, A.; Ranalder, L.; Collier, U.; Dent, C.; Epp, B.; Hareesh Kumar, C.; et al. Renewables 2021-Global Status Report. 2021. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2021_Full_Report.pdf (accessed on 29 September 2021).
- Lappalainen, K.; Valkealahti, S. Experimental study of the maximum power point characteristics of partially shaded photovoltaic strings. Appl. Energy 2021, 301, 117436. [Google Scholar] [CrossRef]
- Hamza Zafar, M.; Mujeeb Khan, N.; Feroz Mirza, A.; Mansoor, M.; Akhtar, N.; Usman Qadir, M.; Ali Khan, N.; Raza Moosavi, S.K. A novel meta-heuristic optimization algorithm based MPPT control technique for PV systems under complex partial shading condition. Sustain. Energy Technol. Assess. 2021, 47, 101367. [Google Scholar] [CrossRef]
- Chen, X.; Du, Y.; Lim, E.; Wen, H.; Yan, K.; Kirtley, J. Power ramp-rates of utility-scale PV systems under passing clouds: Module-level emulation with cloud shadow modeling. Appl. Energy 2020, 268, 114980. [Google Scholar] [CrossRef]
- Belhaouas, N.; Cheikh, M.S.A.; Agathoklis, P.; Oularbi, M.R.; Amrouche, B.; Sedraoui, K.; Djilali, N. PV array power output maximization under partial shading using new shifted PV array arrangements. Appl. Energy 2017, 187, 326–337. [Google Scholar] [CrossRef]
- Bradai, R.; Boukenoui, R.; Kheldoun, A.; Salhi, H.; Ghanes, M.; Barbot, J.P.; Mellit, A. Experimental assessment of new fast MPPT algorithm for PV systems under non-uniform irradiance conditions. Appl. Energy 2017, 199, 416–429. [Google Scholar] [CrossRef]
- Chao, K.H.; Lin, Y.S.; Lai, U.D. Improved particle swarm optimization for maximum power point tracking in photovoltaic module arrays. Appl. Energy 2015, 158, 609–618. [Google Scholar] [CrossRef]
- Mohammadinodoushan, M.; Abbassi, R.; Jerbi, H.; Waly Ahmed, F.; Abdalqadir kh ahmed, H.; Rezvani, A. A new MPPT design using variable step size perturb and observe method for PV system under partially shaded conditions by modified shuffled frog leaping algorithm- SMC controller. Sustain. Energy Technol. Assess. 2021, 45, 101056. [Google Scholar] [CrossRef]
- Laxman, B.; Annamraju, A.; Srikanth, N.V. A grey wolf optimized fuzzy logic based MPPT for shaded solar photovoltaic systems in microgrids. Int. J. Hydrogen Energy 2021, 46, 10653–10665. [Google Scholar] [CrossRef]
- Fares, D.; Fathi, M.; Shams, I.; Mekhilef, S. A novel global MPPT technique based on squirrel search algorithm for PV module under partial shading conditions. Energy Convers. Manag. 2021, 230, 113773. [Google Scholar] [CrossRef]
- Houssein, E.H.; Mahdy, M.A.; Fathy, A.; Rezk, H. A modified Marine Predator Algorithm based on opposition based learning for tracking the global MPP of shaded PV system. Expert Syst. Appl. 2021, 183, 115253. [Google Scholar] [CrossRef]
- González-Castaño, C.; Lorente-Leyva, L.L.; Muñoz, J.; Restrepo, C.; Peluffo-Ordóñez, D.H. An MPPT Strategy Based on a Surface-Based Polynomial Fitting for Solar Photovoltaic Systems Using Real-Time Hardware. Electronics 2021, 10, 206. [Google Scholar] [CrossRef]
- Ghasemi, M.A.; Foroushani, H.M.; Parniani, M. Partial shading detection and smooth maximum power point tracking of PV arrays under PSC. IEEE Trans. Power Electron. 2015, 31, 6281–6292. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Almutairi, K.; Padmanaban, S.; Tirth, V.; Algarni, S.; Irshad, K.; Islam, S.; Zahir, M.H.; Shafiullah, M.; Malik, M.Z. Investigation of MPPT Techniques Under Uniform and Non-Uniform Solar Irradiation Condition—A Retrospection. IEEE Access 2020, 8, 127368–127392. [Google Scholar] [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, optimal, intelligent and classical PV MPPT techniques: A review. CSEE J. Power Energy Syst. 2021, 7, 9–33. [Google Scholar] [CrossRef]
- Guest, P.G.; Guest, P.G. Numerical Methods of Curve Fitting; Cambridge University Press: New York, NY, USA, 2012. [Google Scholar]
- Erickson, R.W.; Maksimovic, D. Fundamentals of Power Electronics, 2nd ed.; Kluwer Academic Publishers: Boston, MA, USA, 2001. [Google Scholar]
- Hart, D.W. Power Electronics; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Corradini, L.; Maksimovic, D.; Mattavelli, P.; Zane, R. Digital Control of High-Frequency Switched-Mode Power Converters; Wiley-IEEE Press: Piscataway, NJ, USA, 2015. [Google Scholar]
- El Aroudi, A.; Martínez-Treviño, B.A.; Vidal-Idiarte, E.; Cid-Pastor, A. Fixed switching frequency digital sliding-mode control of DC-DC power supplies loaded by constant power loads with inrush current limitation capability. Energies 2019, 12, 1055. [Google Scholar] [CrossRef] [Green Version]
- Vidal-Idiarte, E.; Marcos-Pastor, A.; Garcia, G.; Cid-Pastor, A.; Martinez-Salamero, L. Discrete-time sliding-mode-based digital pulse width modulation control of a boost converter. IET Power Electron. 2015, 8, 708–714. [Google Scholar] [CrossRef]
- Vidal-Idiarte, E.; Marcos-Pastor, A.; Giral, R.; Calvente, J.; Martinez-Salamero, L. Direct digital design of a sliding mode-based control of a PWM synchronous buck converter. IET Power Electron. 2017, 10, 1714–1720. [Google Scholar] [CrossRef]
- Farhat, M.; Barambones, O.; Sbita, L. A new maximum power point method based on a sliding mode approach for solar energy harvesting. Appl. Energy 2017, 185, 1185–1198. [Google Scholar] [CrossRef]
- Kamran, M.; Mudassar, M.; Fazal, M.R.; Asghar, M.U.; Bilal, M.; Asghar, R. Implementation of improved Perturb & Observe MPPT technique with confined search space for standalone photovoltaic system. J. King Saud Univ.-Eng. Sci. 2018, 32, 432–441. [Google Scholar]
- Kollimalla, S.K.; Mishra, M.K. A novel adaptive P&O MPPT algorithm considering sudden changes in the irradiance. IEEE Trans. Energy Convers. 2014, 29, 602–610. [Google Scholar]
- Ahmed, J.; Salam, Z. A modified P&O maximum power point tracking method with reduced steady-state oscillation and improved tracking efficiency. IEEE Trans. Sustain. Energy 2016, 7, 1506–1515. [Google Scholar]
- Chapra, S.C. Applied Numerical Methods with MATLAB for Engineers and Scientists; McGraw-Hill: New York, NY, USA, 2012. [Google Scholar]
- Tomczyk, K.; Makowski, T.; Kowalczyk, M.; Ostrowska, K.; Beńko, P. Procedure for the Accurate Modelling of Ring Induction Motors. Energies 2021, 14, 5469. [Google Scholar] [CrossRef]
- Stroock, D.W. Probability Theory: An Analytic View, 2nd ed.; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Zafar, M.H.; Al-shahrani, T.; Khan, N.M.; Feroz Mirza, A.; Mansoor, M.; Qadir, M.U.; Khan, M.I.; Naqvi, R.A. Group teaching optimization algorithm based MPPT control of PV systems under partial shading and complex partial shading. Electronics 2020, 9, 1962. [Google Scholar] [CrossRef]

| Electrical Parameters | Value | |
|---|---|---|
| Maximum power | 200.0 W | |
| Voltage at maximum power | 26.3 V | |
| Current at maximum power | 7.61 A | |
| Short-circuit current | 8.21 A | |
| Open-circuit voltage | 32.9 V | |
| Temperature coefficient of short-circuit current | A/C | |
| Temperature coefficient | V/C |
| Converter | ||||
|---|---|---|---|---|
| Boost |
| Polynomial Models | Equations |
|---|---|
| Degree of Term | 0 | 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | y | ||||||||
| 1 | x | |||||||||
| 2 | - | |||||||||
| 3 | - | - | ||||||||
| 4 | - | - | - | |||||||
| 5 | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Castaño, C.; Restrepo, C.; Revelo-Fuelagán, J.; Lorente-Leyva, L.L.; Peluffo-Ordóñez, D.H. A Fast-Tracking Hybrid MPPT Based on Surface-Based Polynomial Fitting and P&O Methods for Solar PV under Partial Shaded Conditions. Mathematics 2021, 9, 2732. https://doi.org/10.3390/math9212732
González-Castaño C, Restrepo C, Revelo-Fuelagán J, Lorente-Leyva LL, Peluffo-Ordóñez DH. A Fast-Tracking Hybrid MPPT Based on Surface-Based Polynomial Fitting and P&O Methods for Solar PV under Partial Shaded Conditions. Mathematics. 2021; 9(21):2732. https://doi.org/10.3390/math9212732
Chicago/Turabian StyleGonzález-Castaño, Catalina, Carlos Restrepo, Javier Revelo-Fuelagán, Leandro L. Lorente-Leyva, and Diego H. Peluffo-Ordóñez. 2021. "A Fast-Tracking Hybrid MPPT Based on Surface-Based Polynomial Fitting and P&O Methods for Solar PV under Partial Shaded Conditions" Mathematics 9, no. 21: 2732. https://doi.org/10.3390/math9212732
APA StyleGonzález-Castaño, C., Restrepo, C., Revelo-Fuelagán, J., Lorente-Leyva, L. L., & Peluffo-Ordóñez, D. H. (2021). A Fast-Tracking Hybrid MPPT Based on Surface-Based Polynomial Fitting and P&O Methods for Solar PV under Partial Shaded Conditions. Mathematics, 9(21), 2732. https://doi.org/10.3390/math9212732









