Closed-Loop Nash Equilibrium in the Class of Piecewise Constant Strategies in a Linear State Feedback Form for Stochastic LQ Games

Abstract

In this paper, we examine a sampled-data Nash equilibrium strategy for a stochastic linear quadratic (LQ) differential game, in which admissible strategies are assumed to be constant on the interval between consecutive measurements. Our solution first involves transforming the problem into a linear stochastic system with finite jumps. This allows us to obtain necessary and sufficient conditions assuring the existence of a sampled-data Nash equilibrium strategy, extending earlier results to a general context with more than two players. Furthermore, we provide a numerical algorithm for calculating the feedback matrices of the Nash equilibrium strategies. Finally, we illustrate the effectiveness of the proposed algorithm by two numerical examples. As both situations highlight a stabilization effect, this confirms the efficiency of our approach.

1. Introduction

Stochastic control problems governed by Itô’s differential equations have been the subject of intensive research over the last decades. This generated a rich literature and fundamental results such as the $H_2$ and LQ robust sampled-data control problems under a unified framework studied in [1,2], classes of uncertain sampled-data systems with random jumping parameters characterized by finite state semi-Markov process analysed in [3], or stochastic differential games investigated in [4,5,6,7].

Dynamical games have been used to solve many real life problems (see e.g., [8]). For example, the concept of Nash equilibrium is very important for dynamical games, where for controlled systems the closed-loop and open-loop equilibria strategies present special interest. Various aspects of open-loop Nash equilibria are studied for a LQ differential game in [9], other results being reported in [10,11,12]. In addiytion, in [13] applications to gas network optimisation are studied via open-loop sampled-data Nash equilibrium strategy. The framework in which state vector measurements for a class of differential games are available only at discrete times was first studied in [14]. There, a two-player differential game was considered, and necessary conditions for the sample data controls were obtained using a backward translation method starting at the last time interval, and following the previous state measurements. This case has been extended to a stochastic framework in [15], where the players have access to sample-data state information with sampling interval. For other results dealing with closed-loop systems (see, e.g., [16]). Stochastic dynamical games are an important, but more challenging framework. First introduced in [17], stochastic LQ problems have been studied extensively (see, [18,19]).

In the present paper, we consider stochastic differential games governed by Itô’s differential equation, with state multiplicative and control multiplicative white noise perturbations. The original contributions of this work are the following. First, we analyze the design of a Nash equilibrium strategy in a state feedback form in the class of piecewise constant admissible strategies. It is assumed that the state measurements are available only at some discrete times. The original problem is transformed into an equivalent one which asks to find some existence conditions for a Nash equilibrium strategy in a state feedback form for a LQ stochastic differential game described by a system of Itô differential equations controlled by impulses. Necessary and sufficient conditions for the existence of a Nash equilibrium strategy for the new LQ differential game are obtained based on methods from [20,21]. The feedback matrices of the equilibrium strategies for the original dynamical game are obtained from the general result using the structure of the matrix coefficients of the system controlled by impulses. Another major contribution of this paper consists of the numerical methods for computing the feedback matrices of the Nash equilibrium strategy.

To our knowledge, in the stochastic framework, there are few papers dealing with the problem of sampled-data Nash equilibrium strategy in both open-loop and closed-loop forms ([22,23]), the papers [13,14] mentioned before only considering the deterministic framework. In that case, the problem of sampled-data Nash equilibrium strategy can be transformed in a natural way into a problem stated in discrete-time framework. Such a transformation is not possible when the dynamical system contains state multiplicative and control multiplicative white noise perturbations. In [15], the stochastic character is due only to the presence of the additive white noise perturbations. In that case, the approach is not essentially different from the one used in the deterministic case.

The paper is organized as follows. In Section 2, we formulate the problem, introducing the L-players Nash equilibria concept. In Section 2.2, we state an equivalent form of the original problem and we introduce a system of matrix linear differential equations with jumps and algebraic constraints which is involved in the derivation of the feedback matrices of the equilibrium strategies. Then, in Section 2.3, we provide some necessary and sufficient conditions which guarantee the existence of a piecewise constant Nash equilibrium strategy. An algorithm implementing these developments is given in Section 3. The efficiency of the proposed algorithm is demonstrated by two numerical examples illustrating the behavior of the optimal trajectories generated by the equilibrium strategy. Section 4 is dedicated to conclusions.

2. Problem Formulation

2.1. Model Description and Problem Setting

Consider the controlled system having the state space representation described by

$$\begin{array}{cc}\hfill & dx\left(t\right)=[Ax\left(t\right)+\sum _{k=1}^L{B}_k{u}_k\left(t\right)]dt+[Cx\left(t\right)+\sum _{k=1}^L{D}_k{u}_k\left(t\right)]dw\left(t\right),\hfill \\ \hfill & x\left(t_0\right)=x_0,t\in [t_0,t_f],\hfill \end{array}$$

(1)

where $x\left(t\right)\in {\mathbb{R}}^n$ is the state vector, L is a positive integer, $u_k\left(t\right)\in {\mathbb{R}}^{m_k},$$k=1,\dots ,L$ are control parameters, and ${\left\{w\left(t\right)\right\}}_{t\ge 0}$ is a 1-dimensional standard Wiener process defined on a probability space $(\mathsf{\Omega },\mathcal{F},\mathcal{P})$.

In the controlled system there are L players ($k=1,2,\dots ,L$) who change their behavior through their control function $u_k(·),$$k=1,\dots ,L.$ The matrices of the system $A,C\in {\mathbb{R}}^{n\times n}$ and matrices of the players $B_k,D_k\in {\mathbb{R}}^{n\times m_k},$$k=1,\dots ,L,$ are known. In the field of the game theory, the controls $u_k(·)$ are called admissible strategies (or policies) for the players. The different classes of admissible strategies can be defined in various ways, depending on the available information.

Each player aims to minimize its own cost function (performance criterion), and for $k=1,\dots ,L$ we have

$$\begin{array}{cc}\hfill J_k(t_0,x_0;u_1,\dots ,u_L)=& \mathbb{E}\left[x_u^T\left(t_f\right)G_k{x}_u\left(t_f\right)+\underset{t_0}{\overset{t_f}{\int }}(x_u^T\left(t\right)M_k{x}_u\left(t\right)+\sum _{j=1}^L{u}_j^T\left(t\right)R_{kj}{u}_j\left(t\right))dt\right].\hfill \end{array}$$

(2)

We make the following assumption regarding the weights matrices in (2):

H.$G_k\ge 0,$$M_k\ge 0,$$R_{kk}>0,$ and $R_{kl}\ge 0,$ with $k,l=1,\dots ,L,$ and $l\ne k.$

Here we generalize Definition 2.1 given in [23].

Definition 1.

The L-tuple of admissible strategies $({\tilde{u}}_1(·),{\tilde{u}}_2(·),\dots ,{\tilde{u}}_L(·))$ is said to achieve a Nash equilibrium for the differential game described by the controlled system (1), the cost function (2), and the class of the admissible strategies $\mathcal{U}={\mathcal{U}}_1\times {\mathcal{U}}_2\times \cdots \times {\mathcal{U}}_L$, if for all $u_k(·)\in {\mathcal{U}}_k$, $k=1,\dots ,L$ we have

$$\begin{array}{c}\hfill J_k(t_0,x_0;{\tilde{u}}_1,{\tilde{u}}_2,\dots ,{\tilde{u}}_L)\le J_k(t_0,x_0;{\tilde{u}}_1,{\tilde{u}}_2,\dots .,{\tilde{u}}_{k-1},u_k,{\tilde{u}}_{k+1},\dots ,{\tilde{u}}_L).\end{array}$$

(3)

In this paper we consider a special class of closed-loop admissible strategies in which the states $x\left(t\right)$ of the dynamical system are available for measurement at the discrete-times $0\le t_0<t_1<\dots <t_{N-1}<t_N=t_f$, and the set of admissible strategies consists of piecewise constant stochastic processes of the form

$$u_k\left(t\right)=F_k\left(j\right)x\left(t_j\right),t_j\le t<t_{j+1},j=0,1,\dots ,N-1,$$

(4)

with $F_k\left(j\right)\in {\mathbb{R}}^{m_k\times n}$ are arbitrary matrices.

Our aim is to investigate the problem of designing a Nash equilibrium strategy in the class of piecewise constant admissible strategies of type (4) (the closed-loop admissible strategies), for a LQ differential game described by a dynamical system of type (1), under the performance criteria (2). Moreover, we also present a method for the numerical computation of the feedback gains of the equilibrium strategy.

We denote ${\tilde{\mathcal{U}}}^{pc}={\tilde{\mathcal{U}}}_1^{pc}\times {\tilde{\mathcal{U}}}_2^{pc}\times \dots \times {\tilde{\mathcal{U}}}_L^{pc}$ the set of the piecewise constant admissible strategies of type (4).

2.2. The Equivalent Problem

Define $v_k:[t_0,t_f]\to {\mathbb{R}}^{m_k}$ by $v_k\left(t\right)=u_k\left(j\right)$, $t_j\le t<t_{j+1},j=0,1,\dots ,N-1,$ where $u_k\left(j\right)$ are arbitrary $m_k$-dimensional random vectors with finite second moments. If $x\left(t\right)$ is the solution of system (1) determined by the piecewise constant inputs $v_k(·)$, we set $\xi \left(t\right)={(x^T\left(t\right)v_1^T\left(t\right)\dots v_L^T\left(t\right))}^T\in {\mathbb{R}}^{n+m},m={\sum }_{k=1}^L{m}_k$.

Direct calculations show that $\xi \left(t\right)$ is the solution of the initial value problem (IVP) associated to a linear stochastic system with finite jumps often called system controlled by impulses:

$$\begin{array}{cc}\hfill d\xi \left(t\right)& =\mathbf{A}\xi \left(t\right)dt+\mathbf{C}\xi \left(t\right)dw\left(t\right),t_j\le t<t_{j+1}\hfill \end{array}$$

(5a)

$$\begin{array}{cc}\hfill \xi \left(t_j^{+}\right)& ={\mathbf{A}}_d\xi \left(t_j\right)+\sum _{k=1}^L{\mathbf{B}}_{dk}{u}_k\left(j\right),j=0,1,\dots ,N-1,\hfill \end{array}$$

(5b)

$$\begin{array}{cc}\hfill \xi \left(t_0\right)& ={(x_0^T{0}^T\dots 0^T)}^T,\hfill \end{array}$$

(5c)

under the notations:

$$\begin{array}{cc}\hfill & \mathbf{A}=\left(\begin{array}{ccccc}A& B_1& B_2& \cdots & B_L\\ 0_{mn}& 0_{m{m}_1}& 0_{m{m}_2}& \cdots & 0_{m{m}_L}\end{array}\right),\hfill \\ \hfill & \mathbf{C}=\left(\begin{array}{ccccc}C& D_1& D_2& \cdots & D_L\\ 0_{mn}& 0_{m{m}_1}& 0_{m{m}_2}& \cdots & 0_{m{m}_L}\end{array}\right),\hfill \\ \hfill & {\mathbf{A}}_d=\left(\begin{array}{ccccc}{I}_n& 0_{n{m}_1}& 0_{n{m}_2}& \cdots & 0_{n{m}_l}\\ 0_{mn}& 0_{m{m}_1}& 0_{m{m}_2}& \cdots & 0_{m{m}_L}\end{array}\right),\hfill \\ \hfill & {\mathbf{B}}_{dk}={\left(\begin{array}{c}{0}_{n{m}_k}^T{0}_{m_1{m}_k}^T\cdots 0_{m_{k-1}{m}_k}^T{I}_{m_k}{0}_{m_{k+1}{m}_k}^T\cdots 0_{m_L{m}_k}^T\hfill \end{array}\right)}^T,\hfill \end{array}$$

(6)

where $0_{pq}$ denotes the zero matrix of size $p\times q$.

The performance criteria (2) becomes

$$\begin{array}{cc}\hfill J_k(t_0,{\xi }_0;{\mathbf{u}}_1,{\mathbf{u}}_2,\dots ,{\mathbf{u}}_L)=& \mathbb{E}[{\xi }^T\left(t_f\right){\mathbf{G}}_k\xi \left(t_f\right)+\underset{t_0}{\overset{t_f}{\int }}{\xi }^T\left(t\right){\mathbf{M}}_k\xi \left(t\right)dt]\hfill \\ & +\sum _{j=0}^{N-1}\mathbb{E}[\sum _{i=1}^L{u}_i^T\left(j\right){\mathbf{R}}_{ki}\left(j\right)u_i\left(j\right)],\hfill \end{array}$$

(7)

for all ${\mathbf{u}}_k=(u_k\left(0\right),\dots ,u_k(N-1)),$$u_k\left(j\right)$ are $m_k$-dimensional random vectors ${\mathcal{F}}_{t_j}$-measurable such that

$$\mathbb{E}\left[\right|u_k\left(j\right){|}^2]<\infty .$$

Throughout the paper ${\mathcal{F}}_t$ denotes the $\sigma$-algebra generated by the random variables $w\left(s\right),0\le s\le t$. The matrices in (7) can be written as

$$\begin{array}{cc}\hfill & {\mathbf{G}}_k=\mathrm{diag}\left(G_{k}0\right)\in {\mathbb{R}}^{(n+m)\times (n+m)}\hfill \\ \hfill & {\mathbf{M}}_k=\mathrm{diag}\left(M_{k}0\right)\in {\mathbb{R}}^{(n+m)\times (n+m)}\hfill \\ \hfill & {\mathbf{R}}_{ki}\left(j\right)=(t_{j+1}-t_j)R_{ki}.\hfill \end{array}$$

(8)

Let ${\mathcal{U}}^{sd}={\mathcal{U}}_1^{sd}\times {\mathcal{U}}_2^{sd}\times \cdots \times {\mathcal{U}}_L^{sd}$ be the set of the inputs of the form of sampled data linear state feedback, i.e., $\mathbf{u}=({\mathbf{u}}_1,{\mathbf{u}}_2,\dots ,{\mathbf{u}}_L)\in {\mathcal{U}}^{sd}$ if and only if ${\mathbf{u}}_k=(u_k\left(0\right),\dots ,u_k(N-1))$ with

$$u_k\left(j\right)={\mathbf{F}}_k\left(j\right)\xi \left(t_j\right),0\le j\le N-1,$$

(9)

where ${\mathbf{F}}_k\left(j\right)\in {\mathbb{R}}^{m_k\times (n+m)}$ are arbitrary matrices and $\xi \left(t_j\right)$ are the values at the time instants $t_j$ of the solution of the following IVP:

$$\begin{array}{cc}\hfill d\xi \left(t\right)& =\mathbf{A}\xi \left(t\right)dt+\mathbf{C}\xi \left(t\right)dw\left(t\right),t_j<t\le t_{j+1}\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill \xi (t_j^{+})& =({\mathbf{A}}_d+\sum _{k=1}^L{\mathbf{B}}_{dk}{\mathbf{F}}_k\left(j\right))\xi \left(t_j\right),j=0,1,\dots ,N-1,\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill \xi \left(t_0\right)& ={\xi }_0\in {\mathbb{R}}^{n+m}.\hfill \end{array}$$

(10c)

Let ${\mathrm{\Phi }}_k$ be a matrix valued sequence of the form

$$\begin{array}{c}\hfill {\mathrm{\Phi }}_k=({\mathbf{F}}_k\left(0\right),{\mathbf{F}}_k\left(1\right),\dots ,{\mathbf{F}}_k(N-1)),\end{array}$$

(11)

where ${\mathbf{F}}_k\left(i\right)\in {\mathbb{R}}^{m_k\times (n+m)}$ are arbitrary matrices. We consider the set

$$\begin{array}{c}\hfill {\mathcal{U}}_{\mathrm{\Phi }}^{sd}=\{({\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,\dots ,{\mathrm{\Phi }}_L):{\mathrm{\Phi }}_k\mathrm{are}\mathrm{arbitrary}\mathrm{sequences}\mathrm{defined}\mathrm{as}\mathrm{in}\left(11\right)\}.\end{array}$$

(12)

Remark 1.

By (9) and (10), there is a one to one correspondence between the sets ${\mathcal{U}}^{sd}$ and ${\mathcal{U}}_{\mathrm{\Phi }}^{sd}$. Each ${\mathbf{u}}_k$ from ${\mathcal{U}}_k^{sd}$ can be identified with the sequence ${\mathrm{\Phi }}_k=({\mathrm{\Phi }}_k\left(0\right),{\mathrm{\Phi }}_k\left(1\right),\dots ,{\mathrm{\Phi }}_k(N-1))$ of its feedback matrices.

Based on this remark we can rewrite the performance criterion (7) as:

$$\begin{array}{cc}\hfill {\mathcal{J}}_k(t_0,{\xi }_0;{\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,\dots ,{\mathrm{\Phi }}_L)=& \mathbb{E}[{\xi }^T\left(t_f\right){\mathbf{G}}_k\xi \left(t_f\right)+\underset{t_0}{\overset{t_f}{\int }}{\xi }^T\left(t\right){\mathbf{M}}_k\xi \left(t\right)dt]\hfill \\ & +\sum _{j=0}^{N-1}\mathbb{E}[\sum _{i=1}^L{\xi }^T\left(t_j\right){\mathbf{F}}_i^T\left(j\right){\mathbf{R}}_{ki}\left(j\right){\mathbf{F}}_i\left(j\right)\xi \left(t_j\right)],\hfill \end{array}$$

(13)

for all $({\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,\dots ,{\mathrm{\Phi }}_L)\in {\mathcal{U}}_{\mathrm{\Phi }}^{sd}$.

Similarly to Definition 1, one can define a Nash equilibrium strategy for the LQ differential game described by the controlled system (5), the performance criteria (13) and the class of admissible strategies ${\mathcal{U}}_{\mathrm{\Phi }}^{sd}$ described by (12).

Definition 2.

The L-tuple of admissible strategies $({\tilde{\mathrm{\Phi }}}_1,{\tilde{\mathrm{\Phi }}}_2,\dots ,{\tilde{\mathrm{\Phi }}}_L)$ is said to achieve a Nash equilibrium for the differential game described by the controlled system (5), the cost function (13), and the class of the admissible strategies ${\mathcal{U}}_{\mathrm{\Phi }}^{sd}$, if for all $({\mathrm{\Phi }}_1,{\mathrm{\Phi }}_2,\dots ,{\mathrm{\Phi }}_L)\in {\mathcal{U}}_{\mathrm{\Phi }}^{sd}$, we have

$$\begin{array}{c}\hfill {\mathcal{J}}_k(t_0,{\xi }_0;{\tilde{\mathrm{\Phi }}}_1,{\tilde{\mathrm{\Phi }}}_2,\dots ,{\tilde{\mathrm{\Phi }}}_L)\le {\mathcal{J}}_k(t_0,{\xi }_0;{\tilde{\mathrm{\Phi }}}_1,{\tilde{\mathrm{\Phi }}}_2,\dots .,{\tilde{\mathrm{\Phi }}}_{k-1},{\mathrm{\Phi }}_k,{\tilde{\mathrm{\Phi }}}_{k+1},\dots ,{\tilde{\mathrm{\Phi }}}_L).\end{array}$$

(14)

Remark 2.

(a)

Based on the Remark 1 we may infer that if $({\tilde{\mathrm{\Phi }}}_1,{\tilde{\mathrm{\Phi }}}_2,\dots ,{\tilde{\mathrm{\Phi }}}_L)$ is an equilibrium strategy in the sense of the Definition 2, then $({\tilde{\mathbf{u}}}_1,{\tilde{\mathbf{u}}}_2,\dots ,{\tilde{\mathbf{u}}}_L)$ given by (9) using the matrix components of ${\tilde{\mathrm{\Phi }}}_k$, provides an equilibrium strategy for the LQ differential game described by (5), (7) and the family of admissible strategies ${\mathcal{U}}^{sd}$.

(b)

Among the feedback matrices from (9) some have the form:

$$\begin{array}{c}\hfill {\mathbf{F}}_k\left(j\right)=\left(F_k\left(j\right)0_{m_{k}m}\right),\end{array}$$

(15)

where $F_k\left(j\right)\in {\mathbb{R}}^{m_k\times n}$. Hence, some admissible strategies (9) are of type (4). Hence, if the feedback matrices of the Nash equilibrium strategy $({\tilde{\mathrm{\Phi }}}_1,{\tilde{\mathrm{\Phi }}}_2,\dots ,{\tilde{\mathrm{\Phi }}}_L)$ have the structure given in (15), then the strategy of type (9) with these feedback matrices provide the Nash equilibrium strategy for the LQ differential game described by (1), (2) and (4).

To obtain explicit formulae for the feedback matrices of a Nash equilibrium strategy of type (9) (or, equivalently (11), (12)), we use the following system of matrix linear differential equations (MLDEs) with jumps and algebraic constraints:

$$\begin{array}{c}\hfill -{\dot{P}}_k\left(t\right)={\mathbf{A}}^T{P}_k\left(t\right)+P_k\left(t\right)\mathbf{A}+{\mathbf{C}}^T{P}_k\left(t\right)\mathbf{C}+{\mathbf{M}}_k,t_j\le t<t_{j+1}\\ \hfill P_k\left(t_j^{-}\right)={\mathbf{A}}_{[-k]}^T\left(j\right)P_k\left(t_j\right){\mathbf{A}}_{[-k]}\left(j\right)-{\mathbf{A}}_{[-k]}^T\left(j\right)P_k\left(t_j\right){\mathbf{B}}_{dk}\times \end{array}$$

(16a)

$$\begin{array}{c}\hfill \times {({\mathbf{R}}_{kk}\left(j\right)+{\mathbf{B}}_{dk}^T{P}_k\left(t_j\right){\mathbf{B}}_{dk})}^{†}{\mathbf{B}}_{dk}^T{P}_k\left(t_j\right){\mathbf{A}}_{[-k]}\left(j\right)+{\mathbf{M}}_{[-k]}\left(j\right)\\ \hfill \sum _{i=1}^{k-1}{\mathbf{B}}_{dk}^T{P}_k\left(t_j\right){\mathbf{B}}_{di}{\mathbf{F}}_i\left(j\right)+({\mathbf{R}}_{kk}\left(j\right)+{\mathbf{B}}_{dk}^T{P}_k\left(t_j\right){\mathbf{B}}_{dk}){\mathbf{F}}_k\left(j\right)\end{array}$$

(16b)

$$\begin{array}{c}\hfill +\sum _{i=k+1}^L{\mathbf{B}}_{dk}^T{P}_k\left(t_j\right){\mathbf{B}}_{di}{\mathbf{F}}_i\left(j\right)=-{\mathbf{B}}_{dk}^T{P}_k\left(t_j\right){\mathbf{A}}_d\end{array}$$

(16c)

$$\begin{array}{c}\hfill P_k\left(t_N^{-}\right)={\mathbf{G}}_{\mathbf{k}},\mathbf{k}=\mathbf{1},\dots ,\mathbf{L},\end{array}$$

(16d)

where we have denoted

$${\mathbf{A}}_{[-k]}\left(j\right)={\mathbf{A}}_d+\sum _{i=1,i\ne k}^L{\mathbf{B}}_{di}{\mathbf{F}}_i\left(j\right)$$

(17)

and

$${\mathbf{M}}_{[-k]}\left(j\right)=\sum _{i=1,i\ne k}^L{\mathbf{F}}_i^T\left(j\right){\mathbf{R}}_{ki}\left(j\right){\mathbf{F}}_i\left(j\right),$$

(18)

while the superscript † denotes the generalized inverse of a matrix.

Remark 3.

A solution of the terminal value problem (TVP) with algebraic constraints (16) is a 2L-uple of the form $(P_1(·),P_2(·),\dots ,P_L(·);{\mathbf{F}}_1(·),{\mathbf{F}}_2(·),\dots ,{\mathbf{F}}_L(·))$ where, for each $1\le k\le L$, $P_k(·)$ is a solution of the TVP (16a), (16b), (16d) and ${\mathbf{F}}_k\left(j\right)\in {\mathbb{R}}^{m_k\times (n+m)}$, $0\le j\le N-1$. On the interval $[t_{N-1},t_N]$, $P_k(·)$ is the solution of the TVP described by the perturbed Lyapunov-type equation from (16a) and the terminal value given in (16d). On each interval $[t_{j-1},t_j)$, $j\le N-1$, the terminal value $P_k\left(t_j^{-}\right)$ of $P_k(·)$ is computed via (16b) together with (17) and (18) provided that $({\mathbf{F}}_1\left(j\right),{\mathbf{F}}_2\left(j\right),\dots ,{\mathbf{F}}_L\left(j\right))$ to be obtained as solution of (16c). So, the TVPs solved by $P_k(·),1\le k\le L$ are interconnected via (16c).

To facilitate the statement of the main result of this section, we rewrite (16c) in a compact form as:

$$\begin{array}{c}\hfill {\mathrm{\Pi }}_d(P_1\left(t_j\right),\dots ,P_L\left(t_j\right),j)\mathbb{F}\left(j\right)=-{\mathrm{\Gamma }}_d(P_1\left(t_j\right),\dots ,P_L\left(t_j\right)),\end{array}$$

(19)

where $\mathbb{F}\left(j\right)={({\mathbf{F}}_1^T\left(j\right){\mathbf{F}}_2^T\left(j\right)\dots {\mathbf{F}}_L^T\left(j\right))}^T$ and the matrices ${\mathrm{\Pi }}_d(P_1\left(t_j\right),\dots ,$$P_L\left(t_j\right),j)$ and ${\mathrm{\Gamma }}_d(P_1\left(t_j\right),\dots ,P_L\left(t_j\right))$ are obtained using the block components of (16c).

2.3. Sampled Data Nash Equilibrium Strategy

First we derive a necessary and sufficient condition for the existence of an equilibrium strategy of type (9) for the LQ differential game given by the controlled system (5), the performance criteria (7) and the set of the admissible strategies ${\mathcal{U}}^{sd}$. To this end we adapt the argument used in the proof of ([22], Theorem 4).

We prove:

Theorem 1.

Under the assumption $\mathit{H}.$ the following are equivalent:

(i)

the LQ differential game defined by the dynamical system controlled by impulses (5), the performance criteria (7) and the class of the admissible strategies of type (9) has a Nash equilibrium strategy

$$\begin{array}{c}\hfill {\tilde{u}}_k\left(j\right)={\tilde{\mathbf{F}}}_k\left(j\right)\xi \left(t_j\right),0\le j\le N-1,1\le k\le L.\end{array}$$

(20)

(ii)

the TVP with constraints (16) has a solution $({\tilde{P}}_1(·),{\tilde{P}}_2(·),\dots ,{\tilde{P}}_L(·);{\tilde{\mathbf{F}}}_1(·),{\tilde{\mathbf{F}}}_2(·),\dots ,{\tilde{\mathbf{F}}}_L(·))$ defined on the whole interval $[t_0,t_f]$ and satisfying the conditions below for $0\le j\le N-1$:

$$\begin{array}{cc}\hfill {\mathrm{\Pi }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right),j)& {\mathrm{\Pi }}_d{({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right),j)}^{†}{\mathrm{\Gamma }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right))=\hfill \\ \hfill & ={\mathrm{\Gamma }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right)).\hfill \end{array}$$

(21)

If condition (21) holds, then the feedback matrices of a Nash equilibrium strategy of type (9) are the matrix components of the solution of the TVP (16) and are given by

$$\begin{array}{cc}\hfill & {({\tilde{\mathbf{F}}}_1^T\left(j\right){\tilde{\mathbf{F}}}_2^T\left(j\right)\dots {\tilde{\mathbf{F}}}_L^T\left(j\right))}^T=-{\mathrm{\Pi }}_d{({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right),j)}^{†}{\mathrm{\Gamma }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right)),\hfill \\ & 0\le j\le N-1.\hfill \end{array}$$

(22)

The minimal value of the cost of the k-th player is ${\xi }_0^T{\tilde{P}}_k\left(t_0^{-}\right){\xi }_0$.

Proof. 

From (14) and Remarks 1 and 2(a), one can see that a strategy of type (9) defines a Nash equilibrium strategy for the linear differential game described by the controlled system (5), the performance criteria (7) (or equivalently (13)) if and only if for each $1\le k\le L$ the optimal control problem described by the controlled system

$$\begin{array}{cc}\hfill d\xi \left(t\right)& =\mathbf{A}\xi \left(t\right)dt+\mathbf{C}\xi \left(t\right)dw\left(t\right),t_j<t\le t_{j+1}\hfill \end{array}$$

(23a)

$$\begin{array}{cc}\hfill \xi \left(t_j^{+}\right)& ={\tilde{\mathbf{A}}}_{[-k]}\left(j\right)\xi \left(t_j\right)+{\mathbf{B}}_{dk}{u}_k\left(j\right),j=0,1,\dots ,N-1,\hfill \end{array}$$

(23b)

$$\begin{array}{cc}\hfill \xi \left(t_0\right)& ={\xi }_0\in {\mathbb{R}}^{n+m},\hfill \end{array}$$

(23c)

and the quadratic functional

$$\begin{array}{cc}\hfill {\mathcal{J}}_{[-k]}(t_0,{\xi }_0;{\mathbf{u}}_k)=& \mathbb{E}[{\xi }^T\left(t_f\right){\mathbf{G}}_k\xi \left(t_f\right)+\underset{t_0}{\overset{t_f}{\int }}{\xi }^T\left(t\right){\mathbf{M}}_k\xi \left(t\right)dt]\hfill \\ \hfill & +\sum _{j=0}^{N-1}\mathbb{E}[{\xi }^T\left(t_j\right){\tilde{\mathbf{M}}}_{[-k]}\left(j\right)\xi \left(t_j\right)+u_k^T\left(j\right){\mathbf{R}}_{kk}\left(j\right)u_k\left(j\right)],\hfill \end{array}$$

(24)

has an optimal control in a state feedback form. The controlled system (23) and the performance criterion (24) are obtained substituting ${\tilde{u}}_{\ell }\left(j\right)={\tilde{\mathbf{F}}}_{\ell }\left(j\right)\xi \left(t_j\right)$, $1\le k,\ell \le L$, $\ell \ne k$ in (5) and (7), respectively. ${\tilde{\mathbf{A}}}_{[-k]}$ and ${\tilde{\mathbf{M}}}_{[-k]}$ are computed as in (17) and (18), respectively, but with ${\mathbf{F}}_i\left(j\right)$ replaced by ${\tilde{\mathbf{F}}}_i\left(j\right)$.

To obtain necessary and sufficient conditions for the existence of the optimal control in a linear state feedback form we employ the results proved in [20]. First, notice that in the case of the optimal control problem (23)–(24), the TVP (16a), (16b), (16d) plays the role of the TVP (19)–(23) from [20].

Using Theorem 3 in [20] in the case of the optimal control problem described by (23) and (24) we deduce that the existence of the Nash equilibrium strategy of the form (9) for the differential game described by the controlled system (5), the performance criteria (7) (or its equivalent form (13)), is equivalent to the solvability of the TVP described by (16). The feedback matrix ${\tilde{\mathbf{F}}}_k\left(j\right)$ of the optimal control solves the equation:

$$\begin{array}{c}\hfill ({\mathbf{R}}_{kk}\left(j\right)+{\mathbf{B}}_{dk}^T{\tilde{P}}_k\left(t_j\right){\mathbf{B}}_{dk}){\tilde{\mathbf{F}}}_k\left(j\right)=-{\mathbf{B}}_{dk}^T{\tilde{P}}_k\left(t_j\right){\tilde{\mathbf{A}}}_{[-k]}\left(j\right).\end{array}$$

(25)

Substituting the formulae of ${\tilde{\mathbf{A}}}_{[-k]}$ in (25) we deduce that the feedback matrices of the Nash equilibrium strategy solve an equation of the form (16c) written for ${\tilde{\mathbf{F}}}_k\left(j\right)$ instead of ${\mathbf{F}}_k\left(j\right)$. This equation may be written in the compact form:

$$\begin{array}{c}\hfill {\mathrm{\Pi }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right),j)\tilde{\mathbb{F}}\left(j\right)=-{\mathrm{\Gamma }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right)),\end{array}$$

(26)

where $\tilde{\mathbb{F}}\left(j\right)={({\tilde{\mathbf{F}}}_1^T\left(j\right){\tilde{\mathbf{F}}}_2^T\left(j\right)\dots {\tilde{\mathbf{F}}}_L^T\left(j\right))}^T$.

By Lemma 2.7 in [21] we deduce that the Equation (26) has a solution if and only if the condition (21) holds. A solution of the Equation (26) is given by (22). The minimal value of the cost for the k-th player is obtained from Theorem 1 in [20] applied in the case of the optimal control problem described by (23), (24). Thus the proof is complete.□

Remark 4.

When the matrices ${\mathrm{\Pi }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right),j)$ are invertible, the conditions (21) are satisfied automatically. In this case, the feedback matrices ${\tilde{\mathbf{F}}}_k\left(j\right)$ of a Nash equilibrium strategy of type (20) are obtained as the unique solution of the Equation (22), because in this case, the generalized inverse of each matrix ${\mathrm{\Pi }}_d({\tilde{P}}_1\left(t_j\right),\dots ,{\tilde{P}}_L\left(t_j\right),j)$, $0\le j\le N-1$ is the usual inverse.

Combining (6) and (16c), we deduce that the matrices ${\tilde{\mathbf{F}}}_k\left(j\right)$ provided by (22) have the structure ${\tilde{\mathbf{F}}}_k\left(j\right)=({\tilde{F}}_k\left(j\right)0_{m_{k}m})$. Hence, the Nash equilibrium strategy of the differential game described by the dynamical system (5), the performance criteria (7) and the admissible strategies of type (9) have the form

$${\tilde{u}}_k\left(j\right)=({\tilde{F}}_k\left(j\right)0_{m_{k}m})\xi \left(t_j\right)={\tilde{F}}_k\left(j\right)x\left(t_j\right),0\le j\le N-1.$$

Now we obtain the following Nash equilibrium strategy of the differential game.

Theorem 2.

Assume that the conditions $\mathbf{H}.$ and (ii) in Theorem 1 are satisfied. Then, a Nash equilibrium strategy in a state feedback form with sampled measurements of type (4) of the differential game described by the dynamical system (1) and the performance criteria (2) are given by:

$$\begin{array}{c}\hfill {\tilde{u}}_k\left(t\right)={\tilde{F}}_k\left(j\right)x\left(t_j\right),t_j\le t\le t_{j+1},0\le j\le N-1,1\le k\le L.\end{array}$$

(27)

The feedback matrices ${\tilde{F}}_k\left(j\right)$ from (27) are given by the first n columns of the matrices ${\tilde{\mathbf{F}}}_k\left(j\right)$, which are obtained as solutions of Equation (26). In (27), $x\left(t_j\right)$ are the values measured at the times $t_j$, $0\le j\le N-1,$ of the solution of the closed-loop system obtained when (27) is plugged into (1). The minimal value of the cost (2) associated to the k-th player is given by

$$\left(x_0^T{0}_{nm}\right){\tilde{P}}_k\left(t_0^{-}\right){\left(x_0^T{0}_{nm}\right)}^T.$$

In the next section, we present an algorithm which allows the numerical computation of the matrices ${\tilde{F}}_k\left(j\right)$ arising in (27) for an LQ differential game with two players.

3. Numerical Computations and the Algorithm

In what follows we assume that $L=2$ and $t_{j+1}-t_j=h>0.0\le j\le N-1.$

We propose a numerical approach to compute the optimal strategies

$${\tilde{u}}_k\left(j\right)={\tilde{F}}_k\left(j\right)\tilde{x}\left(t_j\right),j=0,1,\dots ,N-1.$$

(28)

The algorithm consists of two steps:

• We first compute the feedback matrices ${\tilde{F}}_k\left(j\right),$$j=0,1,\dots ,N-1,$$k=1,2$ of the Nash equilibrium strategy, based on the solution ${\tilde{P}}_1(·),{\tilde{P}}_2(·)$:

  $$-{\dot{P}}_k\left(t\right)={\mathbf{A}}^T{P}_k\left(t\right)+P_k\left(t\right)\mathbf{A}+{\mathbf{C}}^T{P}_k\left(t\right)\mathbf{C}+{\mathbf{M}}_k,t_j\le t<t_{j+1}.$$

  (29)
  STEP 1.A. We take $P_k\left(t_N^{-}\right)={\mathbf{G}}_k,k=1,2,$ and compute

  $$\begin{array}{c}\hfill {\tilde{P}}_k\left(t_{N-1}\right)=e^{{\mathcal{L}}^{*}h}\left[{\mathbf{G}}_k\right]+{\mathbb{M}}_k,k=1,2,\mathrm{where}\end{array}$$

  (30)

  $$\begin{array}{c}\hfill {\mathbb{M}}_k=h{\mathbf{M}}_k+\frac{h^2}{2}{\mathcal{L}}^{*}\left[{\mathbf{M}}_k\right]+\frac{h^3}{6}{\left({\mathcal{L}}^{*}\right)}^2\left[{\mathbf{M}}_k\right]+\cdots +\frac{h^p}{p!}{\left({\mathcal{L}}^{*}\right)}^{p-1}\left[{\mathbf{M}}_k\right]\end{array}$$

  (31)

  $$e^{{\mathcal{L}}^{*}h}\left[\mathbf{X}\right]\backsimeq \sum _{\ell =0}^q\frac{h^{\ell }}{\ell !}{\mathcal{L}}^{*\ell }\left[\mathbf{X}\right]=\mathbf{X}+h{\mathcal{L}}^{*}\left[\mathbf{X}\right]+\frac{h^2}{2}\left({\mathcal{L}}^{*}\right)\left[{\mathcal{L}}^{*}\left[\mathbf{X}\right]\right]+\dots +\frac{h^q}{q!}{\left({\mathcal{L}}^{*}\right)}^q\left[\mathbf{X}\right],$$

  with $p\ge 1$ and $q\ge 1$ sufficiently large.
  For the operator ${\mathcal{L}}^{*}\left[X\right]$ we have

  $${\mathcal{L}}^{*}\left[X\right]={\mathbf{A}}^{T}X+X\mathbf{A}+{\mathbf{C}}^{T}X\mathbf{C}$$

  (32)

  for all $X=X^T\in {\mathbb{R}}^{(n+m_1+m_2)\times (n+m_1+m_2)}$.
  The iterations ${\mathcal{L}}^{\ell }\left[\mathbf{X}\right]$ are computed from:

  $$\begin{array}{c}\hfill {\mathcal{L}}^{*\ell }\left[\mathbf{X}\right]={\mathbf{A}}^T{\mathcal{L}}^{*(\ell -1)}\left[\mathbf{X}\right]+{\mathcal{L}}^{*(\ell -1)}\left[\mathbf{X}\right]\mathbf{A}+{\mathbf{C}}^T{\mathcal{L}}^{*(\ell -1)}\left[\mathbf{X}\right]\mathbf{C}\end{array}$$

  (33)

  for $\ell \ge 1$ with ${\mathcal{L}}^0\left[\mathbf{X}\right]=\mathbf{X}$ where $\mathbf{X}=P_k(t_{j+1}^{-})$ or $\mathbf{X}={\mathbf{M}}_k$, respectively.
  We compute the feedback matrices ${\tilde{F}}_k(N-1)\in {\mathbb{R}}^{m_k\times n}$ as solutions of the linear equation

  $$\begin{array}{cc}\hfill & \left(\begin{array}{cc}{R}_{11}+h^{-1}{\tilde{P}}_{1,11}\left(t_{N-1}\right)& h^{-1}{\tilde{P}}_{1,12}\left(t_{N-1}\right)\\ h^{-1}{\tilde{P}}_{2,12}^T\left(t_{N-1}\right)& R_{22}+h^{-1}{\tilde{P}}_{2,22}\left(t_{N-1}\right)\end{array}\right)\left(\begin{array}{c}{\tilde{F}}_1(N-1)\\ {\tilde{F}}_2(N-1)\end{array}\right)=\hfill \\ \hfill & -\left(\begin{array}{c}{h}^{-1}{\tilde{P}}_{1,01}^T\left(t_{N-1}\right)\\ h^{-1}{\tilde{P}}_{2,02}^T\left(t_{N-1}\right)\end{array}\right)\hfill \end{array}$$

  (34)
  STEP 1.B. We set

  $${\tilde{\mathbf{F}}}_k(N-1)=({\tilde{F}}_k(N-1)00)\in {\mathbb{R}}^{m_k\times (n+m_1+m_2)},k=1,2.$$
  Next, we compute ${\tilde{P}}_k(t_{N-1}^{-}),$$k=1,2,$:

  $$\begin{array}{cc}\hfill & {\tilde{P}}_1\left(t_{N-1}^{-}\right)={({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(N-1))}^T{\tilde{P}}_1\left(t_{N-1}\right)({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(N-1))\hfill \\ \hfill & -{({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(N-1))}^T{\tilde{P}}_1\left(t_{N-1}\right){\mathbf{B}}_{d1}{(h{R}_{11}+{\mathbf{B}}_{d1}^T{\tilde{P}}_1\left(t_{N-1}\right){\mathbf{B}}_{d1})}^{-1}\hfill \\ \hfill & ·{\mathbf{B}}_{d1}^T{\tilde{P}}_1\left(t_{N-1}\right)({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(N-1))+h{\tilde{\mathbf{F}}}_2^T(N-1)R_{12}{\tilde{\mathbf{F}}}_2(N-1)\hfill \end{array}$$

  (35)

  and

  $$\begin{array}{cc}\hfill & {\tilde{P}}_2(t_{N-1}^{-})={({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(N-1))}^T{\tilde{P}}_2(t_{N-1})({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(N-1))\hfill \\ \hfill & -{({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(N-1))}^T{\tilde{P}}_2(t_{N-1}){\mathbf{B}}_{d2}{(h{R}_{22}+{\mathbf{B}}_{d2}^T{\tilde{P}}_2(t_{N-1}){\mathbf{B}}_{d2})}^{-1}\hfill \\ \hfill & ·{\mathbf{B}}_{d2}^T{\tilde{P}}_2(t_{N-1})({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(N-1))+h{\tilde{\mathbf{F}}}_1^T(N-1)R_{21}{\tilde{\mathbf{F}}}_1(N-1).\hfill \end{array}$$

  (36)
  STEP 2.A. Fix j such that $j\le N-2$. Assuming that ${\tilde{P}}_k(t_{j+1}^{-})$ have already been computed for a $j\le N-2$, $k=1,2$, we compute

  $$\begin{array}{c}\hfill {\tilde{P}}_k(t_j)=e^{{\mathcal{L}}^{*}h}[{\tilde{P}}_k(t_{j+1}^{-})]+{\mathbb{M}}_k,k=1,2,\end{array}$$

  (37)

  where ${\mathbb{M}}_k$ is computed as in (31).
  We compute the feedback gains ${\tilde{F}}_k(j)\in {\mathbb{R}}^{m_k\times n}$ as solution of the linear equation

  $$\begin{array}{c}\hfill \left(\begin{array}{cc}{R}_{11}+h^{-1}{\tilde{P}}_{1,11}\left(t_j\right)& h^{-1}{\tilde{P}}_{1,12}\left(t_j\right)\\ h^{-1}{\tilde{P}}_{2,12}^T\left(t_j\right)& R_{22}+h^{-1}{\tilde{P}}_{2,22}\left(t_j\right)\end{array}\right)\left(\begin{array}{c}{\tilde{F}}_1\left(j\right)\\ {\tilde{F}}_2\left(j\right)\end{array}\right)=-\left(\begin{array}{c}{h}^{-1}{\tilde{P}}_{1,01}^T\left(t_j\right)\\ h^{-1}{\tilde{P}}_{2,02}^T\left(t_j\right)\end{array}\right)\end{array}$$

  (38)
  STEP 2.B. Setting ${\tilde{\mathbf{F}}}_k(j)=\left({\tilde{F}}_k(j)00\right)\in {\mathbb{R}}^{m_k\times (n+m_1+m_2)}$, $k=1,2$ we compute ${\tilde{P}}_k(t_j^{-})$ as in the formulae below

  $$\begin{array}{cc}\hfill & {\tilde{P}}_1(t_j^{-})={({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(j))}^T{\tilde{P}}_1(t_j)({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(j))\hfill \\ \hfill & -{({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(j))}^T{\tilde{P}}_1(t_j){\mathbf{B}}_{d1}{(h{R}_{11}+{\mathbf{B}}_{d1}^T{\tilde{P}}_1(t_j){\mathbf{B}}_{d1})}^{-1}\hfill \\ \hfill & ·{\mathbf{B}}_{d1}^T{\tilde{P}}_1(t_j)({\mathbf{A}}_d+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2(j))+h{\tilde{\mathbf{F}}}_2^T(j)R_{12}{\tilde{\mathbf{F}}}_2(j)\hfill \end{array}$$

  (39)

  and

  $$\begin{array}{cc}\hfill & {\tilde{P}}_2(t_j^{-})={({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(j))}^T{\tilde{P}}_2(t_j)({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(j))\hfill \\ \hfill & -{({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(j))}^T{\tilde{P}}_2(t_j){\mathbf{B}}_{d2}{(h{R}_{22}+{\mathbf{B}}_{d2}^T{\tilde{P}}_2(t_j){\mathbf{B}}_{d2})}^{-1}\hfill \\ \hfill & {\mathbf{B}}_{d2}^T{\tilde{P}}_2(t_j)({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1(j))+h{\tilde{\mathbf{F}}}_1^T(j)R_{21}{\tilde{\mathbf{F}}}_1(j).\hfill \end{array}$$

  (40)
• In the second step, the computation of the optimal trajectory $\tilde{x}(t)$ involves the initial vector $x_0$ and the equilibrium strategy values $u_k(j),$$k=1,2.$
  Then, we illustrate the mean squares of the optimal trajectory $\mathbb{E}\left[\right|\tilde{x}(t){|}^2]$ and of the equilibrium strategy $\mathbb{E}\left[\right|{\tilde{u}}_k(t){|}^2],k=1,2$. We set $\tilde{\xi }(t)={({\tilde{x}}^T(t){\tilde{u}}_1^T(t){\tilde{u}}_2^T(t))}^T$ and define $X(t)=\mathbb{E}[\tilde{\xi }(t){\tilde{\xi }}^T(t)]$.
  We have $t\to X(t)$ solves the forward linear differential equation with finite jumps:

  $$\begin{array}{c}\hfill \dot{X}\left(t\right)=LX\left(t\right),t_j\le t<t_{j+1}.\end{array}$$

  (41)
  For $t_j=jh$ we write:

  $$\begin{array}{c}\hfill X\left(t_j^{+}\right)=({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1\left(j\right)+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2\left(j\right))X\left(t_j\right)·{({\mathbf{A}}_d+{\mathbf{B}}_{d1}{\tilde{\mathbf{F}}}_1\left(j\right)+{\mathbf{B}}_{d2}{\tilde{\mathbf{F}}}_2\left(j\right))}^T\end{array}$$

  (42)
  $0\le j\le N-1,t_j=jh$, where

  $$\begin{array}{c}\hfill LX=\mathbf{A}X+X{\mathbf{A}}^T+\mathbf{C}X{\mathbf{C}}^T.\end{array}$$

  (43)
  Then, we have used the values to make plots

  $$\begin{array}{cc}\hfill \mathbb{E}\left[\right|\tilde{x}(i\delta +jh){|}^2]& =Tr\left[X_{11}(i\delta +jh)\right]\hfill \\ \hfill \mathbb{E}\left[\right|{\tilde{u}}_1(i\delta +jh){|}^2]& =Tr\left[X_{22}(i\delta +jh)\right]\hfill \\ \hfill \mathbb{E}\left[\right|{\tilde{u}}_2(i\delta +jh){|}^2]& =Tr\left[X_{33}(i\delta +jh)\right],\hfill \end{array}$$

  where

  $$X(i\delta +jh)=\left(\begin{array}{ccc}{X}_{11}(i\delta +jh)& X_{12}(i\delta +jh)& X_{13}(i\delta +jh)\\ X_{12}^T(i\delta +jh)& X_{22}(i\delta +jh)& X_{23}(i\delta +jh)\\ X_{13}^T(i\delta +jh)& X_{23}^T(i\delta +jh)& X_{33}(i\delta +jh)\end{array}\right)$$

  such that $X_{11}(i\delta +jh)\in {\mathbb{R}}^{n\times n},X_{22}(i\delta +jh)\in {\mathbb{R}}^{m_1\times m_1}$ and $X_{33}(i\delta +jh)\in {\mathbb{R}}^{m_2\times m_2}$.

This algorithm enables us to compute the equilibrium strategies values $u_k\left(j\right)$ of the players. The experiments illustrate that the optimal strategies are piecewise constant, which seems to indicate that we have a stabilization effect.

Further, we consider two examples for the LQ differential game described by the dynamical system (1), the performance criteria (2) and the class of piecewise constant admissible strategies of type (28).

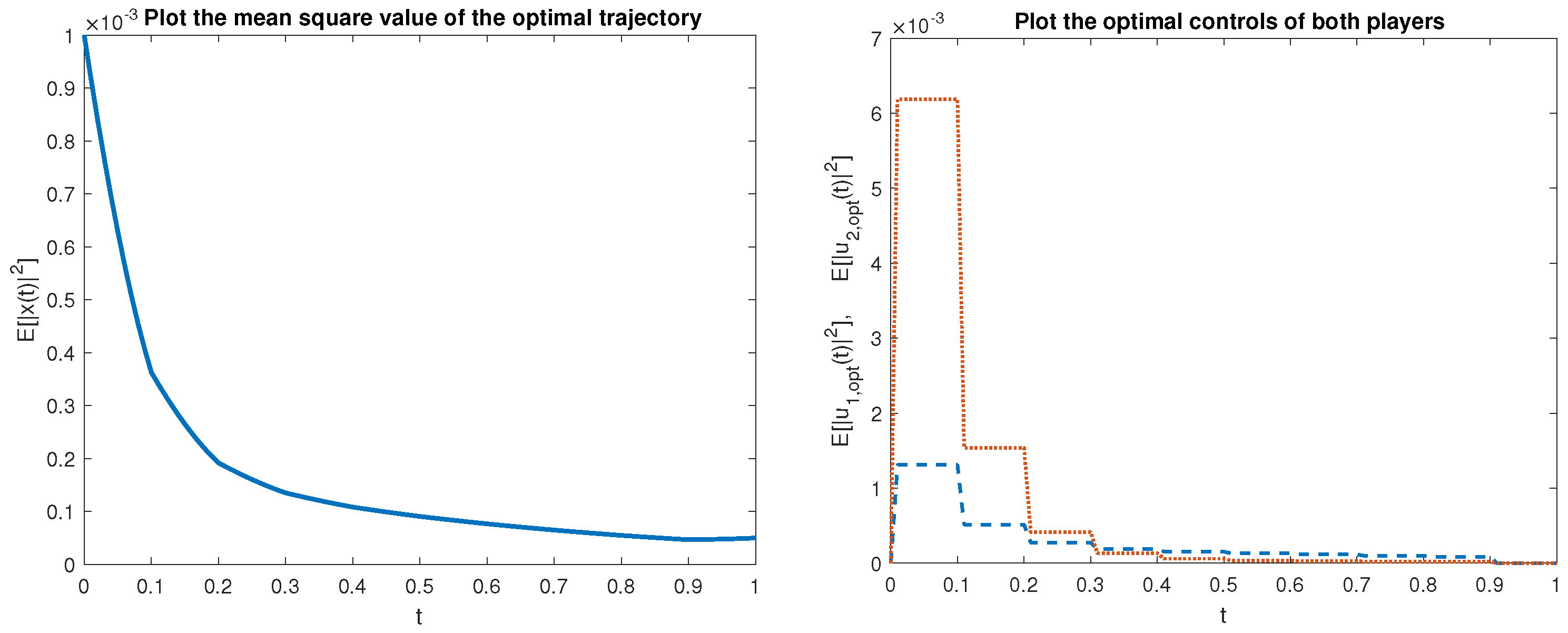
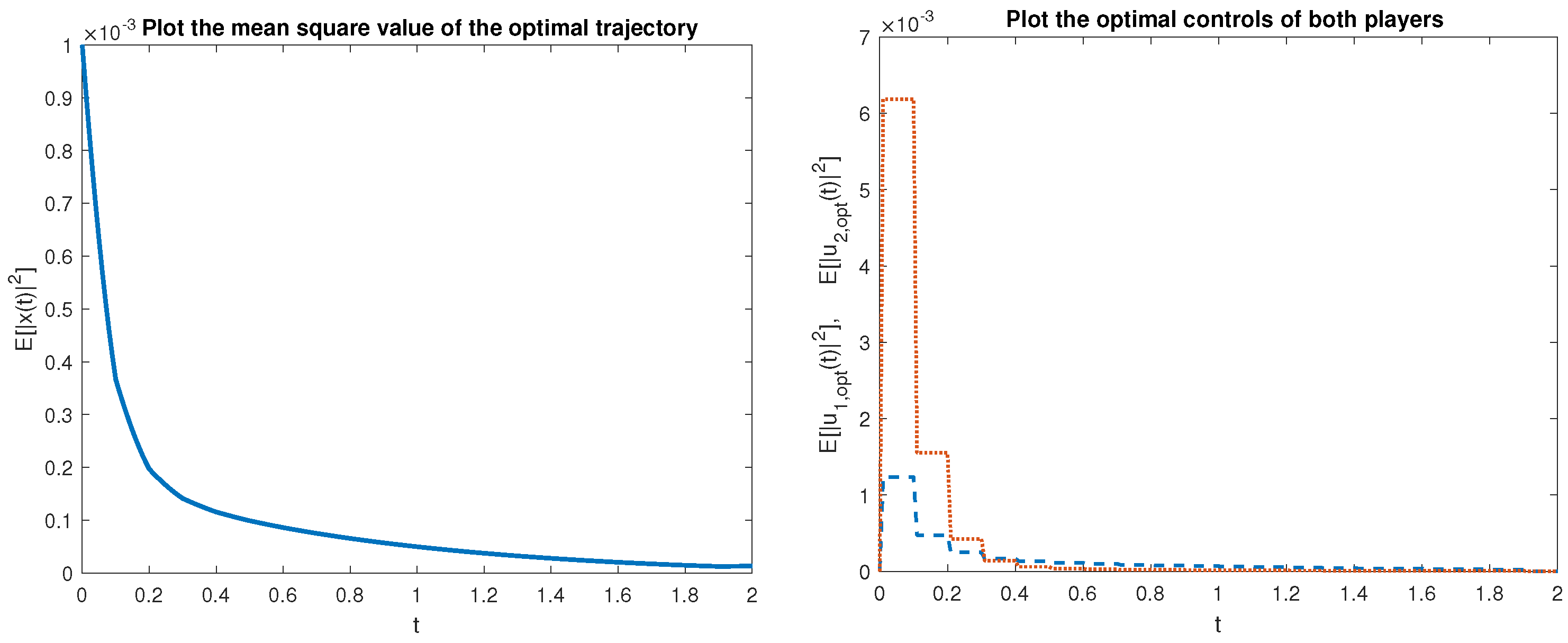
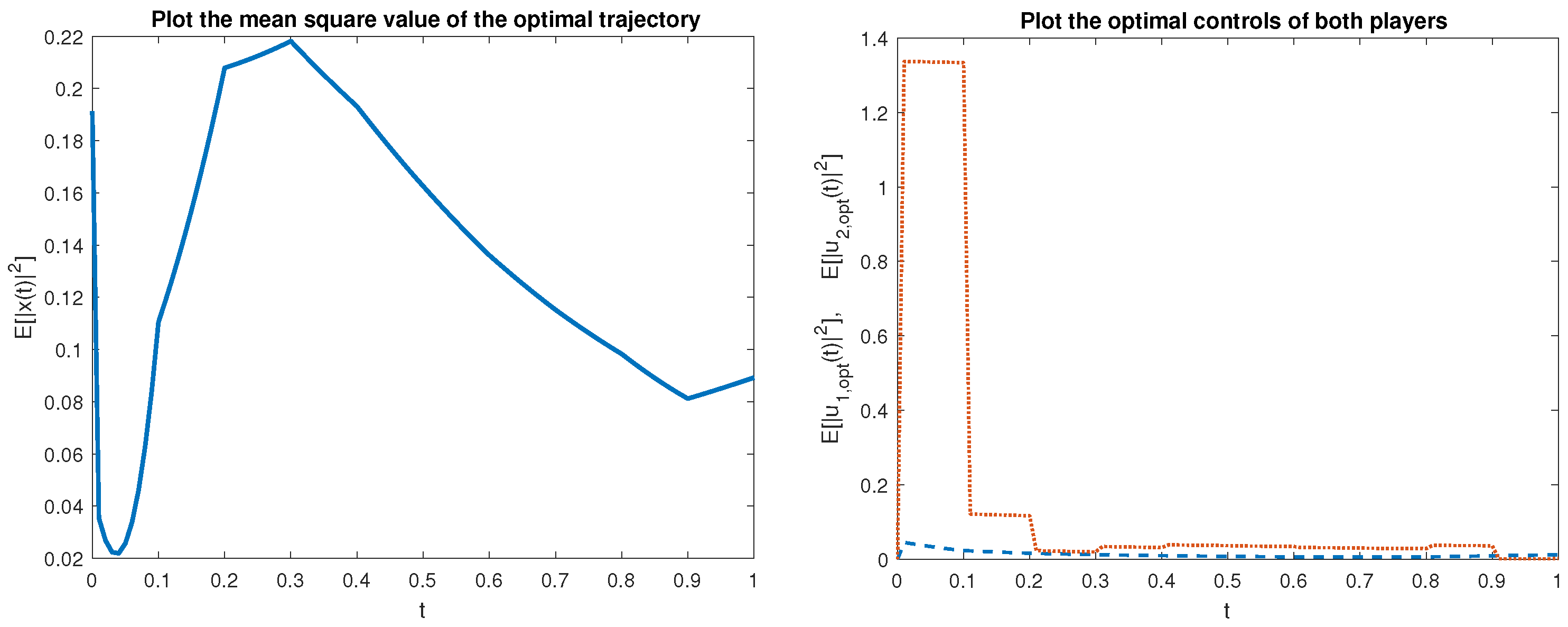
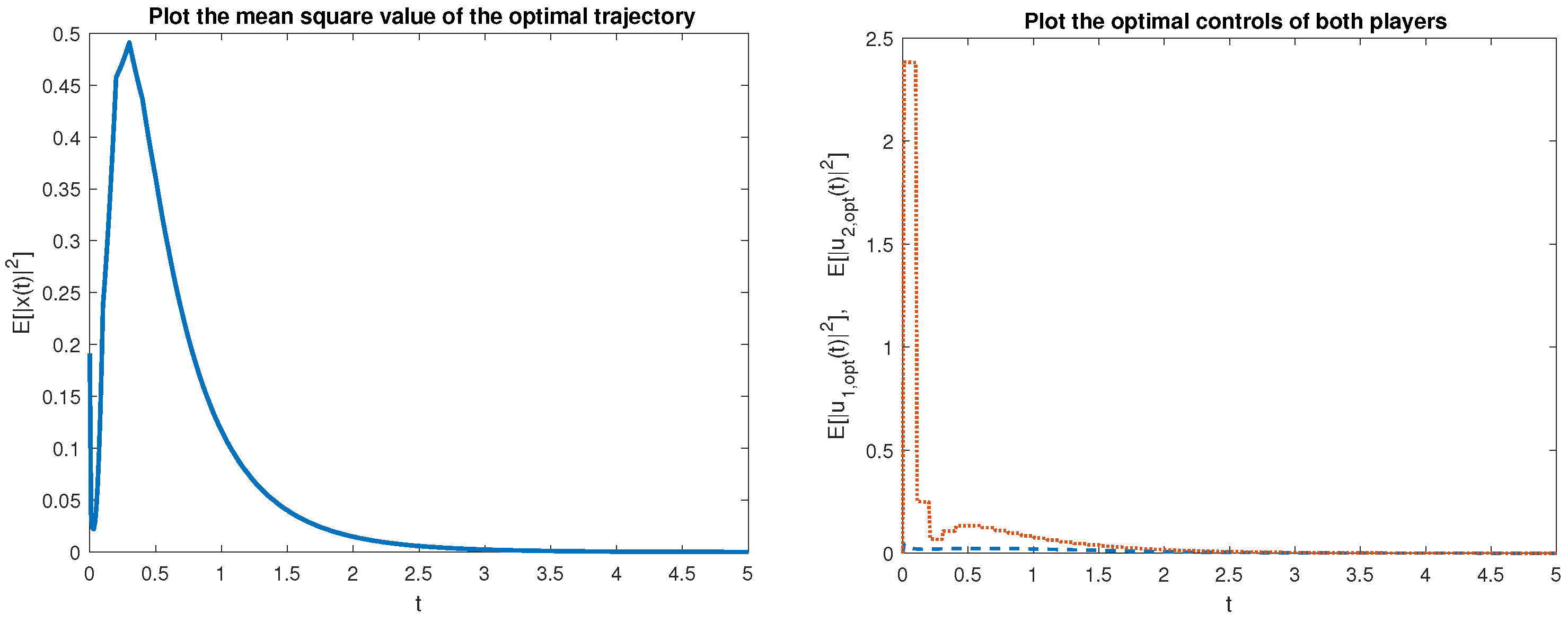
Example 1.

We consider the controlled system (1) in the special form $n=m_1=m_2=2.$ The coefficient matrices $A,$ $B_k,$ $C,$ $D_k,$ $M_k,$ $G_k,$ $R_{kk},$ $R_{k\ell },$ $k,\ell =1,2,$ $k\ne \ell$ are defined as

$$A=\left(\begin{array}{cc}1.5& 0.17\\ 0.07& -1.4\end{array}\right)B_1=\left(\begin{array}{cc}1.5& 0.7\\ 0.3& 0.4\end{array}\right)B_2=\left(\begin{array}{cc}1.2& 0.95\\ 0.8& 0.7\end{array}\right)$$

$$C=\left(\begin{array}{cc}0.7& 0.19\\ 0.24& 0.9\end{array}\right)D_1=\left(\begin{array}{cc}0.2& 0.04\\ 0.4& 0.5\end{array}\right)D_2=\left(\begin{array}{cc}0.1& 0.06\\ 0.2& 0.3\end{array}\right)$$

$$M_1=\left(\begin{array}{cc}0.8& 0.7\\ 0.7& 0.95\end{array}\right)M_2=\left(\begin{array}{cc}0.09& 0.04\\ 0.04& 0.08\end{array}\right)$$

$$G_1=\left(\begin{array}{cc}1.2& 0.45\\ 0.45& 1.5\end{array}\right)G_2=\left(\begin{array}{cc}0.95& 0.8\\ 0.8& 1.15\end{array}\right)$$

$$R_{11}=\left(\begin{array}{cc}0.6& 0.25\\ 0.25& 0.8\end{array}\right)R_{22}=\left(\begin{array}{cc}0.3& 0.15\\ 0.15& 0.4\end{array}\right)$$

$$R_{12}=\left(\begin{array}{cc}0.05& 0.04\\ 0.04& 0.08\end{array}\right)R_{21}=\left(\begin{array}{cc}0.06& 0.07\\ 0.07& 0.09\end{array}\right).$$

The evolution of the mean square values $\mathbb{E}\left[\right|\tilde{x}\left(t\right){\left|\right]}^2$ and $\mathbb{E}\left[\right|u_{opt}\left(t\right){\left|\right]}^2$ of the optimal trajectory $\tilde{x}\left(t\right)$ (with the initial point $x_0^T=\left(0.030.01\right)$) and the equilibrium strategies $u_{1,opt}\left(t\right)$ and $u_{2,opt}\left(t\right)$ is depicted in Figure 1 on the intervals $[0,1]$, and in Figure 2 for $[0,2]$, respectively. The values of the optimal trajectory $\tilde{x}\left(t\right)$ equilibrium strategies of both players are very close to zero in both the short-term and long-term periods.

Figure 1. (left) $\mathbb{E}\left[\right|\tilde{x}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,1]$; (right) $\mathbb{E}\left[\right|u_{1,opt}\left(t\right){|}^2]$ and $\mathbb{E}\left[\right|u_{2,opt}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,1]$.

Figure 2. (left) $\mathbb{E}\left[\right|\tilde{x}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,2]$; (right) $\mathbb{E}\left[\right|u_{1,opt}\left(t\right){|}^2]$ and $\mathbb{E}\left[\right|u_{2,opt}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,2]$.

Example 2.

We consider the controlled system (1) in the special form $n=4$ and $m_1=m_2=2.$ We define the matrix coefficients $A,$ $B_k,$ $C,$ $D_k,$ $M_k,$ $G_k,$ $R_{kk},$ $R_{k\ell },$ $k,\ell =1,2,$ $k\ne \ell$ as follows:

$$A=\left(\begin{array}{cccc}0.5& 0.17& 0.07& 0.9\\ 0.07& 0.54& 0.2& 0.25\\ 0.6& 0.8& 0.92& 0.06\\ 0.35& 0.45& 0.04& -0.99\end{array}\right)B_1=\left(\begin{array}{cc}4.05& -0.4\\ 0.4& -0.8\\ 1& 0.9\\ 0& -0.8\end{array}\right)$$

$$C=\left(\begin{array}{cccc}0.07& 0.19& 0.8& 0\\ 0.4& 0.18& 0.24& 0.7\\ 0.06& 0.3& 0.15& 0.4\\ 0.45& 0.37& 0.09& 0.08\end{array}\right)D_1=\left(\begin{array}{cc}0.15& 0\\ -0.2& 0.25\\ 0& 0.035\\ 0.04& -0.2\end{array}\right)$$

$$B_2=\left(\begin{array}{cc}0.4& 0.05\\ 0.05& -0.07\\ 0& 0.07\\ 0.3& -0.05\end{array}\right)D_2=\left(\begin{array}{cc}0.25& 0.525\\ 1.25& -0.025\\ 0.35& -0.75\\ 0.25& -0.9\end{array}\right)$$

$$M_1=\left(\begin{array}{cccc}0.78& 0& 0& 0\\ 0& 0.82& 0& 0\\ 0& 0& 0.6& 0\\ 0& 0& 0& 0.5\end{array}\right)M_2=\left(\begin{array}{cccc}0.6& 0& 0& 0\\ 0& 0.8& 0& 0\\ 0& 0& 0.48& 0\\ 0& 0& 0& 1.05\end{array}\right)$$

$$G_1=\left(\begin{array}{cccc}0.9& 0.05& 0.25& 0.35\\ 0.05& 1& 0.2& 0.07\\ 0.25& 0.2& 1.05& 0.3\\ 0.35& 0.07& 0.3& 0.9\end{array}\right)G_2=\left(\begin{array}{cccc}1.25& 0.75& 0.21& 0.65\\ 0.75& 0.88& 0.45& 0.76\\ 0.21& 0.45& 1& 0.87\\ 0.65& 0.76& 0.87& 0.99\end{array}\right)$$

$$R_{11}=\left(\begin{array}{cccc}1.26& 0.25& 0.25& 0.8\\ 0.25& 0.95& 0.15& 0.4\\ 0.25& 0.15& 0.96& 0.3\\ 0.8& 0.4& 0.3& 0.88\end{array}\right)R_{22}=\left(\begin{array}{cccc}0.6& 0.15& 0.15& 0.4\\ 0.15& 0.85& 0.36& 0.4\\ 0.15& 0.36& 0.4& 0.25\\ 0.4& 0.4& 0.25& 0.87\end{array}\right)$$

$$R_{12}=\left(\begin{array}{cccc}0.98& 0.04& 0.36& 0.4\\ 0.04& 0.8& 0.36& 0.45\\ 0.36& 0.36& 0.64& 0.1\\ 0.4& 0.45& 0.1& 0.89\end{array}\right)R_{21}=\left(\begin{array}{cccc}0.6& 0.07& 0.35& 0.28\\ 0.07& 0.8& 0.39& 0.25\\ 0.35& 0.39& 1.2& 0.48\\ 0.28& 0.25& 0.48& 1.01\end{array}\right).$$

The evolution of the mean square values $\mathbb{E}\left[\right|\tilde{x}\left(t\right){\left|\right]}^2$ and $\mathbb{E}\left[\right|u_{opt}\left(t\right){\left|\right]}^2$ of the optimal trajectory $\tilde{x}\left(t\right)$ (with the initial point $x_0^T=\left(0.150.010.020.03\right)$) and the equilibrium strategies $u_{1,opt}\left(t\right)$ and $u_{2,opt}\left(t\right)$ on the intervals $[0,1]$ (Figure 3) and $[0,5]$ (Figure 4), respectively. The values of the optimal trajectory $\tilde{x}\left(t\right)$ equilibrium strategies of both players are very close to zero in short-term and long-term period.

Figure 3. (left) $\mathbb{E}\left[\right|\tilde{x}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,1]$; (right) $\mathbb{E}\left[\right|u_{1,opt}\left(t\right){|}^2]$ and $\mathbb{E}\left[\right|u_{2,opt}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,1]$.

Figure 4. (left) $\mathbb{E}\left[\right|\tilde{x}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,5]$; (right) $\mathbb{E}\left[\right|u_{1,opt}\left(t\right){|}^2]$ and $\mathbb{E}\left[\right|u_{2,opt}\left(t\right){|}^2]$; Interval $[t_0,\tau ]=[0,5]$.

4. Concluding Remarks

In this paper, we have investigated the formulation of existence conditions for the Nash equilibria strategy in a state feedback form, in the piecewise constant admissible strategies case. These conditions are expressed through the solvability of the algebraic Equation (26). The solutions of these equations provide the feedback matrices of the desired Nash equilibrium strategy. To obtain such conditions for the existence of a sampled-data Nash equilibrium strategy, we have transformed the original problem into an equivalent one which requires to find a Nash equilibrium strategy in a state feedback form for a stochastic differential game, in which the dynamic is described by Itô type differential equations controlled by impulses. Unlike for the deterministic case, when the problem of finding of a sampled-data Nash equilibrium strategy can be transformed into an equivalent problem in discrete-time, in the stochastic framework when the controlled system is described by Itô type differential equations, such a transformation to the discrete-time case is not possible. The developments from the present work clarify and extend the results from Section 5 of [23], where only the particular case $L=2$ was considered. The key method used for obtaining the feedback matrices of the Nash equilibrium strategy via the Equation (26) is the solution ${\tilde{P}}_k(·),1\le k\le L$ of the TVP (16). On each interval $(t_{j-1},t_j),1\le j\le N,$ (16a) consists of L uncoupled backward linear differential equation. The boundary values ${\tilde{P}}_k(t_j^{-})$ are computed via (16d) for $j=N$ and via (16b) for $j\le N-1$. Finally, we gave an algorithm for calculating the equilibrium strategies of the players, and the numerical experiments suggest a stabilization effect.