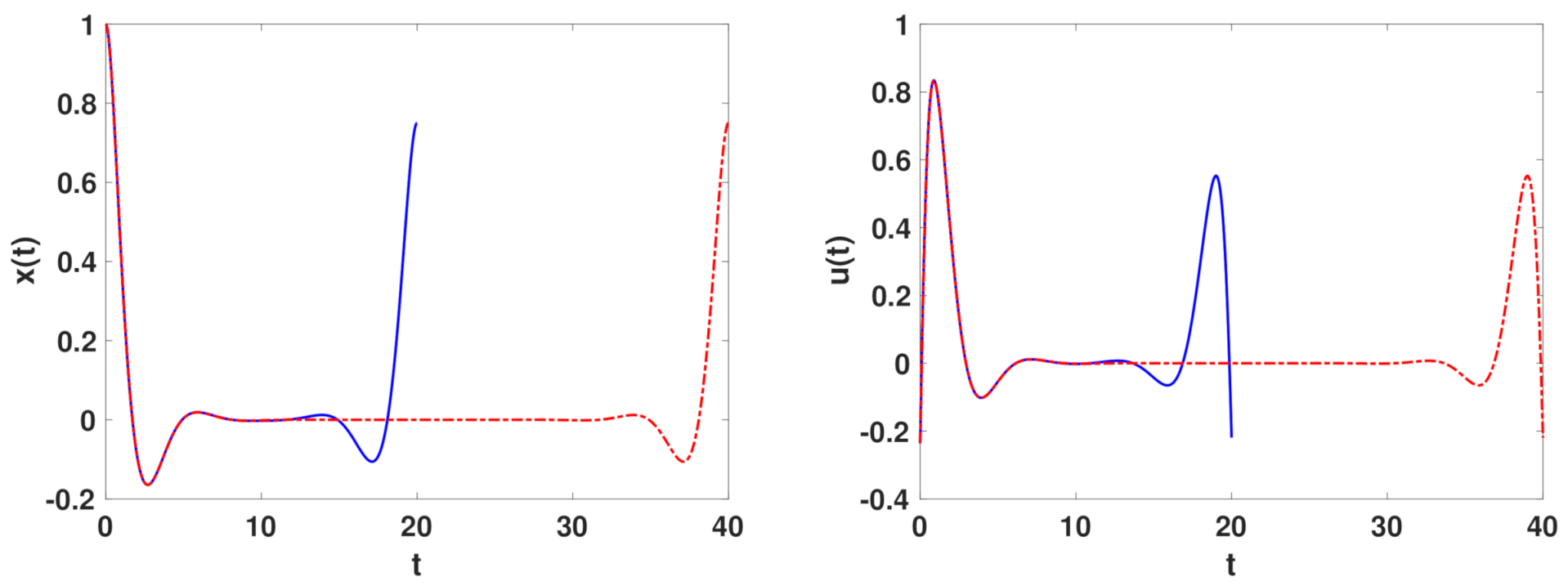
Figure 1.
Mass spring: solution in time for the mass position x on the left and the control u on the right. Final time (blue line) and (red dash-dot line).
Figure 1.
Mass spring: solution in time for the mass position x on the left and the control u on the right. Final time (blue line) and (red dash-dot line).
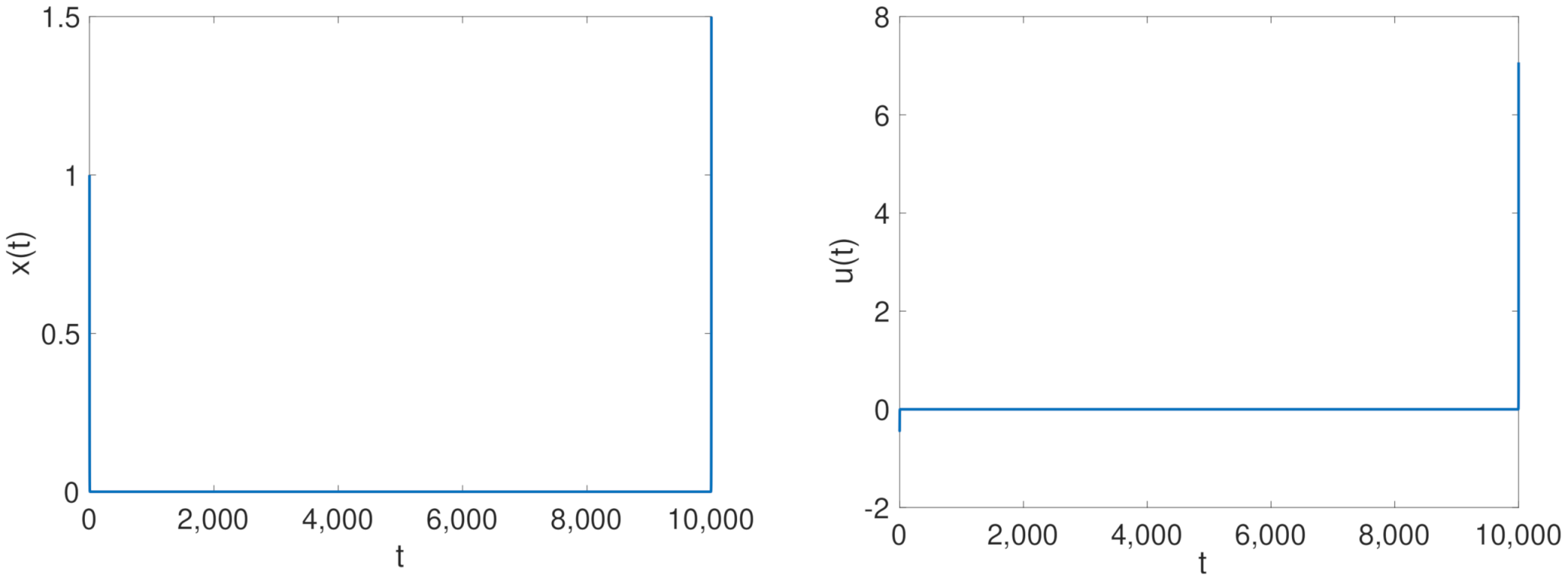
Figure 2.
Hypersensitive: solution in time for the mass position x on the left and the control u on the right, final time .
Figure 2.
Hypersensitive: solution in time for the mass position x on the left and the control u on the right, final time .
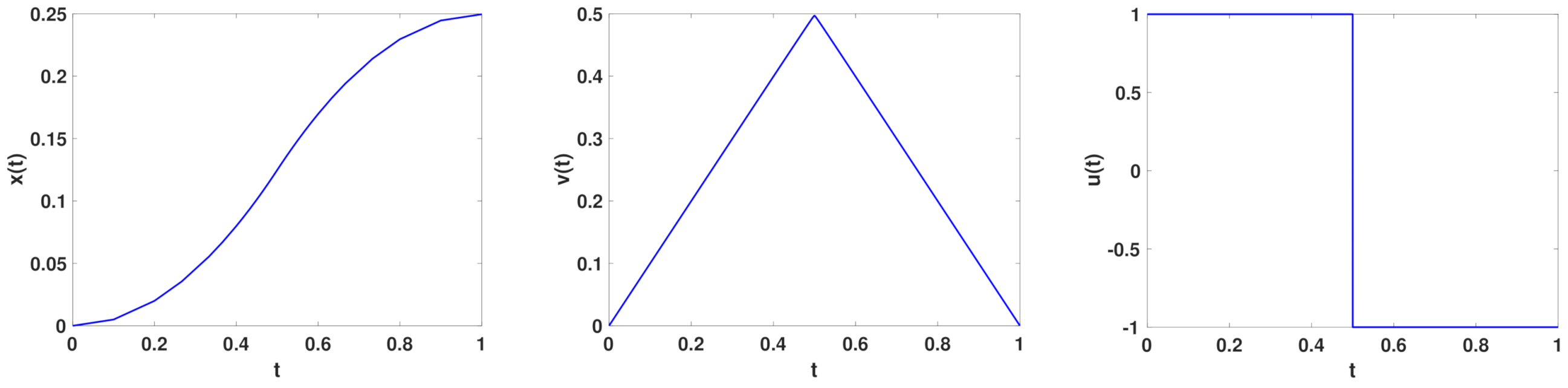
Figure 3.
Bang-Bang, : solution in time for the mass position x on the (left), for the velocity in the (center) and the control u on the (right).
Figure 3.
Bang-Bang, : solution in time for the mass position x on the (left), for the velocity in the (center) and the control u on the (right).
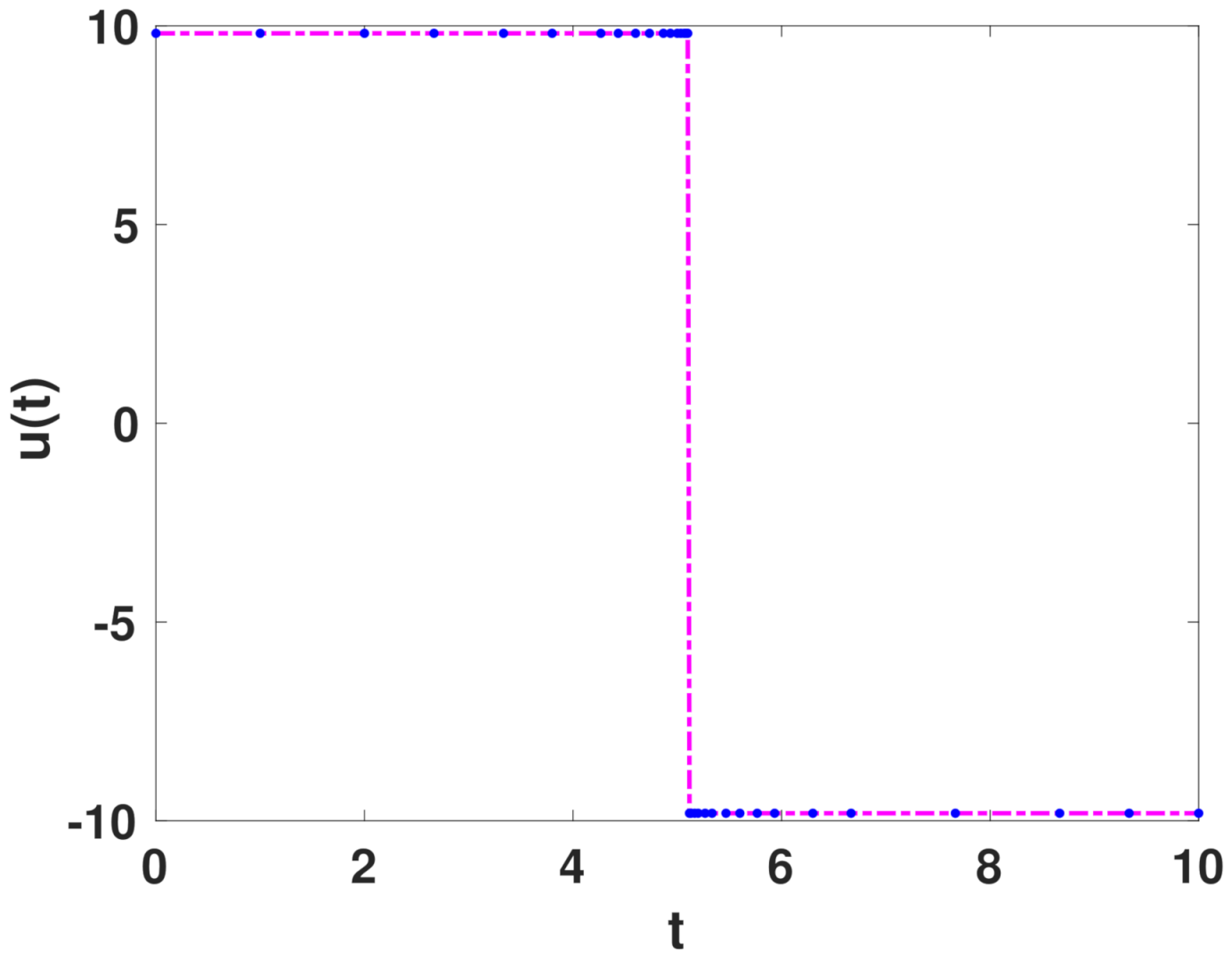
Figure 4.
Longitudinal dynamics of a vehicle, , , , , , , : theoretical (dash-dot line) and numerical (dot line) solution in time for the control u.
Figure 4.
Longitudinal dynamics of a vehicle, , , , , , , : theoretical (dash-dot line) and numerical (dot line) solution in time for the control u.
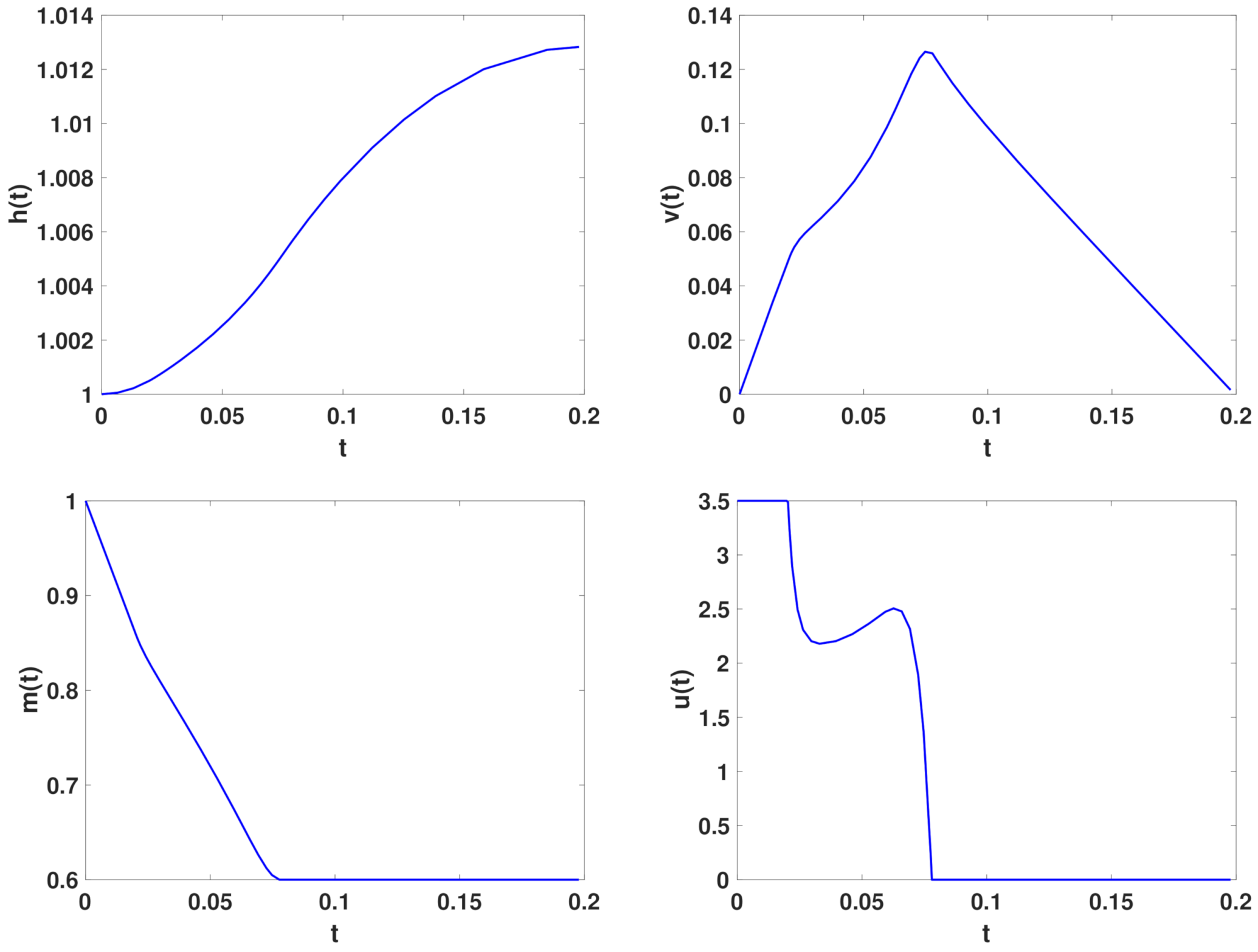
Figure 5.
Goddard rocket, , : from left to right solutions in time for altitude h and mass m (on the top), for velocity v and thrust u (on the bottom).
Figure 5.
Goddard rocket, , : from left to right solutions in time for altitude h and mass m (on the top), for velocity v and thrust u (on the bottom).
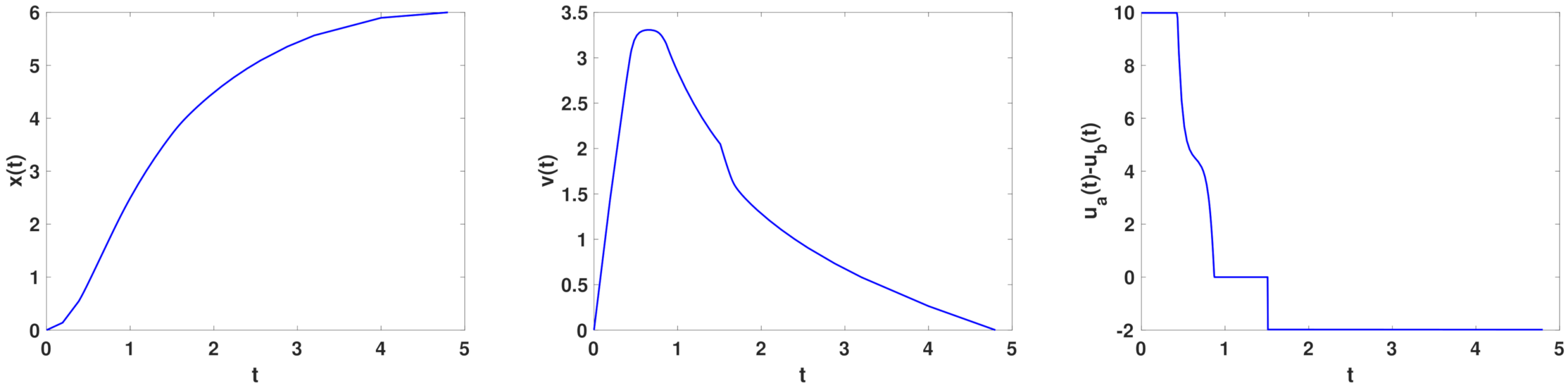
Figure 6.
Minimization of the fuel cost in the operation of a train : from left to right solutions in time for the position x, the velocity v and the difference between the control variables representing the acceleration and the deceleration .
Figure 6.
Minimization of the fuel cost in the operation of a train : from left to right solutions in time for the position x, the velocity v and the difference between the control variables representing the acceleration and the deceleration .
Table 1.
Nonlinear Mass spring: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for . The solution is computed starting from an initial mesh with 16 equidistant points.
Table 1.
Nonlinear Mass spring: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for . The solution is computed starting from an initial mesh with 16 equidistant points.
| | |
|---|
| | | |
|---|
| | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u |
|---|
| bvp4c | 71 | 35 | | | | * | * | * | * | * |
| bvp5c | 294 | 1001 | | | | * | * | * | * | * |
| twpbvp_m | 23 | 52 | | | | 158 | 263 | | | |
| twpbvpc_m | 38 | 52 | | | | 201 | 246 | | | |
| twpbvp_l | 27 | 54 | | | | 97 | 200 | | | |
| twpbvpc_l | 27 | 54 | | | | 104 | 246 | | | |
| tom | 116 | 14 | | | | 426 | 30 | | | |
| tomc | 136 | 16 | | | | 526 | 41 | | | |
| | |
| bvp4c | 254 | 49 | | | | * | * | * | * | * |
| bvp5c | 392 | 1221 | | | | * | * | * | * | * |
| twpbvp_m | 42 | 50 | | | | 254 | 271 | | | |
| twpbvpc_m | 57 | 73 | | | | 306 | 306 | | | |
| twpbvp_l | 48 | 78 | | | | 152 | 207 | | | |
| twpbvpc_l | 58 | 78 | | | | 136 | 253 | | | |
| tom | 196 | 19 | | | | 481 | 33 | | | |
| tomc | 166 | 17 | | | | 511 | 44 | | | |
Table 2.
Nonlinear Mass spring, : final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for , initial mesh with 16 equidistant points.
Table 2.
Nonlinear Mass spring, : final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for , initial mesh with 16 equidistant points.
| | fM | NVF | Error x | Error v | Error u | fVM | NVF | Error x | Error v | Error u |
|---|
| tom | 6266 | 256 | | | | 6266 | 256 | | | |
| tomc | 1291 | 177 | | | | 1236 | 180 | | | |
Table 3.
Nonlinear Mass spring, initial mesh (IM) with 501, 1001 and 2501 equidistant points and : final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for .
Table 3.
Nonlinear Mass spring, initial mesh (IM) with 501, 1001 and 2501 equidistant points and : final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for .
| | IM | fM | NVF | Error x | Error v | Error u |
|---|
| bvp4c | 2501 | 421 | 57 | | | |
| bvp5c | 501 | 261 | 7200 | | | |
| bvp5c | 1001 | 641 | 13,088 | | | |
|
| bvp4c | 2501 | 471 | 71 | | | |
| bvp5c | 501 | 333 | 7578 | | | |
| bvp5c | 1001 | 512 | 13,880 | | | |
Table 4.
Nonlinear Mass spring using the variable , initial mesh with starting mesh with 11 equidistant points and continuation strategy on , final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for .
Table 4.
Nonlinear Mass spring using the variable , initial mesh with starting mesh with 11 equidistant points and continuation strategy on , final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for .
| | |
|---|
| | | | |
|---|
| | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u |
|---|
| bvp4c | 78 | 45 | | | | 199 | 178 | | | | 2093 | 334 | | | |
| bvp5c | 38 | 220 | | | | 148 | 1658 | | | | 1784 | 11,712 | | | |
| twpbvp_m | 24 | 56 | | | | 137 | 233 | | | | 163 | 358 | | | |
| twpbvpc_m | 39 | 81 | | | | 421 | 221 | | | | 141 | 335 | | | |
| twpbvp_l | 28 | 51 | | | | 76 | 346 | | | | 83 | 557 | | | |
| twpbvpc_l | 28 | 51 | | | | 102 | 237 | | | | 139 | 343 | | | |
| tom | 156 | 16 | | | | 481 | 49 | | | | 711 | 73 | | | |
| tomc | 141 | 16 | | | | 681 | 31 | | | | 1356 | 49 | | | |
| acdc | 25 | 155 | | | | 66 | 485 | | | | 110 | 749 | | | |
| acdcc | 25 | 155 | | | | 106 | 375 | | | | 176 | 501 | | | |
| | |
| bvp4c | 296 | 57 | | | | 319 | 160 | | | | 374 | 280 | | | |
| bvp5c | 87 | 464 | | | | 203 | 3535 | | | | 1305 | 19,524 | | | |
| twpbvp_m | 39 | 83 | | | | 178 | 341 | | | | 497 | 459 | | | |
| twpbvpc_m | 50 | 83 | | | | 190 | 255 | | | | 423 | 375 | | | |
| twpbvp_l | 50 | 90 | | | | 114 | 284 | | | | 103 | 446 | | | |
| twpbvpc_l | 61 | 90 | | | | 120 | 246 | | | | 127 | 350 | | | |
| tom | 161 | 17 | | | | 426 | 62 | | | | 751 | 95 | | | |
| tomc | 186 | 19 | | | | 831 | 36 | | | | 826 | 56 | | | |
| acdc | 50 | 158 | | | | 95 | 382 | | | | 89 | 581 | | | |
| acdcc | 50 | 158 | | | | 183 | 371 | | | | 184 | 513 | | | |
Table 5.
Nonlinear Mass spring: conditioning parameters computed using and initial mesh with 11 equidistant points.
Table 5.
Nonlinear Mass spring: conditioning parameters computed using and initial mesh with 11 equidistant points.
| | | | | | |
|---|
|
| twpbvpc_m | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| tomc | | | | | |
Table 6.
Nonlinear Mass spring using the variable : conditioning parameters computed using and initial mesh with 11 equidistant points.
Table 6.
Nonlinear Mass spring using the variable : conditioning parameters computed using and initial mesh with 11 equidistant points.
| | | | | | |
|---|
|
| twpbvpc_m | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| tomc | | | | | |
Table 7.
Hypersensitive problem solved with an initial mesh with 11 equidistant points: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for .
Table 7.
Hypersensitive problem solved with an initial mesh with 11 equidistant points: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for .
| | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u |
|---|
| twpbvp_m | 117 | 239 | | | | 1821 | 394 | | | |
| twpbvpc_m | 140 | 237 | | | | 650 | 456 | | | |
| twpbvp_l | 105 | 224 | | | | * | * | * | * | * |
| twpbvpc_l | 91 | 286 | | | | 1176 | 425 | | | |
| tom | 691 | 33 | | | | 636 | 169 | | | |
| tomc | 681 | 46 | | | | 1941 | 134 | | | |
| | |
| twpbvp_m | 357 | 245 | | | | 1859 | 392 | | | |
| twpbvpc_m | 265 | 239 | | | | 536 | 475 | | | |
| twpbvp_l | 94 | 248 | | | | * | * | * | * | * |
| twpbvpc_l | 91 | 286 | | | | 1176 | 425 | | | |
| tom | 691 | 33 | | | | 691 | 172 | | | |
| tomc | 681 | 46 | | | | 1941 | 134 | | | |
Table 8.
Hypersensitive problem: conditioning parameters computed using and initial mesh with 11 equidistant points.
Table 8.
Hypersensitive problem: conditioning parameters computed using and initial mesh with 11 equidistant points.
| | | | | | |
|---|
|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
Table 9.
Hypersensitive problem using the variable , initial mesh with 11 equidistant points and continuation strategy on T: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for x,v,u.
Table 9.
Hypersensitive problem using the variable , initial mesh with 11 equidistant points and continuation strategy on T: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for x,v,u.
| | |
|---|
| | | |
|---|
| | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u |
|---|
| bvp4c | 107 | 198 | | | | 242 | 170 | | | |
| bvp5c | 70 | 1277 | | | | 132 | 2874 | | | |
| twpbvp_m | 59 | 266 | | | | 124 | 311 | | | |
| twpbvpc_m | 101 | 210 | | | | 190 | 226 | | | |
| twpbvp_l | 45 | 389 | | | | 63 | 306 | | | |
| twpbvpc_l | 76 | 229 | | | | 79 | 234 | | | |
| tom | 571 | 56 | | | | 746 | 59 | | | |
| tomc | 951 | 46 | | | | 1231 | 52 | | | |
| acdc | 56 | 491 | | | | 60 | 425 | | | |
| acdcc | 130 | 672 | | | | 144 | 478 | | | |
Table 10.
Hypersensitive problem using the variable : conditioning parameters computed using and initial mesh with 11 equidistant points.
Table 10.
Hypersensitive problem using the variable : conditioning parameters computed using and initial mesh with 11 equidistant points.
| | | | | | |
|---|
|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
Table 11.
Bang-Bang optimal control Problem (
9): final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
u.
Table 11.
Bang-Bang optimal control Problem (
9): final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
u.
| | |
|---|
| | | |
|---|
| | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u |
|---|
| bvp4c | 25 | 51 | | | 0 | 27 | 97 | | | 0 |
| twpbvp_m | 16 | 11 | | | 0 | 16 | 11 | | | 0 |
| twpbvp_l | 16 | 13 | | | 0 | 16 | 13 | | | 0 |
| tom | 111 | 10 | | | 0 | 31 | 16 | | | 0 |
| tomc | 121 | 10 | | | 0 | 31 | 28 | | | 0 |
| acdc | 9 | 157 | | | 0 | 9 | 221 | | | 0 |
| | |
| bvp4c | 79 | 57 | | | 0 | 47 | 93 | | | 0 |
| twpbvp_m | 10 | 32 | | | 0 | 10 | 32 | | | 0 |
| twpbvp_l | 17 | 66 | | | 0 | 15 | 130 | | | 0 |
| tom | 231 | 19 | | | 0 | 281 | 32 | | | 0 |
| tomc | 201 | 19 | | | 0 | 231 | 40 | | | 0 |
| acdc | 20 | 170 | | | 0 | 17 | 242 | | | 0 |
Table 12.
Bang-Bang optimal control problem-solving (
8) using a piecewise quadratic penalty function with
: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
u.
Table 12.
Bang-Bang optimal control problem-solving (
8) using a piecewise quadratic penalty function with
: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
u.
| | |
|---|
| | | |
|---|
| | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u |
|---|
| twpbvp_m | 16 | 11 | | | | 16 | 11 | | | |
| twpbvp_l | 16 | 13 | | | | 16 | 13 | | | |
| tom | 111 | 10 | | | | 31 | 27 | | | |
| tomc | 126 | 9 | | | | 31 | 20 | | | |
| | |
| twpbvp_m | 8 | 32 | | | | 8 | 32 | | | |
| twpbvp_l | 9 | 93 | | | | 8 | 130 | | | |
| tom | 231 | 19 | | | | 381 | 51 | | | |
| tomc | 261 | 20 | | | | 241 | 56 | | | |
Table 13.
Bang-Bang optimal control problem-solving (
8) using a piecewise quadratic penalty function with
and the continuation strategy: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
u.
Table 13.
Bang-Bang optimal control problem-solving (
8) using a piecewise quadratic penalty function with
and the continuation strategy: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
u.
| | |
|---|
| | | |
|---|
| | | fM | NVF | Error x | Error v | Error u | | fM | NVF | Error x | Error v | Error u |
|---|
| bvp4c | 10 | 12 | 1899 | | | | 5 | 13 | 1214 | | | |
| bvp5c | 10 | 9 | 1551 | | | | 10 | 13 | 1442 | | | |
| acdc | | 4 | 326 | | | | | 4 | 326 | | | |
| | |
| bvp4c | 10 | 16 | 3168 | | | | 10 | 19 | 3421 | | | |
| bvp5c | 10 | 13 | 3235 | | | | 100 | 14 | 21747 | | | |
| acdc | | 9 | 380 | | | | | 9 | 380 | | | |
Table 14.
Bang-Bang optimal control problem: conditioning parameters computed using .
Table 14.
Bang-Bang optimal control problem: conditioning parameters computed using .
| | | | | | |
|---|
|
| twpbvpc_m | 1.8 | 3.3 | 2.0 | 1.3 | 1.6 |
| twpbvpc_l | 1.4 | 3.3 | 2.0 | 1.3 | 1.6 |
| tomc | 1.5 | 3.3 | 2.0 | 1.2 | 1.0 |
|
| twpbvpc_m | 2.0 | 3.2 | 2.0 | 1.2 | 1.6 |
| twpbvp_l | 2.0 | 3.3 | 2.0 | 1.3 | 1.7 |
| tomc | 2.1 | 3.3 | 2.0 | 1.2 | 1.0 |
Table 15.
Bang-Bang optimal control problem with penalty: conditioning parameters computed using .
Table 15.
Bang-Bang optimal control problem with penalty: conditioning parameters computed using .
| | | | | | |
|---|
|
| twpbvpc_m | 1.8 | 3.2 | 2.0 | 1.2 | 1.6 |
| twpbvpc_l | 1.4 | 3.3 | 2.0 | 1.3 | 1.7 |
| tomc | 1.4 | 3.3 | 2.0 | 1.2 | 1.0 |
|
| twpbvpc_m | 2.0 | 3.2 | 2.0 | 1.2 | 1.6 |
| twpbvpc_l | 2.0 | 3.3 | 2.0 | 1.3 | 1.7 |
| tomc | 1.3 | 3.3 | 2.0 | 1.2 | 1.0 |
Table 16.
Longitudinal dynamics of a vehicle , , , , , : final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for x, v, u.
Table 16.
Longitudinal dynamics of a vehicle , , , , , : final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for x, v, u.
| | |
|---|
| | | |
|---|
| | fM | NVF | Error x | Error v | Error u | fM | NVF | Error x | Error v | Error u |
|---|
| bvp4c | 38 | 125 | | | 0 | 32 | 242 | | | 0 |
| bvp5c | 18 | 270 | | | 0 | 18 | 662 | | | 0 |
| twpbvp_m | 38 | 54 | | | 0 | 13 | 146 | | | 0 |
| twpbvp_l | 38 | 57 | | | 0 | 28 | 134 | | | 0 |
| tom | 176 | 23 | | | 0 | 176 | 50 | | | 0 |
| tomc | 131 | 20 | | | 0 | 131 | 48 | | | 0 |
| acdc | 15 | 320 | | | 0 | 8 | 550 | | | 0 |
Table 17.
Longitudinal dynamics of a vehicle , , , , , : conditioning parameters computed using .
Table 17.
Longitudinal dynamics of a vehicle , , , , , : conditioning parameters computed using .
| | | | | | |
|---|
|
|---|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
|
| twpbvpc_m | | | | | |
| twpbvpc_l | | | | | |
| tomc | | | | | |
Table 18.
Goddard Rocket problem (
15) solved using a piecewise quadratic penalty function with
and
: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
h,
v,
m,
T and
u.
Table 18.
Goddard Rocket problem (
15) solved using a piecewise quadratic penalty function with
and
: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
h,
v,
m,
T and
u.
|
|---|
| | fM | NVF | Error h | Error v | Error m | Error T | Error u |
|---|
| bvp4c | 1388 | 8058 | | | | | |
| twpbvp_m | 31 | 86 | | | | | |
| twpbvp_l | 31 | 91 | | | | | |
|
| bvp4c | 1466 | 20,898 | | | | | |
| twpbvp_m | 32 | 142 | | | | | |
| twpbvp_l | 33 | 169 | | | | | |
Table 19.
Goddard Rocket Problem (
15) solved using a piecewise quadratic penalty function with
and the continuation strategy: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
h,
v,
m,
T and
u.
Observe that
acdc for
obtains a solution for
.
Table 19.
Goddard Rocket Problem (
15) solved using a piecewise quadratic penalty function with
and the continuation strategy: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
h,
v,
m,
T and
u.
Observe that
acdc for
obtains a solution for
.
| | |
|---|
| | | |
| | fM | NVF | Error | Error | Error | Error | Error | fM | NVF | Error | Error | Error | Error | Error |
| bvp4c | 47 | 2823 | | | | | | 138 | 46,507 | | | | | |
| twpbvp_m | 16 | 268 | | | | | | 93 | 484 | | | | | |
| twpbvp_l | 16 | 304 | | | | | | 225 | 627 | | | | | |
| tom | 401 | 66 | | | | | | 541 | 224 | | | | | |
| tomc | 291 | 62 | | | | | | 286 | 210 | | | | | |
| acdc | 17 | 341 | | | | | | 24 | 2066 | | | | | |
| | |
| bvp4c | 148 | 9189 | | | | | | 1385 | 52,028 | | | | | |
| twpbvp_m | 29 | 593 | | | | | | 149 | 681 | | | | | |
| twpbvp_l | 32 | 646 | | | | | | 119 | 969 | | | | | |
| tom | 551 | 80 | | | | | | 661 | 279 | | | | | |
| tomc | 321 | 74 | | | | | | 731 | 286 | | | | | |
| acdc | 28 | 496 | | | | | | 58 | 942 | | | | | |
Table 20.
Goddard Rocket problem: conditioning parameters computed using .
Table 20.
Goddard Rocket problem: conditioning parameters computed using .
| | | | | | |
|---|
|
| twpbvpc_m | 4.8 | | | | |
| twpbvpc_l | 4.9 | | | | |
| tomc | 5.4 | | | | |
|
| twpbvpc_m | 5.3 | | | | |
| twpbvpc_l | 5.2 | | | | |
| tomc | 5.5 | | | | |
Table 21.
Minimization of the fuel cost in the operation of a train (
18) using a piecewise quadratic penalty function with
: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
,
.
Table 21.
Minimization of the fuel cost in the operation of a train (
18) using a piecewise quadratic penalty function with
: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
,
.
| | |
|---|
| | | |
| | fM | NVF | Error | Error | Error | Error | fM | NVF | Error | Error | Error | Error |
| bvp4c | 121 | 1747 | | | | | 116 | 2414 | | | | |
| bvp5c | 52 | 3259 | | | | | 56 | 4295 | | | | |
| twpbvp_m | 34 | 132 | | | | | 52 | 124 | | | | |
| twpbvpc_m | 47 | 132 | | | | | 55 | 104 | | | | |
| twpbvp_l | 33 | 136 | | | | | 223 | 124 | | | | |
| twpbvpc_l | 46 | 136 | | | | | 115 | 104 | | | | |
| tom | 1471 | 44 | | | | | 1091 | 45 | | | | |
| tomc | 1406 | 148 | | | | | 2896 | 93 | | | | |
Table 22.
Minimization of the fuel cost in the operation of a train (
18) using a piecewise quadratic penalty function with
and continuation strategy: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
,
.
Table 22.
Minimization of the fuel cost in the operation of a train (
18) using a piecewise quadratic penalty function with
and continuation strategy: final mesh (fM), total number of vectorized function evaluation (NVF) and mixed errors for
x,
v,
,
.
| | |
|---|
| | | |
|---|
| | fM | NVF | Error x | Error v | Error | Error | fM | NVF | Error x | Error v | Error | Error |
|---|
| bvp4c | 69 | 6055 | | | | | 78 | 8213 | | | | |
| bvp5c | 39 | 7180 | | | | | 59 | 8012 | | | | |
| twpbvp_m | 415 | 432 | | | | | 589 | 319 | | | | |
| twpbvpc_m | 132 | 359 | | | | | 589 | 319 | | | | |
| twpbvp_l | 202 | 312 | | | | | 589 | 332 | | | | |
| twpbvpc_l | 202 | 312 | | | | | 589 | 332 | | | | |
| tom | 2201 | 99 | | | | | 2166 | 102 | | | | |
| tomc | 2211 | 218 | | | | | 2886 | 230 | | | | |
| acdc | 36 | 723 | | | | | 40 | 1219 | | | | |
Table 23.
Minimization of the fuel cost in the operation of a train: conditioning parameters computed using , cond is the condition number of the matrix associated with the last nonlinear iteration.
Table 23.
Minimization of the fuel cost in the operation of a train: conditioning parameters computed using , cond is the condition number of the matrix associated with the last nonlinear iteration.
| | | | | | | Cond |
|---|
| | |
| twpbvpc_m | | | | | | |
| twpbvpc_l | | | | | | |
| tomc | | | | | | |
| | |
| twpbvpc_m | | | | | | |
| twpbvpc_l | | | | | | |
| tomc | | | | | | |