A Chemical Analysis of Hybrid Economic Systems—Tokens and Money
Abstract
1. Introduction
2. Materials and Methods
2.1. The Connection between Chemical Reactions and Market Transactions
2.2. Chemical Model
- : X and Y enter the reactions/market in exactly the same quantity.
- and : The presence of the tokens in the reactions is superfluous.
- : In the RM2s context, this means that product Y can be bought with tokens only. This strategy can be used to reward loyal customers instead of introducing vouchers.
- and : Tokens are fully integrated and play an active role in the pricing of the products.
- : By starting with more of product X than Y, one may end up with a surplus of tokens at the end of the reactions that will have to be transferred and accounted for in the subsequent reaction mechanism.
- : One might run out of tokens in this step of the sequence of reaction mechanisms simply because selling product X will not generate enough tokens to buy all of the Y products. This is not an issue in RM2, but might become one in RM2s, where selling Y is restricted to token involvement.
- One can also imagine supplementing the reaction mechanisms with a way to buy X only with tokens at later stages.
2.3. Kinetic Study
2.4. Stability Analysis
2.5. Coefficient Adjustments According to the Supply and Demand Laws
3. Results
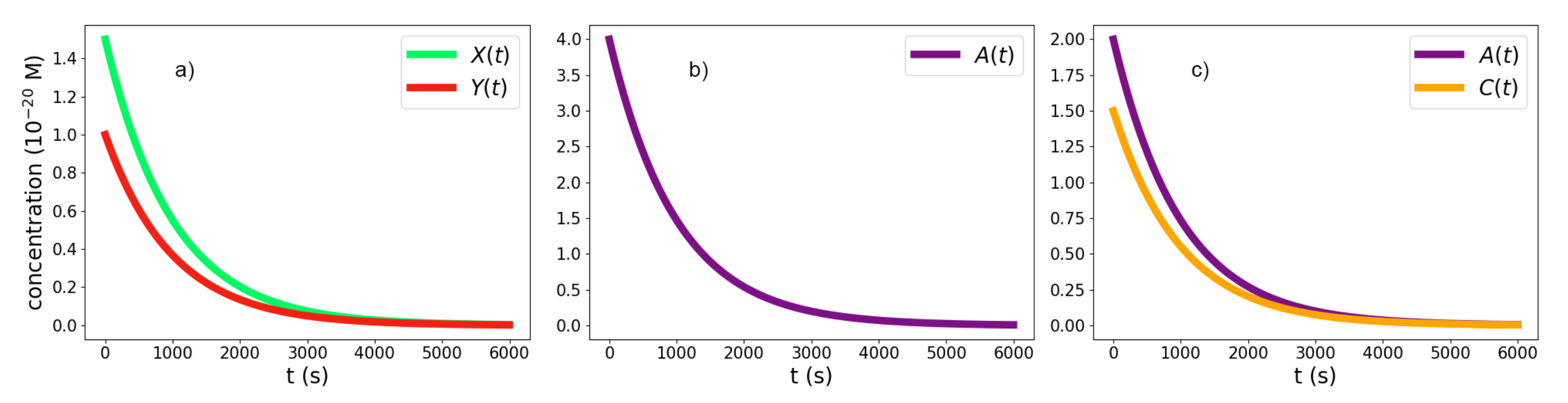
3.1. The Kinetic Study
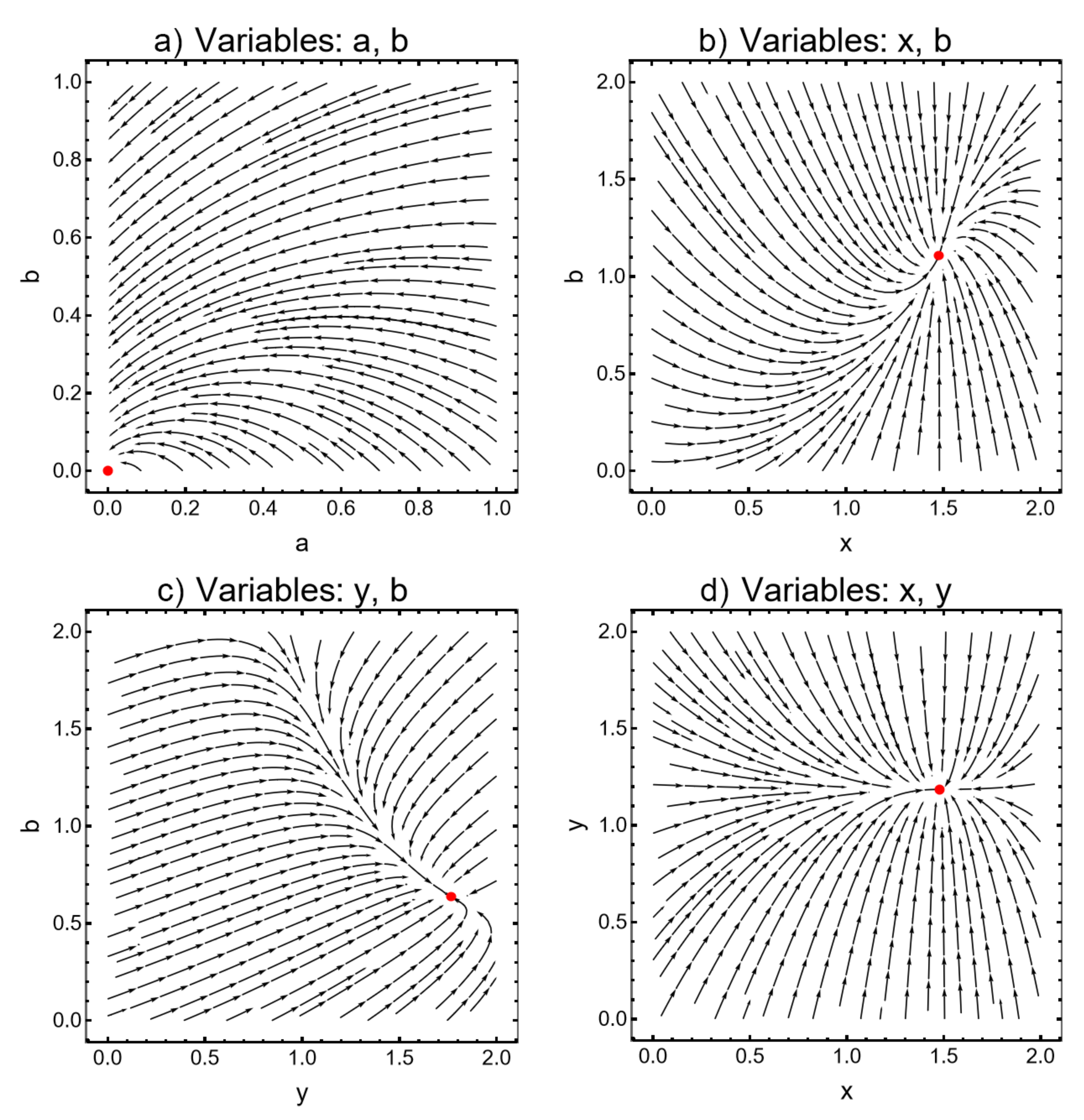
3.2. The Stability Analysis
3.3. Coefficient Adjustments
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DT | Digital technology |
| ICO | Initial Coin Offering |
| Reaction rate | |
| RM1 | Reaction mechanism 1 |
| RM2 | Reaction mechanism 2 |
| RM2s | Reaction mechanism 2 short |
| ODE | Ordinary differential equation |
| Tr(J) | Trace of Jacobian |
| Det(J) | Determinant of Jacobian |
| S(J) | |
| P | Price |
| D | Demand |
| S | Supply |
Appendix A. Integrated Rate Law
Appendix B. Experimental Assumptions
| [X] (M) | [A] (M) | Rate (M/s) | Significance |
|---|---|---|---|
| units of product are sold for units of currency | |||
| and the transaction speed in 10 units/s | |||
| 2 × | doubling the produce concentration does not | ||
| affect the transaction speed | |||
| 2 × | 2 × | doubling the currency concentration | |
| doubles the transaction speed |
| [X] (M) | [A] (M) | Rate (M/s) | Significance |
|---|---|---|---|
| units of product are sold for units of currency | |||
| and the transaction speed in 10 units/s | |||
| 2 × | 2 × | doubling the produce concentration | |
| doubles the transaction speed | |||
| 2 × | doubling the currency concentration | ||
| does not affect the transaction speed |
Appendix C. Scaling Factors
Appendix D. General and Special ODE Solutions
| Nr. | Mec. | Fix. | Var. | Sol. |
|---|---|---|---|---|
| 1 | X | Y, A | ||
| 2 | RM1 | Y | X, A | |
| 3 | - | X, Y, A | solutions exist only for known powers of a | |
| 4 | X, Y | A, B | no sol. | |
| 5 | X, A | Y, B | many sol. | |
| 6 | X, B | Y, A | ||
| 7 | RM2s | Y, A | X, B | |
| 8 | Y, B | X, A | ||
| 9 | A, B | X, Y | ||
| 10 | X | Y, A, B | no sol. | |
| 11 | Y | X, A, B | no sol. | |
| 12 | A | X, Y, B | no sol. (for and ) | |
| many sol. (for ) | ||||
| 13 | B | X, Y, A | no sol. (for ) | |
| 14 | - | X, Y, A, B | no sol. | |
| 15 | X, Y | A, B | no sol. | |
| 16 | RM2 | X, A | Y, B | |
| 17 | X, B | Y, A | ||
| 18 | Y, A | X, B | ||
| 19 | Y, B | X, A | solutions exist only for known powers of a | |
| 20 | A, B | X, Y | ||
| 21 | X | Y, A, B | solutions exist only for known powers of a | |
| 22 | Y | X, A, B | solutions exist only for known powers of a | |
| 23 | A | X, Y, B | ||
| 24 | B | X, Y, A | no sol. (for ) | |
| 25 | - | X, Y, A, B | no sol. |
| Mec. | Fix. | Var. | Sol. | Cond. | Comments |
|---|---|---|---|---|---|
| X | Y, A | (+, −) | |||
| RM1 | Y | X, A | (i, i), (i, i) | ||
| - | X, Y, A | (+, +, −) | |||
| X, A | Y, B | many sol. | - | consistent, dependent | |
| X, B | Y, A | (i, i), (i, i) | |||
| Y, B | X, A | (+, −) | |||
| RM2s | X | Y, A, B | - | inconsistent, independent | |
| Y | X, A, B | - | inconsistent, independent | ||
| A | X, Y, B | many sol. | consistent, dependent | ||
| - | inconsistent, independent | ||||
| B | X, Y, A | - | inconsistent, independent | ||
| X, B | Y, A | (i, i), (i, i) | |||
| Y, B | X, A | (i, i), (i, i) | |||
| (+/−, −), (+/−, −) | |||||
| RM2 | X | Y, A, B | (−, i, i), (−, i, i) | ||
| Y | X, A, B | (−, i, i), (−, i, i) | |||
| A | X, Y, B | (+, +, +) | |||
| B | X, Y, A | - | inconsistent, independent |
References
- UN. Available online: https://www.un.org/sites/un2.un.org/files/un75_new_technologies.pdf (accessed on 2 July 2021).
- UN. Available online: https://www.un.org/sites/un2.un.org/files/un75_final_report_shapingourfuturetogether.pdf (accessed on 2 July 2021).
- Nadkarni, S.; Prügl, R. Digital transformation: A review, synthesis and opportunities for future research. Springer Manag. Rev. Q. 2021, 71, 233–341. [Google Scholar] [CrossRef]
- Fitzgerald, M.; Kruschwitz, N.; Bonnet, D.; Welch, M. Embracing Digital Technology: A New Strategic Imperative. Mit Sloan Manag. Rev. 2013, 55, 1–13. [Google Scholar]
- Ross, J.W.; Sebastian, I.M.; Beath, C.M.; Jha, L.; The Technology Advantage Practice of The Boston Consulting Group. MIT-CISR-Designing-Digital-Survey. Available online: https://media-publications.bcg.com/MIT-CISR-Designing-Digital-Survey.PDF (accessed on 5 July 2021).
- Winden, W.; Carvalho, L. Cities and Digitalization. How Digitalization Changes Cities—Innovation for the Urban Economy of Tomorrow. Available online: https://www.business.ruhr/fileadmin/user_upload/Studie__Cities_and_digitalization__Euricur_wmr.pdf (accessed on 22 July 2021).
- The Climate City Cup. Available online: https://climatecitycup.org (accessed on 22 July 2021).
- Smart City: German Government Funding “Digital Twins” Project. Available online: https://hamburg-news.hamburg/en/location/smart-city-german-government-funding-digital-twins-project (accessed on 22 July 2021).
- Gimpel, H.; Röglinger, M. Digital Transformation: Changes and Chances: Insights based on an Empirical Study. 2015. Available online: http://fim-rc.de/Paperbibliothek/Veroeffentlicht/542/wi-542.pdf (accessed on 2 July 2021).
- Digital Trust & Security—Securing Digital Transformation. Available online: https://www.capgemini.com/de-de/wp-content/uploads/sites/5/2019/10/Securing-Digital-Transformation-Capgemini-Invent.pdf (accessed on 22 July 2021).
- Swan, M. Blockchain: Blueprint for a New Economy; O’Reilly: Beijing, China, 2015. [Google Scholar]
- Kirbac, G.; Tektas, B. The Role of Blockchain Technology in Ensuring Digital Transformation for Businesses: Advantages, Challenges and Application Steps. Proceedings 2021, 74, 17. [Google Scholar] [CrossRef]
- Catalini, C.; Gans, J.S. Some Simple Economics of the Blockchain. NBER Work. Pap. 22952 2016. [Google Scholar] [CrossRef]
- Hileman, G.; Rauchs, M. Global Cryptocurrency Benchmarking Study. Available online: https://www.jbs.cam.ac.uk/wp-content/uploads/2020/08/2017-04-20-global-cryptocurrency-benchmarking-study.pdf (accessed on 22 July 2021).
- Lee, J.Y. A decentralised token economy: How blockchain and cryptocurencies can revolutionise business. Bus. Horizons 2019, 62, 773–784. [Google Scholar]
- Mougayar, M. Tokenomics—A Business Guide to Token Usage, Utility and Value. Available online: https://medium.com/@wmougayar/tokenomics-a-business-guide-to-token-usage-utility-and-value-b19242053416 (accessed on 22 July 2021).
- Matson, J.L.; Estabillo, J.; Matheis, M. Token Economy. Encycl. Personal. Individ. Differ. 2016, 1, 3. [Google Scholar]
- Kleineberg, K.; Helbing, D. A “social bitcoin” could sustain a democratic digital world. Eur. Phys. J. Spec. Top. 2016, 225, 3231–3241. [Google Scholar] [CrossRef][Green Version]
- Dapp, M. Toward a Sustainable Circular Economy Powered by Community-Based Incentive Systems. InBusiness Transformation through Blockchain; Treiblmaier, H., Beck, R., Eds.; Palgrave Macmillan: Cham, Switzerland, 2019; pp. 153–181. [Google Scholar]
- Commons Stack. Realigning Incentives around Public Goods. Available online: https://medium.com/commonsstack (accessed on 6 July 2021).
- Treecycle. We are Fighting Illegal Deforestation by Transforming Fallow Lands into Fast-Growing Sustainable Forests. Available online: https://treecycle.ch/en/ (accessed on 6 July 2021).
- Dusk Network: The Privacy Blockchain for Financial Applications. Available online: https://dusk.network/ (accessed on 6 July 2021).
- Circles. A Basic Income on the Blockchain. Available online: https://joincircles.net/ (accessed on 6 July 2021).
- Forbes: “Reddit Is Launching Ethereum Tokens For Its Subreddits”. Available online: https://www.forbes.com/sites/colinharper/2020/05/14/reddit-launches-ethereum-tokens-for-subbredits-in-new-community-points-campaign/ (accessed on 10 October 2021).
- Tönnissen, S.; Beinke, J.H.; Teuteberg, F. Understanding token-based ecosystems—A taxonomy of blockchain-based business models of start-ups. Electron. Mark. 2020, 30, 307–323. [Google Scholar] [CrossRef]
- Conley, J.P. Blockchain and the Economics of Crypto-tokens and Initial Coin Offerings; Vanderbilt University Department of Economics Working Papers; VUECON-17-00008; Vanderbilt University: Nashville, TN, USA, 2017; p. 37235. [Google Scholar]
- Drasch, B.J.; Fridgen, G.; Manner-Romberg, T.; Nolting, F.M.; Radszuwill, S. The token’s secret: The two-faced financial incentive of the token economy. Electron. Mark. 2020, 30, 557–567. [Google Scholar] [CrossRef]
- Victor, F.; Lüders, B.K. Measuring ethereum-based erc20 token networks. In International Conference on Financial Cryptography and Data Security; Springer: Cham, Switzerland, 2019; pp. 113–129. [Google Scholar]
- Stanley, M.H.R.; Amaral, L.A.N.; Buldyrev, S.V.; Havlin, S.; Leschhorn, H.; Maass, P.; Salinger, M.A.; Stanley, H.E. Scaling behavior in the growth of companies. Nature 1996, 379, 804. [Google Scholar] [CrossRef]
- Rosario, M.N.; Kertész, J. Focus on Statistical Physics Modeling in Economics and Finance. New J. Phys. 2011, 13, 25011. [Google Scholar]
- Chen, S.; Li, S. Econophysics: Bridges over a Turbulent Current. arXiv 2011, arXiv:1107.5373. [Google Scholar] [CrossRef]
- Kutnera, R.; Ausloos, M.; Grechc, D.; Di Matteo, T.; Schinckusg, C.; Stanley, H.E. Econophysics and sociophysics: Their milestones & challenges. Phys. Stat. Mech. Appl. 2019, 516, 240–253. [Google Scholar]
- Helbing, D. Social Self-Organization. Agent-Based Simulations and Experiments to Study Emergent Social Behaviour; Springer: Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2012. [Google Scholar]
- Yochanan, S.; Reuel, S. Do Chemical Reactors Hold the Solution for Global Economic Crises? PIER Working Paper No. 12-010; Penn Institute for Economic Research Department of Economics, University of Pennsylvania: Philadelphia, PA, USA, 2012. [Google Scholar]
- Hartmann, G.C.; Rossler, O.E. Coupled Flare Attractors A Discrete Prototype for Economic Modelling. Discret. Dyn. Nat. Soc. 2012, 1998, 153–159. [Google Scholar]
- Field, R.J. Chaos in the belousov-zhabotinsky reaction. Mod. Phys. Lett. B 2015, 29. [Google Scholar] [CrossRef]
- Kol’tsov, N. Chaotic oscillations in four-step chemical reaction. Russ. J. Phys. Chem. B 2017, 11, 1047–1048. [Google Scholar] [CrossRef]
- Epstein, I.R.; Pojman, J.A. An Introduction to Nonlinear Chemical Dynamics. Oscillations, Waves, Patterns and Chaos; Oxford University Press: New York, NY, USA; Oxford, UK, 1998. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos; Perseus Books: Reading, MA, USA, 1994. [Google Scholar]
- Kim, M.S.; Chung, J.Y. Sustainable growth and token economy design: The case of steemit. Sustainability 2019, 11, 167. [Google Scholar] [CrossRef]
- Voshmgir, S. Token Economy—The Future of Currencies? Available online: https://medium.com/crypto3conomics/token-economy-the-future-of-currencies-d26487fd3945 (accessed on 10 October 2021).
- Kampakis, S. Why do we need tokenomics? JBBA 2018, 1, 1–4. [Google Scholar] [CrossRef]
- Lai, Y.; Gould, H.; Tobochnik, J. Controlling Chaos. Comput. Phys. 1994, 8, 62. [Google Scholar] [CrossRef]
- Santos, R.B.B.; Graves, J.C. Extracting Chaos Control Parameters from Time Series Analysis. J. Phys. Conf. Ser. 2011, 285, 12002. [Google Scholar] [CrossRef]
- Ballandies, M.C.; Dapp, M.M.; Pournaras, E. Decrypting distributed ledger design—Taxonomy, classification and blockchain community evaluation. Clust. Comput. 2021. [Google Scholar] [CrossRef]
- Glatz, F. A Blockchain Token Taxonomy. Available online: https://medium.com/@heckerhut/a-blockchain-tokentaxonomy-fadf5c56139a (accessed on 10 October 2021).
- Ballandies, M.C.; Dapp, M.M.; Degenhart, B.A.; Helbing, D.; Klauser, S.; Pardi, A. Finance 4.0—A Socio-Ecological Finance System. In Finance 4.0—Towards a Socio-Ecological Finance System; Dapp, M., Helbing, D., Klauser, S., Eds.; Springer: Cham, Switzerland, 2021; pp. 53–91. [Google Scholar]
- Fungible vs. Non-Fungible Tokens on the Blockchain, 0xcert. Available online: https://medium.com/0xcert/fungible-vs-non-fungible-tokens-on-the-blockchain-ab4b12e0181a (accessed on 10 October 2021).
- Voshmgir, S. Token Economy: How Blockchain & Smart Contracts Revolutionize the Economy; Token Kitchen: Berlin, Germany, 2019. [Google Scholar]
- Helbing, D.; Klauser, S.; Dapp, M.; Ballandies, M.; Degenhart, B. FuturICT 2.0: Towards a Sustainable Digital Society with a Socio-Ecological Finance System (Finance 4.0); ETH: Zürich, Switzerland, 2020; Available online: ebook.finfour.net (accessed on 22 July 2021).

| Chem. Elem. | Possible Interpretations |
|---|---|
| Z | Total amount of produce coming from a single supplier (e.g., vegetables), Total amount of produced goods, e.g., clothing, furniture |
| X | Products not usually desired by most customers: imperfect products, e.g., tomatoes, used/not new goods, e.g., out-of-fashion clothing, second-hand furniture, recycled paper goods, e.g., notebooks |
| Y | Niche or impactful products: organically sourced produce, traditional products (e.g., clothing) supporting local businesses, environmentally friendly building materials, renewable energy sources, low-power electronics |
| A | Conventional currency |
| B | Token(s) received for actions such as: consuming imperfect fruits and vegetables, buying second-hand goods, donating food and goods to the community, taking part in clean-up projects in nature, volunteering activities that benefit the community, minimising one’s CO footprint |
| T | Market transactions |
| Cases | Reaction Rates in RM1—Equations (2) and (3) | Reaction Rates in RM2s—Equations (6)–(8) |
|---|---|---|
| Mec. | ODE System | Scaled ODE System |
|---|---|---|
| RM1 | ||
| RM2s | ||
| RM2 | ||
| Mec. | Fix. | Var. | Sol. | Cond. | Tr(J), Det(J), S(J) | Node |
|---|---|---|---|---|---|---|
| X, Y | A, B | (0, 0) | 0, 0, 0 | stable | ||
| RM2s | Y, A | X, B | (+,+) | −, +, + | stable | |
| A, B | X, Y | (+,+) | −, +, + | stable | ||
| X, Y | A, B | (0, 0) | 0, 0, 0 | stable | ||
| RM2 | Y, A | X, B | (+,+) | −, +, + | stable | |
| X, A | Y, B | (+,+) | −, +, + | stable | ||
| A, B | X, Y | (+,+) | −, +, + | stable | ||
| A | X, Y, B | (+,+,+) | +, −, + | saddle |
| Product | Status | Difference | New Coefficient |
|---|---|---|---|
| X | surplus | ||
| X | deficit | ||
| Y | surplus | ||
| Y | deficit |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardi, A.-L.; Paolucci, M. A Chemical Analysis of Hybrid Economic Systems—Tokens and Money. Mathematics 2021, 9, 2607. https://doi.org/10.3390/math9202607
Pardi A-L, Paolucci M. A Chemical Analysis of Hybrid Economic Systems—Tokens and Money. Mathematics. 2021; 9(20):2607. https://doi.org/10.3390/math9202607
Chicago/Turabian StylePardi, Anabele-Linda, and Mario Paolucci. 2021. "A Chemical Analysis of Hybrid Economic Systems—Tokens and Money" Mathematics 9, no. 20: 2607. https://doi.org/10.3390/math9202607
APA StylePardi, A.-L., & Paolucci, M. (2021). A Chemical Analysis of Hybrid Economic Systems—Tokens and Money. Mathematics, 9(20), 2607. https://doi.org/10.3390/math9202607






