Cluster Synchronization in Variable-Order Fractional Community Network via Intermittent Control
Abstract
1. Introduction
2. Model and Preliminaries
3. Main Result
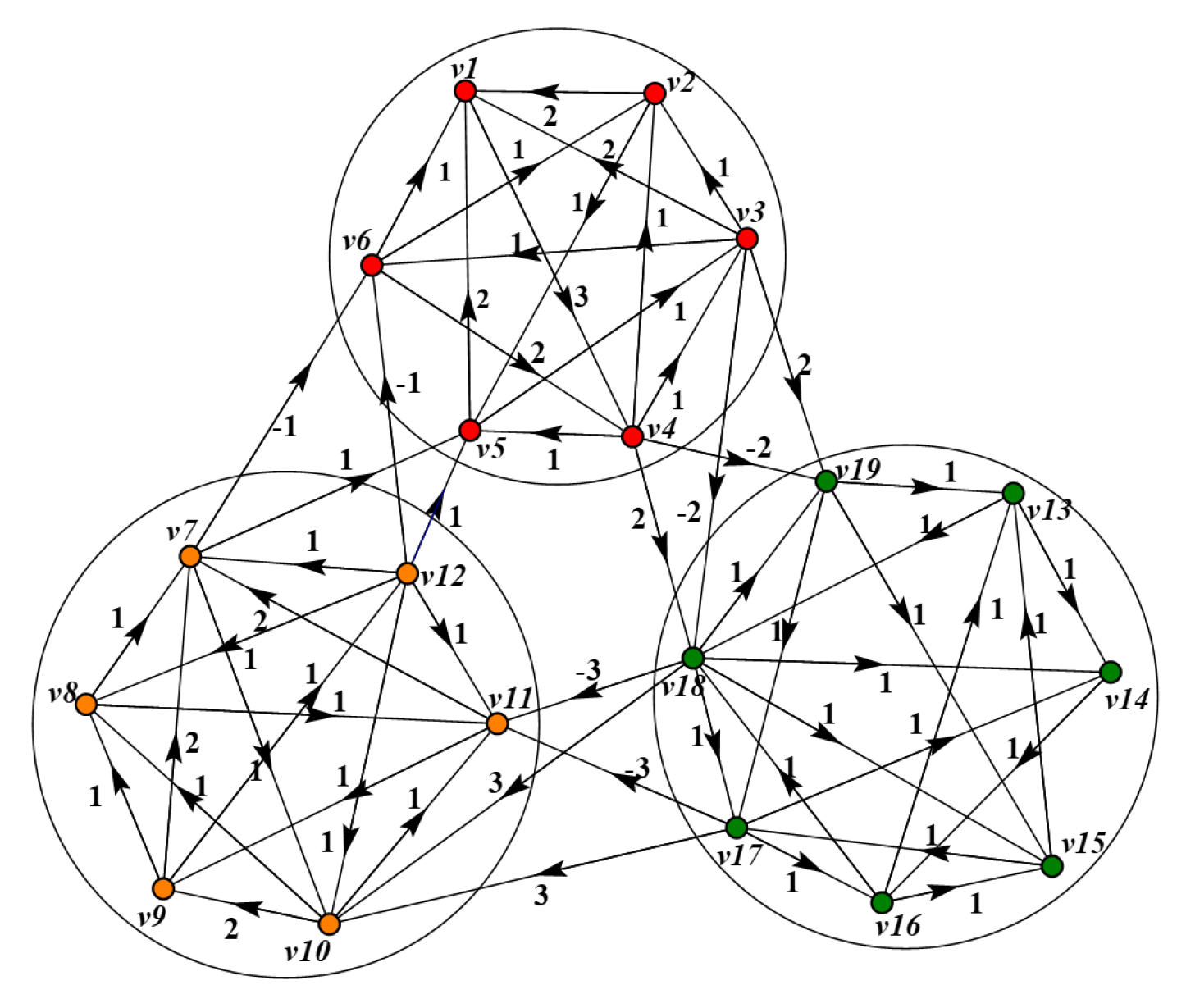
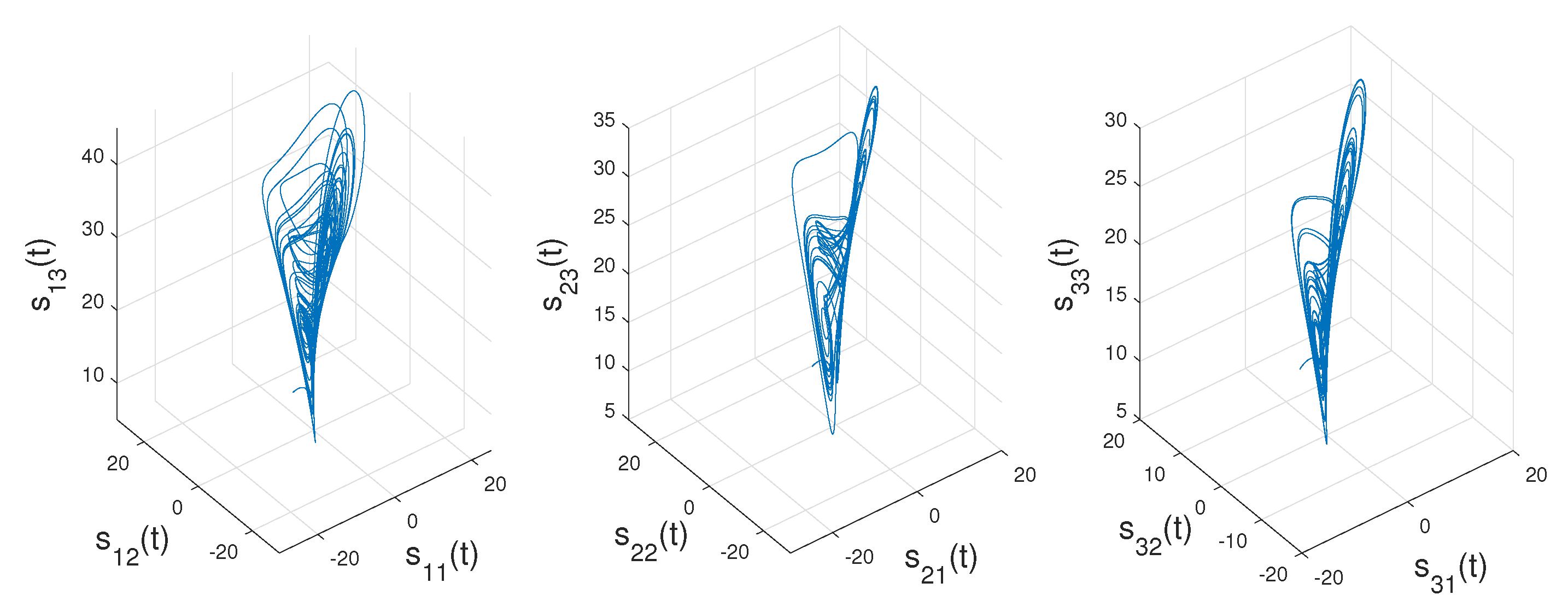
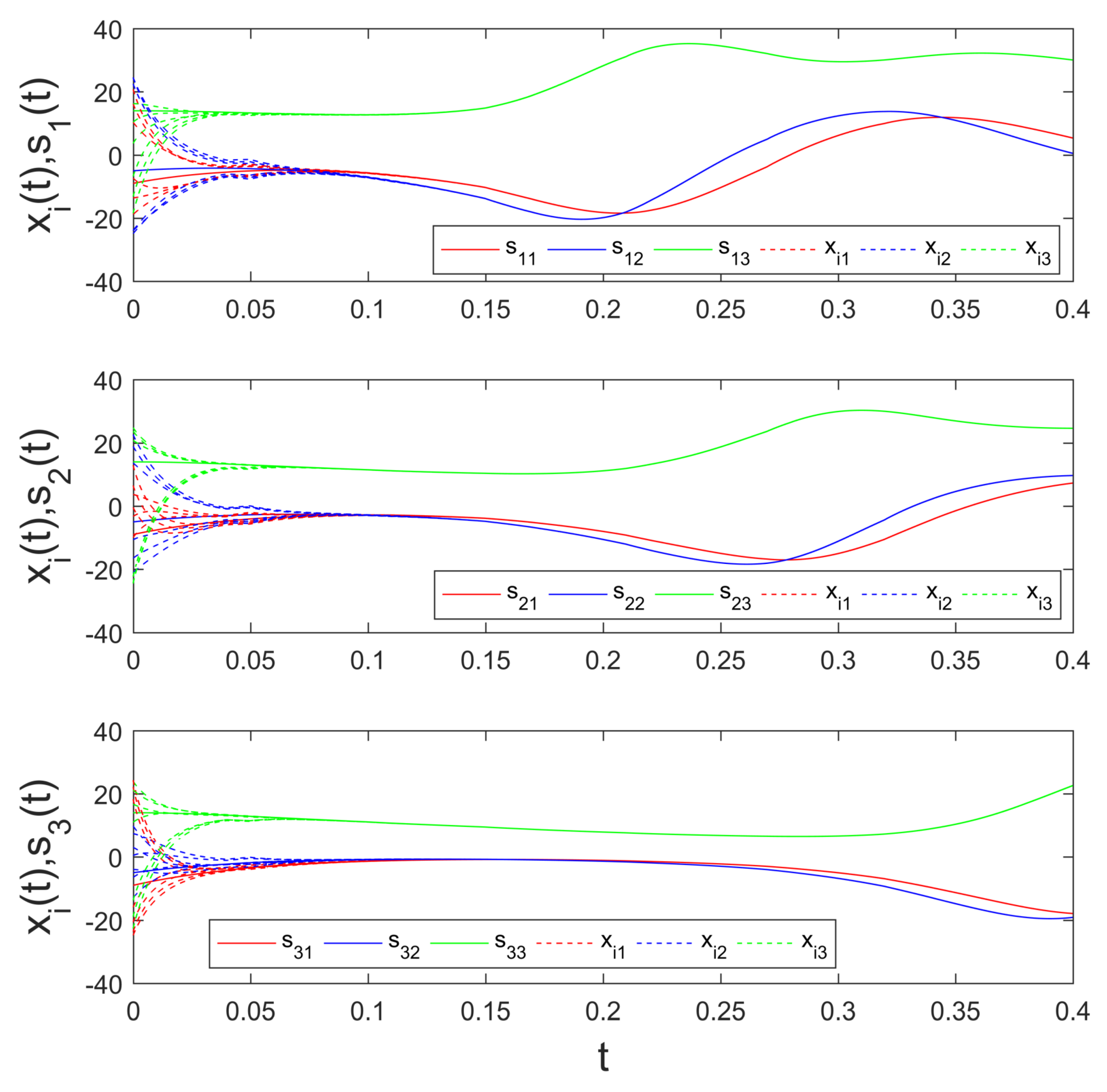
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, P.; Cai, S.; Shen, J.; Liu, Z. Adaptive exponential cluster synchronization in colored community networks via aperiodically intermittent pinning control. Nonlinear Dyn. 2018, 92, 905–921. [Google Scholar] [CrossRef]
- Yang, Q.; Wu, H.; Cao, J. Global cluster synchronization in finite time for complex dynamical networks with hybrid couplings via aperiodically intermittent control. Optim. Control. Appl. Methods 2020, 41, 1097–1117. [Google Scholar] [CrossRef]
- Feng, J.; Yang, P.; Zhao, Y. Cluster synchronization for nonlinearly time-varying delayed coupling complex networks with stochastic perturbation via periodically intermittent pinning control. Appl. Math. Comput. 2016, 291, 52–68. [Google Scholar] [CrossRef]
- Cai, S.; Jia, Q.; Liu, Z. Cluster synchronization for directed heterogeneous dynamical networks via decentralized adaptive intermittent pinning control. Nonlinear Dyn. 2015, 82, 689–702. [Google Scholar] [CrossRef]
- Guan, Z.H.; Yue, D.; Hu, B.; Li, T.; Liu, F. Cluster Synchronization of Coupled Genetic Regulatory Networks with Delays via Aperiodically Adaptive Intermittent Control. IEEE Trans. Nanobiosci. 2017, 16, 585–599. [Google Scholar] [CrossRef]
- Liu, X.; Li, P.; Chen, T. Cluster synchronization for delayed complex networks via periodically intermittent pinning control. Neurocomputing 2015, 162, 191–200. [Google Scholar] [CrossRef]
- Chen, H.; Shi, P.; Lim, C.C. Cluster Synchronization for Neutral Stochastic Delay Networks via Intermittent Adaptive Control. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3246–3259. [Google Scholar] [CrossRef]
- Liu, X.; Chen, T. Cluster synchronization in directed networks via intermittent pinning control. IEEE Trans. Neural Netw. 2011, 22, 1009–1020. [Google Scholar] [CrossRef]
- Kang, Y.; Qin, J.; Ma, Q.; Gao, H.; Zheng, W.X. Cluster synchronization for interacting clusters of nonidentical nodes via intermittent pinning control. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1747–1759. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, K.; Xiang, H.; Liu, Q. Pinning impulsive cluster synchronization of complex dynamical network. Phys. A Stat. Mech. Its Appl. 2020, 545, 123580. [Google Scholar] [CrossRef]
- Pan, L.; Cao, J.; Al-Juboori, U.A.; Abdel-Aty, M. Cluster synchronization of stochastic neural networks with delay via pinning impulsive control. Neurocomputing 2019, 366, 109–117. [Google Scholar] [CrossRef]
- Gong, X.; Gan, L.; Wu, Z. Adaptive impulsive cluster synchronization in community network with nonidentical nodes. Int. J. Mod. Phys. C 2016, 27, 1650010. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; Yang, H.; Zhong, S. An improved impulsive control approach for cluster synchronization of complex networks with parameter mismatches. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2561–2570. [Google Scholar] [CrossRef]
- Du, K.; Ma, Q.; Kang, Y.; Fu, W. Robust Cluster Synchronization in Dynamical Networks With Directed Switching Topology via Averaging Method. IEEE Trans. Syst. Man Cybern. Syst. 2020. [Google Scholar] [CrossRef]
- Zhou, L.; Tan, F.; Yu, F.; Liu, W. Cluster synchronization of two-layer nonlinearly coupled multiplex networks with multi-links and time-delays. Neurocomputing 2019, 359, 264–275. [Google Scholar] [CrossRef]
- Menara, T.; Baggio, G.; Bassett, D.S.; Pasqualetti, F. Stability Conditions for Cluster Synchronization in Networks of Heterogeneous Kuramoto Oscillators. IEEE Trans. Control Netw. Syst. 2020, 7, 302–314. [Google Scholar] [CrossRef]
- Liu, L.; Ding, X.; Zhou, W. Prescribed-time cluster synchronization of uncertain complex dynamical networks with switching via pinning control. Neurocomputing 2021, 419, 136–147. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, Z.; Li, X.; Qiu, J. Cluster Synchronization in Delayed Networks With Adaptive Coupling Strength via Pinning Control. Front. Phys. 2020, 8, 235. [Google Scholar] [CrossRef]
- Liu, X.; Chen, T. Finite-time and fixed-time cluster synchronization with or without pinning control. IEEE Trans. Cybern. 2018, 48, 240–252. [Google Scholar] [CrossRef]
- Liu, P.; Zeng, Z.; Wang, J. Asymptotic and Finite-Time Cluster Synchronization of Coupled Fractional-Order Neural Networks with Time Delay. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4956–4967. [Google Scholar] [CrossRef]
- Zhang, L.; Kartci, A.; Elwakil, A.; Bagci, H.; Salama, K.N. Fractional-Order Inductor: Design, Simulation, and Implementation. IEEE Access 2021, 9, 73695–73702. [Google Scholar] [CrossRef]
- Giraldo-Londoño, O.; Paulino, G.H.; Buttlar, W.G. Fractional calculus derivation of a rate-dependent PPR-based cohesive fracture model: Theory, implementation, and numerical results. Int. J. Fract. 2019, 216, 1–29. [Google Scholar] [CrossRef]
- Wu, G.C.; Zeng, D.Q.; Baleanu, D. Fractional impulsive differential equations: Exact solutions, integral equations and short memory case. Fract. Calc. Appl. Anal. 2019, 22, 180–192. [Google Scholar] [CrossRef]
- Wu, G.C.; Deng, Z.G.; Baleanu, D.; Zeng, D.Q. New variable-order fractional chaotic systems for fast image encryption. Chaos 2019, 29, 083103. [Google Scholar] [CrossRef]
- Wu, F.; Gao, R.; Liu, J.; Li, C. New fractional variable-order creep model with short memory. Appl. Math. Comput. 2020, 380, 125278. [Google Scholar] [CrossRef]
- Xu, L.; Chu, X.; Hu, H. Quasi-synchronization analysis for fractional-order delayed complex dynamical networks. Math. Comput. Simul. 2021, 185, 594–613. [Google Scholar] [CrossRef]
- Zhou, J.; Yan, J.; Wu, Z. Synchronization of fractional-order dynamical network via aperiodically intermittent pinning control. Adv. Differ. Equ. 2019, 2019, 165. [Google Scholar] [CrossRef]
- Liu, P.; Zeng, Z.; Wang, J. Global Synchronization of Coupled Fractional-Order Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2358–2368. [Google Scholar] [CrossRef]
- Zhang, F.; Zeng, Z. Multistability of Fractional-Order Neural Networks with Unbounded Time-Varying Delays. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 177–187. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.Y.; Zheng, F.X.; Shiri, B. Mittag-leffler stability analysis of tempered fractional neural networks with short memory and variable-order. Fractals 2021, 2140029. [Google Scholar] [CrossRef]
- Wu, G.C.; Luo, M.; Huang, L.L.; Banerjee, S. Short memory fractional differential equations for new memristor and neural network design. Nonlinear Dyn. 2020, 100, 3611–3623. [Google Scholar] [CrossRef]
- Ding, D.W.; Yan, J.; Wang, N.; Liang, D. Adaptive Synchronization of Fractional Order Complex-Variable Dynamical Networks via Pinning Control. Commun. Theor. Phys. 2017, 68, 366–374. [Google Scholar] [CrossRef]
- Fan, H.; Zhao, Y. Cluster Synchronization of Fractional-Order Nonlinearly-Coupling Community Networks with Time-Varying Disturbances and Multiple Delays. IEEE Access 2021, 9, 60934–60945. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, Z. Cluster synchronization in fractional-order network with nondelay and delay coupling. Int. J. Mod. Phys. C 2021, 2250006. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, Y.; Wu, Z.Y. Cluster synchronization of fractional-order directed networks via intermittent pinning control. Phys. A Stat. Mech. Its Appl. 2019, 519, 22–33. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, C.; Liu, Y.; Luo, M. Fractional corresponding operator in quantum mechanics and applications: A uniform fractional Schrödinger equation in form and fractional quantization methods. Ann. Phys. 2014, 350, 124–136. [Google Scholar] [CrossRef]
- Zhou, F.X.; Wang, L.Y.; Liu, Z.Y.; Zhao, W.C. A viscoelastic-viscoplastic mechanical model of time-dependent materials based on variable-order fractional derivative. Mech. Time-Depend. Mater. 2021. [Google Scholar] [CrossRef]
- Liu, J.; Wu, F.; Zou, Q.; Chen, J.; Ren, S.; Zhang, C. A variable-order fractional derivative creep constitutive model of salt rock based on the damage effect. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7. [Google Scholar] [CrossRef]
- Dehestani, H.; Ordokhani, Y.; Razzaghi, M. Application of fractional Gegenbauer functions in variable-order fractional delay-type equations with non-singular kernel derivatives. Chaos Solitons Fractals 2020, 140, 110111. [Google Scholar] [CrossRef]
- Ghanbari, B.; Gómez-Aguilar, J.F. Modeling the dynamics of nutrient–phytoplankton–zooplankton system with variable-order fractional derivatives. Chaos Solitons Fractals 2018, 116, 114–120. [Google Scholar] [CrossRef]
- Tang, H.; Wang, D.; Huang, R.; Pei, X.; Chen, W. A new rock creep model based on variable-order fractional derivatives and continuum damage mechanics. Bull. Eng. Geol. Environ. 2018, 77, 375–383. [Google Scholar] [CrossRef]
- Fei, W.; Jie, L.; Quanle, Z.; Cunbao, L.; Jie, C.; Renbo, G. A triaxial creep model for salt rocks based on variable-order fractional derivative. Mech. Time-Depend. Mater. 2021, 25, 101–118. [Google Scholar] [CrossRef]
- Xiang, M.; Yang, D.; Zhang, B. Homoclinic solutions for Hamiltonian systems with variable-order fractional derivatives. Complex Var. Elliptic Equ. 2020, 65, 1412–1432. [Google Scholar] [CrossRef]
- Kachia, K.; Solís-Pérez, J.E.; Gómez-Aguilar, J.F. Chaos in a three-cell population cancer model with variable-order fractional derivative with power, exponential and Mittag-Leffler memories. Chaos Solitons Fractals 2020, 140, 110177. [Google Scholar] [CrossRef]
- Ramirez, L.E.; Coimbra, C.F. A variable order constitutive relation for viscoelasticity. Ann. Der Phys. (Leipz.) 2007, 16, 543–552. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Application of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar] [CrossRef][Green Version]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution (Mathematics in Science and Engineering); Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Wang, F.; Yang, Y. Intermittent synchronization of fractional order coupled nonlinear systems based on a new differential inequality. Phys. A Stat. Mech. Its Appl. 2018, 512, 142–152. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, G. A note on the fractional-order Chen system. Chaos Solitons Fractals 2006, 27, 685–688. [Google Scholar] [CrossRef]
- Li, C.; Chen, G. Chaos in the fractional order Chen system and its control. Chaos Solitons Fractals 2004, 22, 549–554. [Google Scholar] [CrossRef]
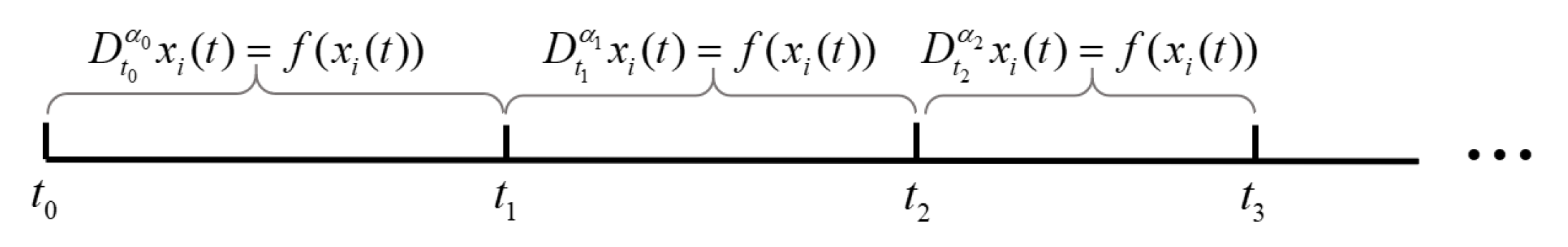
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0.99 | 0.97 | 0.98 | 0.96 | 0.99 | 0.93 | 0.95 | 0.94 | |
| k | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0.97 | 0.95 | 0.96 | 0.95 | 0.97 | 0.99 | 0.98 | 0.98 |
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | ||||||||
| k | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0.42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wu, Z. Cluster Synchronization in Variable-Order Fractional Community Network via Intermittent Control. Mathematics 2021, 9, 2596. https://doi.org/10.3390/math9202596
Wang Y, Wu Z. Cluster Synchronization in Variable-Order Fractional Community Network via Intermittent Control. Mathematics. 2021; 9(20):2596. https://doi.org/10.3390/math9202596
Chicago/Turabian StyleWang, Yi, and Zhaoyan Wu. 2021. "Cluster Synchronization in Variable-Order Fractional Community Network via Intermittent Control" Mathematics 9, no. 20: 2596. https://doi.org/10.3390/math9202596
APA StyleWang, Y., & Wu, Z. (2021). Cluster Synchronization in Variable-Order Fractional Community Network via Intermittent Control. Mathematics, 9(20), 2596. https://doi.org/10.3390/math9202596






