Abstract
Student dropout, defined as the abandonment of a high education program before obtaining the degree without reincorporation, is a problem that affects every higher education institution in the world. This study uses machine learning models over two Chilean universities to predict first-year engineering student dropout over enrolled students, and to analyze the variables that affect the probability of dropout. The results show that instead of combining the datasets into a single dataset, it is better to apply a model per university. Moreover, among the eight machine learning models tested over the datasets, gradient-boosting decision trees reports the best model. Further analyses of the interpretative models show that a higher score in almost any entrance university test decreases the probability of dropout, the most important variable being the mathematical test. One exception is the language test, where a higher score increases the probability of dropout.
1. Introduction
Education is one of the most important factors in the development of a country. A better and more extensive education helps to improve levels of social wellness and economic growth. At the same time, education decreases social inequalities and promotes social mobility. Finally, it also promotes science, technology, and innovation. In summary, it helps to build a better society. According to a report from UNESCO in 2015 [1], the global number of students in high education has grown from 28.5 million in 1970 to 196 million in 2012, and to 250 million in 2021 [2]. However, not all these students necessarily finish their studies, and many of them abandon the university without achieving a degree.
Student dropout, defined as the abandonment of a high education program before obtaining the degree without reincorporation [3], is a problem that affects every higher education institution. It is estimated that half of the students do not graduate [2]. In the United States, the overall dropout rate for undergraduate college students is 40% [4]. In the European Union, the following countries have the lowest dropout rates: United Kingdom, Norway, and France [5] (16%, 17%, and 24% respectively), while Italy has the highest dropout rate (33%), followed by the Netherlands (31%) [5]. In Latin America, 50% of the population between the ages of 25 and 29 who started a university degree did not complete their studies [6].
There are different types of dropouts, and each of them can be analyzed in different ways. Even though a student can drop out of college at any time during his career, most dropouts happen during the first year. In the United States, until 2018, approximately 30% of college freshmen drop out before their sophomore year [4]. In the United Kingdom, 6.3% of young full-time students dropped out during the first year in 2016–2017 [7]. In Latin America, Colombia had a 36% of student dropout in the first year in 2013 [6], while Chile had a 21% in 2019 [8]. For example, Universidad Adolfo Ibáñez and Universidad de Talca, the universities under analysis in this work, have a 12% and 15% of first-year student dropout.
Student dropout is a major issue within the Chilean higher education system. Chilean universities are mostly funded by student fees, and high dropout rates hinder their short-term economic viability. Moreover, the accreditation process in use within the country to evaluate the quality of universities favor high retention rates (in other words, low dropout rates) and penalize low retention rates with lower accreditation rankings. Consequently, Chilean universities try to reduce dropout due to short-term economic requirements, but also focus on the metric to ensure a better accreditation rank which leads to better ranking within the system, opening the door to mid- and long-term benefits, better recruitment possibilities and better indirect funding from the government. The concerns regarding dropout levels also play a major role politically as the government recently introduced new laws that give university education access to all the population through state scholarships. In fact, this research stems from a nationwide publicly funded research project to evaluate the major sources of dropout within the higher educational system during the first year; the two above-mentioned universities were used as the test bed to identify common dropout issues within the full Chilean university system.
The Universidad Adolfo Ibáñez (UAI for short) and the Universidad de Talca (U Talca for short) constitute examples ofthe diversity within the higher education system in Chile. The UAI is one of the leading private universities in the country. The university grew from a business school with the same name, and it has two campuses, one located in Santiago de Chile, the capital of the country, and another in Viña del Mar, in the greater Valparaíso area which is the third most populated area of the country. Most students come from private high schools within the Santiago and Valparaíso region, but also the university also attracts students from different areas of the country due to the perception that the university provides a business-oriented education that covers the needs of the businesses within the country. The university only offers a limited number of academic undergraduate degrees, including engineering, business administration, journalism, psychology, design and law, as well as some Master’s and Ph.D. degrees. The U Talca is a public university located in the Maule region, in the south of the country, and is considered one of the best regional universities within the country. The university has five campuses and offers a wide variety of degrees in multiple topics at undergraduate, graduate and Ph.D. levels. The majority of students come from the Maule region and receive free education through the previously mentioned state scholarships that cover four years of undergraduate education for the population from the six deciles with lower rents. While the differences between these universities are evident, both universities are ranked among the ten best universities in Chile according to the QS university ranking [9].
This work reports the results from machine learning models to identify the major factors involving dropout within these universities for their engineering undergraduate degrees. In order to compare possible dropout predictors between these universities, we propose multiple machine learning models and compare the dissimilarities among the models learned for each university as well as for a joint dataset covering both universities. A posterior analysis of these models will allow us to determine if the same dropout behavior pattern can be observed in both universities, and to evaluate the quality of different models within the same predictive task.
The paper is structured as follows. Section 2 provides a literature review on the area, including the application of machine learning approaches to dropout prediction. Section 3 describes the methodology followed in this work. Section 4 provides an exploratory analysis of the collected data, and Section 5 provides the main results of the study. Section 6 gives some conclusions. We provide an appendix, Appendix B with further details on the comparisons among models.
2. Literature Review
The literature on student dropout is extensive and covers a wide variety of approaches from very different research fields. The problem has been tackled from psychological and economic perspectives, as well as using qualitative and quantitative methods. We organize this section according to the area and methodologies considered within these previous works. Section 2.1 provides a review of work derived from explanatory approaches, while Section 2.2 considers predictive approaches except for machine learning ones, which are discussed in Section 2.3. Finally, Section 2.4 summarizes the conclusions from the literature review and highlights the major differences between our proposal and previous work.
2.1. Explanatory Approaches
The problem of student dropout in higher education has been studied for many years, using different perspectives. One of the first and most popular works have been the adaptation models [10,11,12,13]. These models consider how adaptation and social integration affect the decision to drop out. Ref. [10] considers a model based on Durkheim’s theory of suicide, dropout being the result of a complex social process that includes family and previous educational background, academic potential, normative congruence, friendship support, intellectual development, educational performance, social integration, satisfaction and institutional commitment. In [11], a model considering factors such as student adaptation, the institution and previous academic performance is formulated. Similarly, in [12], a student attrition model is proposed. Ref. [12] argues that student dropout depends on factors that affect directly the student (factors external to the university) as well as their sense of wellness. Ref. [13] proposes a mixed model, where the key factors are related to the quality of the institution, the security in career choice, or the existence of scholarships.
The previous models served as a base for other theoretical investigations. In [14], for example, the authors cluster the theoretical explanatory models into four different groups: (1) the adaptation model, describing the lack of an individual’s integration into the context; (2) the structural model, the university structure, including political, economic, and social, that influences students to dropout; (3) the economic model, describing the student’s choice of an alternative way to invest time, energy, and resources that could offer greater benefits in the future; and (4) the psycho-pedagogic model, that covers a mix of different factors from the adaptation and structural models, plus other dimensions of a psycho-educative nature, such as learning strategies.
Other studies, mainly based on interviews and manual analysis, have reached diverse conclusions [15,16,17,18]. Ref. [15] concluded that previous academic performance variables are the best predictors of university performance; however, aside from this, time management is also important. Ref. [16] uses surveys to young deserters and concludes that dropouts is mostly related to socioeconomic or individual problems. Similarly, ref. [17] inferred that the primary cause of dropout is the lack of funding of students. Consequently, [17] proposes that the actions of the welfare department within universities should be more proactive and guide students in the financing options they can access. Ref. [18] states that the causes of dropout for one student may not apply to another student, meaning that each student dropout may occur for different reasons.
2.2. Predictive Approaches
An alternative line of research focuses on the application of mathematical models to predict student dropout. The range of methods used within these works is varied and is comprised of genetic algorithms to multivariate and survival analysis [19,20,21,22,23]. These works add a new perspective and generate new conclusions. Ref. [19] collected data from a web-based system and used a genetic algorithm to predict student performance. Specifically, the work analyzes the time students spent on resources from the university web system, rendering a 10% improvement in accuracy over previous classifiers. Ref. [20] applied correlational analysis, relating the student dropout with four different variables: previous academic performance, first-year college performance, attendance, and date of enrollment (students whose enroll after the start of the academic year have a higher dropout rate). Ref. [21] used a static econometric model and concludes that previous academic performance and funding are some of the best indicators for dropout. Ref. [22] used a rule-based knowledge discovery system to identify relevant causes for student dropout in the first and second year of an engineering degree. For first-year students, the most important aspects are: who funds the student and the number of years from the end of secondary school to university entrance. However, these factors change for second-year students, where a common dropout denominator is the “number of subjects not attended as full-time students”, i.e., full-time students are most likely to finish their career. Recently, ref. [23], in a world where the massification of technology has been mostly adopted by the younger population, included the role of procrastination as a factor in student dropout. The work shows an association between high levels of procrastination and low academic performance in students. The conclusions show that procrastination can be evaluated with entry tests and can be overcome by training.
Statistical models have also been applied for this type of analysis. Ref. [24] used maximum likelihood probit models to estimate the effects of specific factors that may lead to student dropout, concluding that better results on national high school exams substantially reduce the risk of dropout, and that female students also have a relatively lower estimated dropout probability. Ref. [25] used the multivariate analysis technique to determine factors that affect university dropout, using a questionnaire to collect data. The authors conclude that the factors that affect student dropout the most are economical (individual and family), institutional (management, institutional intervention, and monitoring student), mental (psychosocial and family support), and personal (motivational and social relationship).
Finally, more complex statistical models, such as survival models, have also been applied to analyze this problem. Ref. [26] analyzed socioeconomic characteristics and personal factors related to dropouts using duration analysis (the dropout is analyzed as a process in time, and the model evaluates the students that are more likely to graduate). Among the conclusions in [26] we highlight that men, students who previously dropout from other studies, and working students are more likely to dropout. Ref. [27] employed a discrete-time competing risks survival model to identify risk factors associated with high education dropout in the Pontificia Universidad Católica de Chile. The authors propose a Bayesian variable selection framework that handles covariate selection. The authors conclude that there is a high degree of heterogeneity among the programs at the university; hence, building a common model for the entire university was not recommended.
2.3. Machine Learning Approaches
Recently, institutions have collected their data to generate value from them through machine learning models. This has fueled several works, from simple predictions to variable analysis through interpretative models. In this section, we provide a review of the application of machine learning models for student dropout analysis.
2.3.1. Decision Trees
The decision trees are structures used to classify based on decisions, where each leaf determines a class label [28]. One of the first decision tree models applied to dropout is provided in [29]. This work compares multiple training processes for Decision trees applied to dropout prediction, i.e., ID3, C4.5, and ADT, and concludes that ADT provides the best decision tree. The tree has a precision rate of 82.8%, but does not provide informative conclusions. Similarly, ref. [30] applied different decision tree training algorithms to predict student dropout at Simón Bolívar University (Colombia). Even though the work mentions that decision trees are a suitable model, the work does not reach any conclusion regarding the most important features, as different training algorithms selected dissimilar variables within their decision trees. Finally, ref. [31] determined that decision trees with parameter optimization results provide better precision when compared to other models. Moreover, the work determines three variables that could explain dropouts: grades, years of advancement in the career, and admission test university scores.
2.3.2. Logistic Regression
A logistic regression is a probability model introduced in [32], in which each variable is associated with a parameter showing its relevance. Ref. [33] provides a methodology to apply a logistic regression model to the student dropout problem. The work focuses on providing basic information to educational researchers following the model. Ref. [34] analyzed dropout in Chilean higher education at a university level, concluding that the dropout is related to socioeconomic level, previous academic performance, score in the university admission test, academic scholarships, and financial credits. Government financial credits and scholarships have among the strongest correlations with persistence in higher education programs, implying important financial constraints within the Chilean higher education system. Finally, ref. [35] analyzes over seventeen variables to determine seven variables that affect dropout: gender, time of study (day or evening), age group, school of origin, lives with family, score in the university admission test, and father’s occupation; the admission test score is the most important feature among them.
2.3.3. Naive Bayes
The Naive Bayes model is a probabilistic model based on the Bayes theorem, which can also be interpreted [36]. Ref. [37] analyzed data from Dr. R.M.L. Awadh University, India, identifying factors that are highly correlated with previous academic performance, living location, language of teaching (mixed classes in native language and English, or only in English), mother’s education, student habits, family annual income, and student family status. Later, ref. [38] applied a naive Bayes model for data from the Amrita School of Arts & Sciences to predict early dropout. In this study, the most relevant variables were academics, demographic, psychological, and health factors.
2.3.4. K-Nearest Neighbors (KNN)
KNN classifies each observation according to the vote of its K more similar (i.e., closer) neighbors. This closeness is determined according to some distance function [39]. To date, there is not much research dedicated to predicting university student dropout or similar problems using KNN Neighbor methods. Ref. [40] used KNN to predict student performance in a touch-typing online course. Specifically, it identified at an early stage of the course those students who have a high risk of failing, using variables collected from course lessons, such as typing speed, accuracy, time spent in the lesson, and exam attempts. Recently, ref. [41] used a KNN model to predict student dropout based on welfare-related variables, such as parental involvement, education, and annual income.
2.3.5. Neural Networks
An artificial neural network is a biologically inspired method capable of creating complex non-linear predictive models [42]. The generated models are considered to be black box models, implying that the parameters learned from the model are difficult to interpret [43]. Ref. [44] used student surveys, telephone interviews, and administrative data related to predict student dropout in a school of medicine. The characteristics deemed important can be summarized into personal, parental features, location, previous academic performance, and university admission test scores. The network obtained a precision between 65% and 84% in its predictions. A posterior sensitive analysis determined that the most important variables were family education, school origin, lack of pre-university guidance, study with friends, and motivation. Another example of this type of model is the work of [45], where a multilayer perceptron obtained a prediction rate of 96.3% (96.8% using a radial base function), using variables that can be summarized in whether the student has children, knowledge in software used in the university major, family commitment, adaptation to the university, university ranking and student’s perspective on his or her integration into the labor market.
2.3.6. Support Vector Machine
A Support Vector Machine (SVM), initially known as Support-Vector Networks, uses a hyperplane to separate between classes [46,47]. The algorithm searches for the hyperplane that maximizes the margin between the classes, classifying the data points according to their position with respect to the defined hyperplane. In the case of classes that are not linearly separable, a kernel is used to increase the dimension of the data points, finding a hyperplane in this new dimension. Ref. [48] predicts degree completion within three years by STEM community college students, on a small dataset of 282 students and 9 variables. Recently, [49] compares the performance of linear support vector machines against other machine learning models, proving that SVM obtain good results predicting student performance.
2.3.7. Random Forest
Random forest is a method that constructs tree-based classifiers whose capacity can be arbitrarily expanded to increase accuracy. It builds multiple decision trees, each of them using a random sample of the original variables. The class label of a data point is determined using a weighted vote scheme with the classification of each decision tree [50]. Ref. [51] compares random forest against boosted decision tree on high-school dropout from the National Education Information System (NEIS) in South Korea. Ref. [52] predicts university dropout in Germany using random forest. The study determines that one of the most important variables is the final grade at secondary school.
2.3.8. Gradient Boosting Decision Tree
A general gradient descent boosting paradigm is developed for additive expansions based on any fitting criterion. When used with decision trees, it uses regression trees to minimize the error of the prediction. A first tree predicts the probability of a data point to belong to a class; the next tree models the error of the first tree, minimizing it and calculating a new error, which is the new input for a new error-modeling tree. This boosting improve the performance, where the final model is the sum of the output of each tree [53]. Given its popularity, gradient boosting is being used as one of the method to compare dropout in several papers, especially in the Massive Open Online Course [54,55,56].
2.3.9. Multiple Machine Learning Models Comparisons
Besides the previously described works, several investigations have used and compared more than one model to predict university dropout. Ref. [3] compared decision trees, neural networks, support vector machines, and logistic regression, concluding that a support vector machine provided the best performance. The work also concluded that the most important predictors are past and present educational success and financial help. Ref. [57] analyzed dropout from engineering degrees at Universidad de Las Americas, comparing neural networks, decision trees, and K-median with the following variables: score in the university admission test, previous academic performance, age and gender. Unfortunately, the research had no positive results because of unreliable data. Ref. [58] compared decision trees, Bayesian networks, and association rules, obtaining the best performance with decision trees. The work identified previous academic performance, origin, and age of student when they entered the university as the most important variables. Additionally, it identified that during the first year of the degree is where containment, support, tutoring and all the activities that improve the academic situation of the student are more relevant. Lately, two similar works [59,60] used Bayesian networks, neural networks, and decision trees to predict student dropout. Both works found that the most influential variables were the university admission test scores and the economic benefits received by the students (scholarships and credits). Finally, ref. [61] compares logistic regression with decision trees. This work obtains slightly better results with decision trees than with logistic regression and concludes that the most relevant factors to predict study success and dropout are combined features such as the count and the average of passed and failed examinations or average grades.
2.4. Opportunities Detected from the Literature Review
An analysis of previous work shows that the literature is extensive, with multiple alternative approaches. Specifically, each work is focused on the use of a single or a few approaches to a specific case study.
In this work, we differ from previous works in these two major issues.
First, we consider multiple, eight, machine learning models and compare their results both in terms of their ability to predict results and in terms of their ability to explain the phenomenon under investigation. On the one hand, the analysis of multiple models will allow us to evaluate what is the real contribution of each model and, on the other hand, the identification of explanatory variables will enable us to extract general conclusions regarding the major features that affect dropout regardless of the method in use.
Second, we consider data from two different universities. Using these two universities will allow us to examine the applicability of a single model within different settings. Moreover, it will allow us to draw conclusions that try to transcend the limitations of considering only data from one university to find out dropout sources. Specifically, we investigate what we can draw from one university to a different university.
In summary, this work builds upon the previous literature by providing a larger comparison of methods and a comparative study with data from two different universities regarding dropout issues. As a result, we remove the possible bias associated to a specific university and draw conclusions on the problem of dropout itself and the applicability of distinct machine learning methods to dropout prediction.
Note that the focus of our work is the prediction of dropout chances among first-year students only with the information available before the start of the courses; that is, information provided during their application steps. This problem is specially relevant for our case of study as it provides means to universities to focus their early retention policies among those students that have a major risk of abandoning the university in early stages.
3. Methodology
In this paper, we compare the learned patterns from machine learning models for two different universities (UAI and U Talca) and analyze the dissimilarities among prediction models. In order to perform the comparison, we create multiple models that try to predict dropout in engineering undergraduate degrees using datasets from these two Chilean Universities. A posterior analysis of the constructed models is used to determine if the same dropout behavior patterns are observed in both universities or if there are major differences between them.
In order to reach these objectives, the research was structured as follows:
In a first stage, an exploratory data analysis is performed. The objective is to understand the data and their variables. The analysis also includes data pre-processing and data cleaning.
In this phase, we gathered initial information from the data through the description of each variable; we study the distribution of each variable, its possible values, and we identify missing data from the datasets. During this process, we clean the data by discarding variables gathered during the first year, since we cannot use them for first-year dropout prediction. Other unnecessary variables are also deleted, as well as problematic observations, such as old records or observations with numerous missing values. We also grouped potential values from some variables (i.e., changing the address of a student by its region of origin) in order to improve the quality of this variable and to reduce the complexity of the dataset. We also analyze missing data, searching for a pattern in their variable distribution to be used as a replacement. Finally, we also perform outlier detection. In our case, outliers did not require special treatment, as most of them were indirectly eliminated when deleting older data.
In the second stage, we implemented all the machine learning models. This step includes a parameter-tuning phase for the hyper-parameters of each model, and a variable selection process, per model, based on a forward selection procedure.
We implemented eight different models: a K-Nearest Neighbor (KNN) [62], a Support Vector Machine (SVM) [63], a decision tree [28], a random forest [64], a gradient-boosting decision tree [53], a naive Bayes [36], a logistic regression [65], and a neural network [66]. All models were implemented using python and the libraries scikit-learn [67] and Keras [68].
For each of the eight models, we performed a hyper-parameter tuning procedure to select the variables included in each model according to their performance. For the tuning process, we performed a grid search over the most common parameters for each of these models. For KNN, we searched K from 1 to 100. With the SVM, we evaluated all combinations for and three kernels: polynomial, radial basis function, and sigmoid.
For tree-related models (decision tree, random forest, and gradient boosting) we used one-hot encoding for nominal variables and tried multiple parameter combinations. In the case of the decision tree, we analyzed a variable number of minimum samples to constitute a leaf, changing its value from 10 to 200. The results provided by decision tress constructed according to this method outperformed the results provided by trees selected according to their maximum depth. For random forest and gradient-boosting methods, we tried all combinations among the minimum number of samples at a leaf, , number of trees, , and the number of sampled features per tree, .
For the Naive Bayes method, we considered numerical and nominal variable separately and tried the following Laplace smoothing coefficients, . For logistic regression, we use the method from Broyden–Fletcher–Goldfarb–Shanno [69,70,71,72] and a “L2” regularization penalty [73].
Finally, for neural networks, we tried multiple architectures, varying the number of hidden layers from 1 to 5 and the number of neurons from 5 to 20. The networks were trained using a binary cross-entropy loss function, and “adam” as the optimizer [74].
The selection of variables in each model was performed using a forward selection approach [75]. Forward selection starts with an empty model, and, at each iteration, it selects among all variables the one that provides the best performance. This process is iterated until all variables belong to the model or the results do not improve.
In the third stage, we evaluate all the models using a k-fold cross-validation procedure [76]. This procedure will allow us to extract information from the data.
In this stage, we estimate the mean and standard deviation error through 10-fold cross-validation on different measures (accuracy and score for both classes). Ten-fold cross-validation helps us to estimate the error distribution by splitting the datasets into 10 folds. Then, 9 folds are selected for training and tested in the other fold. This process is repeated until all folds are used for testing, and the error estimation is given by the average over error folds. In addition, considering that we will model student dropout, there is likely to be an important difference in the proportion of data between students that dropout and students that do not dropout, leading to an unbalanced data problem. Unbalanced issues will be minimized through undersampling. Specifically, the majority class is reduced through random sampling, so that the proportion between the majority and the minority class is the same. To combine both methods (10-fold cross-validation with an undersampling technique), we apply the undersampling technique over each training set produced after a K-fold split and then evaluate in the original test fold. With that, we avoid possible errors of double-counting duplicated points in the test sets when evaluating them.
We measure the performance of each model using the accuracy, the score for both classes, and the precision and the recall for the positive class, all of them explained considering the values of the confusion matrix; true positives (TP); true negatives (TN); false positives (FP); and false negatives (FN).
Accuracy, Equation (1), is one of the basic measures used in machine learning and indicates the percentage of correctly classified points over the total number of data points. An accuracy index varies between 0 and 1, where a high accuracy implies that the model can predict most of the data points correctly. However, this measure behaves improperly when a class is biased because high accuracy is achievable labeling all data points as the majority class.
To solve this problem, we will use other measures that avoid the TN reducing the impact of biased datasets. The recall (Equation (2)) is the number of TP over the total points which belong to the positive class (). The recall varies between 0 and 1, where a high recall implies that most of the points which belong to the positive class are correctly classified. However, we can have a high value of FP without decreasing the recall.
The precision (Equation (3)) is the number of TP over the total points classified as positive class (). The precision varies between 0 and 1, where a high precision implies that most of the points classified as positive class are correctly classified. With precision, it is possible to have a high value of FN without decreasing its value.
To solve the problems from recall and precision, we also use the score, Equation ((4)). The score is the harmonic average of the precision and recall, and tries to balance both objectives, improving the score on unbalanced data. The score varies between 0 and 1, and a high score implies that the model can classify the positive class and generates a low number of false negatives and false positives. Even though true positives are associated with the class with fewer labels, we report the score using both classes as true positive, avoiding misinterpretation of the errors.
In the final fourth stage, we perform an interpretation process, where the patterns or learned parameters from each model are analyzed to generate new information applicable to future incoming processes.
In this stage, we only consider some of the constructed models. Specifically, decision trees, random forests, gradient-boosting decision trees, logistic regressions, and naive Bayes models are interpretable models, meaning that we can identify which variables or pattern behaviors are important. This is especially relevant for dropout students, where early actions can be taken to avoid dropout. Identifying common features among students that dropout may allow decision makers to generate policies to apply within the university to mitigate the issue. For models based on tree (decision tree, random forest, and gradient boosting), we analyzed the significance of the features within the trees. With the logistic regression model, we analyzed the model parameters, values, to identify the most relevant attributes; higher absolutes values are associated with the most relevant variables related to dropout.
4. Exploratory Data Analysis
The data used in this study were provided by two Chilean universities, Universidad Adolfo Ibáñez (UAI) and Universidad de Talca (U Talca). For each dataset, we describe and analyze both variables and perform data cleaning operations. Finally, we also merge both datasets into a single dataset that considers both universities. The merged dataset will be used to evaluate the validity of a joint approach.
4.1. Universidad Adolfo Ibáñez
The data provided by the UAI contain 31,714 observations, each with 40 variables. Each observation corresponds to a student from the University. This work only considers engineering students, reducing the original dataset to 8416 observations. The dataset contains several null values and variables that did not contribute to the prediction task, hence, these variables were deleted from the dataset.
Among the deleted variables, we highlight two groups. A group of five variables whose removal was based on data quality or students that enrolled themselves into the university but never registered a course. The second group of variables were eliminated because their information was gathered after the student completes their first year in the university. Therefore the data does not apply to first-year dropout prediction. Finally, for nominal variables with many values, their values were changed to increase their significance. These preprocessing steps reduced the datasets to 3750 observations and 14 variables.
We can categorize the variables of the final dataset in the following personal variables: gender, place of residence (variable commune) and region of origin (variable region); high school data, such as the type of school (variable school, i.e., private, subsidized, or public), average high school grades (variable nem), student ranking according to their school (variable ranking); university application (variable admission, whether the application submitted via a normal or special process), year (year where the student entered the university), the preference ranking (variable preference, whether the degree they enrolled onto was listed as their first, second or lower in their list of preferences within the national system to assign students to universities); and the university admission test scores, which include scores for mathematics (variable mat), language (variable lang), science or history (variable optional), and average among all tests (variable pps). Note that this last set of scores come from standardized tests performed by all students that enroll within a Chilean university for a year. Finally, we include a class label (DROPOUT).
After an initial analysis of the variables conditioned according to the DROPOUT variable (Figure 1), we observed that lower values in variables nem, mat, optional, pps and ranking seem to increase dropout probabilities. This was to be expected, since all these variables are related to the performance of the student. Moreover, students coming from public schools or schools with state support (i.e., subsidized) have lower dropout probabilities. This effect could be explained because the UAI is a private university, and students with lower resources entered the university through scholarships granted to them based on their academic performance, hence they have a previous track of being successful students. For details about categorical variables, please refer to the Table A1 column UAI at Appendix A.
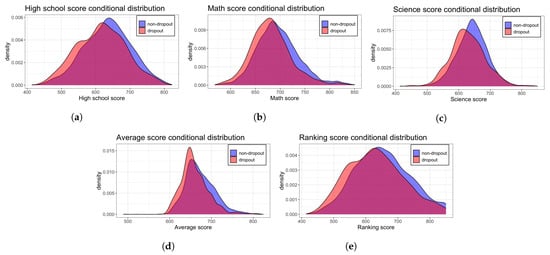
Figure 1.
Score conditional distributions based on the DROPOUT variable, with respect to each variable within the Universidad Adolfo Ibáñez dataset. (a) Variable nem. (b) Variable mat. (c) Variable optional. (d) Variable pps. (e) Variable ranking.
4.2. Universidad de Talca
The data provided by the U Talca includes four datasets, with a total of 73,067 observations and 99 variables. Even though there is a large quantity of data, the datasets contained several null values and variables that did not contribute to the prediction of first year dropout, which were eliminated.
In what follows, we described the data cleaning procedure, justifying the elimination of some data and the deletion of unnecessary variables and observations.
First, we analyzed the datasets for useless data for first-year dropout prediction. We discarded two of the datasets completely. One dataset contains first-year university grades and the second dataset to students in special situations. As these datasets provide information regarding the student during their university period, they cannot be used to predict dropout of newly enrolled student. A third dataset is used to generate the label variable (DROPOUT) as it includes the date of enrolment and the current status of the student. The fourth dataset includes most of the variables related to the student itself, its previous educational record and personal information. The resulting combined dataset contains 5652 observations and 40 variables, and still needs some preprocessing to reduce unnecessary variables and observations.
This preprocessing step started by discarding five variables because of data quality (most of the observations correspond to NULL values). A second set of variables was eliminated because their information is gathered after the first year is completed; therefore, this is not useful for first-year dropout prediction. Finally, for nominal variables with a large number of possible values, we grouped in order to create meaningful classes. These processes reduce the datasets to 2201 observations and 17 variables. From the 17 variables, both universities share 14 of them, while the remaining three corresponding to the engineering degree that the student enroll to, and the information about the education of the father and their family income. The first of these variables, specific engineering degree, is not recorded within the UAI as the university offers a common first year and students only select a specific engineering degree after their second year, while students from U Talca enter specific engineering degrees as freshmen. We contacted Universidad Adolfo Ibáñez regarding the availability of the two other variables, but they have only been recorded in the last two years, making them unavailable for most of the observations.
After an initial analysis of the variables conditioned by the DROPOUT variable, see Figure 2, we observed that lower values in variables pps, mat, optional and ranking increase the probability of dropout. This could be expected since all these variables are related to the previous performance of the student. We also observed that lower family incomes and non-professional parents increase the probability of dropout. It is also important to note that the selected engineering degree also affects dropout probability. Specifically, computer, mining, and bioinformatics have higher dropouts than other degrees. For details about categorical variables, please refer to Table A1 column U. Talca at Appendix A.
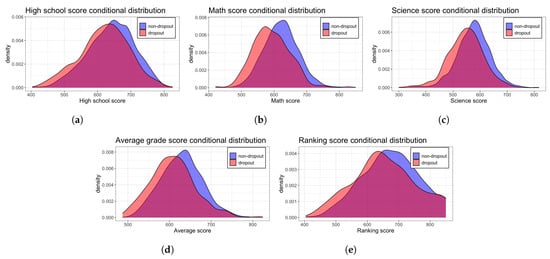
Figure 2.
Score conditional distributions based on the DROPOUT variable, with respect to each variable within the Universidad de Talca dataset. (a) Variable nem. (b) Variable mat. (c) Variable optional. (d) Variable pps. (e) Variable ranking.
4.3. Unification of Both Datasets
After the analysis of both datasets, we unified them by creating a new dataset containing the 14 shared variables. This new dataset contains 5951 observations, each with 14 variables. It is important to note that there are more observations from Universidad Adolfo Ibáñez (3750 observations); hence, this imbalance must be handled within the machine learning models.
Figure 3 compares the score distributions of the student from both universities. Each plot shows an estimated distribution over the score used in this paper. As it can be observed, both students have very similar high school scores, see Figure 3e). This could be explained because there is no standardization among the grades from different schools. This means that two schools could have very similar grades for their students, but the level of each school could be drastically different. UAI students have better scores in all standardized tests (Figure 3a–d). In contrast, students from Universidad de Talca have better ranking scores, meaning that Universidad de Talca receives more top high school students than UAI.
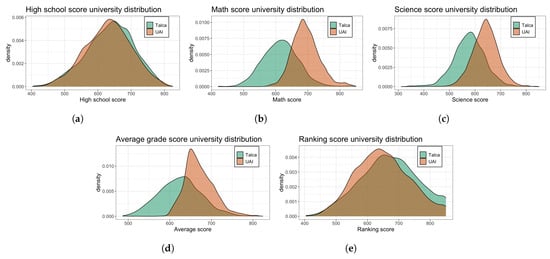
Figure 3.
Score conditional distributions based on the DROPOUT variable, with respect to each variable within the combined dataset. (a) Variable nem. (b) Variable mat. (c) Variable optional. (d) Variable pps. (e) Variable ranking.
Table 1 provides a list of the variables used within the datasets (combined dataset, UAI and U Talca datasets). For the U Talca dataset we can also include three additional variables only available for the said university. We refer to the dataset using these three additional variables as U Talca All.

Table 1.
Common variables within the datasets.
5. Analysis and Results
In this section, we discuss the results of each model after the application of variable and parameter selection procedures. After discussing the models, we analyze the results of the interpretative models.
5.1. Results
All results correspond to the score (positive and negative), precision (positive class), recall (positive class), and the accuracy of the 10-fold cross-validation test with the best tuned model provided by each machine learning method. We applied the following models: KNN, SVM, decision tree, random forest, gradient-boosting decision tree, naive Bayes, logistic regression, and a neural network, over four different datasets: The unified dataset containing both universities, see Section 4.3 and denoted as “combined”; the datasets from UAI, Section 4.1 and denoted as “UAI”; and U Talca, Section 4.2 denoted as “U Talca”, using the common subset of 14 variables between both universities; and the dataset from U Talca with the 17 available variables (14 common variables and three exclusive variables), Section 4.2 denoted as “U Talca All”. We also included a random model as a baseline to assess if the proposed models behave better than a random decision. Variable selection was completed using forward selection, and the hyper-parameters of each model were searched through the evaluation of each potential combination of parameters, see Section 4. The best performing models were:
- KNN: combined ; UAI ; U Talca and U Talca All .
- SVM: combined ; UAI ; U Talca and U Talca All ; polynomial kernel for all models.
- Decision tree: minimum samples at a leaf: combined 187; UAI 48; U Talca 123; U Talca All 102.
- Random forest: minimum samples at a leaf: combined 100; UAI 20; U Talca 150; U Talca All 20.
- Random forest: number of trees: combined 500; UAI 50; U Talca 50; U Talca All 500.
- Random forest: number of sampled features per tree: combined 20; UAI 15; U Talca 15; U Talca All 4.
- Gradient boosting decision tree: minimum samples at a leaf: combined 150; UAI 50; U Talca 150; U Talca All 150.
- Gradient boosting decision tree: number of trees: combined 100; UAI 100; U Talca 50; U Talca All 50.
- Gradient boosting decision tree: number of sampled features per tree: combined 8; UAI 20; U Talca 15; U Talca All 4.
- Naive Bayes: Gaussian distribution were assumed.
- Logistic regression: Only variable selection was applied.
- Neural Network: hidden layers-neurons per layer: combined 2–15; UAI 1–18; U Talca 1–18; U Talca All 1–5.
The results from all models are summarized in Table 2, Table 3, Table 4, Table 5 and Table 6. Each table shows the results for one metric over all datasets (combined, UAI, U Talca, U Talca all). In every table, “-” means that the models use the same variables for U Talca and U Talca All. Table 7 shows all variables that were important for at least one model, on any dataset. The notation used codes variable use as “Y” or “N” values, indicating if the variable was considered important by the model or not, while “-” means that the variable did not exist on that dataset (for example, a nominal variable in a model that only uses numerical variables). To summarize all datasets, the display of the values has the following pattern: “combined,UAI,U Talca,U Talca All”.

Table 2.
score + class, for each dataset.

Table 3.
score − class, for each dataset.

Table 4.
Recall + class, for each dataset.

Table 5.
Precision + class, for each dataset.

Table 6.
Accuracy, for each dataset.

Table 7.
Feature importance, for each model and dataset. The pattern of each cell represents the datasets “combined,UAI,U Talca,U Talca All”.
Table 2 shows the score of each model for the + class (since the data were highly unbalanced). Based on the results, it was not possible to select a single model as the best for all datasets. The best model could be gradient boosting, which had the higher average score in two of the four datasets, but this model was not significantly better than some other models, from a statistical point of view, i.e., a hypothesis test with a p-value lower than 0.05. Based only on the score, we could discard decision trees, since it had the lowest score in two datasets, and did not excel in any dataset. When comparing the performance per dataset, U Talca datasets have higher scores for every model. This may imply a better data quality from this university, but it could also be due to their higher dropout rate within the said dataset. The results for combined dataset show scores in an intermediate value between U Talca and UAI. This could be expected, as we trained using data from both universities. U Talca All showed a higher score in the logistic regression and neural network, suggesting that the addition of the non-shared variables improved the performance, at least when considering these models. However, these differences are not statistically significant compared to the U Talca dataset.
Table 3 shows the score for the − class for all models and datasets. The scores are higher than in the positive class, which was expected since the negative class corresponds to the majority class (non-dropout students). Even though we balanced the data when training, the test data (and the real-world data) is still unbalanced, which may have an influence. Similarly to the score for the + class, it is also difficult to select a single model as the best, since random forests could be considered the best in the combined and UAI datasets; however, KNN had better performance on U Talca and U Talca All. Even though it could be difficult to discard a model, the neural network had one of the lowest performances among all models. This may be because the tendency of over fitting from neural networks and their dependency on very large datasets for training. When comparing the performance by dataset, the combined dataset has higher scores (unlike the previous measure, where it had an intermediate value). U Talca scores were similar when including non-shared variables, but random forest surprises with a lower average score (even if the difference is not statistically significant). This result may be explained because the model selects random variables per tree generation. Then, the selection of these new variables, instead of the most important variables, such as the mathematics score, could negatively affect the performance of the model.
Table 4 and Table 5 show the recall (/( + )) and precision (/( + )) score of the + class for all models and datasets. In case of the precision, most models behave similarly among them. In contrast, we can observe some differences in recall. Logistic regression obtains a better recall than most models in all datasets. Decision tree behaves well in each dataset by itself, but behaves poorly when both datasets are combined. Comparing both tables, the recall is always higher than precision. This means that the number of False Negatives is lower than the number of False Positives. In practice, there is a low number of students that drop out of the university, which is not predicted by the model. However, students that were predicted to drop out continue after the first year. Unfortunately, we do not have the data to corroborate if those students were helped by each university during their first year.
The next performance measure is accuracy, which is shown in Table 6. The results show that the random forest could be considered the best in the combined and the UAI datasets, but KNN had better performance on U Talca and U Talca all; yet again, some differences are not statistically significant. In contrast, the neural network could be selected as a model to discard, since it had the lowest score among the entire table. When comparing the performance by dataset, the results are likethe score for the − class, with the both datasets having the higher scores with the same models. Random forest U Talca All also showed a lower average score (but no statistically significant difference) compared to U Talca.
As a summary, all results show similar performance among models and datasets. If we were to select one model for implementing a dropout prevention system, we would select a gradient-boosting decision tree because we prioritize the scores with the score + class measure, since the data were highly unbalanced and we are interested in improving retention. Recall that the score for the + class would focus on correctly classifying students who dropout (keeping a balance with the other classification), without achieving a high score when labeling all students if they do not drop out (the situation of most students). Note that, from a practical standpoint, the costs of missing a student that drops out is larger than considering multiple students at risk of dropping out and providing them with support.
5.2. Variable Analysis
Based on the models generated by the interpretative models, we proceeded to analyze the influence of individual variables. Recall that the pattern to read the importance of the variable in Table 7 is “both, UAI, UTalca, Utalca All vars”, and the values Y or N imply the use of that variable within the best model for the said combination of method and dataset. Note that, in the last dataset, we only report results if the final models differed from the model provided to the U Talca and the U Talca All datasets. For more detailed results, including the learned parameters of the logistic regression and the feature importance of the models based on a decision tree, please refer to Appendix B.
Given all models, the most important variable is mat, i.e., the score in the mathematics test performed within the national unified test to select university. This variable was considered by practically all models except by a single case (UAI−Logistic regression). Here, the variable pps could have included part of the information of mat, since it had a strong negative value, and probably the addition of variable region affected the results in some way (since this is the only model where the region variable is used). The second most important variables are pps and lang, which are shared by most models, but not for all the datasets. Naive Bayes did not consider these variables (except for pps in both datasets, where the unification of datasets may be the reason for its use), and they were mostly considered in the combined and UAI datasets. This could be explained since the conditional distribution of the classes is sufficiently similar not to be considered by the model, or simply because they were not selected in the tuning process. Ranking was considered in some datasets in all the models with exception of the logistic regression, which did not consider this variable in any dataset. It was probably not used in some models because of co-linearitywith variables such as pps or nem. The optional variable showed similar results. Some datasets considered this variable important, but the decision tree did not consider it in any dataset. Recall that the optional variable was the unification of 2 optional tests (history or science), which may have affected its use for prediction. Note that gradient boosting considered all the previous variables as important in every dataset. Since this model predicts using the errors, it would be expected that using numerical variables, which have many values, would be preferable, instead of using one-hot encoded categorical variables. The variable nem was important for a few models, which was to be expected, since it was discarded from some models due to collinearity problems, specifically with the variable ranking.
The discrete variables were important only in a few models and datasets. Preference and admission were statistically significant in U Talca-Logistic regression, where a lower value in preference (higher preference for the university) and entering through regular admission decreases dropout. The region variable was important in the UAI-Logistic regression, where being from the Metropolitan or the Valparaiso regions, the regions where the university is located, decrease dropout. The variables degree and family income were non-shared variables included in U Talca All; however, the fact that they were important in some models may imply that some patterns could not be found using only the shared variables. Note that in the U Talca dataset, the variables preference and admission seem to be replaced by the variable degree. This variable, degree, is a categorical variable that takes as its values the degrees of mechanical engineering (which decreases dropout), civil engineering (also decreases dropout), and bioinformatic engineering (which increases dropout). Finally, when comparing universities, it seems that the feature importance at the UAI defined the importance in the combined dataset in most of the cases, which may be caused because the dataset from this university is bigger than the dataset from the Universidad de Talca.
Qualitative Analysis
We now proceed to explain the importance of some variables found within the models. The variable mat could be the most important variable because of courses such as calculus or physics, which use several mathematical logic and are found within the first year of engineering degrees. In fact, Universidad Adolfo Ibáñez currently performs several efforts during the first undergraduate year to improve the mathematical knowledge of their students, such as helping with the creation of study groups and preparatory classes before every test and examination. These courses also used to have high failure rates. Therefore, it will not be surprising to note that low mathematical scores will be positively related to failures in mathematical courses. The importance of variable pps could be explained by its relation to other variables. Recall that variable pps is a weighted average of all other national tests, being math one of the most important among them. Then, a high math score should imply a high score in pps too.
The variable lang has a different behavior than previous variables. In interpretative models, a higher score in lang increases the probability of dropout. At Universidad Adolfo Ibáñez, the low quantity of language-related courses and their low failure rates could explain this. Only 3 (out of 12) first-year subjects evaluate reading and/or writing skills.
The variable ranking is a score that compares the student with other students from their high school. Therefore, it seems reasonable that excellent students in any high school continue to be excellent students in the university, hence its importance. It is common to observe that excellent students become friends within the university and start generating common study habits from the first semester, for example, using their free time between classes to study or to work on some homework.
Among the discrete variables, it is striking that the variable region was considered important only for UAI. Here, students from the same region than the university location fare better. This result can be explained because these students tend to live with their parents, and this may translate into better habits and, thus, lower dropout probability. This could be expected given the implications of the experience involved in moving to a new place without parents. First-year students that live alone have more freedom and responsibilities. In several cases, this freedom could imply more recreational parties and depression (due to loneliness), affecting negatively their performance during the first year.
6. Conclusions
This work compared the performance and learned patterns from machine learning models for two universities when predicting student dropout of first-year engineering students. Four different datasets were compared: combined dataset (students from both of the universities and shared variables), UAI dataset (students from this university and all variables, which are the same as the shared variables), U Talca (students from this university and the shared variables), and U Talca All (the same than Universidad de Talca, but includes non-shared variables).
From the numerical perspective, the results show similar performance among most models in each dataset. If it we were to select one model for implementing a dropout prevention system, we would prioritize the scores with the score + class measure, since the data were highly unbalanced. Considering this, the best option would be a gradient-boosting decision tree, since it showed the higher average score in the combined and UAI datasets, with good scores in the U Talca and U Talca All datasets. Following that priority, it would be reasonable to discard the decision tree based on its lower average score when using that measure. Note that the differences are minimal among models, showing that the capabilities of different models to predict first-year dropout are more heavily related to the sources of information than to the model itself.
The interpretive models (decision tree, random forest, gradient boosting, naive Bayes, and logistic regression) showed that the most important variable is mat (mathematical test score from the national tests to enter university), since this variable was considered in almost every model and datasets. In all the cases, a higher score of this variable decreased the probability of dropout. The importance of this variable makes sense since many of the efforts done inside the universities during the first year are focused on courses such as calculus or physics, which are mathematically heavy courses (e.g., study groups organized by the university and student organizations). Moreover, these courses have high failure rates, which ultimately leads to dropout. Other variables, such as pps and ranking, were also considered by most models, and a higher score in them also decreased the probability of dropout. The variable lang was considered by some models too, but a higher score increased the probability of dropout, which could be explained by the fact that we were analyzing engineering students, and reading and writing skills are barely evaluated during first year. On the opposite, most categorical variables were not considered important by most of the models. The few exceptions are preference and admission in U Talca dataset, region in UAI and family income and degree as non-shared variables in U Talca All, where the last variable seems to replace the information of preference and admission, showing the limitations unifying datasets. Specifically, these non-shared variables were selected in many U Talca All models, suggesting differences between the universities.
Finally, when comparing among universities, the unification of datasets resulted in an intermediate performance (between the score of the two universities) in two of four measures, revealing that one university would become a limitation in the performance of the other when a general model is used. For that, it would be preferable to use a single model per university, instead of a general model. A single model would focus more accurately on the patterns of each university, while a general model may lose information when trying to generalize them. Moreover, and given the broad diversity of data collected among different universities, the application of common methods to ascertain dropout seems to be difficult or inadvisable.
As future work, it would be important to collect more (and different) variables to include in the models. A better model could be generated using data related to the adaptation and social integration information of the students, which was used in older studies. Additionally, if required to predict dropout during the semester (and not only after enrollment), it would be useful to collect day-to-day information through learning content managements such as Moodle, or the one available in the university of interest.
Author Contributions
Conceptualization, E.Á.-M., S.M. and J.P.; methodology, E.Á.-M., S.M. and J.P.; software, D.O.; validation, S.M. and J.P.; formal analysis, E.Á.-M., D.O., S.M. and J.P.; investigation, E.Á.-M., D.O., S.M. and J.P.; resources, E.Á.-M. and J.P.; data curation, D.O.; writing—original draft preparation, D.O., S.M. and J.P.; writing—review and editing, E.Á.-M., S.M. and J.P.; visualization, D.O.; supervision, E.Á.-M., S.M., and J.P.; funding acquisition, E.Á.-M. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
E. Álvarez-Miranda acknowledges the support of the Complex Engineering Systems Institute ANID PIA/BASAL AFB180003. All authors acknowledges the support of ANID through the grant FONDEF IDeA I+D ID18I10216 “Desarrollo de tecnologías de Big Data para aumentar la retención y el éxito de estudiantes universitarios”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Due to Non disclosure agreements, the data used in this work cannot be provided. More detailed aggregated results are available upon request to the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Categorical Variables Description
This appendix shows the details of the categorical variables in Table A1. We show most categorical variables with their total frequency and the dropout frequency for each university. The number of students that did not dropout was omitted for space, but it can be calculated by subtracting the dropout frequency from the total frequency. Commune and Region were omitted given its large number of possible values.

Table A1.
Description of categorical variables.
Table A1.
Description of categorical variables.
| UAI | U. Talca | ||||
|---|---|---|---|---|---|
| Variable | Value | Total | Dropout | Total | Dropout |
| Frequency | Frequency | Frequency | Frequency | ||
| Dropout | 3750 | 536 | 2201 | 472 | |
| Gender | male | 2893 | 428 | 1694 | 360 |
| female | 857 | 108 | 507 | 112 | |
| School | private | 2856 | 436 | 128 | 24 |
| subsidized | 538 | 61 | 1172 | 251 | |
| public | 115 | 13 | 872 | 187 | |
| null | 241 | 26 | 29 | 10 | |
| Admission | regular | 3457 | 491 | 2155 | 457 |
| special | 286 | 43 | 46 | 15 | |
| null | 7 | 2 | 0 | 0 | |
| Preference | first | 1972 | 255 | 1592 | 310 |
| second | 825 | 151 | 310 | 77 | |
| third | 407 | 58 | 160 | 37 | |
| forth or posterior | 302 | 45 | 132 | 45 | |
| null | 244 | 27 | 7 | 3 | |
| Engineering degree | Bioinformatics | – | – | 137 | 49 |
| Civil | – | – | 285 | 47 | |
| Industrial | – | – | 542 | 72 | |
| Informatics | – | – | 324 | 96 | |
| Mechanics | – | – | 208 | 34 | |
| Mechatronics | – | – | 285 | 67 | |
| Mines | – | – | 420 | 107 | |
Appendix B. Comparison Details
This appendix shows the details of the interpretative models. The results from this section are summarized in Table 7. Specifically, we show the parameters or feature importance for the selected variables from logistic regression, decision tree, random forest, and gradient boosting.
Table A2 shows the learned parameters for each model. A value means that the variable was not selected for the model. In all cases, a negative parameter decreases the probability of dropout. As we can observe, higher values in the mathematical, average, science, and high school degree scores reduced the probability f dropout. Among them, mathematics is the most important variable in three of the four cases. On the contrary, a higher language score increases the probability of dropout. In the case of the degree, bioinformatic engineering increases the dropout probability, while mechanical and civil engineering decreases the probability of dropout. In the case of Universidad de Talca, the dropout is related to the preference of the student (preference). If the degree or university was not the first option of the student, the student is more likely to dropout during the first year. Students that enroll in the university through the test scores have a lower probability of dropout compared to the students that enroll through special methods, such as sports scholarship. Finally, for Universidad Adolfo Ibáñez, people living close to the university, possibly with their families (Valparaiso and Metropolitan region), have a lower probability of dropout than students coming from other regions and living on their own.

Table A2.
Learned parameters for the logistic regression for all datasets, parameters with p-value over 0.01 are not shown.
Table A2.
Learned parameters for the logistic regression for all datasets, parameters with p-value over 0.01 are not shown.
| Var | Both | UAI | U Talca | U Talca All Vars |
|---|---|---|---|---|
| mat | −2.28 ± 0.27 | – | −2.72 ± 0.23 | −2.94 ± 0.28 |
| pps | −1.54 ± 0.19 | −2.46 ± 0.39 | −0.80 ± 0.24 | – |
| lang | 1.23 ± 0.26 | 1.26 ± 0.38 | 0.43 ± 0.16 | – |
| optional | −1.44 ± 0.34 | – | – | – |
| nem | – | – | −0.57 ± 0.25 | −0.85 ± 0.23 |
| mechanical degree | – | – | – | −0.52 ± 0.12 |
| civil degree | – | – | – | −0.41 ± 0.16 |
| bioinformatics degree | – | – | – | 0.45 ± 0.18 |
| preference | – | – | 0.74 ± 0.34 | – |
| admission test | −0.37 ± 0.08 | – | −0.57 ± 0.27 | – |
| region Valparaiso | – | −0.67 ± 0.19 | – | – |
| region Metropolitana | – | −0.43 ± 0.15 | – | – |
Figure A1 shows the feature importance for the decision tree model in each dataset. Please note that we use a 10-fold cross validation. Consequently, we can obtain a standard deviation for the importance of each variable from this model. The most important variables differ according to the models, but lang, math, ranking, and pps are consistently among most models. Further analysis of the learned decision trees shows similar behavior to the conclusions obtained through the logistic regression.
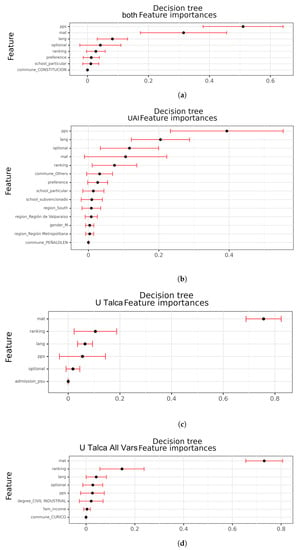
Figure A1.
Feature importance for decision trees. Black dots correspond to the means, while red bars represent one standard deviation. (a) Both. (b) UAI. (c) U Talca. (d) U Talca All Vars.
Figure A2 shows the feature importance for the random forest model in each dataset. UAI has several variables with a low score (influencing the combined dataset). In contrast, in U Talca and U Talca All, the mat score is the most important, with a considerably high score.
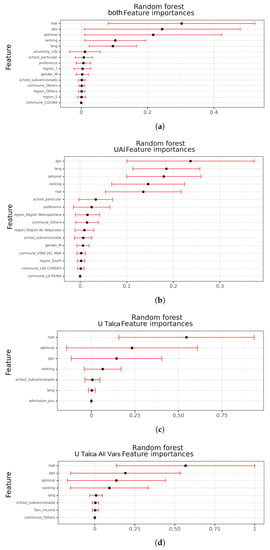
Figure A2.
Feature importance for random forest. Black dots correspond to the means, while red bars represent one standard deviation. (a) Both. (b) UAI. (c) U Talca. (d) U Talca All Vars.
Figure A3 shows the feature importance for the gradient boosting model in each dataset. In all cases, the numerical variables are considerably more important than the rest of the variables.
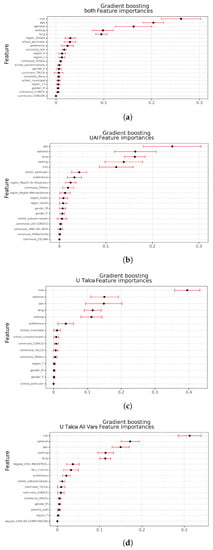
Figure A3.
Feature importance for gradient boosting. Black dots correspond to the means, while red bars represent one standard deviation. (a) Both. (b) UAI. (c) U Talca. (d) U Talca All Vars.
References
- Draft Preliminary Report Concerning the Preparation of a Global Convention on the Recognition of Higher Education Qualifications. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000234743 (accessed on 3 September 2021).
- 23 Remarkable Higher Education Statistics. Available online: https://markinstyle.co.uk/higher-education-statistics/ (accessed on 3 September 2021).
- Delen, D. A comparative analysis of machine learning techniques for student retention management. Decis. Support Syst. 2010, 49, 498–506. [Google Scholar] [CrossRef]
- College Dropout Rates. Available online: https://educationdata.org/college-dropout-rates/ (accessed on 3 September 2021).
- UK Has ‘Lowest Drop-Out Rate in Europe’. Available online: https://www.timeshighereducation.com/news/uk-has-lowest-drop-out-rate-in-europe/2012400.article (accessed on 3 September 2021).
- At a Crossroads: Higher Education in Latin America and the Caribbean. Available online: https://openknowledge.worldbank.org/handle/10986/26489 (accessed on 3 September 2021).
- Why Are Dropout Rates Increasing in UK Universities? Available online: https://www.studyinternational.com/news/dropping-out-university/ (accessed on 3 September 2021).
- Informes Retención de Primer año. Available online: https://www.mifuturo.cl/informes-retencion-de-primer-ano/ (accessed on 3 September 2021). (In Spanish).
- QS Latin America University Rankings 2022. Available online: https://www.topuniversities.com/university-rankings/latin-american-university-rankings/2022 (accessed on 3 September 2021). (In Spanish).
- Spady, W. Dropouts from higher education: An interdisciplinary review and synthesis. Interchange 1970, 1, 64–85. [Google Scholar] [CrossRef]
- Tinto, V. Dropout from Higher Education: A Theoretical Synthesis of Recent Research. Rev. Educ. Res. 1975, 45, 89–125. [Google Scholar] [CrossRef]
- Bean, J. Student attrition, intentions, and confidence: Interaction effects in a path model. Res. High. Educ. 1981, 17, 291–320. [Google Scholar] [CrossRef]
- Pascarella, E.; Terenzini, P. How College Affects Students: Findings and Insights from Twenty Years of Research; Jossey-Bass Publishers: San Francisco, CA, USA, 1991. [Google Scholar]
- Cabrera, L.; Bethencourt, J.; Álvarez, P.; González, M. El problema del abandono de los estudios universitarios. [The dropout problem in university study]. Rev. Electron. Investig. Eval. Educ. 2006, 12, 171–203. [Google Scholar]
- Broc, M. Voluntad para estudiar, regulación del esfuerzo, gestión eficaz del tiempo y rendimiento académico en alumnos universitarios. Rev. Investig. Educ. 2011, 29, 171–185. [Google Scholar]
- Bejarano, L.; Arango, S.; Johana, K.; Durán, H.; Ortiz, C. Caso de estudio: Caracterización de la deserción estudiantil en la Fundación Universitaria Los Libertadores 2014-1–2016-1. Rev. Tesis Psicol. 2017, 12, 138–161. [Google Scholar]
- Sinchi, E.; Ceballos, G. Acceso y deserción en las universidades. Alternativas de financiamiento. Alteridad 2018, 13, 274–287. [Google Scholar] [CrossRef]
- Quintero, I. Análisis de las Causas de Deserción Universitaria. Master’s Thesis, Universidad Nacional Abierta y a Distancia UNAD, Colombia, Bogata, Colombia, 2016. [Google Scholar]
- Minaei-Bidgoli, B.; Kashy, D.; Kortemeyer, G.; Punch, W. Predicting student performance: An application of data mining methods with an educational Web-based system. In Proceedings of the Frontiers in Education Conference, Westminster, CO, USA, 5–8 November 2003; Volume 1, p. T2A-13. [Google Scholar]
- Bernardo, A.; Cerezo, R.; Núñez, J.; Tuero, E.; Esteban, M. Prediction of university drop-out: Explanatory variables and preventine measures. Rev. Fuentes 2015, 16, 63–84. [Google Scholar]
- Larroucau, T. Estudio de los factores determinantes de la deserción en el sistema universitario chileno. Rev. Estud. de Políticas Públicas 2015, 1, 1–23. [Google Scholar]
- Kuna, H.; Garcia-Martinez, R.; Villatoro, F. Pattern discovery in university students desertion based on data mining. Adv. Appl. Stat. Sci. 2010, 2, 275–285. [Google Scholar]
- Garzón, A.; Gil, J. El papel de la procrastinación académica como factor de la deserción universitaria. Rev. Complut. Educ. 2016, 28, 307–324. [Google Scholar] [CrossRef]
- Jia, P.; Maloney, T. Using predictive modelling to identify students at risk of poor university outcomes. High. Educ. 2015, 70, 127–149. [Google Scholar] [CrossRef]
- Martelo, R.; Acevedo, D.; Martelo, P. Análisis multivariado aplicado a determinar factores clave de la deserción universitaria. Rev. Espac. 2018, 39, 13. [Google Scholar]
- Giovagnoli, P. Determinants in university desertion and graduation: An application using duration models. Económica 2005, 51, 59–90. [Google Scholar]
- Vallejos, C.; Steel, M. Bayesian survival modelling of university outcomes. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2017, 180, 613–631. [Google Scholar] [CrossRef]
- Quinlan, J. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Bharadwaj, B.; Pal, S. Mining Education Data to Predict Student’s Retention: A comparative Study. Int. J. Comput. Sci. Inf. Secur. 2012, 10, 113–117. [Google Scholar]
- Heredia, D.; Amaya, Y.; Barrientos, E. Student Dropout Predictive Model Using Data Mining Techniques. IEEE Lat. Am. Trans. 2015, 13, 3127–3134. [Google Scholar] [CrossRef]
- Ramírez-Correa, P.; Grandón, E. Predicción de la Deserción Académica en una Universidad Pública Chilena a través de la Clasificación basada en Árboles de Decisión con Parámetros Optimizados. Form. Univ. 2018, 11, 3–10. [Google Scholar] [CrossRef]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc. Ser. B (Methodol.) 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Cabrera, A. Logistic Regression Analysis in Higher Education: An Applied Perspective. In Higher Education: Handbook of Theory and Research; Springer: Berlin/Heidelberg, Germany, 1994; Volume 10, pp. 225–256. [Google Scholar]
- Santelices, V.; Catalán, X.; Horn, C.; Kruger, D. Determinantes de Deserción en la Educación Superior Chilena, con Énfasis en Efecto de Becas y Créditos; Technical report; Pontificia Universidad Católica de Chile: Santiago, Chile, 2013. [Google Scholar]
- Matheu, A.; Ruff, C.; Ruiz, M.; Benites, L.; Morong, G. Modelo de predicción de la deserción estudiantil de primer año en la Universidad Bernardo O’Higgins. Educação e Pesquisa 2018, 44. [Google Scholar] [CrossRef] [Green Version]
- Langley, P.; Iba, W.; Thompson, K. An analysis of Bayesian classifiers. In Proceedings of the Tenth National Conference on Artificial Intelligence; AAAI: Cambridge, MA, USA, 1992; pp. 223–228. [Google Scholar]
- Kumar, B.; Pal, S. Data Mining: A prediction of performer or underperformer using classification. Int. J. Comput. Sci. Inf. Technol. 2011, 2, 686–690. [Google Scholar]
- Hegde, V.; Prageeth, P. Higher education student dropout prediction and analysis through educational data mining. In Proceedings of the 2018 2nd International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2018; pp. 694–699. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Tanner, T.; Toivonen, H. Predicting and preventing student failure–using the k-nearest neighbour method to predict student performance in an online course environment. Int. J. Learn. Technol. 2010, 5, 356–377. [Google Scholar] [CrossRef]
- Mardolkar, M.; Kumaran, N. Forecasting and Avoiding Student Dropout Using the K-Nearest Neighbor Approach. SN Comput. Sci. 2020, 1, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G. Neural networks for classification: A survey. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2000, 30, 451–462. [Google Scholar] [CrossRef] [Green Version]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Siri, A. Predicting Students’ Dropout at University Using Artificial Neural Networks. Ital. J. Sociol. Educ. 2015, 7, 225–247. [Google Scholar]
- Alban, M.; Mauricio, D. Neural Networks to Predict Dropout at the Universities. Int. J. Mach. Learn. Comput. 2019, 9, 149–153. [Google Scholar] [CrossRef] [Green Version]
- Boser, B.; Guyon, I.; Vapnik, V. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory; ACM Press: New York, NY, USA, 1992; pp. 144–152. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cardona, T.A.; Cudney, E. Predicting Student Retention Using Support Vector Machines. Procedia Manuf. 2019, 39, 1827–1833. [Google Scholar] [CrossRef]
- Mesbah, M.; Naicker, N.; Adeliyi, T.; Wing, J. Linear Support Vector Machines for Prediction of Student Performance in School-Based Education. Math. Probl. Eng. 2020, 2020, 4761468. [Google Scholar]
- Ho, T. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, p. 278. [Google Scholar]
- Lee, S.; Chung, J. The Machine Learning-Based Dropout Early Warning System for Improving the Performance of Dropout Prediction. Appl. Sci. 2019, 9, 3093. [Google Scholar] [CrossRef] [Green Version]
- Behr, A.; Giese, M.; Teguim, H.; Theune, K. Early Prediction of University Dropouts—A Random Forest Approach. Jahrbücher für Natl. und Statistik 2020, 240, 743–789. [Google Scholar] [CrossRef]
- Friedman, J. Stochastic gradient-boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Tenpipat, W.; Akkarajitsakul, K. Student Dropout Prediction: A KMUTT Case Study. In Proceedings of the 1st International Conference on Big Data Analytics and Practices (IBDAP), Bangkok, Thailand, 25–26 September 2020; pp. 1–5. [Google Scholar]
- Liang, J.; Li, C.; Zheng, L. Machine learning application in MOOCs: Dropout prediction. In Proceedings of the 11th International Conference on Computer Science Education (ICCSE), Nagoya, Japan, 23–25 August 2016; pp. 52–57. [Google Scholar]
- Liang, J.; Yang, J.; Wu, Y.; Li, C.; Zheng, L. Big Data Application in Education: Dropout Prediction in Edx MOOCs. In Proceedings of the IEEE Second International Conference on Multimedia Big Data (BigMM), Taipei, Taiwan, 20–22 April 2016; pp. 440–443. [Google Scholar]
- Fischer, E. Modelo Para la Automatización del Proceso de Determinación de Riesgo de Deserción en Alumnos Universitarios. Master’s Thesis, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Santiago, Chile, 2012. [Google Scholar]
- Eckert, K.; Suenaga, R. Análisis de Deserción-Permanencia de Estudiantes Universitarios Utilizando Técnica de Clasificación en Minería de Datos. Form. Univ. 2014, 8, 3–12. [Google Scholar] [CrossRef] [Green Version]
- Miranda, M.; Guzmán, J. Análisis de la Deserción de Estudiantes Universitarios usando Técnicas de Minería de Datos. Form. Univ. 2017, 10, 61–68. [Google Scholar] [CrossRef]
- Viloria, A.; Garcia, J.; Vargas-Mercado, C.; Hernández-Palma, H.; Orellano, N.; Arrozola, M. Integration of Data Technology for Analyzing University Dropout. Procedia Comput. Sci. 2019, 155, 569–574. [Google Scholar] [CrossRef]
- Kemper, L.; Vorhoff, G.; Wigger, B. Predicting student dropout: A machine learning approach. Eur. J. High. Educ. 2020, 10, 1–20. [Google Scholar] [CrossRef]
- Dudani, S. The Distance-Weighted k-Nearest-Neighbor Rule. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 325–327. [Google Scholar] [CrossRef]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Cox, D. Some procedures associated with the logistic qualitative response curve. In Research Papers in Statistics: Festschrift for J. Neyman; David, F., Ed.; Wiley: New York, NY, USA, 1966; pp. 55–71. [Google Scholar]
- Rumelhart, D.; McClelland, J. Learning Internal Representations by Error Propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition: Foundations; MIT Press: Cambridge, MA, USA, 1987; pp. 318–362. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Keras. Keras: The Pyton Deep Learning API, 2015. Available online: https://keras.io (accessed on 3 September 2021).
- Broyden, C. The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Fletcher, R. A new approach to variable metric algorithms. Comput. J. 1970, 13, 317–322. [Google Scholar] [CrossRef] [Green Version]
- Goldfarb, D. A Family of Variable-Metric Methods Derived by Variational Means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Ng, A. Feature selection, L1 vs. L2 regularization, and rotational invariance. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 78. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Efroymson, M. Multiple regression Analysis. In Mathematical Methods for Digital Computers; Wiley: Hoboken, NJ, USA, 1960. [Google Scholar]
- Browne, M.W. Cross-Validation Methods. J. Math. Psychol. 2000, 44, 108–132. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).