Abstract
Recently developed GeoGebra tools for the automated deduction and discovery of geometric statements combine in a unique way computational (real and complex) algebraic geometry algorithms and graphic features for the introduction and visualization of geometric statements. In our paper we will explore the capabilities and limitations of these new tools, through the case study of a classic geometric inequality, showing how to overcome, by means of a double approach, the difficulties that might arise attempting to ‘discover’ it automatically. On the one hand, through the introduction of the dynamic color scanning method, which allows to visualize on GeoGebra the set of real solutions of a given equation and to shed light on its geometry. On the other hand, via a symbolic computation approach which currently requires the (tricky) use of a variety of real geometry concepts (determining the real roots of a bivariate polynomial by reducing it to a univariate case through discriminants and Sturm sequences, etc.), which leads to a complete resolution of the initial problem. As the algorithmic basis for both instruments (scanning, real solving) are already internally available in GeoGebra (e.g., via the Tarski package), we conclude proposing the development and merging of such features in the future progress of GeoGebra automated reasoning tools.
1. Introduction
In recent years we are witnessing a rich interaction between two geometric instruments which were initially born with different intentions in mind, but are converging and joining forces nowadays to create a new generation of software for doing Geometry. On the one hand there were the Geometric Automatic Theorem Provers (GATPs), which can be traced back to the seminal work by Wu [1], with an increasing variety of methods and approaches developed along the years, such as the Gröbner Basis Method, the Area Method, the Full-Angle Method.... These methods have succeeded to automatically prove a large collection of geometric statements, as can be seen for instance [2].
On the other hand, there were the Dynamic Geometry Software (DGS) programs (some of the pioneers being The Geometric Supposer, Cabri, The Geometer’s Sketchpad, Geometry Inventor or Thales) which initially were conceived as a tool for teaching Geometry in schools, as a kind of digital assistant for the constructions traditionally made by ruler and compass on the blackboard.
The GATPs based on algebraic techniques, such as Wu’s Method ([1,3]) or the Gröbner Basis method ([4,5]), require frequently the manipulation of a large set of polynomials, which represents a given geometric construction. Unfortunately, this translation of geometric properties into algebraic equations can be a tedious process. Dynamic Geometry programs turned out to be an ideal interface to introduce geometric information, and the extension of this software with convenient algebraic tools allowed the creation of a natural environment to work on automated proving in Geometry. This fruitful cooperation was put into practice in several DGS programs such as Geometry Expert, GDI or GCLC, with GeoGebra joining this list in recent years. Since its inception, GeoGebra put special emphasis on becoming something more than a DGS, but a Mathematical Software where not only the geometrical objects, but their algebraic counterparts, could be accessible and visualized simultaneously. This, together with its increasing worldwide popularity ([6,7,8]) and free access for non-commercial use, makes GeoGebra a top choice for carrying out this integration process with algebraic proving tools.
At present, GeoGebra is actively developing a set of new Geometric Automated Reasoning Tools (GARTs) which not only are capable of proving geometric equalities or inequalities, but allow the user to explore and discover facts about geometric figures. The present work is aimed at showing some of these new tools, implemented in recent versions of GeoGebra Discovery (an experimental version of GeoGebra), emphasizing their ability to handle geometric inequalities. We also comment on its current strengths and limitations, and how the visualization possibilities that offer the graphic view of GeoGebra can illuminate the automatic resolution of geometric problems which involve certain difficulties, due to the high complexity of some elements appearing along the process (see [9] for an unpublished paper with a similar approach). To that end, we will focus our attention on re-discovering and proving by computational means the geometric inequality 5.3 of the collection [10]:
Proposition 1.
If the lengths of the sides of a triangle are a, b, c, and the length of its circumradius is R, then
Equality holds if and only if .
In summary, our research goal is to show how to approach this Proposition through the combination of a dynamic color scanning method and (real algebra) symbolic computations, exemplifying the need to automatize this combination of tools, to address and to solve some automated reasoning challenging issues that arise in the current GeoGebra Discovery version.
In Section 2, we briefly describe the tools that are already available in the official releases of GeoGebra, and which allow proving and discovering geometric equalities in a given construction. In Section 3, we present new tools for dealing with geometric inequalities, currently implemented in GeoGebra Discovery, an experimental version of GeoGebra maintained by the first author where GARTs are first checked before official release. In Section 4, we introduce the Dynamic Color Scanning Method, a powerful and flexible visualization technique devised by the second author on GeoGebra that can be helpful when symbolic computations or other visualization methods fail. To illustrate how the previous tools can be employed and combined, in Section 5, we approach the task of automatically proving the classical geometric inequality in Proposition 1, highlighting the accomplishments that the new symbolic tools in GeoGebra Discovery achieve when investigating geometric relations and inequalities, but commenting also on the current limitations that hinder a full resolution of the problem. Section 6 combines the visualization power of the dynamic color scanning method, together with the algebraic capabilities of the software Maple to definitely settle Proposition 1. Finally, in Section 7, we include some conclusions and propose lines of research to improve the performance and versatility of GeoGebra in future versions.
2. The GeoGebra Automated Reasoning Tools
Since 2014, GeoGebra is making a systematic and permanent effort in order to develop new Geometric Automated Reasoning Tools (GARTs) based on algebraic computations that go beyond proving geometric statements, providing better feedback than just deciding the truth or falsehood of a statement, and introducing instruments that actually lead to the discovery of geometric facts (see [11,12], for some papers both dealing with the algebraic algorithms and their implementation in GeoGebra). Given the school environment where DGS programs are mainly utilized, these new features are aimed at providing students with a kind of expert companion, a Geometer Automata (GA) as described in [13], to help them explore geometric configurations and gain insight into the relations that exist among its elements.
Currently, the CAS engine embedded in GeoGebra that performs the symbolic computations required to use these reasoning tools is Giac ([14,15]), which has support for symbolic computations such as finding the Gröbner basis of a polynomial ideal or determining whether a polynomial belongs or not to a given ideal. At present, the GARTs in GeoGebra make use of Giac in order to establish equality relations among the elements of a geometric construction. In the next section, we will present new developments that expand the possibilities of these tools.
To give a rough sketch of how things work, let us start by setting up the basic scenario. Let us assume that K (usually ) is a field with an algebraically closed extension L (usually ). Roughly speaking, let us assume that we have a geometric construction and that we want to show whether a thesis concerning this construction always holds. The construction starts by placing some free points , , with their coordinates taken in the field K. From these points we can construct new elements (points, segments, lines, circles, etc.) that depend on the initial free points, eventually introducing new free variables in the construction. These elements satisfy geometric relations that can be expressed in form of polynomial equations ( we often make an abuse of notation by identifying a polynomial with its corresponding polynomial equation and/or its set of solutions) . Among the variables we can choose a maximal set of independent variables (that is, which do not hold polynomial relations among them). Usually, this set of independent variables contains the coordinates of the initial free points, and its cardinal is related to the degrees of freedom of the configuration. As a simple example, let us consider the construction
Take a point P in the perpendicular bisector of a segment .
We require two free points , , and a third point that must lie in the perpendicular bisector of the segment , whose equation is given by
We are using here six variables, and there is one polynomial relation among them. Intuitively speaking, our construction has five degrees of freedom (four for the coordinates of the points A, B, plus one more that decides the height of the point P on the bisector). Of course, for more complex constructions we would get not just one, but a collection of polynomials . The points in satisfying the polynomials in H form the hypothesis variety, and each of these points correspond to a particular instance of the figure under study.
Now, after having settled our construction we would like to prove something. Let us suppose we want to prove the following thesis (see Figure 1):
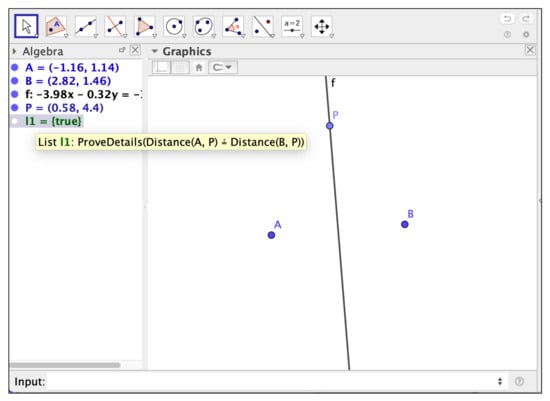
Figure 1.
Proving with GeoGebra that the distances from a point P in the perpendicular bisector of segment to its extremes are equal.
The distances from P to A and B are equal.
This thesis can also be expressed as a polynomial:
and the set of its solutions in is called the thesis variety. Now, the proposition
If P is a point on the perpendicular bisector of the segment , then the distances from P to A and B are equal.
Would be proved if we check that, for each possible configuration satisfying the relation , then also holds. In other words, if we check that . Using the language of algebraic geometry, this amounts to say that the hypothesis variety is contained in the thesis variety . Now, in this new algebraic setting, we can take advantage of all the machinery related to varieties, polynomial rings and ideals (with coefficients in the algebraically closed field L). Since proving that is equivalent to show that , by adding an extra variable t and considering all our polynomials in we are led to show that . By the Nullstellensatz Theorem, this is the case if the ideal is . However, checking that 1 belongs to an ideal given by a set of generators can be algorithmically decided by checking whether a Gröbner basis of the ideal reduces to ([16], (Chapter 2)).
Remark 1.
Notice that in the example above we actually have , since . In other words, the hypothesis and the thesis are equivalent.
Unfortunately, working in a Euclidean Geometry environment introduces certain complications in the description given above, due to several reasons:
- (i)
- The use of complex versus real geometry tools: Points in the Euclidean plane have real coordinates, while the algebraic algorithms used within this framework are designed for algebraically closed fields. Therefore, when we state that we are including points in with complex coordinates, which is more than what we actually need. We could be missing valid theses which hold for all real points in , but not on the whole complex variety (see [17,18]). For example, let us consider the following statement, usually called Clough’s conjecture [19], namely, the equality of
- -
- the sum of segments , , and , where are the feet of the perpendiculars to the sides of an equilateral triangle from an arbitrary point D,
- -
- and , where p is the length of side , i.e., is half the perimeter of the equilateral triangle .
See [20] for detailed synthetic and algebraic proofs. Now, the algorithms we have implemented in GeoGebra, if asked about the Relation between and , proceed, first, checking the numerically approximate equality of both quantities and, if it holds, starting a symbolic protocol by considering the ideal generated by all the polynomial equations describing the hypotheses. We emphasize here the terms polynomial equations, because all the lengths are described by expressing as the sum of the squares of the differences of the coordinates of the extremes of the corresponding segments, say, , etc. There are neither square roots nor choice of positive signs for defining , as this approach would require real algebraic geometry methods. Thus, our hypotheses ideal includes much more cases (in the complex geometry context) than intuitively expected, and the thesis , holds only on some of them (for example, on those cases where are positive).Accordingly, GeoGebra Discovery declares that the formulated statement is “true on parts, false on parts”, see Figure 2. This means that the underlying algorithm detects, without having to compute a primary decomposition of the involved hypotheses ideal, that the statement holds true on some components and is false on some others, see item iii) below.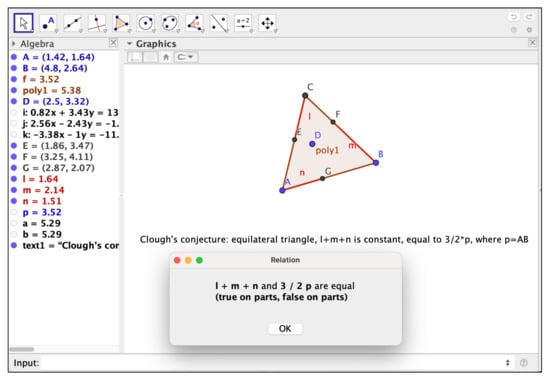 Figure 2. Checking Clough’s conjecture through GeoGebra Discovery yields “true on parts”.On the other hand, asking directly for the proof of Clough’s statement, see Figure 3, an affirmative answer is obtained, together with a list (too long in this case to be fully displayed in the Figure) of construction instances that should be avoided for the truth of the statement: degenerate cases such as when the triangle collapses and, also, variants of the thesis statement that hold just on the primary components of the hypotheses where the given thesis is false.
Figure 2. Checking Clough’s conjecture through GeoGebra Discovery yields “true on parts”.On the other hand, asking directly for the proof of Clough’s statement, see Figure 3, an affirmative answer is obtained, together with a list (too long in this case to be fully displayed in the Figure) of construction instances that should be avoided for the truth of the statement: degenerate cases such as when the triangle collapses and, also, variants of the thesis statement that hold just on the primary components of the hypotheses where the given thesis is false.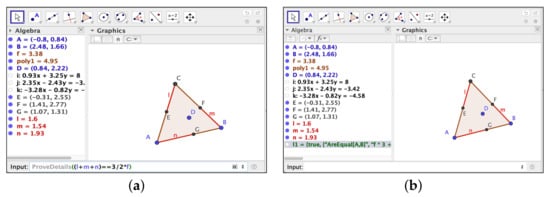 Figure 3. (a) Asking GeoGebra Discovery to prove that the sum is equal to the semiperimeter . (b) GeoGebra Discovery replies that the statement is true except in some degenerate cases (described in the list after true in the last line of the Algebra window).This is related to the possibility, in this case, to modify the thesis so that it collects all possible sign choices for , by multiplying by all possible variants of such formula, changing signs for , such as , , etc. See [21] for a detailed study of this way of understanding real statements in a complex geometry context.Of course, the reason for choosing a complex algebraic geometry approach for GeoGebra automated reasoning tools is because algorithms based on complex geometry are generally much more efficient than their real counterparts, and this aspect is of special relevance for the implementation of GARTs in software with educational purposes.
Figure 3. (a) Asking GeoGebra Discovery to prove that the sum is equal to the semiperimeter . (b) GeoGebra Discovery replies that the statement is true except in some degenerate cases (described in the list after true in the last line of the Algebra window).This is related to the possibility, in this case, to modify the thesis so that it collects all possible sign choices for , by multiplying by all possible variants of such formula, changing signs for , such as , , etc. See [21] for a detailed study of this way of understanding real statements in a complex geometry context.Of course, the reason for choosing a complex algebraic geometry approach for GeoGebra automated reasoning tools is because algorithms based on complex geometry are generally much more efficient than their real counterparts, and this aspect is of special relevance for the implementation of GARTs in software with educational purposes. - (ii)
- Non-degeneracy conditions: In Geometry statements, whenever we mention objects such as line segments, polygons, circles..., we implicitly assume certain conditions on the points that are used to define those figures and render a theorem as true. As an example, in a theorem on triangles we always assume that its vertices are non-collinear points of the plane. These conditions are not easy to interpret by the GATPs and require special care when dealing with them. The problem of non-degeneracy conditions, which depends upon the choice of independent variables in the construction, the way the construction itself is carried out, or the interpretation we can give to what a degenerate construction is, has been studied extensively in the literature and the reader is referred to [12,22,23,24,25] or [26] to gain a better understanding of the intricacies surrounding it.
- (iii)
- True on parts, false on parts statements: As already explained in item i), quite often the hypothesis variety that is obtained from the algebraization process (via complex geometry algorithms which avoid the computationally costly decomposition of the hypothesis variety into irreducible components) can have irreducible, non-degenerate components of maximal dimension, such that the thesis holds on some of the components, while not on others. This situation was thoroughly treated in [27], and gave rise to a new category of true on parts, false on parts geometric statements.
However, our latest developments want to go further, providing tools that actually discover geometric theorems, not just prove them. Some of the strategies behind the algebraic approach to this endeavor (see also [12,24,28]) are briefly described below:
Strategy 1.
We want to show the implication . As seen before, we proceed to check that the ideal . What if we do not get as response to our query? Let us assume that our CAS system produces an output such as this:
If we set , where the variables form a maximal set of independent variables in , it is easy to see that the points in the variety cannot satisfy the thesis condition, and must be excluded from the hypothesis variety in order to obtain a valid statement, which would take the form
Of course, a new check should be made to confirm the validity and interest of this new formulation.
In other words, an algorithm has provided us automatically with the missing hypothesis that turn our initial statement into a true one. Depending on the form and complexity that the polynomials take, the interpretation of these new conditions in geometric terms can be more or less affordable. In fact, some of them are closely related to the non-degeneracy conditions we already mentioned.
Strategy 2.
We have obtained from a geometric construction our hypothesis ideal H, and we are curious about when a certain property holds among some of its elements. If we express this property through an algebraic relation , then we can think of the ideal
and if the variables form a maximal set of independent variables in we can eliminate the variables to obtain an ideal
that provides the conditions that the independent variables must fulfill in the construction in order to obtain the wanted property.
Strategy 3.
Another possibility for implementing discovering tools which combine a numerical and a symbolic approach can proceed as follows: Given a geometric configuration, proceed firstly to search (by using fast performing numerical computations) for properties held among the elements of the construction (parallelism, concurrency, collinearity, concyclicity,...) and set them as possible conjectures. In a second stage, these conjectures will be handled by the algebraic prover to decide whether they can be settled as true statements or rejected.
GeoGebra makes use of these techniques in several commands, some of them already implemented in the official releases of GeoGebra (for technical details concerning their inner workings, see [28,29]):
- Relation(<list of objects>): This higher level command performs two distinct operations: In the first place it proceeds to make a numerical comparison of the objects, and outputs an answer concerning geometric properties such as equality/inequality, parallelism, collinearity, concurrency, etc. Together with this numerical output, the user finds a “More...” button that, when clicked, gives way to a deeper, symbolic analysis of the numerical result previously obtained, resorting to the commands that mention below and proving or rejecting its truthfulness. See Figure 2.
- Prove(<Boolean Expression>): This command is the basic symbolic automatic theorem prover in GeoGebra, and its output can be (generally) true, (generally) false or undefined/? (when GeoGebra cannot decide the question). In order to introduce easily the Boolean expressions of geometric nature, GeoGebra offers a number of different commands such as AreParallel(<line>,<line>), AreCollinear(<Point>,<Point>, <Point>), AreConcyclic(<Point>,<Point>,<Point>,<Point>), etc.
- ProveDetails(<Boolean Expression>): Improved version of the previous command, offering as output more information on degeneracy conditions whenever they are easy to translate into a simple statement. See Figure 3.
- LocusEquation(<Arguments>): This command offers the possibility of finding the algebraic equation for a geometric locus, obtained also by symbolic means. Besides, the command shows on the graphic window the curve corresponding to the equation. Among the several options for choosing the arguments, one which will be useful later to our purposes is LocusEquation(<Boolean expression>, <Point>); this command will find the equation for the locus of points satisfying the given Boolean expression.
- Discover(<Point>): This command, one of the latest additions in GeoGebra Discovery, provides as output from a geometric construction a whole set of geometric statements concerning properties about the lines, segments and other geometric elements related to the point provided as argument. The inner workings of the command follow the idea exposed in Strategies 1 and 3 above.
3. New Tools in GeoGebra Discovery: Handling Geometric Inequalities
In the previous paragraphs we summarily described how automated reasoning tools have been implemented in GeoGebra for proving geometric equalities. However, many classic theorems and results in Geometry are not stated in the form of an equality, but through the use of inequalities—and immediately comes to mind as an essential example the triangle inequality. However, working with inequalities forces us to enter into the realm of Real Algebraic Geometry and its corresponding set of instruments, so that the methods based on polynomials in closed algebraic fields do not suffice to cover this interesting family of geometric results.
In this respect, we believe that at present GeoGebra is pioneering the implementation of automated reasoning tools for proving and discovering geometric inequalities in a DGS environment, and aims at being able to produce proofs in a reasonable timeframe for a wide collection of results.
These new tools are currently in the development stage, and have not yet been implemented in official releases of GeoGebra. Nevertheless, they can be accessed through an experimental version of GeoGebra denominated GeoGebra Discovery ([30]). The (real) algebraic methods that are at the root of dealing with this new set of geometric propositions are based on real quantifier elimination and a derived technique denominated Cylindrical Algebraic Decomposition (CAD). The following is a brief description of the basic ideas involved when performing a CAD.
We start with a given geometric construction that, in a similar way as in the previous case when considering geometric equalities, is defined by a collection of polynomial relations. However, now we introduce two main differences: On the one hand, we restrict our variables to take values in the field , so that we focus our attention in the real plane. On the other hand, we allow them to be only positive or negative, or to hold inequality relations among them. In this way, we obtain a better, more precise description of the set of instances available for our Euclidean construction. Therefore, instead of working with complex varieties, our set of constructions can be represented by a subset of of a type that generalizes that of a variety, called a semialgebraic set. These sets can be expressed (see [31]), (Chapter 3) as a union of sets of the form
The possibility of working in a real geometry environment allows us to consider details that escaped our previous complex geometry approach. To see how naturally semialgebraic sets appear in geometric constructions, let us translate into algebraic form the statement
Given two points in the plane, take a point P in the interior of the line segment .
If we set coordinates , and , then the algebraic translation would give the following semialgebraic set of points defined by the following equations and inequalities:
Here is where a CAD becomes handy. A CAD is a partition of in semialgebraic sets. Let us consider first the projections , . Given a set , a cylinder is a set of the form , and a stack is a partition of a cylinder of the form , induced by a sequence of continuous functions on S so that:
- If j is odd, then
- If j is even, then
Notice that we have for each j. Now we can define a CAD inductively as follows:
- For , a CAD of is a finite partition of the real line in k points and the open intervals which constitute their complement (it can be viewed as a stack over a point). A point is called a 0-cell and an open interval a 1-cell of the CAD.
- For , a CAD of is a partition of in stacks , whose elements are semialgebraic sets, and such that the collection , is a CAD of (here we have renamed and reindexed the elements of the —dimensional CAD to avoid accumulation of subindices). If is a k-cell, then is either a -cell (if j is odd) or a k-cell (if j is even). Besides, and, by the recursive nature of the construction, the collection of sets (with repeated elements) forms a CAD of .
Now, given a finite set of polynomials , there are algorithms whose output is a CAD, together with a sample point in each of its elements, and so that for all the points in each of the elements of the partition and each only one of the relations , , holds. We then say that the CAD is compatible with P (see Figure 4 for an example).
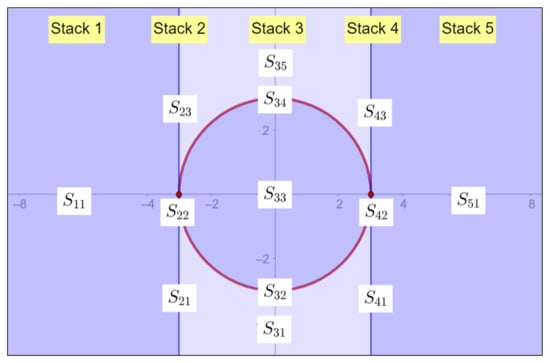
Figure 4.
CAD compatible with the polinomial .
Therefore, if we describe a geometric construction by the hypothesis semialgebraic set and our thesis is represented by an inequality , we can construct a CAD for the collection of all polynomials defining the hypothesis and thesis sets. For each set in the resulting partition, either or . Since the CAD provides also a complete sample of points for all the pieces and the sign of T on each piece does not change on each of them, we can verify whether the inequality is satisfied on all the sets that constitute H by verifying that for each of them, and this would mean that our geometric statement is true. Unfortunately, the computational complexity of performing a CAD is very high, being doubly exponential on the number of variables (see [32]), and this renders the process unpractical in complex configurations. Nonetheless, some clever implementations, combined with other algebraic techniques that simplify the process, have been already successful, time ago, to automatically prove a wide number of classic, non-trivial results ([33,34,35]).
However, we can take advantage of the semialgebraic set H in order to discover new inequalities as well. Let us assume that we want to investigate the relationship between two quantities , that have a geometric meaning in our construction, and find out whether there is a constant p such that an inequality of the form (or a similar one) holds. Then we can include in the space of variables where our Hypothesis semialgebraic set lies (p as first coordinate), together with the defining polynomials for u and v and the equation that defines p as the ratio of the quantities u, v. Thus, we obtain a hypothesis set in some which also contains as coordinates the variables . Recall that each point of H corresponds to an instance of our geometric construction. Now, if we proceed to construct a CAD and use it to project H on the coordinate p-axis we will get a semialgebraic subset in this axis, which is the collection of intervals or points for which there exists geometric constructions providing the corresponding value p. The CAD algorithm facilitates the computation of this projection set, and if we obtain, for example, an interval of the form , this leads to a proof of the inequality . Thus, this algorithm turns out to be a suitable tool for the discovery of new geometric facts.
A detailed description of the algebraic and geometric aspects of the construction of a CAD can be found in [36,37]. There are implementations of the corresponding algorithms in several software programs such as Mathematica, Maple, Reduce or QEPCAD, and GeoGebra Discovery, in its most recent versions, has incorporated them through its realgeom extension, see [38]. In its most recent release, GeoGebra Discovery embeds the Tarski/QEPCAD B program (see [39,40,41]) to perform these CADs, opening the possibility of proving geometric inequalities without resorting to external programs. The commands in GeoGebra that put in action this new set of tools are the following:
- Compare(<Expression, Expression>): This command performs a sequence of tasks that can be briefly described as follows (see [40]):
- The first two points of the construction are identified with (0,0) and (1,0). This reduces the number of variables required, and avoids some degenerate configurations.
- By using only the equalities defining the hypothesis, there is a first trial to check for an equality relation between the input expressions. This is handled by the Giac CAS embedded in GeoGebra.
- If equality relations are not found, the set of equations in the hypothesis is processed, eliminating unnecessary variables and generating a quantified formula.
- Now, via the Tarski/QEPCAD B software, this quantified formula is converted into a quantifier-free formula, by means of a CAD algorithm that outputs an inequality for the quotient of the input expressions.
- This inequality is translated and displayed into a simple form, easy to understand by the user.
See Figure 5 for an example of the performance of the Compare command regarding the statement of Proposition 1.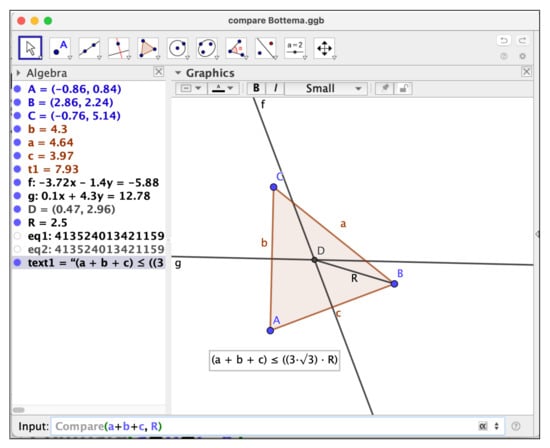 Figure 5. Discovering the inequality between the perimeter and the radius of the circumcenter of a triangle.
Figure 5. Discovering the inequality between the perimeter and the radius of the circumcenter of a triangle. - Relation(<list of objects>): As mentioned before, this higher level command performs two distinct operations ([28]): first, proceeds to make a numerical comparison of the objects, and outputs an answer concerning geometric properties, including—this is the more recent improvement—inequalities, etc. Then the user finds a “More...” button that, if clicked, starts a deeper, symbolic analysis of the numerical result previously obtained, proving or rejecting its truthfulness. A detailed example is developed in Section 5, and shown in Figures 10 and 11.
4. Visualization of Real Curves and the Dynamic Color Scanning Method
Nowadays, computer visualization of mathematical objects is an active area of research, which finds applications in a great variety of disciplines. In particular, the graphic representation of real algebraic curves (especially in the neighborhood of a singularity) poses a number of challenges that, although have been faced by numerical and also by symbolic methods (see [42] and its many references, as well as [43] as a more recent contribution), still lack accuracy in current computer software implementations, even in apparently innocent-looking examples.
Example 1.
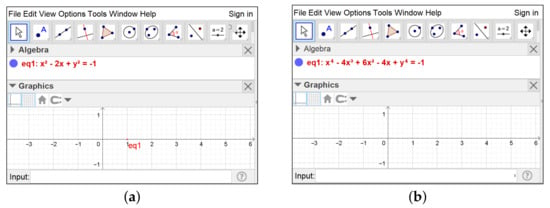
Within GeoGebra, introduce in the input line the command
ImplicitCurve((x-1)^2+y^2),
whose output corresponds to the curve C with equation . It is obvious that the real part of C contains only the point . GeoGebra will display correctly the curve, as shown in Figure 6a. If we want to visualize now the curve given by , whose real part coincides with that of C, and introduce

Figure 6.
GeoGebra output for the implicit curves (success, subfigure (a)) and (failure, subfigure (b)).
ImplicitCurve((x-1)^4+y^4),
GeoGebra will display nothing on its graphic view, as shown in Figure 6b. These issues can also affect the commandLocusEquation(), since it makes use ofImplicitCurve()to represent loci graphically.
Example 2.
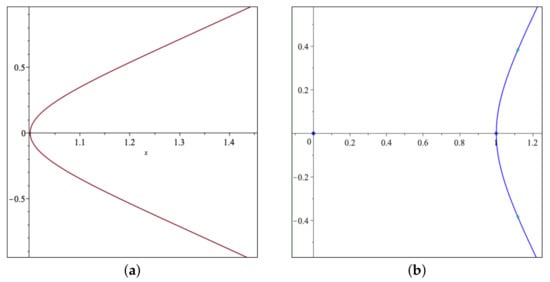
Even advanced mathematical software packages such as Maple face similar problems with its plotting commands. The graphic output of the set of instructions
with(plots);
implicitplot(x^2+y^2-x^3, x=-1..1, y=-1..1);
will miss the real point that belongs to this cubic curve, see Figure 7a. This is due to the fact that the implicitplot command uses a sample-based method which is not able to detect accurately isolated points. However, Maple includes other representation options that allow a more precise output for the case of real algebraic curves, by means of the package algcurves. Executing now

Figure 7.
Graphic output of Maple for the curve (a) with the implicitplot() command; (b) with the plot_real_curve() command.
with(algcurves);
plot_real_curve(x^2+y^2-x^3, x, y);
our previous missing point will appear on screen, as shown in Figure 7b.
Being the case that important characteristics of algebraic curves can be lost when making use of these plotting commands, it is interesting to explore other ways to approach the problem of visualizing (real) algebraic curves. This is the moment to take a closer look at some of GeoGebra’s special functionalities. Since this program was mainly designed as a software to be used for the teaching and learning of Mathematics, it incorporates a set of tools that facilitates the visualization of geometric constructions and their properties, making them more attractive and comprehensible to students. It turns out that these tools can also be employed as a powerful resource to explore diverse problems where complex geometric configurations arise. In particular, the combined use of the properties Show Trace and Dynamic color that can be assigned to objects in the graphic window of GeoGebra creates a scanning tool capable of showing hidden relations among the elements of a given construction. We refer to this technique as the dynamic color scanning method.
The basic idea behind this method lies in the ability to assign a color to each point in the plane depending on its position in relation to a geometric construction, element or property we have to deal with. Whether working with distances and other measures, with operations performed on a set of these quantities, or with equations corresponding to geometric loci, the scanning method in GeoGebra is easy to implement, reasonably fast and reliable, and produces outstanding visual information that can provide insight in a complex scenario. Pioneer work in the use of this technique in the GeoGebra environment can be attributed to the second author, who has a nice collection of applications in [44] (see Figure 8).

Figure 8.
(a) The classic Mandelbrot set, created with the dynamic color scanning method. (b) An application to investigate the Fermat point of an arbitrary triangle.
Let us describe briefly how this visual method works by showing a simple example (for those unacquainted with GeoGebra, its reference manual can be found at [45]). Let us assume that we have three given points A, B, C on the plane, that we can display in the graphic window of GeoGebra. Let us denote the distance between two points P and Q by .
Problem 1.
Find the geometric locus of points P such that .
This locus is easy to display with the ImplicitCurve command in GeoGebra, see Figure 9a. Now, in order to exemplify how to visualize this locus through our dynamic color scanning method approach, let us start associating some colors to point , as follows. First, we remark that GeoGebra allows to set independently dynamic values of the three color channels RGB that colorize an object in GeoGebra. The numeric value for each channel ranges between 0 (no color) and 1 (full color), and for other values z outside this range GeoGebra applies a periodic pattern given by
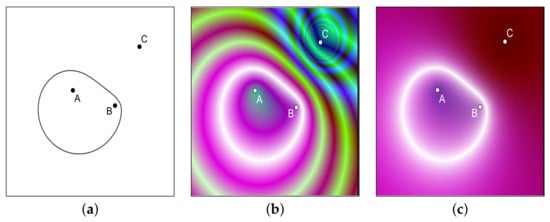
Figure 9.
Locus of P such that , displayed (a) with the traditional GeoGebra tools, (b,c) with the dynamic color scanning method.
In particular, if we set the values (R,G,B) to integers of the form (even, even, even) we get black, and by setting them to integers (odd, odd, odd) we obtain white. Besides, if all three channels have equal values, a color in the scale of greys is produced. Now, for instance, let us set dynamic values for the point P as follows:
- Red: c/s
- Green: 1-abs(s-c)
- Blue: s/c,
where c = Distance(P,C) and s = Distance(P,A)+Distance(P,B). Observe that we will get for the point P the white color only when , since values assigned to red and blue channels are positive and mutually inverse, and all three channels will give odd numbers (in fact, 1) only in this case.
Now, if we activate the trace for the point P and drag it, after covering the region we are interested in, we obtain the color scanning of the area, and we will have a visualization of the locus (the set of points white-colored) we are looking for. It is interesting to make here several remarks concerning the output image:
- The periodic patterns that frequently arise in form of concentric rings of similar colors are due to the periodic behavior of the dynamic colors when the values introduced in the RGB channels move outside the range, as previously mentioned (see Figure 9b).
- A way to restrict the values for the dynamic color channels in the range is obtained by using exponential expressions of the form
- Red: e^(-abs(f(P)))
- Green: e^(-abs(g(P)))
- Blue: e^(-abs(h(P))),
so that only when simultaneously the functions , depending on point P, are equal to 0 the white color will be assigned to P. In our example, by assigning to the color channels the values- Red: e^(-abs(1-c/s))
- Green: e^(-abs(s-c))
- Blue: e^(-abs(1-s/c)),
we obtain Figure 9c.Besides, if we substitute in a given RGB channel, for instance the red one, the expression in the exponent by , where k is a convenient positive constant, we get the mantissa of , which drops abruptly to zero when crosses integer values, producing distinct lines because of the sudden color change in the red channel. This trick leads to the appearance of level curves connecting points P with the same value, which will be more densely distributed by choosing a greater value for the constant k. We will make use of this technique later in Section 6.1. - Since we have three different channels that can hold independent values, by playing wisely with them, we have at our disposal up to three different properties to visualize in our scanning method. An illustration of how to take advantage of this feature is shown in Figure 8b, where an investigation on the Fermat’s Point is carried out (see the section on “Escáner del Punto Fermat” in [44], for details on the construction).
Now, to improve the output of the process and avoid the cumbersome dragging of point P all over the graphic view we can benefit from other resources included in GeoGebra and proceed as follows:
- Set a rectangular region to be scanned. Let us say it has as upper left corner the point , and dimensions .
- Shrink the size of the radius for the point P to its minimum size.
- Create a slider t that will be used as the x-coordinate of P, and runs from to .
- Set the coordinates of P to and rename the point to . This trick allows us to automatically assign the point P to the cell of the GeoGebra spreadsheet. Now we can create a list of points , , by taking advantage of the spreadsheet features, starting first by adding the point , with the same properties as A1, and dragging downwards (as it is usually done when working with spreadsheets) the cell A2. This column of points (all of them inheriting the properties we set up for ) translates in the graphic window into a scanning vertical segment, which will sweep the region as the slider t runs through its defined range. A recommended value for is in order to obtain a good quality of the scanning image. Therefore, for covering our rectangular region of height h we should create around h points.
We will see below how this method proves useful when trying to understand geometric configurations that lead to demanding computational tasks that cannot be handled by the GeoGebra CAS. Other variations of these dynamic coloring methods in GeoGebra that show their flexibility and visualization potential can be found in [46] (see also [44,47]).
Remark 2.
Similar visualization techniques to those presented here can be also employed in other DGS programs such as Cinderella [48] and its companion open project CindyJS [49], some of them inspired in Losada’s scanning method for GeoGebra (see for instance [50]).
5. A Case Study: Relation between the Perimeter and Circumradius of a Triangle
Now we center our attention on Proposition 1, and let us see how GeoGebra can help us discover this proposition automatically, without having to provide any clue whatsoever as an input, apart from the basic construction required to set the scenario for our investigation.
We start by constructing the three vertices A, B, C of a triangle. Without loss of generality, we can assume A and B to be the points and . The third vertex C has free coordinates . Now we draw the segments , and , with respective lengths a, b, c, and the perpendicular bisectors l and m to and respectively. Let us denote by the point of intersection of the two previous bisectors. The segment of length R is the circumradius of the triangle . Our construction is all set. Now we introduce in the GeoGebra input line the command Relation(, R) and we obtain (see Figure 10) an initial, numerical output indicating that the quantities and R do not coincide. Not very informative indeed, but if we press the “More...” button (see Figure 11) the realgeom extension enters in action and quickly shows that the relation holds.
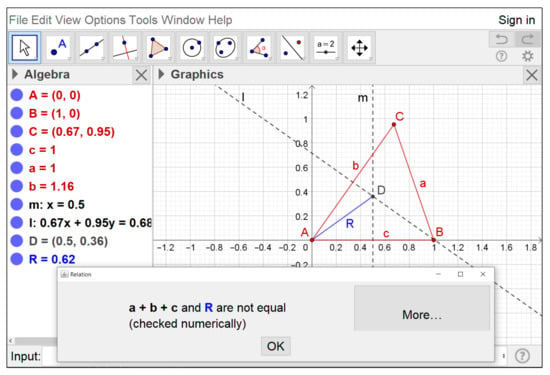
Figure 10.
Numerical output of the Relation tool.
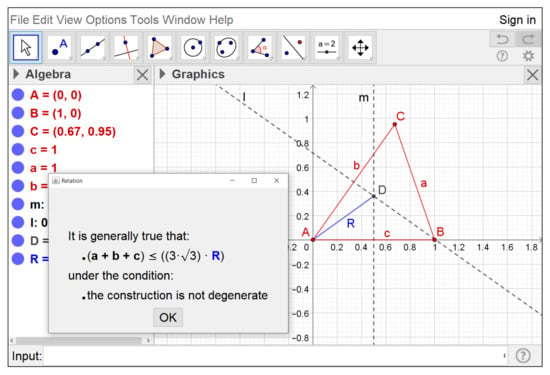
Figure 11.
Symbolic output of the Relation tool.
However, Proposition 1 not only asserts that this inequality holds. It also states that the corresponding equality is true if and only if the triangle is equilateral. How can we prove this with our set of tools? Well, for this task the command LocusEquation(<Boolean Condition>, <Point>) becomes handy, since if we ask GeoGebra to provide us with the geometric locus of the points in the plane satisfying the equality relation we should obtain an algebraic curve giving us information on the set of points we are looking for. Were Proposition 1 correct, this locus should reduce to the points and , which are the only ones producing equilateral triangles together with A and B.
Having therefore a clear strategy to settle down the equality part of our statement, we type in the input bar LocusEquation(, C), obtaining the following equation for this geometric locus:
The degree of this polynomial equation is 16 and, unfortunately, GeoGebra is not capable of producing any points of the corresponding curve in the graphical window (see Figure 12, where all elements apart from the locus have been hidden to allow a better visualization). Our strategy fails! In principle, it could be the case that the curve had no real points, but a quick inspection of the polynomial is enough to see that at least the point must belong to it. Therefore, something is going wrong here... It is time to look for another way to find out what is the real aspect of this curve.
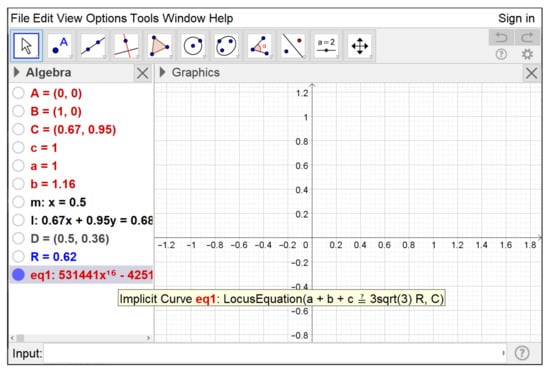
Figure 12.
The algebraic curve does not appear on-screen.
6. Combining Visual and Symbolic Strategies to Overcome Difficulties
6.1. The Visual Approach Using the Dynamic Color Scanning Method
After the difficulties that we have encountered when trying to study the algebraic curve by means of the LocusEquation() command, let us approach the problem from a more visual strategy, by using the dynamic color scanning method described in Section 4. Let us choose as scanning area the rectangle R with two opposite vertices located at and , which contains points A, B of our construction. We have to assign dynamic values to the three RGB color channels of the scanning points, and these values should depend on some kind of measure of the “distance” of the point to the curve . As an initial choice, we could just choose the values for each point , but the high values that the polynomial P attains on the considered region (for instance, ) produces undesirable effects in the visualization process, so that it is better to adjust these values in order to obtain a better display. A good choice to get a neat output is obtained by assigning to each point of the scanning segment the following values (see Figure 13 and Figure 14):
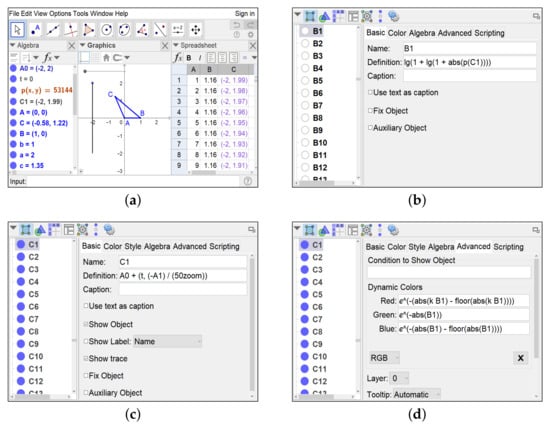
Figure 13.
(a) Setting up the dynamic color scanner. (b,c) Basic parameters of the scanning points. (d) Parameter values for the RGB channels.
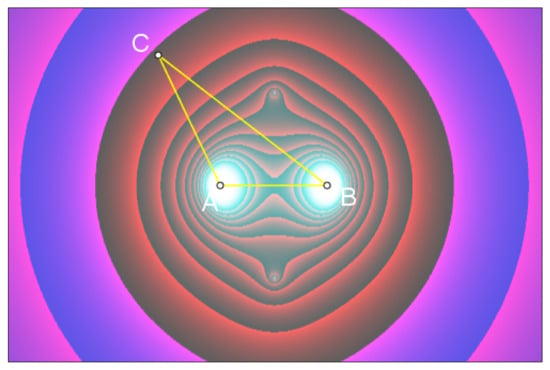
Figure 14.
Output after a dynamic color scanning of the plane for the locus .
- Red: e^(-(abs(k Bi)-floor(abs(k Bi))))
- Green: e^(-abs(Bi))
- Blue: e^(-(abs(Bi)-floor(abs(Bi)))),
Here, recommended values for the values k, are and .
As already seen, the “curve” of white points in the scanned region would represent the part of the geometric locus contained in R. However, instead of a curve we perceive four whitened areas: two of them, more visible, with centers located around and , and two smaller ones (these ones are trickier to spot, and the technique described in Section 4 for producing isolines, applied to the red and blue channels, helps detecting them) with centers lying on the line . This leads us to state the following conjecture:
Conjecture 1.
The number of real points of the curve is finite and equal to four. Besides, two of them have as x-coordinate the value , while the two others have x-coordinates and respectively.
So, the dynamic color scanning method has helped us approach the solution to our question on the conditions that correspond to the equality case in Proposition 1. Of course, this cannot be considered a formal proof, but the information that we have obtained from this visual exploration allows us to return to a symbolic approach, this time with a conjecture in mind, and with Maple and its algebraic toolkit as auxiliary assistant.
6.2. The Symbolic Approach Using Maple Commands
Thanks to the previous section we now have a better intuition about the geometric locus corresponding to the equality , and we can try to resort to more powerful tools in order to definitely settle the question that has resisted our analysis so far. From now on, we will use Maple and a variety of its available tools to perform a thorough algebraic study of the situation in order to completely elucidate the set of real points in .
In the first place, since we already have some familiarity with CADs, we will use higher level commands implemented in recent versions of Maple to quickly settle down Proposition 1. To achieve this, we need the RegularChains package and its commands to perform CADs:
- >
- with(RegularChains):with(ChainTools):with(SemiAlgebraicSetTools):R:=PolynomialRing([y,x])cad:=CylindricalAlgebraicDecompose(P,R,method = recursive,output=piecewise)
Here, P represents the polynomial detailed in the precedent Equation (5). Executing this group of instructions we get
which graphically corresponds to the CAD shown in Figure 15.
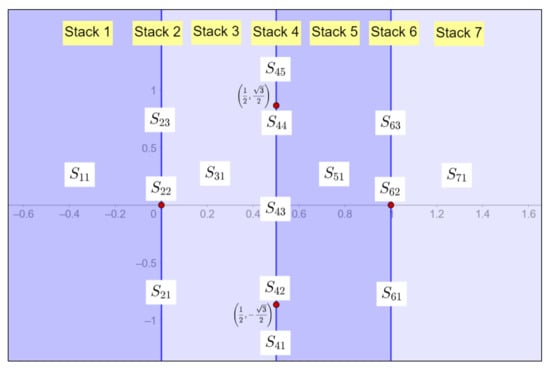
Figure 15.
CAD compatible with the set of solutions of .
This confirms at once our Conjecture 1, as well as the equality case in Proposition 1, and we are done.
However... what kind of symbolic calculations lie behind performing a CAD compatible with a set of given polynomials? In order to gain a better understanding of how Maple is capable of completing these tasks related to working with polynomials in real coefficients, in the sequel, we proceed to give a more guided, step-by-step treatment of the problem, by using lower level Maple commands that can also be translated to other software packages such as the Xcas/Giac environment.
We start by translating into algebraic form our initial construction (see Table 1).

Table 1.
Algebraic translation of geometric construction in GeoGebra.
Notice that we take care of expressing all our relations concerning distances and other measures in polynomial form. This allows the use of the algebraic tools implemented in Maple. We define now the ideal containing our hypothesis, which we denote by Hypo:
- >
- restart:with(PolynomialIdeals):Hypo:=PolynomialIdeal(u-(1/2),(x-1)*(u-((x+1)/2))+y*(v-(y/2)),h^2-(x-u)^2-(y-v)^2,a^2-(x-1)^2-y^2,b^2-x^2-y^2,c^2-1, variables={x,y,u,v,h,a,b,c});
The Hilbert dimension of this ideal gives us information on the number of maximal independent variables, giving us the degrees of freedom of the construction:
- >
- HilbertDimension(Hypo);EliminationIdeal(Hypo,{x,y});
Therefore, we can consider as free variables the coordinates x, y of the point C, since we can drag this point on the plane and its position determines the whole construction. Now we introduce the polynomial related to the locus equation (together with the relation defining ) to obtain ideal T, which should decrease its Hilbert dimension by one:
- >
- T:=PolynomialIdeal(u-(1/2),(x-1)*(u-((x+1)/2))+y*(v-(y/2)),h^2-(x-u)^2-(y-v)^2,a^2-(x-1)^2-y^2,b^2-x^2-y^2,c^2-1,r^2-3,a+b+c-3*r*h,variables={x,y,u,v,h,a,b,c,r});HilbertDimension(T);
Therefore, the variables are not free anymore, and a polynomial relation among them must hold. If we type now
- >
- P:=EliminationIdeal(T,{x,y});
we obtain the same polynomial appearing in Equation (5) (with a different order of terms), confirming the good job done by GeoGebra when computing the locus equation for the equality . Our intuition, reinforced through our visualization approach in Section 6.1, invites us to think that this algebraic curve should have only two real points (apart from degenerate cases that already have been considered). Therefore, our mission consists now in finding all the real points belonging to the curve . Since Maple also includes graphic tools to plot real algebraic curves, in the same spirit as we tried with GeoGebra we can see whether Maple outputs (see Figure 16) successfully the real set of points for this curve:
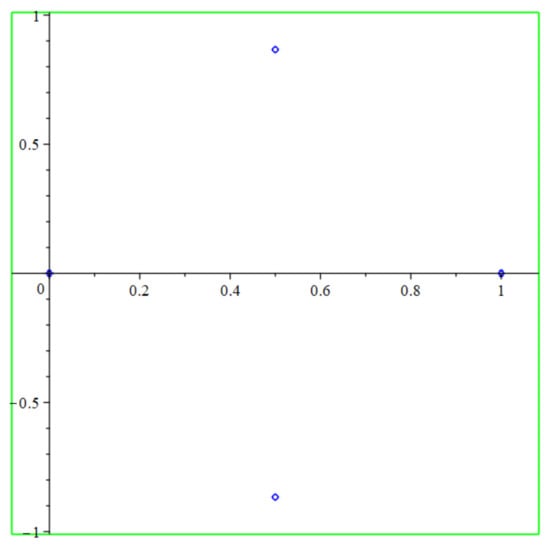
Figure 16.
Maple output for locus equation .
- >
- with(algcurves): plot_real_curve(P(x,y),x,y);
Indeed, it seems that this time the picture looks complete: The graphic output shows four points that certainly could correspond to the degenerate cases and , together with the elusive points and , which correspond to the two possible equilateral triangle configurations. We are getting closer to our goal, but we have learned that, even though the visual approach has provided us with clues to settle the problem, at the same time it can be an inaccurate technique.
Now, in order to verify rigorously that these are the only real points of our curve, we will proceed as follows:
- Step 1:
- Check that for has real solutions in y, and determine them all.
- Step 2:
- Check that for has not real solutions in y.
These two facts will lead to a full determination of the set of real points in our geometric locus.
- Step 1:
- We first set and compute , factorizing the result.
- >
- simplify(subs(x=0,P(x,y))); factor(%);
From the first factor it follows that there exists the real solution , and to exclude any other possibilities it is enough to count real roots by using the Sturm sequence of the second factor (since the third factor has symmetric real roots, being obtained from the second through the substitution ).
- >
- sturmseq(297*y^4 + 432*y^3 + 658*y^2 + 432*y + 297,y);sturm(%,y, -infinity, infinity);
For the value , we proceed similarly and obtain
- >
- simplify(subs(x=1,P(x,y)));
Since this polynomial coincides with the one in case , we again have that is the only real root for .
Finally, let us study the case . Now,
- >
- simplify(subs(x=1/2,P(x,y)));
The last factor in this expression has roots , while the others do not produce further real roots:
- >
- sturmseq(1936*y^4 + 744*y^2 + 81,y);sturm(%,y, -infinity, infinity);
- >
- sturmseq(432*y^4 + 152*y^2 + 27,y);sturm(%,y, -infinity, infinity);
Therefore, after we finish Step 1 we have checked that the curve contains the real points , , and . However... Are these the only real points?
- Step 1:
- We start by considering again the polynomial , but now displayed as a polynomial in , that is, as a polynomial in the variable y with coefficients in the domain :
- >
- P(y):=collect(P(x,y),y);
Now we consider the discriminant of , i.e., the following poynomial in the variable x.
- >
- F(x):=discrim(P(y),y);
The output is a factorized polynomial in that we can express in the form . The first factor is a monomial containing , which gives the real root . The two other factors , (one of them squared) need a more careful examination. Let us see first whether they can be further factorized.
- >
- factor(F_1);factor(F_2);
Now it is clear that has only one real solution (with multiplicity 8). With respect to , the factors and do not contribute with real roots, and the factors and contribute with real solutions and (with multiplicities 6 and 32 respectively). Finally, we study the Sturm sequence for the larger factor in order to see whether we are missing other real roots of .
- >
- sturmseq(221709312*x^10 - 1108546560*x^9 + 5547202304*x^8−15537529856*x^7 + 23360155968*x^6 - 20355008960*x^5+10731606224*x^4 - 3448222560*x^3 + 658900764*x^2−70266636*x + 3485889,x);sturm(%,x,-infinity, infinity);
Therefore, no new real roots appear, and we conclude that the only real roots of the discriminant are 0, and 1. These three values split into four intervals and on their interiors does not vanish. Now the following result concerning discriminants becomes handy (see for example [51], (pp. 320–321) for a proof of this fact):
Proposition 2.
Between consecutive roots of the discriminant of a bivariate polynomial (regarded as a function of y alone), the number of real zeros of is independent of x.
Therefore, we can use again Sturm’s sequences to check the number of real roots for the variable y for specifying particular values of x lying in each of the aforementioned intervals, let us say , , and .
- >
- subs(x=-1,P(y)); sturmseq(%,y):sturm(%,y,-infinity, infinity);
- >
- subs(x=1/3,P(y)); sturmseq(%,y):sturm(%,y,-infinity,infinity);
- >
- subs(x=2/3,P(y)); sturmseq(%,y):sturm(%,y,-infinity,infinity);
- >
- subs(x=2,P(y)); sturmseq(%,y):sturm(%,y,-infinity,infinity);
Therefore, for any outside the finite set there are no real solutions for , and we can conclude that , , and are the only real points of the curve , and this concludes our scaffolded, computational-based proof of Proposition 1.
Certainly, there are still people loving human-made proofs. If the reader is among them and is curious about a more classical approach, see [10] or [52].
7. Conclusions and Further Research
We have seen that the current graphic and symbolic tools available in diverse mathematical software packages, due to high complexity issues, present some limitations for visualizing appropriately geometric objects such as loci defined by algebraic curves. In order to gain some insight on the geometry of these objects we have resorted to an alternative visualization technique, the dynamic color scanning method, which takes advantage of the possibility of working with dynamic colors in the GeoGebra graphic view. The visual guidance provided by this method allows us to approach the extreme case of a geometric inequality more effectively, this time using symbolic tools available in external software such as Maple.
The authors consider that future releases of GeoGebra could benefit from the inclusion of new commands that:
- (i)
- perform straightforwardly a dynamic color scanning, avoiding the setup process which is needed at present and improving its performance;
- (ii)
- utilize the Giac and Tarski/QEPCAD embedded systems to increase the power of the GART’s tools present in GeoGebra, rendering unnecessary to make use of external software to visualize and study certain geometric problems (see for instance [53]) which can involve equalities or inequalities in their formulation.
We hope to accomplish these tasks in a near future, with the help of the many colleagues already involved in the development of the GeoGebra automated reasoning tools project.
Author Contributions
Writing—original draft, T.R., R.L., Z.K. and C.U. All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
First and third authors were partially supported by a grant PID2020-113192GB-I00 (Mathematical Visualization: Foundations, Algorithms and Applications) from the Spanish MICINN.
Acknowledgments
Thanks to Laureano González-Vega for some clever hints concerning Section 6.2.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CAD | Cylindric Algebraic Decomposition |
| CAS | Computer Algebra System |
| DGS | Dynamic Geometry Software |
| GART | Geometry Automated Reasoning Tool |
| GATP | Geometry Automated Theorem Prover |
References
- Wu, W.T. On the decision problem and the mechanization of theorem-proving in elementary geometry. Sci. Sin. 1978, 21, 159–172, Reprinted in: Automated Theorem Proving: After 25 Years; Bledsoe, W.W., Loveland, D.W., Eds.; Contemporary Mathematics, 29; AMS: Providence, RI, USA, 1984; pp. 213–234. [Google Scholar]
- Quaresma, P. Thousands of Geometric problems for geometric Theorem Provers (TGTP). In Automated Deduction in Geometry, 8th International Workshop, ADG 2010; Schreck, P., Narboux, J., Richter-Gebert, J., Eds.; LNAI 6877; Springer: Berlin/Heidelberg, Germany, 2011; pp. 169–181. [Google Scholar]
- Chou, S.C. An Introduction to Wu’s Method for Mechanical Theorem Proving in Geometry. J. Autom. Reason. 1988, 4, 237–267. [Google Scholar] [CrossRef]
- Buchberger, B. Introduction to Gröbner Bases. In Gröbner Bases and Applications; Buchberger, B., Winkler, F., Eds.; LMSLN 251; Cambridge University Press: Cambridge, UK, 1998; pp. 3–31. [Google Scholar]
- Kapur, D. Using Gröbner bases to reason about geometry problems. J. Symb. Comput. 1986, 2, 399–408. [Google Scholar] [CrossRef]
- About GeoGebra. Available online: https://www.geogebra.org/m/pR5DME5S#material/uy93nfzr (accessed on 21 August 2021).
- Cevikbas, M.; Kaiser, G. A Systematic Review on Task Design in Dynamic and Interactive Mathematics Learning Environments (DIMLEs). Mathematics 2021, 9, 399. [Google Scholar] [CrossRef]
- Ondes, R.N. Research trends in dynamic geometry software: A content analysis from 2005 to 2021. World J. Educ. Technol. Curr. Issues 2021, 13, 236–260. [Google Scholar] [CrossRef]
- Kovács, Z.; Montag, A.; Vajda, R. On Euler’s inequality and automated reasoning with dynamic geometry. arXiv 2020, arXiv:1708.02993. [Google Scholar]
- Bottema, O.; Djordjević, R.Ž.; Janić, R.R.; Mitrinović, D.S.; Vasić, P.M. Geometric Inequalities, 1st ed.; Wolters-Noordhoff Publishing: Groningen, Germany, 1969. [Google Scholar]
- Hohenwarter, M.; Kovács, Z.; Recio, T. Using GeoGebra automated reasoning tools to explore geometric statements and conjectures. In Proof Technology in Mathematics Research and Teaching; Hanna, G., de Villiers, M., Reid, D., Eds.; Mathematics Education in the Digital Era 14; Springer: Berlin/Heidelberg, Germany, 2019; pp. 215–236. [Google Scholar]
- Recio, T.; Vélez, M.P. Automatic Discovery of Theorems in Elementary Geometry. J. Autom. Reason. 1999, 23, 63–82. [Google Scholar] [CrossRef]
- Botana, F.; Kovács, Z.; Recio, T. A Mechanical Geometer. Math.Comput. Sci. 2020. [Google Scholar] [CrossRef]
- De Graeve, R.; Parisse, B. Giac/Xcas (v. 1.7.0). 2021. Available online: https://www-fourier.ujf-grenoble.fr/~parisse/giac.html (accessed on 29 July 2021).
- Kovács, Z.; Parisse, B. Giac and GeoGebra—Improved Gröbner Basis Computations. In Computer Algebra and Polynomials; Gutiérrez, J., Schicho, J., Weimann, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2015; pp. 12–138. [Google Scholar]
- Cox, D.A.; Little, J.; O’Shea, D. Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra, 3rd ed.; Springer: Cham, Germany, 2015. [Google Scholar]
- Conti, P.; Traverso, C. Algebraic and semialgebraic proofs: Methods and paradoxes. In Proc. 3rd International Workshop on Automated Deduction in Geometry (ADG 2000); Richter-Gebert, J., Wang, D., Eds.; LNAI, 2061; Springer: Berlin/Heidelberg, Germany, 2000; pp. 83–103. [Google Scholar]
- Dolzmann, A.; Sturm, T.; Weispfenning, V. A New Approach for Automatic Theorem Proving in Real Geometry. J. Autom. Reason. 1998, 21, 357–380. [Google Scholar] [CrossRef]
- De Villiers, M. Clough’s conjecture: A Sketchpad investigation. In Proceedings of the 10th Annual National Congress of the Association for Mathematics Education of South Africa; Nieuwoudt, S., Froneman, S., Nkhoma, P., Eds.; AMESA: Potchefstroom, South Africa, 2004; Volume 2, pp. 52–56. [Google Scholar]
- De Villiers, M. An illustration of the explanatory and discovery functions of proof. Pythagoras 2012, 33, 8. [Google Scholar] [CrossRef]
- Kovács, Z.; Recio, T.; Sólyom-Gecse, C. Rewriting input expressions in complex algebraic geometry provers. Ann. Math. Artif. Intell. 2018, 85, 73–87. [Google Scholar] [CrossRef]
- Chou, S.C. Mechanical Geometry Theorem Proving, 1st ed.; D. Reidel Publishing Company: Dordrecht, Holland, 1988. [Google Scholar]
- Kovács, Z.; Recio, T.; Tabera, L.F.; Vélez, M.P. Dealing with Degeneracies in Automated Theorem Proving in Geometry. Mathematics 2021, 9, 1964. [Google Scholar] [CrossRef]
- Kapur, D. A Refutational Approach to Geometry Theorem Proving. Artif. Intell. 1988, 37, 61–93. [Google Scholar] [CrossRef]
- Bulmer, M.; Fearnley-Sander, D.; Stokes, T. The kinds of truth of geometric theorems in automated deduction in geometry. In Proc. 3rd International Workshop on Automated Deduction in Geometry (ADG 2000); Richter-Gebert, J., Wang, D., Eds.; LNAI, 2061; Springer: Berlin/Heidelberg, Germany, 2000; pp. 129–142. [Google Scholar]
- Guan, H.; Rao, Y.S.; Zhang, J.Z.; Cao, S.; Qin, X.L. Method for Processing Graph Degeneracy in Dynamic Geometry Based on Domain Design. J. Comput. Sci. Technol. 2021, 36, 910–921. [Google Scholar] [CrossRef]
- Kovács, Z.; Recio, T.; Vélez, M.P. Detecting truth, just on parts. Rev. MatemáTica Complut. 2019, 32, 451–474. [Google Scholar] [CrossRef]
- Kovács, Z. The Relation Tool in GeoGebra 5. In Proceedings of the 10th International Workshop on Automated Deduction in Geometry (ADG 2014), Coimbra, Portugal, 9–11 July 2014; Botana, F., Quaresma, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 53–71. [Google Scholar]
- Botana, F.; Hohenwarter, M.; Janičić, P.; Petrović, I.; Recio, T.; Weitzhofer, S. Automated Theorem Proving in GeoGebra: Current Achievements. J. Autom. Reason. 2015, 55, 39–59. [Google Scholar] [CrossRef]
- GeoGebra Discovery. Available online: https://github.com/kovzol/geogebra-discovery (accessed on 29 July 2021).
- Bochnak, J.; Coste, M.; Roy, M.F. Real Algebraic Geometry, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Davenport, J.; Heintz, J. Real quantifier elimination is doubly exponential. J. Symb. Comput. 1988, 5, 29–35. [Google Scholar] [CrossRef]
- Xia, B.; Yang, L.; Hou, X. Automated discovering and proving for geometric inequalities. In ADG’98: Proceedings of the Second International Workshop on Automated Deduction in Geometry, Beijing, China, 1–3 August 1998; Gao, X.-S., Wang, D., Yang, L., Eds.; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Xia, B.; Yang, L. Automated Inequality Proving and Discovering; World Scientific Publishing Company: Hackensack, NJ, USA, 2017. [Google Scholar]
- Yang, L. Recent advances in automated theorem proving on inequalities. J. Comput. Sci. Technol. 1999, 14, 434–446. [Google Scholar] [CrossRef]
- Collins, G.E. Quantifier elimination for real closed fields by cylindrical algebraic decomposition. In Proc. 2nd GI Conference on Automata. Theory and Formal Languages; Brakhage, H., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1975; Volume 33, pp. 134–183. [Google Scholar]
- Chen, C.; Maza, M.M. Quantifier Elimination by Cylindrical Algebraic Decomposition based on Regular Chains. J. Symb. Comput. 2016, 75, 74–93. [Google Scholar] [CrossRef]
- Kovács, Z.; Vajda, R. GeoGebra and the realgeom reasoning tool. In Proceedings of the Fifth International Workshop on Satisfiability Checking and Symbolic Computation, Paris, France, 5 July 2020; Fontaine, P., Korovin, K., Kotsireas, I.S., Rümmer, P., Tourret, S., Eds.; CEUR Workshop Proceedings. RWTH: Aachen, Germany, 2020; Volume 2752, pp. 204–219. [Google Scholar]
- Brown, C.W. QEPCAD. Extended Tarski Formulas. Available online: https://www.usna.edu/Users/cs/wcbrown/qepcad/B/user/ETF.html (accessed on 12 August 2021).
- Brown, C.W.; Kovács, Z.; Vajda, R. Supporting Proving and Discovering Geometric Inequalities in GeoGebra by Using Tarski. In Proceedings of the 13th International Workshop on Automated Deduction in Geometry (ADG2021), Hagenberg, Austria, 15–17 September 2021. [Google Scholar]
- Brown, C.W. An Overview of QEPCAD B: A Tool for Real Quantifier Elimination and Formula Simplification. J. JSSAC 2003, 10, 13–22. [Google Scholar]
- Cheng, J.; Lazard, S.; Peñaranda, L.; Pouget, M.; Rouillier, F.; Tsigaridas, E. On the topology of real algebraic plane curves. Math. Comput. Sci. 2010, 4, 113–137. [Google Scholar] [CrossRef]
- Chen, C.; Wu, W.; Feng, Y. Visualizing Planar and Space Implicit Real Algebraic Curves with Singularities. J. Syst. Sci. Complex. 2020, 33, 1252–1274. [Google Scholar] [CrossRef]
- Losada, R. Color Dinámico (Spanish). Available online: https://www.geogebra.org/m/d6j2nhYG (accessed on 19 July 2021).
- GeoGebra Manual. Available online: https://wiki.geogebra.org/en/Manual (accessed on 23 August 2021).
- Losada, R. El Color Dinámico de GeoGebra (Spanish). Gaceta De La Real Sociedad Matematica Española 2014, 17, 525–547. [Google Scholar]
- Losada, R.; Recio, T.; Valcarce, J.L. Equal Bisectors at a Vertex of a Triangle. In Computational Science and Its Applications—ICCSA 2011; Murgante, B., Gervasi, O., Iglesias, A., Taniar, D., Apduhan, B.O., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6785, pp. 328–341. [Google Scholar]
- Cinderella Homepage. Available online: https://cinderella.de/tiki-index.php (accessed on 20 August 2021).
- CindyJS. Available online: https://cindyjs.org/ (accessed on 22 August 2021).
- Montag, A.; Richter-Gebert, J. Bringing Together Dynamic Geometry Software and the Graphics Processing Unit. arXiv 2018, arXiv:1808.04579. [Google Scholar]
- Schwartz, J.T.; Sharir, M. On the “Piano Movers” Problem. II. General Techniques for Computing Topological Properties of Real Algebraic Manifolds. Adv. Appl. Maths. 1983, 4, 298–351. [Google Scholar] [CrossRef]
- Bottema, O. Inequalities for R, r and s. Publikacije Elektrotehničkog Fakulteta. Serija Matematika i Fizika 1971, 338/352, 27–36. [Google Scholar]
- Kovács, Z.; Recio, T.; Vélez, M.P. Merging Maple and GeoGebra Automated Reasoning Tools. In Maple in Mathematics Education and Research; Corless, R.M., Gerhard, J., Kotsireas, I., Eds.; Communications in Computer and Information Science; Springer Nature: Cham, Switzerland, 2021. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).