Abstract
We consider the coefficient inverse problem for the first-order hyperbolic system, which describes the propagation of the 2D acoustic waves in a heterogeneous medium. We recover both the denstity of the medium and the speed of sound by using a finite number of data measurements. We use the second-order MUSCL-Hancock scheme to solve the direct and adjoint problems, and apply optimization scheme to the coefficient inverse problem. The obtained functional is minimized by using the gradient-based approach. We consider different variations of the method in order to obtain the better accuracy and stability of the appoach and present the results of numerical experiments.
1. Introduction
In this article, we deal with the numerical solution of the coefficient inverse problem, which corresponds to the problems of ultrasound tomography. The problems of developing methods and algorithms to use the ultrasound to recognize the genesis of breast cancer in its early stages have been studied extensively lately [1,2,3,4]. On the mathematical level, such problems are usually considered as inverse problems, when one has to recover the parameters of the model (that in our case describes the propagation of the ultrasound through the object of investigation) by using some measurement data [5,6,7,8]. The inverse problems are known for their ill-posedness and a requirement for a large number of computational resources for the numerical solution. Hence, the goal is to use a numerical algorithm that utilizes the provided data in an effective manner.
The mathematical models for ultrasound acoustics usually have the form of either the second-order equation or the first-order system of PDE equations. The models, based on the second-order wave equation are usually easier to study, and therefore, there are more ways to efficiently solve the direct problem. The first-order system of acoustics, that we consider in this paper, requires more computational resources for solving. Its advantage relies on its close connection to the physics of wave propagation, since the equations can be derived straight from the conservation laws. We mention several papers [9,10,11,12,13,14], where authors investigated inverse problems for a system of hyperbolic partial differential equations. One can also mention the following papers [15,16], where authors considered the direct problems for linear hyperbolic systems and studied their well-posedness.
Since we use the model, that based on the two-dimensional system of acoustic equations, its parameters, that we aim to recover, are the density of the medium and the speed of waves propagation—both are the functions of the two spatial variables. The reconstruction of two coefficients in the partial differential equations with a finite number of observations is very challenging.
The inverse problem of determining several coefficients in scalar hyperbolic equation by data given on the part of the boundary was investigated in [17]. The Carleman estimate was obtained to prove the uniqueness and a Lipschitz stability estimate for the coefficient inverse problem.
In [18] authors considered the reconstruction of three coefficients depended on space variables in the dynamical isotropic system of elasticity from two boundary measurements and proved the uniqueness and a Hölder stability using Carleman estimates in Sobolev spaces of negative order.
The inverse problem of recovering several coefficients in Maxwell’s equations was investigated in [19,20,21] by a finite number of measurements. For the coefficient inverse problem, the Lipschitz stability estimate was proven by using the Carleman estimate.
The coefficient inverse problem for the dynamic Maxwell equations was considered [22]. Hölder stability and global Carleman estimate for the inverse problem were proved.
The coefficient inverse problem of the recovering of the magnetic permeability and dielectric permittivity of Maxwell’s system in three dimensions by data of the electric field given on the part of the boundary was considered in [23]. The authors applied the Carleman estimates to get the theoretical stability. The inverse problem was reformulated as an optimization problem. The hybrid finite element and difference method was implemented for solving the direct and adjoint problem.
An inverse problem of finding two coefficients in a hyperbolic acoustic equation of the second-order by interior data was considered in [24]. The authors applied a Carleman technique estimates to obtain the Lipschitz stability estimates and therefore unique reconstruction of both coefficients was guaranteed. Numerical experiments of recovering both coefficients by data with noise were presented.
The continuation and coefficient inverse problem of recovering dielectric permeability and conductivity in application to ground penetrating radar was investigated in [25]. The inverse problems were reformulated as optimization problems. To minimize the cost functional gradient method was applied.
The numerical algorithms, based on the S. K. Godunov scheme [26,27] is applied for solving direct problems. Such kinds of methods allow us to construct the effective numerical realization of the physical process and benefits from the usage of the piecewise-smooth structure of the state variables on each time step. If one uses the methods, based on finite approximation, for solving the forward problem in the case of piecewise-smooth medium, then one has to add special conditions on the interface. Such conditions are very hard to add in the case of complex media interfaces and impossible to realize when solving the inverse problem, when one does not have the knowledge of media interfaces.
For the solution of the coefficient inverse problems gradient methods [25,28,29,30,31] and global-convergence [6,32,33,34,35] are applied. We should also mention the family of Newton-type methods. However, their drawback is the solution of the additional linear inverse problem, which has to be solved on each iteration. When considering the multidimensional problems, this necessity to deal with that additional linear problem tends to become too complicated.
An optimization approach to a three-dimensional acoustic inverse problem was considered in the time-domain [28]. The velocity and the density were reconstructed by minimizing an objective functional. The gradient of the cost functional was found with an explicit expression via the solution of adjoint problem. The parameters were reconstructed by the conjugate gradient method. The uniqueness of the solution was proved.
The problem of modeling the acoustic radiation pattern of source was considered in [36]. The problem is formulated in the form of control problem for the 2D first-order system of hyperbolic equations. The modelling of the acoustic radiation patterns of sources could allow to improve the resolution of acoustic tomography.
2. Direct Problem
2.1. Problem Formulation
From the conservation laws of impulse in direction x and y, and the conservation law of mass [12] let us consider the direct problem of acoustic wave propagation through the 2D medium in the domain :
Here is the velocity vector with respect to x, is the velocity vector with respect to y, is the exceeded pressure, is the density of the medium, is the wave speed. Such system is often used to describe the propagation of the ultrasound through the fluid medium, and the acoustic parameters of the models, that were considered during the numerical experiments are close to fluid. is the characteristic function of the source location, has the following form:
Here, is a frequency.
2.2. Methods for Solving the Direct Problem
In this subsection we consider the brief description of the two methods, that we used for solving the direct problem during the experiments. Both of them originates from the upwind scheme, developed by S.K. Godunov [26,27]. His approach was based on using the integral form of the problem, piecewise-constant approximation of the state variables inside the numerical cell and the solution of the Riemann problem-the initial problem with conditions represented by two constant states separated by a discontinuity. The MUSCL-Hancock scheme, first published by van Leer [37], extends the ideas behind the Godunov scheme in order to obtain higher accuracy of the method and nowadays is one of the common approaches for dealing with the hyperbolic systems. One can find more detailed reviews of papers, related to both methods, in [37,38,39].
In order to describe methods, used for solving the direct problem (1)–(4), we use a generalized formulation of the Equations (1) and (2) of the following form:
Here is the vector of state variables, and are the vectors of fluxes correspondingly. After introducing the discretizing the computational domain into the finite number of cells, one can obtain:
The Equation (7) corresponds to the numerical cell , where the sub-indexes indicate the state values on the current time step, and sup-indexes-on the next time step, are the grid steps with respect to the spatial coordinates and time correspondingly. The values on the each boundary of the cell considered, are the solutions of the Riemann (or discontinuity decay) problem [27]. For example, the approximation (7) of the first of the Equation (1) has the following form:
The value is the solution of the discontinuity decay problem, that arises on the boundaries of the cell considered. The formula has the following form:
The two other equations of the system can be considered in the same manner. The right-hand side of the equation can also be easily taken into account. We skip the rest of the formulas, yet one can find them, for example, in [27], as well as the study of the stability of the scheme.
Another approach, that we used for solving the direct problem is MUSCL-Hancock scheme. First, we summarize the basic Godunov approach as the combination of the two following steps:
- Obtaining the flux values by solving the Riemann problem;
- Updating the state variables on the next time step, using the solution of the Riemann problem.
One should mention, that the Godunov approach based on the piecewise-constant approximation of the parameters of each of the cells. The MUSCL-Hancock scheme uses the piecewise-linear approximation of the parameters, based on the slope limited approximation. Another feature of the scheme is the solution of the Riemann problem on the half-step, which corresponded to . Such update allows the described scheme to second-order accuracy [39]. The workflow of the scheme can now be summarized as follows:
- Reconstruction of the state variables on the current time step, using piecewise-linear extrapolation;
- Evolution of the reconstructed state variables by conservation laws with a time ;
- Obtaining the flux values for the “midpoint” time step by solving the Riemann problem for evolved state variables;
- Updating the state values from the current time step on the next time step by conservation laws with a time .
We skip the formulas for the sake of brevity. However, the precise description of the MUSCL-Hancock scheme can be found in [37,38,39].
3. Inverse Problems
While solving the direct problem for the system (1)–(4) we suppose, that parameters of the system are known. However, when considering the possible applications, one usually has to solve the problem of calculating these parameters using the additional data-the inverse problem.
In this paper we suppose, that we obtain the data of inverse problem by measuring the pressure inside the receivers:
Here we consider the system of N receivers, each located in the corresponded domain . The inverse problem, therefore, is to recover functions , in (1)–(4) using the additional information (10).
Inverse problems of acoustics are usually considered in the case of data, given on the part of the boundary. The theoretical study of different methods in the case of spatially distributed receivers is very challenging (even in the case of mathematical models, based on the second-order equation). Thus, we consider the formulated inverse problem from a numerical point of view.
Let us reduce the inverse problem (1)–(4), (10) to minimization problem of the following cost functional:
We use the gradient-based approach to minimize the functional (12) by considering the following iteration scheme:
Here is descent parameter, is the gradient of the functional. Let us note [40,41] that
Here is adjoint of Frechet derivative of the operator A.
One can choose the parameter of the descent differently, for example, one can fix throughout the iterations (Landweber iterations), or search for the best parameter on each step of the optimization process (steepest descent). The initial approximation for the gradient descent is often connected with the prior information about the solution. We mention the structure of initial approximation in the next chapter. Using a priori information about the solution of the coefficient inverse problem in algorithm allowed us to decrease the number of iteration extremely [42]. The theorem of strong convergence of the Landweber iteration method for the coefficient inverse problems for hyperbolic equations was proved in [29].
The gradient of the functional can be computed as follows [11]. Let us introduce the adjoint problem [25,42]:
Then the gradient has the following form:
Thus, in order to make one step of the gradient descent, one has to solve the direct problem (1)–(4), using the current approximation of the parameters, then solve the adjoint problem (14)–(18), and after that, using the solution of both problems, compute the gradient of the cost functional, using (19) and (20). Since the adjoint problem (14)–(18) also has the form of the hyperbolic system, one can use Godunov-type methods, considered earlier, to compute the solution of the adjoint problem as well.
As we mentioned in the introduction, it is possible to consider the Newton method for solving the inverse problem, which tends to have second-order convergence, as opposed to the first order of gradient-based approaches. For operator formulation of inverse problem (11) the Newton method can be described as follows
The drawback of the Newton method is the necessity to solve the additional problem on each iteration, that corresponds to the inversion of the Frechet derivative of the operator, in contrast to gradient methods (13), where one only has to solve the adjoint problems. In our case, the linear two-dimensional inverse problem has the following form:
This formulation corresponds to the problem of the reconstruction of the density (yet it changes slightly when considering the reconstruction of the speed of sound). The problem is to find the function using the following additional information:
Thus, we have to deal with the additional inverse problem on every iteration (or, in the case of quasi-Newton methods, every fixed number of iterations) of the scheme. Such an increase in the complexity of each iteration sometimes outweighs the decrease in the total number of iterations in the case of multidimensional problems in Hilbert spaces. Thus, despite the fact the question of efficiency of the Newton-type methods for the problem considered remains interesting, we leave it to future work and focus on the gradient descent in the present paper.
4. Numerical Results
In this section, we present the results of numerical computations. In this paper, we use synthetic data to study the proposed algorithms. Throughout the computations, we use the following setup, which consists of the test object and the water zone outside the object, where the transducers are located. The radius of the object is m, the transducers are uniformly placed in a circle (of the radius m) around the object. The acoustic parameters (density, speed of waves propagation) inside the object are chosen as equal to the parameters of the normal human tissue ( kg/m, km/s). We also consider different inclusions inside the object (their quantity and form varies from one model to another), which has different parameters (density varies from kg/m to kg/m in different inclusions, speed of sound varies from km/s to km/s). The initial approximation was considered as an object without any inclusions, and we seek to identify said inclusions by solving the inverse problem. Physical size of computational domain meters. The grid parameters was chosen as follows: .
We start with the model, presented in Figure 1. It consists of an object and two inclusions, located one inside the other.
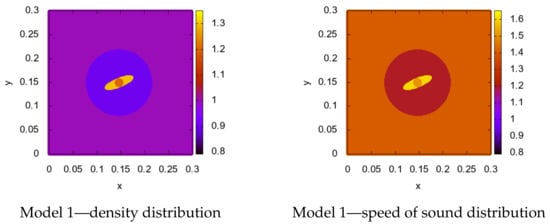
Figure 1.
Test 1—exact model.
During the first experiments, we considered the problems of recovering the density and the velocity independently. While one of the medium parameters was unknown, the other one was given exactly (in this case we have the exact values of the second parameter in the whole domain) or inexactly (in this case we do not have the information about the inclusions in the given parameter).
The computational results for this test are presented in Figure 2 and Figure 3. We considered the system of 16 transducers during the computations, and we considered 1000 iterations of the gradient descent. We should mention, that during iteration each position of the source runs through the transducers. When the location of the source is fixed, other transducers work as the receivers. Since that, we work with the array of gradients, each corresponded to the fixed source location, on each iteration. The problem of usage of such data for the better performance of the gradient descent was considered in [14]. The descent parameters were chosen by the trial and error method. One can see, that while the result of recovering one parameter of the system, while the other is given exactly, is accurate enough (graphs a) and (c) on the (Figure 2), the situation changes drastically, when the other parameter is given inexactly (graphs b) and (d) on the (Figure 2). The errors, introduced in the model by inexact fixed parameter, leads to the fact, that solution, obtained by the gradient descent, tends to drift from the true solution, starting from a certain number of iteration, while the residual functional still decreases. The more precise behavior of the relative errors and residual is presented in Figure 3, where red lines correspond to the exact setup of the fixed parameter, and green lines correspond to the inexact setup of the fixed parameter. Such a situation (when the number of iterations should be chosen according to the errors in the data of inverse problem or in the model itself) arises often, when solving inverse problems. However, such behavior provides additional difficulties, when recovering both parameters simultaneously, as in the following tests.
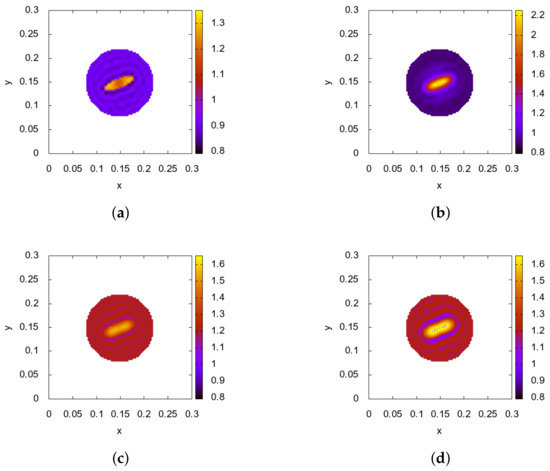
Figure 2.
Test 1—recovering of the density with exact (a) and inexact (b) speed of sound distribution; recovering of the speed of sound with exact (c) and inexact (d) density distribution. The upper scale of the graph (b) was changed a little due to the errors in the solution.
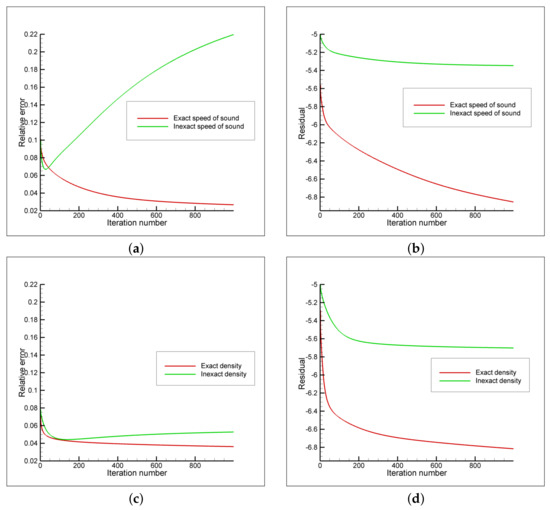
Figure 3.
Test 1—the convergence of the descent process: relative errors (a) and the residual behaviour (b) for the density recovering, relative errors (c) and the residual behaviour (d) for the speed of sound recovering.
For the next test, we considered a different model, presented in the figure. In this case, we have one relatively small inclusion in the left part of the object. The model is presented in Figure 4.
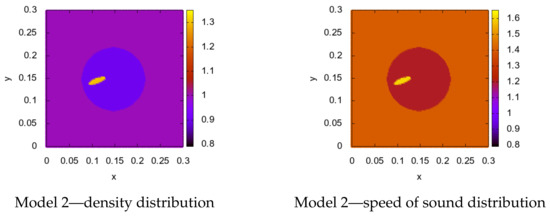
Figure 4.
Test 2—exact model.
During the following series of experiments, we considered both the density and speed of sound to be determined. However, because we have only an initial approximation for both functions, the inaccuracy of the model increases, compared to the first series of tests. During the computations, it leads to the accumulation of inaccuracy. In order to overcome such behavior, we proposed the following scheme. We spend some fixed number of iteration, updating only one of the desired parameters (for example, the density). The other parameter (speed of sound) is fixed. After the fixed number of iterations, we switch the fixed-function and the changeable function (start to update the values of the speed of sound, while the density is fixed). Such a scheme allows us to avoid the situation, when the convergence of the descent process, based on minimization of the cost functional, is overwhelmed by the negative effect of the gradient descent with an inaccurate model (demonstrated in the first series of experiments). We considered the several variations of such approach-switch (between updating the density and updating the speed of sound) every 100, 50 and 1 iteration of the gradient descent.
The computational results are presented in Figure 5 and Figure 6. One can see that the simultaneous update of both parameters lead to increasing oscillations in the relative errors (Figure 5, red curves). The proposed switch scheme allows us to improve the performance of the descent process (some traces of the oscillation behaviour could be seen by considering the green curves). The regular switch between the updates of the density and the speed of sound leads to a more stable and smooth decrease of both the relative errors and the residual. When considering the reconstruction results (Figure 6), this allows us to obtain the solution with less number of artifacts, while the inclusion is clearly visible.
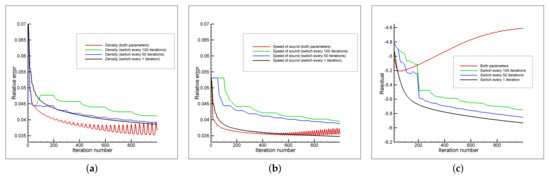
Figure 5.
Test 2—the convergence of the descent process: (a) the behaviour of density’s relative errors, (b) the speed of sound relative error’s behaviour, (c) the residual. Here red curves corresponds to the simultaneous update of both the density and the velocity, green curves correspond to the switch between the update of the parameters every 100 iterations, blue curves—every 50 iteration; black curves—every iteration.
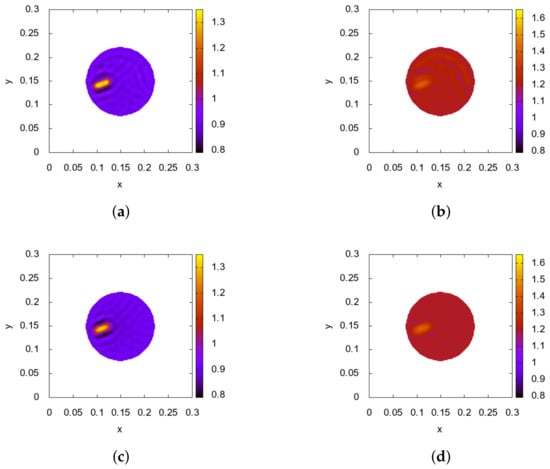
Figure 6.
Test 2—the reconstruction results of the density (left graphs) and the velocity (right graphs): (a,b) corresponds to the simultaneous update of both parameters, (c,d) switch between the update of the parameters every (1) iteration.
2
The results of the third series of tests are presented in Figure 7 and the Table 1 and Table 2. The exact solution is presented on the upper graphs of Figure 7. It consists of several inclusions inside the objects with different forms and sizes. The diameter of the smallest inclusion is 1cm, which corresponds to the earliest stages of breast cancer genesis. According to the comparative results for the second model, we used the regular switch of the gradient descent between the updates of the density and the speed of sound. The results of the reconstruction for the exact data are presented on the lower graphs of Figure 7. One can see that all three inclusions are visible (despite the fact that the complex structure of the inclusion in the left part of the object is not clearly distinguishable).
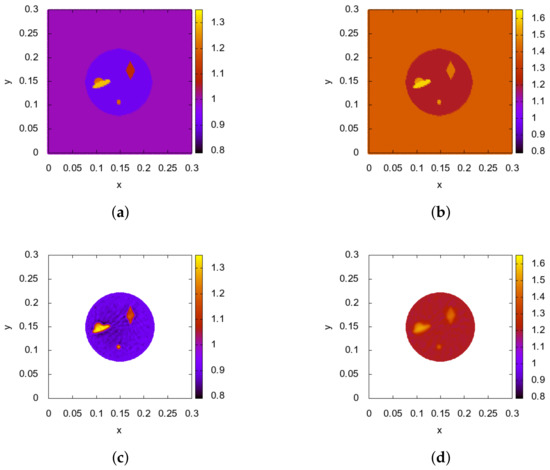
Figure 7.
Test 3—the reconstruction results of the density (left graphs) and the velocity (right graphs): (a,b) exact solution, (c,d) result of the reconstruction.

Table 1.
Mesh dependence—case of exact data.

Table 2.
Mesh dependence—cased of noised data.
5. Discussion
In this work we considered the coefficient inverse problem of recovering two coefficients (density and the speed of sound) of the first order hyperbolic system, that describes the propagation of the 2D acoustic waves in a heterogeneous medium. We used the second-order MUSCL-Hancock scheme to solve the direct and adjoint problems, and applied optimization scheme to the coefficient inverse problem.
The presented numerical results illustrate the acceptable accuracy and stability of the proposed algorithm. The ways to improve the method, that we plan to consider in the future work, related to the study of better methods of choosing the descent parameters, consideration of the different ways to measure the data and other related problems. We are also planning to extend the formulation of the problem by considering the attenuation of the waves in the medium.
Author Contributions
Conceptualization M.S.; methodology, D.K., N.N. and M.S.; software D.K.; formal analysis N.N.; writing—original draft preparation, D.K.; writing—review and editing, D.K., N.N. and M.S.; project administration, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been supported by the RSCF under grant 19-11-00154 “Developing of new mathematical models of acoustic tomography in medicine. Numerical methods, HPC and software”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article.
Acknowledgments
Authors wish to thank the reviewers for their comments and efforts towards improving this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burov, V.A.; Zotov, D.I.; Rumyantseva, O.D. Reconstruction of the sound velocity and absorption spatial distributions in soft biological tissue phantoms from experimental ultrasound tomography data. Acoust. Phys. 2015, 61, 231–248. [Google Scholar] [CrossRef]
- Duric, N.; Littrup, P.; Li, C.; Roy, O.; Schmidt, S.; Janer, R.; Cheng, X.; Goll, J.; Rama, O.; Bey-Knight, L.; et al. Breast ultrasound tomography: Bridging the gap to clinical practice. Proc. SPIE 2012, 8320, 832000. [Google Scholar]
- Jirik, R.; Peterlik, I.; Ruiter, N.; Fousek, J.; Dapp, R.; Zapf, M.; Jan, J. Sound-speed image reconstruction in sparse-aperture 3D ultrasound transmission tomography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 254–264. [Google Scholar] [CrossRef] [PubMed]
- Wiskin, J.; Malik, B.; Natesan, R.; Lenox, M. Quantitative assessment of breast density using transmission ultrasound tomography. Med. Phys. 2019, 46, 2610–2620. [Google Scholar] [CrossRef]
- Filatova, V.; Danilin, A.; Nosikova, V.; Pestov, L. Supercomputer Simulations of the Medical Ultrasound Tomography Problem. Commun. Comput. Inf. Sci. 2019, 1063, 297–308. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. Synthesis of global convergence and adaptivity for a hyperbolic coefficient inverse problem in 3D. J. Inverse Ill-Posed Probl. 2010, 18, 85–132. [Google Scholar] [CrossRef]
- Klibanov, M.V. Travel time tomography with formally determined incomplete data in 3D. Inverse Probl. Imaging 2019, 13, 1367–1393. [Google Scholar] [CrossRef]
- Klibanov, M.V. On the travel time tomography problem in 3D. J. Inverse Ill-Posed Probl. 2019, 27, 591–607. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Kulikov, I.M.; Shishlenin, M.A. An Algorithm for Recovering the Characteristics of the Initial State of Supernova. Comp. Math. Math. Phys. 2020, 60, 1008–1016. [Google Scholar] [CrossRef]
- Kulikov, I.M.; Novikov, N.S.; Shishlenin, M.A. Mathematical modeling of propagation of ultrasonic waves in the medium: Direct and inverse problem. Siberian Electronic Mathematical Reports. 2015, 12, C219–C228. [Google Scholar]
- Kabanikhin, S.I.; Klyuchinskiy, D.V.; Novikov, N.S.; Shishlenin, M.A. Numerics of acoustical 2D tomography based on the conservation laws. J. Inverse Ill-Posed Probl. 2020, 28, 287–297. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Klychinskiy, D.V.; Kulikov, I.M.; Novikov, N.S.; Shishlenin, M.A. Direct and Inverse Problems for Conservation Laws. In Continuum Mechanics, Applied Mathematics and Scientific Computing: Godunov’s Legacy; Demidenko, G., Romenski, E., Toro, E., Dumbser, M., Eds.; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Romanov, V.G.; Kabanikhin, S.I. Inverse Problems for Maxwell’s Equations; VSP: Utrecht, The Netherlands, 1994. [Google Scholar]
- Klyuchinskiy, D.; Novikov, N.; Shishlenin, M. A Modification of gradient descent method for solving coefficient inverse problem for acoustics equations. Computation 2020, 8, 73. [Google Scholar] [CrossRef]
- Bastin, G.; Coron, J.-M. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. In Progress in Nonlinear Differential Equations and Their Applications; Birkhauser: Boston, MA, USA, 2016. [Google Scholar]
- Blokhin, A.M.; Trakhinin, Y.L. Well-Posedness of Linear Hyperbolic Problems: Theory and Applications; Nova Publishers: Hauppauge, NY, USA, 2006. [Google Scholar]
- Bellassoued, M.; Jellal, D.; Yamamoto, M. Lipschitz stability in in an inverse problem for a hyperbolic equation with a finite set of boundary data. Appl. Anal. 2008, 87, 1105–1119. [Google Scholar] [CrossRef]
- Imanuvilov, O.Y.; Isakov, V.; Yamamoto, M. An inverse problem for the dynamical Lame system with two sets of boundary data. Comm. Pure Appl. Math. 2003, 56, 1366–1382. [Google Scholar] [CrossRef]
- Li, S. An inverse problem for Maxwell’s equations in bi-isotropic media. SIAM J. Math. Anal. 2005, 37, 1027–1043. [Google Scholar] [CrossRef]
- Li, S.; Yamamoto, M. An inverse source problem for Maxwell’s equations in anisotropic media. Appl. Anal. 2005, 84, 1051–1067. [Google Scholar] [CrossRef]
- Li, S.; Yamamoto, M. An inverse problem for Maxwell’s equations in anisotropic media in two dimensions. Chin. Ann. Math. Ser. B 2007, 28, 35–54. [Google Scholar] [CrossRef]
- Bellassoued, M.; Cristofol, M.; Soccorsi, E. Inverse boundary value problem for the dynamical heterogeneous Maxwell’s system. Inverse Probl. 2012, 28, 095009. [Google Scholar] [CrossRef]
- Beilina, L.; Cristofol, M.; Niinimaki, K. Optimization approach for the simultaneous reconstruction of the dielectric permittivity and magnetic permeability functions from limited observations. Inverse Probl. Imaging 2015, 9, 1–25. [Google Scholar] [CrossRef]
- Beilina, L.; Cristofol, M.; Li, S.; Yamamoto, M. Lipschitz stability for an inverse hyperbolic problem of determining two coefficients by a finite number of observations. Inverse Probl. 2017, 34, 015001. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Nurseitov, D.B.; Shishlenin, M.A.; Sholpanbaev, B.B. Inverse problems for the ground penetrating radar. J. Inverse Ill-Posed Probl. 2013, 21, 885–892. [Google Scholar] [CrossRef]
- Godunov, S.K. Differential method for numerical computation of noncontinuous solutions of hydrodynamics equations. Matematicheskiy Sbornik 1959, 47, 271–306. (In Russian) [Google Scholar]
- Godunov, S.K.; Zabrodin, A.V.; Ivanov, M.Y.; Kraikov, A.N.; Prokopov, G.P. Numerical Solution for Multidimensional Problems of Gas Mechanics; Nauka: Moscow, Russia, 1976. [Google Scholar]
- He, S.; Kabanikhin, S.I. An optimization approach to a three-dimensional acoustic inverse problem in the time domain. J. Math. Phys. 1995, 36, 4028–4043. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Scherzer, O.; Shishlenin, M.A. Iteration methods for solving a two dimensional inverse problem for a hyperbolic equation. J. Inverse Ill-Posed Probl. 2003, 11, 87–109. [Google Scholar] [CrossRef]
- Beilina, L. Adaptive Finite Element Method for a coefficient inverse problem for the Maxwell’s system. Appl. Anal. 2011, 90, 1461–1479. [Google Scholar] [CrossRef]
- Beilina, L.; Hosseinzadegan, S. An adaptive finite element method in reconstruction of coefficients in Maxwell’s equations from limited observations. Appl. Math. 2016, 61, 253–286. [Google Scholar] [CrossRef]
- Beilina, L.; Klibanov, M.V. A posteriori error estimates for the adaptivity technique for the Tikhonov functional and global convergence for a coefficient inverse problem. Inverse Probl. 2010, 26, 045012. [Google Scholar] [CrossRef][Green Version]
- Xin, J.; Beilina, L.; Klibanov, M. Globally convergent numerical methods for some coefficient inverse problems. Comput. Sci. Eng. 2010, 12, 64–76. [Google Scholar]
- Beilina, L.; Klibanov, M.V. Globally strongly convex cost functional for a coefficient inverse problem. Nonlinear Anal. Real World Appl. 2015, 22, 272–288. [Google Scholar] [CrossRef]
- Klibanov, M.V. Carleman estimates for global uniqueness, stability and numerical methods for coefficient inverse problems. J. Inverse Ill-Posed Probl. 2013, 21, 477–560. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Klyuchinskiy, D.V.; Novikov, N.S.; Shishlenin, M.A. On the problem of modeling the acoustic radiation pattern of source for the 2D first-order system of hyperbolic equations. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1715, p. 012038. [Google Scholar]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Berthon, C. Why the MUSCL-Hancock scheme is L 1 -stable. Numer. Math. 2006, 104, 27–46. [Google Scholar] [CrossRef]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Hanke, M.; Neubauer, A.; Scherzer, O. A convergence analysis of the Landweber iteration for nonlinear ill-posed problems. Numer. Math. 1995, 72, 21–37. [Google Scholar]
- Kabanikhin, S.I.; Kowar, R.; Scherzer, O. On the Landweber iteration for the solution of a parameter identification problem in a hyperbolic partial differential equation of second order. J. Inverse Ill-Posed Probl. 1998, 6, 403–430. [Google Scholar] [CrossRef]
- Kabanikhin, S.I.; Shishlenin, M.A. Quasi-solution in inverse coefficient problems. J. Inverse Ill-Posed Probl. 2008, 16, 705–713. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).