On the Complexity of Finding the Maximum Entropy Compatible Quantum State
Abstract
1. Introduction
2. Background and Problem Statement
- Input: A family of circuitsthat construct the family of marginal density operators.
- Accept: ifis admissible.
- Reject: ifis not admissible.
- Input: A family of circuits promised to construct an admissible , and a real value k.
- Accept: if there exists a such that
- Reject: otherwise.
3. Hardness of Comparing Entropy of a Compatible Chain
- Input: Two quantum circuits and that generate tripartite density operators and , respectively, over the same Hilbert space of the form , promised that:
- ▸
- ;
- ▸
- ;
- ▸
- ;
then, - Accept: if ;
- Reject: if .
- Input: Two quantum circuits and , acting on m qubits, that prepare the states or promised that
- ▸
- either ;
- ▸
- or ;
then, - Accept:,
- Reject:.
- ;
- .
4. Quantum Markov Chains and Trees
- it admits a QMT in the compatibility space iff every sub-3-chain is compatible with a QMC—Theorem 3;
- the QMT coincides with the density operator that maximizes the von Neumann entropy, constrained by the provided set of two-body marginals—Corollary 1;
- defining a proper order in the graph—constructive ordering—we can construct the unique compatible QMT directly from the marginals. The Lagrange multipliers in the optimization problem are then obtained through Theorem 2.
4.1. Background on Quantum Markov Chains
- 1.
- is a QMC over the chain .
- 2.
- , where .
- 3.
- and preserves the partial trace .
- 4.
- .
4.2. Definition of Quantum Markov Trees
4.3. QMT as Max-Entropy Density Operator
- (i)
- ;
- (ii)
- we havefor some constructive ordering .
- ;
- .
- and,
- .
4.4. Compatibility with a QMT
4.5. QMT and the MECM Problem
- 1.
- is a spanning tree
- 2.
- is a QMC constructed in polynomial-time (with respect with the number of nodes n) where and for some given constructive order of .
4.6. QMT and Chow–Liu Algorithm
| Algorithm 1 Chow–Liu Algorithm |
|
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | linear dichroism |
| QSZK | Quantum Statistical Zero Knowledge |
| CPTP | Completely Positive Trace Preserving |
| QMA | Quantum Merlin Arthur |
| QCMP | Quantum Compatible Marginal Problem |
| MECMP | Maximum Entropy Compatible Marginal Problem |
| BQP | Bounded-Error Quantum Polynomial Time |
| (3c)QED | (3-chain) Quantum Entropy Difference |
| QSD | Quantum Statistical Difference |
| QMC | Quantum Markov Chain |
| QMT | Quantum Markov Tree |
Appendix A. Lemmas for Theorem 1
Appendix B. Proof of the Central Lemma 1
- (i)
- ;
- (ii)
- ;
- (3 ⇒ 1) This implication comes for free from the definition of QMC. Moreover, the map is clearly CPTP. The complete positivity indeed comes for free from the Hermitianicity of and , then of their square-roots.
- (1 ⇒ 3) Equation (A8) for t = 0 gives exactly the Petz map in (3), so the implication comes as corollary of Theorem A3.
- (1 ⇔ 2) This follows from the statement of Theorem A3.
- (2 ⇔ 4) It comes as corollary of Theorem A2, using the settings in Corollary A1.
Appendix C. Lemmas for Theorem 2 and 3
- (a)
- If the associate graphis a chain A-B-C-D (i.e.,) then
- (b)
- If the associate graphis a star centered in B (i.e.,)
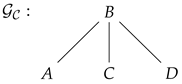
- (i)
- , s.t. and
- (ii)
- , s.t. .
Appendix D. Number of 3-Chains
References
- D’Ariano, M.; G Paris, M.G.; Sacchi, M.F. Quantum tomography. Adv. Imaging Electron. Phys. 2003, 128, 206–309. [Google Scholar]
- Huber, F.M.; Gühne, O. Characterizing ground and thermal states of few-body Hamiltonians. Phys. Rev. Lett. 2016, 117, 010403. [Google Scholar] [CrossRef] [PubMed]
- Cotler, J.; Wilczek, F. Quantum overlapping tomography. Phys. Rev. Lett. 2020, 124, 100401. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620. [Google Scholar] [CrossRef]
- Bairey, E.; Arad, I.; Lindner, N.H. Learning a local Hamiltonian from local measurements. Phys. Rev. Lett. 2019, 122, 020504. [Google Scholar] [CrossRef] [PubMed]
- Bairey, E.; Guo, C.; Poletti, D.; Lindner, N.H.; Arad, I. Learning the dynamics of open quantum systems from their steady states. New J. Phys. 2020, 22, 032001. [Google Scholar] [CrossRef]
- Wiebe, N.; Granade, C.; Ferrie, C.; Cory, D.G. Hamiltonian Learning and Certification Using Quantum Resources. Phys. Rev. Lett. 2014, 112, 190501. [Google Scholar] [CrossRef]
- Biamonte, J.; Wittek, P.; Pancotti, N.; Rebentrost, P.; Wiebe, N.; Lloyd, S. Quantum machine learning. Nature 2017, 549, 195. [Google Scholar] [CrossRef]
- Anshu, A.; Arunachalam, S.; Kuwahara, T.; Soleimanifar, M. Sample-efficient learning of quantum many-body systems. arXiv 2020, arXiv:2004.07266. [Google Scholar]
- Cao, N.; Xie, J.; Zhang, A.; Hou, S.Y.; Zhang, L.; Zeng, B. Supervised learning for quantum maximum entropy estimation. arXiv 2020, arXiv:2005.01540. [Google Scholar]
- Klyachko, A.A. Quantum marginal problem and N-representability. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2006; Volume 36, p. 72. [Google Scholar]
- Liu, Y.K. Consistency of local density matrices is QMA-complete. In Approximation, Randomization, and Combinatorial Optimization Algorithms and Techniques; Springer: Berlin/Heidelberg, Germany, 2006; pp. 438–449. [Google Scholar]
- Higuchi, A.; Sudbery, A.; Szulc, J. One-qubit reduced states of a pure many-qubit state: Polygon inequalities. Phys. Rev. Lett. 2003, 90, 107902. [Google Scholar] [CrossRef] [PubMed]
- Bravyi, S. Requirements for Compatibility between Local and Multipartite Quantum States. Quantum Inf. Comput. 2004, 4, 12–26. [Google Scholar]
- Huber, F.M. Quantum States and Their Marginals: From Multipartite Entanglement to Quantum Error-Correcting Codes. Ph.D. Thesis, University of Siegen (DE), Siegen, Germany, 2018. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Dagum, P.; Luby, M. Approximating probabilistic inference in Bayesian belief networks is NP-hard. Artif. Intell. 1993, 60, 141–153. [Google Scholar] [CrossRef]
- Valiant, L.G. The complexity of computing the permanent. Theor. Comput. Sci. 1979, 8, 189–201. [Google Scholar] [CrossRef]
- Chow, C.K.; Liu, C.N. Approximating discrete probability distributions with dependence trees. IEEE Trans. Inf. Theory 1968, 14, 462–467. [Google Scholar] [CrossRef]
- Leifer, M.S.; Spekkens, R.W. Towards a formulation of quantum theory as a causally neutral theory of Bayesian inference. Phys. Rev. A 2013, 88, 052130. [Google Scholar] [CrossRef]
- Fitzsimons, J.F.; Jones, J.A.; Vedral, V. Quantum correlations which imply causation. Sci. Rep. 2015, 5, 18281. [Google Scholar] [CrossRef]
- Horsman, D.; Heunen, C.; Pusey, M.F.; Barrett, J.; Spekkens, R.W. Can a quantum state over time resemble a quantum state at a single time? Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20170395. [Google Scholar] [CrossRef]
- Watrous, J. Quantum computational complexity. arXiv 2008, arXiv:0804.3401. [Google Scholar]
- Bernstein, E.; Vazirani, U. Quantum complexity theory. Siam J. Comput. 1997, 26, 1411–1473. [Google Scholar] [CrossRef]
- Watrous, J. Limits on the power of quantum statistical zero-knowledge. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 16–19 November 2002; IEEE: New York, NY, USA, 2002; pp. 459–468. [Google Scholar]
- Arora, S.; Barak, B. Computational Complexity: A Modern Approach; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Ben-Aroya, A.; Schwartz, O.; Ta-Shma, A. Quantum Expanders: Motivation and Construction. Theory Comput. 2020, 6, 47–79. [Google Scholar] [CrossRef]
- Fawzi, O.; Renner, R. Quantum conditional mutual information and approximate Markov chains. Commun. Math. Phys. 2015, 340, 575–611. [Google Scholar] [CrossRef]
- Giorgio, S.D.; Mateus, P.; Mera, B. Recoverability from direct quantum correlations. J. Phys. A Math. Theor. 2020, 53, 185301. [Google Scholar] [CrossRef]
- Wang, Y.J. Compatibility among Marginal Densities. Biometrika 2004, 91, 234–239. [Google Scholar] [CrossRef]
- De Loera, J.; Onn, S. The Complexity of Three-Way Statistical Tables. Siam J. Comput. 2004, 33, 819–836. [Google Scholar] [CrossRef][Green Version]
- Fritz, T.; Chaves, R. Entropic Inequalities and Marginal Problems. IEEE Trans. Inf. Theory 2013, 59, 803–817. [Google Scholar] [CrossRef]
- Watrous, J. Succinct quantum proofs for properties of finite groups. In Proceedings of the 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; IEEE: New York, NY, USA, 2000; pp. 537–546. [Google Scholar]
- Aaronson, S. Quantum computing, postselection, and probabilistic polynomial-time. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 3473–3482. [Google Scholar] [CrossRef]
- Sutter, D. Approximate Quantum Markov Chains. In Approximate Quantum Markov Chains; Springer International Publishing: Cham, Switzerland, 2018; pp. 75–100. [Google Scholar]
- Sutter, D.; Fawzi, O.; Renner, R. Universal recovery map for approximate Markov chains. Proc. R. Soc. A 2016, 472, 20150623. [Google Scholar] [CrossRef]
- Choi, M.D. Completely positive linear maps on complex matrices. Linear Algebra Appl. 1975, 10, 285–290. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Aharonov, D.; Kitaev, A.; Nisan, N. Quantum circuits with mixed states. In Proceedings of the Thirtieth Annual ACM Symposium on Theory of Computing, Berkeley, CA, USA, 28–30 May 1998; pp. 20–30. [Google Scholar]
- Löwner, K. Über monotone matrixfunktionen. Math. Z. 1934, 38, 177–216. [Google Scholar] [CrossRef]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Cayley, A. A theorem on trees. Quart. J. Math. 1889, 23, 376–378. [Google Scholar]
- Ambainis, A.; Nayak, A.; Ta-Shma, A.; Vazirani, U. Dense quantum coding and quantum finite automata. J. Assoc. Comput. Mach. (JACM) 2002, 49, 496–511. [Google Scholar] [CrossRef]
- Umegaki, H. Conditional expectation in an operator algebra, IV (entropy and information). In Kodai Mathematical Seminar Reports; Department of Mathematics, Tokyo Institute of Technology: Tokyo, Japan, 1962; Volume 14, pp. 59–85. [Google Scholar]
- Uhlmann, A. Relative entropy and the Wigner-Yanase-Dyson-Lieb concavity in an interpolation theory. Commun. Math. Phys. 1977, 54, 21–32. [Google Scholar] [CrossRef]
- Petz, D. Monotonicity of quantum relative entropy revisited. Rev. Math. Phys. 2003, 15, 79–91. [Google Scholar] [CrossRef]
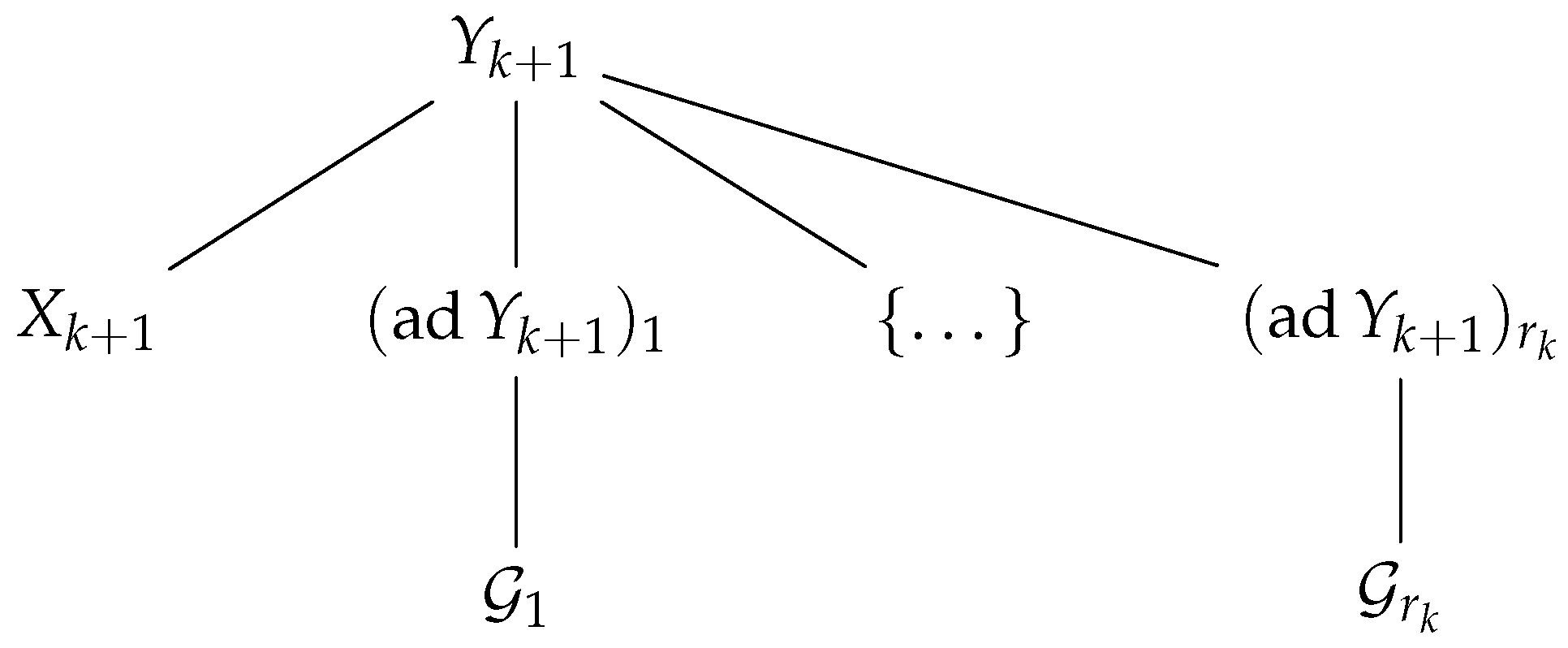
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Giorgio, S.; Mateus, P. On the Complexity of Finding the Maximum Entropy Compatible Quantum State. Mathematics 2021, 9, 193. https://doi.org/10.3390/math9020193
Di Giorgio S, Mateus P. On the Complexity of Finding the Maximum Entropy Compatible Quantum State. Mathematics. 2021; 9(2):193. https://doi.org/10.3390/math9020193
Chicago/Turabian StyleDi Giorgio, Serena, and Paulo Mateus. 2021. "On the Complexity of Finding the Maximum Entropy Compatible Quantum State" Mathematics 9, no. 2: 193. https://doi.org/10.3390/math9020193
APA StyleDi Giorgio, S., & Mateus, P. (2021). On the Complexity of Finding the Maximum Entropy Compatible Quantum State. Mathematics, 9(2), 193. https://doi.org/10.3390/math9020193





