Figure 1.
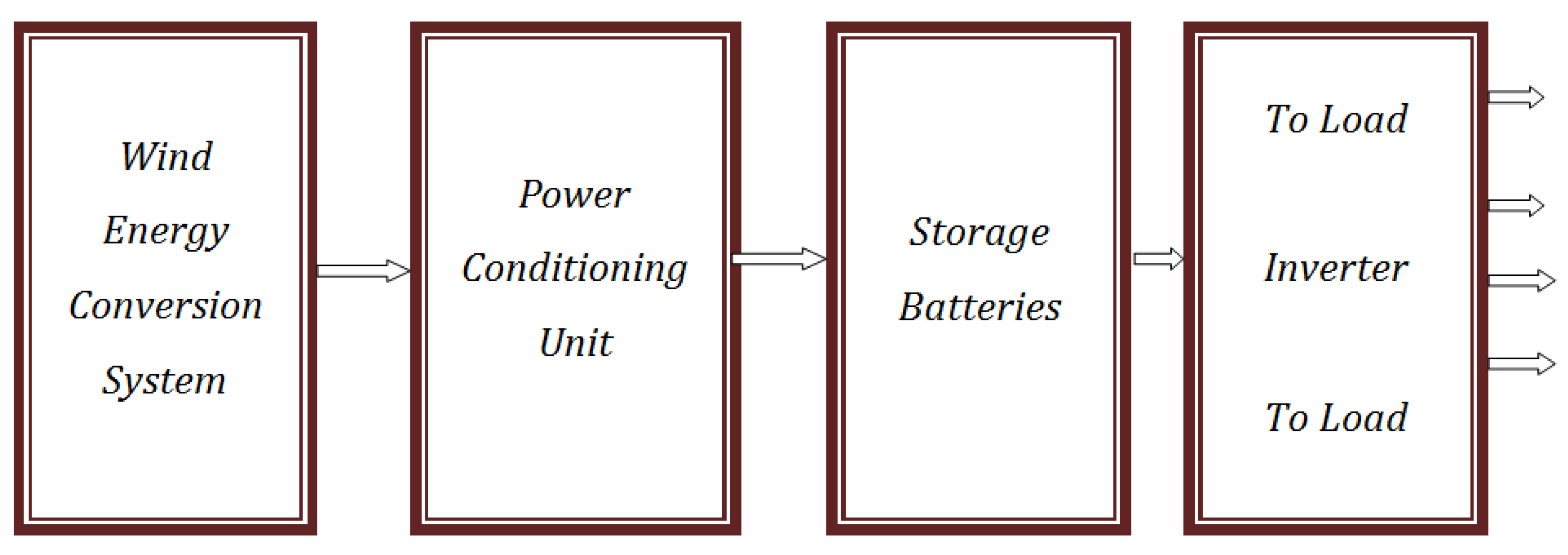
Block diagram of a wind energy generation system.
Figure 1.
Block diagram of a wind energy generation system.
Figure 2.
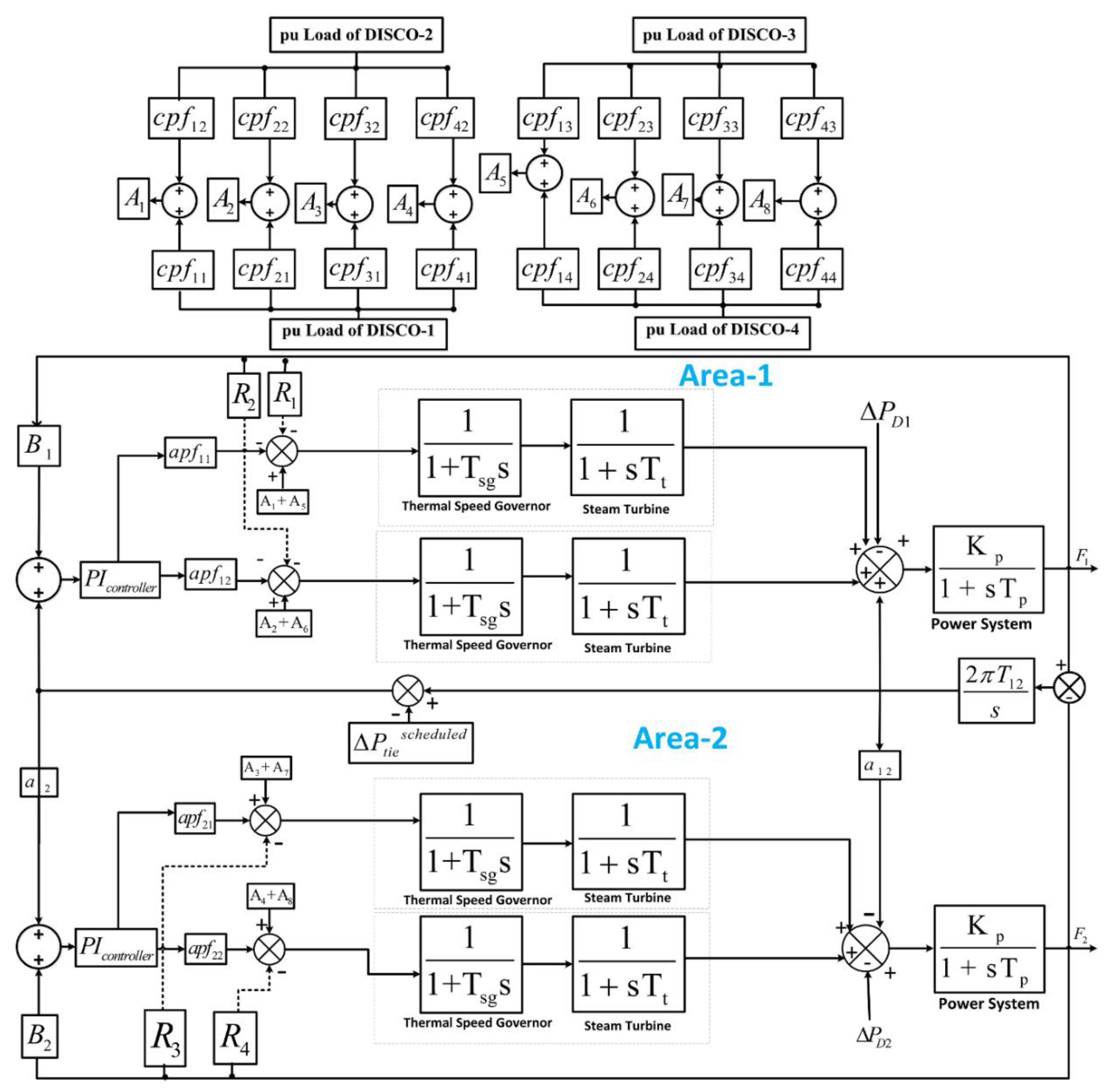
Transfer function model.
Figure 2.
Transfer function model.
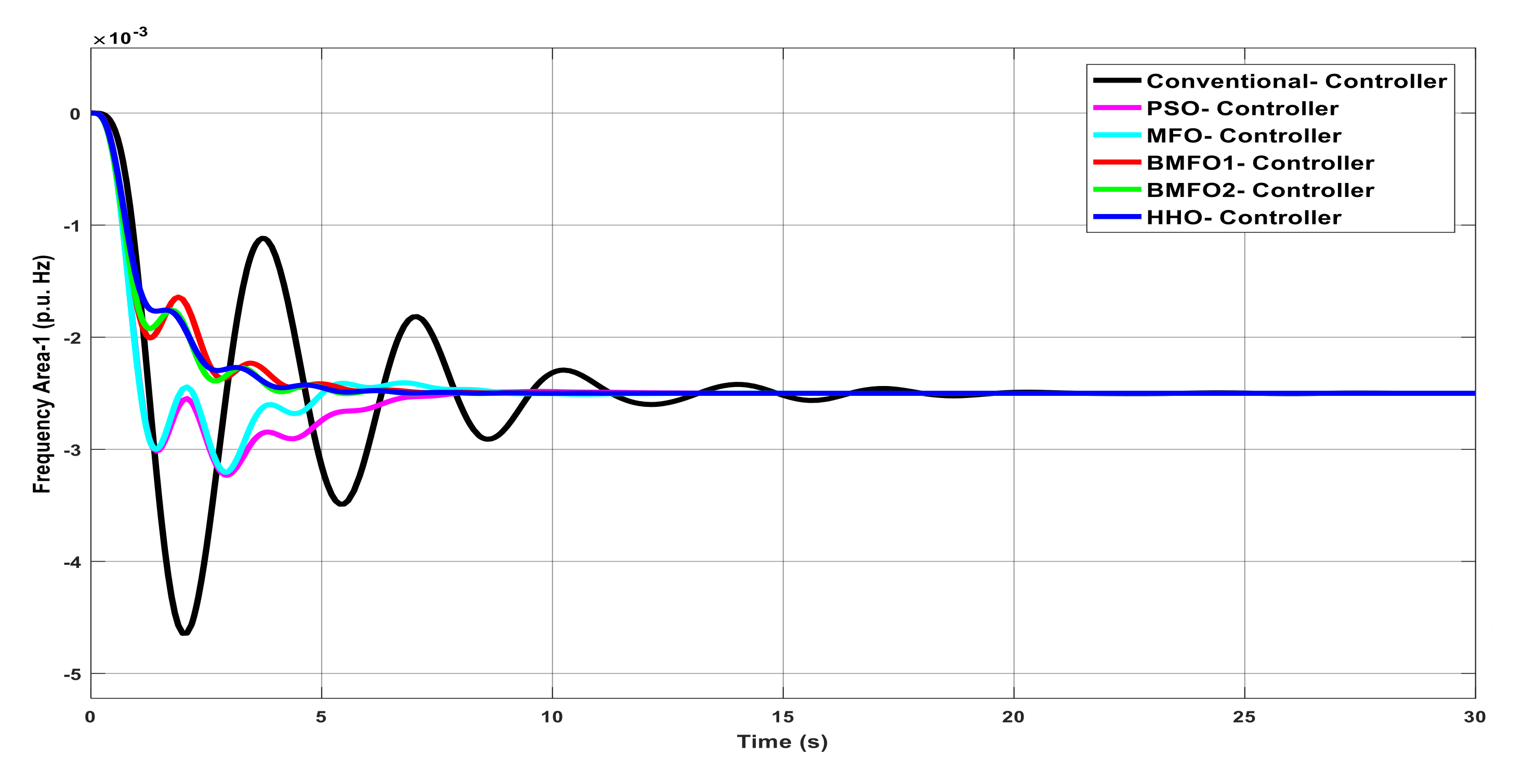
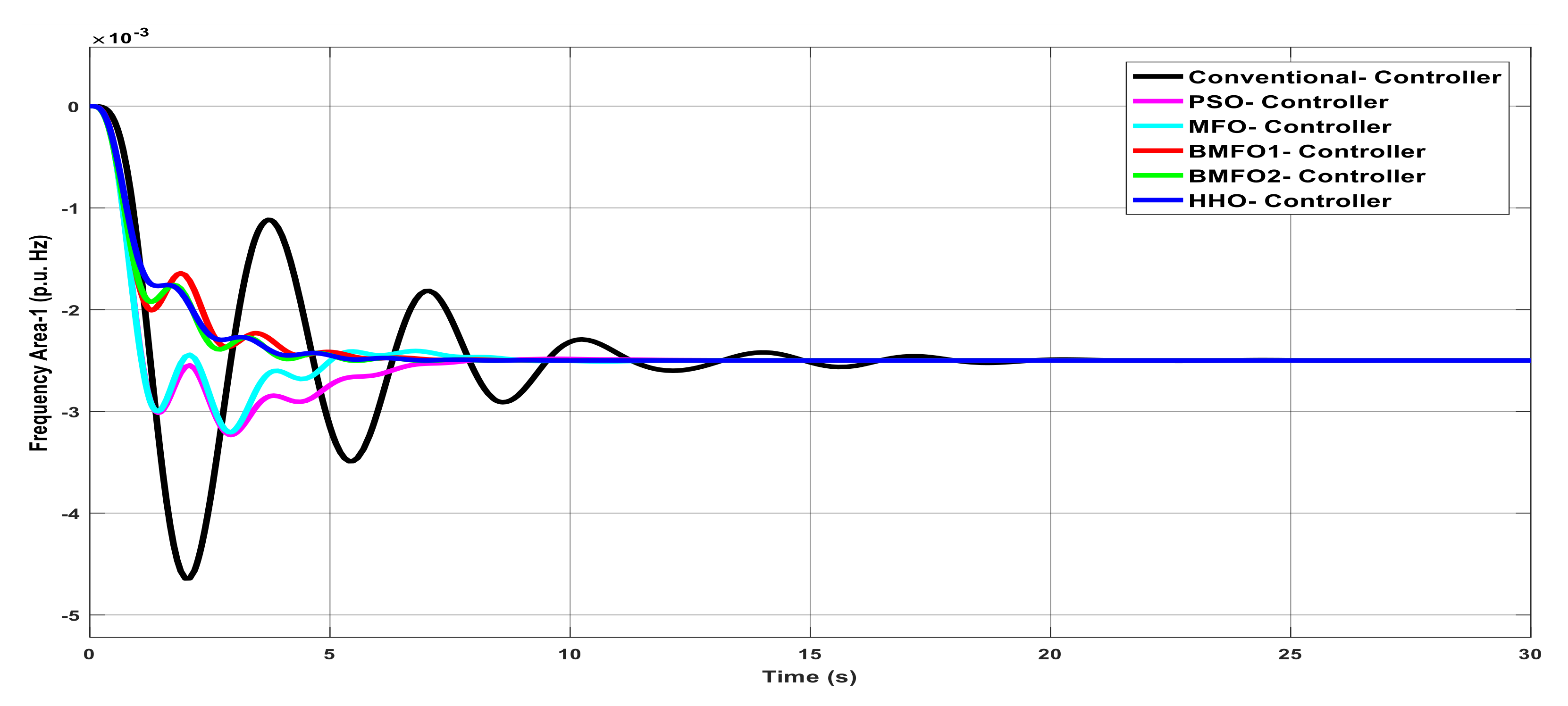
Figure 3.
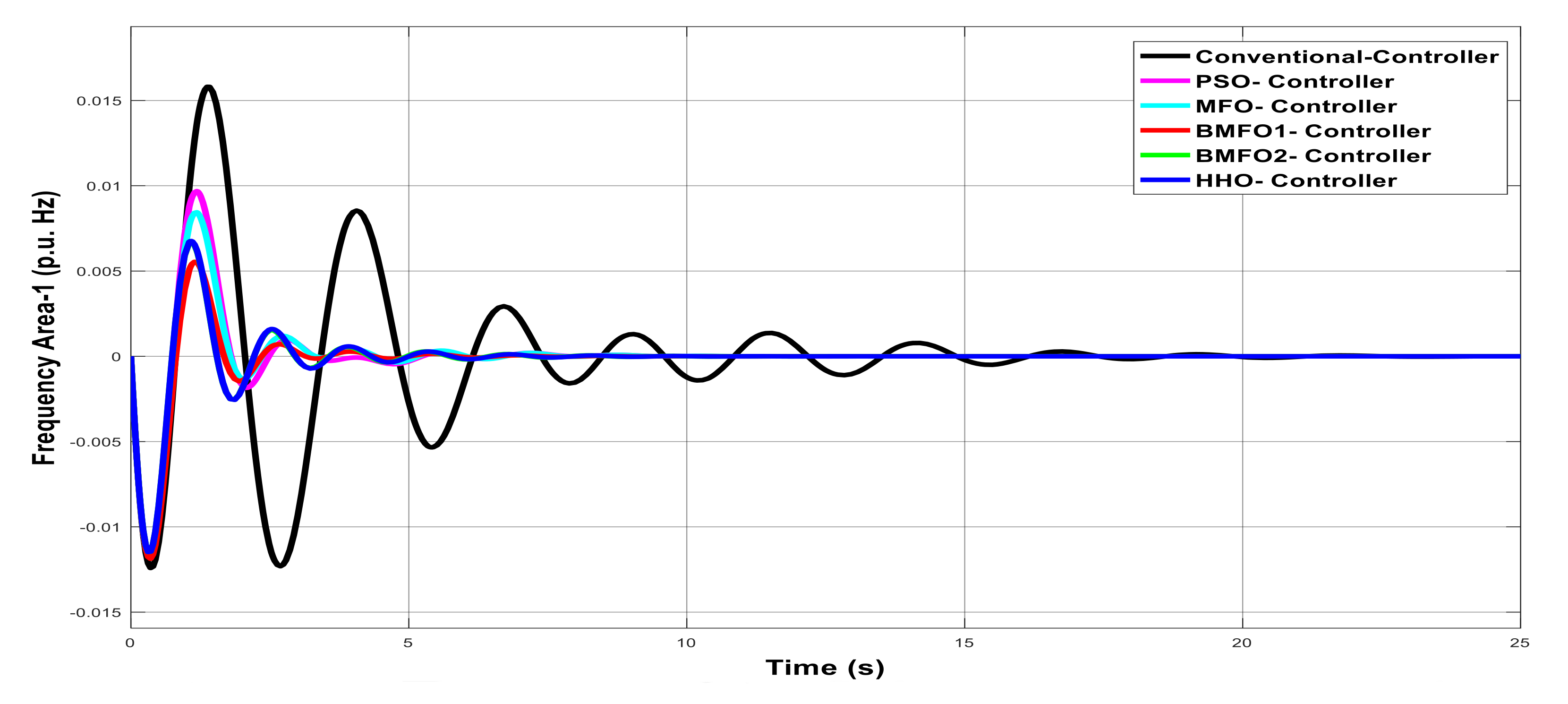
Dynamic response of Area1 frequency with various controllers under unilateral contract.
Figure 3.
Dynamic response of Area1 frequency with various controllers under unilateral contract.
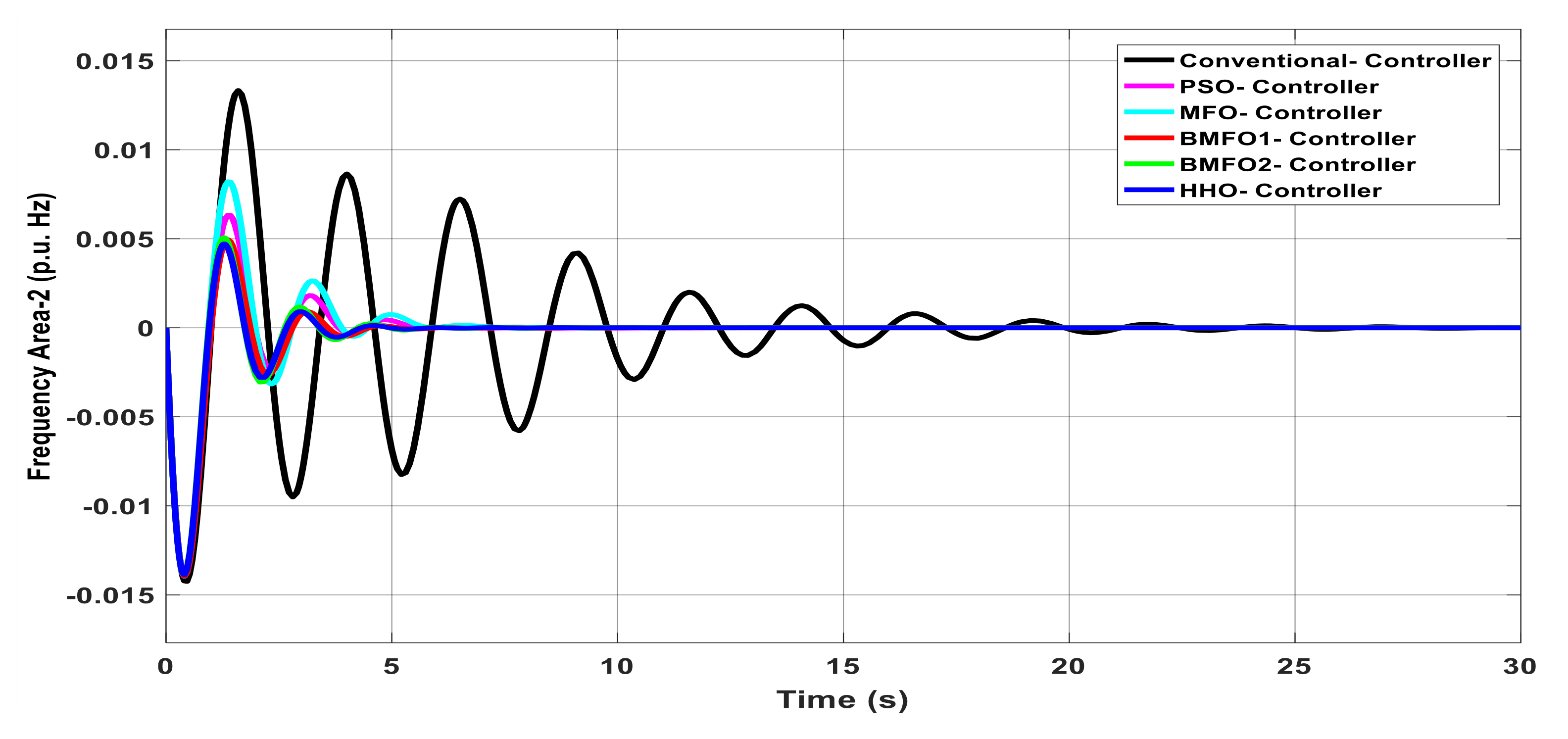
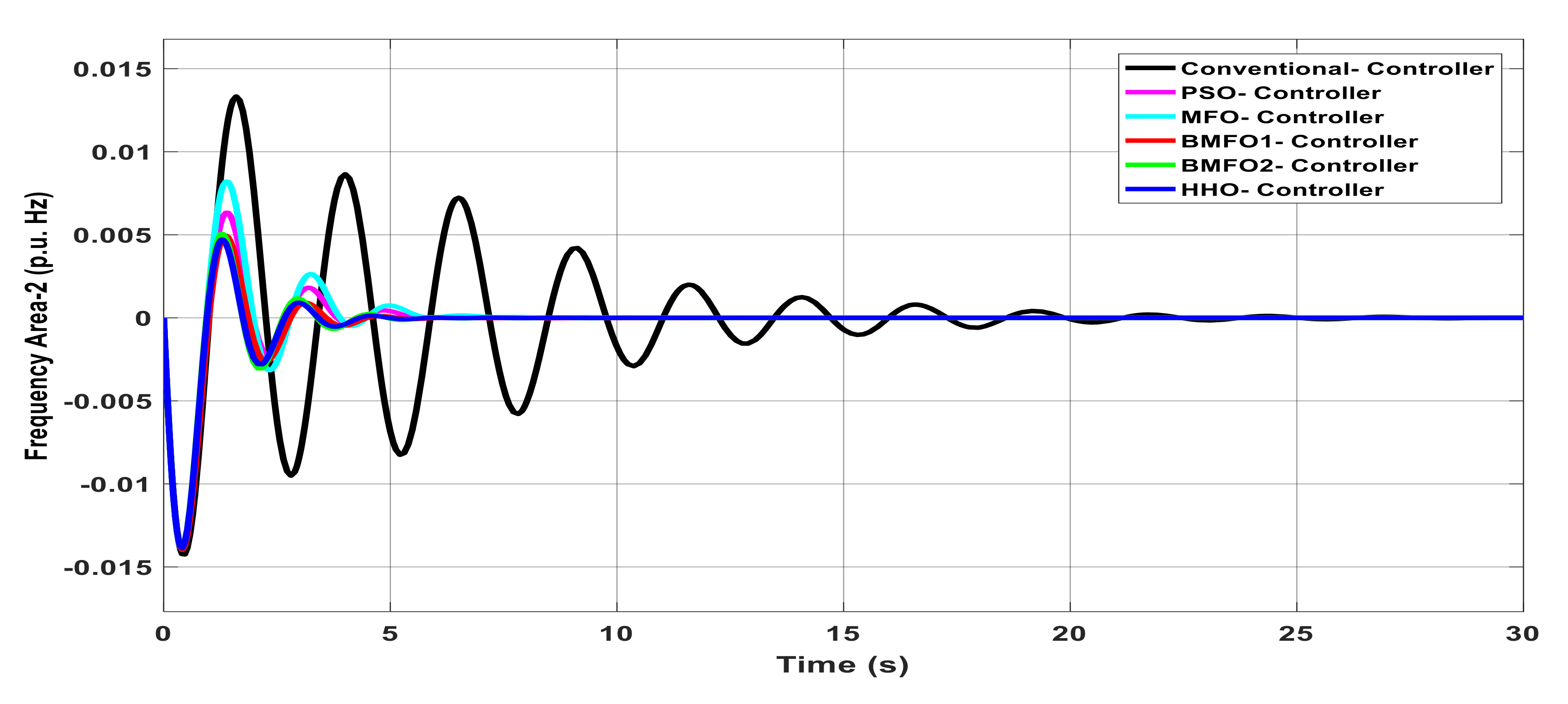
Figure 4.
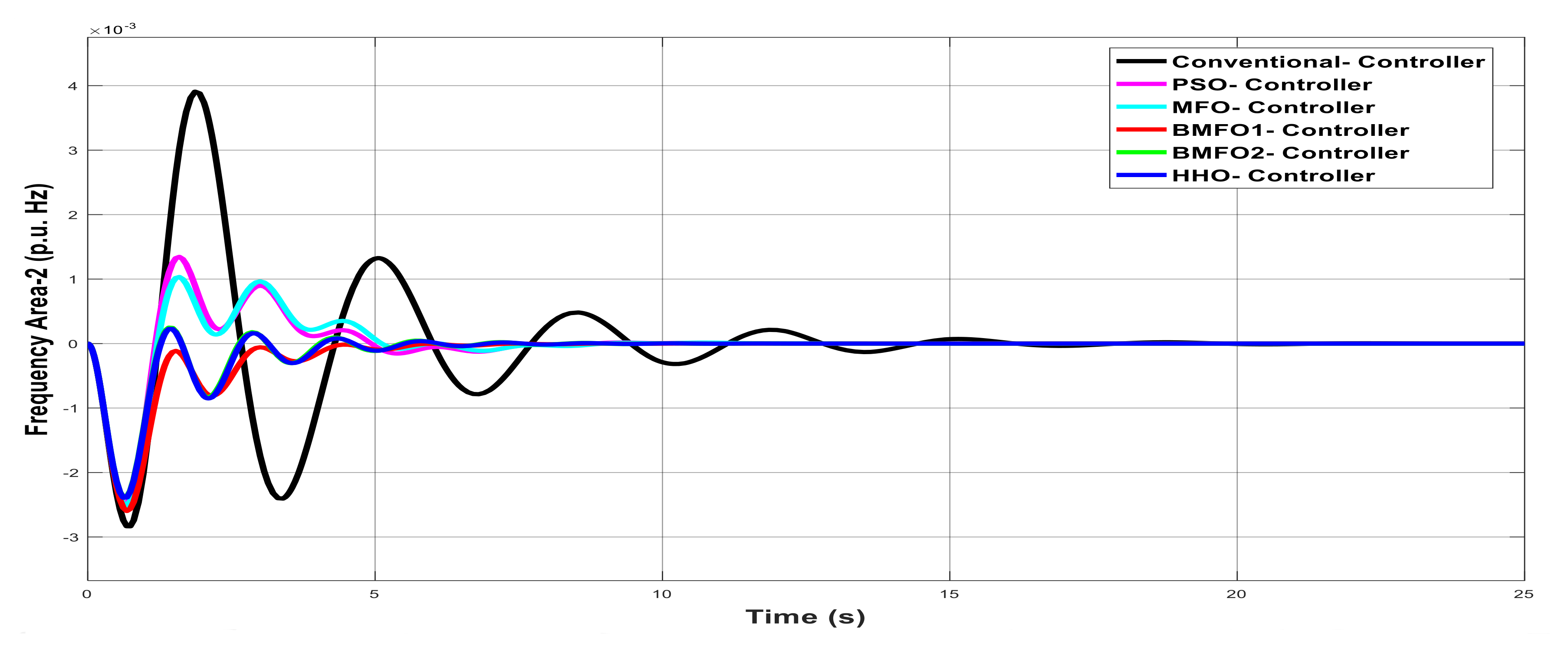
Dynamic response of Area2 frequency with various controllers under unilateral contract.
Figure 4.
Dynamic response of Area2 frequency with various controllers under unilateral contract.
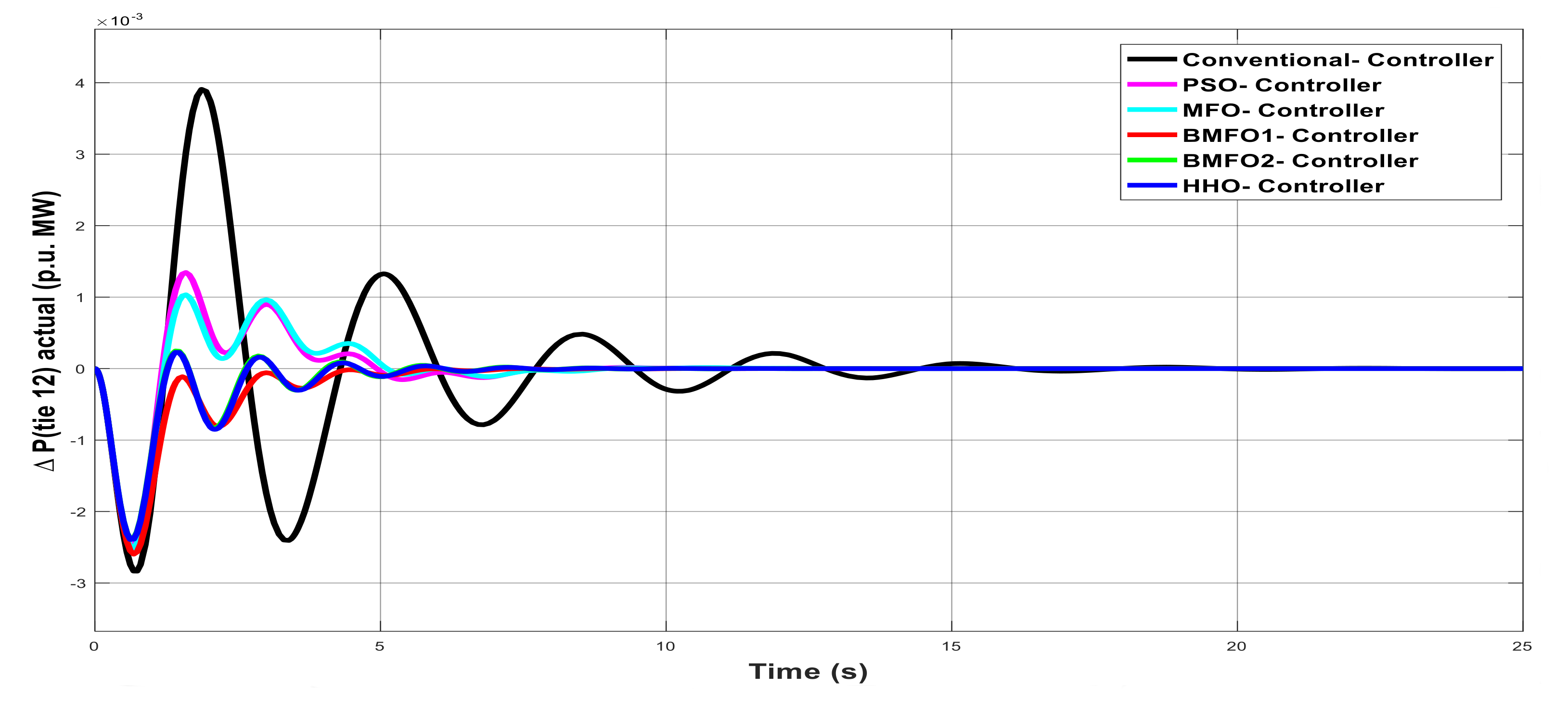
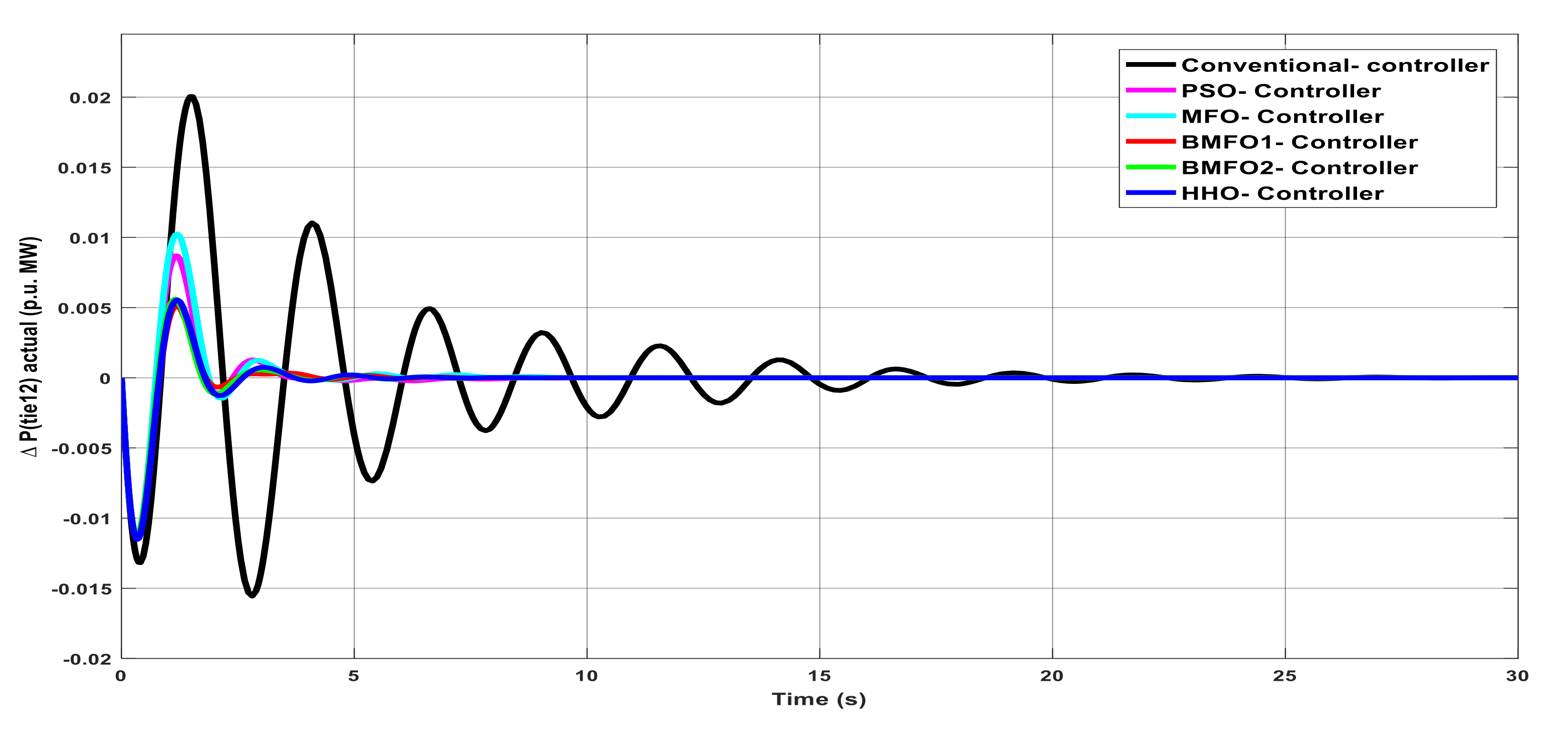
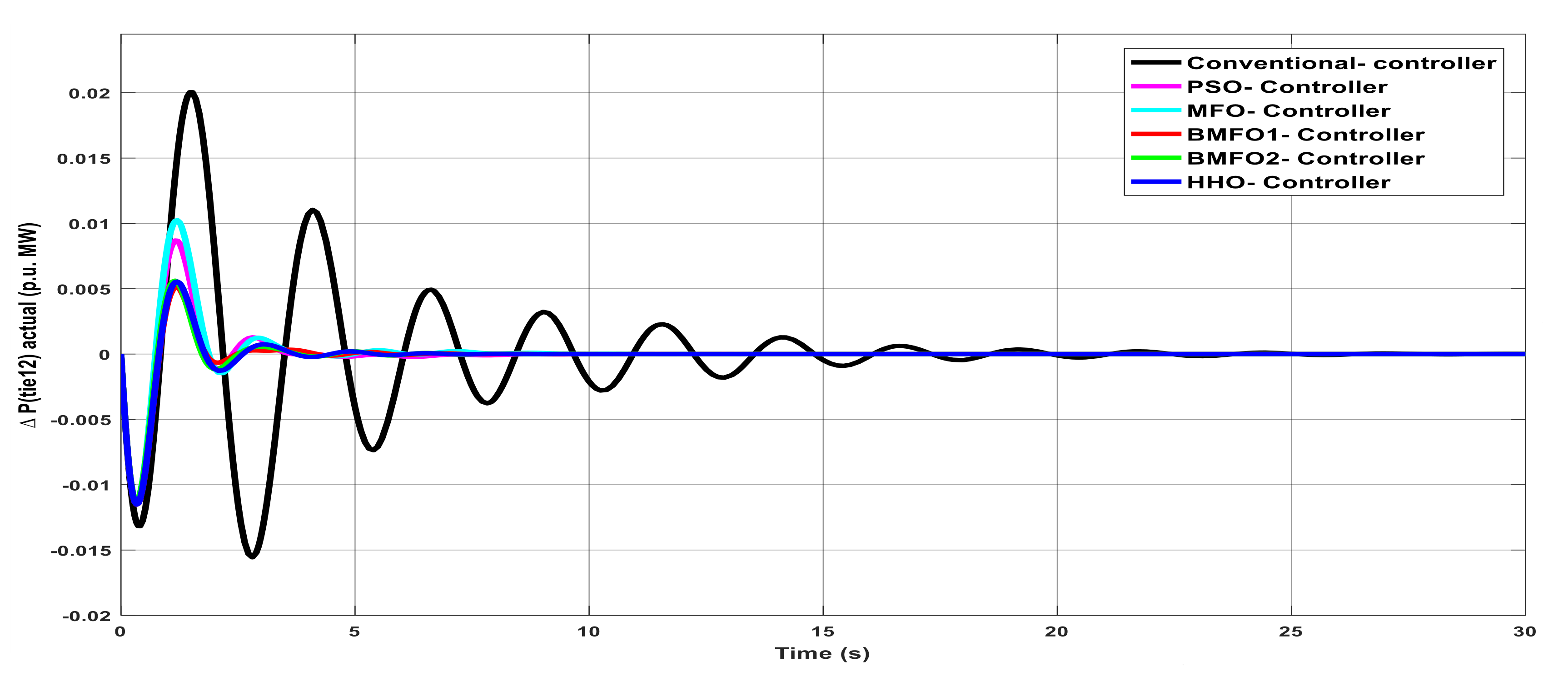
Figure 5.
Deviation in actual tie-line power flow with various controllers under unilateral contract.
Figure 5.
Deviation in actual tie-line power flow with various controllers under unilateral contract.
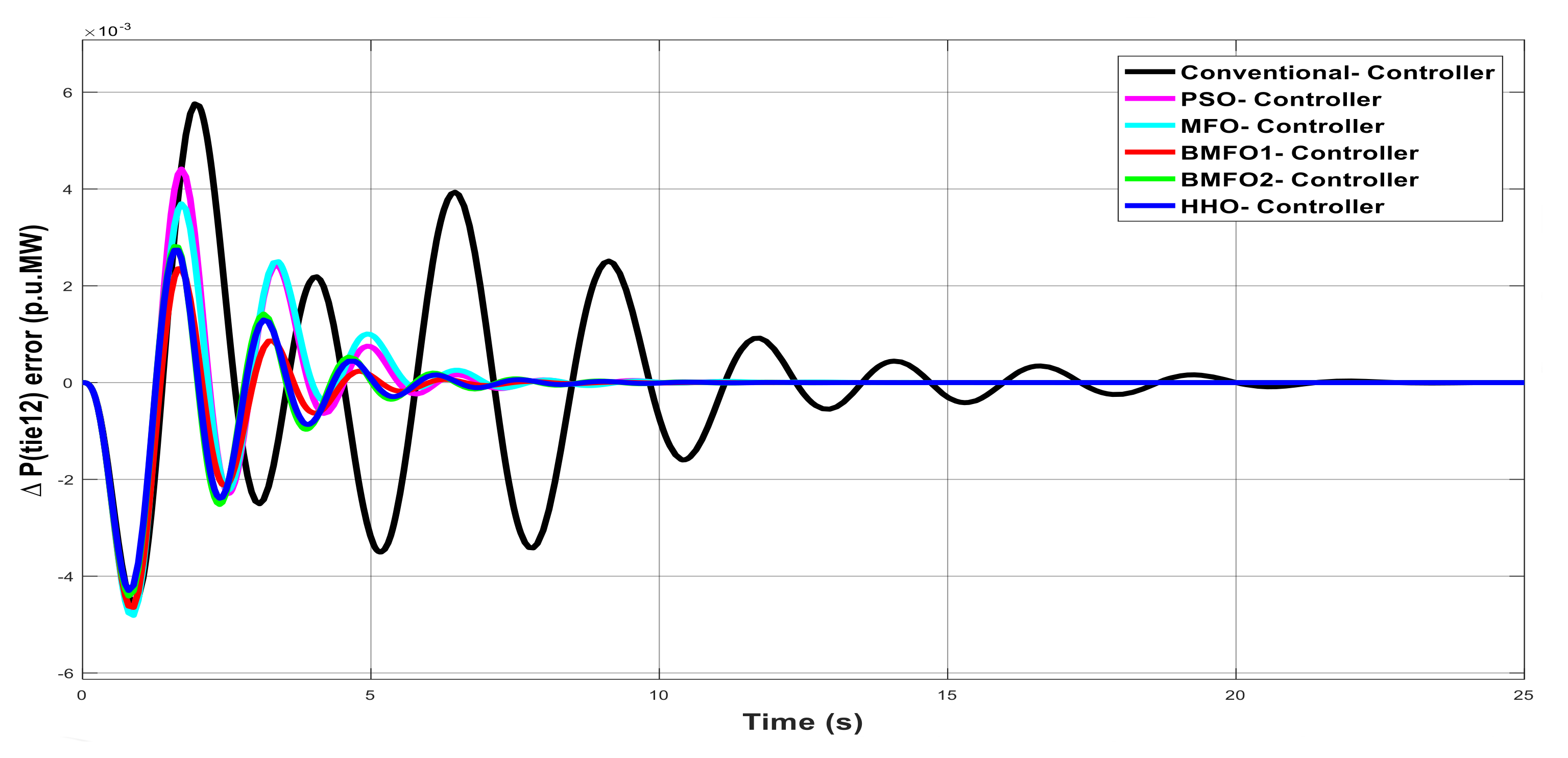
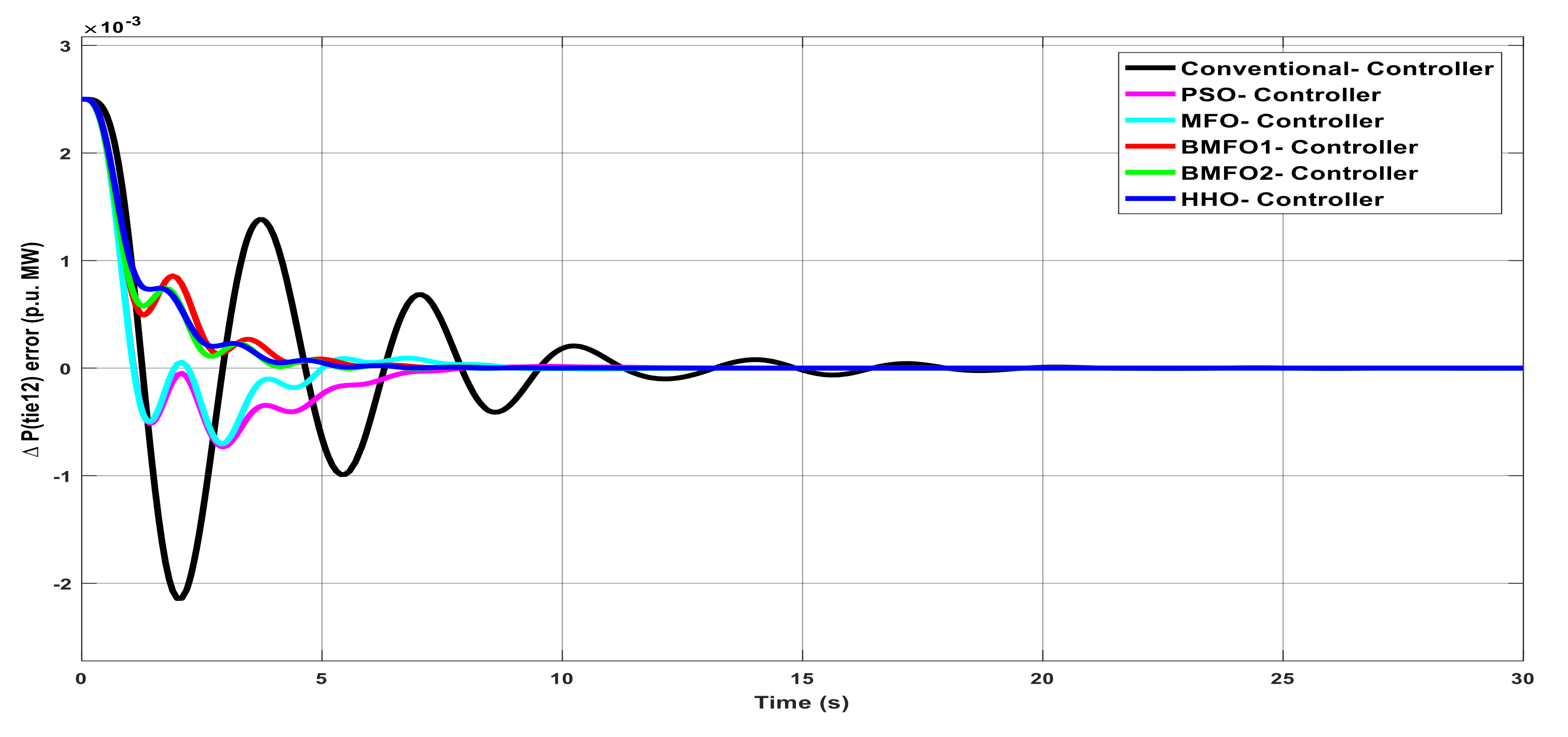
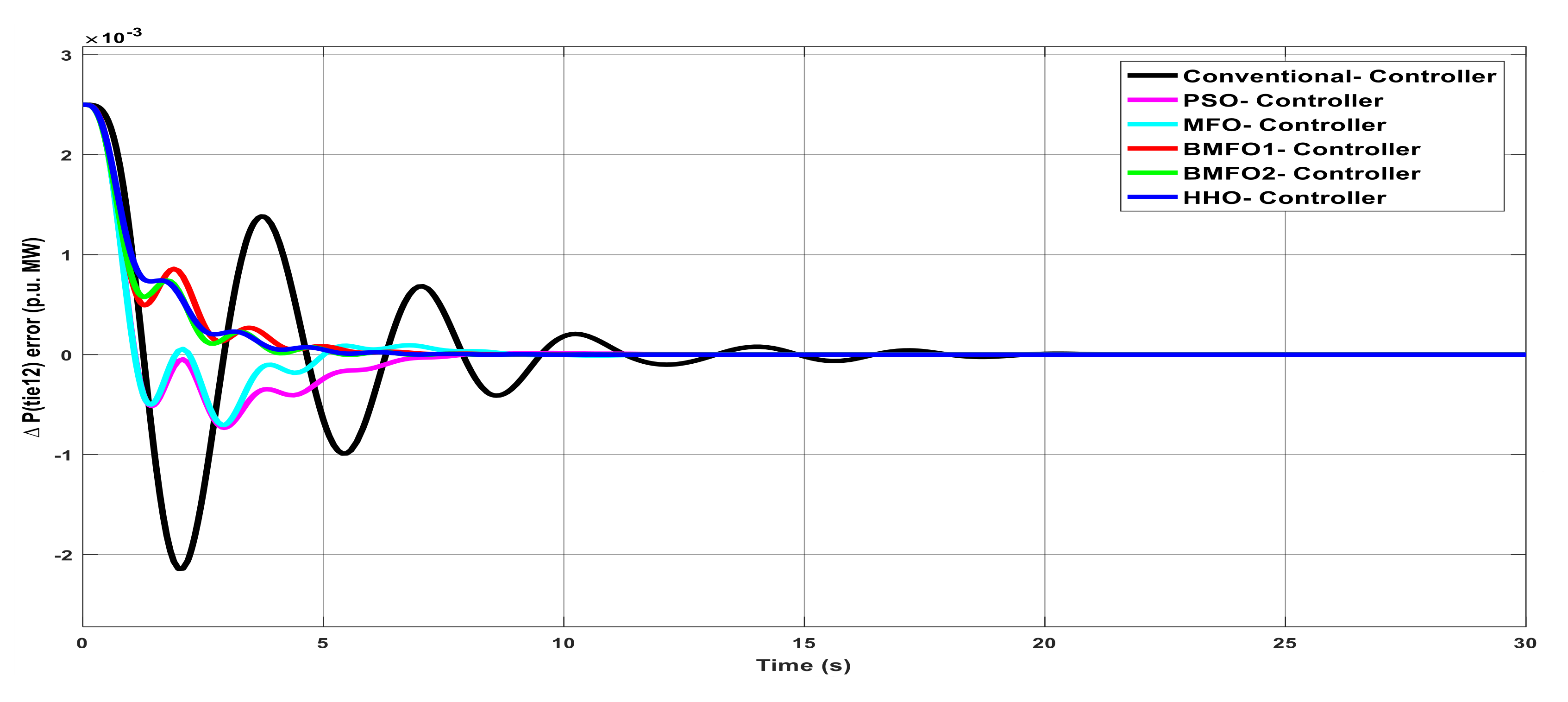
Figure 6.
Deviation in tie-line error with various controllers under unilateral contract.
Figure 6.
Deviation in tie-line error with various controllers under unilateral contract.
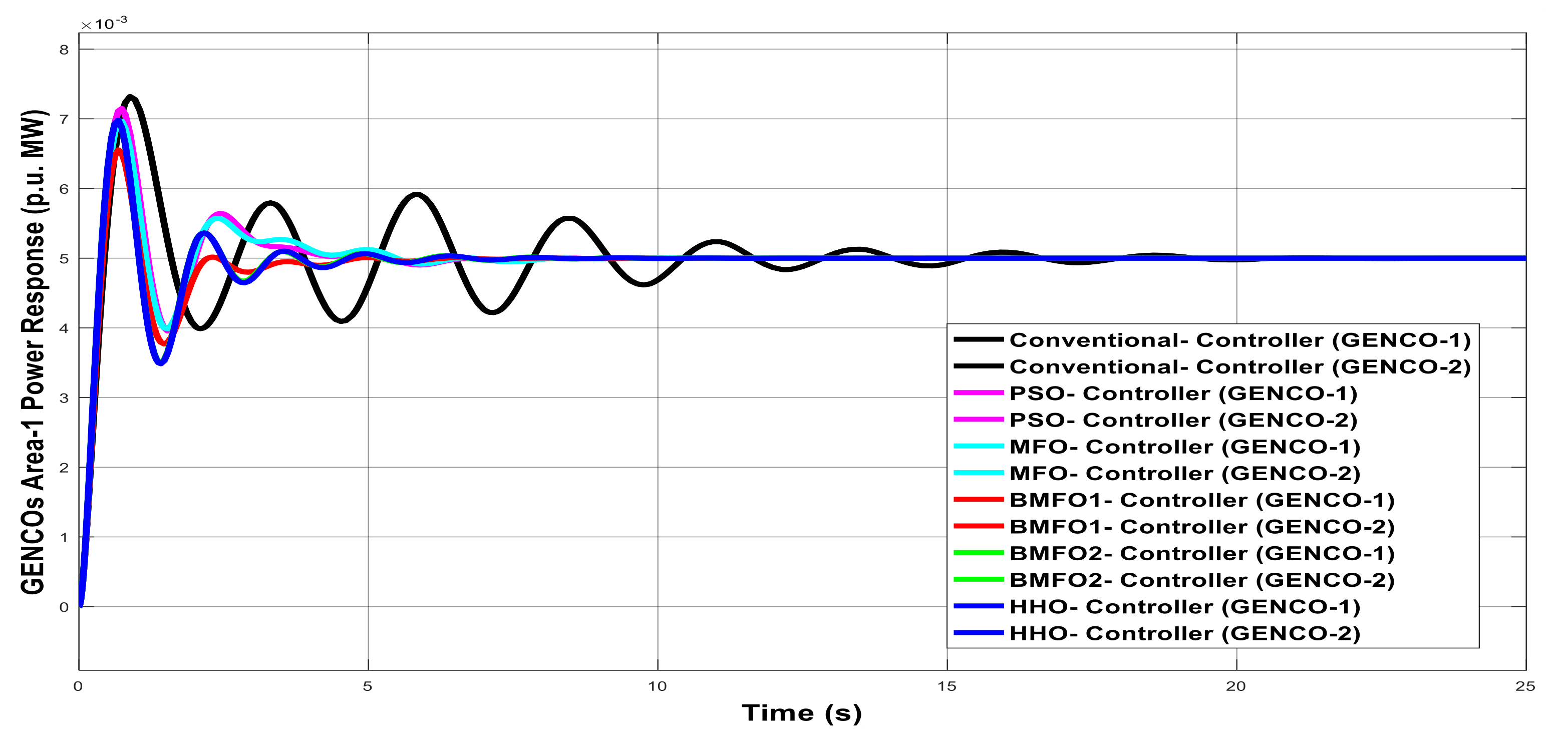
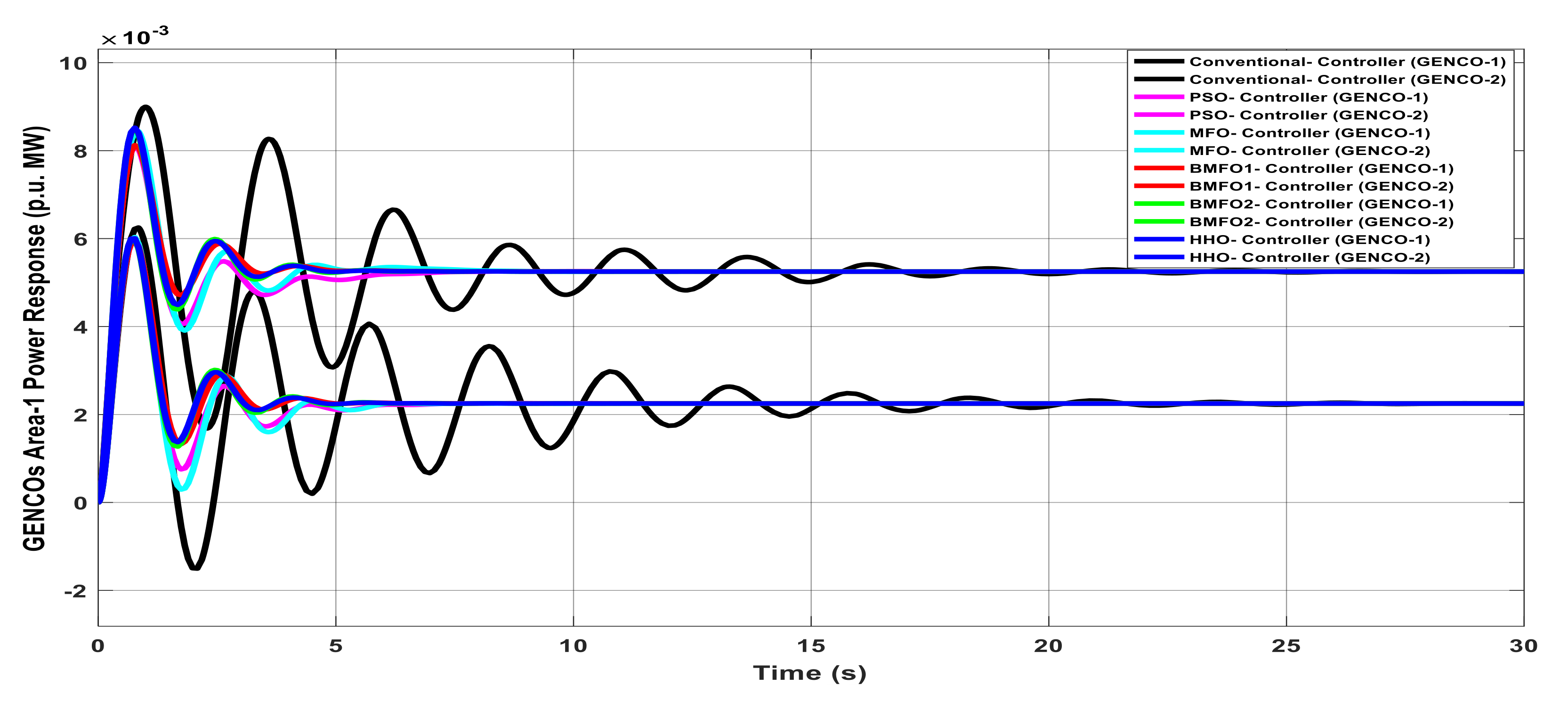
Figure 7.
Generation Companies (GENCOs) generation response of Area1 with various controllers under unilateral contract.
Figure 7.
Generation Companies (GENCOs) generation response of Area1 with various controllers under unilateral contract.
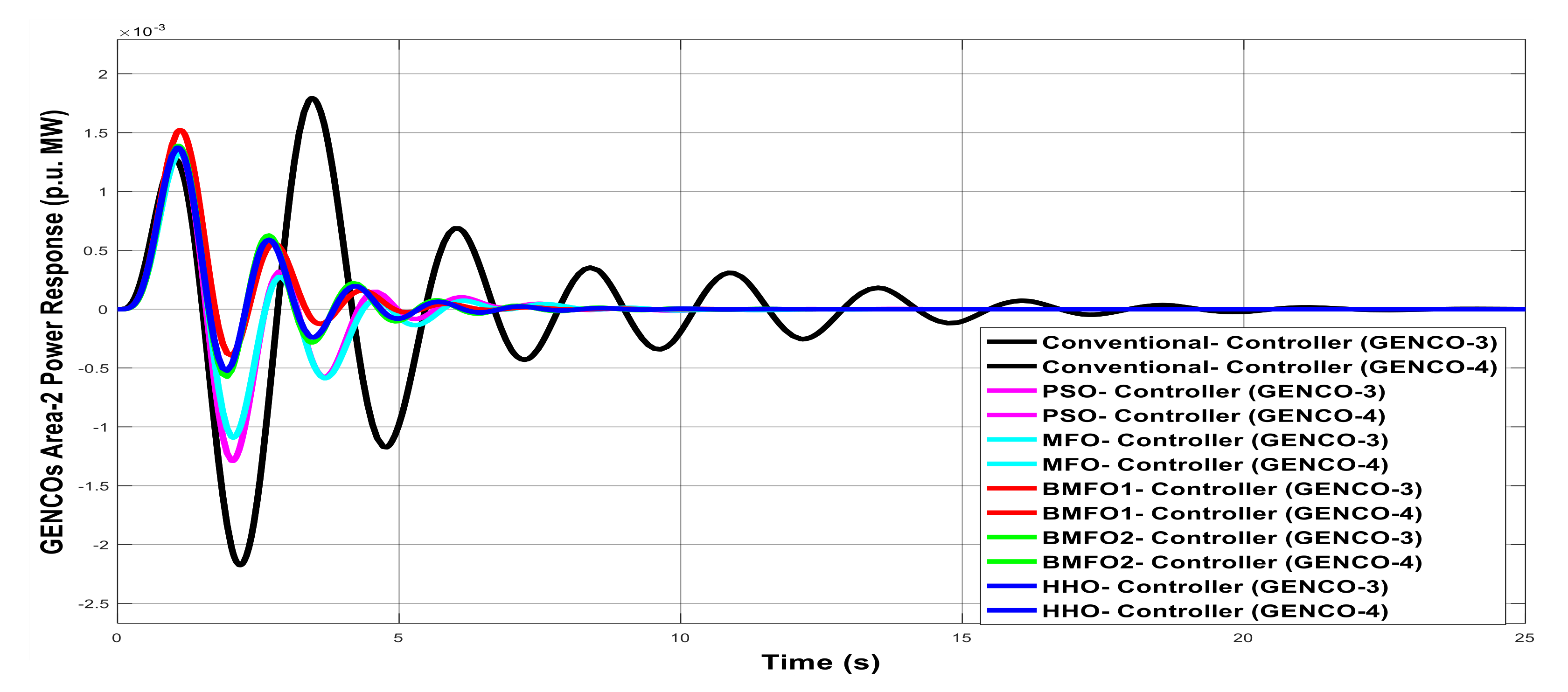
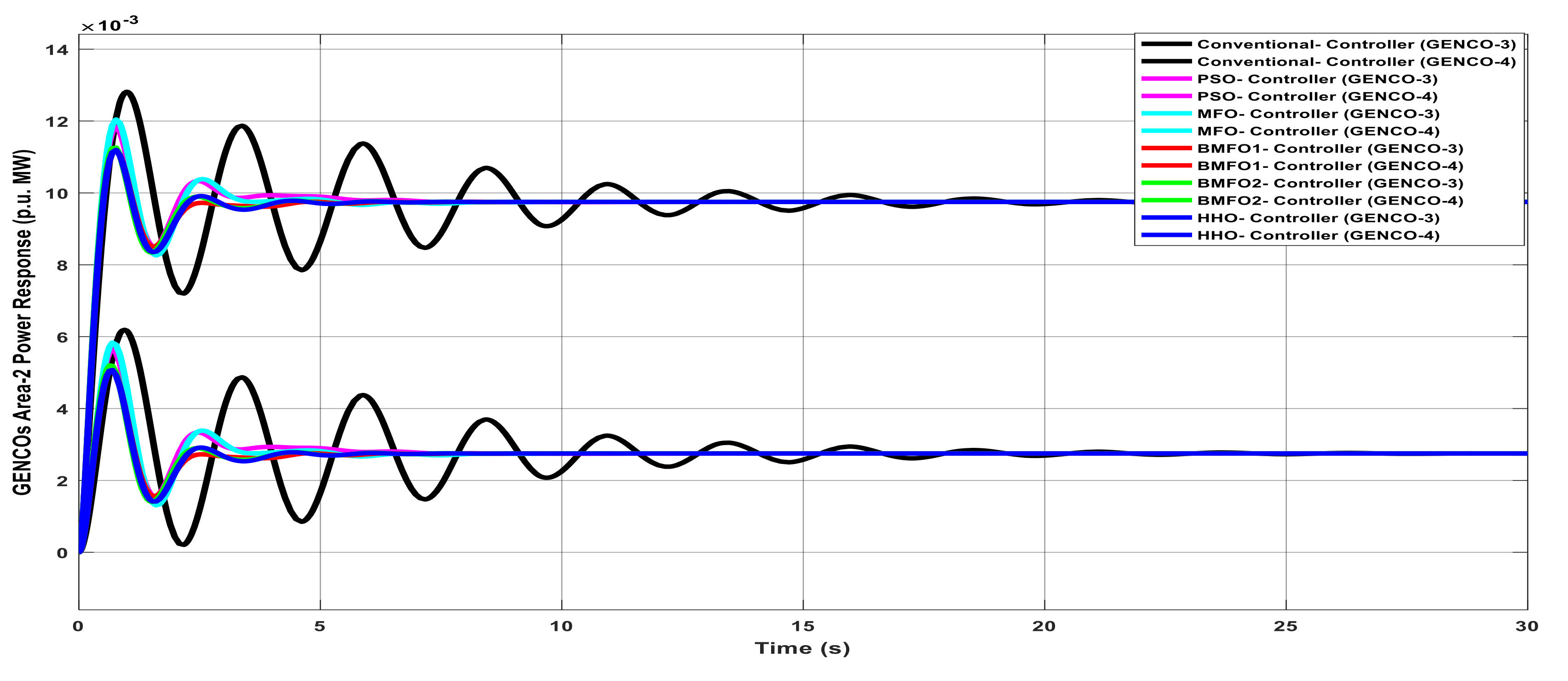
Figure 8.
GENCOs generation response of Area2 with various controllers under unilateral contract.
Figure 8.
GENCOs generation response of Area2 with various controllers under unilateral contract.
Figure 9.
Dynamic response of Area1 frequency with various controllers under bilateral contract.
Figure 9.
Dynamic response of Area1 frequency with various controllers under bilateral contract.
Figure 10.
Dynamic response of Area2 frequency with various controllers under bilateral contract.
Figure 10.
Dynamic response of Area2 frequency with various controllers under bilateral contract.
Figure 11.
Deviation in actual tie-line power flow with various controllers under bilateral contract.
Figure 11.
Deviation in actual tie-line power flow with various controllers under bilateral contract.
Figure 12.
Deviation in tie-line error with various controller under bilateral contract.
Figure 12.
Deviation in tie-line error with various controller under bilateral contract.
Figure 13.
GENCOs generation response of Area1 with various controllers under bilateral contract.
Figure 13.
GENCOs generation response of Area1 with various controllers under bilateral contract.
Figure 14.
GENCOs generation response of Area2 with various controllers under bilateral contract.
Figure 14.
GENCOs generation response of Area2 with various controllers under bilateral contract.
Figure 15.
Dynamic response of Area1 frequency with various controllers under contract violation case.
Figure 15.
Dynamic response of Area1 frequency with various controllers under contract violation case.
Figure 16.
Dynamic response of Area2 frequency with various controller under contract violation case.
Figure 16.
Dynamic response of Area2 frequency with various controller under contract violation case.
Figure 17.
Deviation in actual tie-line power flow with various controllers under contract violation case.
Figure 17.
Deviation in actual tie-line power flow with various controllers under contract violation case.
Figure 18.
Deviation in tie-line error with various controllers under contract violation case.
Figure 18.
Deviation in tie-line error with various controllers under contract violation case.
Figure 19.
GENCOs generation response of Area1 with various controllers under contract violation case.
Figure 19.
GENCOs generation response of Area1 with various controllers under contract violation case.
Figure 20.
GENCOs generation response of Area2 with various controllers under contract violation case.
Figure 20.
GENCOs generation response of Area2 with various controllers under contract violation case.
Table 1.
Performance of various algorithms in the proposed system.
Table 1.
Performance of various algorithms in the proposed system.
| Parameter | No. of Trials | Mean | Standard Deviation | Best | Worst |
|---|
| PSO | 50 | 1.13807 | 1.00846 | 1.02774 | 1.05084 |
| MFO | 50 | 0.0489 | 0.00644 | 0.02835 | 0.05073 |
| BMFO1 | 50 | 0.0284 | 0.00083 | 0.02745 | 0.03216 |
| BMFO2 | 50 | 0.0272 | 0.00011 | 0.02764 | 0.02811 |
| HHO | 50 | 7.62 × 10−93 | 1.39 × 10−93 | 1.4 × 10−112 | 4.17 × 10−92 |
Table 2.
Improved gain values of Proportional Integral (PI) controller for the expected scheme with various algorithms.
Table 2.
Improved gain values of Proportional Integral (PI) controller for the expected scheme with various algorithms.
| Controller Type | Controller Parameters |
|---|
| Area1 | Area2 |
|---|
| K1p | K1Int | K2P | K2Int |
|---|
| PSO | 0.53007 | −7.12 × 10−6 | 0.28516 | −0.84672 |
| MFO | 0.52333 | −0.70889 | 0.31424 | −0.92724 |
| BMFO1 | 0.53126 | −0.0034 | 0.28435 | 9.83 × 10−6 |
| BMFO2 | 0.55025 | −8.07 × 10−7 | 0.28545 | −1.89 × 10−6 |
| HHO | 0.15025 | −9.059 × 10−9 | 0.18293 | −1.91 × 10−9 |
Table 3.
Graph analysis of Area1 frequency with various controllers under unilateral contract.
Table 3.
Graph analysis of Area1 frequency with various controllers under unilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 1.05 | 1.186 | 1.375 | 22 |
| PSO | 0.8833 | 1.05 | 1.186 | 21.430 |
| MFO | 0.8833 | 1.05 | 1.145 | 21.3 |
| BMFO1 | 0.9667 | 1.05 | 1.145 | 21.02 |
| BMFO2 | 0.8833 | 1.05 | 1.087 | 20.1 |
| HHO | 0.8833 | 0.9667 | 1.07 | 19.8 |
Table 4.
Graph analysis of Area2 frequency with various controller under unilateral contract.
Table 4.
Graph analysis of Area2 frequency with various controller under unilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 1.474 | 1.654 | 1.868 | 23.39 |
| PSO | 1.336 | 1.414 | 1.594 | 21.17 |
| MFO | 1.336 | 1.474 | 1.594 | 21.01 |
| BMFO1 | −1.201 | −1.414 | −1.534 | 21.43 |
| BMFO2 | 1.297 | 1.375 | 1.414 | 21.43 |
| HHO | 1.297 | 1.375 | 1.414 | 20.86 |
Table 5.
Graph analysis of deviation in actual tie-line power flow with various controllers under unilateral contract.
Table 5.
Graph analysis of deviation in actual tie-line power flow with various controllers under unilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 1.935 | 3.478 | 3.865 | 23.39 |
| PSO | 0.664 | 1.195 | 1.325 | 21.17 |
| MFO | 0.535 | 0.975 | 1.068 | 21.01 |
| BMFO1 | 0.435 | −0.778 | −0.865 | 21.43 |
| BMFO2 | 0.535 | 0.957 | 1.063 | 21.43 |
| HHO | 0.162 | 0.292 | 0.324 | 20.86 |
Table 6.
Graph analysis of deviation in tie-line error with various controller under unilateral contract.
Table 6.
Graph analysis of deviation in tie-line error with various controller under unilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 2.935 | 5.280 | 5.865 | 22 |
| PSO | 2.118 | 3.814 | 4.235 | 21.430 |
| MFO | 1.955 | 3.498 | 3.886 | 21.3 |
| BMFO1 | 1.115 | 2.002 | 2.224 | 21.02 |
| BMFO2 | 1.988 | 3.555 | 3.950 | 20.1 |
| HHO | 1.157 | 2.085 | 2.315 | 19.8 |
Table 7.
Graph analysis of GENCOs generation response of Area1 with various controllers under unilateral contract.
Table 7.
Graph analysis of GENCOs generation response of Area1 with various controllers under unilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 3.665 | 6.595 | 7.325 | 23.39 |
| PSO | 3.598 | 6.478 | 7.195 | 21.17 |
| MFO | 3.508 | 6.315 | 7.015 | 21.01 |
| BMFO1 | 3.335 | 6.002 | 6.668 | 21.43 |
| BMFO2 | 3.503 | 6.305 | 7.005 | 21.43 |
| HHO | 3.335 | 6.002 | 6.668 | 20.86 |
Table 8.
Graph analysis of GENCOs generation response of Area2 with various controllers under unilateral contract.
Table 8.
Graph analysis of GENCOs generation response of Area2 with various controllers under unilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 0.888 | 1.598 | 1.775 | 22 |
| PSO | 0.725 | 1.305 | 1.450 | 21.430 |
| MFO | 0.734 | 1.333 | 1.468 | 21.3 |
| BMFO1 | 0.755 | 1.355 | 1.505 | 21.02 |
| BMFO2 | 0.723 | 1.300 | 1.445 | 20.1 |
| HHO | 0.695 | 1.251 | 1.390 | 19.8 |
Table 9.
Graph analysis of Area1 frequency with various controllers under bilateral contract.
Table 9.
Graph analysis of Area1 frequency with various controllers under bilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | −2.414 | −4.205 | −4.668 | 23.39 |
| PSO | −1.508 | −2.715 | −3.015 | 21.17 |
| MFO | −1.503 | −2.705 | −3.005 | 21.01 |
| BMFO1 | −1.003 | −1.805 | −2.005 | 21.43 |
| BMFO2 | −0.978 | −1.766 | −1.955 | 21.43 |
| HHO | −0.835 | −1.499 | −1.665 | 20.86 |
Table 10.
Graph analysis of Area2 frequency with various controllers under bilateral contract.
Table 10.
Graph analysis of Area2 frequency with various controllers under bilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 0.0066 | 0.0118 | 0.0131 | 23.39 |
| PSO | 0.0031 | 0.0047 | 0.0052 | 21.17 |
| MFO | 0.0045 | 0.0074 | 0.0082 | 21.01 |
| BMFO1 | 0.0026 | 0.0046 | 0.0051 | 21.43 |
| BMFO2 | 0.0027 | 0.0048 | 0.0053 | 21.43 |
| HHO | 0.0023 | 0.0041 | 0.0045 | 20.86 |
Table 11.
Graph analysis of deviation in actual tie-line power flow with various controllers under bilateral contract.
Table 11.
Graph analysis of deviation in actual tie-line power flow with various controllers under bilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 0.0106 | 0.0190 | 0.0211 | 23.39 |
| PSO | 0.0043 | 0.0077 | 0.0085 | 21.17 |
| MFO | 0.0063 | 0.0114 | 0.0125 | 21.01 |
| BMFO1 | 0.0033 | 0.0059 | 0.0065 | 21.43 |
| BMFO2 | 0.0031 | 0.0055 | 0.0061 | 21.43 |
| HHO | 0.0029 | 0.0053 | 0.0058 | 20.86 |
Table 12.
Graph analysis of deviation in tie-line error with various controller under bilateral contract.
Table 12.
Graph analysis of deviation in tie-line error with various controller under bilateral contract.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 1.284 | 2.311 | 2.568 | 22 |
| PSO | 1.278 | 2.299 | 2.555 | 21.430 |
| MFO | 1.277 | 2.298 | 2.554 | 21.3 |
| BMFO1 | 1.277 | 2.297 | 2.553 | 21.02 |
| BMFO2 | 1.277 | 2.296 | 2.552 | 20.1 |
| HHO | 1.276 | 2.295 | 2.551 | 19.8 |
Table 13.
(a). Graphanalysis of GENCOs to Distribution Companies (DISCOs) generation response of Area1 with various controllers under bilateral contract. (b). Graph analysis of DISCOs to GENCOs generation response of Area1 with various controllers under bilateral contract.
Table 13.
(a). Graphanalysis of GENCOs to Distribution Companies (DISCOs) generation response of Area1 with various controllers under bilateral contract. (b). Graph analysis of DISCOs to GENCOs generation response of Area1 with various controllers under bilateral contract.
| (a) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 3.130 | 5.630 | 6.255 | 23.39 |
| PSO | 3.116 | 5.608 | 6.231 | 21.17 |
| MFO | 3.056 | 5.514 | 6.112 | 21.01 |
| BMFO1 | 3.056 | 5.514 | 6.112 | 21.43 |
| BMFO2 | 3.044 | 5.478 | 6.088 | 21.43 |
| HHO | 3.006 | 5.411 | 6.012 | 20.86 |
| (b) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 4.508 | 8.114 | 9.015 | 22 |
| PSO | 4.335 | 7.799 | 8.665 | 21.430 |
| MFO | 4.335 | 7.799 | 8.665 | 21.3 |
| BMFO1 | 4.258 | 7.663 | 8.514 | 21.02 |
| BMFO2 | 4.258 | 7.663 | 8.514 | 20.1 |
| HHO | 4.224 | 7.600 | 8.445 | 19.8 |
Table 14.
(a). Graph analysis of GENCOs to DISCOs generation response of Area2 with various controllers under bilateral contract. (b). Graph analysis of DISCOs to GENCOs generation response of Area2 with various controllers under bilateral contract.
Table 14.
(a). Graph analysis of GENCOs to DISCOs generation response of Area2 with various controllers under bilateral contract. (b). Graph analysis of DISCOs to GENCOs generation response of Area2 with various controllers under bilateral contract.
| (a) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 3.114 | 5.591 | 6.212 | 23.39 |
| PSO | 2.943 | 5.297 | 5.885 | 21.17 |
| MFO | 2.998 | 5.397 | 5.996 | 21.01 |
| BMFO1 | 2.857 | 5.143 | 5.714 | 21.43 |
| BMFO2 | 2.663 | 4.792 | 5.324 | 21.43 |
| HHO | 2.506 | 4.511 | 5.012 | 20.86 |
| (b) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 6.434 | 11.579 | 12.865 | 22 |
| PSO | 6.006 | 10.811 | 12.012 | 21.430 |
| MFO | 6.066 | 10.901 | 12.112 | 21.3 |
| BMFO1 | 6.066 | 10.901 | 12.112 | 21.02 |
| BMFO2 | 5.885 | 10.595 | 11.770 | 20.1 |
| HHO | 5.564 | 10.001 | 11.112 | 19.8 |
Table 15.
Graph analysis of Area1 frequency with various controllers under contract violation case.
Table 15.
Graph analysis of Area1 frequency with various controllers under contract violation case.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | −2.414 | −4.205 | −4.668 | 23.39 |
| PSO | −1.508 | −2.715 | −3.015 | 21.17 |
| MFO | −1.503 | −2.705 | −3.005 | 21.01 |
| BMFO1 | −1.003 | −1.805 | −2.005 | 21.43 |
| BMFO2 | −0.978 | −1.766 | −1.955 | 21.43 |
| HHO | −0.835 | −1.499 | −1.665 | 20.86 |
Table 16.
Graph analysis of Area2 frequency with various controller under contract violation case.
Table 16.
Graph analysis of Area2 frequency with various controller under contract violation case.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 0.0066 | 0.0118 | 0.0131 | 23.39 |
| PSO | 0.0031 | 0.0047 | 0.0052 | 21.17 |
| MFO | 0.0045 | 0.0074 | 0.0082 | 21.01 |
| BMFO1 | 0.0026 | 0.0046 | 0.0051 | 21.43 |
| BMFO2 | 0.0027 | 0.0048 | 0.0053 | 21.43 |
| HHO | 0.0023 | 0.0041 | 0.0045 | 20.86 |
Table 17.
Graph analysis of deviation in actual tie-line power flow with various controller under contract violation case.
Table 17.
Graph analysis of deviation in actual tie-line power flow with various controller under contract violation case.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 0.0106 | 0.0190 | 0.0211 | 23.39 |
| PSO | 0.0043 | 0.0077 | 0.0085 | 21.17 |
| MFO | 0.0063 | 0.0114 | 0.0125 | 21.01 |
| BMFO1 | 0.0033 | 0.0059 | 0.0065 | 21.43 |
| BMFO2 | 0.0031 | 0.0055 | 0.0061 | 21.43 |
| HHO | 0.0029 | 0.0053 | 0.0058 | 20.86 |
Table 18.
Graph analysis of deviation in tie-line error with various controllers under contract violation case.
Table 18.
Graph analysis of deviation in tie-line error with various controllers under contract violation case.
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
|---|
| Conventional | 1.284 | 2.311 | 2.568 | 22 |
| PSO | 1.278 | 2.299 | 2.555 | 21.430 |
| MFO | 1.277 | 2.298 | 2.554 | 21.3 |
| BMFO1 | 1.277 | 2.297 | 2.553 | 21.02 |
| BMFO2 | 1.277 | 2.296 | 2.552 | 20.1 |
| HHO | 1.276 | 2.295 | 2.551 | 19.8 |
Table 19.
(a). Graph analysis of GENCOs to DISCOs generation response of Area1 with various controllers under contract violation case. (b). Graph analysis of DISCOs to GENCOs generation response of Area1 with various controllers under contract violation case.
Table 19.
(a). Graph analysis of GENCOs to DISCOs generation response of Area1 with various controllers under contract violation case. (b). Graph analysis of DISCOs to GENCOs generation response of Area1 with various controllers under contract violation case.
| (a) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 3.130 | 5.630 | 6.255 | 23.39 |
| PSO | 3.116 | 5.608 | 6.231 | 21.17 |
| MFO | 3.056 | 5.514 | 6.112 | 21.01 |
| BMFO1 | 3.056 | 5.514 | 6.112 | 21.43 |
| BMFO2 | 3.044 | 5.478 | 6.088 | 21.43 |
| HHO | 3.006 | 5.411 | 6.012 | 20.86 |
| (b) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 4.508 | 8.114 | 9.015 | 22 |
| PSO | 4.335 | 7.799 | 8.665 | 21.430 |
| MFO | 4.335 | 7.799 | 8.665 | 21.3 |
| BMFO1 | 4.258 | 7.663 | 8.514 | 21.02 |
| BMFO2 | 4.258 | 7.663 | 8.514 | 20.1 |
| HHO | 4.224 | 7.600 | 8.445 | 19.8 |
Table 20.
(a). Graph analysis of GENCOs to DISCOs generation response of Area2 with various controllers under contract violation case. (b). Graph analysis of DISCOs to GENCOs generation response of Area2 with various controllers under contract violation case.
Table 20.
(a). Graph analysis of GENCOs to DISCOs generation response of Area2 with various controllers under contract violation case. (b). Graph analysis of DISCOs to GENCOs generation response of Area2 with various controllers under contract violation case.
| (a) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 3.114 | 5.591 | 6.212 | 23.39 |
| PSO | 2.943 | 5.297 | 5.885 | 21.17 |
| MFO | 2.998 | 5.397 | 5.996 | 21.01 |
| BMFO1 | 2.857 | 5.143 | 5.714 | 21.43 |
| BMFO2 | 2.663 | 4.792 | 5.324 | 21.43 |
| HHO | 2.506 | 4.511 | 5.012 | 20.86 |
| (b) |
| Controller | Delay Time | Rise Time | Peak Overshoot Time | Settling Time |
| Conventional | 6.434 | 11.579 | 12.865 | 22 |
| PSO | 6.006 | 10.811 | 12.012 | 21.430 |
| MFO | 6.066 | 10.901 | 12.112 | 21.3 |
| BMFO1 | 6.066 | 10.901 | 12.112 | 21.02 |
| BMFO2 | 5.885 | 10.595 | 11.770 | 20.1 |
| HHO | 5.564 | 10.001 | 11.112 | 19.8 |