Estimation for Varying Coefficient Models with Hierarchical Structure
Abstract
1. Introduction
2. Modeling and Estimation
- (1)
- Take the non-penalized estimator as the initial estimator .
- (2)
- According to the method discussed above, iterate (7) until convergence; specifically, the iteration stops when is less than . For model sparsity, and should be set 0 when they are less than a small real value (in our simulation, we choose ).
- (3)
- Get the KLasso estimator .
3. Theoretical Properties
- C1.
- For , the covariate is independent of the error .
- C2.
- The covariate has finite p-order moment, i.e., , where .
- C3.
- The density function of U, , is continuous and has second-order derivative.
- C4.
- has second-order derivative, while and are both bounded.
- C5.
- is a symmetric kernel function, which satisfies , , , .
- C6.
- and are all bounded and have second-order continuous derivatives for and .
- (1)
- as
- (2)
- as
4. Simulation Study and Real Data Analysis
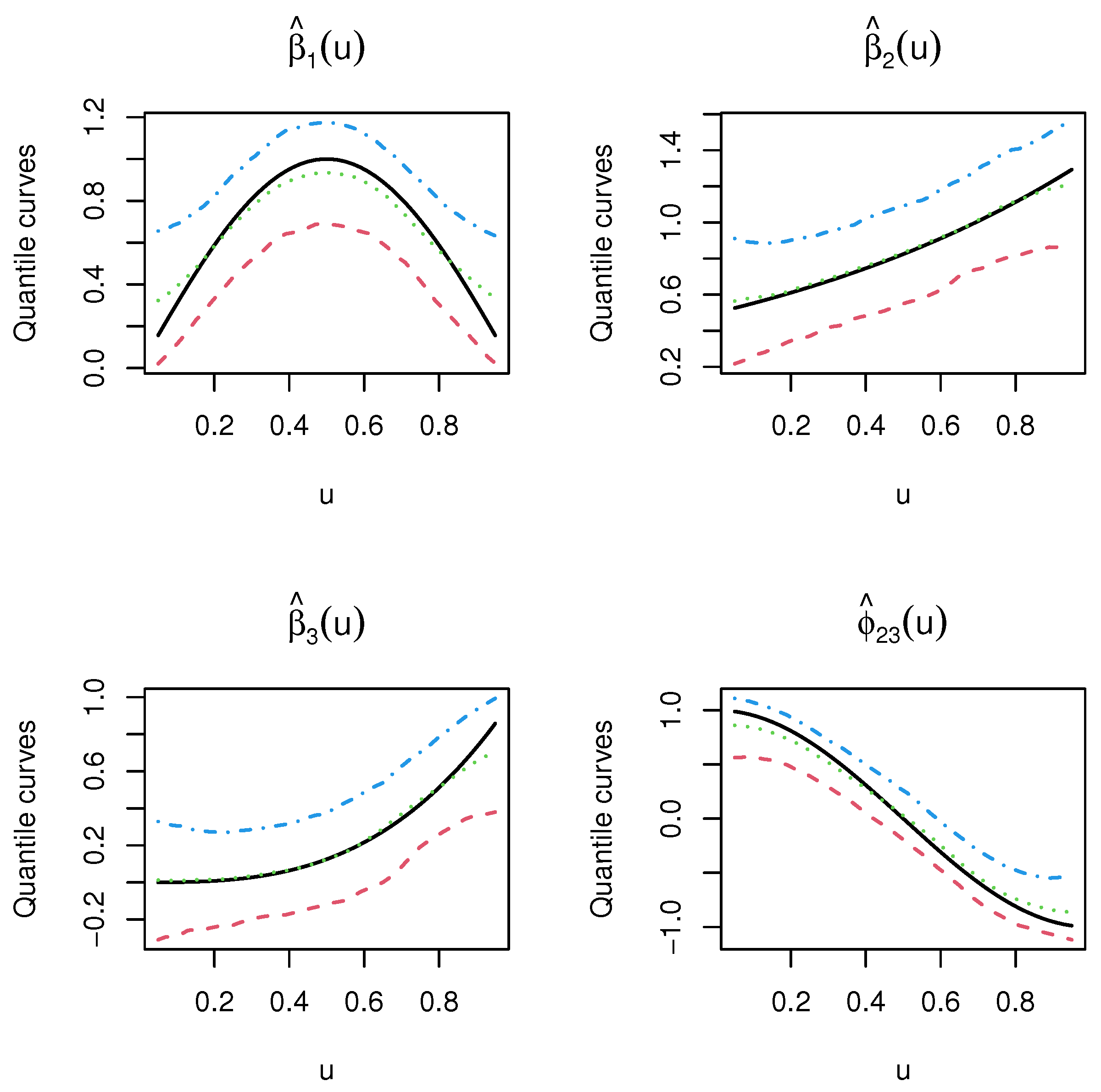
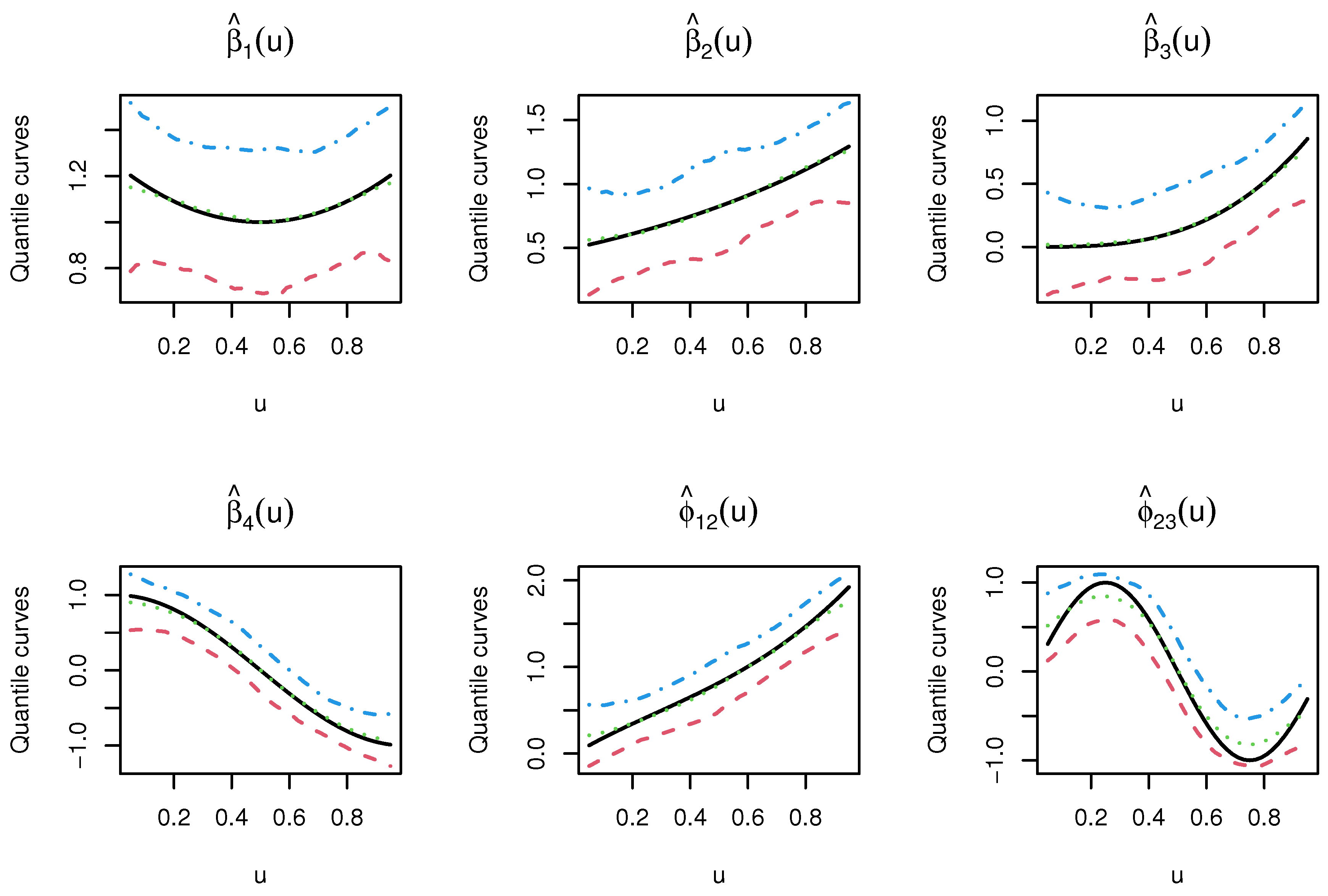
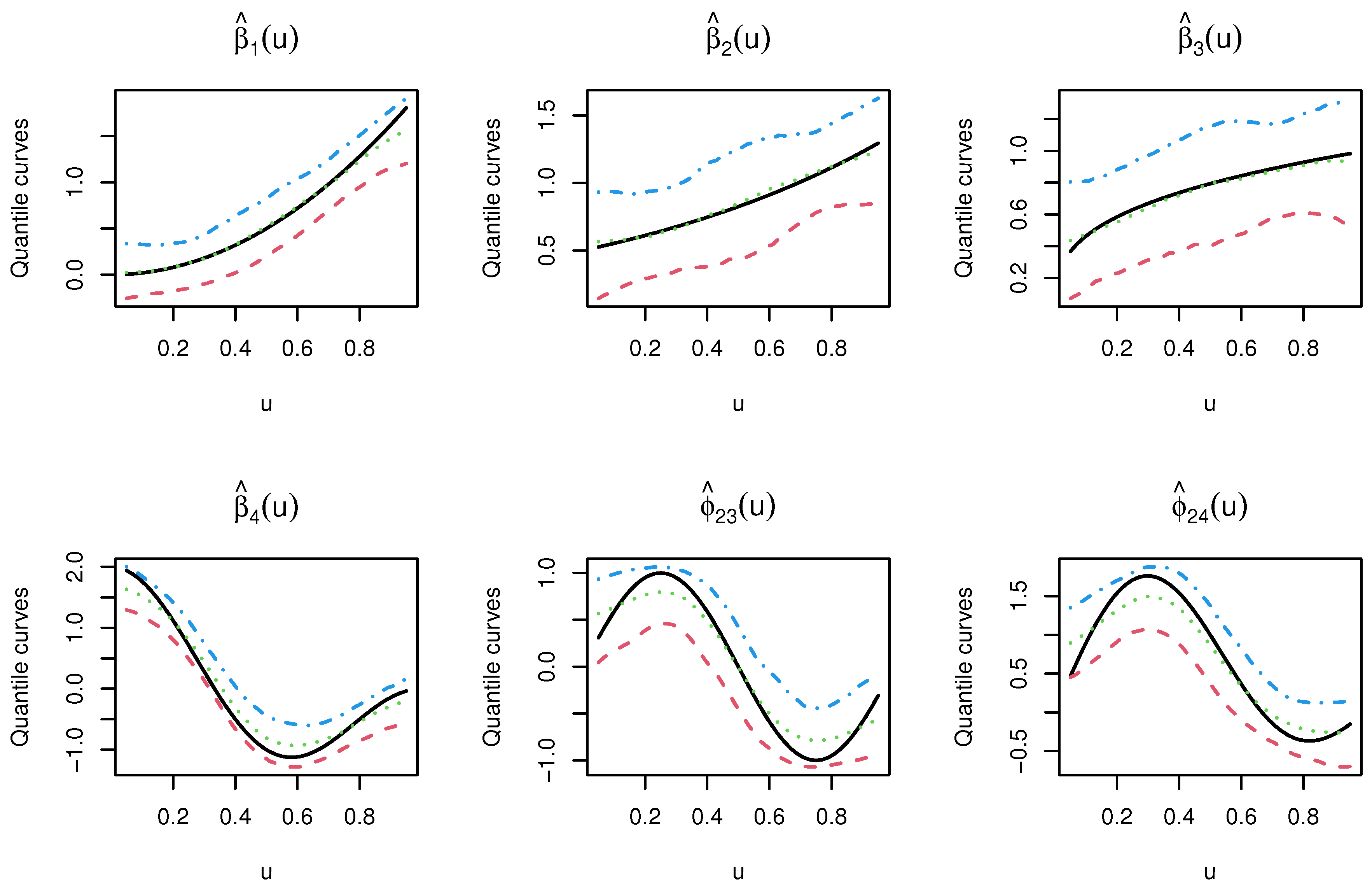
4.1. Simulation Study
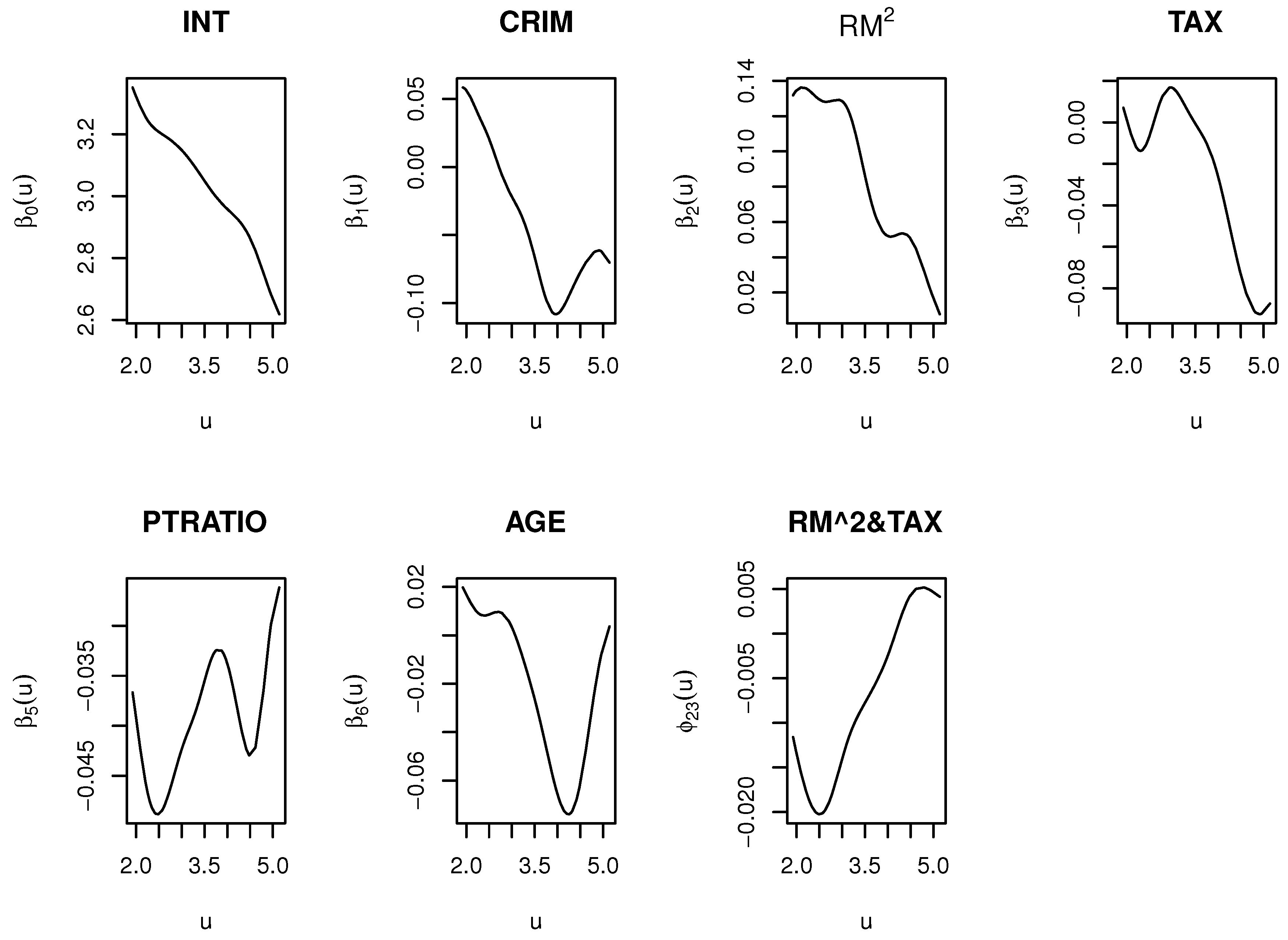
4.2. The Boston Housing Data Analysis
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- (1)
- , and ;
- (2)
- , and and ; and
- (3)
- , and .
References
- Hastie, T.; Tibshirani, R. Varying-coefficient models. J. R. Stat. Soc. Ser. B 1993, 55, 757–779. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, W. Statistical estimation in varying coefficient models. Ann. Stat. 1999, 27, 1491–1518. [Google Scholar]
- Fan, J.; Huang, T. Profile likelihood inferences on semiparametric varying-coefficient partially linear models. Bernoulli 2005, 11, 1031–1057. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, W. Simultaneous confidence bands and hypothesis testing in varying-coefficient models. Scand. J. Stat. 2000, 27, 715–731. [Google Scholar] [CrossRef]
- Zhu, N.H. Two-stage local Walsh average estimation of generalized varying coefficient models. Acta Math. Appl. Sin. Engl. Ser. 2015, 31, 623–642. [Google Scholar] [CrossRef]
- Li, Z.H.; Liu, J.S.; Wu, X.L. Variable bandwidth and one step local M-estimation of varying coefficient models. Appl. Math. A J. Chin. Univ. 2009, 4, 379–390. [Google Scholar]
- Wang, H.; Xia, Y. Shrinkage estimation of the varying coefficient model. J. Am. Stat. Assoc. 2009, 104, 747–757. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zhao, P.; Xue, L. Variable selection for semiparametric varying coefficient partially linear models. Stat. Probab. Lett. 2009, 79, 2148–2157. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, H.J.; Zhu, Z.; Song, X. A unified variable selection approach for varying coefficient models. Stat. Sin. 2012, 22, 601–628. [Google Scholar] [CrossRef]
- Li, D.; Ke, Y.; Zhang, W. Model selection and structure specification in ultra-high dimensional generalised semi-varying coefficient models. Ann. Stat. 2015, 43, 2676–2705. [Google Scholar] [CrossRef]
- He, K.; Lian, H.; Ma, S.; Huang, J. Dimensionality reduction and variable selection in multivariate varying-coefficient models with a large number covariates. J. Am. Stat. Assoc. 2018, 113, 746–754. [Google Scholar] [CrossRef]
- Hall, P.; Xue, J.H. On selecting interacting features from high-dimensional data. Comput. Stat. Data Anal. 2014, 71, 694–708. [Google Scholar] [CrossRef]
- Niu, Y.S.; Hao, N.; Zhang, H.H. Interaction screening by partial correlation. Stat. Interface 2018, 11, 317–325. [Google Scholar] [CrossRef]
- Kong, Y.; Li, D.; Fan, Y.; Lv, J. Interaction pursuit in high-dimensional multi-response regression via distance correlation. Ann. Stat. 2017, 45, 897–922. [Google Scholar] [CrossRef]
- Radchenko, P.; James, G. Variable selection using adaptive nonlinear interaction structure in high dimensions. J. Am. Stat. Assoc. 2010, 105, 1541–1553. [Google Scholar] [CrossRef]
- Choi, N.; Li, W.; Zhu, J. Variable selection with strong heredity constraint and its oracle property. J. Am. Stat. Assoc. 2010, 105, 354–364. [Google Scholar] [CrossRef]
- Bien, J.; Taylor, J.; Tibshirani, R. A lasso for hierarchical interactions. Ann. Stat. 2013, 41, 1111–1141. [Google Scholar] [CrossRef]
- Zhao, P.; Rocha, G.; Yu, B. The composite absolute penalties family for grouped and hierarchical variable selection. Ann. Stat. 2009, 37, 3468–3497. [Google Scholar] [CrossRef]
- Lim, M.; Hastie, T. Learning interactions via hierarchical group lasso regularization. J. Comput. Graph. Stat. 2015, 24, 627–654. [Google Scholar] [CrossRef] [PubMed]
- Nelder, J.A. The statistics of linear models: Back to basics. Stat. Comput. 1994, 4, 221–234. [Google Scholar] [CrossRef]
- Hamada, M.; Wu, C.J. Analysis of designed experiments with complex aliasing. J. Qual. Technol. 1992, 24, 130–137. [Google Scholar] [CrossRef]
- Haris, A.; Witten, D.; Simon, N. Convex modeling of interactions with strong heredity. J. Comput. Graph. Stat. 2016, 25, 981–1004. [Google Scholar] [CrossRef] [PubMed]
- Ning, H.; Zhang, H.H. A note on high-dimensional linear regression with interactions. Am. Stat. 2017, 71, 291–297. [Google Scholar]
- Ning, H.; Yang, F.; Zhang, H.H. Model selection for high dimensional quadratic regression via regularization. J. Am. Stat. Assoc. 2018, 113, 615–625. [Google Scholar]
- She, Y.; Wang, Z.; Jiang, H. Group regularized estimation under structural hierarchy. J. Am. Stat. Assoc. 2018, 113, 445–454. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Hu, T.; Xia, Y. Adaptive semi-varying coefficient model selection. Stat. Sin. 2012, 22, 575–599. [Google Scholar] [CrossRef]
- Hunter, D.; Li, R. Variable selection using MM algorithms. Ann. Stat. 2005, 33, 1617–1642. [Google Scholar] [CrossRef]
- Craven, P.; Wahba, G. Estimating the correct degree of smoothing by the method of generalized cross-validation. Numer. Math. 1979, 31, 377–403. [Google Scholar] [CrossRef]
- Zou, H.; Li, R. One-step sparse estimates in nonconcave penalized likelihood models. Ann. Stat. 2008, 36, 1509–1533. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computating; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 16 March 2020).
- Venables, W.; Ripley, B. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2020; ISBN 0-387-95457-0. [Google Scholar]
- Harrison, D. and Rubinfeld D. Hedonic housing prices and the demand for clean air. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
| Estimator | |||
|---|---|---|---|
| 0.0684 (0.0856) | 0.0285 (0.0189) | 0.0174 (0.0087) | |
| 0.0553 (0.0385) | 0.0277 (0.0181) | 0.0170 (0.0087) | |
| 0.0531 (0.0508) | 0.0309 (0.0213) | 0.0213 (0.0110) | |
| 0.0476 (0.0406) | 0.0305 (0.0211) | 0.0211 (0.0107) | |
| 0.0483 (0.0403) | 0.0277 (0.0199) | 0.0183 (0.0096) | |
| 0.0410 (0.0325) | 0.0256 (0.0167) | 0.0169 (0.0086) | |
| 0.0811 (0.0715) | 0.0231 (0.0256) | 0.0124 (0.0082) | |
| 0.0435 (0.0343) | 0.0198 (0.0134) | 0.0111 (0.0056) |
| Estimator | |||
|---|---|---|---|
| 0.0605 (0.0433) | 0.0332 (0.0215) | 0.0173 (0.0084) | |
| 0.0576 (0.0407) | 0.0329 (0.0212) | 0.0172 (0.0083) | |
| 0.0832 (0.0608) | 0.0428 (0.0278) | 0.0221 (0.0107) | |
| 0.0789 (0.0551) | 0.0426 (0.0270) | 0.0221 (0.0106) | |
| 0.0820 (0.0584) | 0.0411 (0.0253) | 0.0221 (0.0116) | |
| 0.0753 (0.0498) | 0.0419 (0.0254) | 0.0225 (0.0117) | |
| 0.0866 (0.0882) | 0.0358 (0.0323) | 0.0182 (0.0095) | |
| 0.0605 (0.0429) | 0.0325 (0.0212) | 0.0173 (0.0088) | |
| 0.0815 (0.0685) | 0.0329 (0.0213) | 0.0147 (0.0081) | |
| 0.0658 (0.0486) | 0.0317 (0.0202) | 0.0143 (0.0077) | |
| 0.1695 (0.1023) | 0.0486 (0.0328) | 0.0185 (0.0093) | |
| 0.1123 (0.0652) | 0.0428 (0.0242) | 0.0168 (0.0082) |
| Estimator | |||
|---|---|---|---|
| 0.0784 (0.0751) | 0.0357 (0.0232) | 0.0188 (0.0096) | |
| 0.0702 (0.0536) | 0.0345 (0.0224) | 0.0189 (0.0096) | |
| 0.0938 (0.0753) | 0.0483 (0.0338) | 0.0253 (0.0127) | |
| 0.0918 (0.0717) | 0.0484 (0.0334) | 0.0253 (0.0125) | |
| 0.0819 (0.0654) | 0.0435 (0.0305) | 0.0242 (0.0119) | |
| 0.0795 (0.0595) | 0.0435 (0.0297) | 0.0244 (0.0119) | |
| 0.2343 (0.1158) | 0.0658 (0.0385) | 0.0227 (0.0113) | |
| 0.2127 (0.1052) | 0.0628 (0.0367) | 0.0216 (0.0104) | |
| 0.1462 (0.1213) | 0.0734 (0.0660) | 0.0247 (0.0126) | |
| 0.1265 (0.0897) | 0.0668 (0.0483) | 0.0239 (0.0118) | |
| 0.2088 (0.1638) | 0.0933 (0.0616) | 0.0330 (0.0166) | |
| 0.1842 (0.1159) | 0.0909 (0.0534) | 0.0305 (0.0152) |
| n | CM | CZ | CS | |
|---|---|---|---|---|
| 100 | 0.922 | 0.711 | 0.658 | |
| Model 1 | 200 | 0.996 | 0.985 | 0.982 |
| 500 | 1.000 | 1.000 | 1.000 | |
| 100 | 0.884 | 0.575 | 0.524 | |
| Model 2 | 200 | 0.987 | 0.972 | 0.960 |
| 500 | 1.000 | 1.000 | 1.000 | |
| 100 | 0.932 | 0.533 | 0.517 | |
| Model 3 | 200 | 0.973 | 0.952 | 0.937 |
| 500 | 1.000 | 1.000 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Li, Y.; Feng, S. Estimation for Varying Coefficient Models with Hierarchical Structure. Mathematics 2021, 9, 132. https://doi.org/10.3390/math9020132
Li F, Li Y, Feng S. Estimation for Varying Coefficient Models with Hierarchical Structure. Mathematics. 2021; 9(2):132. https://doi.org/10.3390/math9020132
Chicago/Turabian StyleLi, Feng, Yajie Li, and Sanying Feng. 2021. "Estimation for Varying Coefficient Models with Hierarchical Structure" Mathematics 9, no. 2: 132. https://doi.org/10.3390/math9020132
APA StyleLi, F., Li, Y., & Feng, S. (2021). Estimation for Varying Coefficient Models with Hierarchical Structure. Mathematics, 9(2), 132. https://doi.org/10.3390/math9020132





