Synthetic Data Augmentation and Deep Learning for the Fault Diagnosis of Rotating Machines
Abstract
1. Introduction
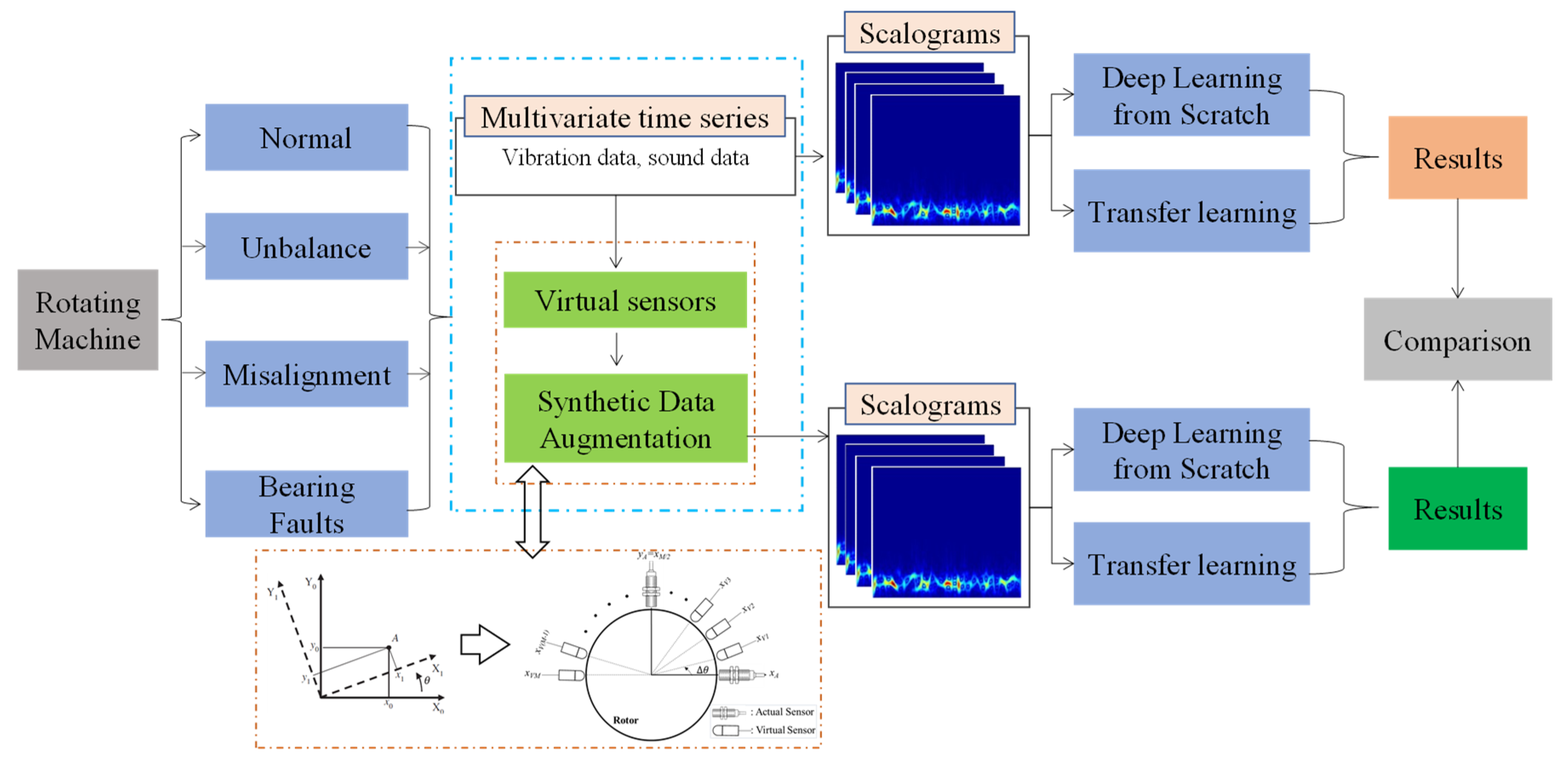
2. Proposed Methodology
2.1. Description of Dataset
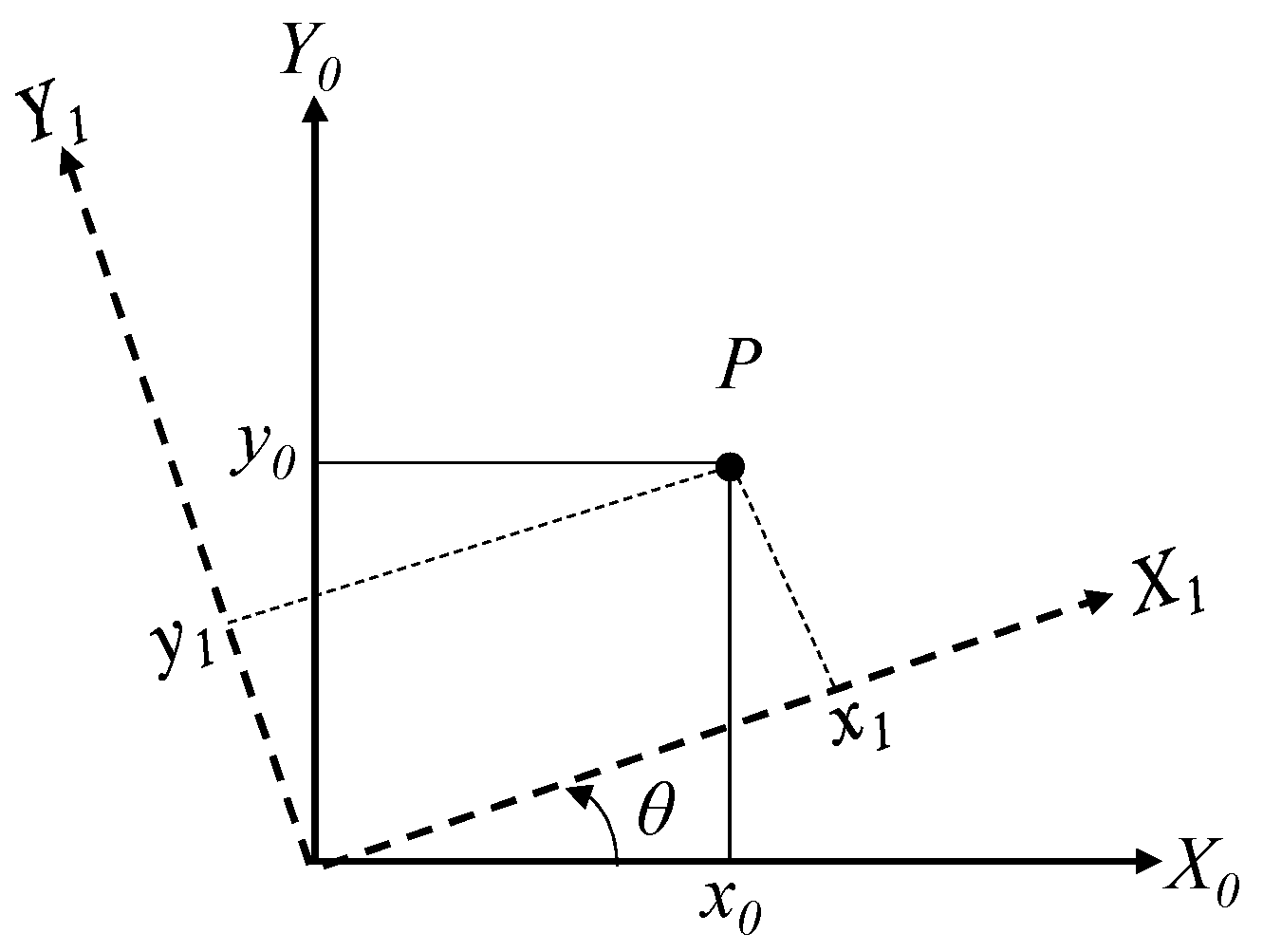
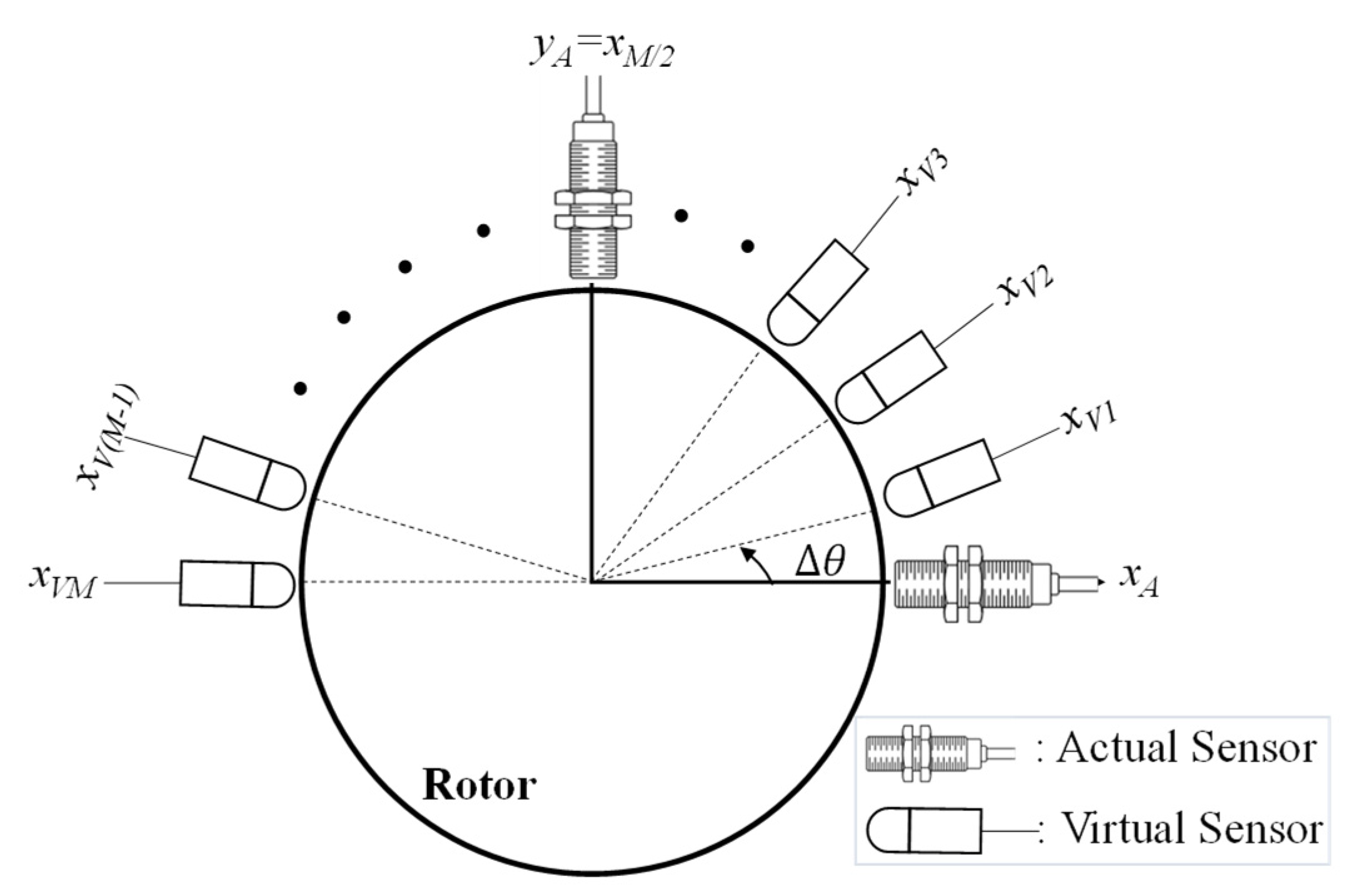
2.2. Synthetic Data Augmentation
2.3. Scalograms of Vibration Signals
3. Deep Learning Models
4. Results on the Original Data
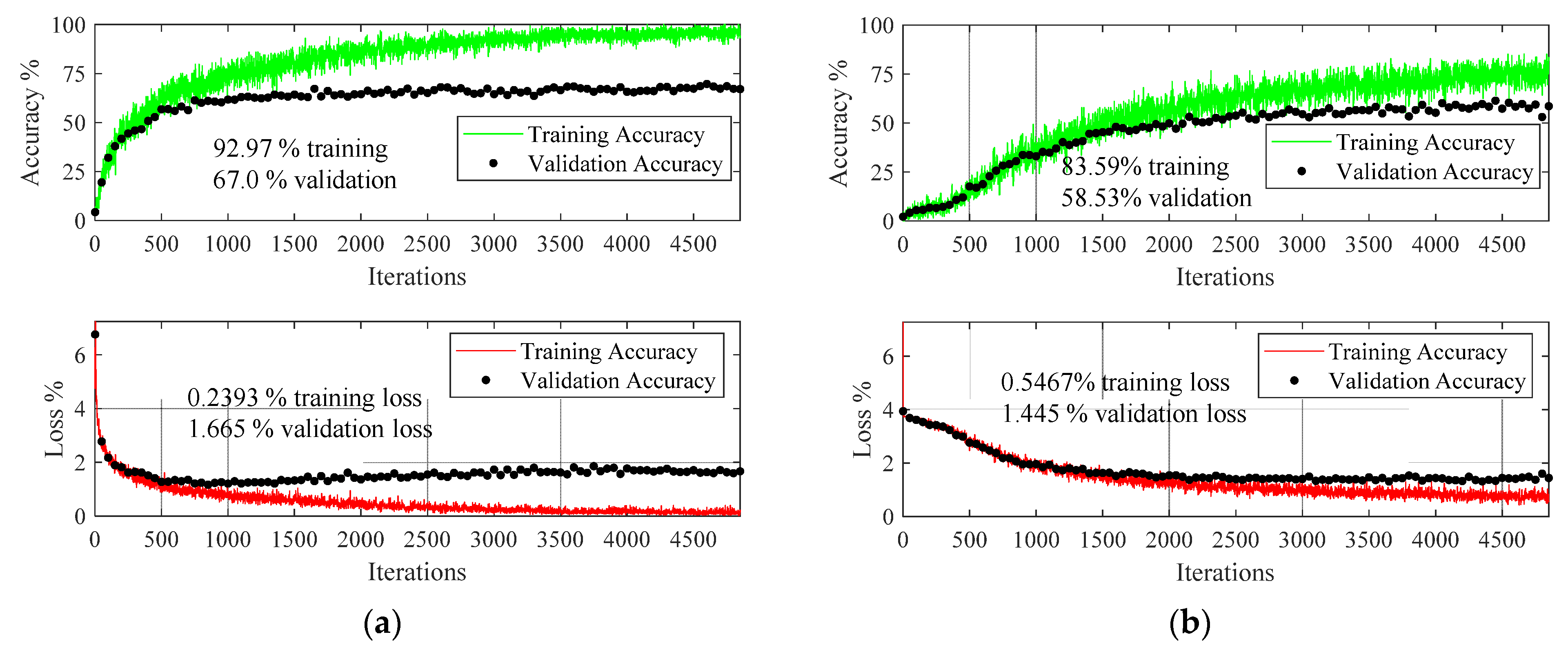
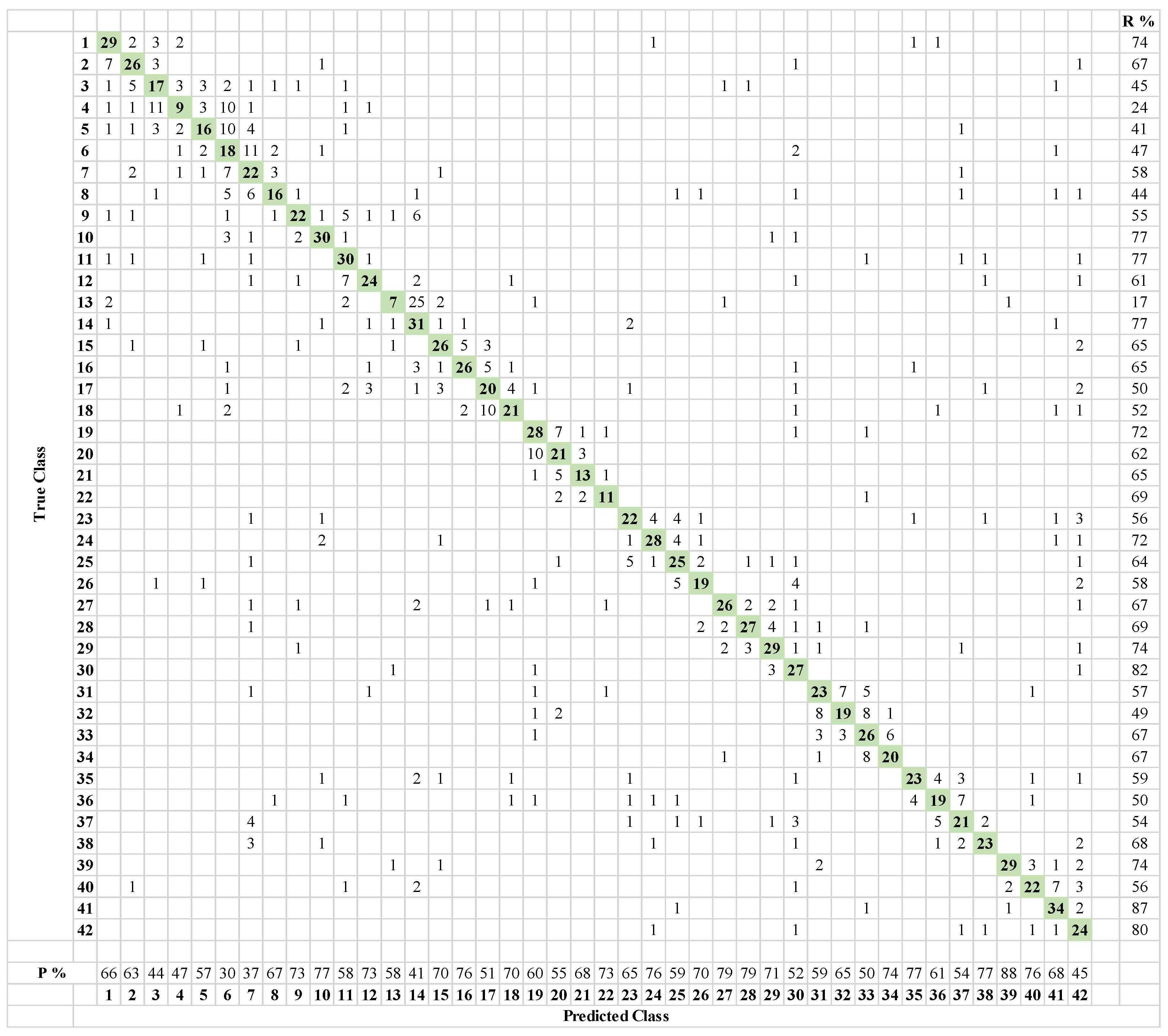
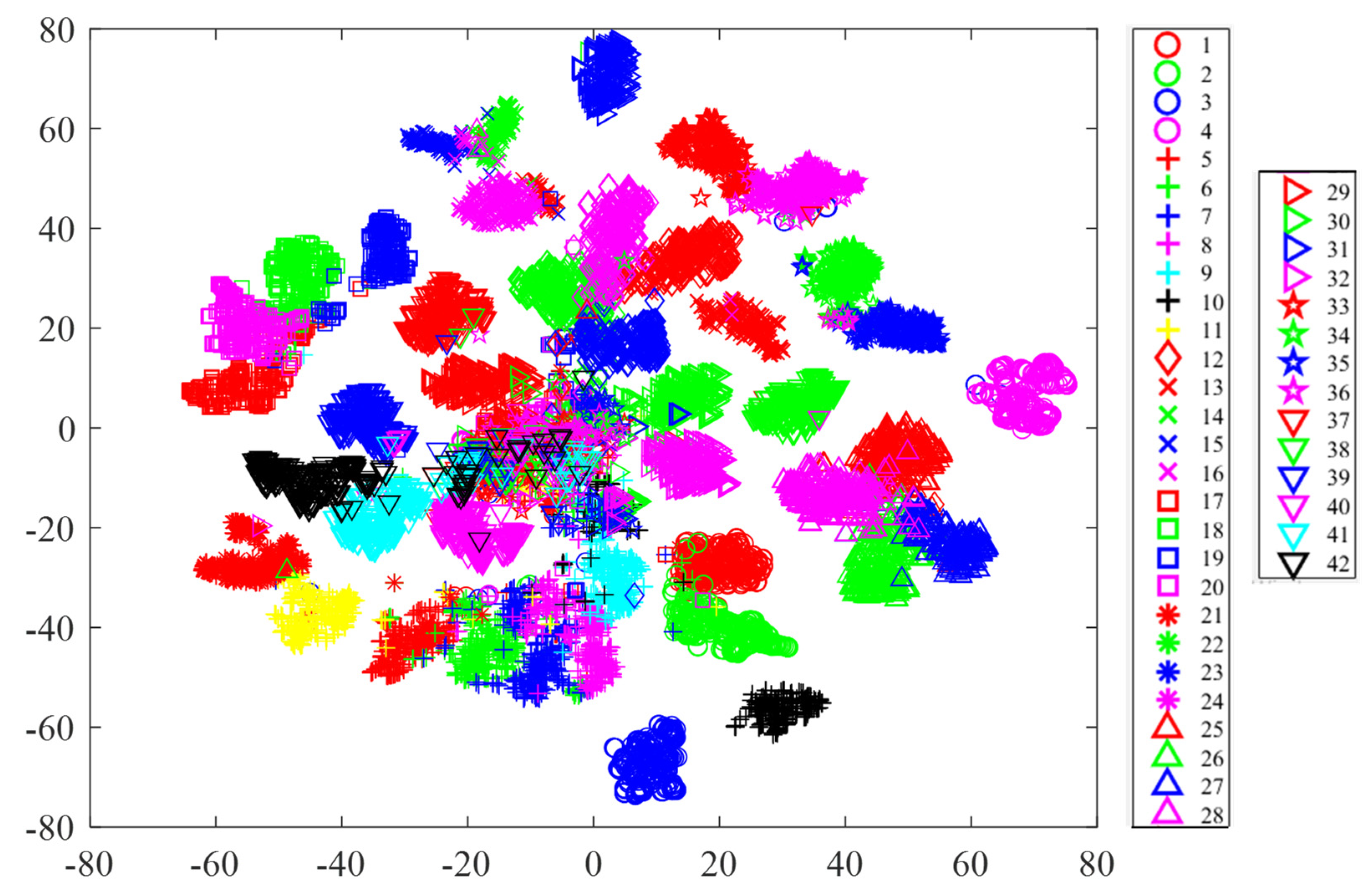
4.1. Transfer Learning Results
4.2. Results from the Customized CNN
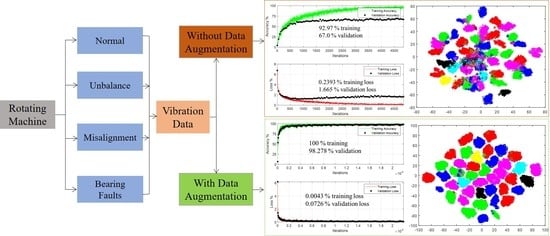
5. Results on Augmented Data
Transfer Learning via ResNet18
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Explanation |
| CNN | Convolutional Neural Network |
| PCA | Principal Component Analysis |
| t-SNE | t-Distributed Stochastic Neighbor Embedding |
| CWT | Continuous Wavelet Transform |
| ∆θ | incremental angle of rotation for virtual sensors |
| xVm | m-th virtual signal along x-axis |
| yVm | m-th virtual signal along y-axis |
| DSource | Source Dataset |
| DTarget | Target Dataset |
| Parameters of the deep learning model on source data | |
| Parameters of the deep learning model on target data | |
| γ | Rescaling parameter |
| β | Offsetting parameter |
| ReLU | Rectified Linear Unit |
References
- Liu, J.; Wang, W.; Golnaraghi, F. An Enhanced Diagnostic Scheme for Bearing Condition Monitoring. IEEE Trans. Instrum. Meas. 2010, 59, 309–321. [Google Scholar] [CrossRef]
- De Lima, A.A.; Prego, T.D.M.; Netto, S.L.; Da Silva, E.A.B.; Gutierrez, R.H.R.; Monteiro, U.A.; Troyman, A.C.R.; Silveira, F.J.D.C.; Vaz, L. On fault classification in rotating machines using fourier domain features and neural networks. In Proceedings of the 2013 IEEE 4th Latin American Symposium on Circuits and Systems (LASCAS), Cusco, Peru, 27 February–1 March 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–4. [Google Scholar]
- Li, P.; Kong, F.; He, Q.; Liu, Y. Multiscale slope feature extraction for rotating machinery fault diagnosis using wavelet analysis. Measurement 2013, 46, 497–505. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- Yang, H.; Mathew, J.; Ma, L. Vibration Feature Extraction Techniques for Fault Diagnosis of Rotating Machinery: A Literature Survey. In Proceedings of the Asia-Pacific Vibration Conference, Gold Coast, Australia, 12–14 November 2003; pp. 801–807. [Google Scholar]
- Walker, R.; Perinpanayagam, S.; Jennions, I.K. Rotordynamic Faults: Recent Advances in Diagnosis and Prognosis. Int. J. Rotating Mach. 2013, 2013, 856865. [Google Scholar] [CrossRef]
- Shen, C.; Wang, D.; Kong, F.; Tse, P.W. Fault diagnosis of rotating machinery based on the statistical parameters of wavelet packet paving and a generic support vector regressive classifier. Measurement 2013, 46, 1551–1564. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.; Xu, M.; Huang, W. A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy 2019, 21, 409. [Google Scholar] [CrossRef] [PubMed]
- Manikandan, S.; Duraivelu, K. Fault diagnosis of various rotating equipment using machine learning approaches—A review. Proc. Inst. Mech. Eng. Part E J. Process. Mech. Eng. 2021, 235, 629–642. [Google Scholar] [CrossRef]
- Kolar, D.; Lisjak, D.; Pająk, M.; Pavković, D. Fault Diagnosis of Rotary Machines Using Deep Convolutional Neural Network with Wide Three Axis Vibration Signal Input. Sensors 2020, 20, 4017. [Google Scholar]
- Qian, W.; Li, S.; Yi, P.; Zhang, K. A novel transfer learning method for robust fault diagnosis of rotating machines under variable working conditions. Measurement. 2019, 138, 514–525. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional Neural Network Based Fault Detection for Rotating Machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Rego, D.M.; Fontenla-Romero, O.; Alonso-Betanzos, A. Power wind mill fault detection via one-class ν-SVM vibration signal analysis. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 511–518. [Google Scholar]
- Li, K.; Chen, P.; Wang, S. An Intelligent Diagnosis Method for Rotating Machinery Using Least Squares Mapping and a Fuzzy Neural Network. Sensors 2012, 12, 5919–5939. [Google Scholar] [CrossRef] [PubMed]
- Umbrajkaar, A.M.; Krishnamoorthy, A.; Dhumale, R.B. Vibration Analysis of Shaft Misalignment Using Machine Learning Approach under Variable Load Conditions. Shock. Vib. 2020, 2020, 1650270. [Google Scholar] [CrossRef]
- Yan, J.; Hu, Y.; Guo, C. Rotor unbalance fault diagnosis using DBN based on multi-source heterogeneous information fusion. Procedia Manuf. 2019, 35, 1184–1189. [Google Scholar] [CrossRef]
- Cerrada, M.; Sánchez, R.-V.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vasquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Patel, R.K.; Giri, V. Feature selection and classification of mechanical fault of an induction motor using random forest classifier. Perspect. Sci. 2016, 8, 334–337. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Y.; Zhao, Z.; Wang, J. Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding. Sensors 2015, 15, 16225–16247. [Google Scholar] [CrossRef]
- Zhang, R.; Peng, Z.; Wu, L.; Yao, B.; Guan, Y. Fault Diagnosis from Raw Sensor Data Using Deep Neural Networks Considering Temporal Coherence. Sensors 2017, 17, 549. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Machine Learning and Deep Learning Algorithms for Bearing Fault Diagnostics—A Comprehensive Review. arXiv 2019, arXiv:1901.08247. [Google Scholar]
- Zhang, S.; Zhang, S.; Wang, B.; Habetler, T.G. Deep Learning Algorithms for Bearing Fault Diagnostics-a Review. In Proceedings of the 2019 IEEE 12th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Toulouse, France, 27–30 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 257–263. [Google Scholar]
- Shah, R.; Sands, T. Comparing Methods of DC Motor Control for UUVs. Appl. Sci. 2021, 11, 4972. [Google Scholar] [CrossRef]
- Sands, T. Development of Deterministic Artificial Intelligence for Unmanned Underwater Vehicles (UUV). J. Mar. Sci. Eng. 2020, 8, 578. [Google Scholar] [CrossRef]
- Jia, F.; Lei, Y.; Lu, N.; Xing, S. Deep normalized convolutional neural network for imbalanced fault classification of machinery and its understanding via visualization. Mech. Syst. Signal Process. 2018, 110, 349–367. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Data Preprocessing Techniques in Convolutional Neural Network Based on Fault Diagnosis Towards Rotating Machinery. IEEE Access 2020, 8, 149487–149496. [Google Scholar] [CrossRef]
- Dellana, R.; Roy, K. Data augmentation in CNN-based periocular authentication. In Proceedings of the 2016 6th International Conference on Information Communication and Management (ICICM), Hertfordshire, UK, 29–31 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 141–145. [Google Scholar]
- Nalepa, J.; Marcinkiewicz, M.; Kawulok, M. Data Augmentation for Brain-Tumor Segmentation: A Review. Front. Comput. Neurosci. 2019, 13, 83. [Google Scholar] [CrossRef]
- Taylor, L.; Nitschke, G. Improving Deep Learning Using Generic Data Augmentation. arXiv 2017, arXiv:1708.06020. [Google Scholar]
- Cui, Z.; Chen, W.; Chen, Y. Multi-Scale Convolutional Neural Networks for Time Series Classification. arXiv 2016, arXiv:1603.06995. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Data Augmentation Using Synthetic Data for Time Series Classification with Deep Residual Networks. arXiv 2018, arXiv:1808.02455. [Google Scholar]
- Le Guennec, A.; Malinowski, S.; Tavenard, R. Data Augmentation for Time Series Classification Using Convolutional Neural Networks. In Proceedings of the ECML/PKDD Workshop on Advanced Analytics and Learning on Temporal Data, Riva del Garda, Italy, 19–23 September 2016. [Google Scholar]
- Wen, Q.; Sun, L.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time Series Data Augmentation for Deep Learning: A Survey. arXiv 2020, arXiv:2002.12478. [Google Scholar]
- Iwana, B.K.; Uchida, S. An Empirical Survey of Data Augmentation for Time Series Classification with Neural Networks. arXiv 2021, arXiv:2007.15951. [Google Scholar]
- Fu, Q.; Wang, H. A Novel Deep Learning System with Data Augmentation for Machine Fault Diagnosis from Vibration Signals. Appl. Sci. 2020, 10, 5765. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.-Q. Intelligent rotating machinery fault diagnosis based on deep learning using data augmentation. J. Intell. Manuf. 2020, 31, 433–452. [Google Scholar] [CrossRef]
- Hu, T.; Tang, T.; Lin, R.; Chen, M.; Han, S.; Wu, J. A simple data augmentation algorithm and a self-adaptive convolutional architecture for few-shot fault diagnosis under different working conditions. Measurement 2020, 156, 107539. [Google Scholar] [CrossRef]
- Kamycki, K.; Kapuscinski, T.; Oszust, M. Data Augmentation with Suboptimal Warping for Time-Series Classification. Sensors 2019, 20, 98. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Zhang, Z.; Cui, R. Efficient Time Series Augmentation Methods. In Proceedings of the 2020 13th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Chengdu, China, 17–19 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1004–1009. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 770–778. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-Level Accuracy with 50× Fewer Parameters and <0.5 MB Model Size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Georgoulas, G.; Mustafa, M.; Tsoumas, I.; Antonino-Daviu, J.; Climente-Alarcon, V.; Stylios, C.; Nikolakopoulos, G. Principal Component Analysis of the start-up transient and Hidden Markov Modeling for broken rotor bar fault diagnosis in asynchronous machines. Expert Syst. Appl. 2013, 40, 7024–7033. [Google Scholar] [CrossRef]
- Zhu, W.; Webb, Z.T.; Mao, K.; Romagnoli, J. A Deep Learning Approach for Process Data Visualization Using t-Distributed Stochastic Neighbor Embedding. Ind. Eng. Chem. Res. 2019, 58, 9564–9575. [Google Scholar] [CrossRef]
- MAFAULDA: Machinery Fault Database [Online]. Available online: http://www02.smt.ufrj.br/~offshore/mfs/page_01.html (accessed on 18 February 2021).
- SpectraQuest Inc. Available online: https://spectraquest.com/ (accessed on 22 February 2021).
- Souza, R.M.; Nascimento, E.G.; Miranda, U.A.; Silva, W.J.; Lepikson, H.A. Deep learning for diagnosis and classification of faults in industrial rotating machinery. Comput. Ind. Eng. 2021, 153, 107060. [Google Scholar] [CrossRef]
- Marins, M.A.; Ribeiro, F.M.; Netto, S.L.; da Silva, E.A. Improved similarity-based modeling for the classification of rotating-machine failures. J. Frankl. Inst. 2018, 355, 1913–1930. [Google Scholar] [CrossRef]
- Pestana-Viana, D.; Zambrano-Lopez, R.; De Lima, A.A.; Prego, T.D.M.; Netto, S.L.; da Silva, E. The influence of feature vector on the classification of mechanical faults using neural networks. In Proceedings of the 2016 IEEE 7th Latin American Symposium on Circuits & Systems (LASCAS), Florianopolis, Brazil, 28 February–2 March 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 115–118. [Google Scholar]
- Ribeiro, F.M.; Netto, S.L.; da Silva, E.A. Application of Machine Learning to Evaluate Unbalance Severity in Rotating Machines. In Proceedings of the 10th International Conference on Rotor Dynamics–IFToMM; Springer: Seoul, Korea, 2019; Volume 2, p. 144. [Google Scholar]
- Ali, M.A.; Bingamil, A.A.; Jarndal, A.; Alsyouf, I. The Influence of Handling Imbalance Classes on the Classification of Mechanical Faults Using Neural Networks. In Proceedings of the 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Zallaq, Bahrain, 15–17 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Saufi, S.R.; Bin Ahmad, Z.A.; Leong, M.S.; Lim, M.H. Differential evolution optimization for resilient stacked sparse autoencoder and its applications on bearing fault diagnosis. Meas. Sci. Technol. 2018, 29, 125002. [Google Scholar] [CrossRef]
- Jung, J.H.; Jeon, B.C.; Youn, B.D.; Kim, M.; Kim, D.; Kim, Y. Omnidirectional regeneration (ODR) of proximity sensor signals for robust diagnosis of journal bearing systems. Mech. Syst. Signal Process. 2017, 90, 189–207. [Google Scholar] [CrossRef]
- Sands, T. Virtual Sensoring of Motion Using Pontryagin’s Treatment of Hamiltonian Systems. Sensors 2021, 21, 4603. [Google Scholar] [CrossRef]
- Srivastava, A.; Oza, N.; Stroeve, J. Virtual sensors: Using data mining techniques to efficiently estimate remote sensing spectra. IEEE Trans. Geosci. Remote. Sens. 2005, 43, 590–600. [Google Scholar] [CrossRef]
- Van Der Auweraer, H.; Tamarozzi, T.; Risaliti, E.; Sarrazin, M.; Croes, J.; Forrier, B.; Naets, F.; Desmet, W. Virtual Sensing Based on Design Engineering Simulation Models. In Proceedings of the ICEDyn2017, Ericeira, Portugal, 3–5 July 2017; pp. 1–16. [Google Scholar]
- Zaidan, M.A.; Motlagh, N.H.; Fung, P.L.; Lu, D.; Timonen, H.; Kuula, J.; Niemi, J.V.; Tarkoma, S.; Petaja, T.; Kulmala, M.; et al. Intelligent Calibration and Virtual Sensing for Integrated Low-Cost Air Quality Sensors. IEEE Sens. J. 2020, 20, 13638–13652. [Google Scholar] [CrossRef]
- Guo, S.; Yang, T.; Gao, W.; Zhang, C. A Novel Fault Diagnosis Method for Rotating Machinery Based on a Convolutional Neural Network. Sensors 2018, 18, 1429. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.; Lundgren, J. Drill Fault Diagnosis Based on the Scalogram and Mel Spectrogram of Sound Signals Using Artificial Intelligence. IEEE Access 2020, 8, 203655–203666. [Google Scholar] [CrossRef]
- Xing, S.; Halling, M.W.; Meng, Q. Structural Pounding Detection by Using Wavelet Scalogram. Adv. Acoust. Vib. 2012, 2012, 805141. [Google Scholar] [CrossRef][Green Version]
- Lee, D.T.; Yamamoto, A. Wavelet Analysis: Theory and Applications. Hewlett Packard J. 1994, 45, 44. [Google Scholar] [CrossRef]
- Olhede, S.; Walden, A. Generalized Morse wavelets. IEEE Trans. Signal Process. 2002, 50, 2661–2670. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S. Higher-Order Properties of Analytic Wavelets. IEEE Trans. Signal Process. 2009, 57, 146–160. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Cao, P.; Zhang, S.; Tang, J. Preprocessing-Free Gear Fault Diagnosis Using Small Datasets with Deep Convolutional Neural Network-Based Transfer Learning. IEEE Access 2018, 6, 26241–26253. [Google Scholar] [CrossRef]
- Li, C.; Zhang, S.; Qin, Y.; Estupinan, E. A systematic review of deep transfer learning for machinery fault diagnosis. Neurocomputing 2020, 407, 121–135. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation Functions: Comparison of trends in Practice and Research for Deep Learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Khan, A.; Kim, H.S. Classification and prediction of multidamages in smart composite laminates using discriminant analysis. Mech. Adv. Mater. Struct. 2020, 1–11. [Google Scholar] [CrossRef]
- Saxe, A.M.; McClelland, J.; Ganguli, S. A mathematical theory of semantic development in deep neural networks. Proc. Natl. Acad. Sci. USA 2019, 116, 11537–11546. [Google Scholar] [CrossRef] [PubMed]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.S.; Asari, V.K. A State-of-the-Art Survey on Deep Learning Theory and Architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Huang, K.; Hussain, A.; Wang, Q.-F.; Zhang, R. Deep Learning: Fundamentals, Theory and Applications; Springer: Seoul, Korea, 2019; Volume 2. [Google Scholar]
- Rice, L.; Wong, E.; Kolter, Z. Overfitting in Adversarially Robust Deep Learning. In Proceedings of the International Conference on Machine Learning, PMLR, Vienna, Austria, 12–18 July 2020; pp. 8093–8104. [Google Scholar]
- Ying, X. An Overview of Overfitting and Its Solutions. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2019; Volume 1168, p. 022022. [Google Scholar]
- Van Der Maaten, L. Barnes-Hut-Sne. arXiv 2013, arXiv:1301.3342. [Google Scholar]


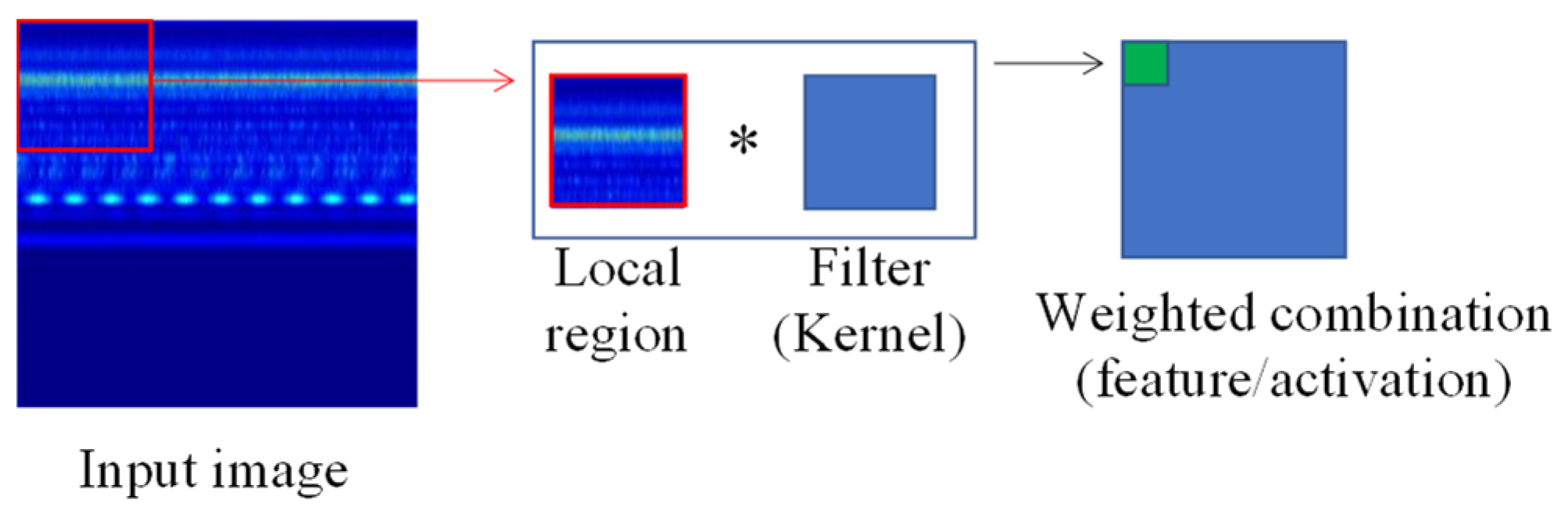



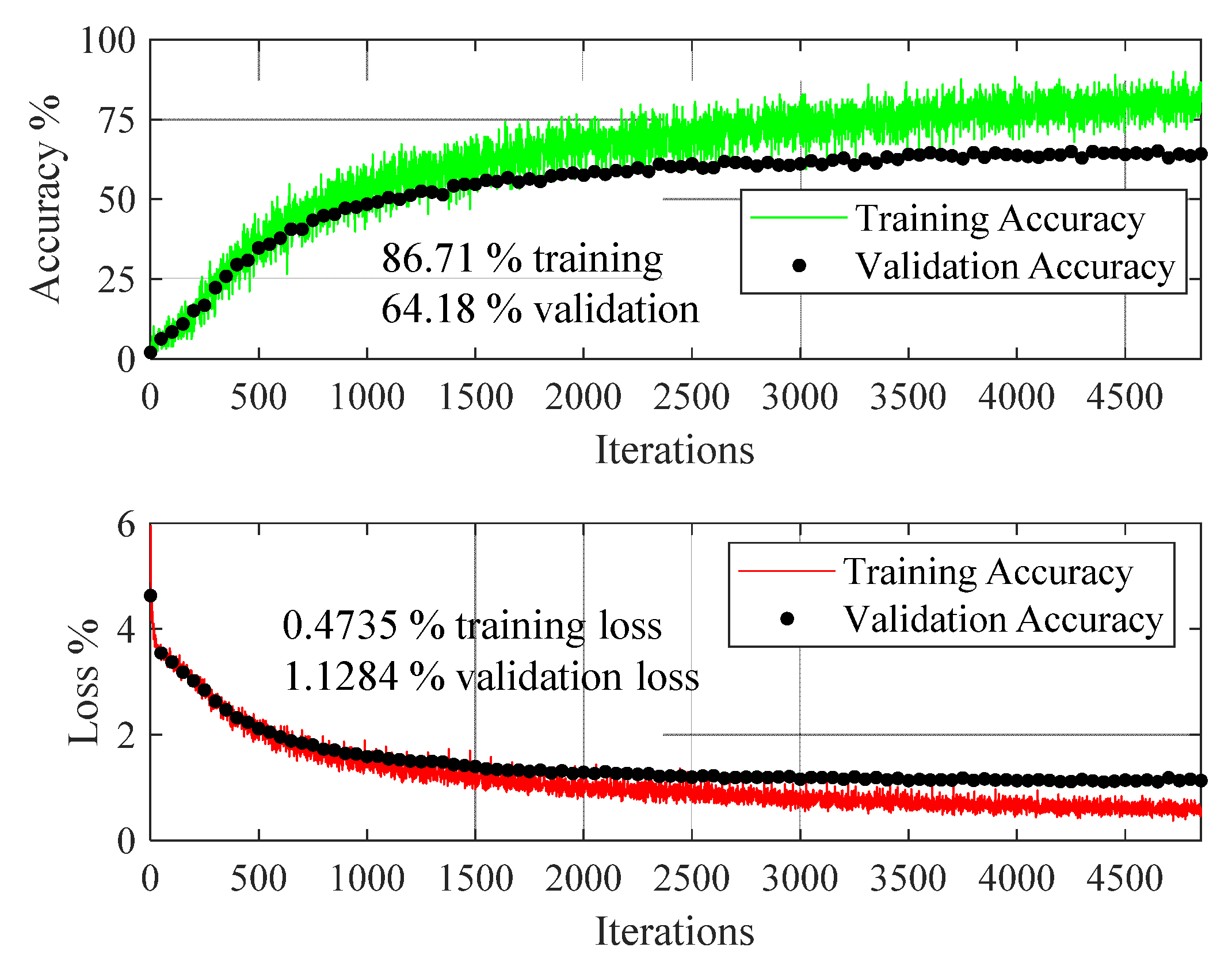
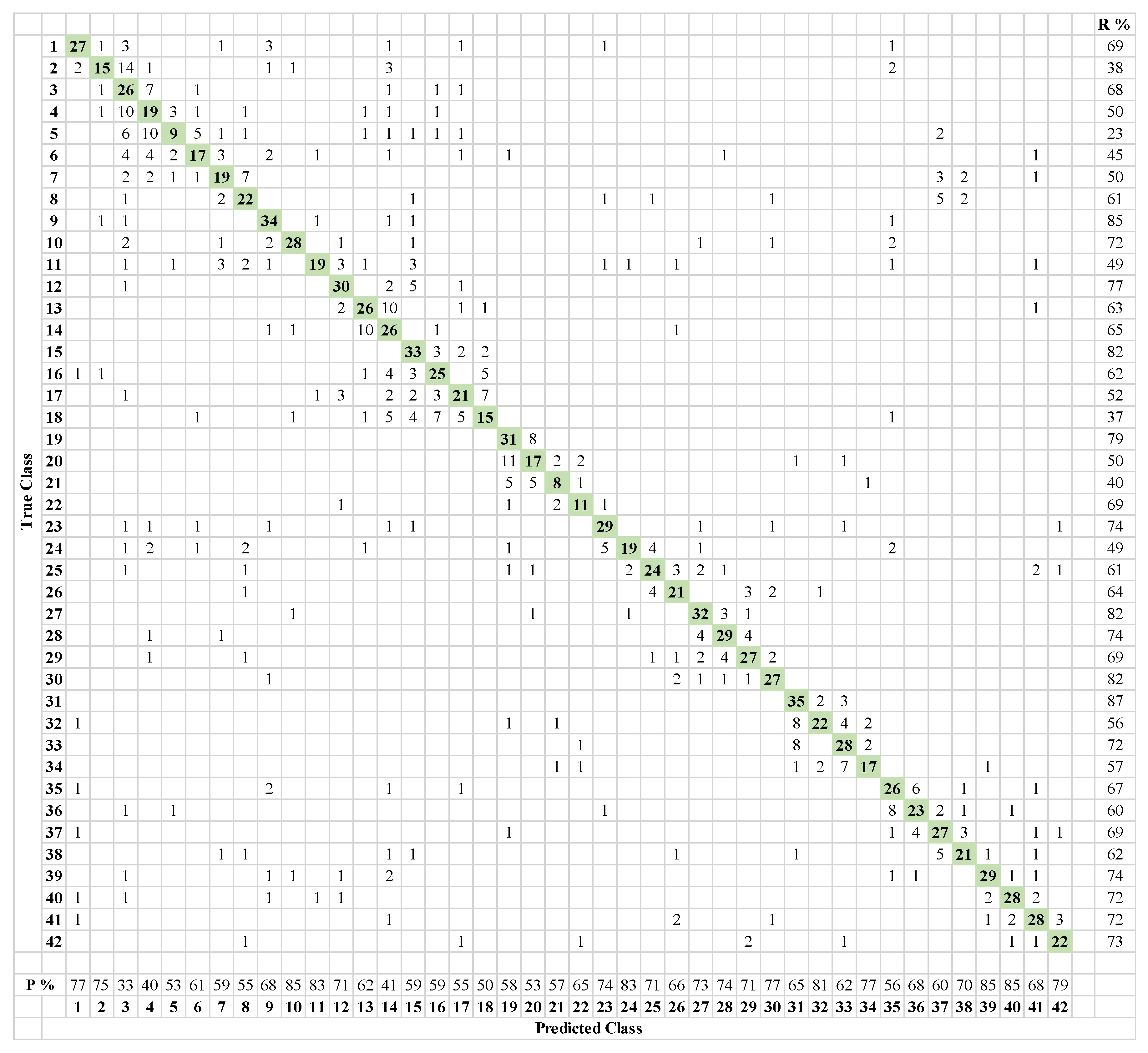
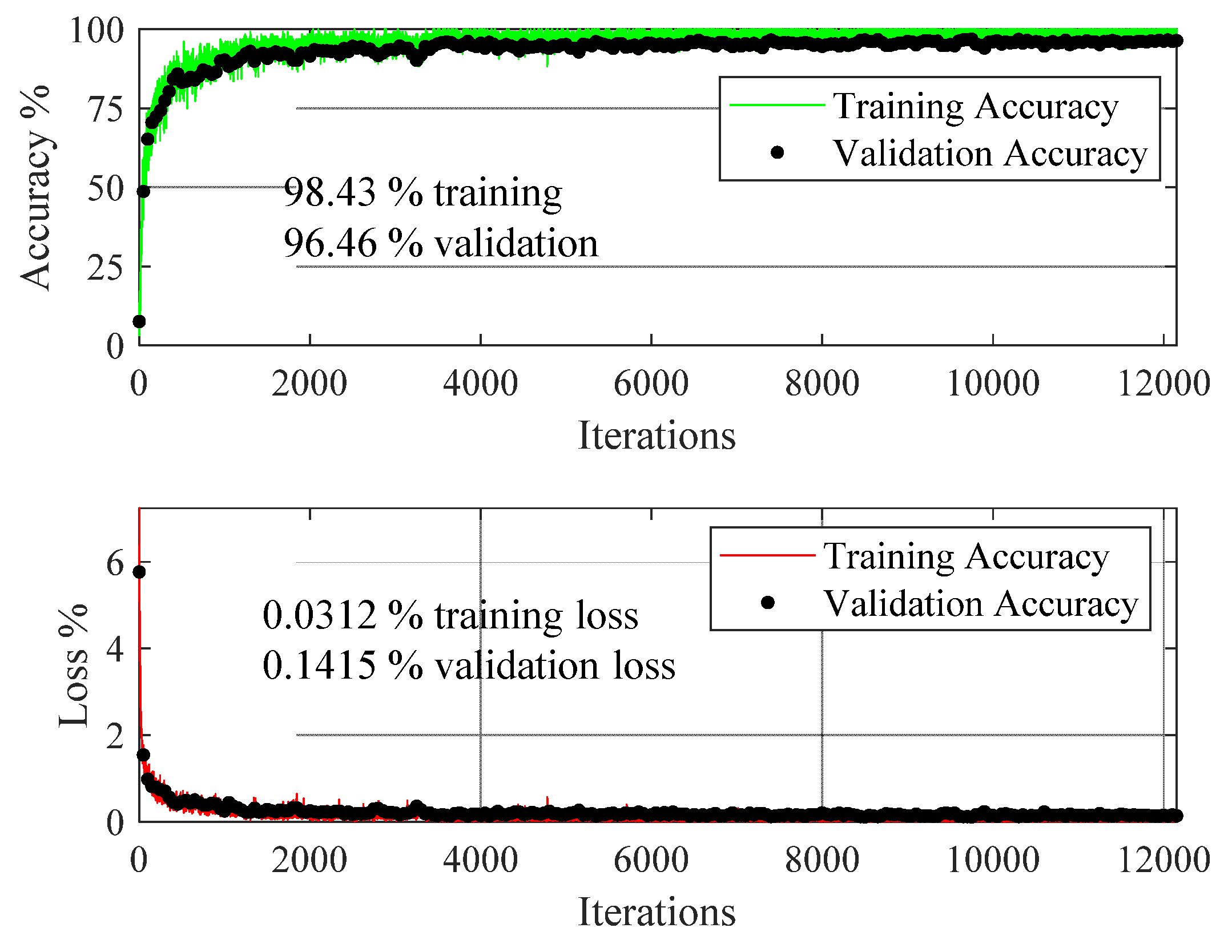
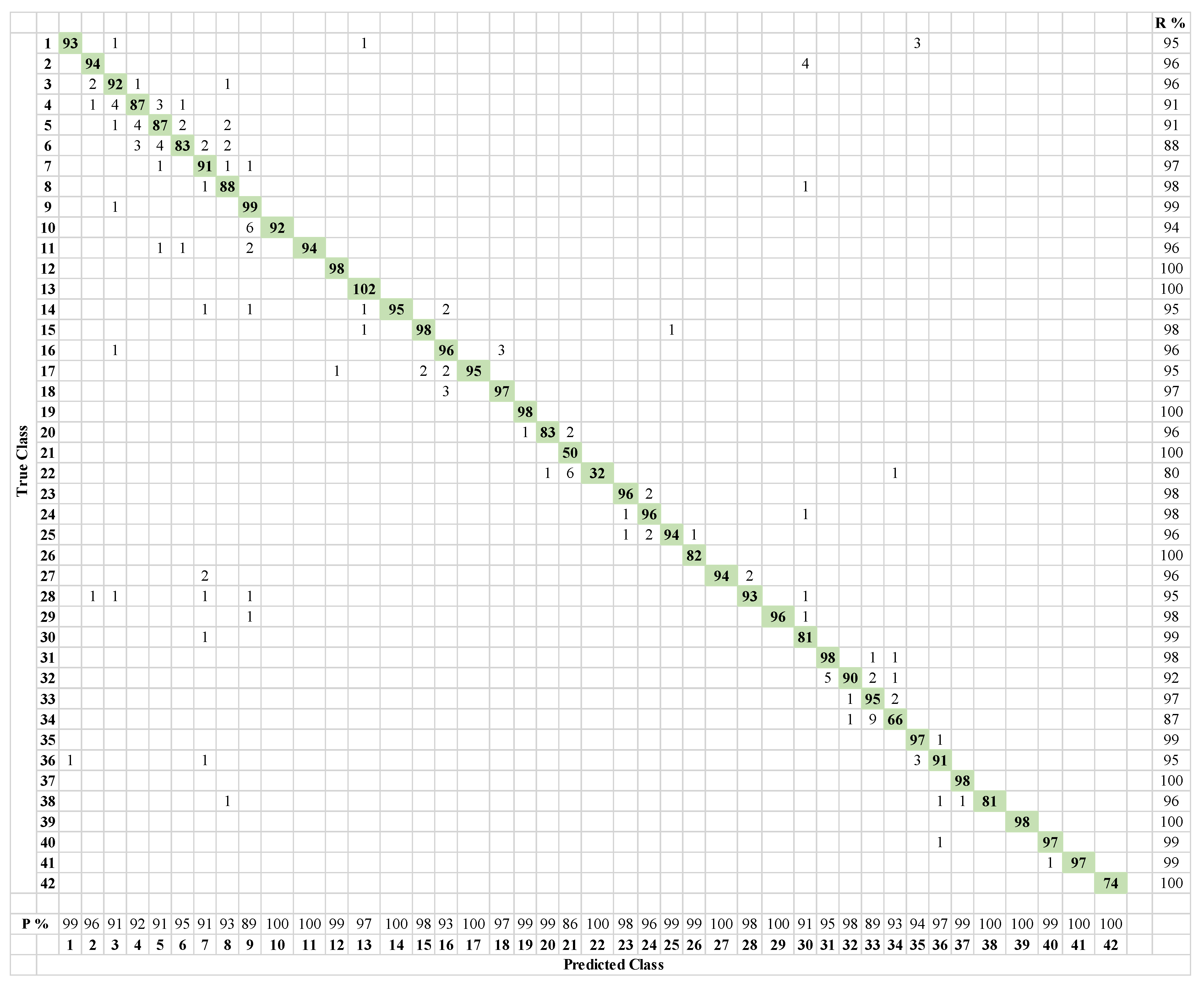
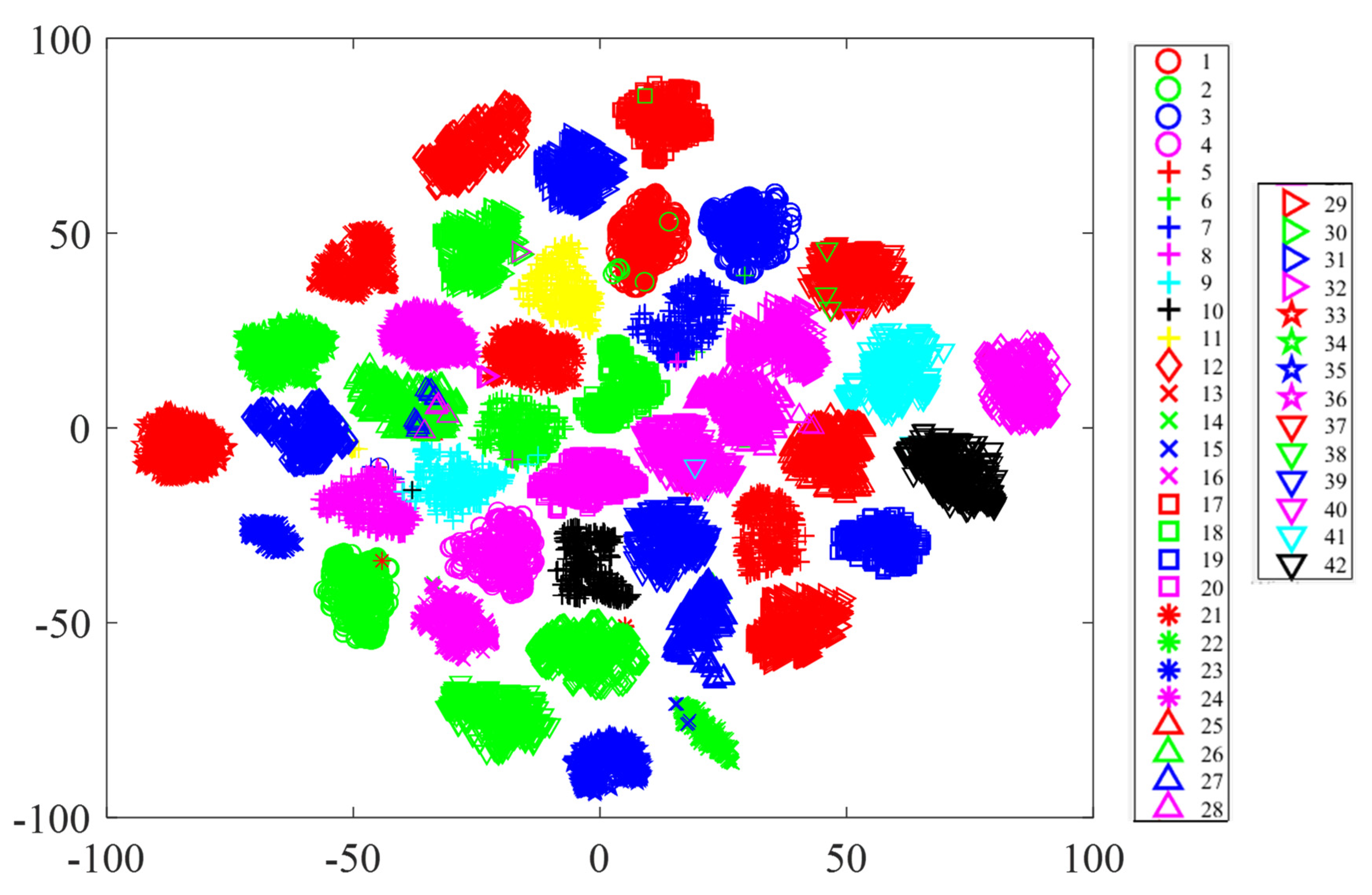
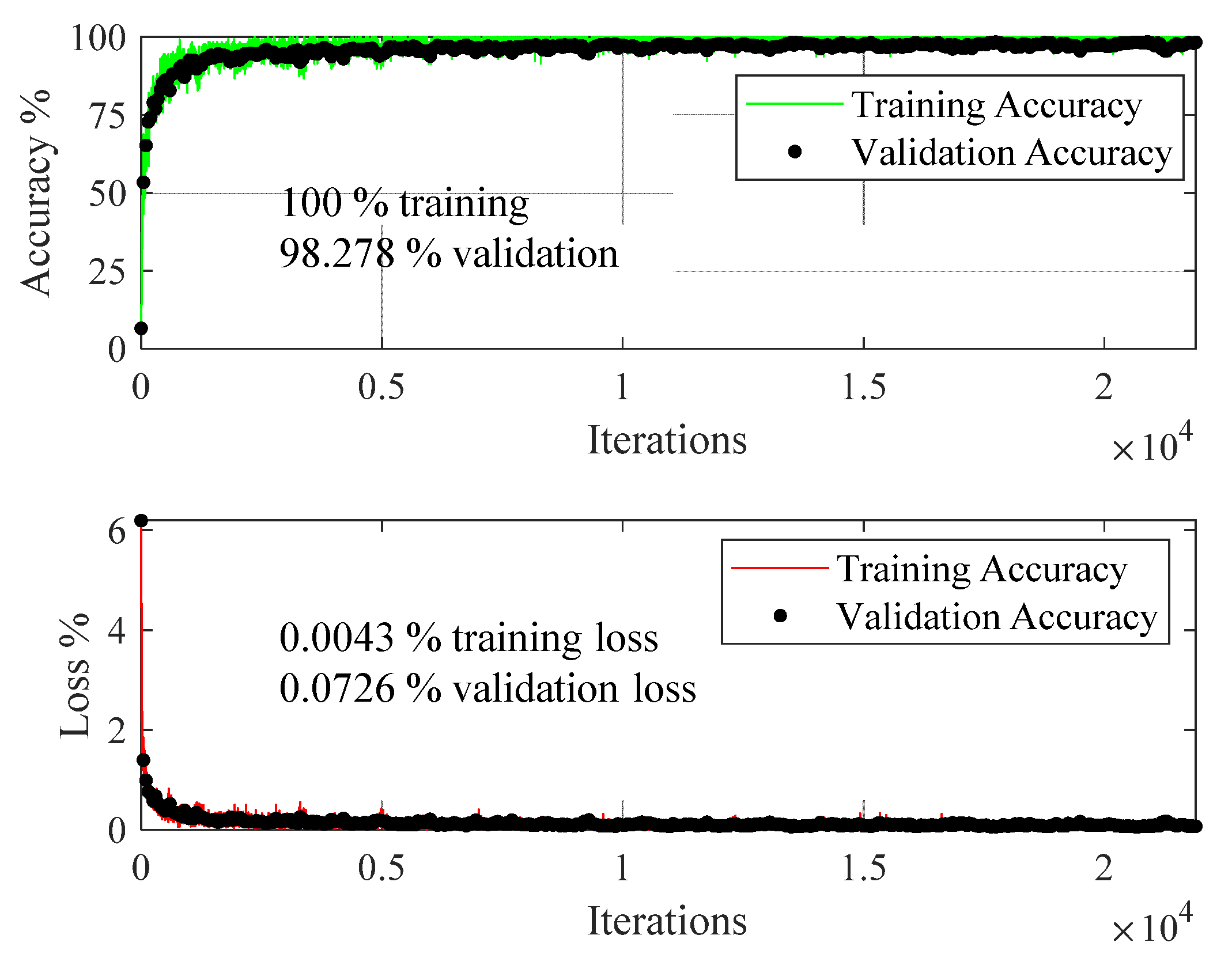
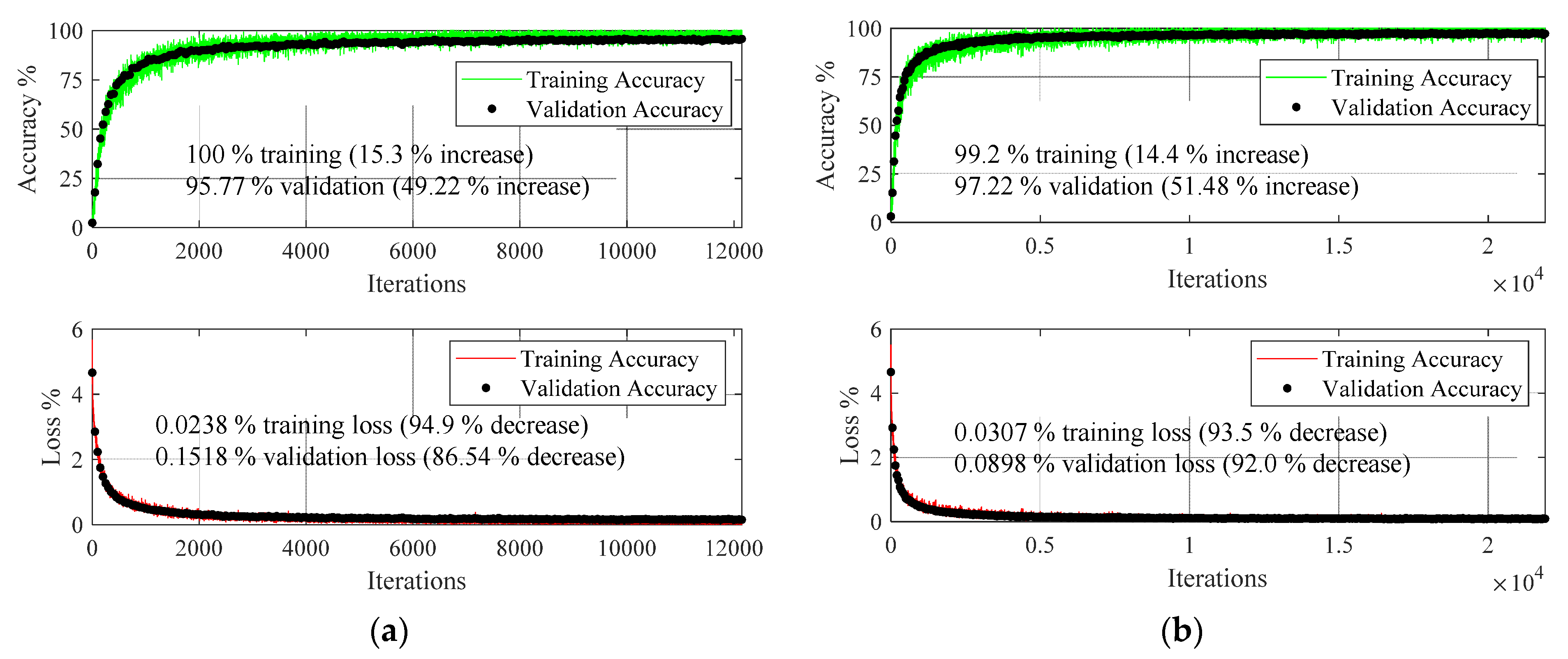
| Health State | Severity Levels | Speed of Operation and Number of Measurements |
|---|---|---|
| Normal | No fault | 49 speeds (737 to 3886 rpm) Total 49 × 8 = 392 time series |
| Unbalance | 10 g, 15 g, 20 g, 25 g, 30 g, 35 g | 6 g >> 49 speeds, 10 g >> 48 speeds, 15 g >> 48 speeds 20 g >> 49 speeds, 25 g >> 47 speeds, 30 g >> 47 speeds 35 g >> 45 speeds (Total 333 × 8 = 2664 time series) |
| Horizontal Misalignment | 0.5 mm, 1.0 mm, 1.5 mm, 2.0 mm | 0.5 mm >> 50 speeds, 1.0 mm >> 49 speeds, 1.5 mm >> 49 speeds, 2 mm >> 49 speeds (Total 197 × 8 = 1576 time series) |
| Vertical Misalignment | 0.51 mm, 0.63 mm, 1.27 mm, 1.4 mm, 1.78 mm, 1.9 mm | 0.51 mm >> 51 speeds, 0.63 mm >> 50 speeds, 1.27 mm >> 50 speeds, 1.4 mm >> 50 speeds, 1.78 mm >> 50 speeds, 1.90 mm >> 50 speeds (301 × 8 = 2408 time series) |
| Bearing Faults | Underhang Position (between rotor and motor): Outer Race fault Rolling Element fault Inner Race fault | Outer race fault: {0 g >> 49 speeds, 6 g >> 48 speeds, 20 g >> 49 speeds, 35 g >> 42 speeds (188 × 8 = 1504 time series)} Rolling element fault: {0 g >> 49 speeds, 6 g >> 49 speeds, 20 g >> 49 speeds, 35 g >> 37 speeds (184 × 8 = 1472 time series)} Inner race fault: {0 g >> 50 speeds, 6 g >> 49 speeds, 20 g >> 49 speeds, 35 g >> 38 speeds (186 × 8 = 1488 time series)} |
| Overhang Position (rotor between bearing and motor): Outer Race fault Rolling Element fault Inner Race fault | Outer race fault: {0 g >> 49 speeds, 6 g >> 49 speeds, 20 g >> 49 speeds, 35 g >> 41 speeds (188 × 8 = 1504 time series)} Rolling element fault: {0 g >> 49 speeds, 6 g >> 49 speeds, 20 g >> 49 speeds, 35 g >> 41 speeds (188 × 8 = 1504 time series)} Inner race fault: {0 g >> 49 speeds, 6 g >> 43 speeds, 20 g >> 25 speeds, 35 g >> 20 speeds (137 × 8 = 1096 time series)} |
| # | Method | Type of Features | Results | Reference |
|---|---|---|---|---|
| 1 | Similarity-based modeling | Statistical time and frequency domain features | Classification of faults in general without considering severity of different defects | [48] |
| 2 | Optimize number of features and multilayer perceptron | Statistical Features | General classification of normal, unbalance, and misalignment only, without considering severity of different defects | [49] |
| 3 | Multilayer perceptron and division of normal state data | Fourier domain features | General classification of normal, unbalance, and misalignment only, without considering severity of different defects | [2] |
| 4 | Similarity based model and kernel discriminant analysis | Feature vector from discrete-time Fourier transform, kurtosis, and entropy of signal | Categorize the unbalance health state only into high, medium, and low | [50] |
| 5 | Synthetic minority over-sampling technique for imbalance class data | Statistical features and rotational frequency | Classification of faults in general without considering severity of different defects | [51] |
| 6 | Deep learning and t-SNE | Autonomous features from wavelet scalograms | Bearing faults classification only with the effect of unbalance mass on each defect | [52] |
| 7 | Ensemble convolutional neural network (EnCNN) | Autonomous feature extraction from sensor signals | Fault classification using normal, horizontal misalignment and vertical misalignment data with severities. | [47] |
| Layer Name | Description |
|---|---|
| image input layer | 100 × 100 × 3 Scalograms |
| Convolution 1, Pooling 1 | Convolution layer (Filter 3 × 3, 16 Filters) |
| Batch Normalization | |
| ReLU layer | |
| Max-pooling Layer (Filter 2 × 2, strides 2) | |
| Convolution 2, Pooling 2, drop-out 1 | Convolution layer (Filter 3 × 3, 32 Filters) |
| Batch Normalization | |
| ReLU layer | |
| Max-pooling Layer (Filter 2 × 2, strides 2) | |
| dropout layer (0.2 drop out probability) | |
| Convolution 3, drop-out 2 | Convolution layer (Filter 3 × 3, 48 Filters) |
| Batch Normalization | |
| ReLU layer | |
| dropout layer (0.2 drop out probability) | |
| Convolution 4, Pooling 4, drop-out 3 | Convolution layer (Filter 3 × 3, 64 Filters) |
| Batch Normalization | |
| ReLU layer | |
| Max-pooling Layer (Filter 2 × 2, strides 2) | |
| dropout layer (0.2 drop out probability) | |
| Convolution 5, drop-out 5 | Convolution layer (Filter 3 × 3, 64 Filters) |
| Batch Normalization | |
| ReLU layer | |
| dropout layer (0.2 drop out probability) | |
| Convolution 6 | Convolution layer (Filter 3 × 3, 64 Filters) |
| Batch Normalization | |
| ReLU layer | |
| Global pooling | Max-pooling Layer ([1 13]) |
| Fully connected layer | 42 classes |
| classification layer | with SoftMax function for classification |
| Network | Training Accuracy% | Validation Accuracy% | Training Loss% | Validation Loss% |
|---|---|---|---|---|
| ResNet18 (8 virtual sensors) | Increased by 5.87 | Increased by 43.97 | Decreased by 86.96 | Decreased by 91.5 |
| Customized CNN (8 virtual sensors) | Increased by 7.56 | Increased by 46.68 | Decreased by 98.2 | Decreased by 95.64 |
| ResNet18 (16 virtual sensors) | Increased by 15.3 | Increased by 49.2 | Decreased by 94.9 | Decreased by 93.5 |
| Customized CNN (16 virtual sensors) | Increased by 14.4 | Increased by 41.5 | Decreased by 86.5 | Decreased by 92.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.; Hwang, H.; Kim, H.S. Synthetic Data Augmentation and Deep Learning for the Fault Diagnosis of Rotating Machines. Mathematics 2021, 9, 2336. https://doi.org/10.3390/math9182336
Khan A, Hwang H, Kim HS. Synthetic Data Augmentation and Deep Learning for the Fault Diagnosis of Rotating Machines. Mathematics. 2021; 9(18):2336. https://doi.org/10.3390/math9182336
Chicago/Turabian StyleKhan, Asif, Hyunho Hwang, and Heung Soo Kim. 2021. "Synthetic Data Augmentation and Deep Learning for the Fault Diagnosis of Rotating Machines" Mathematics 9, no. 18: 2336. https://doi.org/10.3390/math9182336
APA StyleKhan, A., Hwang, H., & Kim, H. S. (2021). Synthetic Data Augmentation and Deep Learning for the Fault Diagnosis of Rotating Machines. Mathematics, 9(18), 2336. https://doi.org/10.3390/math9182336