Abstract
The topic of similarity plays an essential role in developing students’ deductive reasoning. However, knowing how to teach similarity and understanding how to incorporate deductive reasoning and proof along with plane geometry remain a challenge to both school curriculum creators and teachers. This study identified the problems and characteristics regarding how similarity is treated in secondary mathematics textbooks in Hong Kong in the past half century. The content analysis method was used to analyze six secondary mathematics textbook series published in different periods. From the epistemological perspective of the textbook contents, our analysis shows the historical context and learning trajectories of how similarity was treated in school curriculum. The natural axiomatic geometry paradigm is not emphasized too much at different stages and most of the textbooks did not provide formal proofs of similarity. The intuitive idea was gradually consolidated into a formal definition of similarity. Furthermore, the way that rigorous geometric deduction can be performed from intuitive concepts and experimental geometry to the idea of proofs and formal proofs is also discussed.
1. Introduction
Historically, debates and changes in the goals of geometry instruction have arisen during the twentieth century [1]. One of the main goals of teaching geometry has been to help students acquire deductive reasoning as part of human culture [1,2,3]. According to commonly accepted notions, deductive reasoning is the process of inferring conclusions from known information (premises) based on formal logic rules, where conclusions are necessarily derived from the given information, and there is no need to validate them by experiments [4]. Even though deductive reasoning plays a central position in school geometry, how to teach deductive reasoning does not always have a clear process. For example, it is still not clear which concepts or definitions should be taught at the beginning stage before teaching students how to write proofs in school teaching, as well as which statement should be used as a starting point to deduce another theorem. It is also discussed whether teachers shall emphasize the rigid logic reasoning process or students’ intuitive and hands-on experience. In a recent review on geometry education in one of ICME-13 Monographs, Herbst and his colleagues found that there was attention to spatial thinking and to aspects of deductive reasoning from conjecturing to proving across different countries [5] (p. 3). New teaching approaches, such as tool-based task design, inquiry-based learning, and DGS dragging mode, have been applied to teaching secondary school geometry frequently [6]. Meanwhile, it is noted that the traditional Euclidean approaches still existed in the classroom. Thus, it remains challenging to determine how deductive geometry should be inserted back into the curriculum.
In geometry, the names of many geometrical concepts related to images do not necessarily belong to the geometrical concept, which can hinder the understanding of the concepts by using properties [7] (p. 211). For instance, similarity constitutes an equivalence relationship between shapes/figures. The topic of similarity not only connects the strand of measurement (length, angle, area, and volume) to geometric figures (shape and space) but also contributes to developing students’ processing abilities such as problem solving reasoning and proof, communications, and connections [8]. However, because the term similar is used in both mathematical and non-mathematical situations, students often have difficulties with its mathematical definition. Young children already have extensive experiences from daily life that contribute to their intuitions about similarity [9] (p. 4). That intuitive knowledge did affect their perceptions of similar shapes but was not helpful for them to conceptualize the definition of similarity [10]. In the research literature, similarity often appears in the context of proportional reasoning. In Piaget ’s research [11], the results showed that eight-year-old students could employ visual perception and pre-proportional strategies to solve similarity tasks. However, it is not always the case. Lamon [12] found that many Grade 6 students relied on visual perception strategies but not on proportional reasoning when solving problems involving similarity, even if they were able to reason correctly with proportions. Through clinical interviews, Cox [9] also found that secondary school students who could do proportional reasoning in numeric context are not doing well in similarity tasks, which emphasized the geometric nature of similarity and made it different from other contexts for reasoning. There is no doubt that proportional relationships between similar figures are essential, while how to teach similarity and how to introduce deductive reasoning to students remain difficult.
In the school curriculum, the topic of similarity usually spans several sections from daily life geometry to deductive geometry. Traditionally, the teaching of geometry in Hong Kong mainly adopts the Euclidean axiomatic approach. In the mid-1960s, like many other Asian educational regions, Hong Kong experienced the “Modern Mathematics” period (i.e., the New Math), whose motto was “down with Euclid” [13,14,15]. Some activists at the time argued that it would be more straightforward to teach logic (inclusive of deduction) via statement calculus (symbolic logic) than via traditional plane geometry [16]. Consequently, some hands-on activities were added to geometry learning, which emphasized more on experimental experience, but the effects of developing students’ deductive reasoning were not so good [17]. It was not until the middle of the 1990s that plane geometry and proofs began to be appreciated again, although the relationship between traditional teaching approaches (axiomatic approach) and other approaches (e.g., hands-on activities) was unclear. In the 2000s, spatial sense and spatial ability have been emphasized in the new curriculum reform in Hong Kong [18]. Some new topics, such as geometric transformations, symmetries, and perspective patterns, were added into the reformed mathematics curriculum [19]. In the recently revised mathematics curriculum, integration with ICT or e-learning into mathematics instruction, including geometry teaching, has been advocated [20].
However, helping students understand the geometric nature of similarity is not easy. With the erratic evolution of teaching geometry mentioned above, secondary school teachers are facing the challenge of teaching deductive reasoning that they do not know well and deciding from where they should begin to teach [19]. On the one hand, many teachers have learned geometry by the axiomatic approach and were trained in this approach in university. On the other hand, they are required to adapt to the intuitive approach, deductive approach, and analytical approach, which are advocated by the mathematics curriculum or textbooks.
The instructional approach suggested by curriculum materials including textbooks has often influenced teachers’ pedagogical strategies [21]. Stein, Remillard, and Smith argued that “what mathematical topics are covered in a given set of curriculum materials is of fundamental importance” [22] (p. 237). In this paper, we want to explore how we can incorporate deductive reasoning as well as proofs along with plane geometry. If we want to understand how to teach deductive reasoning, specifically on the topic of similarity in this study, we should know how the concept is formed and organized within the whole mathematics knowledge structure. Thus, understanding the evolution of how similarity is treated in textbooks, especially the content and arrangement at different times, can provide us with insights and inspire us to teach deductive reasoning. Using epistemological analysis, we examined the topic of similarity in six textbook series running from the 1960s (or earlier) to the present day in Hong Kong. It is hoped that reviewing how similarity has been treated can shed light on how to understand the topic within a historical context and how it can be better presented and taught in schools, not only in Hong Kong but also in other regions in the world. We also hope that the reflections on teaching deductive reasoning can be extended to other topics in the school mathematics curriculum.
2. Background of the Study and Research Questions
The teaching of geometry, apart from the spatial sense, is all about deduction. It involves both deductive reasoning and rigor in the process of deduction. Although proofs and proving play a crucial role in learning geometry [23], the difficulties in teaching and learning of proofs and proving are well-recognized internationally [24] (p. 224). Jones pointed out that the intuitive approaches and the axiomatics or formal approaches could sometimes be two extremes for teaching a chosen topic in geometry [25]. To understand the teaching of deductive reasoning in secondary school geometry, we select the topic of similarity for analysis in this study, which is one of the critical concepts of deductive geometry. To understand the nature of similarity, we should first define the concept.
2.1. Definition of Similarity in Mathematics
Among different definitions, equiangularity and proportionality of lengths are the two fundamental properties of similarity. There is a close relationship between these two properties (some may use corresponding angles and lengths) and the notion of similarity in Euclidean geometry. Seago et al. [26] called this a “static” approach to define the concept of similarity, which emphasized the proportional relationships when comparing corresponding lengths between similar figures or within similar figures. Meanwhile, for students who hold and apply a static definition of similarity, there could be a challenge for them to determine which parts of the given figures are corresponding. As shown in Figure 1, ② and ③ can be treated as equivalent to the definition of similarity, even though they are sometimes treated as definitions themselves (i.e., without ① in Figure 1). Let us look at some commonly used starting points.
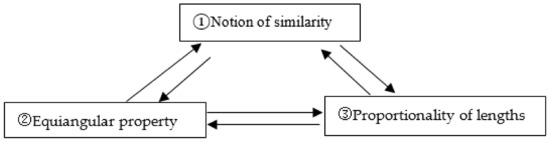
Figure 1.
The properties of similarity and their relationships.
2.1.1. Definition of Similarity in Euclid’s Elements
The classical mathematics book Elements has a great influence on the school mathematics curriculum. Definition 1 in Book 6 in the Elements provides the premise for similarity in figures [27], which is after Book 5 (the theory of proportion). It states that “[s]imilar rectilinear figures are such as have their angles severally equal and the sides about the equal angles proportional” (p. 156). Accordingly, it uses ② + ③ as the definition, without the overarching definition ①. One can also see that the definitions are confined to rectilinear figures. What remains is to show that either ② or ③ can suffice, that is, proving that ② ⬄ ③. Accordingly, in the Propositions 1 and 2 (they are the 4th and 5th propositions in the Elements) below, the context is not confined to rectilinear figures but also triangles, which makes the proofs considerably more straightforward.
Proposition 1.
In equiangular triangles, the sides about the equal angles are proportional where the corresponding sides are opposite the equal angles.
Proposition 2.
If two triangles have their sides proportional, then the triangles are equiangular with the equal angles opposite the corresponding sides.
In their book, Geometry Revised, Coxeter, and Greitzer observed that Euclidean geometry is characterized by a group of similarities [28] (p. 80), which are angle-preserving transformations. Under the umbrella of transformation, similarities are categorized into isometry, dilatations, and spiral similarities [28] (p. 101). Isometry is also called congruence transformation, which preserves the distance. Dilatation is the simplest kind of similarity, which can transform each line into a parallel line. Any dilatation is called a central dilatation because all the lines joining the corresponding points of the figure and its image are concurrent. The spiral similarity is the combination of a dilatation and a rotation about the same center, which is not a dilatation, though it is still a direct similarity [28] (p. 95). Based on the definition of spiral similarity of two triangles, Coxeter and Greitzer further noted that “[a]ny two directly similar figures are related either by a translation or by a spiral similarity” [28] (p. 97). The spiral similarity leaves one point fixed and preserves the sense of rotation (anticlockwise or clockwise), which preserves angles in both the magnitude and the sign. This is precisely the ② in Figure 1, again, without ①. As corresponding angles are mentioned, the definition is not confined to rectilinear figures.
2.1.2. The Notion of Enlargement: Similarity in 1980s’ Textbooks
It is well known that historically Euclid’s Elements is written for mature persons preparing for the study of philosophy. Euclidean geometry is only one of many geometries, each having its own primitive concepts, axioms, and theorems [28] (p. 80). One can also start with the primitive notion of enlargement (reduction inclusive) and take it as a definition, as shown in Figure 2.
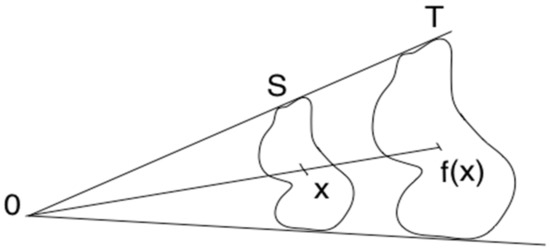
Figure 2.
Enlargement.
When spelling out in mathematical terms,
(*) S and T are similar if they can be placed in suitable positions so that there is a bijection f: S → T, a point O as well as r > 0 such that
f (O) = O and d (O, f (x)) = r d(O, x), ∀ x ∈ S.
This description has been commonly used as the definition of similarity in Hong Kong mathematics textbooks since the 1980s, as shown in Figure 3. It is illustrative, but it is not straightforward to translate such a definition into either preserving angles or preserving sides in proportion [29] (p. 86).
Figure 3.
Illustration of similarity found in a 1980s’ textbook.
A variation is as follows (without needing to find point O, or to place S and T in suitable positions):
S and T are similar if there is a bijection f: S → T as well as r > 0 such that
d(f (x), f (y)) = r d(x, y), ∀ x, y ∈ S.
This is a commonly used definition. It has several advantages. Firstly, it is not confined to rectilinear figures (and thus considers distances rather than side lengths) or figures on the same plane. Secondly, it refers to both two-dimensional and three-dimensional figures at the same time. However, like Euclid’s Elements, it is not easily understood by school-age students. In conclusion, there are three propositions that can serve as starting points for discussing the definition of similarity. They are as follows:
The definition of similarity in Euclid’s Elements used is ② + ③ [24], although this is confined to rectilinear figures. To shorten the presentation of the relation, let us call ④ be the result of ② + ③, which is “Corresponding angels and corresponding lengths in proportion”. Before we explore which of the above definitions should be used as a starting point to introduce similarity in school mathematics, we shall keep in mind that whatever is defined in geometry (mathematics) is not always the same as that adopted in textbooks. A school mathematics curriculum has its own learning objectives and trajectory, and it may be changed at different times. Textbooks are the main curriculum material. To understand and interpret the contents of textbooks, we will first introduce the epistemological analysis in mathematics education in the next session and then show how mathematics textbooks are developed in Hong Kong.
2.2. Epistemological Analysis in Mathematics Education
Epistemology is concerned with the nature of knowledge, and ways of knowing and learning about social reality, which allows us to reflect on the manner in which objects of knowledge appear in school practices, which consist of offering means through which to understand the formation of knowledge, and provides the most visibility to epistemology in teaching [30]. In mathematics education, epistemology can be taken to include both the nature of mathematical knowledge, including its means of verification, and the processes of coming to know it or learn it. Although epistemological analysis has been refined in the last 20 years [31], the function of epistemology is not always as transparent as it looks. Radford [30] pointed out that epistemological analysis cannot be conducted without attempting to show how knowledge is tied to culture and without showing the conditions of possibility of knowledge in different historical-cultural contexts.
In mathematics education, textbooks have a strong influence on the content taught and learned. Teachers’ teaching sequence is often parallel to that of textbooks [21]. Thus, the analysis of the contents in mathematics textbooks is meaningful. In this study, we analyzed the contents of similarity in textbooks by using epistemological analysis. Thus, we need to take account of the historical dimension when we reflect on the topic of similarity in textbooks. Textbook analysis can help one see how to approach the topic of similarity, how to draw some important rules or conclusions in each textbook, and the evolution of the arrangement during the periods. By addressing the historical–cultural aspects of similarity, we could become more familiar with the context we teach and the connections across different topics in school mathematics curricula.
2.3. Historical Development of Mathematics Textbooks: The Case in Hong Kong
Before proceeding to further analysis, we may briefly review the historical development of the mathematics curriculum and mathematics textbooks in Hong Kong. Like many other regions, Hong Kong experienced the Modern Mathematics period in the mid-1960s and returned to the basics in the 1980s. A target-oriented curriculum was introduced in the mid-1990s [15,32]. The mathematics curriculum underwent further revisions thereafter (The precise years have been omitted here because there are always several years of difference in the publication of a curriculum document and its initial and subsequently full implementation). Since the establishment of the Hong Kong Curriculum Development Committee in 1990, the curricula of different subjects in Hong Kong have been centrally developed by the government in consultation with the community. Before that, there was only examination syllabi. Under the Curriculum Development Committee, commercial companies have developed textbooks, but they have been required to undergo a review process. Textbooks must conform to the syllabi and the curriculum and assessment guides issued by the Curriculum Development Council (CDC). They must reflect the curriculum aims and the expected learning outcomes for the students and contain the core elements of the curriculum. During the last half century of social change, mathematics textbooks in Hong Kong have changed from being foreign-produced to being locally produced. Authors of textbooks have also been changed from local teachers and scholars to publishers.
Regardless of the stage, textbooks have always played an important role in the school curriculum. They have been the primary source of the content covered and pedagogical styles implemented in the Hong Kong classrooms. They have provided a framework for teachers to plan what to be taught, how they will teach, and what homework or activities to be assigned [33]. They have also influenced the output of teaching [34] and have provided students with opportunities to learn. Reys, Reys, Lapan, Holliday, and Wasman [21] pointed out that teachers’ pedagogical strategies have often been influenced by the instructional approaches set out in learning materials. Their sequences of instruction have often been parallel to the learning trajectory of the teaching topics in the textbooks [35,36].
Based on this understanding, we conducted a historical-epistemological analysis to determine how the topic of similarity in Hong Kong textbooks has been treated, specifically to identify the learning trajectory of the topic. Examining textbooks during different times could provide interesting and informative perspectives on deductive geometry. Specifically, there are several research questions explored in this study: (1) what have been the core characteristics of the topic at different times, and how has it changed? and (2) how can the topic be better presented and organized to teach deductive geometry? Reflecting on the topic of similarity can improve our understanding of the nature of similarity and how to teach deductive geometry, which may provide insights into teaching other topics in school mathematics.
3. Methodology
3.1. Content Analysis of Textbooks
Across different times, the nature of defining and interpreting a mathematical construct could have undergone significant epistemological shifts (i.e., the concept of function [37]). In order to know how the notion of similarity has changed, and the structure and arrangements of the concept of similarity in Hong Kong secondary mathematics textbooks, we used the content analysis method. Content analysis is a research tool of qualitative research used to determine the presence and meaning of concepts, terms, or words in one or more pieces of recorded communication [38]. Mesa emphasized that analyzing the contents in textbooks could help one discover the authors’ epistemological decisions while selecting specific content concerning what has led to the legitimization of a preferred piece of knowledge, what would students learn if they followed the text entirely, how would students construct meaning from the text in the textbooks, and what notions would the students develop by reading the text alone [39,40]. In Charalambous, Delaney, Hsu, and Mesa’s comparative analysis of primary mathematics textbooks, they found three approaches to textbook analysis, which was classified as horizontal, vertical, and contextual analysis [41]. In the horizontal analysis, the textbook is examined in the educational system, and the focus is on general textbook characteristics (e.g., physical appearance, the organization of the content across the book, etc.). The vertical analysis examines how textbooks treat a single mathematical concept and views the textbook as an environment for the construction of knowledge. The contextual analysis focuses on how textbooks are used in instructional activities by either instructors or students. In this study, because we only focused on the contents of textbooks at different periods, we adopted the horizontal and vertical analysis of textbooks and did not include the contextual approach. The horizontal analysis gives us a whole structure of the contents, and the vertical analysis offers more focused and in-depth analyses of the mathematical content.
3.2. Textbook Sampling
Mathematics education in Hong Kong went through various stages of development during British colonial rule. In the early days, the colonial government did not invest too much into Hong Kong education. Hong Kong did not have its textbooks [15]. The mathematics textbooks used in schools were imported worldwide, such as from Britain, Malaysia, and Mainland China. After the introduction of Modern Mathematics to Hong Kong, local textbooks began to appear. With the establishment of the Curriculum Development Committee, Hong Kong mathematics textbooks entered the so-called era of Basic Mathematics. After China returned to sovereignty in 1997, the Hong Kong government allowed multiple publishers to write textbooks. For example, publishers could use their own writing styles, and select their contents and teaching activities. Schools or teachers could choose the textbooks freely; however, these selected textbooks and learning materials had to be written in line with curriculum and assessment guides issued by the CDC. With these backgrounds, we chose six series (We originally analyzed eight series of textbooks. However, since those in the 1990s and 2000s are basically “isomorphic” with the current textbooks, we combined them into one category which is named “current.”) of Hong Kong mathematics textbooks from different periods to analyze the topic of similarity across half a century since the 1960s. The criteria for the textbook selection depended on the importance and popularity of the books in Hong Kong at different times. Information about the representative textbooks in different periods in Hong Kong are obtained by consulting experienced school mathematics teachers in Hong Kong. Among these, there have been four phases of development and revisions of Hong Kong mathematics textbooks across almost 50 years: 1960s, 1906s–1980s, 1980s–1990s, and 2000s–now (see Table 1).

Table 1.
Textbooks selected for analysis.
3.3. Data Analysis
Content analysis has been defined as a systematic, replicable technique for compressing many words of text into fewer content categories based on explicit rules of coding [48]. The coding process followed the ideas of the grounded theory approach [49]. At first, we analyzed the topic of similarity in previous textbooks and the current textbook, then we compared and analyzed how it has been defined in Hong Kong textbooks in different periods. To understand the notation and arrangement of similarity, selected textbooks from all four phases were studied on any chapter/section that was titled “similarity”, “similar figures”, “similar triangles”, or “similar solids”. All contents including texts, problems, examples, and exercises were considered in all selected chapters or sections. To ensure the reliability of the coding process, two coders (the first author and the second author) first selected about 10% of the sample of pages from each textbook to code the contents individually. Then, the coders compared the results to check the agreements. When there were disagreements on the coding, two coders discussed every difference to reach a consensus. Based on the agreements, the first author completed all the coding of selected textbooks.
As for the horizontal analysis, we examined the organization and sequence of the content, which included the number of units/lessons, the structure of units/lessons, topic covered, sequencing of topics, etc. For the vertical analysis, we focused on how the textbooks conveyed the concept of similarity to students, and the connection between texts, problems, examples, and exercises. Based on the analysis, we summarized the entire structure of similarity in the school curriculum and proposed two possible approaches to introducing deductive geometry at the secondary level. Specifically, the analysis of each series of textbooks included three categories: how similarity was defined (Definition), how the concept of similarity was introduced (Arrangement), and how the proof of similarity was presented (Proof). If there is a clear definition or statement about similar figures or similarity in one textbook, we will code this as Definition of Similarity. For example, in Leung, Chen, and Chan, the definition is presented as “two objects are similar if they have exactly the same shape, but not necessarily the same size.” [46] (p. 1). In Parkin, Teng, and Wills, there was a section titled as “Defining similarity”, which was followed by two statements “(1) Corresponding angles must be equal; (2) Corresponding sides must be proportional” [45] (p. 80). These two statements are coded as Definition of Similarity in this textbook. We also investigated the whole arrangement within the contents about similarity to examine the connections among different topics, including the concept of similarity, condition for similarity, and properties. Examples and exercises in each subsection in textbooks were also counted for the vertical analysis.
4. Results
4.1. Definition: How Similarity Is Defined in Mathematics Textbooks across Time?
From a historical perspective, we examined the definitions of similarity used in these selected textbooks. Details are presented in Table 2. It showed that, during different periods, there are different approaches to define the concept of similarity. Intuitive considerations (such as enlargement and reduction) were mostly adopted as a starting point by many textbooks. Some started with general figures and then moved on to triangles, while some textbooks confined to triangles at the beginning and then extended to rectilinear figures.

Table 2.
Definition of similarity in previous mathematics textbooks in different periods.
As mentioned earlier, the scope of the discussion (whether limited to rectilinear figures or even triangles) determines how easy it is to follow the definition and how restricted the notion is when it is applied. However, it is noted that, during the traditional mathematics period (I), a spiral-type approach was used. The discussion was confined to triangles from the start in Stage A (and thus made learning easier), and the whole thing was revisited in Stage B when the notion was extended to rectilinear figures. Starting with triangles and rectilinear figures and extending to other figures (and solids) was quite common in the textbooks. However, carrying the definitions and properties over without justification introduced non-rigorous arguments during learning.
4.2. Arrangement: How the Contents of Similarity Are Arranged in Textbooks?
4.2.1. How Was the Content of Similarity Arranged in Current Textbooks?
First, let us look at how a current popular Hong Kong textbook [VI] addresses the issue. Illustrations, such as those shown in Figure 3, are presented in Book 1 (which is for Secondary 1 or Grade 7 students). However, as the entire discussion is immediately confined to triangles, it becomes simple and can be easily followed by Secondary 1 students. The subsequent discussion is straightforward too, as shown in Figure 4 (In this paper, “SAS” refers to “two sides in proportion with the inscribed angles being equal.”). The arrangement and structure in Figure 4 follow the sequence of contents in the textbook.
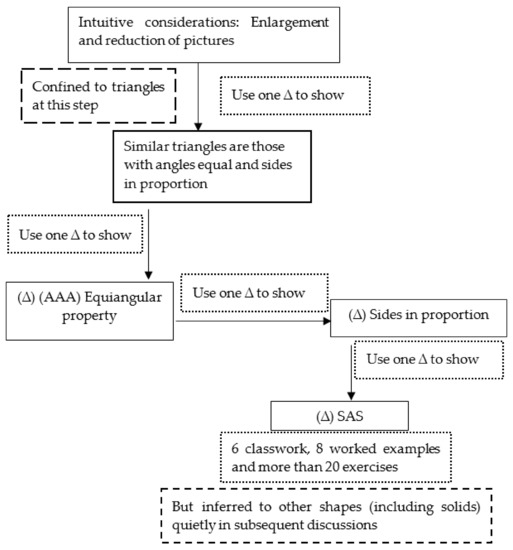
Figure 4.
Introduction of similar figures in current textbooks [47].
After inferring all the properties of other shapes (and solids) without explanation, these properties were recalled briefly in Book 3A (to be used in the first term of Secondary 3), and the students were trained to solve various problems through an abundance of exercises. Then, in Book 3B (to be used in the second term of Secondary 3), areas, surface areas, and volumes of similar figures/solids were discussed without proofs. The above flow has been found in all Hong Kong textbooks from the 1980s to the present. It has not been easy to discuss cases beyond triangles. Nonetheless, one must be able to apply these properties to the other (even non-rectilinear) figures ultimately. In the following parts, we will see how mathematics textbooks in different periods have treated the topic, and whether we can gain some inspirations from them.
4.2.2. How Was Similarity Introduced in Previous Textbooks?
After reviewing all the topics of similarity in textbooks, it was found that most of the textbooks used intuitive approaches to introducing the concept of similarity. It is not strange that these textbooks might assume that secondary students already shared an intuitive idea of what similarity is. Fischbein emphasized that the intuitive structures are essential components of every form of active understanding and of productive thinking [50]. Meanwhile, different textbooks had some subtle differences in emphasizing the intuitive experience of similarity. For example, some started with triangles (e.g., textbook [I]), while some even moved one step back to the notion of similar shapes (similar in shape but potentially not in size; “equivalence” refers to the same shape plus the same size) (e.g., textbook II and [VI]). Some used enlargements and made use of triangular grids (e.g., textbook [III]) [44] (p. 27). The target definition of the above textbooks was often introduced by a series of oral examples, physical examples, and non-examples. It is worth looking at the treatment of [I], which was first published more than 75 years ago. It initiated an oral discussion in class (Figure 5). Please note that this was more of a guideline for teachers to follow for so-called guided discovery than it was a “seat work” for the students. Specifically, it used “examples of oral discussion,” suggesting that the teacher could do more. In textbook [II], there were also some similar treatment of classroom discussion about similarity. It seems that authors were discussing the concept with readers but not told the readers directly. For example, at the beginning of the section of Similar Shapes, the textbook first raised several real-life questions for discussion [43] (pp.165–166):
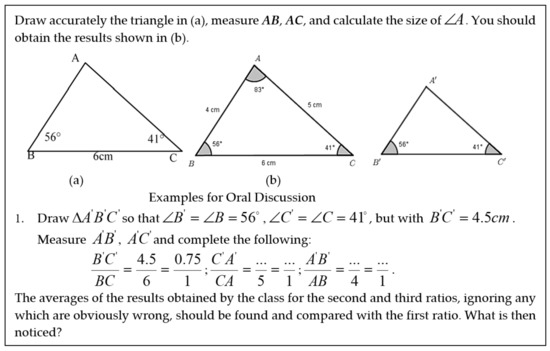
Figure 5.
Oral discussion in textbook I [42] (p. 70).
- (a)
- Are yellow and brown similar colors?
- (b)
- Are orange and red similar colors?
- (c)
- Are English and Chinese similar languages?
- (d)
- Are all the pupils in your class similar sizes?
- (e)
- Are all circles similar shapes?
- (f)
- Are all triangles similar shapes?
- (g)
- Are all equilateral triangles similar shapes?
- (h)
- Are all pencils similar?
After these questions, it suggested that students might discuss the above questions to compare what the word “similar” meant in daily life and mathematics: “in everyday use, the word ‘similar’ usually means ‘roughly the same’; in mathematics ‘similar’ has a very exact meaning” [43] (p. 166). Then, the textbook drew a statement that two objects are similar if they have exactly the same shape. The focus of discussion about “similar” has naturally shifted from daily life to mathematical figures through the discussion questions.
4.3. Proof: How Was the Proof of Similarity Introduced in Previous Textbooks
After establishing the definition of similarity, the next task is to arrive at the equivalences of different properties, as shown in Figure 4. Even if one starts with ④, which is ② + ③ (and confined to triangles), one should show that either ② or ③ is enough, i.e., one must show ② ⬄ ③. Although the formal proof can be found in the Elements (e.g., the Proposition 1 and Proposition 2 mentioned in Section 2.1), none except [VI] offered a proof. It offered a simpler proof of Proposition 5 (SSS for similarity) via the consideration of proportional line segments. Furthermore, although a detailed proof can be found in the book, only a sketch is only provided in the conclusion. In other books, ② ⬄ ③ is merely illustrated or arrived at (through inspection) via special examples.
Once ② ⬄ ③ is established, it is not too difficult (at least for those trained in mathematics) to generalize it to non-rectilinear figures by considering the triangles formed by the points under inspection (Figure 6). However, the equivalences between (*) (which has often been used as a starting point before) and others have not been commonly found in textbooks, probably because the proofs are not straightforward.
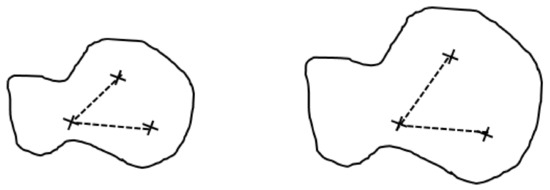
Figure 6.
Similarity in the case of non-rectilinear figures.
As discussed above, mathematical proofs have been eliminated from these textbooks. This has been the same for the topics of areas and volumes of similar figures. Some authors have simply arrived at the results for cases of rectangles/cuboids and then jumped to conclusions for other figures without any articulating sound reasons. The converse is also true. It is worth mentioning that, in [III], a proof was provided for the result (i.e., ‘for similar triangles with ratio m: n, the ratio of the areas is m2:n2’) only by using the area formula of a triangle (). This would not work if the teaching sequence of the area of the triangle formula came after the topic of similarity. Besides, [IV] devoted a separate section to the meaning of deductive geometry, which has become quite common nowadays.
4.4. Topics of Similarity and Its Structure in Geometry Curriculum
Based on the above analysis, we could ascertain the structure of the topic of similarity in secondary mathematics textbooks. The definition of similarity was introduced first. Afterwards, the conditions for checking similarity were given (and proved in some books). This was accompanied by an abundance of working examples and exercises. In some textbooks, the discussion was narrowed to rectilinear figures or even triangles in some cases. In the latter case, criteria such as “sides in proportion”, “AAA”, and even “SAS” arrived. Subsequently, various applications were introduced in the books. These applications included scales in enlargements and reductions, the pantograph, and areas/volumes of similar figures or solids. The scope of the topic in the school curriculum is summarised in Figure 7.
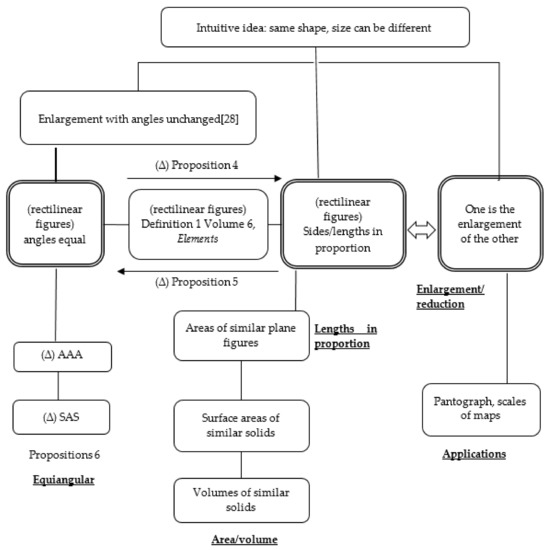
Figure 7.
The overall structure of the topic of similarity.
5. Discussion
No matter which mathematics topic is taught at school, the learning trajectory of the topic is not necessarily organized according to the knowledge structure of mathematics but has to be logical. In this study, we explored how the topic of similarity is introduced in school mathematics (geometry). The epistemological analysis is adopted. Artigue discussed three functions of epistemological analysis in teaching and learning mathematics. First, epistemology allows us to reflect on how objects of knowledge appear in school practice. The second function consists of offering a means through which to understand the formation of knowledge. The third function is the one found under the idea of epistemological obstacles, providing the most visibility to epistemology in teaching [51].
Different arrangements of the mathematical concepts in textbooks may reflect the different approaches to teaching and learning geometric. As mentioned above in the introduction, several approaches to geometry teaching, including the axiomatic, intuitive, and deductive approaches, were emphasized in the history of mathematics education. How to handle these different approaches in secondary geometry teaching is still unclear. Fishbein also expressed similar viewpoints: “The interactions and conflicts between the formal, the algorithmic, and the intuitive components of mathematical activity are very complex and usually not easily identified or understood” [52] (p. 244).
By inspecting the topic of similarity in secondary mathematics textbooks across different historical periods in Hong Kong, it was found that the approaches to teaching the concept of similarity were different at four phases. Although different textbooks had different emphases on arranging the contents of similarity, the changes were among the above three approaches. In the study, all the textbooks across different times chose the intuitive approach to teaching similar figures as the starting point. Deductive reasoning and proofs were emphasized in textbooks during the period of traditional mathematics and modern mathematics. After universal education was implemented at the end of 1970s in Hong Kong, this emphasis on formal geometric proofs in textbooks has declined. Since 2000, although there are more examples and activity experiences about similar figures in the textbooks, there was no mathematical proof of similarity and more differentiated exercises are provided for students.
The similarity is just one geometric topic in secondary school mathematics. These changes in textbooks seem to reflect a shift from the content-centered with subject knowledge focus to a student-centered with learning diversity focus, which may be related to the goals of mathematics curriculum reforms at different periods [53]. However, we may argue what kinds of geometry education we shall provide to secondary students, or what types of learning experiences students shall have when learning geometry. According to the analysis of the concept of similarity and arrangement in mathematics textbooks, the results in teaching school geometry also reflect different epistemologies of mathematics and mathematics teaching across the historical trajectory.
Recently, Kuzniak [54] ever proposed three geometric paradigms into the field of didactics of geometry to account for the different styles in school geometry education. They are natural geometry, natural axiomatic geometry, and formal axiomatic geometry. In natural geometry, valid assertions are generated by using arguments based upon perception, experiment, and deduction. Dynamic and experimental proofs are acceptable. This paradigm is close to intuitive approaches, which emphasized students’ intuitions and experiences. The natural axiomatic geometry is close to Euclidean geometry, which emphasized the deductive reasoning. The third geometric paradigm is not usual in compulsory education but is what mathematics teachers should know in teacher education [54] (pp. 10–11), which is close to the axiomatic approach. From the results, we found that the natural geometry paradigms frequently appeared at different phases. In contrast, the natural axiomatic geometry paradigm is not apparent. Several realistic situations, such as enlargement, projection, and a pantograph, were used to introduce the intuitive idea that “similarity refers to the same shape but not necessarily the same size”. Students have extensive experience in their daily lives that contribute to their intuition. This intuitive idea is gradually consolidated into a formal definition.
In the above discussion, we have pointed out the importance of the choice and domain of the definition (whether confined to triangles, rectilinear figures or otherwise). It is a disappointment that most of the textbooks investigated did not provide formal proofs of similarity. In that sense, the natural axiomatic geometry paradigm is not emphasized too much. Mathematics textbooks have a strong influence on taught and learned content. If teachers do not know the necessity of introducing a proof and do not know the logical circularity of the proof, students could lose the opportunity to understand the nature of concept (similarity) and relevant properties in context. A proof with logical circularity provides a good opportunity for students to understand what a proof is, what roles do premises have, how the two kinds of deductive reasoning work, and so on [24] (p. 237). Without these learning experience, students may get used to memorizing definitions or properties and reciting the procedures without a deep understanding of how and why it should be conducted in the suggested way.
The content analysis shows that it was more undesirable in those textbooks that some statements were either taken for granted or implied without providing good reasons for them. One example of this was discussed above. After showing that if the ratio of the corresponding lengths is m:n, then the ratio of the corresponding areas is m2:n2 for rectangles/cuboids. It was assumed that the converse is true and the same for other figures/solids. Indeed, some of these proofs might have been too difficult for younger students to understand, but it should at least be mentioned that proofs are needed (and are not being provided for the time being).
With the emphasis on deductive reasoning and geometric thinking worldwide, it has become a trend to put deductive geometry back into the school curriculum, from which it was once removed (This is not applicable to regions such as the Chinese mainland, which did not experience the Modern Mathematics movement) from the textbooks. Still, as mentioned at the start of this article, the challenge has been how to do so. In the article about intuition and proof, Fischbein suggested a synthetic approach to learn formal proof, which proposed that the intuitive and the analytical forms of knowledge shall be complementary and deeply interrelated [50]. Below, we suggest two possible ways of addressing this challenge to help teachers introduce deductive geometry.
5.1. Approach 1: Using Local Axiomatics and Experimental Geometry
When scholars such as H. Wu and W. Hsiang (Hung-Hsi Wu and Wu-Yi Hsiang are professors of mathematics at the University of California at Berkeley) suggested that deductive geometry should be re-introduced, they were not simply advocating that the topic taught in the 1950s should be reintegrated into curriculums. Instead, Wu put forth the idea of “local axiomatics”, and Hsiang suggested that the starting point should be experimental geometry. In brief, geometry deductions should not start from axioms and postulates (as the Elements did) but from some intermediate starting points. Wu specifically recommended the 22 School Mathematics Study Group axioms [55], and by incorporating Hsiang’s idea, it is found that these axioms could be established through experimental geometry. Experimental geometry indeed has been emphasized for a long time in geometry textbooks [56]. The experimental tasks have a vital role in building on pupils’ geometrical intuition effectively. Perhaps it is not realistic for teachers to conduct a real experimental task in the classroom. However, the dynamic geometry software or system will help conduct “virtual” experiments [19], which has the potential to bridge the gap between practical and deductive geometry [57]. The dynamic geometry software or system has not only provided tools for students to develop or express their understanding but also has the capacity to record students’ work through keystrokes or dragging [6,58]. These records could potentially reflect students’ thinking process which in turn helps teachers diagnose students’ learning difficulties in deductive geometry. With the rapid development of e-learning or learning management systems nowadays, it is worthy of exploring the effectiveness of further developing students’ deductive reasoning with a dynamic geometry environment.
5.2. Approach 2: Using the Idea of Proofs (Idoofs)
In an earlier research, Chazan [59] identified three aspects of similarity related to concepts that students had the most difficulty with: (1) notions of similarity; (2) proportional reasoning; and (3) dimensional growth. He pointed out that using the term “similar” could mislead students who had strongly associated images of the term learned in non-mathematical contexts.
As mentioned above, the content of deductive proof is reduced from the mathematics textbook. The reasons may be due to the difficulties of proofs or the requirement of the curriculum reform. Thus, it is important for teachers to provide students with some proof experience to enrich students’ learning opportunities in deductive proofs. If we remove all the proof from textbooks or curriculum material, there is not much left other than memorizing various formulas (the criteria for similarity in this case) by rote and then using them to tackle numerous problems. However, for average students, formal proofs are not easy for them to write and understand. A big bridge is needed to help students in writing and understanding proofs. The notion of idoof, i.e., the idea of proof, has often been put forth. If a proof is too difficult to be shown to students, it helps if the skeleton of the proof can be illustrated.
Coming back to the specific topic of similarity, if we want to teach deductive reasoning by plane geometry, having a logical flow is of utmost importance. Vollrath suggested that teaching the concept of similarity could be natural to start with similarity transformation [7] (p. 223). Indeed, in the Common Core State Standards for Mathematics (CCSSM), a “transformations-based” approach to similarity is advocated [26], which focuses on rotating, reflecting, and translating to determine congruence, and enlarging or reducing figures proportionally to create a class of similar figures. In particular, it helps us to “understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.” [60] (p. 56). The transformation-based approach is more dynamic and intuitive than a static approach. However, we may argue that this is not enough. A formal proof or even the idea of proof (idoofs) should be introduced to students. After introducing the intuitive concepts of similarity through various real-life objects, we can choose a starting point (i.e., formal definition) from which different deductive consequences (criteria for similarity in this case) can be arrived at logically, one by one. This can be achieved through formal proofs, idoofs, or even experiments, e.g., with the help of a dynamic geometry system (DGS). In fact, in the conclusion of Herbst et al.’s review [5], they proposed those new technologies could be integrated into research and practices in secondary geometry education. Technologies and tools used in teaching secondary geometry can provide students with an opportunity to investigate geometric conceptions used in solving problems and bring geometric thinking closer to what secondary students can do.
6. Conclusions
In conclusion, the analysis and results in this paper contribute to a greater understanding of how deductive reasoning and the topic of similarity is arranged in mathematics textbooks. Because the content analysis of textbooks is adopted in the study, the research findings of this work will contribute to the creation of some key design features for future mathematics textbooks. Although the study investigated some old textbooks published in different periods and some insights were gained from the contents, someone may argue that old textbooks are unlikely to be useful in informing ways of improving current teaching practice, whereas Herbst suggested that “the history of how instruction responded to past curriculum change efforts can serve as a source of information, encouragement, and caution” [3] (p. 285). Despite that this paper focuses on the evolution of mathematics textbooks in Hong Kong, these changes are also closely related to the development of mathematics curriculum in the rest of the world. The findings will also have some inspiration for mathematics teaching in other regions. There still are some limitations in the present study. Mathematics textbooks in Hong Kong have undergone an evolution over the past fifty years. Only six series of textbooks are selected for analysis. The findings from this study may not be generalizable, and they are portable. The selection of textbooks mainly relies on school teachers’ experiences, which may not reflect the actual situation in each period. We adopted the horizontal and vertical content analysis in the study. This could be deeper and the context analysis dimension could be considered in future studies.
If deductive reasoning is our objective in secondary geometry education, this purpose will not be served by rapidly generating these propositions after investigating only a couple of examples. One should refrain from transferring only those propositions shown (e.g., triangles) to other figures without explanation. To accept correctness of a mathematical proof, students need to interrelate the intuitive knowledge and analytical knowledge in productive mathematical activities. Only through this way can students be brought up in an environment where there is a reason for everything in mathematics, and where every reason shall be rational and supported by valid evidences.
Author Contributions
Conceptualization, Q.-P.Z. and N.-Y.W.; methodology, N.-Y.W.; validation, Q.-P.Z. and N.-Y.W.; formal analysis, Q.-P.Z. and N.-Y.W.; investigation, Q.-P.Z. and N.-Y.W.; resources, N.-Y.W.; writing—original draft preparation, Q.-P.Z.; writing—review and editing, N.-Y.W.; supervision, N.-Y.W. Both authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the FLASS Dean’s Research Funds, the Education University of Hong Kong, grant number Ref.: FLASS/DRF/04629.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Authors would like to thank the reviewers for their useful comments and suggestions on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- González, G.; Herbst, P. Competing arguments for the geometry course: Why were American high school students supposed to study geometry in the 20th century? Int. J. Hist. Math. Educ. 2006, 1, 7–33. [Google Scholar]
- Clements, D.H.; Battista, M.T. Geometry and spatial reasoning. In Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics; Grouws, D.A., Ed.; Macmillan: New York, NY, USA, 1992; pp. 420–464. [Google Scholar]
- Herbst, P. Establishing a custom of proving in American school geometry: Evolution of the two-column proof in the early 20th century. Educ. Stud. Math. 2002, 49, 283–312. [Google Scholar] [CrossRef]
- Ayalon, M.; Even, R. Mathematics educators’ views on mathematics learning and the development of deductive reasoning. Int. J. Sci. Math. Educ. 2010, 8, 1131–1154. [Google Scholar] [CrossRef]
- Herbst, P.; Cheah, U.H.; Richard, P.R.; Jones, K. (Eds.) International Perspectives on the Teaching and Learning of Geometry in Secondary Schools (ICME-13 Monographs); Springer: Cham, Switzerland, 2018. [Google Scholar]
- Sinclair, N.; Bartolini-Bussi, M.; Villiers, M.D.; Jones, K.; Koretenkamp, U.; Leung, A.; Owens, K. Geometry education, including the use of new technologies: A survey of recent research. In Proceedings of the 13th International Congress on Mathematical Education. ICME-13 Monographs, Hamburg, Germany, 24–31 July 2016; Kaiser, G., Ed.; Springer: Cham, Switzerland, 2017; pp. 277–287. [Google Scholar]
- Vollrath, H.J. The understanding of similarity and shape in classifying tasks. Educ. Stud. Math. 1977, 8, 211–224. [Google Scholar] [CrossRef]
- NCTM. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Cox, D.C. Similarity at the crossroads of geometry and number. Math. Think. Learn. 2013, 15, 3–23. [Google Scholar] [CrossRef]
- Kallia, M.; Panagiotis, S. The role of teaching in the development of basic concepts in geometry: How the concept of similarity and intuitive knowledge affect student’s perception of similar shapes. In Proceedings of the CERME 6, Lyon, France, 28 January–1 February 2009; Durand-Guerrier, V., Soury-Lavergne, S., Arzarello, F., Eds.; INRP: Lyon, France, 2010; pp. 736–745. [Google Scholar]
- Piaget, J. The Child’s Conception of Space; Routledge: Oxfordshire, UK, 1966. [Google Scholar]
- Lamon, S.J. Ratio and proportion: Connecting content and children’s thinking. J. Res. Math. Educ. 1983, 24, 41–61. [Google Scholar] [CrossRef]
- Dieudonné, J. New Thinking in School Mathematics; The Royaumont Seminar: Asnière-sur-Oise, France, 1959. [Google Scholar]
- Meder, A. What is wrong with Euclid? Math. Teach. 1958, 51, 578–584. [Google Scholar] [CrossRef]
- Wong, N.Y.; Tang, K.C. Mathematics education in Hong Kong under colonial rule. BSHM Bull. J. Br. Soc. Hist. Math. 2012, 27, 119–125. [Google Scholar] [CrossRef]
- Hersh, R.; John-Steiner, V. Loving and Hating Mathematics: Challenging the Myths of Mathematical Life; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Wong, N.Y. (Ed.) The Long and Winding Road of Hong Kong Mathematics Education in the Past Half a Century: Starting the Discourse from the Modern Mathematics Movement; Hong Kong Association for Mathematics Education: Hong Kong, China, 2001. (In Chinese) [Google Scholar]
- Curriculum Development Council. Mathematics Education Key Learning Area Curriculum Guide (Primary 1—Secondary 3); Hong Kong SAR Government Logistic Department: Hong Kong, China, 2002.
- Cheung, K.L.; Wong, N.Y.; Lam, C.C. Reconstructing school geometry curriculum—Why and how should deductive geometry be taught? Mathmedia 2010, 34, 13–33. (In Chinese) [Google Scholar]
- Curriculum Development Council. Mathematics Education Key Learning Area Curriculum Guide (Primary 1—Secondary 6); Hong Kong SAR Government Logistic Department: Hong Kong, China, 2017.
- Reys, R.; Reys, B.; Lapan, R.; Holliday, G.; Wasman, D. Assessing the impact of standards-based middle grades mathematics curriculum materials on student achievement. J. Res. Math. Educ. 2003, 34, 74–95. [Google Scholar] [CrossRef]
- Stein, M.; Remillard, J.; Smith, M. How curriculum influences students’ learning. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; Information Age: Charlotte, NC, USA, 2007; pp. 557–628. [Google Scholar]
- Hanna, G.; de Villiers, M. (Eds.) Aspects of proof in mathematics education. In Proof and Proving in Mathematics Education: The ICMI Study; Springer: New York, NY, USA, 2012; pp. 1–10. [Google Scholar]
- Miyazaki, M.; Fujita, T.; Jones, K. Students’ understanding of the structure of deductive proof. Educ. Stud. Math. 2017, 94, 223–239. [Google Scholar] [CrossRef] [Green Version]
- Jones, K. Deductive and intuitive approaches to solving geometrical problems. In Perspectives on the Teaching of Geometry for the 21st Century; Mammana, C., Villani, V., Eds.; Kluwer: Dordrecht, The Netherlands, 1998; pp. 78–83. [Google Scholar]
- Seago, N.M.; Jacobs, J.K.; Heck, D.J.; Nelson, C.L.; Malzahn, K.A. Impacting teachers’ understanding of geometric similarity: Results from field testing of the learning and teaching geometry professional development materials. Prof. Dev. Educ. 2014, 40, 627–653. [Google Scholar] [CrossRef]
- Fitzpatrick, R. Euclid’s Elements of Geometry. In The Greek Text of J.L. Heiberg (1883–1885) from Euclidis Element; University of Texas at Austin: Austin, TX, USA, 2007; Available online: http://farside.ph.utexas.edu/Books/Euclid/Elements.pdf (accessed on 9 August 2021).
- Coxeter, H.S.M.; Greitzer, S.L. Geometry Revisited; Mathematical Association of America: Washington, DC, USA, 1967. [Google Scholar]
- Chan, L.K.F.; Leung, C.T.; Wise, S.R. Mathematics for Hong Kong; Canotta Publishing Company: Hong Kong, China, 1988. [Google Scholar]
- Radford, L. Epistemology as a research category in mathematics teaching and learning. In The Didactics of Mathematics: Approaches and Issues; Hodgson, B.R., Kuzniak, A., Lagrange, J.B., Eds.; Springer: Cham, Switzerland, 2016; pp. 31–41. [Google Scholar]
- Barbin, E.; Stehlíková, N.; Tzanakis, C. History and Epistemology in Mathematics Education; Vydavatelský Servis: Prague, Czech, 2008. [Google Scholar]
- Wong, N.Y. The Hong Kong mathematics curriculum: 1997 × MATH × ED = Period of Change. In Reforms and Issues in School Mathematics in East Asia; Leung, F.K.S., Li, Y., Eds.; Sense Publications: Rotterdam, The Netherlands, 2010; pp. 33–57. [Google Scholar]
- Nicol, C.C.; Crespo, S.M. Learning to teach with mathematics textbooks: How preservice teachers interpret and use curriculum materials. Educ. Stud. Math. 2006, 62, 331–355. [Google Scholar] [CrossRef]
- Haggarty, L.; Pepin, B. An investigation of mathematics textbooks and their use in English, French, and German Classrooms: Who gets an opportunity to learn what? Br. Educ. Res. J. 2002, 28, 567–590. [Google Scholar] [CrossRef]
- Simon, M.; Tzur, R. Explicating the role of mathematical tasks in conceptual learning: An elaboration of the hypothetical learning trajectory. Math. Think. Learn. 2004, 6, 91–104. [Google Scholar] [CrossRef]
- Weber, E.; Walkington, C.; McGalliard, W. Expanding notions of “learning trajectories” in mathematics education. Math. Think. Learn. 2015, 17, 253–272. [Google Scholar] [CrossRef]
- Siu, M.K. Concept of function: Its history and teaching. In Learn from the Masters: Proceedings of Workshop on History of Mathematics Kristiansand; Swetz, T.F., Fauvel, J., Bekken, O., Johansson, B., Katz, V., Eds.; Mathematics Association of America: Washington DC, USA, 1995; pp. 105–121. [Google Scholar]
- Mills, A.J.; Durepos, G.; Wiebe, E. (Eds.) Encyclopedia of Case Study Research; Sage: Thousand Oaks, CA, USA, 2010; Volume 1, pp. 225–230. [Google Scholar]
- Mesa, V. Characterizing practices associated with functions in middle school textbooks: An empirical approach. Educ. Stud. Math. 2004, 56, 255–286. [Google Scholar] [CrossRef]
- Weinberg, A.; Wiesner, E. Understanding mathematics textbooks through reader-oriented theory. Educ. Stud. Math. 2011, 76, 49–63. [Google Scholar] [CrossRef]
- Charalambous, C.Y.; Delaney, S.; Hsu, H.Y.; Mesa, V. A comparative analysis of the addition and subtraction of fractions in textbooks from three countries. Math. Think. Learn. 2010, 12, 117–151. [Google Scholar] [CrossRef] [Green Version]
- Durell, C.V. A New Geometry for Schools; G. Bell & Sons Ltd.: London, UK, 1939. [Google Scholar]
- Millo, B.A.; Millo, C.A. School Mathematics Project for Hong Kong; Eastern University Press: Hong Kong, China, 1967. [Google Scholar]
- School Mathematics Monoid. Modern Mathematics; United College Press: Hong Kong, China, 1966. [Google Scholar]
- Parkin, F.; Teng, S.B.; Wills, G. New Curriculum Mathematics; Revised edition; Oxford University Press: Hong Kong, China, 1977. [Google Scholar]
- Leung, K.T.; Chen, D.L.C.; Chan, C.L. Basic Mathematics; Longman Group (Far East) Ltd.: Hong Kong, China, 1975. [Google Scholar]
- Man, P.F.; Yeung, C.M.; Yueng, K.H.; Kowk, Y.F.; Cheung, H.Y. Mathematics in Action, 2nd ed.; Pearson: Hong Kong, China, 2014. [Google Scholar]
- Krippendorff, K. Content Analysis: An Introduction to Its Methodology; Sage Publications: Newbury Park, CA, USA, 1980. [Google Scholar]
- Strauss, A.; Corbin, J.M. Basics of Qualitative Research: Grounded Theory Procedures and Techniques; Sage Publications: Thousand Oaks, CA, USA, 1990. [Google Scholar]
- Fischbein, E. Intuition and proof. For. Learn. Math. 1982, 3, 9–24. [Google Scholar]
- Artigue, M. The role of epistemology in the analysis of teaching/learning relationships in mathematics education. In Proceedings of the 1995 Annual Meeting of the Canadian Mathematics Education Study Group, Ontario, Canada, 26–30 May 1995; Pothier, Y.M., Ed.; University of Western Ontario: London, ON, Canada, 1995; pp. 7–21. [Google Scholar]
- Fischbein, E. Intuition in Science and Mathematics: An Educational Approach; Reidel: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Wong, N.Y.; Han, J.W.; Lee, P.Y. The mathematics curriculum: Towards globalisation or Westernisation? In How Chinese Learn Mathematics: Perspectives from Insiders; Fan, L., Wong, N.Y., Cai, J., Li, S., Eds.; World Scientific: Singapore, 2004; pp. 27–70. [Google Scholar]
- Kuzniak, A. Thinking about the teaching geometry through the lens of the theory of geometric working spaces. In International Perspectives on the Teaching and Learning of Geometry in Secondary Schools (ICME-13 Monographs); Herbst, P., Cheah, U.H., Richard, P.R., Jones, K., Eds.; Springer: Cham, Switzerland, 2018; pp. 5–24. [Google Scholar]
- California State Board of Education. Mathematics Framework for California Public Schools: Kindergarten through Grade Twelve; California State Board of Education: Sacramento, CA, USA, 1999.
- Fujita, T.; Jones, K. The place of experimental tasks in geometry teaching: Learning from the textbook designs of the early 20th century. Res. Math. Educ. 2003, 5, 47–62. [Google Scholar] [CrossRef] [Green Version]
- Jones, K.; Gutiérrez, A.; Mariotti, M.A. (Eds.) Proof in dynamic geometry environments: A special issue. Educ. Stud. Math. 2000, 44, 1–3. [Google Scholar] [CrossRef]
- Leung, A.; Lee, A.M.S. Students’ geometrical perception on a task-based dynamic geometry platform. Educ. Stud. Math. 2013, 82, 361–377. [Google Scholar] [CrossRef]
- Chazan, D. Similarity: Exploring the Understanding of a Geometric Concept; Technical Report 88–15; Educational Technology Center: Cambridge, MA, USA, 1998. [Google Scholar]
- Common Core State Standards Initiative. Common Core States Standards for Mathematics; National Governors Association Center for Best Practices and the Council of Chief State School Officers: Washington, DC, USA, 2010. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).