Flow Increment through Network Expansion

Abstract

The network expansion problem is a very important practical optimization problem when there is a need to increment the flow through an existing network of transportation, electricity, water, gas, etc. In this problem, the flow augmentation can be achieved either by increasing the capacities on the existing arcs, or by adding new arcs to the network. Both operations are coming with an expansion cost. In this paper, the problem of finding the minimum network expansion cost so that the modified network can transport a given amount of flow from the source node to the sink node is studied. A strongly polynomial algorithm is deduced to solve the problem.

1. Introduction

Currently, the networks around us are continuously expanded to enlarge the transport capacity of electricity, gas, water, data, etc. This can be done either by increasing the transport capacities of the wires, pipes, or the bandwidth, whenever this is possible, or by adding new connections. Of course, the increase of the capacities is restricted by an upper limit and comes with a cost. Adding new connections also has a cost.

There are two network flow optimization problems that are related to this work since they involve modifications of the capacities on arcs: the inverse and the reverse maximum flow problems. The inverse maximum flow problem is to transform a given feasible flow from a given network G into a maximum flow by modifying the capacities of G as little as possible. The distance between the initial vector of capacities and the modified one is measured using different norms. The inverse maximum flow problem under $L_{\infty }$ can be solved in a binary search manner [1]. In the case of $L_k$ norm, a strongly polynomial algorithm is deduced that mainly involves the computation of a minimum cut in a special network [2,3]. The more general case when there are losses or gains on arcs is proved to be NP-Hard [4].

The reverse maximum flow problem was studied by [5]. Here, the goal is to look for a new capacity vector such that the maximum flow value in the new network is lower bounded by a given value $v_0$, while minimizing the Chebyshev distance between the initial and the new capacity vectors. A polynomial algorithm, which works in two phases, was developed to solve this problem. In the first phase, a binary search is performed to find an interval containing the optimal value of the flow $v_0$, and, in the second phase, the Newton method [6] is used to obtain the optimal capacity vector.

In an electrical, pipeline, wireless, or road transportation network, the expansion becomes indispensable in time to increment the amount of flow that can be transported through that network [7,8,9,10,11].

The problem of network expansion under budget constraint was studied by [12]. In this problem, given a budget, a maximum possible edge capacity expansion function and a cost function for the expansion of the edge capacity, the objective is to efficiently use the budget, such that the flow in the network is maximized. The problem is known as the budget-constrained flow expansion problem (BFEP). The main idea for solving this problem is to increase the flow in the network, iteratively, by one unit, using the cheapest path from the source to the sink. At each iteration, the remaining budget is updated, and the process stops when the whole budget was used. Their solution is based on two polynomial algorithms. One algorithm returns the edges that need to be expanded in order to increase the flow by one unit at minimum cost. The second one iteratively calls the first and checks if the imposed budget limit was reached.

In the present paper, we analyze the Minimum Cost Network Expansion Problem (MCNEP). Starting with a given network G, the objective is to obtain a new network $G^{\prime }$, by increasing the capacities of the arcs from G within some given limits, or by adding new arcs, such that the cost of the modification is minimum, and in $G^{\prime }$, w units of flow can be transported from source to sink. The cost function for the capacity augmentation/arc insertion operations is a linear function with respect to the modification of the respective capacities. Both problems, MCNEP and BFEP, study the possibility of expansion of an existing network. In BFEP, there is a budget to be spend for the expansion in order to obtain a maximum flow from source to sink, and the amount of money to be spend cannot exceed the given budget. On the other hand, in MCNEP, when the maximum flow that can be transported in the given network from source to sink becomes insufficient, the network should be expanded so that a given amount of flow can be transported in the modified network, and the cost of expansion is minimized.

Our paper is organized as follows. In Section 2, we provide an overview of the network flow problem. In Section 3, the Minimum Cost Network Expansion Problem (MCNEP) is formally described and a strongly polynomial algorithm for solving this problem is presented. Section 4 provides an example and finally, Section 5 concludes our work and points out future research directions.

2. Network Flow

Let $G=(V,A,s,t,u)$ be an $s-t$ directed network, where V is the set of $n>0$ so called vertices (nodes), and $A\subseteq V\times V$ is the set of $m\ge 0$ so-called arcs (directed edges), each arc $a=(i,j)\in A$ connects two nodes i and j from V, s is a special node called source, and t is a node called sink. In G, we define the capacity function $u:A\to {\mathbb{R}}_{+}^{*}$. The value $u\left(a\right)$ is the maximum flow that can be transported from node i to node j on the arc $a=(i,j)\in A$.

If a network has multiple sources and multiple sinks, a super source and a super sink can be introduced. The super source is linked with the initial sources, and the initial sinks are linked with the super sink. The resulting $s-t$ network is equivalent with the initial one [13]. So, without restricting the generality of the problem, we shall consider from now on that the network has one source and one sink, i.e., it is an $s-t$ network.

A (feasible) flow in an $s-t$ directed network G is a function $f:A\to {\mathbb{R}}_{+}$ satisfying the boundary restrictions (1) and the conservation conditions from (2).

$$0\le f\left(a\right)\le u\left(a\right),\forall a=(i,j)\in A$$

(1)

$$\sum _{\begin{array}{c}j\in V,\\ (i,j)\in A\end{array}}f(i,j)-\sum _{\begin{array}{c}j\in V,\\ (j,i)\in A\end{array}}f(j,i)=\left\{\begin{array}{c}0,\mathrm{if}i\in V-\{s,t\}\hfill \\ v_f,\mathrm{if}i=s\hfill \\ -v_f,\mathrm{if}i=t\hfill \end{array}\right.$$

(2)

where $v_f=v\left(f\right)\ge 0$ is the so-called value of the flow f.

A feasible flow $f^{*}$ is a maximum flow if it has the maximum value among all the feasible flows in the network G, i.e.,

$$v\left(f^{*}\right)=max\{v\left(f\right)\mid f\mathrm{is}\mathrm{a}\mathrm{feasible}\mathrm{flow}\mathrm{in}G\}$$

(3)

In (3), $v\left(f^{*}\right)$ represents the maximum amount of flow that can be transported in the network G, from s to t. Now, we suppose that this value must be increased.

3. Flow Increment through Network Expansion

Since the increment of the arcs’ capacities comes with a cost, a cost function $c:A\to {\mathbb{R}}_{+}^{*}$ is introduced, where $c\left(a\right)$ is the per unit cost of modification of the capacity on the arc $a\in A$. Therefore, if the capacity of the arc a is increased with d units, the cost of changing the capacity of a is $c\left(a\right)·d$. An upper limit modification function $\alpha :A\to {\mathbb{R}}_{+}^{*}$ for the capacities is also introduced so that $u\left(a\right)+\alpha \left(a\right)$ is the maximum capacity allowed on an arc a.

Let Q be the set of arcs that can be added to the network. Of course, $Q\subseteq V\times V$, and $Q\cap A=\varphi$, i.e., $Q\subseteq V\times V-A$. A cost function $c_Q:Q\to {\mathbb{R}}_{+}^{*}$ is also introduced, where $c_Q\left(a\right)$ is the per unit cost of the capacity if the arc $a\in Q$ is added to the network. Therefore, if the arc $a\in Q$ having the capacity $u_Q\left(a\right)>0$ is introduced into the network, then the cost of adding a to the network is $c_Q\left(a\right)·u_Q\left(a\right)$. An upper limit function $\beta :Q\to {\mathbb{R}}_{+}^{*}$ for the capacities of the arcs in Q is also introduced, where $\beta \left(a\right)$ is the maximum allowed capacity for the arc $a\in Q$ if it is introduced into the network, i.e., $u_Q\left(a\right)\le \beta \left(a\right)$, where $u_Q\left(a\right)>0$ is the capacity of a.

The minimum cost expansion of the network G (by increasing the capacities of the arcs and by adding new arcs) has to be found so that in the resulting network $G^{\prime }$, w units of flow can be transported from s to t, i.e., there exists a feasible flow of value w in $G^{\prime }$. Thus, the following problem is to be solved:

$$\left\{\begin{array}{c}min\{{\displaystyle \sum _{a\in A}}(c\left(a\right)·(v\left(a\right)-u\left(a\right))+{\displaystyle \sum _{a\in Q}}(c_Q\left(a\right)·u_Q\left(a\right))\}\hfill \\ u\left(a\right)\le v\left(a\right)\le u\left(a\right)+\alpha \left(a\right),\forall a\in A\hfill \\ 0\le u_Q\left(a\right)\le \beta \left(a\right),\forall a\in Q\hfill \\ \mathrm{there}\mathrm{exists}\mathrm{a}\mathrm{feasible}\mathrm{flow}\mathrm{of}\mathrm{value}w\mathrm{in}{G}^{\prime }=(V,A^{\prime },s,t,u^{\prime })\hfill \\ A^{\prime }=A\cup \{a\in Q\mid u_Q\left(a\right)>0\}\hfill \\ u^{\prime }\left(a\right)=\left\{\begin{array}{c}v\left(a\right),a\in A\hfill \\ u_Q\left(a\right),a\in A^{\prime }-A\hfill \end{array}\right.,\forall a\in A^{\prime }\hfill \end{array}\right.$$

(4)

We shall name the problem from Equation (4) as the minimum cost network expansion problem, and denote it as MCNEP. We have the following result:

Theorem 1.

If $v\left(f^{*}\right)\ge w$, where $f^{*}$ is the maximum flow in the network G, then G is the solution of MCNEP.

Proof. 

Let $f^{*}$ be the maximum flow in the network G. We suppose that $v\left(f^{*}\right)\ge w$. It results that there exists a feasible flow f in G so that $v\left(f\right)=w$. Thus, G is a feasible solution of MCNEP. Since the cost of the objective function in Equation (4) for G is 0, it is clear that G is optimum solution for MCNEP. □

Now, let us study the feasibility of MCNEP. The maximum value of the flow that can be transported from s to t is achieved when the capacities of all the arcs from A are all increased to their maximum and all the arcs from Q are added to the network having the maximum allowed capacities, i.e., the maximum value of flow that can be transported from s to t is obtained in the network $G^{″}=(V,A\cup Q,s,t,u^{″})$, where:

$$u^{″}\left(a\right)=\left\{\begin{array}{c}u\left(a\right)+\alpha \left(a\right),a\in A\hfill \\ \beta \left(a\right),a\in Q\hfill \end{array}\right.$$

(5)

We shall call $G^{″}$ as the maximum extended network since all the capacities of the arcs from $A\cup Q$ are set to their maximum.

We have the following feasibility theorem for MCNEP:

Theorem 2.

MCNEP is feasible if and only if $v\left(g^{*}\right)\ge w$, where $g^{*}$ is a maximum flow in $G^{″}$.

Proof. 

Let us consider that MCNEP is feasible and $v\left(g^{*}\right)<w$, where $g^{*}$ is a maximum flow in $G^{″}$. Since MCNEP is feasible, it result that there is a network $G^{\prime }=(V,A^{\prime },s,t,u^{\prime })$ so that $u\left(a\right)\le u^{\prime }\left(a\right)\le u\left(a\right)+\alpha \left(a\right)$, $\forall a\in A$, $0\le u^{\prime }\left(a\right)\le \beta \left(a\right),\forall a\in Q$, and there is a feasible flow $f^{\prime }$ in $G^{\prime }$ so that $v\left(f^{\prime }\right)=w$. It is clear from (5) that $f^{\prime }$ is a feasible flow in $G^{″}$, and since $f^{*}$ is a maximum flow in $G^{″}$ the results show that $v\left(g^{*}\right)\ge v\left(f^{\prime }\right)=w$, which is a contradiction with the initial supposition that $v\left(g^{*}\right)<w$.

Now, for the inverse implication, we suppose that for the maximum flow $g^{*}$ in $G^{″}$ we have $v\left(g^{*}\right)\ge w$. It results that there is a feasible flow $f^{″}$ in $G^{″}$ so that $v\left(f^{″}\right)=w$. So, $G^{″}$ is a feasible solution for Equation (4). □

If $v\left(f^{*}\right)<w$, where $f^{*}$ is the maximum flow in the network G (G is not the solution of MCNEP, see Theorem 1) and MCNEP passes the feasibility test given by Theorem 2, a solution for MCNEP exists and has to be found. To do that, a new network denoted $G^e=(V^e,A^e,s,t,u^e,c^e)$ is constructed. The set $V^e$ contains the nodes from V, and for each arc $a\in A$, a new node denoted $i_a$ is introduced in $V^e$, i.e.,

$$V^e=V\cup V_A,V_A=\{i_a\mid a\in A\}$$

(6)

The set $A^e$ contains all the arcs from $A\cup Q$, and for each arc $a=(i,j)\in A$ two new arcs are introduced, $(i,i_a)$, and, respectively, $(i_a,j)$, i.e.,

$$A^e=A\cup Q\cup A_1^e\cup A_2^e,$$

(7)

where:

$$A_1^e=\{(i,i_a)\mid a=(i,j)\in A\},A_2^e=\{(i_a,j)\mid a=(i,j)\in A\}$$

(8)

The capacity function $u^e$ is defined as follows:

$$u^e(i,j)=\left\{\begin{array}{c}u(i,j),\mathrm{if}(i,j)\in A\hfill \\ \beta (i,j),\mathrm{if}(i,j)\in Q\hfill \\ \alpha \left(a\right),\mathrm{if}j=i_a\mathrm{or}i=i_a\mathrm{where}{i}_a\in V_A\hfill \end{array}\right.$$

(9)

The cost function $c^e$ is constructed as follows:

$$c^e(i,j)=\left\{\begin{array}{c}0,\mathrm{if}(i,j)\in A\hfill \\ c_Q(i,j),\mathrm{if}(i,j)\in Q\hfill \\ c\left(a\right)/2,\mathrm{if}j=i_a\mathrm{or}i=i_a\mathrm{where}{i}_a\in V_A\hfill \end{array}\right.$$

(10)

Let $f^e$ be a minimum cost flow of value w in $G^e$, i.e., $f^e$ is a feasible flow of value w in $G^e$ having the minimum cost among all feasible flows of value w in $G^e$, where the cost of a feasible flow f in $G^e$ denoted $c^e\left(f\right)$ is defined as follows:

$${\displaystyle c^e\left(f\right)=\sum _{a\in A^e}{c}^e\left(a\right)·f\left(a\right)}$$

(11)

The following network denoted $G^{*}=(V,A^{*},s,t,u^{*})$ is constructed, where:

$$A^{*}=A\cup A^{{*}^{\prime }},A^{{*}^{\prime }}=\{a\in Q\mid f^e\left(a\right)>0\}$$

(12)

and

$$u^{*}\left(a\right)=\left\{\begin{array}{c}u\left(a\right)+f^e(i,i_a),\mathrm{if}a\in A\hfill \\ f^e\left(a\right),\mathrm{if}a\in A^{*}-A\hfill \end{array}\right.$$

(13)

Theorem 3.

The network $G^{*}=(V,A^{*},s,t,u^{*})$ defined using Equations (12) and (13) is the optimum solution of MCNEP.

Proof. 

We recall the fact that $G^{*}$ is constructed using a minimum cost flow $f^e$ of value w calculated in the network $G^e=(V^e,A^e,s,t,u^e,c^e)$, i.e., $f^e$ is the solution of the problem:

$$\left\{\begin{array}{c}{\displaystyle min\{\sum _{a\in A^e}{c}^e\left(a\right)·f\left(a\right)\}}\hfill \\ f\mathrm{is}\mathrm{a}\mathrm{feasible}\mathrm{flow}\mathrm{of}\mathrm{value}w\mathrm{in}{G}^e\hfill \end{array}\right.$$

(14)

We have:

$$\begin{array}{c}\hfill \begin{array}{c}\sum _{a\in A^e}{c}^e\left(a\right)f^e\left(a\right)=\hfill \\ {\displaystyle =\sum _{a\in A}{c}^e\left(a\right)f^e\left(a\right)+\sum _{a\in Q}{c}^e\left(a\right)f^e\left(a\right)+\sum _{a\in A_1^e}{c}^e\left(a\right)f^e\left(a\right)+\sum _{a\in A_2^e}{c}^e\left(a\right)f^e\left(a\right)=}\hfill \\ {\displaystyle =\sum _{a\in Q}{c}_Q\left(a\right)f^e\left(a\right)+\sum _{a=(i,j)\in A}{c}^e(i,i_a)f^e(i,i_a)+\sum _{a=(i,j)\in A}{c}^e(i_a,j)f^e(i_a,j)=}\hfill \\ {\displaystyle =\sum _{a\in Q}{c}_Q\left(a\right)f^e\left(a\right)+\sum _{a=(i,j)\in A}c\left(a\right)/2(f^e(i,i_a)+f^e(i_a,j))=}\hfill \\ {\displaystyle =\sum _{a\in Q}{c}_Q\left(a\right)f^e\left(a\right)+\sum _{a=(i,j)\in A}c\left(a\right)f^e(i,i_a)=}\hfill \\ {\displaystyle =\sum _{a\in Q}{c}_Q\left(a\right)u^{*}\left(a\right)+\sum _{a\in A}c\left(a\right)(u^{*}\left(a\right)-u\left(a\right)).}\hfill \end{array}\end{array}$$

(15)

Using Equations (14) and (15), the following optimization problem is obtained:

$${\displaystyle min\{\sum _{a\in A}c\left(a\right)·(u^{*}\left(a\right)-u\left(a\right))+\sum _{a\in Q}{c}_Q\left(a\right)·u^{*}\left(a\right)\}}$$

(16)

Using Equation (13), we have:

$$0\le u^{*}\left(a\right)-u\left(a\right)=f^e(i,i_a)\le \alpha \left(a\right),\forall a\in A$$

(17)

$$0<u^{*}\left(a\right)=f^e\left(a\right)\le \beta \left(a\right),\forall a\in Q\mathrm{and}{f}^e\left(a\right)>0$$

(18)

$$0=u^{*}\left(a\right)\le \beta \left(a\right),\forall a\in Q,\mathrm{and},\mathrm{by}\mathrm{convention},f^e\left(a\right)=0.$$

(19)

We construct the following flow denoted $f^{*}$ in $G^{*}$:

$$f^{*}\left(a\right)=\left\{\begin{array}{c}{f}^e\left(a\right)+f^e(i,i_a),\mathrm{if}a\in A\hfill \\ f^e\left(a\right),\mathrm{if}a\in A^{*}-A\hfill \end{array}\right.$$

(20)

Since $f^e$ is a feasible flow in $G^e$, the results show that $f^{*}$ respects the conservation conditions in $G^{*}$, and from Equation (13) the results show that $f^{*}$ satisfies the boundary conditions in $G^{*}$. Thus, $f^{*}$ is a feasible flow in $G^{*}$. Using Equation (16)–(19) the results show that $u^{*}$ is optimum solution of Equation (4). □

Corollary 1.

The cost of network expansion from G to the optimum solution $G^{*}$ of MCNEP is $v\left(f^e\right)$, where $f^e$ is the minimum cost flow in $G^e$.

Proof. 

The result is immediate from Equation (15). □

Using Theorems 1–3, the following algorithm (Algorithm 1) for solving MCNEP is developed.

Algorithm 1: Algorithm for solving MCNEP (AMCNEP)

Input: $G=(V,A,s,t,u),c,\alpha ,\beta ,Q,c_Q,w$;

Output: $G^{*}=(V,A^{*},s,t,u^{*})$;

Compute a maximum flow $f^{*}$ in G;

If $v\left(f^{*}\right)\ge w$ then

It is no need to modify G. A feasible flow of value w can be computed in G;

Stop.

End if;

Build the network $G^{″}$ using Equation (5);

Compute a maximum flow $g^{*}$ in $G^{″}$;

If $v\left(g^{*}\right)<w$ then

MCNEP is not feasible;

Stop.

End if;

Build the network $G^e=(V^e,A^e,s,t,u^e,c^e)$ using Equations (6)–(10);

Compute a minimum cost flow $f^e$ in $G^e$;

Build the network $G^{*}=(V,A^{*},s,t,u^{*})$ using $f^e$, Equations (12) and (13);

The network $G^{*}$ is the optimum solution for MCNEP.

Theorem 4.

The time complexity of Algorithm 1 (AMCNEP) is

$$O({(m+q)}^2·logn+(m+q)·m·{log}^{2}n)$$

where n is the number of vertices in G, m is the number of arcs of the network G, and q the number of arcs from Q (that can be added to the network G).

Proof. 

Algorithm 1 needs to calculate two maximum flows, one in G, and the other in $G^{″}$. Today’s best known algorithm for the maximum flow problem is due to Orlin [14]. It has a time complexity of $O(m·n)$ (when applied in G). In $G^{″}$ there are n vertices and $m+q$ arcs. Thus, the time complexity of finding the maximum flow in $G^{″}$ is $O\left(\right(m+q)·n)$.

A minimum cost flow has to be calculated in $G^e$. The algorithms for minimum cost flow are designed to work on integer values [13]. Since in $G^e$ the cost of the arcs from $A_1^e\cup A_2^e$ are integer values divided by 2 (see Equation (10), before applying the algorithm for minimum cost flow, all the costs of the arcs from $A^e$ are multiplied by 2, and, in the end, the cost of the obtained flow $f^e$ is divided by 2. Today’s best known algorithm for the minimum cost flow problem is also due to Orlin [15]. Since $G^e$ has $m+n$ nodes and $3m+q$ arcs, if applied in $G^e$, this algorithm for minimum cost flow has a time complexity of $O({(m+q)}^2·logn+(m+q)·m·{log}^{2}n)$.

So, the time complexity of the whole algorithm is $O({(m+q)}^2·logn+(m+q)·m·{log}^{2}n)$. □

4. Example

We shall take an example to illustrate how AMCNEP works. In Figure 1, a given network G is presented. The arcs from Q (that can be added to the network) are drawn using dashed lines. This network is intended to be extended with the minimum cost so that it can support a flow of value $w=8$.

In Figure 2, the maximum flow $f^{*}$ calculated in G is presented. Its value is $v\left(f^{*}\right)=5$. Since $v\left(f^{*}\right)<w$, the network $G^{″}$ from Figure 3 is built next.

The maximum flow $g^{*}$ in $G^{″}$ has the value $v\left(g^{*}\right)=14>w$. Thus, MCNEP is feasible.

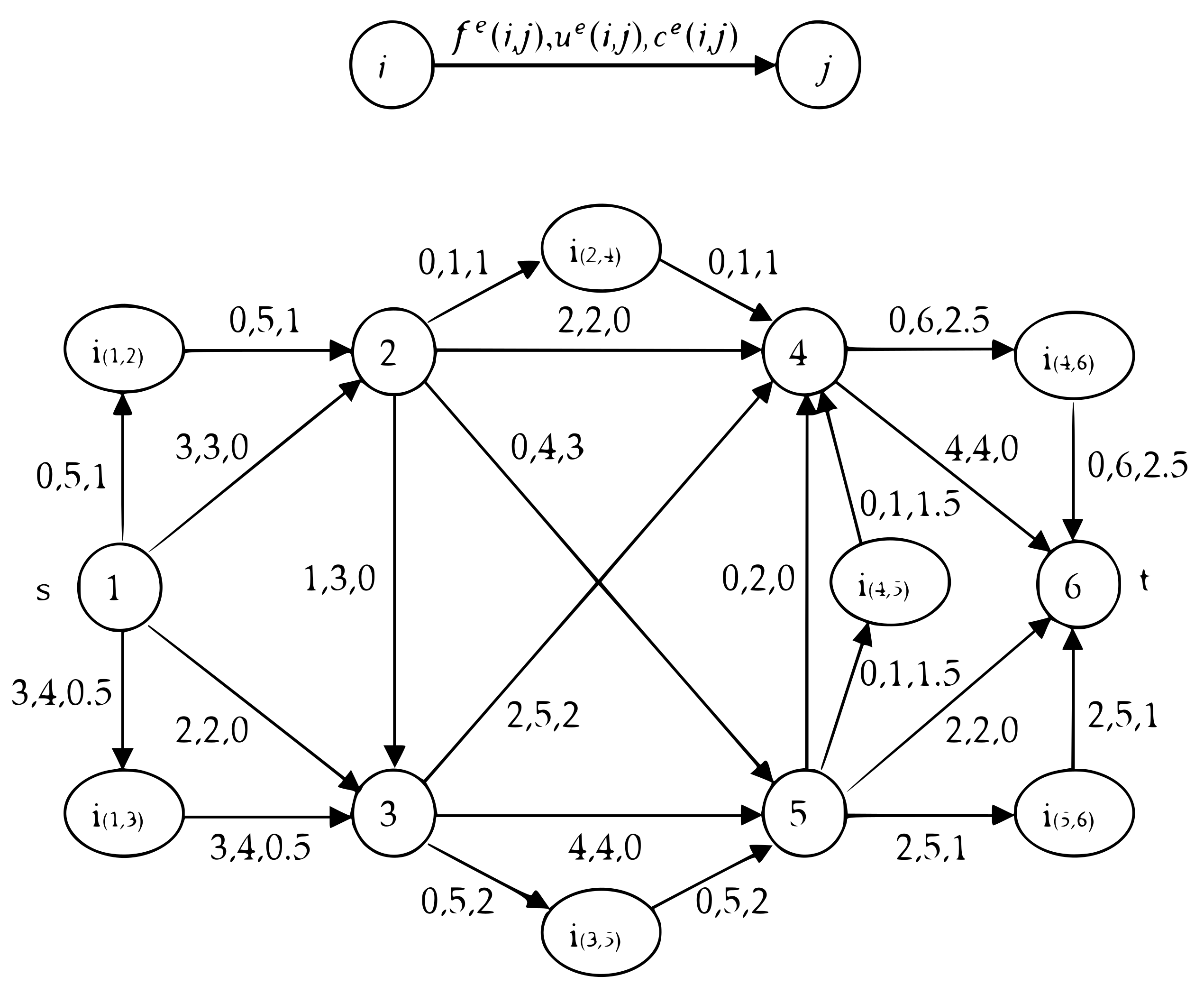
In Figure 4, the network $G^e$ is built. Since the capacity of the arc (2, 3) cannot be increased ($\alpha (2,3)=0$), it is no need to introduce the node $i_{(2,3)}$ and the corresponding arcs $(2,i_{(2,3)})$ and $(i_{(2,3)},3)$. The minimum cost flow $f^e$ of value $v\left(f^e\right)=w$ is computed in $G^e$. The cost of $f^e$ is $v\left(f^e\right)=11$.

In Figure 5, the solution $G^{*}$ of MCNEP is presented.The modified capacities are in bold. The capacity of the arc $(1,3)$ was increased from 2 to 5, and the capacity of the arc $(5,6)$ was increased from 2 to 4. The arc $(3,4)$ was added with the capacity 2. The total cost of network expansion from G to $G^{*}$ is $3\times 1+2\times 2+2\times 2=11$. This value can be calculated comparing $G^{*}$ with G, or using the value of the minimum cost flow $v\left(f^e\right)$ from Figure 4 (see Corollary 1).

5. Conclusions

This paper considered the minimum cost network expansion problem (MCNEP). The problem arises in cases where a given network must be modified to allow an increase in the amount of flow going from the source to the sink node. In this study, we considered that the transport capacities can be increased, and new arcs can be added to the network, and the cost of these operations is minimized. A strongly polynomial algorithm (Algorithm 1) was introduced to solve MCNEP.

A future work could consider a generalization of MCNEP, where the cost of the modification of arc capacities and the cost of introducing new arcs are not linear.