Abstract
In recent years, learning-based approaches for 3D reconstruction have gained much popularity due to their encouraging results. However, unlike 2D images, 3D cannot be represented in its canonical form to make it computationally lean and memory-efficient. Moreover, the generation of a 3D model directly from a single 2D image is even more challenging due to the limited details available from the image for 3D reconstruction. Existing learning-based techniques still lack the desired resolution, efficiency, and smoothness of the 3D models required for many practical applications. In this paper, we propose voxel-based 3D object reconstruction (V3DOR) from a single 2D image for better accuracy, one using autoencoders (AE) and another using variational autoencoders (VAE). The encoder part of both models is used to learn suitable compressed latent representation from a single 2D image, and a decoder generates a corresponding 3D model. Our contribution is twofold. First, to the best of the authors’ knowledge, it is the first time that variational autoencoders (VAE) have been employed for the 3D reconstruction problem. Second, the proposed models extract a discriminative set of features and generate a smoother and high-resolution 3D model. To evaluate the efficacy of the proposed method, experiments have been conducted on a benchmark ShapeNet data set. The results confirm that the proposed method outperforms state-of-the-art methods.
1. Introduction
In recent years, imaging devices such as cameras have become common, and people have easy access to these devices; however, most of these devices can only capture the scene in 2D format. Originally, the real-world scenes exist in a 3D format, but the third dimension gets lost during image acquisition. The recovery of the lost dimension is important for many applications such as robotic vision, medical imaging, 3D printing, and the TV industry. In a 2D image, a basic element is known as a pixel having coordinates, X and Y. In contrast, in a 3D model, the basic element is a voxel consisting of three coordinates X, Y, and Z [1], as shown in Figure 1. Interpreting 3D shapes is a primary function of the human visual system. Hence, we can easily infer the object’s 3D shape by viewing it from one or more viewpoints. However, it is quite a trivial task for machines to infer the lost third dimension due to the absence of important geometrical information in the 2D format.

Figure 1.
2D image and its corresponding 3D model.
Literature confirms that different approaches have been employed for 3D reconstruction over the last few decades, such as generating a 3D model from point cloud data and generating a 3D model directly from 2D images. The point-cloud-based approach employs skeletons, meshes, and Voronoi diagrams for 3D reconstruction [2]. The point cloud data are the 3D unstructured data gathered using a 3D laser scanner and 3D cameras [3]. Constructing a 3D model from point cloud data is highly mathematical because complex geometrical information is required. However, some approaches are data-driven in which machine learning techniques are used for 3D reconstruction from point cloud data [3]. In the second approach, initially, researchers proposed several methods for 3D reconstruction using a large collection of images of the same object. For this purpose, the geometrical properties were extracted from images using direct minimization of projection errors or dense matching. In addition to this, implicit volumetric reconstruction or explicit mesh-based techniques were also used for 3D reconstruction. However, in both cases, a large amount of input data and mathematical knowledge are required to estimate sufficient geometrical properties [4].
Recently, after the availability of large 3D data sets such as ShapeNet [5] and advancement in machine learning techniques, several successful attempts have been made for 3D reconstruction directly from 2D images using learning-based methods [6,7,8,9]. These techniques include multiple-view-based methods [10], panoramic-view-based methods [11], and single-view-based methods [12]. In multiple-view-based methods, special image capturing devices, such as 3D cameras, are required to capture the multiview images of an object or scene used for 3D model reconstruction. In contrast, the panoramic image of a scene or object estimates the geometry and reconstructs the layout in a 3D model. Both approaches are quite tedious because extensive mathematical information is required for 3D reconstruction using these methods. Constructing a 3D model from a single view 2D image is more promising because of the easy availability of single-view image capturing devices. Several methods have been proposed for 3D reconstruction from a single 2D image; however, there is still a need to address many issues such as low resolution, inefficiency, and low accuracy of existing methods [13,14,15].
In this work, simple-autoencoder (AE)- and variational-autoencoder (VAE)-based methods are presented for 3D reconstruction from a single 2D image. Our contribution is twofold. First, to the best of the authors’ knowledge, it is the first time that VAE have been employed for the 3D reconstruction problem. Second, the model is designed in such a way that it could extract a discriminative set of features for improving reconstruction results. The proposed method is evaluated on the ShapeNet benchmark data set, and the results confirm that it outperforms state-of-the-art methods for 3D reconstruction. The rest of the paper is organized as follows. In Section 2, related work for 3D model reconstruction is presented. In Section 3, we elaborate regarding the proposed methodology. Experimentation results and discussion are presented in Section 4. Finally, the paper is concluded in Section 5.
2. Related Work
In this section, we provide background information and discuss state-of-the-art methods used for 3D model reconstruction. These methods can be divided into geometry-based reconstruction and learning-based reconstruction methods.
2.1. Background Study
Recovering the lost dimension during image acquisition from any normal camera has been a hot research area in the field of computer vision for more than a decade. The literature review shows that the research methodology has been changed from time to time. More precisely, we can divide the conversion of 2D images to 3D model reconstruction into three generations. The first generation learns the 3D to 2D image projection process by utilizing the mathematical and geometrical information using some mathematical or algorithmic solution. These types of solutions usually require multiple images that are captured using specially calibrated cameras. For example, using some multiview of an object with constant angle changing that can cover all the 360 degrees of an object, we can compute the geometrical points of the object [16]. Using some triangularization techniques, we can join these points to make a 3D model [2]. The second generation of 2D to 3D model conversion utilizes the accurately segmented 2D silhouettes. This generation leads to a reasonable 3D model generation, but it requires specially designed calibrated cameras to capture the image of the same object from every different angle. This type of technique is not feasible or more practical because of the complex image capturing techniques [10,17].
Humans can assume the shape of the object using prior knowledge about some objects and predict what an object will look like from another unseen viewpoint. The computer-vision-based techniques are inspired by human vision to convert 2D images to 3D models. With the availability of large-scale data sets, deep learning research has evolved in 3D reconstruction from a single 2D image. A deep-belief-network-based 3D model was proposed [12] to learn the 3D model from a single 2D image. It is considered one of the earlier neural-network-based data-driven models to reproduce the 3D model. Although the results were not promising, it was considered a good start in 3D reconstruction using the computer-vision-based method. After this success, another research study based on a recurrent neural network became popular for 3D reconstruction [13]. This method employed encoder–decoder-based architecture while considering single or multiple images as input. The latent vector was produced using input, and then this latent layer vector was given to the decoder module with a residual network to reproduce the 3D model. This also became an achievement in computer vision, but the quality of results depended on the number of images given as input.
Similarly, the authors of some other studies such as [15] proposed an attentional aggregation module (AttSets) between the latent layer vector and decoder. This method could work as an intermediary between latent vector space and decoder to generate the 3D model using single-view 2D or multiview images. This study also uses a recurrent-based 3D decoder to decode latent space to generate a 3D volumetric grid. Moreover, other studies such as [18,19,20,21,22,23] used a similar kind of encoder–decoder-based architecture with some alterations to perform direct 3D model reconstruction from a 2D image.
2.2. Geometry-Based Reconstruction
The 3D reconstruction using geometry-based methods requires complex geometrical information, and most of these methods are scene-dependent. A method for 3D human reconstruction was proposed based on geometric information [24,25]. Some other methods focused on improving the quality of 3D sensory inputs such as multiview cameras and 3D scanners and then converting these data into a 3D model [26,27]. However, all of these methods required more than one view of an object to capture sufficient geometry for 3D reconstruction. For 3D reconstruction from a single 2D image, it is difficult to extract geometrical information, making it difficult to formulate a 3D model. Moreover, we need to preserve the depth information of the scene or object to reconstruct the model in 3D [28].
2.3. Learning-Based Reconstruction
Learning-based reconstruction approaches utilize data-driven volumetric 3D model synthesis. The research community has leveraged improvements in deep learning to enable efficient modeling of a 2D image into a 3D model. With the availability of large-scale data sets such as ShapeNet [5], most researchers focus on developing a 3D voxelized model from a single 2D image. Recently, various approaches have been proposed for achieving this task. One study shows that a 3D morphable shape can be generated from an image of a human face, but it requires many manual interactions and high-quality 3D scanning of the face. Some methods suggest learning a 3D shape model from key points or silhouettes [29]. In some studies, the single image’s depth map is first calculated using machine-learning-based techniques, and then a 3D model is constructed using RGB-D images [30].
A convolutional neural network (CNN) has recently become popular to predict the geometry directly from a single image by using an encoder–decoder-based architecture. The encoder extracts the features from the single image, while the decoder generates the model based on features extracted by the encoder [31]. In another study, deep-CNN-based models were learned, in which a single input image is directly mapped to output 3D representation for the 3D model generation in a single step. The authors of another study proposed a 3D recurrent-reconstruction-neural-network (RRNN)-based technique, in which the generation of the 3D model is performed in steps using a 2D image as input [13]. Some studies, such as [32], used a 2D image along with depth information as input to the 3D-based U-Net architecture. For 3D appearance rendering, Groueix et al. [33] used a convolutional encoder–decoder-based architecture to generate the 3D scene from a single image as an input. Then, Haoqiang et al. [34], by incorporating a differentiable appearance sampling mechanism, further improved the quality of the generated 3D scene.
The literature suggests that generating a 3D model from a single 2D image using learning-based methods is comparatively less explored [35]. In this direction, we propose a simple yet effective deep-learning-based framework that can estimate the 3D shape from a single 2D image in an end-to-end manner.
3. Methodology
The proposed V3DOR approach consists of two different architectures, i.e., autoencoder (AE) and variational autoencoder (VAE). The AE consists of two modules in which the encoder extract features, and the decoder is responsible for generating output. Our shape learning architectures generate the 3D model in the 1-channel volume of voxels. The reason for 1-channeled volume reconstruction is to reduce the computational cost. The complete methodology is presented in subsequent sections.
3.1. Autoencoder-Based Technique
Autoencoders (AE) basically helps in approximation of identity mapping using encoding and decoding blocks. The latent representation of input in compact form is learned in encoding stage and tries to rebuild the input using the encoded features in decoding stage. Previously autoecoders have been popular in dimentionality reduction and image compression tasks, but It has gained much attention recently in the 3D reconstruction related tasks as well. It is observed that most promising results are obtained in 3D reconstruction from single 2D image using autoencoder-based architecture. In this research The conversion of 2D images to 3D models has been studied widely and the proposed approach stands out from existing techniques as we used more deeper networks that can extract best features from the input. The proposed automatic conversion of 2D to 3D models is shown in Figure 2 and explained as follows.
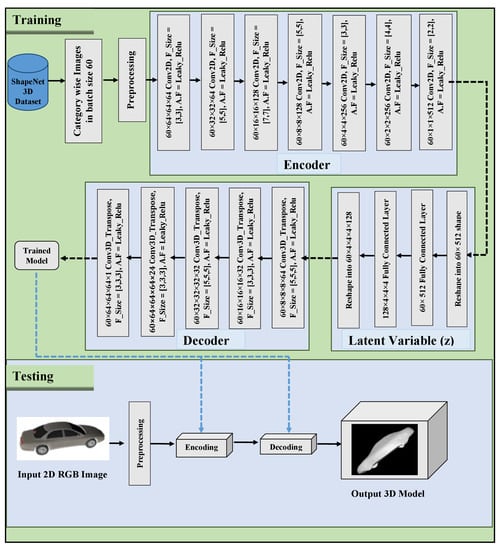
Figure 2.
Detailed Architecture of the Proposed Autoencoder Approach.
3.1.1. Preprocessing
Given an input, a 2D image, say I. Convert 2D image into gray-scale and normalize is to make every kind of image acceptable for the model. Image normalizing includes (1) resize the image into 128 × 128 pixels so that the complexity and memory limitations can be overcome. (2) pixel normalizing to make pixel values in specified range i.e., 0–255. (3) object centring, it is observed that if the object is in center of the image it can learn the good geometrical representation so pixel centering techniques have been applied.
3.1.2. Encoder
We proposed a deep encoder with two extra number of convolution layers as compared to decoder block which helps us to learn the complex geometrical features. The encoder network h(.) learns a latent representation concerning I. The latent representation is invariant to size and angle. This helps us to make the 3D model, which is rotate-able at every angle. The encoder architecture consists of seven 2D convolution layers can be expressed as (64, 3 × 3, 2), (64, 5 × 5, 2), (128, 7 × 7, 2), (128, 5 × 5, 2), (256, 3 × 3, 2), (256, 4 × 4, 2), (512, 2 × 2, 2) the format is (filter channels, spatial filter dimensions, stride). The learned representation has the final shape of 1D vector of size 512. After encoding process a fully-connected layer is being added to increase the dimension of the latent variable from 512 to 8192 which helps to extract even fine details from the encoded vector.
3.1.3. Decoder
The learned representation is then given to the decoder model g to do the generation of shape into the volume V such that V = g(h(I)). The decoder decodes the latent space vector into one channel occupancy volume of the object having fine details. The decoder consists of 5 layers of 3D transpose with following format (filter channels, filter dimensions, stride) can be expressed as (64, 5 × 5 × 5, 2), (32, 3 × 3 × 3, 2), (32, 5 × 5 × 5, 2), (21, 3 × 3 × 3, 2), (1, 3 × 3 × 3, 1). The output of the 3D structure is in shape .
3.1.4. Loss Estimation
The ground truth in volumetric shape V is available; the loss function uses the generated volumetric shape and ground truth to calculate the loss function. The volumetric shape obtained has some sparseness to handle its variation of cross-entropy loss named as Mean Squared False Cross-Entropy Loss (MSFEL) is used. The MSFEL was proposed in [36]. The MSFEL is expressed as:
where is known as false positive cross-entropy loss of vacant voxel of the ground truth shape volume, and is the false negative cross-entropy loss of occupied voxels. Which can be represented as:
where P is the number of occupied voxels; is the nth unoccupied voxel and N is the total number of unoccupied voxels of V, and is the pth occupied voxel; and are the prediction of and , respectively.
3.2. Variational-Autoencoder-Based Technique
Recently, generative networks like GANs [37] and Variational Autoencoders (VAE) [38] has gained too much attention in computer vision. Some work has been conducted in 3D modeling using VAE’s, but to the best of our knowledge, no literature has been found to convert the 3D model directly from a simple 2D image [31]. In this approach, encoding and decoding are performed, but VAE is used to generate the 3D model. The VAE is a stochastic model; it uses as a generative model. The main advantage of using VAE over simple autoencoders is that synthetic data can be generated. The parameters of enocoder and decoder are trained joinlty to improve the laerning capability and decrease the training loss. The overall network setting of the encoder and decoder is the same as in our proposed autoencoder approach. However, in simple autoencoders, the encoder outputs a latent variable of size n where n is the number of pixels. But, the proposed variational autoencoder outputs two computed vectors of size n: a vector of means values µ and a vector of standard deviation values as a latent vector fed to the decoder, as shown in Figure 3. The decoder then decodes the latent representation into a 3D model. The loss function used here is the same as it was used in our proposed autoencoder approach. Using this approach, new 3D models can be generated with similar characteristics to the input data but not real.
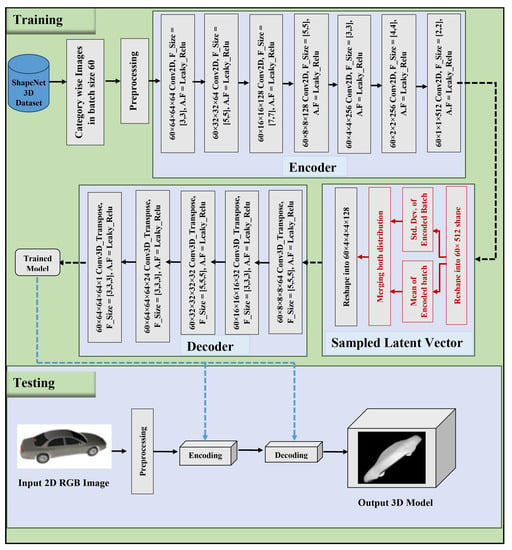
Figure 3.
Detailed Architecture of the Proposed Variational Autoencoder Approach.
4. Experimentations and Results
4.1. Data Set
Several public benchmark data sets are available for evaluation algorithms for 3D modeling, including IKEA 3D [39], PASCAL 3D [40], ModelNet [12], and ShapeNet [5]. ShapeNet [5] is a well-known data set consisting of fifty object categories and used by many researchers to evaluate their techniques. This study has used a subset of the ShapeNet [5] data set, including cars, chairs, guitar, and table categories as used by [41]. Each category has images taken from all the angle which covers the 360 of an object and its corresponding 3D model. There are 3389 objects of cars, 2199 objects of a chair, 631 objects of guitar, and 2539 objects of table category. Each object has its corresponding 3D model as a ground truth.
4.2. Comparison with State-of-the-Art Methods
To analyze and investigate the proposed methodology, the experiments were conducted using the subset of the ShapeNet data set. The data were divided into 70% for training, 10% for validation, and 20% for testing. Each object has its corresponding 3D model available, which acts as a ground truth. The steps involved in testing are: (1) Input the image. (2) Use a trained model to compute its latent representation. (3) The computed latent representation is then given to the trained decoder to compute the 3D model.
The evaluation metric used for a generated 3D object is intersection over union (). computes the ratio between the area of the overlap part and the area of the union part. The formula of is given by:
It is currently a standard evaluation metric for comparing the 3D shape and prediction. It compares all the pixels or voxels and compares them with the corresponding ground truth. To check the quality of the computed 3D model by using our proposed approach, the evaluation as mentioned above metric is used.
The popular 3D volumetric reconstruction model named 3D-Recons [42] and OCCNet [14] have been adapted as a baseline for performance and quality evaluation. Both types of research generate a 3D model in volumetric shapes. OCCNet [14] uses an occupancy-based network module that refines the reconstructed model. In contrast, 3D-Recons [42] used an autoencoder-based technique for 3D model construction.
Table 1 is showing the comparison between the state-of-the-art approaches for 3D surface reconstruction from single 2D image on the basis of . The experiments also confirms that the proposed approach achieves better results than the state-of-the-art. These results were obtained even with fewer epochs than the 3D-Recons approach [43]. This happens due to the use of a modern approach for 3D modeling using neural networks.

Table 1.
Comparison with state-of-the-art methods in terms of .
The visual results of generated 3D model using our approach and other baselines are shown in Table 2. It is observed that most of the methods based on CNN [9,14,42,44] can learn the 3D geometry correctly. However, a rough 3D model is generated by an LSTM-based method [13]. In contrast, surface reconstructed by the proposed approach and OccNet [14] can capture a complex geometrical structure.

Table 2.
Visual comparison with competitive approaches.
5. Conclusions
Two different approaches of voxel-based 3D object reconstruction (V3DOR) have been proposed, one using an autoencoder (V3DOR-AE) and another using a variational autoencoder (V3DOR-VAE). The proposed methodology has three main steps. First, the encoder part is used to learn the geometrical constraints in compressed representation from the input 2D image. Second, in the simple AE approach, the latent representation of the input image is obtained during the encoding process. However, in the proposed 3D-VAEN approach, two encoded vectors of mean and standard deviation are computed from input in encoding phase. Third, the decoding process is performed to generate the learned encoded representation into a 3D model. The decoding process is the same for both of the proposed approaches. To show the quality of the proposed method, is being used as an evaluation metric. Both of the proposed methodologies are validated by performing rigorous experimentation and comparison with existing methods. Results show that both approaches have a better mean than the state-of-the-art approaches. It is also seen that the model reconstructed using our proposed approach is of good quality and has fine details. However, at the moment, we are not expecting reasonable performance on cross-data-set validation. This is a special validation where the model is trained and tested on a data set and is then retested on a different data set. So far, we could not find state-of-the-art following this ideal approach of validation. This could be part of our future research work. In addition to this, reconstruction of the complex 3D object with colorful effects from a single 2D image can also be considered as a future research direction.
Author Contributions
R.T., A.B.S. and Z.H. conceived and designed the experiments; R.T. performed the experiments; A.B.S. and Z.H. analyzed the data; A.B.S. and R.T. contributed reagents/materials/analysis tools; R.T. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the PDE-GIR project which has received funding from the European Unions Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement No 778035.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shin, D.; Fowlkes, C.; Hoiem, D. Pixels, voxels, and views: A study of shape representations for single view 3d object shape prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3061–3069. [Google Scholar]
- Berger, M.; Tagliasacchi, A.; Seversky, L.; Alliez, P.; Guennebaud, G.; Levine, J.; Sharf, A.; Silva, C. A survey of surface reconstruction from point clouds. Comput. Graph. Forum 2017, 36, 301–329. [Google Scholar] [CrossRef] [Green Version]
- Goel, S.; Bansal, R. Surface Reconstruction Using Scattered Cloud Points. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 242–245. [Google Scholar]
- Lee, P.; Huang, J.; Lin, H. 3D model reconstruction based on multiple view image capture. In Proceedings of the 2012 International Symposium on Intelligent Signal Processing and Communications Systems, Tamsui, Taiwan, 4–7 November 2012; pp. 58–63. [Google Scholar]
- Chang, A.; Funkhouser, T.; Guibas, L.; Hanrahan, P.; Huang, Q.; Li, Z.; Savarese, S.; Savva, M.; Song, S.; Su, H.; et al. Shapenet: An information-rich 3d model repository. arXiv 2015, arXiv:1512.03012. [Google Scholar]
- Jimenez Rezende, D.; Eslami, S.; Mohamed, S.; Battaglia, P.; Jaderberg, M.; Heess, N. Unsupervised learning of 3d structure from images. In Proceedings of the Advances In Neural Information Processing Systems, Annual Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29, pp. 4996–5004. [Google Scholar]
- Zeng, G.; Paris, S.; Quan, L.; Lhuillier, M. Surface reconstruction by propagating 3d stereo data in multiple 2d images. In Proceedings of the European Conference On Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 163–174. [Google Scholar]
- Hu, F.; Zhao, J.; Huang, Y.; Li, H. Structure-aware 3D reconstruction for cable-stayed bridges: A learning-based method. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 89–108. [Google Scholar] [CrossRef]
- Kato, H.; Ushiku, Y.; Harada, T. Neural 3d mesh renderer. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3907–3916. [Google Scholar]
- Liu, J.; Yu, F.; Funkhouser, T. Interactive 3D modeling with a generative adversarial network. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 126–134. [Google Scholar]
- Zou, C.; Colburn, A.; Shan, Q.; Hoiem, D. Layoutnet: Reconstructing the 3d room layout from a single rgb image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2051–2059. [Google Scholar]
- Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d shapenets: A deep representation for volumetric shapes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1912–1920. [Google Scholar]
- Choy, C.; Xu, D.; Gwak, J.; Chen, K.; Savarese, S. 3d-r2n2: A unified approach for single and multi-view 3d object reconstruction. In Proceedings of the European Conference On Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 628–644. [Google Scholar]
- Mescheder, L.; Oechsle, M.; Niemeyer, M.; Nowozin, S.; Geiger, A. Occupancy networks: Learning 3d reconstruction in function space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4460–4470. [Google Scholar]
- Yang, Y.; Liu, S.; Pan, H.; Liu, Y.; Tong, X. PFCNN: Convolutional neural networks on 3d surfaces using parallel frames. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13578–13587. [Google Scholar]
- Liu, S.; Acosta-Gamboa, L.; Huang, X.; Lorence, A. Novel low cost 3D surface model reconstruction system for plant phenotyping. J. Imaging 2019, 3, 39. [Google Scholar] [CrossRef] [Green Version]
- Gwak, J.; Choy, C.; Chandraker, M.; Garg, A.; Savarese, S. Weakly supervised 3d reconstruction with adversarial constraint. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 263–272. [Google Scholar]
- Tulsiani, S.; Zhou, T.; Efros, A.; Malik, J. Multi-view supervision for single-view reconstruction via differentiable ray consistency. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2626–2634. [Google Scholar]
- Xie, H.; Yao, H.; Sun, X.; Zhou, S.; Zhang, S. Pix2vox: Context-aware 3d reconstruction from single and multi-view images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 2690–2698. [Google Scholar]
- Girdhar, R.; Fouhey, D.; Rodriguez, M.; Gupta, A. Learning a predictable and generative vector representation for objects. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 484–499. [Google Scholar]
- Gadelha, M.; Maji, S.; Wang, R. 3d shape induction from 2d views of multiple objects. In Proceedings of the 2017 International Conference On 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 402–411. [Google Scholar]
- Wu, J.; Zhang, C.; Xue, T.; Freeman, W.; Tenenbaum, J. Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 82–90. [Google Scholar]
- Smith, E.; Meger, D. Improved adversarial systems for 3d object generation and reconstruction. In Proceedings of the Conference On Robot Learning, Mountain View, CA, USA, 13–15 November 2017; pp. 87–96. [Google Scholar]
- Häne, C.; Tulsiani, S.; Malik, J. Hierarchical surface prediction for 3d object reconstruction. In Proceedings of the 2017 International Conference on 3D Vision (3DV), Qingdao, China, 10–12 October 2017; pp. 412–420. [Google Scholar]
- Toshev, A.; Szegedy, C. Deeppose: Human pose estimation via deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1653–1660. [Google Scholar]
- Zhang, C.; Pujades, S.; Black, M.; Pons-Moll, G. Detailed, accurate, human shape estimation from clothed 3D scan sequences. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4191–4200. [Google Scholar]
- Kar, A.; Tulsiani, S.; Carreira, J.; Malik, J. Category-specific object reconstruction from a single image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1966–1974. [Google Scholar]
- Lu, Y.; Wang, Y.; Lu, G. Single image shape-from-silhouettes. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 3604–3613. [Google Scholar]
- Čavojská, J.; Petrasch, J.; Mattern, D.; Lehmann, N.; Voisard, A.; Böttcher, P. Estimating and abstracting the 3D structure of feline bones using neural networks on X-ray (2D) images. Commun. Biol. 2020, 3, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Cao, M.; Zheng, L.; Liu, X. Single View 3D Reconstruction Based on Improved RGB-D Image. IEEE Sens. J. 2020, 20, 12049–12056. [Google Scholar] [CrossRef]
- Biffi, C.; Cerrolaza, J.; Tarroni, G.; Marvao, A.; Cook, S.; O’Regan, D.; Rueckert, D. 3D high-resolution cardiac segmentation reconstruction from 2D views using conditional variational autoencoders. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 1643–1646. [Google Scholar]
- Wu, J.; Wang, Y.; Xue, T.; Sun, X.; Freeman, W.; Tenenbaum, J. Marrnet: 3d shape reconstruction via 2.5 d sketches. arXiv 2017, arXiv:1711.03129. [Google Scholar]
- Groueix, T.; Fisher, M.; Kim, V.; Russell, B.; Aubry, M. AtlasNet: A Papier-Mâché Approach to Learning 3D Surface Generation. arXiv 2018, arXiv:1802.05384. [Google Scholar]
- Fan, H.; Su, H.; Guibas, L. A point set generation network for 3d object reconstruction from a single image. In Proceedings of the IEEE Conference On Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 605–613. [Google Scholar]
- Fu, K.; Peng, J.; He, Q.; Zhang, H. Single image 3D object reconstruction based on deep learning: A review. Multimed. Tools Appl. 2021, 80, 463–498. [Google Scholar] [CrossRef]
- Wang, S.; Liu, W.; Wu, J.; Cao, L.; Meng, Q.; Kennedy, P. Training deep neural networks on imbalanced data sets. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 4368–4374. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.; Welling, M. An introduction to variational autoencoders. arXiv 2019, arXiv:1906.02691. [Google Scholar] [CrossRef]
- Lim, J.; Pirsiavash, H.; Torralba, A. Parsing ikea objects: Fine pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2992–2999. [Google Scholar]
- Xiang, Y.; Mottaghi, R.; Savarese, S. Beyond pascal: A benchmark for 3d object detection in the wild. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Steamboat Springs, CO, USA, 24–26 March 2014; pp. 75–82. [Google Scholar]
- Sun, Y.; Liu, Z.; Wang, Y.; Sarma, S. Im2avatar: Colorful 3d reconstruction from a single image. arXiv 2018, arXiv:1804.06375. [Google Scholar]
- Zhu, Y.; Zhang, Y.; Feng, Q. Colorful 3d reconstruction from a single image based on deep learning. In Proceedings of the 2020 3rd International Conference on Algorithms, Computing and Artificial Intelligence, Sanya, China, 24–26 December 2020; pp. 1–7. [Google Scholar]
- Pons-Moll, G.; Romero, J.; Mahmood, N.; Black, M. Dyna: A model of dynamic human shape in motion. ACM Trans. Graph. (TOG) 2015, 34, 1–14. [Google Scholar] [CrossRef]
- Liu, S.; Li, T.; Chen, W.; Li, H. Soft rasterizer: A differentiable renderer for image-based 3d reasoning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 7708–7717. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

















