Abstract
The industry–academic collaboration (IAC) in developed and developing countries enables these economies to gain momentum in continuous innovation and, thus, economic growth. Patent commercialization is one major channel of knowledge flow in IAC. However, very few studies consider the flow of knowledge between industrial firms and universities. Moreover, ways that the patent commercialization performance of IACs can be evaluated are rarely discussed. Therefore, defining an analytic framework to evaluate the performance of IAC from the aspect of patent commercialization is critical. Traditionally, data envelopment analysis (DEA) models have widely been adopted in performance evaluation. However, traditional DEA models cannot accurately evaluate the performance of IACs with complex university–industry interconnections, the internal linkages, or linking activities of knowledge-flow within the decision-making units (DMUs), i.e., the IACs. In order to solve the abovementioned problems, this study defines a multiple objective programming (MOP)-based network DEA (NDEA), with weighting derived from the decision-making trial and evaluation laboratory (DEMATEL)-based analytic network process (ANP), or the DANP. The proposed analytic framework can evaluate the efficiency of decision-making units (DMUs) with a network structure (e.g., supply chains, strategic alliances, etc.) based on the weights that have been derived, based on experts’ opinions. An empirical study based on the performance of the patent commercialization of Taiwanese IACs was used to demonstrate the feasibility of the proposed framework. The results of the empirical research can serve as a basis for improving the performance of IAC.
1. Introduction
In the era of the knowledge-based economy, knowledge has become the major factor driving the economic growth of major and fast-catching-up minor economies. The accumulation, creation, and application of knowledge have become the main sources of national competitiveness. Industry–academic collaboration (IAC) enables firms to obtain new techniques and patents from university research [1]. Thus, over the past few decades, pharmaceutical, engineering, and software firms have increasingly enhanced their cooperation with universities [2]. In addition to their own research and development (R&D), firms also need universities’ R&D of new technologies.
IACs have a long tradition in numerous countries all over the world [3]. The logic behind IAC refers to the cooperation between firms and universities. Such collaborations between firms and universities have gradually become a key component of an effective national innovation system. The motivations of policymakers and higher-education institutes to develop “third missions” besides the two conventional basic missions of lecturing and academic research, and to commercialize academic knowledge through various approaches like patent applications and commercialization, technology licensing and transfer, incubation has strengthened the appropriateness of IACs [4,5,6]. IAC also promotes technological innovation, and the transfer of scientific technology can be promoted through the acquisition and use of knowledge created by the IAC, innovative start-ups, and spin-offs [7].
Much evidence has demonstrated that effective knowledge and technology transfer are vital for a successful IAC [8]. An effective transfer is able to enhance innovation performance [9], improve the technology’s novelty [10], and enhance product development [6,11]. Thus, the evaluation of effective knowledge and technology transfer in IAC is very important. Performance evaluation is the formal process of measuring employees’ productive work and achievements, based on job responsibilities. In general, performance management is a systematic management process used to organize the way that individuals achieve common goals. It can provide directions for organizations or employees to improve or communicate the results being achieved [12].
Numerous scholars have tried to evaluate the performance of IAC. For example, Anderson et al. [13] evaluated the performance of university technology transfers, while Rast et al. [14] defined an evaluation framework for assessing IAC. Crescenzi et al. [15] used co-patenting to detect the closeness and innovative collaborations of university–industry linkages. Furthermore, Crescenzi et al. [15] argued that collaborative research projects, scientific publications, and patenting are three major channels for shaping knowledge transmission in IAC. Apparently, patents are an important indicator of IAC.
Therefore, scholars have started to investigate the related issues of patent commercialization by universities, due to the low percentage rate of patents that have been commercialized by universities [16]. Whether university patents can successfully be commercialized is very important for the sustainable economic growth of certain fast-growing economies like that of mainland China. Recently, according to Hsu et al. [17], in spite of the economic importance of patented university research, it is hard to quantify the monetary value of patents by universities and to observe the extent to which higher-education institutes are capable of capturing such value from patent commercialization. Apparently, the way that IAC can be evaluated according to the performance of patent licensing and commercialization is very important for evaluating the knowledge transmission in AIC and is worthy of further investigation.
However, almost no studies consider the flow of knowledge between industrial firms and universities; nevertheless, this knowledge flow is critical to IAC in a knowledge-based economy. In reality, there is a growing awareness of the very limited understanding that we have about the connections that link universities and industrial firms together [18]. Consequently, a growing number of scholars have mentioned the need to investigate further the appropriateness of current sources for evaluating “third missions” or IAC performance, as well as for the development of novel possible evaluation criteria [19].
Traditionally, data envelopment analysis (DEA) was widely adopted for tackling performance evaluation problems. However, the conventional DEA models (e.g., the CCR [20] and BCC [21] models) have some limitations in solving IAC problems, especially when taking into account the complexity of university–industry interconnections [19]. According to Tone and Tsutsui [22], many organizations comprise numerous linked divisions (see Figure 1a, from [22], for a typical example of an organization consisting of three linked divisions). The traditional DEA models usually adopt either the aggregation (e.g., the CCR [20] and BCC [21] models) or the separation (e.g., Seiford and Zhu [23]) methods. (Typical configurations for the aggregation and separation models of DEA can be found in Figure 1b,c). For the aggregation models, the decision-making unit (DMU) is usually regarded as a black box (see Figure 1b), while the internal linkages or linking activities within the DMU are neglected; therefore, the performance of individual divisions within the DMUs cannot be evaluated [24]. In contrast, the DEA models based on the separation method usually treat each division as an independent unit (see Figure 1c for a typical example); linkages among other divisions are completely neglected [24].
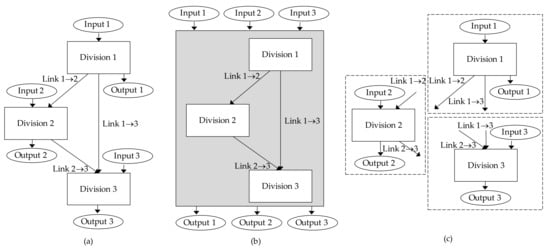
Figure 1.
(a) A DMU with three linked divisions; (b) an aggregation mode; (c) a separation model. Note: graphic adapted from Tone and Tsutsui [22].
Thus, the multiple objective programming (MOP)-based NDEA approach, or the NDEA-MOP, proposed by Kao et al. [24], is adopted to resolve the abovementioned problem in evaluating the patent commercialization performance of IACs. Based on the CCR model [20] or BCC model [21], the total and divisional efficiencies of a DMU are defined according to different objective functions to be measured cohesively in the NDEA-MOP. Furthermore, very few works on MOP problems in general, and NDEA-MOP problems in particular, adopt the real weights associated with goals. Thus, the authors propose a decision-making trial and evaluation laboratory (DEMATEL)-based analytic network process (ANP) [25] or DANP framework to derive the influence weights associated with the objectives, based on the opinions of experts familiar with IAC. The analytic results derived by the DANP-based NDEA-MOP model with real weights will be very important for solving real-world management problems. An empirical study, based on the open database of the Ministry of Education, Taiwan, will be used to evaluate the IAC performance of Taiwanese technical universities.
The rest of this paper is organized as follows. In Section 2, past works on IAC, patent commercialization, performance evaluations of IAC, and NDEA are reviewed. In Section 3, the DANP-based NDEA-MOP analytic model is proposed. In Section 4, an empirical study based on the performance evaluation of the patent commercialization of Taiwanese IACs is introduced to verify the feasibility of the proposed analytic framework. Then, a discussion will be presented in Section 5. Finally, Section 6 will conclude the paper with observations, conclusions, and recommendations for further study.
2. IAC, Patent Commercialization and Performance Evaluation
In the era of the knowledge economy, IAC has already become one of the most important methods for diffusing knowledge that is embedded in techniques or inventions, from higher institutes to industrial firms. During recent years, the patent commercialization of universities has become a research focus due to its dominant role in enhancing economic growth [26]. Therefore, the way in which the performance of the patent commercialization of IACs can be evaluated is very important. Specifically, the way that the inputs and outputs of the IACs should be determined so that the performance of IAC in general, and the evaluation of the patent commercialization in IACs in particular, can be evaluated is worth further investigation. Traditionally, DEA-based methods have already been adopted widely in performance evaluation. However, the conventional DEA methods neglect the interconnections within DMUs [24]. Thus, NDEA-based methods that include the divisions inside the DMU and the connections between the DMUs can cross the research gap and evaluate the efficiency of patent commercialization correctly. The NDEA-MOP further advances the NDEA models from the aspect of considering multiple objectives of management in performance evaluation. Thus, the NDEA-MOP will be very useful in evaluating patent commercialization performance in IACs. This section first reviews the definitions regarding IAC. Then, it reviews the literature on patent commercialization. After that, past works on the performance evaluation of IAC and on NDEA are reviewed.
2.1. IAC
Collaboration between universities and industries can expand the research relationships that public enterprises carry out, promote the commercialization of public R&D results, increase labor mobility between the public and private sectors, and contribute to new products and patents [1]. Thus, IAC has widely been adopted. Such cooperation is conducive to knowledge-cooperation so that different innovative capabilities can be integrated to create new and useful items [27]. There are many different types and goals and categories of ways in which IAC can be formulated [28]. Cooperation can be formal or informal; the former includes formal equity partnerships, signing contracts, setting research projects, and licensing a variety of patents [29]. The IAC is a win-win approach for both universities and industrial firms. Universities can improve the quality of their research and teaching through their practical cooperation experiences with industrial firms, while the industrial firms can increase the differentiation of their products and/or services, as well as reducing operating costs via innovative concepts developed through collaborative research. Universities and industries share not only their knowledge and abilities but also their R&D facilities and staff members [30].
2.2. Patent Commercialization by Universities
Patent commercialization is a vital stage in enhancing organizational performance [31]. The scope of patent commercialization consists of the sales, transfer, or license of patented technologies to industrial firms; founding start-ups that are based on the grounds of licensed patent technologies; or commercializing patented technologies in designs, products, and manufacturing or the service process of licensees [31]. The patents held by firms or universities are, by nature, different [16]. On the one hand, patents held by firms are driven primarily by possible market benefits. On the other hand, patents held by universities are more dependent on the governmental patent policy and the missions or characteristics of a specific university [16,32,33]. Effective patent commercialization increase returns and thus improves the innovation performance of specific firms or universities [31].
One vital mechanism by which universities contribute to economic growth is the conversion of academic inventions into patent commercialization [34]. Consequently, over the past three decades, research interests on the transfer of academic knowledge to industrial firms have increased radically [35] in developed countries like the United States (e.g., [36]), Spain (e.g., [37]), The Netherlands (e.g., [38]), Portugal (e.g., [39,40]), Japan (e.g., [41]), and in quickly evolving economies like China (e.g., [42]). Furthermore, this transfer has been regarded as a natural phase in the development of modern higher-education institutes [35,43]. Thus, researchers have started to investigate the commercialization of university patents [44,45,46] and the formation of spin-offs [35,47,48,49]. Giuri et al. [35] also presented a similar finding that patent sales, licensing, and academic spinoffs are three exploitation channels of academic patents.
2.3. Performance Evaluation of the IAC
The concept of “performance evaluation” was proposed by Drucker [50]. In 1954, he promoted the phrase “management by objectives”, with the goal of assessing performance by comparing the performances of personnel, whether individually or as members of a team. According to Ahmed et al. [51], performance evaluation is crucial for the effective management of the manpower behind an organization and the evaluation of employees, which can assist in the development of staff, improve organizational effectiveness, and feed into business planning. Recently, Murphy [52] defined performance evaluation as a process in which one or more individuals (typically, supervisors or managers) in organizations observe and gain information about the employees’ work performance.
Under the leadership of Drucker, many scholars have proposed specific methods that focus on setting goals and then comparing performance against these goals. For example, Huang et al. [53] proposed a multiple objective programming-based DEA model for evaluating the performance of leading fabless integrated-circuit design houses. Wu et al. [54] developed a professional performance evaluation system for pre-service automobile repair vocational high-school teachers in Taiwan. Han and Trimi [55] proposed a fuzzy technique for order preference according to its similarity to the ideal solution (TOPSIS) method. This method was used to evaluate the performance of reverse logistics in social commerce platforms. Kao et al. [56] evaluated the performance of systemic innovation problems regarding the Internet of Things (IoT) in manufacturing industries, using novel MCDM methods.
Performance evaluation can address both general (e.g., employee performance evaluation [57]) and specific (e.g., leanness evaluation metrics for manufacturing organizations [58]) issues. The resources for performance measurement are usually part of the organizational infrastructure, where the assessment is targeted. Performance evaluation can focus on goal setting, which is the basis of traditional performance management processes. Goals enable the alignment of individual and team performance with organizational-level performance. Goal setting can help managers increase engagement by clarifying expectations, leading to more challenging work [59].
When discussing the relative performance of the DMUs of a decision-making problem in a specific field, the main input and output variables should be considered at the very beginning. The possible inputs that can be used to evaluate IAC problems include manpower, financial resources, material input, and human input. Manpower includes the number of teachers, such as the professors and lecturers, as well as support personnel. Financial resources include government funds, tuition fees, private grants, self-raised income by universities, and other incomes. Material investment mainly includes fixed assets and equipment investment. The educational output primarily refers to the university’s achievements in the process of operation, education, teaching, and talent training, and the rewards and achievements of academic and scientific research [60].
Three input factors of IAC, namely, resources, researchers’ capabilities, and researchers’ motivations, are usually those that are considered. Furthermore, expense is a key input factor in any type of R&D activity [61]. The easiest way to measure researchers’ capabilities is with bibliographic metrics. In academia, one of the major criteria for evaluating researchers’ quality is the number of journal publications they have. However, the quality of journals and individual journal articles varies, so the publication number is not a trustworthy method of evaluating the influence of a researcher; therefore, the number of citations is a better method for measurement. Citation calculations record the number of times a writer’s publications have been cited by others in the bibliographical databases, e.g., the Science Citation Index (SCI) and Social Science Citation Index (SSCI), being developed by the Institute for Scientific Information [62]. Sometimes, measuring researchers’ motivation directly is very tough, but the academic atmosphere and other factors associated with the academic department can be adopted for assessment. Previous studies have shown that the atmosphere is one of the most important predictors of participation in industry activities [63,64].
According to Perkmann et al. [2], IAC has three major categories of outputs. First, the technological output of IAC projects can be measured by patent applications or patents granted. Second, publications in peer-reviewed journals can serve as a major performance indicator in academic institutions. Third, several staffing indicators have also been successfully evaluated in terms of staff skills and training [2]. Crescenzi et al. [15] argued that patenting is one of the major channels for shaping knowledge transmission in AIC. Apparently, patent applications or patents granted should be one of the major indicators for evaluating the performance of IAC [35]. One typical example is the recent exploration by Nugent et al. [65] of the impact of university–industry-targeted (U-I-targeted) grants by governments, based on the economic benefit from patent applications that have been filed and granted.
Albats et al. [66] summarized seven factors to be considered when evaluating the performance of an IAC. (1) The evaluation system should take into account the peculiarities of particular collaborations. (2) Individual and expert assessments should be conducted in high-tech and/or niche markets, rather than by official indicators collected. (3) The introductions of agile principles that have been widely adopted in the iterative development process of the information and communications technology (ICT) products to other more traditional industries may help shorten the time-frame of IAC project implementation and assessment [66]. (4) Especially in an era when an open innovation approach is emerging rapidly, or if the company is moving into science-intensive sectors, the prominence of publications in academic journals, as well as the entire strategic cooperation with academia, must be well-thought-out. (5) The cooperation amongst the performers, such as round-tables, conferences, meetings on funding, regional events, etc., should be included. (6) As a suggestion for policymakers and researchers, a number of regional background checks should be conducted on a large-scale basis to respond to the link between the actors’ priorities and relevant key performance indicators for IAC. (7) Finally, based on new indicators developed and related to previous indicators, optional indicators should be provided so that actors can select the most relevant indicators [66].
Albeit evaluating IAC is very important, according to Perkmannet al. [2], the performance of IAC is often hard to evaluate for the following four reasons. First, the outputs from projects are often intangible and are thus not possible to measure directly. While this know-how is relevant to achieving specific goals, it is difficult to quantify its value. Second, outputs from these projects are very complicated, combining the goals of the university and firm. Third, the benefits from these projects may only be comprehended over the long term [67]. It takes a long time to realize the benefits of these projects. Fourth, it is difficult to judge performance according to the reference value or target with which the performance indicator should be compared. The objectives, outputs, and organizational structure of IAC in different fields of science vary widely.
2.4. NDEA
The DEA is a method proposed by Charnes et al. [20] to mathematically contrast the productivities of distinct DMUs, according to various inputs and outputs. A DMU will be regarded as efficient when the relative efficiency is one and all the slack variables are zero [20]. Other DMUs with ratios lower than 1 are regarded as “less efficient” with respect to the efficient ones. (Please refer to the original work by Charnes et al. [20] for the fundamental concepts of how the relative efficiencies of DMUs can be derived.) Due to the fact that the weights associated with the input and output variables of DMUs are derived to maximize the ratio and are then compared with the most efficient DMUs, the measured productivity is also called “relative efficiency” [68].
One disadvantage of conventional DEA models is their ignorance of internal activities. For example, suppose the target firm has three departments that are closely interrelated. Each department uses its own input resources to generate its own output. However, in most cases, a department may use the partial or full outputs of other departments as its inputs. Such a scenario cannot be formulated using the traditional DEA model, where each input or output belongs only to one specific department [22].
To measure the efficiency of systems with linkage(s) inside, the NDEA models proposed by Färe and Grosskopf [69] can provide complete access to the underlying information of the black box and can evaluate the overall performance of the DMUs and individual components thereof. Following the efforts by Färe and Grosskopf [69], various scholars have proposed methods to tackle NDEA problems. Tone and Tsutsui [22] proposed a generic slack-based NDEA method, or the so-called network SBM, which can formally tackle intermediate products. Cook et al. [70] proposed a specific two-stage NDEA model, where the output from the first stage is the sole input to the second stage. Moreover, Cook et al. [71] explored the generic problem of an open multi-stage process by presenting overall efficiency as an additive-weighted average of the efficiencies of every single component or stage. Following Tone and Tsutsui’s effort [22], Fukuyama and Mirdehghan [72] proposed an NDEA method for deriving the efficiency of each DMU and the divisions inside, to prevent incorrect decisions caused by multiple optima [24].
MOP features a set of objective functions that should be optimized at the same time, and a set of well-defined constraints to be fulfilled [73]. In recent years, several scholars have proposed the NDEA-MOP model. Kao et al. [24] proposed models for NDEA-MOP methods. Despotis et al. [74] adopted an MOP model for evaluating efficiency through a two-stage process. Recently, Koronakos et al. [75] re-formulated some fundamental NDEA methodologies in a generic MOP framework. Compared with traditional NDEA approaches, NDEA-MOP has been verified as effective and discriminatory in an evaluation and manifests the following merits [76]. First, with MOP, the efficiency of the DMU and of its divisions can be optimized simultaneously [76]. Second, from the perspective of multi-level decision-making, the DMU level and the divisional level can work collaboratively to optimize their efficiencies [76]. Due to the advantages of the NDEA-MOP model in tackling real-world performance evaluation problems, an analytic framework based on this method will be introduced to tackle the performance evaluation of patent commercialization in IACs.
3. Research Methods
The first subsection introduces the modified Delphi method. The second subsection introduces NDEA. The third subsection defines the parameters and model of the NDEA-MOP, which will serve as the research method of this study, and evaluates the performance of IAC. Finally, the structure of the NDEA model is configured, which will serve as the basis for the empirical case study in Section 4.
3.1. Modified Delphi Method
The Delphi method, a research method for collective decision-making by anonymous experts [77], was proposed by the RAND Corporation in 1950. The way to solve a problem by the Delphi method is to repeat interviews or dispatch questionnaires for several iterations until a consensus can be reached. Although applicable to solving real-world problems, the traditional Delphi method wastes time and provides uncontrollable front and rear views of the expert group on a contradictory situation. Thus, Murry and Hommons [78] proposed a modified Delphi method to conquer the shortcomings of the traditional Delphi method. Based on this modified Delphi method, any criterion or alternative should be included in the decision-making problem when more than 75% of the experts invited to provide opinions agree with the specific criterion or alternative.
3.2. DEMATEL
DEMATEL was first proposed by Gabus and Fontela [79] to resolve complicated problems in the world. This graph theory-based method can be adopted to understand the influencing relationships among the criteria of an MCDM problem. In the past decade, the DEMATEL-based analytic framework and hybrid MCDM methods have been extensively implemented to resolve many decision-making problems, which include policy, management (e.g., [80,81,82]), education (e.g., [83,84,85,86]), engineering (e.g., [87]), medical devices (e.g., [88,89]), and other social problems (e.g., [90]).
The analytic procedure of DEMATEL can be formulated according to Tzeng and Huang [81], Yang et al. [91], and Huang et al. [87], as follows. At first, the initial direct relation matrix (IDRM) can be constructed according to the expert opinion questionnaires. The IDRM can be defined as , where is the number of objectives. Here, a 5-point Likert scale is adopted, where 5 indicates the highest degree of influence, while 1 indicates the lowest degree of influence. Then, the influence from the objective to the objective is denoted as , and is filled into the elements of the row and column in the IDRM. After that, the IDRM is normalized by multiplying the matrix with the factor , i.e., , where the maximum row sum and the maximum column sum can be selected;
is equal to the reciprocal of the larger one of the two numbers. That is:
The total relation matrix (TRM), , can be derived accordingly as follows:
where , is the identity matrix. The row sum and column sum vectors of the TRM can be derived as and , respectively. The sum of elements belonging to the -row and the -column can be denoted by and , respectively. The influence relation map (IRM) of all the objectives can be derived by demonstrating the influence relationships, where and represent the horizontal and vertical axes of the IRM.
3.3. DANP
DANP, a method proposed by Prof. Gwo-Hshiung Tzeng [92,93,94], is an analytic method that integrates DEMATEL and ANP. The traditional ANP-based analytic framework requires a pre-defined structure of the decision-making problem. Usually, an IRM that is being defined by DEMATEL (e.g., [80]) or a structure being derived by other decision-making methods will be adopted. The derivations of such a structure need extra time. The DANP method that transforms the TRM being derived by DEMATEL into the supermatrix of the AN, as proposed by Saaty [25], can reduce the time needed for structure derivations. Here, the process of the DANP method is summarized below, based on [87,95].
Let be equal to the transposed matrix of derived in Section 3.2. That is . The can be divided into submatrices, according to the number of aspects () to which the objectives belong. In other words, The submatrices can be denoted as , where and . Here, ni and nj are the numbers of objectives that belong to the ith aspect, , and the jth aspect, , respectively (see Equation (A11) of [87]). Then, every column of the submatrix, , should further be normalized by (see Equation (A12) of [87]). The normalized submatrix of can be formulated as according to Equation (A13) of [87]. The normalized TRM, , can serve as the unweighted supermatrix, , according to Equation (A6) of [87]. To derive the weighted supermatrix, the values of the elements belonging to each submatrix that belongs to the matrix can be summed and filled into the matrix , in which is the sum of all the elements belonging to the submatrix . Then, the matrix can be normalized as by normalizing each column to unity as follows, where . The weighted supermatrix, , can thus be calculated by multiplying the transposed matrix, , to , i.e., . Then, the weighted supermatrix can be calculated by raising the weighted supermatrix to its limiting powers, or . Detailed further explanations of the above process can be found in [87]. The global priority vectors can be derived accordingly, along with the weights associated with every objective.
3.4. NDEA-MOP Model
In this study, the NDEA model proposed by Kao et al. [24] will be adopted as the basis for developing the theoretic framework, where the multiple-objective decision-making method is used to develop the NDEA-MOP model. In this section, the MOP model for the compensatory solution is shown below.
The MOP Model is based on the BCC model. The notations are defined, following the work performed by Tone and Tsutsui [22] and Kao et al. [24]. We assume a total of DMUs can be found in the performance evaluation problem. Each DMU consists of divisions . We also assume that and are the numbers of inputs to and outputs from the division. The link streaming from Division to Division can be represented by and the set of links by . The observed input resources to at Division are ; the output products from at Division are ; the linking intermediate products from Division to Division are , where is the number of items in Link . Based on the above notations, the formula for the BCC-MOP model can be defined as follows:
Here, the objective equation is defined to evaluate the efficiency of in Division . and are the input and the outputs of the . is the weight of the input . is the weight of the output . is the weight associated with the incoming link . is the weight associated with the outgoing link . is a non-negative minimum that ensures that all weights are non-negative. is a constant with no positive or negative restrictions. To solve the mathematical programming problem, will be added to the original BCC model, so that the nonlinear programming problem can be transformed into a linear mathematical programming model. A feasible solution can thus be derived easily.
In order to solve the MOP problem, this research uses the NDEA-MOP method proposed by Kao et al. [24] to develop the following algorithms and proposes the following solutions. At first, the ideal solution for each objective is optimized independently. For , is maximized independently, where . Thus, the maximum values, , can be derived accordingly. After that, the anti-ideal solution for every objective will be derived independently; that is, for every objective equation, is minimized as . Then, the membership function for every objective can be defined as
Finally, the solutions can be derived according to Lee and Li [96]. The compensatory solution maximizes the weighted mean membership function of all objectives, as follows:
where is the weight for Division . In this work, we adopt the structural model proposed by [22], as seen in Figure 2. The problem can easily be solved by using LINGO.
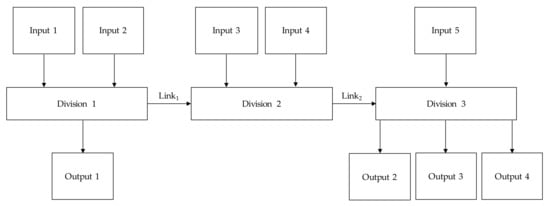
Figure 2.
Structure Model of NDEA. Note: graphic adapted from Tone and Tsutsui [22].
In general, the analytic process can be summarized as follows. First, users define DMUs, based on the literature review results. Then, the input and output data are formulated, according to the NDEA-MOP model defined in Section 3.3. The solution can be defined by LINGO, accordingly. Then, the performance of the DMUs can be evaluated. The process is demonstrated in Figure 3.

Figure 3.
Analytic Process.
4. Empirical Study
In this section, the IAC performance of major Taiwanese universities of technology will be evaluated, based on the NDEA-MOP introduced in Section 3. First, the development and current status of IAC and the patent commercialization of higher-education institutes in Taiwan will be introduced in Section 4.1. Then, the modified Delphi method will be introduced to confirm the input and output variables to be fed into the NDEA-MOP models in Section 4.2. The weights associated with the objectives of the NDEA-MOP models will be derived in Section 4.3, using the DANP method. The patent commercialization problem in IAC will be modeled in Section 4.4. Finally, the analytic results will be demonstrated in Section 4.5.
4.1. IAC and Patent Commercialization in Taiwan
The IACs of Taiwan originated from the establishment of work-study programs provided by vocational senior high schools in 1969. Over the past 50 years, these work-study programs have already provided sufficient workforces to the industrial firms and have thus accelerated the economic growth and competitiveness of the state. During the past three decades, the need to upgrade Taiwanese industries to technology and service ones [97] has given birth to the IAC model. In the initiation of IACs in Taiwan, numerous limitations were placed on the collaboration between industrial firms and universities, due to the government’s restrictions on the development of such collaborations [98]. However, the Taiwanese government changed its policy and has encouraged collaboration between industrial firms and academic institutes since the 1980s [98]. To cross the gap between university education and the industrial requirements for manpower, and to enhance the capabilities of industrial innovation, the Taiwanese government aggressively encourages IAC. Nowadays, the Taiwanese Ministry of Science and Technology (MOST) plays the dominant role in developing IAC, focusing on patent applications, technology transfer, and commercialization [98,99].
Currently, most of the patented technologies developed by Taiwanese universities are being transferred to enterprises in the form of IAC [100]. However, most schools still need to rely on external resources for help with patent commercialization [100]. According to Wang et al. [101], in comparison with top foreign universities, Taiwanese universities are weaker when it comes to commercializing their research results into products; moreover, these products are usually less valuable in the market. According to the Taiwanese Ministry of Economic Affairs [102], about 5,000 patents were granted to Taiwanese universities in 2016. In general, only three out of every one thousand patents granted to Taiwanese universities can be commercialized [102]; thus, the patent commercialization rate of Taiwanese universities is on around the same scale and is still very limited [102]. It is clear that an evaluation of IAC’s patent commercialization performance can meaningfully enhance Taiwan’s innovation capability.
Higher education in Taiwan features a dual-track system of general universities alongside universities of technology [103]. The universities of technology aim to develop a higher-level workforce in the fields of technology, engineering, and management [104]. For some of the leading institutions, like the Taiwan University of Science and Technology, AIC is always the university’s main mission [105]. Thus, 20 Taiwanese universities of technology will be adopted as the focus for empirical studies of the performance evaluation of patent commercialization in IAC, based on the DANP-based NDEA-MOP.
4.2. Confirmation of Input and Output Variables Using the Modified Delphi Method
First, the structure model was adapted from the work by Tone and Tsutsui [22]. The indicators for IAC patent commercialization were collected from the Ministry of Education, Taiwan (https://udb.moe.edu.tw/ReportCategories; accessed on 6 July 2021). Then, the modified Delphi method was introduced to confirm the input and output of and linkages between the divisions of the structure model, based on the opinions collected from industry experts (see Table 1). Based on the modified Delphi method, all these inputs, outputs, or linkages are agreed upon by more than 75% of the experts polled and are regarded as acceptable (see Table 2) for the NDEA-MOP model.

Table 1.
The list of experts.

Table 2.
The result from the questionnaire for the input and outputs.
4.3. Derivations of the Weights Associated with the Divisions
Based on the opinions provided by the polled experts, the influence of division on division is denoted as in the IDRM. By adopting the process introduced in Section 3.2, the IRM can be derived as shown in Table 3, while the TRM can be derived as shown in Table 4. Then, the row sum and column sum vectors of the TRM can be derived as and , respectively. All these aspects, as well as and versus each aspect, are demonstrated in Table 5. The IRM is demonstrated in Figure 4. Furthermore, the influence weights versus each division can be derived according to the procedure outlined in Section 3.3. Here, the academic department is defined as Division 1, while the university is defined as Division 2 of an IAC.

Table 3.
IRM.

Table 4.
TRM.

Table 5.
Variables for and weights versus each aspect.
Figure 4.
The IRM.
The significant confidence test proposed by Lu et al. [106] was introduced to verify whether the experts’ opinions are consistent, based on the IRM in Table 3. The significant confidence level can be derived according to Lu et al. [106], where which is smaller than 5%. That is, the significant confidence is 99.997%. Here, denotes the number of experts; is the average influence of the objective on the objective ; and denotes the number of objectives. Thus, the experts’ opinions are consistent.
4.4. The NDEA-MOP Model with Variables and Data
The NDEA-MOP problem can thus be formulated. In the structure model, two divisions, which include the department and the university, are included (see Figure 5). The inputs to the academic department include government grants and industry grants in New Taiwan Dollars (NTD). The output of the university division is the number of patents, which includes, but is not limited to, contractual research, authorization fees, royalties, and technology transfer fees. However, due to the availability of the open data, only the license fee and royalty, as well as the number of patents licensed, are included in the model. The unit of “license fee of IP” is in NTD. is the output from Division 1 to Division 2. The variable is defined as the total number of patents granted to the faculty belonging to a specific DMU or the technical university under investigation. In general, all the inputs, outputs, and linkages are summarized in Table 6.
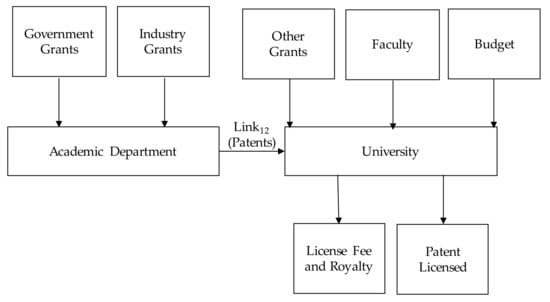
Figure 5.
Structure Model.

Table 6.
Input, output, and link variables of IAC.
After configuring the research model, the open data for these DMUs were collected from the Ministry of Education, Taiwan (https://udb.moe.edu.tw/ReportCategories; accessed on 6 July 2021). The original data for inputs, outputs, and linkages are given in Table 7. The data are further normalized by dividing by the maximum number of their respective columns, as shown in Table 8.

Table 7.
The original data of inputs, outputs and linkages (as of the year 2016).

Table 8.
Normalized inputs, outputs, and linkage.
4.5. The Efficiency of DMUs
In this subsection, the efficiency of the DMUs associated with each division will be derived separately. First, the ideal solution and the anti-ideal solution will be derived by using the BCC and CCR models, respectively, with LINGO. For Division 1, the inputs are government grants () and industry grants (), while the output is the number of patents () granted to the faculty. The number of patents () granted to the faculty also serves as the linkage and one of the inputs to Division 2. Except for the number of patents, other grants (), the number of faculty (), and budgets () will serve as the inputs of Division 2, while patents licensed to industrial firms and other institutes (), as well as license fees and royalties (), will serve as the outputs. The mathematical programming equations for the BCC of DMU1 are provided below as an example. The compensatory results for other DMUs can be derived in the same style:
The CCR results for every DMU can also be derived by removing from the above equations. The results derived by both the CCR and BCC models are demonstrated in Table 9. For the evaluations of the DMUs with the CCR model from the Division 1 aspect (academic departments), DMU A7 is the most efficient unit (Table 9). For the evaluations of the DMUs with the CCR model from the Division 2 aspect (university level), DMUs A1, A3, A4, A5, A11, A12, A13, A14, A18, and A19 are efficient. Further, regarding DMU evaluations with the BCC model from the Division 1 aspect (academic departments), DMUs A7, A9, and A10 are the efficient units, while A1, A3, A4, A5, A11, A12, A13, A14, A18, A19, and A20 are efficient for Division 2 evaluations (Table 9).

Table 9.
The results of the separation models.
Following the performance evaluations of independent divisions by the BCC and CCR models, the compensatory solution for evaluating the performance of two linked divisions will be derived. First, the performance will be evaluated using the BCC model, based on the structure model demonstrated in Figure 5 and the normalized inputs, outputs, and linkage in Table 8. Based on Equations (3)–(5), as well as the ideal solutions demonstrated in Table 9, the compensating solution to maximize a weighted average of all the membership functions of the target can be derived. (Here, the anti-ideal solutions are all 0s.) Because the overall performance, , will be measured for every DMU, by adopting the weights derived using the DANP in Section 4.3, the weights associated with Divisions 1 and 2, which are 0.488 and 0.512, will be adopted. The equation is:
Thus, the mathematical programming model for DMU A1, based on the BCC model, can be formulated as follows:
The CCR model can easily be formulated simply by removing and from the above equations. The results derived by both the BCC and CCR models are given in Table 10. Based on the analytic results derived by the CCR model, A14 and A15 are efficient DMUs in Division 1 (academic department level) (Table 10). For Division 2 (university level) evaluations, DMUs A1, A2, A3, A4, A11, A14, A18, and A19 are efficient. For the evaluation of overall performance by the CCR model, DMUs A14 and A18 top other DMUs and are ranked first and second, respectively. From the perspective of the BCC model (Table 10), A14 and A15 are efficient DMUs in Division 1. For Division 2 (university level) evaluations, DMUs A1, A2, A3, A4, A11, A12, A14, A18, and A19 are efficient. Finally, the evaluation of overall performance by the BCC model generates the same results as the ones generated by using the CCR model. DMUs A14 and A18 are ranked as the first and second, respectively (Table 10).

Table 10.
The results of compensatory models.
5. Discussion
The traditional DEA models have been widely adopted for solving performance evaluation problems. Though these models are very popular, they cannot correctly evaluate the performance of systems, e.g., supply chains, value networks, industrial–academic collaborations, etc. In particular, the linkages between the components of the systems have always been neglected. Thus, the traditional DEA models are not suitable for calculating the efficiency of such systems. The NDEA-MOP, an NDEA framework considering multiple objectives proposed in this work, can resolve this kind of problem and can evaluate the relative performance of systems. Especially, the integration of the DANP with the NDEA-MOP is very useful for solving performance evaluation problems in the real world. Compared with traditional DEA models, this approach is indeed a better one. In the following section, the managerial implications, advances in research methods, as well as limitations and future research possibilities, will be discussed.
5.1. Managerial Implications
According to the empirical results in Section 4, the managerial implications can be discussed from the aspect of the necessity of analyzing IAC problems in patent commercialization from the NDEA-MOP perspective, the advancement of research in the patent commercialization of IAC, the discussion of school management, and the influence of the relationship between the university administration and academic departments.
We cannot ignore the role of the intermediate data when we evaluate the relative efficiency of DMUs, in the case of multiple inputs and multiple outputs [107]. It is common in IAC that part of the outputs of Division 1 become the inputs of Division 2. Although traditional DEA methods have been applied to measure the relative efficiency of DMUs, based on their inputs and outputs, the DEA model is unable to evaluate the transfer of inputs and outputs inside a DMU. NDEA-MOP takes the input/output transfer among divisions inside a DMU into consideration. To provide a more precise performance evaluation of IAC, we suggest that decision-makers should use the NDEA-MOP model.
There are at least two divisions in a DMU in IAC. It is important to determine the appropriate weights in different divisions in order to evaluate the overall performance of IAC. This study suggests that it is appropriate to adopt the weights derived by the DANP in Section 4.3, instead of letting decision-makers determine the weights themselves.
The overall patent commercialization performance of IAC in DMUs is affected by the efficiency of both Divisions 1 and 2. We find that the overall performance may not be good when one division is efficient but the other one is inefficient, for example, in the results derived by the compensatory models (Table 10), A15 is an efficient DMU in Division 1. However, the DMU is inefficient from both the aspect of Division 2 and the overall performance. Similarly, the DMU A19 is efficient from the perspective of Division 2. However, the DMU is inefficient, from the perspectives of Division 1 and the overall performance. Thus, we suggest that universities that want to improve their overall performance in IAC patent commercialization should simultaneously monitor the efficiency of Divisions 1 and 2. The way to improve the efficiency of Division 1, or the academic department, is to encourage the faculty to apply for patents after they complete the IAC. To increase the possibility of obtaining patents, government administrators or firm managers who decide to provide grants to universities should evaluate the past performance of IAC, the capabilities of the research teams, and the potential of proposals from the patent commercialization aspect. In addition, it is important to continue to monitor performance during the lifespan of projects. From the Division 2 perspective, one way to improve efficiency is via budget-planning for patent commercialization. Inventions in the faculties should be checked regularly (e.g., quarterly or annually) for patentable technologies. Furthermore, key performance indicators can be defined to help monitor the performance of university patent commercialization in general, and the patent commercialization performance of IACs in particular.
Regarding the performance evaluation results, we found that about one-half of the university administrations were already efficient, whether seen from the perspective of the separation model or of the compensatory solution. Table 11 below summarizes the results of the separation model and the compensatory solution from Table 9 and Table 10.

Table 11.
Efficient DMUs in different analytic models.
Based on the separation model, 1 DMU of the CCR model and 3 DMUs of the BCC model are efficient from the perspective of Division 1 (see Table 11). Based on Division 2, 10 DMUs of the CCR model and 11 DMUs of the BCC model are efficient. However, no single example of the DMUs is efficient. Since each division in a DMU is treated as an independent unit and the linking activities between other divisions are totally neglected, the separation model is insufficient for evaluating the efficiencies [24]. Therefore, the results derived from the separation model can only serve as a contrast, which can help demonstrate the effectiveness of the compensatory solution as a way to derive meaningful performance evaluation results.
Based on the compensatory solution, 9 DMUs of the CCR model and 10 DMUs of the BCC model are efficient, from the perspective of Division 2 (see Table 11). However, no DMU was efficient from the perspective of Division 1. The analytic results may be due to the universities’ aggressive pursuit of every kind of government grant from the Ministry of Education (e.g., the Aim for the Top University Project, Higher Education SPROUT Project, etc.). Furthermore, due to the historical faculty promotion system, most Taiwanese professors were dedicated to pursuing academic publications in indexed journals (e.g., SCI and SSCI journals). Few faculty members were dedicated to applying for patents. The analytic results are also consistent with the work of Hsu et al. [108], who argued that Taiwan’s universities are dedicated to basic research in pursuit of academic publications rather than to applied research; the criteria of university faculty promotion in Taiwan tend to emphasize academic publications [108]. Thus, the performances of academic departments in IAC were less satisfactory.
From the aspect of the overall performance of IAC, A1, A2, A4, A11, A12, A14, and A18 is higher than 0.6. The results suggest that these DMUs are more efficient. However, the overall performance of all DMUs is still far from satisfactory. The results are consistent with the current status of Taiwanese patent commercialization. As has already been mentioned in Section 4.1, only three out of every one thousand patents granted to Taiwanese citizens can be commercialized [102], not to mention the commercialization of patents granted to Taiwanese universities. Furthermore, the overall performance of some DMUs is poor because their academic divisions are less efficient, which may be due to the overemphasizing of academic publications in the current system.
Except for the aspect of performance evaluation, the current study has advanced the research on higher education, especially on vocational education. In the past, very few works have tried to study the influence of relationships between the university administration (Division 2) and academic departments (Division 1). Furthermore, very few works have tried to explore the dominance of both parties. In this work, we found that the academic department is playing a more influential role in developing industrial–academic cooperation. In contrast, the university administration is influenced by the academic departments. In Taiwan, traditionally, it was widely recognized that professors initiated the IAC projects. The university administration helped finish the administrative work. This analytic result is consistent with traditional cognition. Furthermore, although academic departments play a more influential role, both parties have almost equal weights in the collaboration. Even so, the university administration is a little more important in such performance evaluation or in resolving decision-making problems. The result may be due to the influence of universities’ resources on industry cooperation, as was argued by Nam et al. [109]. Another possible way that the university administration can influence the performance of academic departments by aggressively pursuing IAC is the compensation policy initiated by several Taiwanese universities in recent years. In this arrangement, the faculty will receive monetary and other rewards. Such reward policies encourage the faculty to aggressively initiate or pursue IAC projects and commercialize patents. Such an influence relationship can also be reflected in the weights of both parties in the IAC.
5.2. Advances in the Research Method
This work mainly advances research methods in the integration of MCDM and MODM methods, in the introduction of real weights into the NDEA-MOP models for performance evaluation in general, and in the evaluations of IAC in particular. Solving MCDM problems by combining different methods is not new, as many authors have used this approach. For example, Lu et al. [106] adopted DEMATEL, DANP and VIseKriterijumska Optimizacija I Kompromisno Resenje (VIKOR) to evaluate the factors that influence the adoption of radio frequency identification (RFID). Yang et al. [91] integrated DEMATEL, DANP, and VIKOR to evaluate and select disaster-recovery sites for information systems of academic big data. Huang et al. [88] evaluated the investment projects of spinal medical device firms, using the real option and DANP, with modified VIKOR (DANP-mV)-based MCDM methods. In fact, the DANP method has been widely adopted for weighting criteria in other studies. However, very few scholars have tried to integrate DANP to derive the weights associated with the objectives of an MODM problem. However, the mutual influence relationships among objectives can always be found in an MODM problem in general, and MOP-based DEA problems in particular. Such influential relationships among the objectives are always crucial and cannot be neglected. For example, in the empirical case in this work, the mutual influence relationships between the objective of academic departments and the objective of a university (see Figure 4) are very significant and meaningful (see Section 5.1 for an analysis of the influences of university administrations on the IAC-performance of academic departments).
Furthermore, people were used to dealing with MCDM and MODM problems separately. As mentioned above, numerous works have been dedicated to DEMATEL- or DANP-based research. However, the influence of relationships and the weights derived therefrom were seldom introduced into real-world mathematical programming problems with multiple objectives. However, such integrations are very important. So, the integration of real weights into the MODM programs crosses the research gap of fusing MCDM and MODM problems in resolving real-world problems.
5.3. Limitations and Future Possibilities
In this work, only Taiwanese universities of technology were investigated. Furthermore, due to the very low availability of financial information from the industry, the patent commercialization performance of IAC was only investigated based on the open data from the Taiwanese Ministry of Education. Thus, the results may be controversial. In the future, the outputs of the university division may include more detailed information (e.g., authorization fees, royalties, and technology transfer fees) when available. The introduction of industry data into the analytic framework, as well as analyses based on the data of multiple periods, will also be very helpful in offering more insights into performance evaluation.
6. Conclusions
IAC is mutually beneficial to firms and universities. Through industrial collaboration, universities obtain funding to undertake research and have the opportunities to take an invention or product from conception to market. Through cooperation with universities, firms that are aligned with early-stage research may find opportunities to get a head start on their competition. IAC has become a trend in recent years. Patent commercialization is one of the major channels for transferring the academic knowledge embedded in technology to industrial firms or for realizing the benefits of IAC. However, the rates of the successful commercialization of academic patents belonging to higher-education institutions in most countries are still low. Thus, finding ways to evaluate the patent commercialization performance of IAC becomes a critical issue.
Universities that undertake industry–academic projects vary in size, resources, and faculty capabilities. In addition, at least two divisions (departments and universities) are interrelated. The outputs of IAC from departments, such as patents, are the inputs of universities. These characteristics make the DEA unsuitable for evaluating the performance of IAC. In order to evaluate the performance of IAC, this study not only considers the variables of the inputs and outputs from the industry–university cooperation but also uses NDEA-MOP to consider the link between the university and its departments.
In this work, the performance of the patent commercialization of major Taiwanese universities of technology was evaluated, based on the NDEA-MOP model. From interpreting the analytic results, it is shown that the academic departments and the faculty play a more influential role in the patent commercialization in IAC. About half of the university administrations have been efficient. However, the performance of most academic departments should be enhanced. The reasons for the inefficiency of academic departments may be due to the overemphasis of journal paper publications in the promotion system. Further, university administrations play a more important role than academic departments in IAC, due to the compensation policy initiated by Taiwanese universities in recent years. The policy can encourage the faculty to aggressively pursue IACs and commercializing patents.
This study has various suggestions for future research. First, this research uses only one year’s data, obtained from the government’s public information, for the analyses. Future research can collect multi-year data to evaluate the performance of IAC. Second, this study uses 20 universities of technology as the sample. Thus, the outputs of IAC mainly consider the number of patents, patents licensed, license fees, and royalties. Future research can use corporate-sponsored research projects in business schools in universities as a sample to evaluate the overall performance of IAC. These studies should choose other outputs for their analyses.
Author Contributions
C.-Y.H. designed, performed research, and analyzed the data, wrote, and revised the paper. M.-J.Y. analyzed the data and wrote portions of the empirical study case. J.-F.L. wrote the background of the empirical case of industrial academic cooperation. H.C. discussed and concluded the whole article. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially granted by National Taiwan Normal University and MOST, Taiwan (MOST 106-2221-E-003-019-MY3; MOST 107-2629-M-492-001-MY2; MOST 110-2621-M-003-005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Marotta, D.; Mark, M.; Blom, A.; Thorn, K. Human Capital and University-Industry Linkages’ Role in Fostering Firm Innovation: An Empirical Study of Chile and Colombia; The World Bank: Washington, DC, USA, 2007. [Google Scholar]
- Perkmann, M.; Neely, A.; Walsh, K. How should firms evaluate success in university–industry alliances? A performance measurement system. R D Manag. 2011, 41, 202–216. [Google Scholar] [CrossRef]
- Ankrah, S.; Omar, A.-T. Universities–industry collaboration: A systematic review. Scand. J. Manag 2015, 31, 387–408. [Google Scholar] [CrossRef]
- Marhl, M.; Pausits, A. Third mission indicators for new ranking methodologies. Eval High Educ. 2011, 5, 43–64. [Google Scholar] [CrossRef]
- Perkmann, M.; Tartari, V.; McKelvey, M.; Autio, E.; Broström, A.; D’este, P.; Fini, R.; Geuna, A.; Grimaldi, R.; Hughes, A. Academic engagement and commercialisation: A review of the literature on university–industry relations. Res. Policy 2013, 42, 423–442. [Google Scholar] [CrossRef]
- Rybnicek, R.; Königsgruber, R. What makes industry–university collaboration succeed? A systematic review of the literature. J. Bus. Econ. 2019, 89, 221–250. [Google Scholar] [CrossRef] [Green Version]
- Guimón, J. Promoting University-Industry Collaboration in Developing Countries. The Innovation Policy Platform; World Bank: New York, NY, USA, 2013. [Google Scholar]
- Philbin, S.P. Developing and Managing University-Industry Research Collaborations through a Process Methodology/Industrial Sector Approach. J. Res. Adm. 2010, 41, 51–68. [Google Scholar]
- Jiang, M.; Zhou, P. Research on the patent innovation performance of university–industry collaboration based on complex network analysis. J. Bus.-to-Bus. Mark 2014, 21, 65–83. [Google Scholar]
- Guan, J.C.; Yam, R.C.; Mok, C.K. Collaboration between industry and research institutes/universities on industrial innovation in Beijing, China. Technol. Anal. Strateg. Manag. 2005, 17, 339–353. [Google Scholar] [CrossRef]
- George, G.; Zahra, S.A.; Wood, D.R. The effects of business–university alliances on innovative output and financial performance: A study of publicly traded biotechnology companies. J. Bus. Ventur. 2002, 17, 577–609. [Google Scholar] [CrossRef]
- Perrini, F.; Tencati, A. Sustainability and stakeholder management: The need for new corporate performance evaluation and reporting systems. Bus. Strategy Environ. 2006, 15, 296–308. [Google Scholar] [CrossRef]
- Anderson, T.R.; Daim, T.U.; Lavoie, F.F. Measuring the efficiency of university technology transfer. Technovation 2007, 27, 306–318. [Google Scholar] [CrossRef]
- Rast, S.; Khabiri, N.; Senin, A.A. Evaluation framework for assessing university-industry collaborative research and technological initiative. Procedia Soc. Behav. Sci. 2012, 40, 410–416. [Google Scholar] [CrossRef] [Green Version]
- Crescenzi, R.; Filippetti, A.; Iammarino, S. Academic inventors: Collaboration and proximity with industry. J. Technol. Transf. 2017, 42, 730–762. [Google Scholar] [CrossRef]
- Gong, H.; Peng, S. Effects of patent policy on innovation outputs and commercialization: Evidence from universities in China. Scientometrics 2018, 117, 687–703. [Google Scholar] [CrossRef]
- Hsu, D.H.; Hsu, P.-H.; Zhou, T.; Ziedonis, A.A. Benchmarking U.S. university patent value and commercialization efforts: A new approach. Res. Policy 2021, 50, 104076. [Google Scholar] [CrossRef]
- D’Este, P.; Patel, P. University–industry linkages in the UK: What are the factors underlying the variety of interactions with industry? Res. Policy 2007, 36, 1295–1313. [Google Scholar] [CrossRef]
- Ramos-Vielba, I.; Fernández-Esquinas, M.; Espinosa-de-los-Monteros, E. Measuring university–industry collaboration in a regional innovation system. Scientometrics 2010, 84, 649–667. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Tone, K.; Tsutsui, M. Network DEA: A slacks-based measure approach. Eur. J. Oper. Res. 2009, 197, 243–252. [Google Scholar] [CrossRef] [Green Version]
- Seiford, L.M.; Zhu, J. Profitability and marketability of the top 55 US commercial banks. Manag. Sci. 1999, 45, 1270–1288. [Google Scholar] [CrossRef] [Green Version]
- Kao, H.-Y.; Chan, C.-Y.; Wu, D.-J. A multi-objective programming method for solving network DEA. Appl. Soft Comput. 2014, 24, 406–413. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Han, J. Technology commercialization through sustainable knowledge sharing from university-industry collaborations, with a focus on patent propensity. Sustainability 2017, 9, 1808. [Google Scholar] [CrossRef] [Green Version]
- Wang, J. Knowledge creation in collaboration networks: Effects of tie configuration. Res. Policy 2016, 45, 68–80. [Google Scholar] [CrossRef] [Green Version]
- Perkmann, M.; Walsh, K. University–industry relationships and open innovation: Towards a research agenda. Int. J. Manag. Rev. 2007, 9, 259–280. [Google Scholar] [CrossRef]
- Hagedoorn, J.; Link, A.N.; Vonortas, N.S. Research partnerships1. Res. Policy 2000, 29, 567–586. [Google Scholar] [CrossRef]
- D’Este, P.; Guy, F.; Iammarino, S. Shaping the formation of university–industry research collaborations: What type of proximity does really matter? J. Econ. Geogr. 2012, 13, 537–558. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-H.; Wang, M.-Y. Complementary assets, appropriability, and patent commercialization: Market sensing capability as a moderator. Asia Pacific Manag. Rev. 2015, 20, 141–147. [Google Scholar] [CrossRef]
- Baldini, N.; Grimaldi, R.; Sobrero, M. To patent or not to patent? A survey of Italian inventors on motivations, incentives, and obstacles to university patenting. Scientometrics 2007, 70, 333–354. [Google Scholar] [CrossRef]
- Ambos, T.C.; Mäkelä, K.; Birkinshaw, J.; d’Este, P. When does university research get commercialized? Creating ambidexterity in research institutions. J. Manag. Stud. 2008, 45, 1424–1447. [Google Scholar] [CrossRef]
- Wu, Y.; Welch, E.W.; Huang, W.-L. Commercialization of university inventions: Individual and institutional factors affecting licensing of university patents. Technovation 2015, 36–37, 12–25. [Google Scholar] [CrossRef]
- Giuri, P.; Munari, F.; Pasquini, M. What determines university patent commercialization? Empirical evidence on the role of IPR ownership. Ind. Innov. 2013, 20, 488–502. [Google Scholar] [CrossRef]
- Agrawal, A.; Henderson, R. Putting patents in context: Exploring knowledge transfer from MIT. Manag. Sci. 2002, 48, 44–60. [Google Scholar] [CrossRef]
- Ripoll Feliu, V.; Diaz Rodriguez, A. Knowledge transfer and university-business relations: Current trends in research. Intang. Cap. 2017, 13, 697–719. [Google Scholar] [CrossRef] [Green Version]
- De Wit-de Vries, E.; Dolfsma, W.A.; van der Windt, H.J.; Gerkema, M.P. Knowledge transfer in university–industry research partnerships: A review. J. Technol. Transf. 2019, 44, 1236–1255. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, J.J.; Carayannis, E.G. University-industry knowledge transfer-unpacking the “black box”: An introduction. Knowl. Manag. Res. Pract. 2019, 17, 353–357. [Google Scholar] [CrossRef]
- De Almeida, M.V.; Ferreira, J.J.; Ferreira, F.A. Developing a multi-criteria decision support system for evaluating knowledge transfer by higher education institutions. Knowl. Manag. Res. Pract. 2018, 17, 358–372. [Google Scholar] [CrossRef]
- Kang, B.; Motohashi, K. Academic contribution to industrial innovation by funding type. Scientometrics 2020, 124, 169–193. [Google Scholar] [CrossRef]
- Hou, B.; Hong, J.; Chen, Q.; Shi, X.; Zhou, Y. Do academia-industry R&D collaborations necessarily facilitate industrial innovation in China? The role of technology transfer institutions. Eur. J. Innov. Manag. 2019, 22, 717–746. [Google Scholar]
- Rothaermel, F.T.; Agung, S.D.; Jiang, L. University entrepreneurship: A taxonomy of the literature. Ind. Corp. Chang. 2007, 16, 691–791. [Google Scholar] [CrossRef]
- Shane, S. Selling university technology: Patterns from MIT. Manag. Sci. 2002, 48, 122–137. [Google Scholar] [CrossRef]
- Thursby, J.G.; Thursby, M.C. Who is selling the ivory tower? Sources of growth in university licensing. Manag. Sci. 2002, 48, 90–104. [Google Scholar] [CrossRef] [Green Version]
- Sine, W.D.; Shane, S.; Gregorio, D.D. The halo effect and technology licensing: The influence of institutional prestige on the licensing of university inventions. Manag. Sci. 2003, 49, 478–496. [Google Scholar] [CrossRef] [Green Version]
- Shane, S.; Stuart, T. Organizational endowments and the performance of university start-ups. Manag. Sci. 2002, 48, 154–170. [Google Scholar] [CrossRef] [Green Version]
- Wright, M.; Lockett, A.; Clarysse, B.; Binks, M. University spin-out companies and venture capital. Res. Policy 2006, 35, 481–501. [Google Scholar] [CrossRef]
- Munari, F.; Toschi, L. Do venture capitalists have a bias against investment in academic spin-offs? Evidence from the micro-and nanotechnology sector in the UK. Ind. Corp. Chang. 2011, 20, 397–432. [Google Scholar] [CrossRef]
- Drucker, P.S. The Practice of Management: A study of the Most Important Function in America Society; Harper & Row: New York, NY, USA, 1954. [Google Scholar]
- Ahmed, I.; Sultana, I.; Paul, S.K.; Azeem, A. Employee performance evaluation: A fuzzy approach. Int. J. Product. Perform. Manag. 2013, 62, 718–734. [Google Scholar] [CrossRef]
- Murphy, K.R. Performance evaluation will not die, but it should. Hum. Resour. Manag. J. 2020, 30, 13–31. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.-Y.; Tzeng, G.H.; Chen, Y.T.; Chen, H. Performance evaluation of leading fabless integrated circuit design houses by using a multiple objective programming based data envelopment analysis approach. Int. J. Innov. Comput. Inf. Control. 2012, 8, 5899–5916. [Google Scholar]
- Wu, M.-J.; Huang, C.-Y.; Kao, Y.-S.; Lue, Y.-F.; Chen, L.-C. Developing a professional performance evaluation system for pre-Service automobile repair vocational high school teachers in Taiwan. Sustainability 2018, 10, 3537. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Trimi, S. A fuzzy TOPSIS method for performance evaluation of reverse logistics in social commerce platforms. Expert Syst. Appl. 2018, 103, 133–145. [Google Scholar] [CrossRef]
- Kao, Y.-S.; Nawata, K.; Huang, C.-Y. Evaluating the performance of systemic innovation problems of the IoT in manufacturing industries by novel MCDM methods. Sustainability 2019, 11, 4970. [Google Scholar] [CrossRef] [Green Version]
- Islam, R.; bin Mohd Rasad, S. Employee performance evaluation by the AHP: A case study. Asia Pacific Manag. Rev. 2006, 11, 163–176. [Google Scholar]
- Karim, A.; Arif-Uz-Zaman, K. A methodology for effective implementation of lean strategies and its performance evaluation in manufacturing organizations. Bus. Process Manag. J. 2013, 19, 169–196. [Google Scholar] [CrossRef]
- Mone, E.M.; London, M. Employee Engagement Through Effective Performance Management: A Practical Guide for Managers, 2nd ed.; Routledge: New York, NY, USA, 2018. [Google Scholar]
- Zhang, L.; Luo, Y. Evaluation of input output efficiency in higher education based on data envelope analysis. Int. J. Database Theory Appl. 2016, 9, 221–230. [Google Scholar] [CrossRef]
- Kerssens-van Drongelen, I.; Nixon, B.; Pearson, A. Performance measurement in industrial R&D. Int. J. Manag. Rev. 2000, 2, 111–143. [Google Scholar]
- Moed, H.F. Citation Analysis in Research Evaluation; Springer Science & Business Media: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Louis, K.S.; Blumenthal, D.; Gluck, M.E.; Stoto, M.A. Entrepreneurs in academe: An exploration of behaviors among life scientists. Adm. Sci. Q. 1989, 1, 110–131. [Google Scholar] [CrossRef]
- Bercovitz, J.; Feldman, M. Academic entrepreneurs: Organizational change at the individual level. Organ. Sci. 2008, 19, 69–89. [Google Scholar] [CrossRef] [Green Version]
- Nugent, A.; Chan, H.F.; Dulleck, U. Government Funding of University-Industry Collaboration: Exploring the Impact of Targeted Funding on University Patent Activity [Working Paper]; QUT Business School: Brisbane, QLD, Australia, 2019. [Google Scholar]
- Albats, E.; Fiegenbaum, I.; Cunningham, J.A. A micro level study of university industry collaborative lifecycle key performance indicators. J. Technol. Transf. 2018, 43, 389–431. [Google Scholar] [CrossRef]
- Voytek, K.P.; Lellock, K.L.; Schmit, M.A. Developing performance metrics for science and technology programs: The case of the manufacturing extension partnership program. Econ. Dev. Q. 2004, 18, 174–185. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Erol, S. The DEA–FUZZY ANP department ranking model applied in Iran Amirkabir University. Acta Polytech. Hung. 2010, 7, 103–114. [Google Scholar]
- Färe, R.; Grosskopf, S. Productivity and intermediate products: A frontier approach. Econ. Lett. 1996, 50, 65–70. [Google Scholar] [CrossRef]
- Cook, W.D.; Liang, L.; Zhu, J. Measuring performance of two-stage network structures by DEA: A review and future perspective. Omega 2010, 38, 423–430. [Google Scholar] [CrossRef]
- Cook, W.D.; Zhu, J.; Bi, G.; Yang, F. Network DEA: Additive efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 1122–1129. [Google Scholar] [CrossRef]
- Fukuyama, H.; Mirdehghan, S.M. Identifying the efficiency status in network DEA. Eur. J. Oper. Res. 2012, 220, 85–92. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Huang, J.-J. Fuzzy Multiple Objective Decision Making; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Despotis, D.K.; Koronakos, G.; Sotiros, D. Composition versus decomposition in two-stage network DEA: A reverse approach. J. Product. Anal. 2016, 45, 71–87. [Google Scholar] [CrossRef] [Green Version]
- Koronakos, G.; Sotiros, D.; Despotis, D.K. Reformulation of Network Data Envelopment Analysis models using a common modelling framework. Eur. J. Oper. Res. 2019, 278, 472–480. [Google Scholar] [CrossRef] [Green Version]
- Kao, H.-Y.; Bold, T. Evaluating Human Resource Efficiencies of Mongolian Hospitals with network DEA. Int. J. Inf. 2017, 28, 177–194. [Google Scholar]
- Brady, S.R. Utilizing and adapting the Delphi method for use in qualitative research. Int. J. Qual. Methods 2015, 14, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Murry, J.W., Jr.; Hammons, J.O. Delphi: A versatile methodology for conducting qualitative research. Rev. High. Educ. 1995, 18, 423–436. [Google Scholar] [CrossRef]
- Gabus, A.; Fontela, E. World Problems, an Invitation to Further Thought within the Framework of DEMATEL; Battelle Geneva Research Center: Geneva, Switzerland, 1972. [Google Scholar]
- Huang, C.-Y.; Shyu, J.Z.; Tzeng, G.-H. Reconfiguring the innovation policy portfolios for Taiwan’s SIP Mall industry. Technovation 2007, 27, 744–765. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Huang, C.-Y. Combined DEMATEL technique with hybrid MCDM methods for creating the aspired intelligent global manufacturing & logistics systems. Ann. Oper. Res. 2012, 197, 159–190. [Google Scholar]
- Kao, Y.-S.; Nawata, K.; Huang, C.-Y. Systemic functions evaluation based technological innovation system for the sustainability of IoT in the manufacturing industry. Sustainability 2019, 11, 2342. [Google Scholar] [CrossRef] [Green Version]
- Shyu, J.Z.; Huang, C.-Y. Configuring the knowledge diffusion policy portfolio of higher education institutes. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 5685–5734. [Google Scholar]
- Huang, C.-Y.; Kao, Y.-S.; Lu, H.-H.; Wu, M.-J. Curriculum development for enhancing the imagination in the technology commercialization process. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 6249–6283. [Google Scholar]
- Shiau, S.J.; Huang, C.-Y.; Yang, C.-L.; Juang, J.-N. A derivation of factors influencing the innovation diffusion of the OpenStreetMap in STEM education. Sustainability 2018, 10, 3447. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.-Y.; Wang, H.-Y.; Yang, C.-L.; Shiau, S.J. A derivation of factors influencing the diffusion and adoption of an open source learning platform. Sustainability 2020, 12, 7532. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Chung, P.-H.; Shyu, J.Z.; Ho, Y.-H.; Wu, C.-H.; Lee, M.-C.; Wu, M.-J. Evaluation and selection of materials for particulate matter MEMS sensors by using hybrid MCDM methods. Sustainability 2018, 10, 3451. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.-Y.; Hsieh, H.-L.; Chen, H. Evaluating the investment projects of spinal medical device firms using the real option and DANP-mV based MCDM methods. Int. J. Environ. Res. Public Health 2020, 17, 3335. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Tung, I. Strategies for heterogeneous r&d alliances of in vitro diagnostics firms in rapidly catching-up economies. Int. J. Environ. Res. Public Health 2020, 17, 3688. [Google Scholar]
- Yang, C.-L.; Shieh, M.-C.; Huang, C.-Y.; Tung, C.-P. A derivation of factors influencing the successful integration of corporate volunteers into public flood disaster inquiry and notification systems. Sustainability 2018, 10, 1973. [Google Scholar] [CrossRef] [Green Version]
- Yang, C.-L.; Huang, C.-Y.; Kao, Y.-S.; Tasi, Y.-L. Disaster Recovery Site Evaluations and Selections for Information Systems of Academic Big Data. Eurasia J. Math. Sci. Technol. Educ. 2017, 13, 4553–4589. [Google Scholar]
- Liu, C.-H.; Tzeng, G.-H.; Lee, M.-H. Improving tourism policy implementation—The use of hybrid MCDM models. Tour. Manag. 2012, 33, 413–426. [Google Scholar] [CrossRef]
- Phillips-Wren, G.; Jain, L.C.; Nakamatsu, K.; Howlett, R.J. Advances in Intelligent Decision Technologies: Proceedings of the Second Kes International Symposium Idt 2010; Springer: Berlin, Germany, 2010. [Google Scholar]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Huang, C.-Y.; Yang, C.-L.; Hsiao, Y.-H. A Novel Framework for Mining Social Media Data Based on Text Mining, Topic Modeling, Random Forest, and DANP Methods. Mathematics 2021, 9, 2041. [Google Scholar] [CrossRef]
- Lee, E.S.; Li, R.J. Fuzzy multiple objective programming and compromise programming with Pareto optimum. Fuzzy Sets Syst. 1993, 53, 275–288. [Google Scholar]
- Lo, W.Y.W. Taiwan’s Higher Education System in Context; University Rankings; Springer: Singapore, 2014; pp. 15–39. [Google Scholar]
- Huang, C.-Y.; Yang, C.-W.; Fang, S.-C. The contrasting interaction effects of university-industry collaboration motivation with demographic characteristics on university-industry collaboration performance in Taiwan. Technol. Anal. Strateg. Manag. 2019, 31, 1048–1062. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chen, M.H.; Yang, I.S. Policy Instruments to Foster University-Industry Links: A Comparative Study of U.K., U.S. and Taiwan; Ministry of Economic Affair Conference: Taipei, Taiwan, 2002.
- Executive Yuan. Program for the Promotion of Invention Patent Industrialization; Executive Yuan: Taipei, Taiwan, 2010. [Google Scholar]
- Wang, M.-Y.; Lin, J.-H.; Lo, H.-C. Influential factors of the commercialization of academic patents: The Taiwan experience. In Proceedings of the PICMET’12: Technology Management for Emerging Technologies, Vancouver, BC, Canada, 29 July–2 August 2012. [Google Scholar]
- Intellectual Property Office. The Incubation Mechanism of University Spin-Off Companies of R&D Services. Available online: https://pcm.tipo.gov.tw/PCM2010/pcm/commercial/show/article_detail.aspx?aType=1&Articletype=1&aSn=629 (accessed on 27 July 2021).
- Department of Higher Education. Higher Education in Taiwan 2012–2013; Department of Higher Education, Ministry of Education: Taipei, Taiwain, 2012.
- Lee, L.-S. Technological and Vocational Education in Taiwan. In Proceedings of the Conference of the Japan Academic Society for Industrial Education (JASIE), 8 July 2000; Available online: https://eric.ed.gov/?id=ED441956 (accessed on 27 July 2021).
- Ho, M.H.-C.; Liu, J.S.; Kuan, M.C.-H. Torn between academic publications and university–industry collaboration. Res. Eval. 2016, 25, 151–160. [Google Scholar] [CrossRef]
- Lu, M.-T.; Lin, S.-W.; Tzeng, G.-H. Improving RFID adoption in Taiwan’s healthcare industry based on a DEMATEL technique with a hybrid MCDM model. Decis. Support Syst. 2013, 56, 259–269. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S. Network DEA. Socio Econ. Plan. Sci. 2000, 1, 35–49. [Google Scholar] [CrossRef]
- Hsu, D.W.; Shen, Y.-C.; Yuan, B.J.; Chou, C.J. Toward successful commercialization of university technology: Performance drivers of university technology transfer in Taiwan. Technol. Forecast. Soc. Chang. 2015, 92, 25–39. [Google Scholar] [CrossRef]
- Nam, G.M.; Kim, D.G.; Choi, S.O. How resources of universities influence industry cooperation. J. Open Innov. Technol. Mark. Complex. 2019, 5, 9. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).