A Posteriori Fractional Tikhonov Regularization Method for the Problem of Analytic Continuation
Abstract
1. Introduction
2. An A Posteriori Regularization Parameter Choice Rule for the Fractional Tikhonov Method and the Convergence Estimate
- (a)
- is a continuous function;
- (b)
- ;
- (c)
- ;
- (d)
- is a strictly increasing function over .
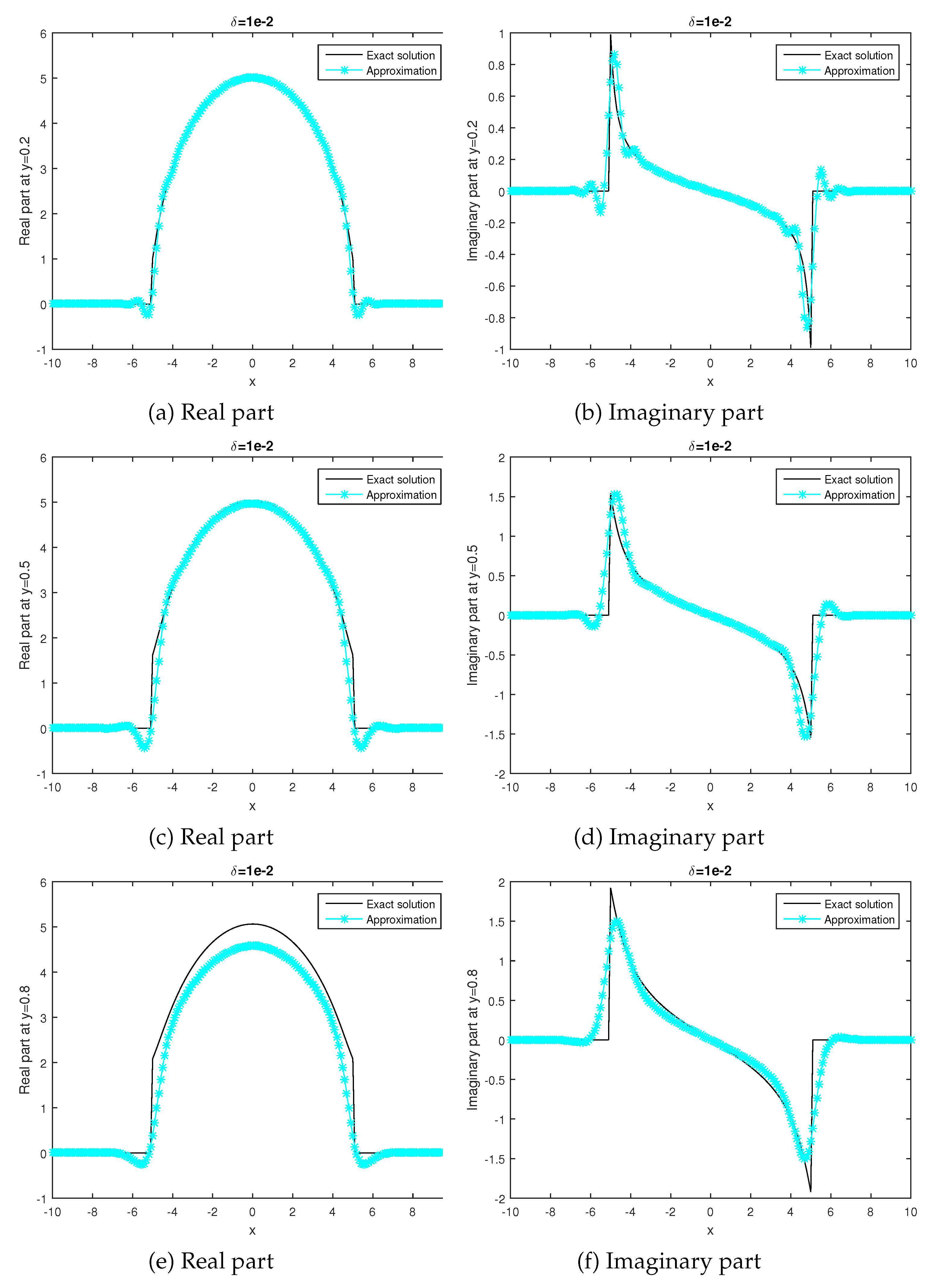
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franklin, J. Analytic contiunation by the fast Fourier transform. SIAM. Sci. Stat. Comput. 1990, 11, 112–122. [Google Scholar] [CrossRef][Green Version]
- Ramm, A.G. The ground-penetrating radar problem. J. Inverse Ill-Posed Problem. 2000, 8, 23–30. [Google Scholar] [CrossRef][Green Version]
- Stefanescu, I.S. On the stable analytic continuation with a condition of uniform boundedness. J. Math. Phys. 1986, 27, 2657–2686. [Google Scholar] [CrossRef]
- Natterer, F. Image reconstruction in quantitative susceptibility mappling. SIAM J. Imaging Sci. 2016, 9, 1127–1131. [Google Scholar] [CrossRef]
- Airapetyan, R.G.; Ramm, A.G. Numerical inversion of the Laplace transform from the real axis. J. Math. Anal. Appl. 2000, 248, 572–587. [Google Scholar] [CrossRef]
- Epstein, C.L. Philadelphia. In Introduction to the Mathematics of Medical Imaging; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Miller, K.; Viano, G.A. On the necessity of nearlybestpossible methods for analytic continuation of scattering data. J. Math. Phys. 1973, 14, 1037–1048. [Google Scholar] [CrossRef]
- Fu, C.L.; Deng, Z.L.; Feng, X.L.; Dou, F.F. A modified Tikhonov regularization for stable analytic continuation. SIAM J. Numer. Anal. 2009, 47, 2982–3000. [Google Scholar] [CrossRef]
- Engl, H.W.; Hanke, M.; Neubauer, A. Regularization of Inverse Problem; Kluwer Academic: Boston, MA, USA, 1996. [Google Scholar]
- Hao, D.N.; Shali, H. Stable analytic continuation by mollification and the fast Fourier transform. In Method of Complex and Clifford Analysis; ICAM: Hanoi, Vietnam, 2004; pp. 143–152. [Google Scholar]
- Deng, Z.L.; Fu, C.L.; Feng, X.L.; Zhang, Y.X. A mollification regularization method for stable analytic continuation. Math. Comput. Simul. 2011, 81, 1593–1608. [Google Scholar] [CrossRef]
- Fu, C.L.; Dou, F.F.; Feng, X.L.; Qian, Z. A simple regularization method for stable analytic continuation. Inverse Probl. 2008, 24, 065003. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Fu, C.L.; Yan, L. Approximate inverse method for stable analytic continuation in a strip domain. J. Comput. Appl. Math. 2011, 235, 2979–2992. [Google Scholar] [CrossRef][Green Version]
- Cheng, H.; Fu, C.L.; Feng, X.L. An optimal filtering method for stable analytic continuation. J. Comput. Appl. Math. 2012, 236, 2582–2589. [Google Scholar] [CrossRef]
- Feng, X.L.; Ning, W.T. A wavelet regularization method for solving numerical analytic continuation. Int. J. Comput. Math. 2015, 92, 1025–1038. [Google Scholar] [CrossRef]
- Xiong, X.T.; Zhu, L.Q.; Li, M. Regularization methods for a problem of analytic continuation. Math. Comput. Simulat. 2011, 82, 332–345. [Google Scholar] [CrossRef]
- Cheng, H.; Fu, C.L.; Zhang, Y.X. An iteration method for stable analytic continuation. Appl. Math. Comput. 2014, 233, 203–213. [Google Scholar] [CrossRef]
- Xiong, X.T.; Cheng, Q. A modified Lavrentiev iterative regularization method for analytic continuation. J. Comput. Appl. Math. 2018, 327, 127–140. [Google Scholar] [CrossRef]
- Yang, F.; Wang, Q.C.; Li, X.X. A fractional Landweber iterative regularization method for stable analytic continuation. AIMS Math. 2021, 6, 404–419. [Google Scholar] [CrossRef]
- Klann, E.; Maass, P.; Ramlau, R. Two-step regularization methods for linear inverse problems. J. Inverse Ill-Posed Probl. 2006, 14, 583–609. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Klann, E.; Ramlau, R. Regularization by fractional filter methods and data smoothing. Inverse Probl. 2008, 24, 045005. [Google Scholar] [CrossRef]
- Hochstenbach, M.E.; Reichel, L. Fractional Tikhonov regularization for linear discrete ill-posed problems. BIT Numer. Math. 2011, 51, 197–215. [Google Scholar] [CrossRef]
- Gerth, D.; Klann, E.; Ramlau, R.; Reichel, L. On fractional Tikhonov regularization. J. Inverse Ill-Posed Probl. 2015, 23, 611–625. [Google Scholar] [CrossRef]
- Morigi, S.; Reichel, L.; Sgallari, F. Fractional Tikhonov regularization with a nonlinear penalty term. J. Comput. Appl. Math. 2017, 324, 142–154. [Google Scholar] [CrossRef]
- Bianchi, D.; Buccini, A.; Donatelli, M.; Serra-Capizzano, S. Iterated fractional Tikhonov regularization. Inverse Probl. 2015, 31, 055005. [Google Scholar] [CrossRef]
- Bianchi, D.; Donatelli, M. On generalized iterated Tikhonov regularization with operator-dependent seminorms. Electron. Trans. Numer. Anal. 2017, 47, 73–99. [Google Scholar] [CrossRef]
- Xiong, X.T.; Xue, X.M.; Qian, Z. A modified iterative regularization method for ill-posed problems. Appl. Numer. Math. 2017, 122, 108–128. [Google Scholar] [CrossRef]
- Li, M.; Xiong, X.T. On a fractional backward heat conduction problem: Application to deblurring. Comput. Math. Appl. 2012, 64, 2594–2602. [Google Scholar] [CrossRef]
- Qian, Z. A new generalized Tikhonov method based on filtering idea for stable analytic continuation. Inverse. Probl. Sci. Eng. 2018, 26, 362–375. [Google Scholar] [CrossRef]
- Morozov, V.A. Regularization of incorrectly posed problems and the choice of regularization parameter. USSR Comput. Math. Math. Phys. 1966, 6, 242–251. [Google Scholar] [CrossRef]
- Xiong, X.T. A regularization method for a Cauchy problem of the Helmholtz equation. J. Comput. Appl. Math. 2010, 233, 1723–1732. [Google Scholar] [CrossRef][Green Version]

| y | 0.2 | 0.5 | 0.8 | |
|---|---|---|---|---|
| 0.0725 | 0.1009 | 0.2769 | ||
| 0.0168 | 0.0732 | 0.2684 | ||
| 0.0857 | 0.2866 | 0.7765 | ||
| 0.0238 | 0.2774 | 0.7227 |
| y | 0.2 | 0.5 | 0.8 | |
|---|---|---|---|---|
| 1.2201 | 3.2006 | 5.1905 | ||
| 1.2208 | 2.0412 | 2.8628 | ||
| 1.6075 | 5.6605 | 6.5887 | ||
| 1.7714 | 3.5022 | 3.7275 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, X.; Xiong, X. A Posteriori Fractional Tikhonov Regularization Method for the Problem of Analytic Continuation. Mathematics 2021, 9, 2255. https://doi.org/10.3390/math9182255
Xue X, Xiong X. A Posteriori Fractional Tikhonov Regularization Method for the Problem of Analytic Continuation. Mathematics. 2021; 9(18):2255. https://doi.org/10.3390/math9182255
Chicago/Turabian StyleXue, Xuemin, and Xiangtuan Xiong. 2021. "A Posteriori Fractional Tikhonov Regularization Method for the Problem of Analytic Continuation" Mathematics 9, no. 18: 2255. https://doi.org/10.3390/math9182255
APA StyleXue, X., & Xiong, X. (2021). A Posteriori Fractional Tikhonov Regularization Method for the Problem of Analytic Continuation. Mathematics, 9(18), 2255. https://doi.org/10.3390/math9182255





