Convective Heat Transfer of a Hybrid Nanofluid over a Nonlinearly Stretching Surface with Radiation Effect
Abstract
:1. Introduction
2. Mathematical Model
3. Numerical Approach
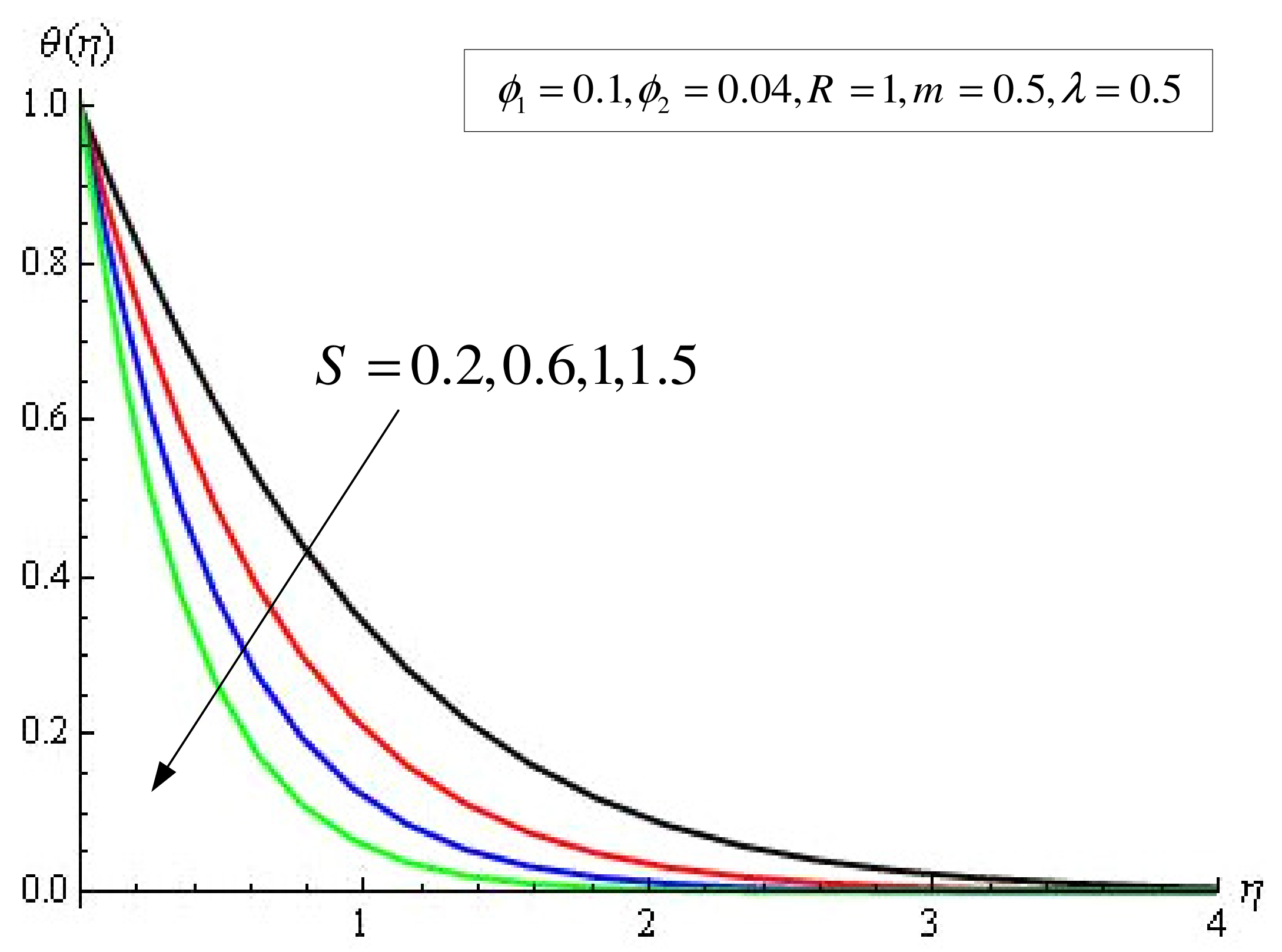
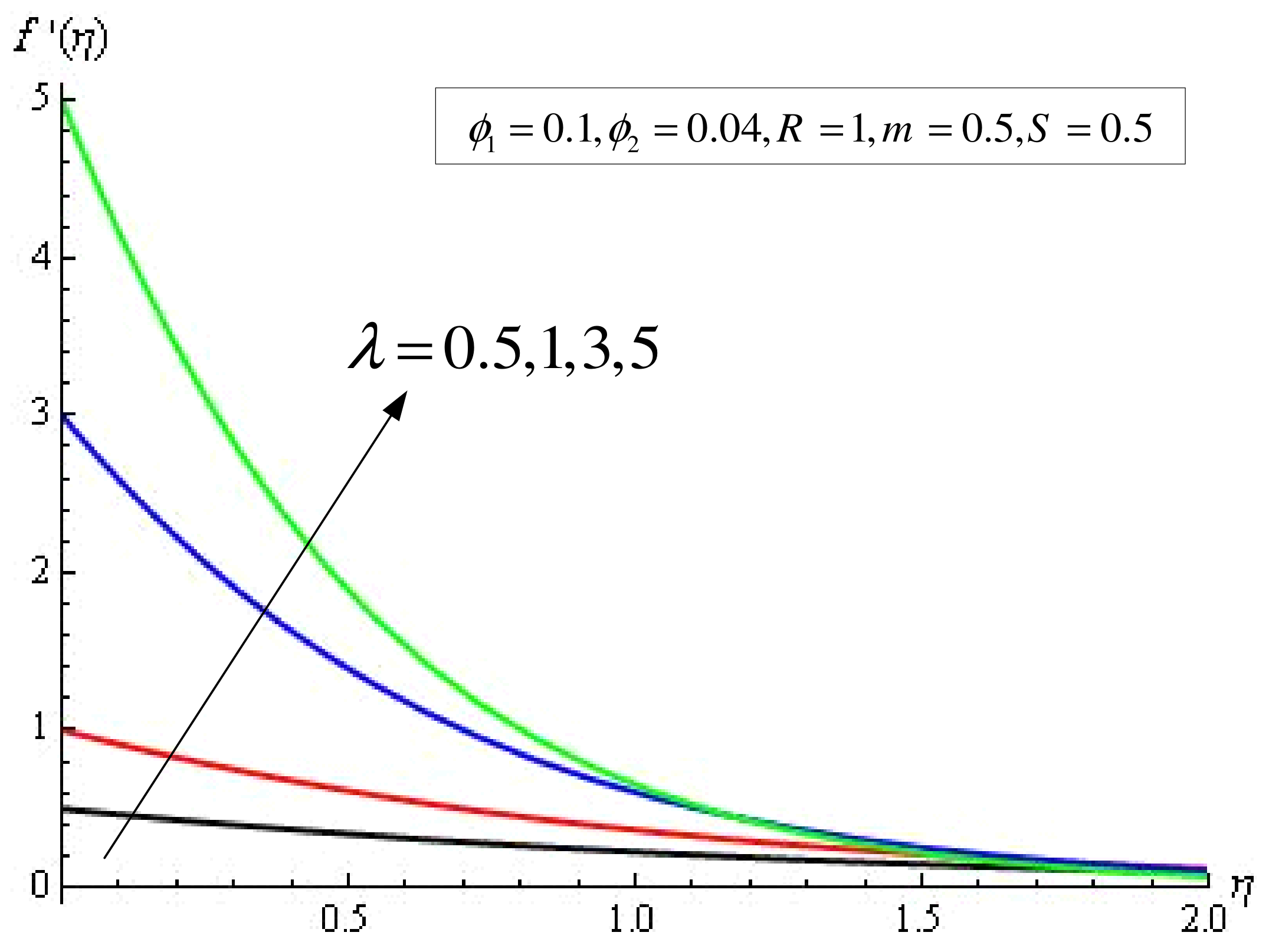
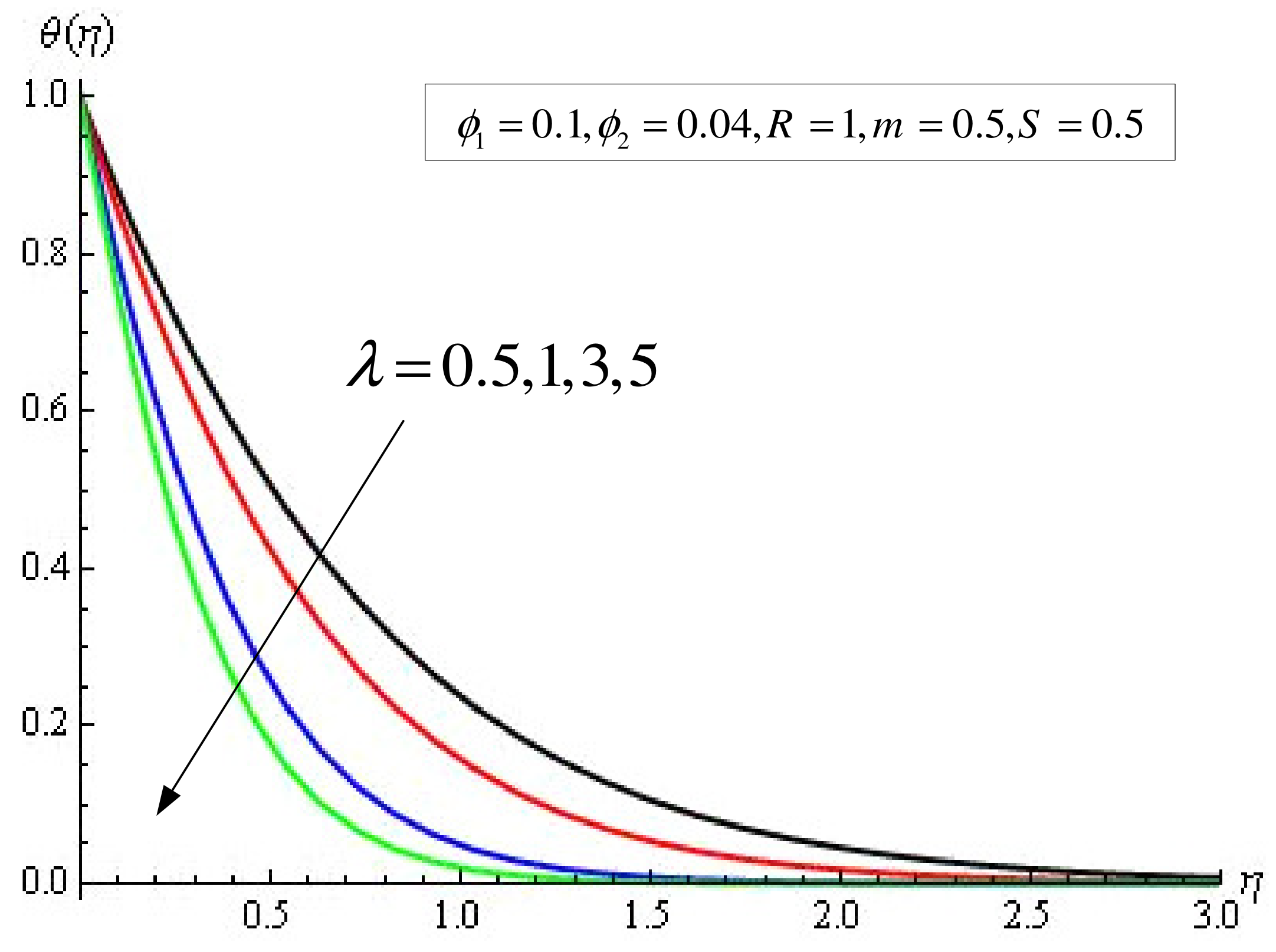
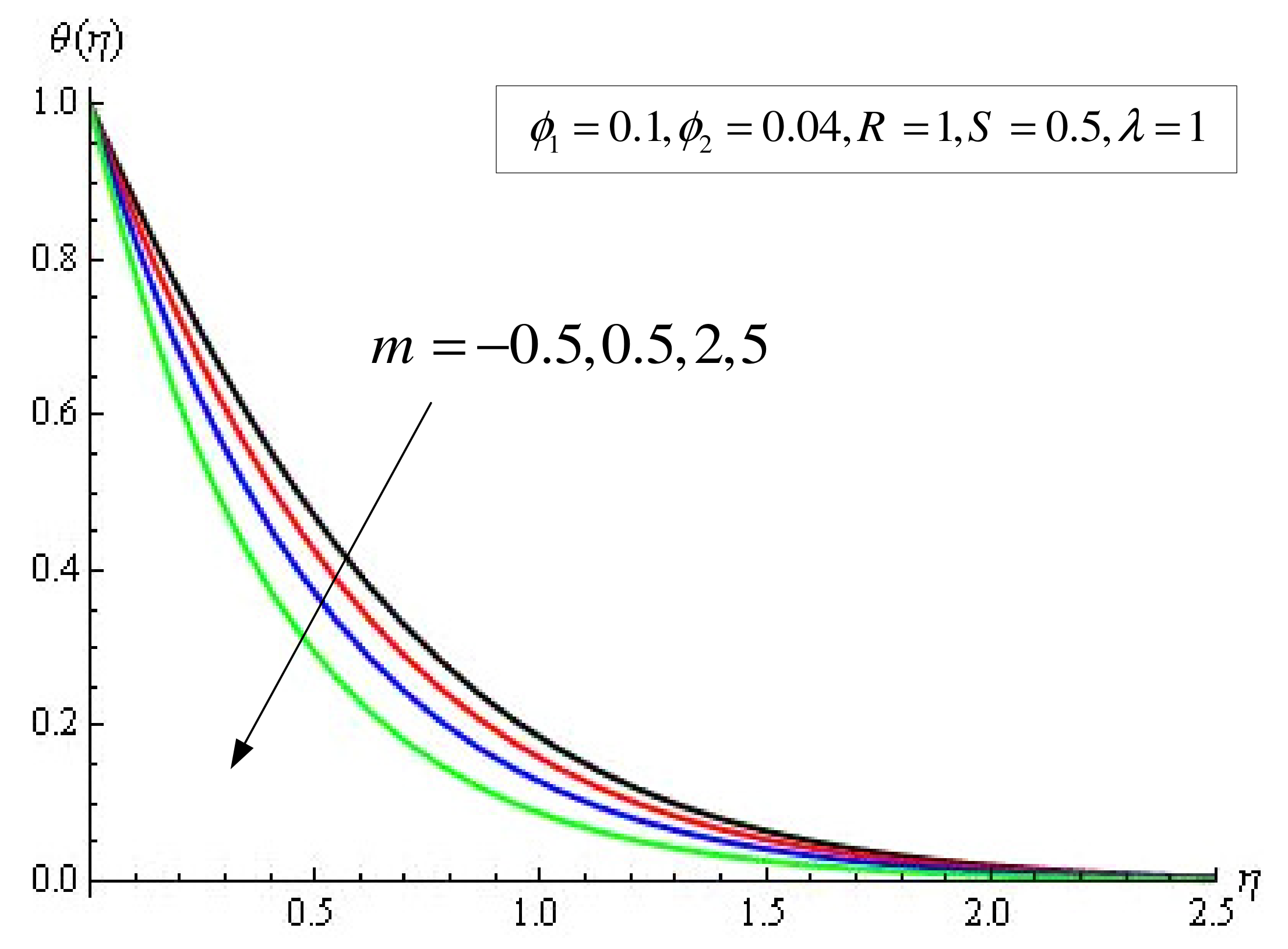
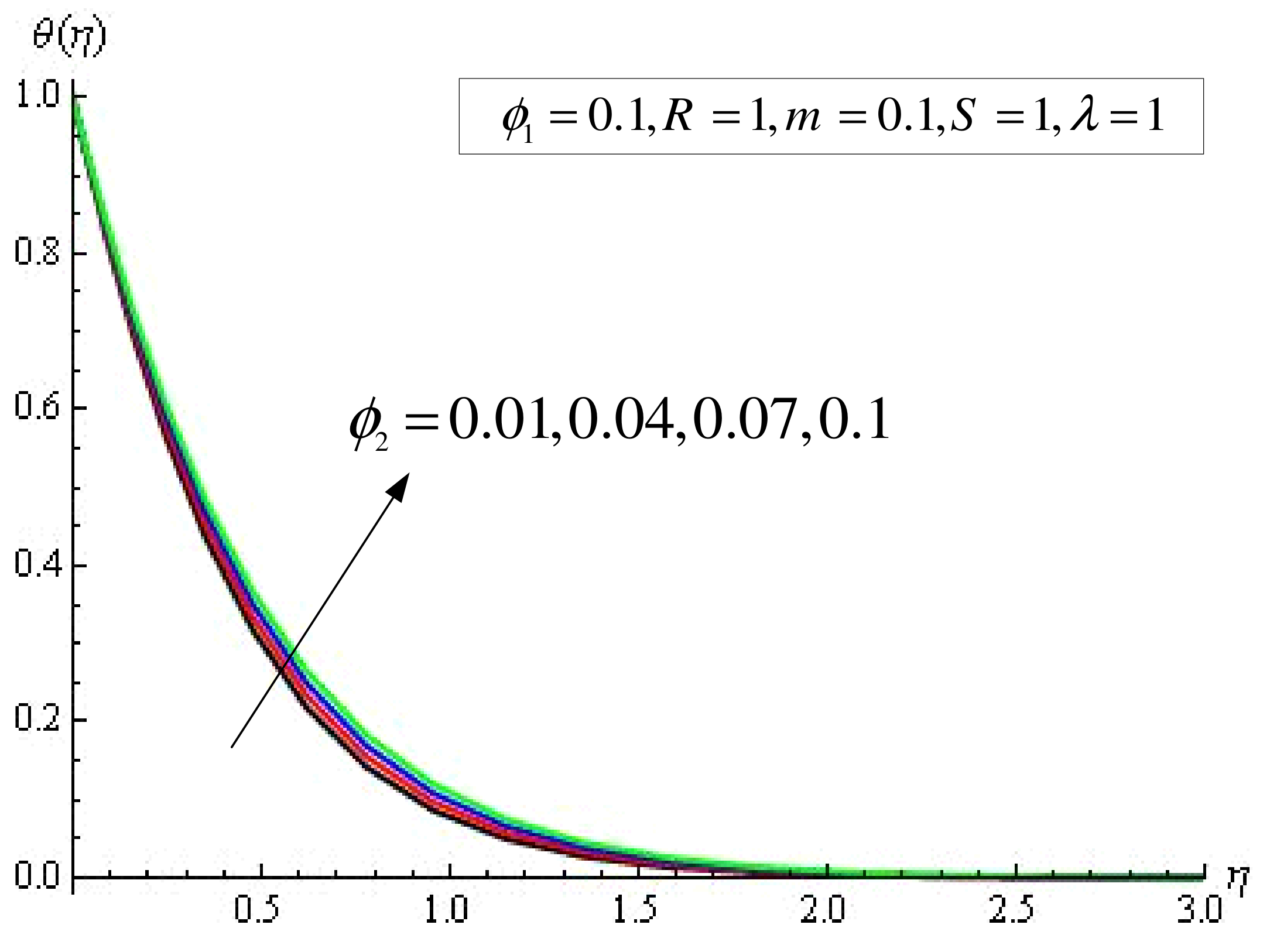
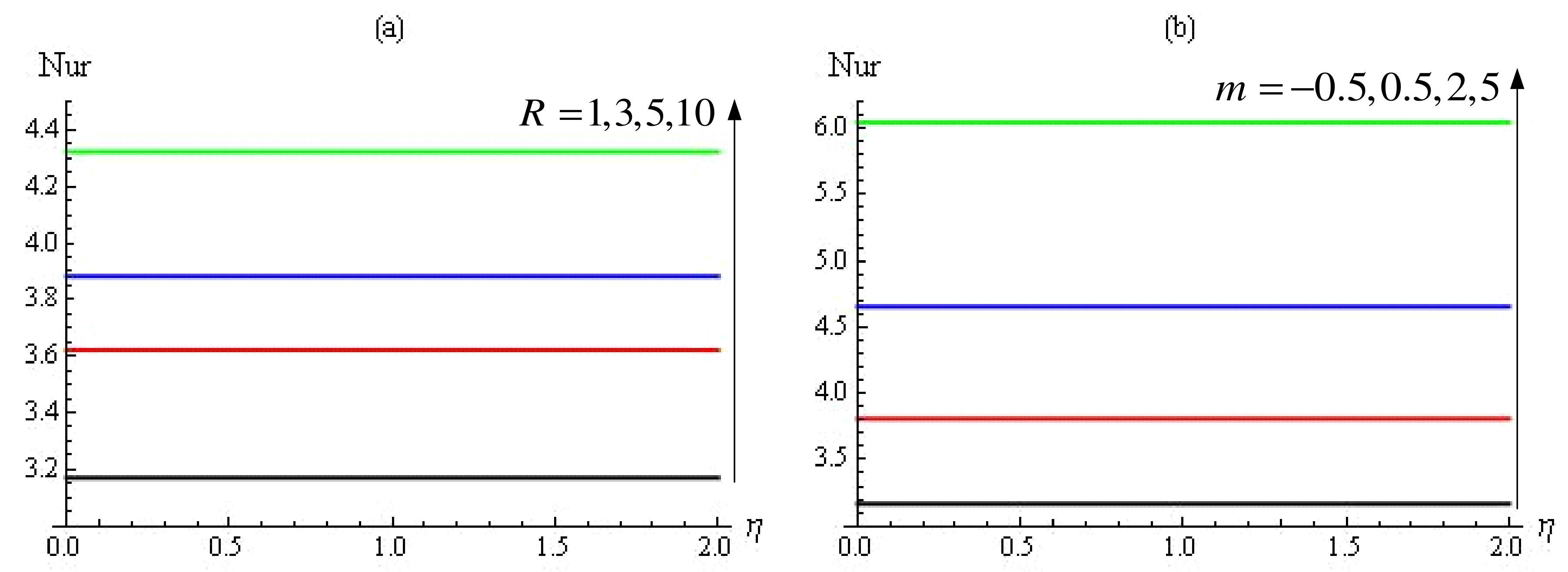
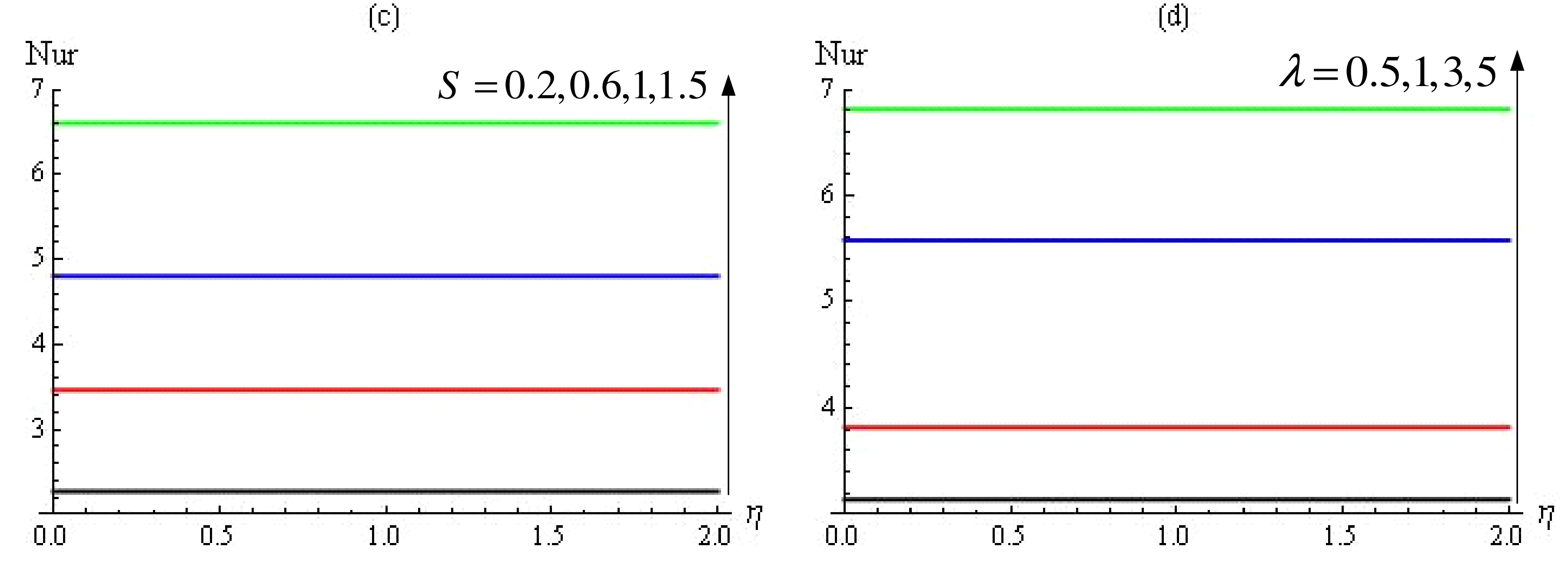
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fisher, E.G. Extrusion of Plastics, 3rd ed.; Halsted Press: New York, NY, USA, 1976. [Google Scholar]
- Tidmore, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Polymer Science and Engineering Series; Van Norstrand: New York, NY, USA, 1970. [Google Scholar]
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. (ZAMP) 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; ASME, FED 231/MD 66. pp. 99–105. [Google Scholar]
- Khanafer, K.; Vafai, K.; Lightstone, M.F. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications—A state-of-the-art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. Merkin and Needham wall jet problem for hybrid nanofluids with thermal energy. Eur. J. Mech. B/Fluids 2020, 83, 195–204. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD flow and heat transfer near stagnation point over a stretching/shrinking surface with partial slip and viscous dissipation: Hybrid nanofluid versus nanofluid. Powder Technol. 2020, 367, 192–205. [Google Scholar] [CrossRef]
- Pop, I.; Roşca, N.C.; Roşca, A.V. Additional results for the problem of MHD boundary-layer flow past a stretching/shrinking surface. Int. J. Numrical Methods Heat Fluid Flow 2016, 26, 2283–2294. [Google Scholar] [CrossRef]
- Roşca, N.C.; Roşca, A.V.; Pop, I. Cross flow and heat transfer past a permeable stretching/shrinking sheet in a hybrid nanofluid. Int. J. Numrical Methods Heat Fluid Flow 2021, 31, 1295–1319. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–297. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer along a permeable stretching/shrinking curved surface in a hybrid nanofluid. Phys. Scr. 2019, 94, 105219. [Google Scholar] [CrossRef]
- Devi, S.U.S.; Devi, S.P.A. Heat transfer enhancement of Cu-Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids Recent research, development and applications. Renew. Sustain. Energy Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Akilu, S.; Baheta, A.T.; Sharma, K.V. Experimental measurements of thermal conductivity and viscosity of ethylene glycol-based hybrid nanofluid with TiO2-CuO/C inclusions. J. Mol. Liq. 2017, 246, 396–405. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Adamu, I.M.; Muhammad, M.J. Preparation methods and thermal performance of hybrid nanofluids. J. Adv. Res. Mater. Sci. 2019, 56, 1–10. [Google Scholar]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energy Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Kazemia, M.A.; Jafari, S.S.; Musavi, S.M.; Nejati, M. Analytical solution of convective heat transfer of a quiescent fluid over a nonlinearly stretching surface using Homotopy analysis method. Results Phys. 2018, 10, 164–172. [Google Scholar] [CrossRef]
- Devi, S.A.; Devi, S.S. Numerical investigation of hydromagnetic hybrid Cu-Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int. J. Nonlinear Sci. Numer. Simul. 2016, 17, 249–257. [Google Scholar] [CrossRef]
- Cortell, R. Radiation effects for the Blasius and Sakiadis flows with a convective surface boundary condition. Appl. Math. Comput. 2008, 206, 832–840. [Google Scholar]
- Aly, E.H. Dual exact solutions of graphene–water nanofluid flow over stretching/shrinking sheet with suction/injection and heat source/sink: Critical values and regions with stability. Powder Technol. 2019, 342, 528–544. [Google Scholar] [CrossRef]
- Aly, E.H.; Benlahsen, M.; Guedda, M. Similarity solutions of a MHD boundary–layer flow past a continuous moving surface. Int. J. Eng. Sci. 2007, 45, 486–503. [Google Scholar] [CrossRef]
- Guedda, G.; Aly, E.H.; Ouahsine, A. Analytical and ChPDM analysis of MHD mixed convection over a vertical flat plate embedded in a porous medium filled with water at 4 ∘C. Appl. Math. Model. 2011, 35, 5182–5197. [Google Scholar] [CrossRef]
- Aly, E.H.; Vajravelu, K. Exact and numerical solutions of MHD nano boundary–layer flows over stretching surfaces in a porous medium. Appl. Math. Comput. 2014, 232, 191–204. [Google Scholar] [CrossRef]
- Aly, E.H.; Sayed, H.M. Magnetohydrodynamic and thermal radiation effects on the boundary-layer flow due to a moving extensible surface with the velocity slip model: A comparative study of four nanofluids. J. Magn. Magn. Mater. 2017, 422, 440–451. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. Radiation and mixed convection magnetohydrodynamics boundary layer of hybrid Cu-Al2O3/water nanofluid flow over a wall jet. J. Nanofluids 2020, 9, 152–160. [Google Scholar] [CrossRef]


| Physical | Base Fluid | Nanoparticles | |
|---|---|---|---|
| Properties | Water | Cu | |
| (kg m) | 997.1 | 3970 | 8933 |
| (J kg K) | 4179 | 765 | 385 |
| k (W m K) | 0.613 | 40 | 401 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aly, E.H.; Roşca, A.V.; Roşca, N.C.; Pop, I. Convective Heat Transfer of a Hybrid Nanofluid over a Nonlinearly Stretching Surface with Radiation Effect. Mathematics 2021, 9, 2220. https://doi.org/10.3390/math9182220
Aly EH, Roşca AV, Roşca NC, Pop I. Convective Heat Transfer of a Hybrid Nanofluid over a Nonlinearly Stretching Surface with Radiation Effect. Mathematics. 2021; 9(18):2220. https://doi.org/10.3390/math9182220
Chicago/Turabian StyleAly, Emad H., Alin V. Roşca, Natalia C. Roşca, and Ioan Pop. 2021. "Convective Heat Transfer of a Hybrid Nanofluid over a Nonlinearly Stretching Surface with Radiation Effect" Mathematics 9, no. 18: 2220. https://doi.org/10.3390/math9182220
APA StyleAly, E. H., Roşca, A. V., Roşca, N. C., & Pop, I. (2021). Convective Heat Transfer of a Hybrid Nanofluid over a Nonlinearly Stretching Surface with Radiation Effect. Mathematics, 9(18), 2220. https://doi.org/10.3390/math9182220







