Using Tangram as a Manipulative Tool for Transition between 2D and 3D Perception in Geometry
Abstract
1. Introduction
1.1. Students’ Difficulties in Acquiring Spatial Skills
1.2. Theoretical Framework
1.3. Research Questions
2. Materials and Methods
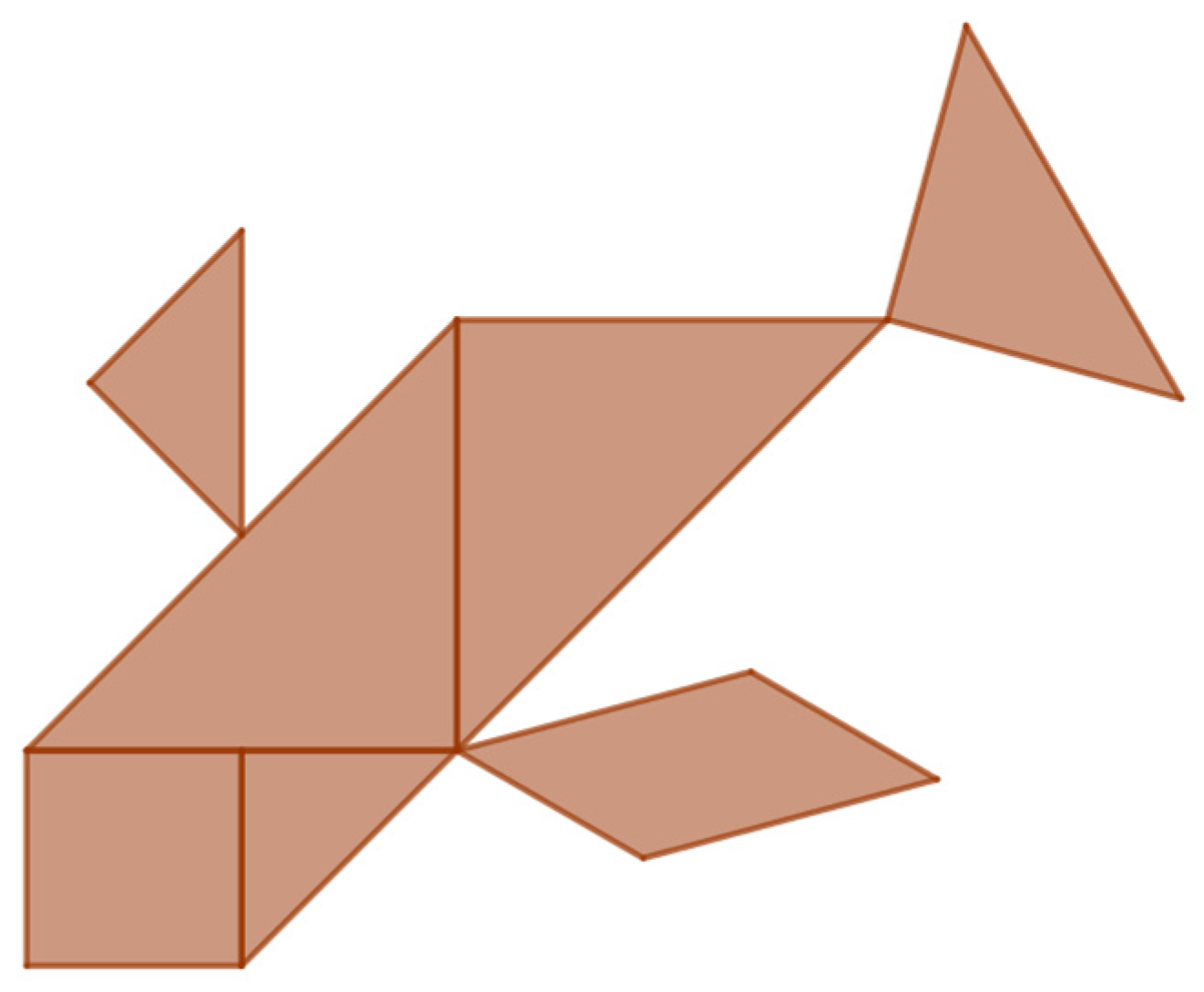
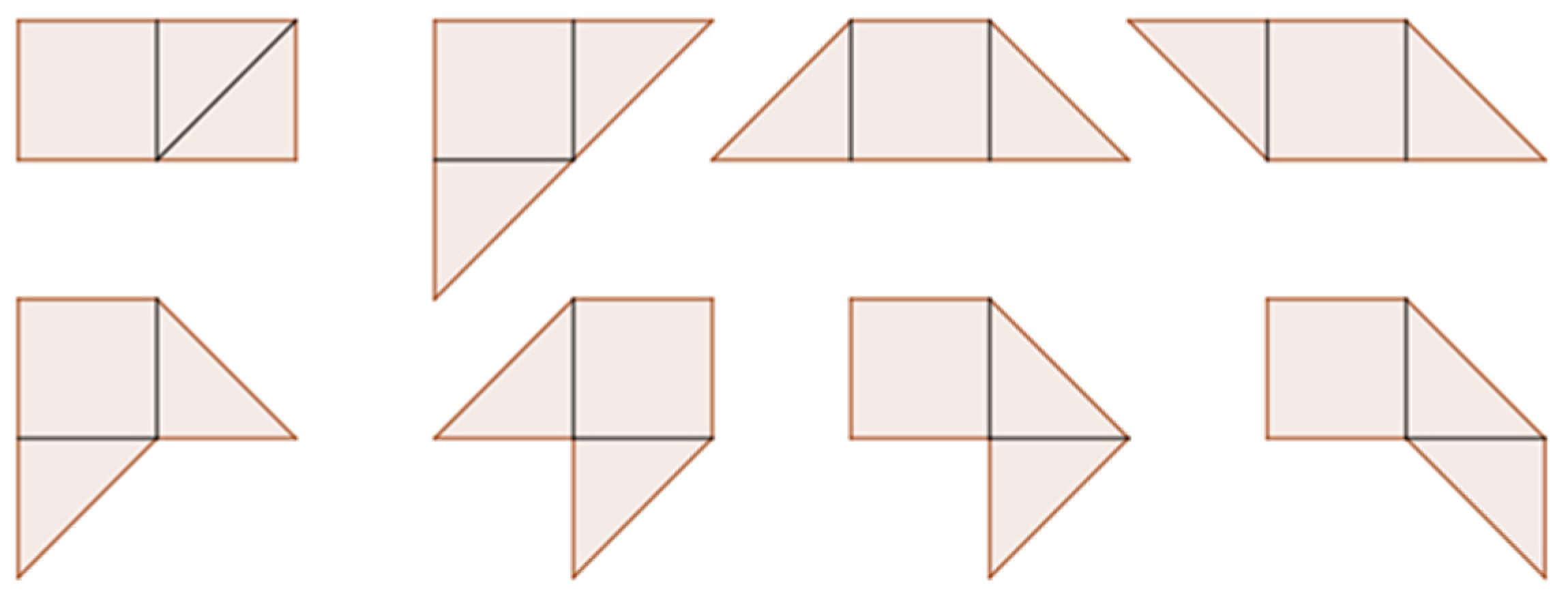
2.1. Tangram
2.2. Action Research
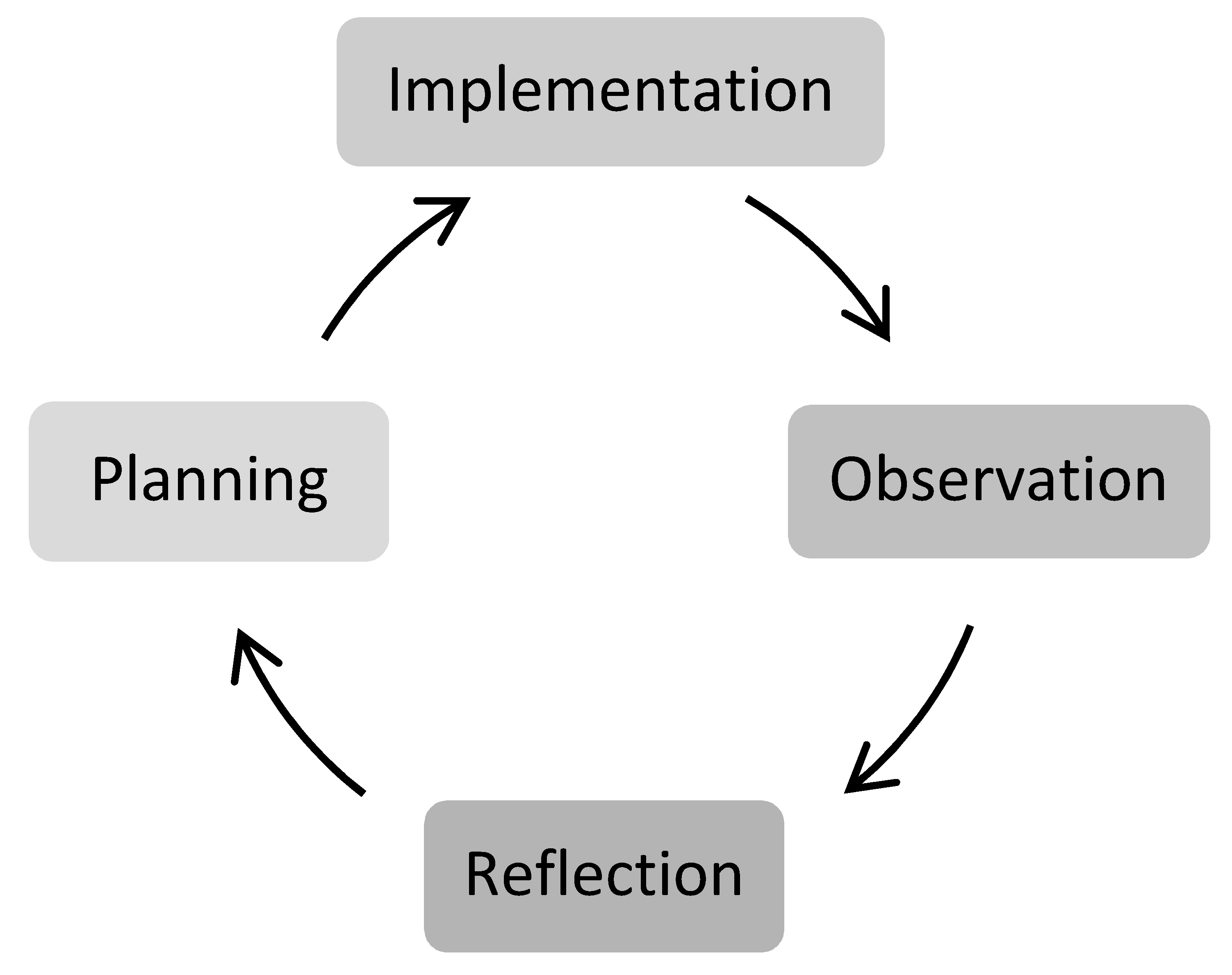
2.2.1. The Action Research Cycle
- (1)
- Reconnaissance or observation
- (2)
- Planning
- (3)
- Acting or monitoring
- (4)
- Reflecting or evaluating
2.3. Participants
Characteristics of the Participants
2.4. Measures
2.4.1. Pre-Test
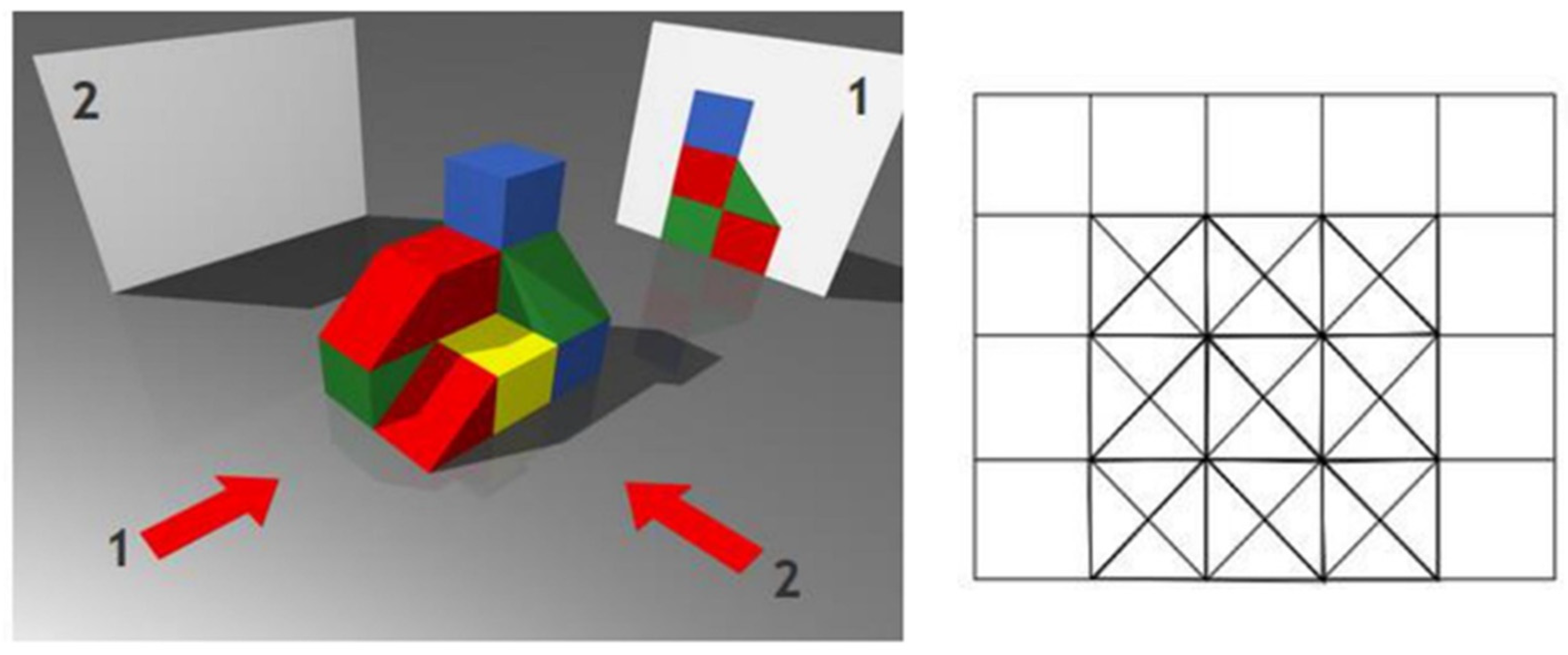
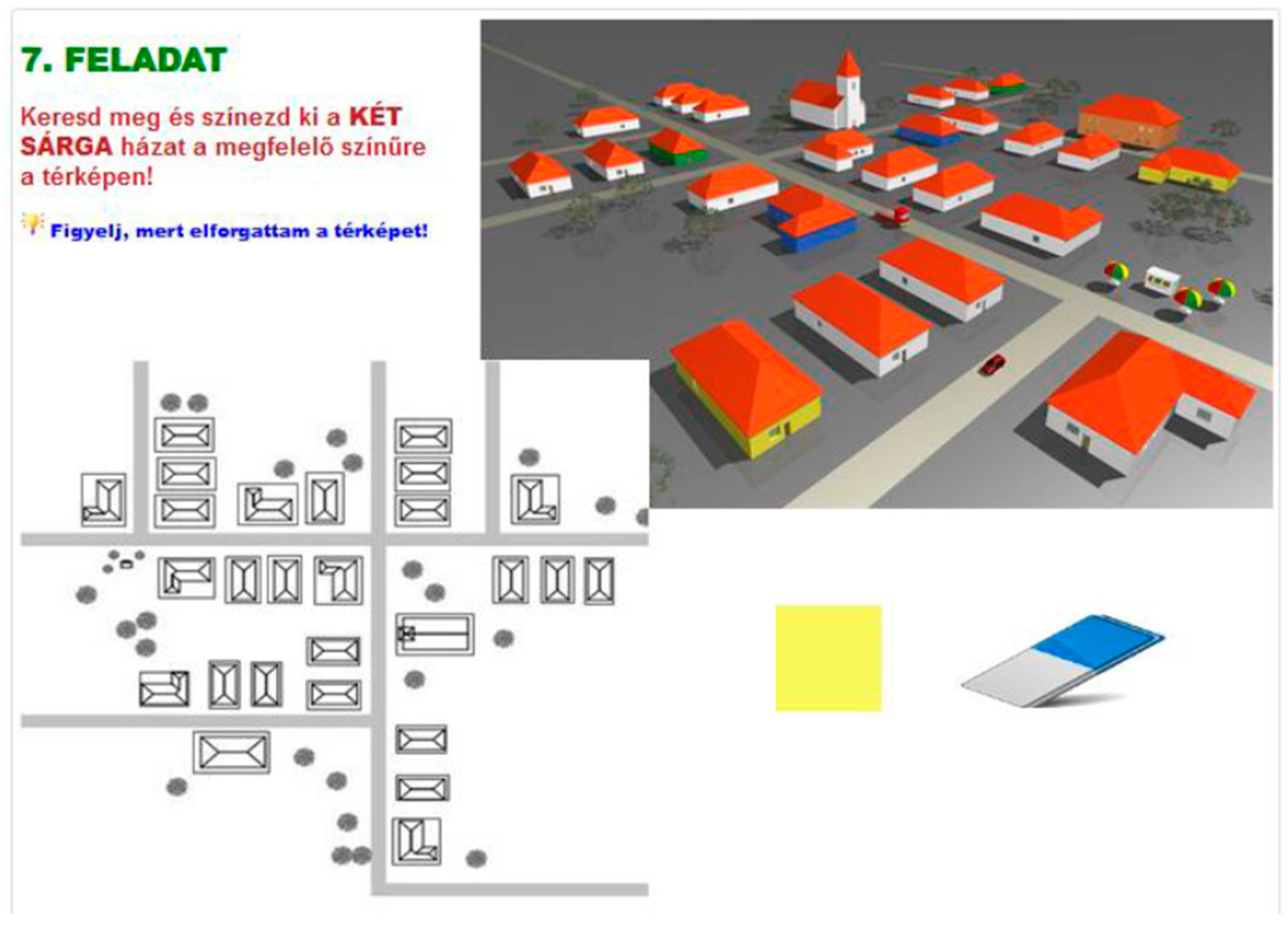
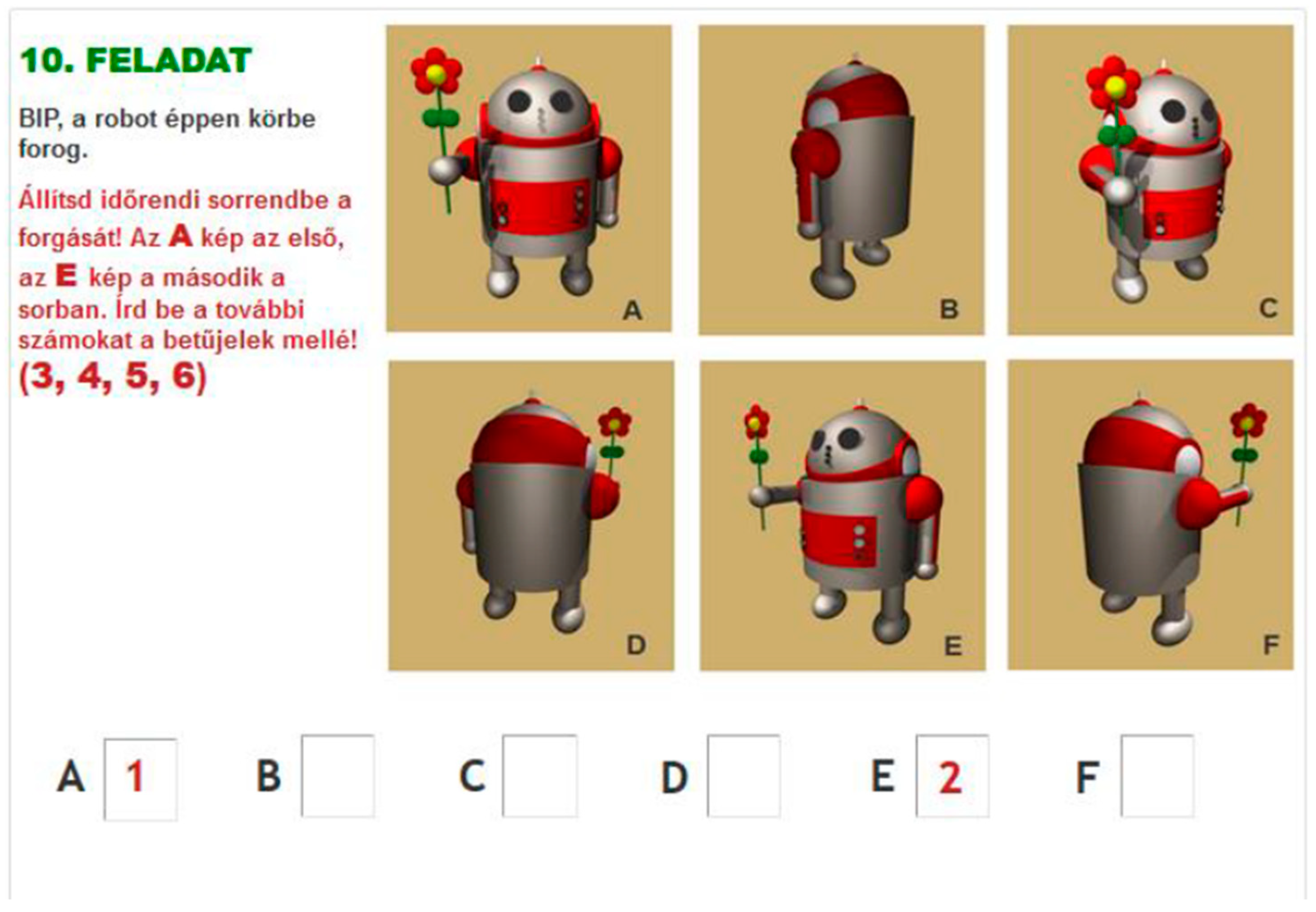
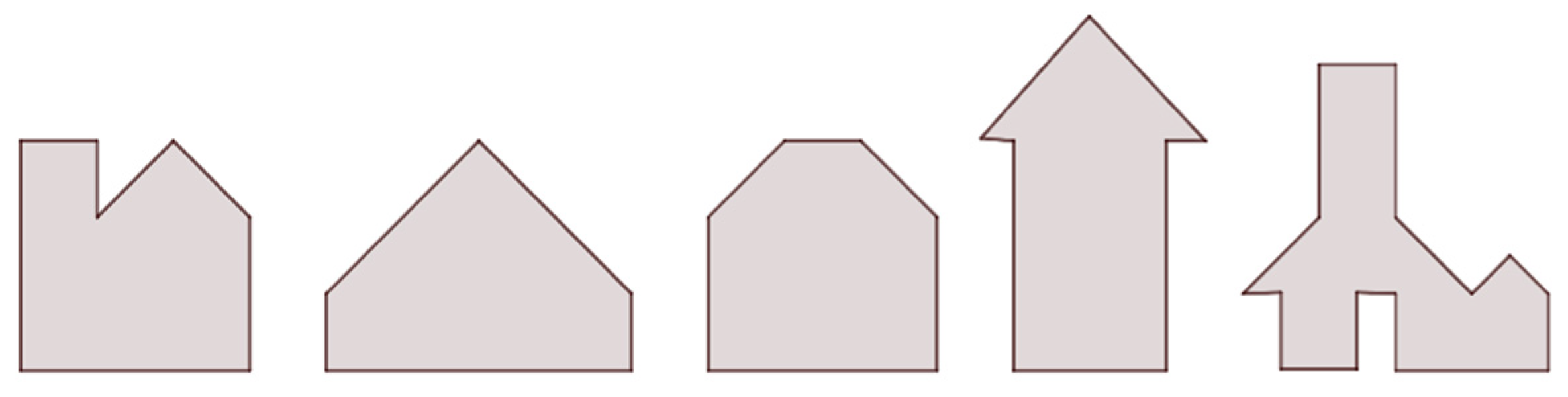
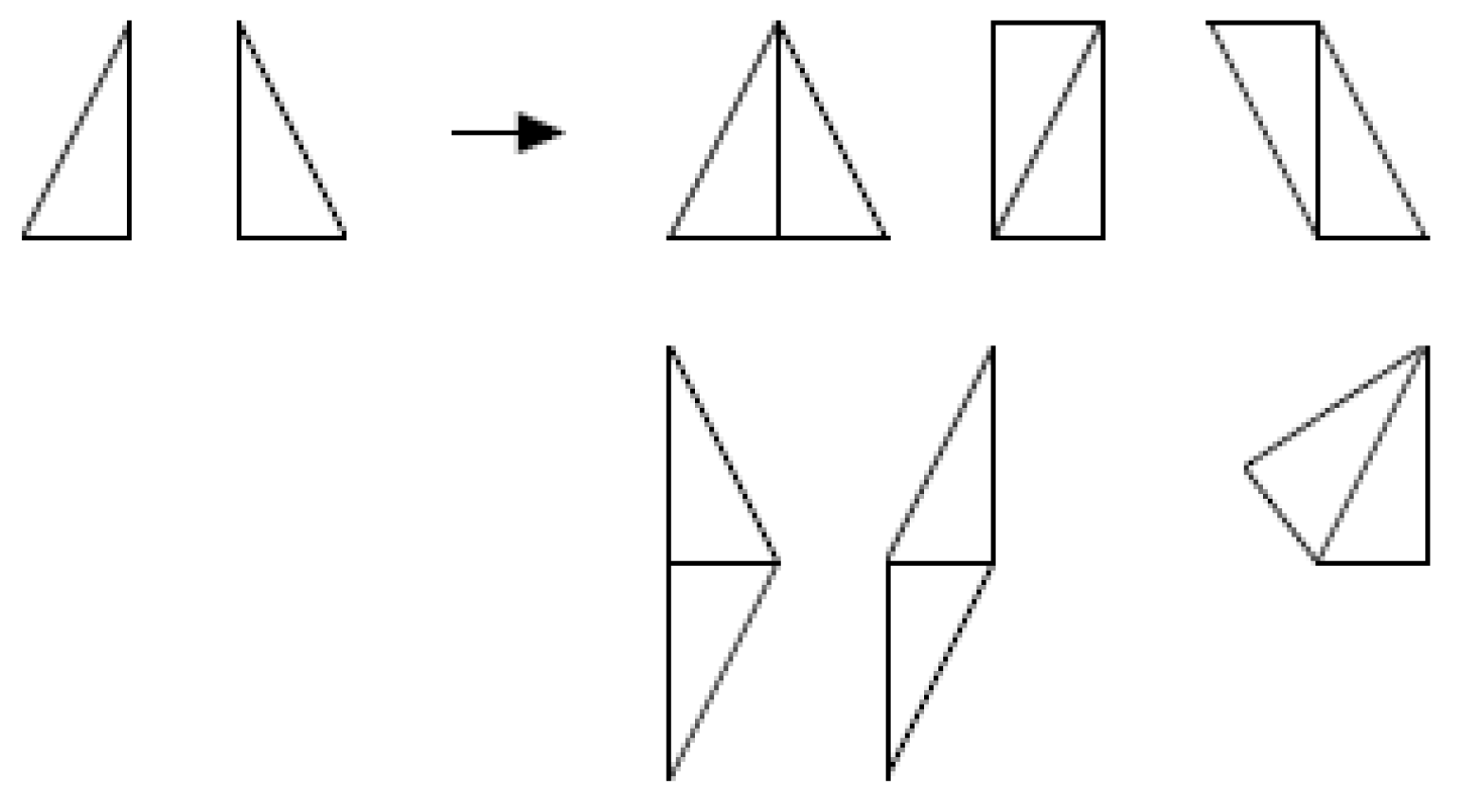
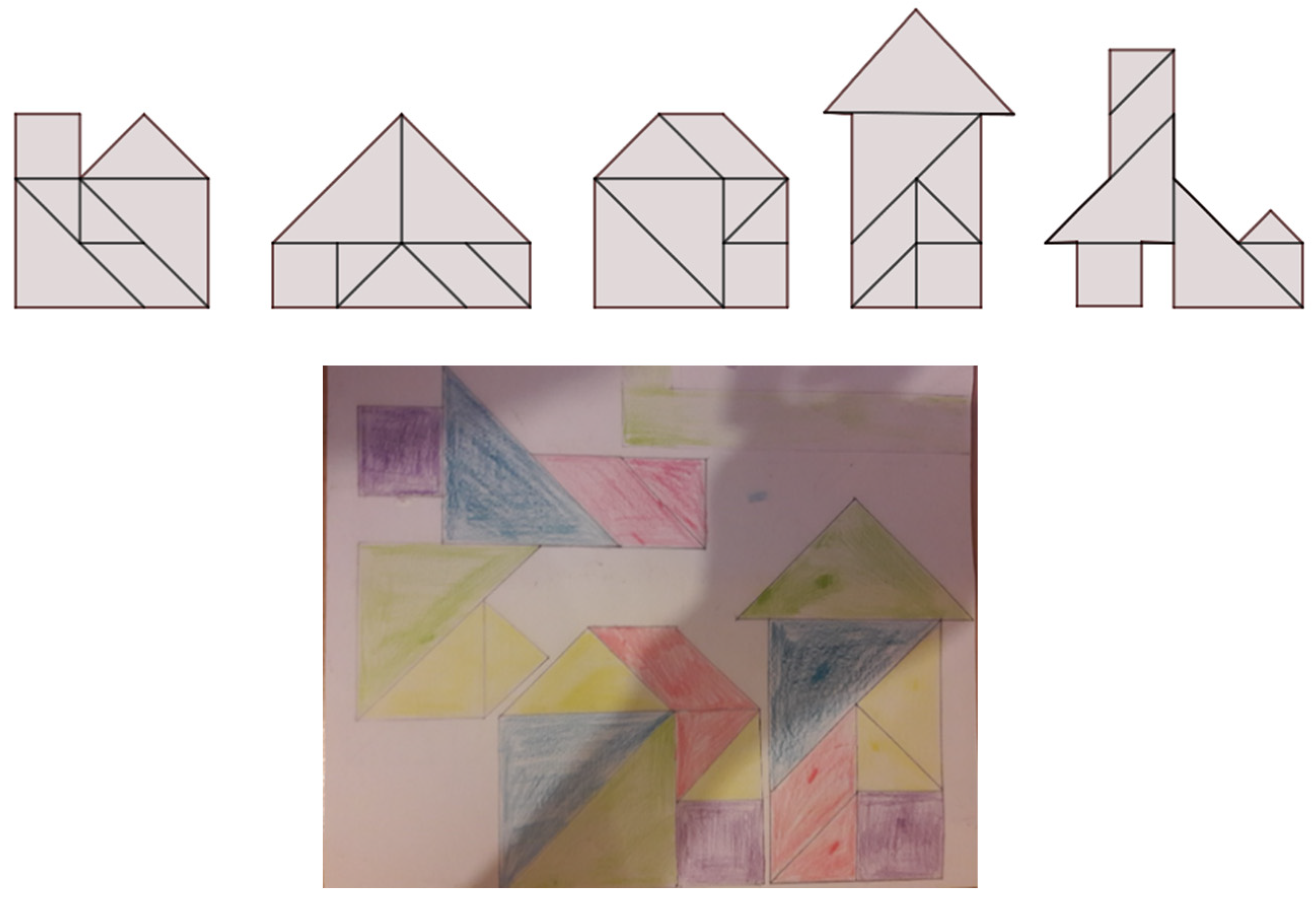
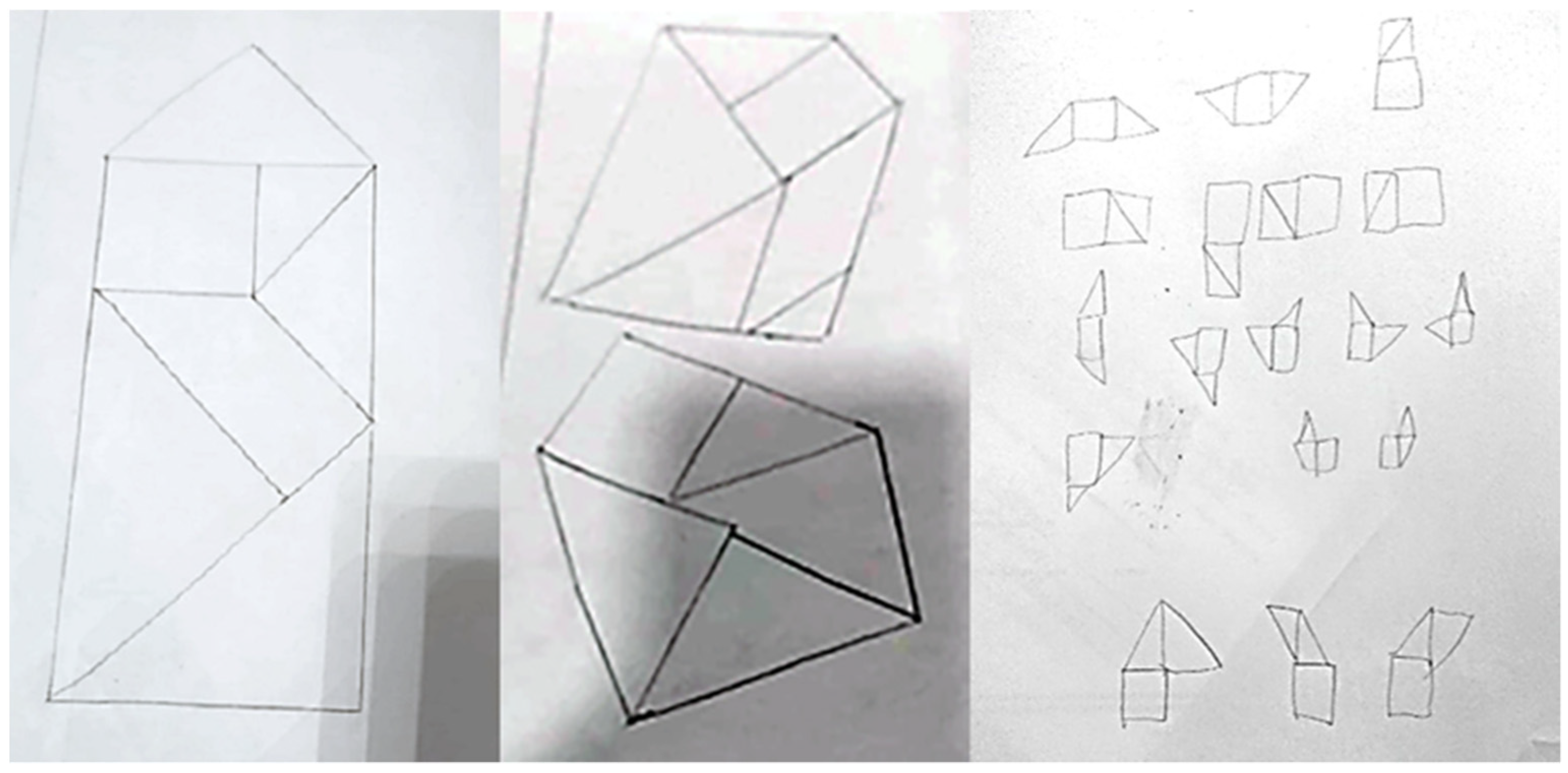
2.4.2. The Tangram Tasks
- Draw a house, e.g., a square with a triangle on it. Divide the figure into two or more pieces (like puzzle pieces) and give them to a schoolmate to figure out what shape was cut out. The puzzle pieces can be put together individually and then exchanged between the children.
- Measure the sizes of a sample Tangram and then try to copy it on a sheet of paper.
- Discuss, what are the important data to look out for, when constructing on the paper.
- Make a Tangram out of cardboard, put it in an envelope, it will serve the class. Not all parts have to be used what enables free creation. Use items also from multiple sets at once. Make photographs of the results.
- Lay out new pictures, draw them around, and add lines to divide them into pieces.
3. Results
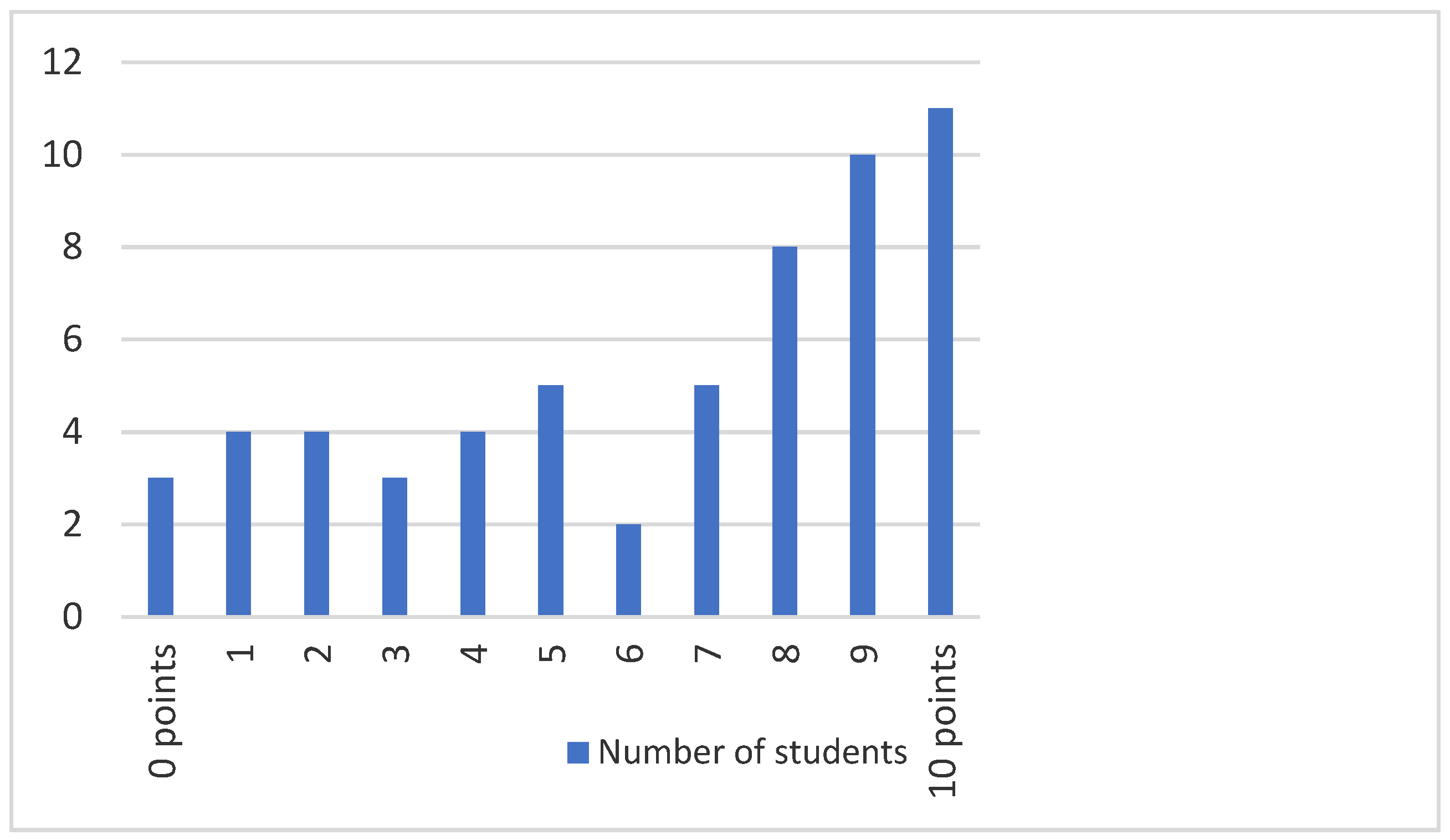
3.1. Results of the Pre-Test
3.2. Evaluation of the Tangram Tasks
4. Discussion
- Spatial perception such as: orientation in space, experiencing space, understanding spatial relationships.
- Spatial representation (mostly in 2D) such as: representing mutual positions in space or mutual positions in a mental visual image, representation of motion in space through time, reconstruction of space elements.
- Creation of spatial objects in 2D or 3D such as: modelling and construction.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
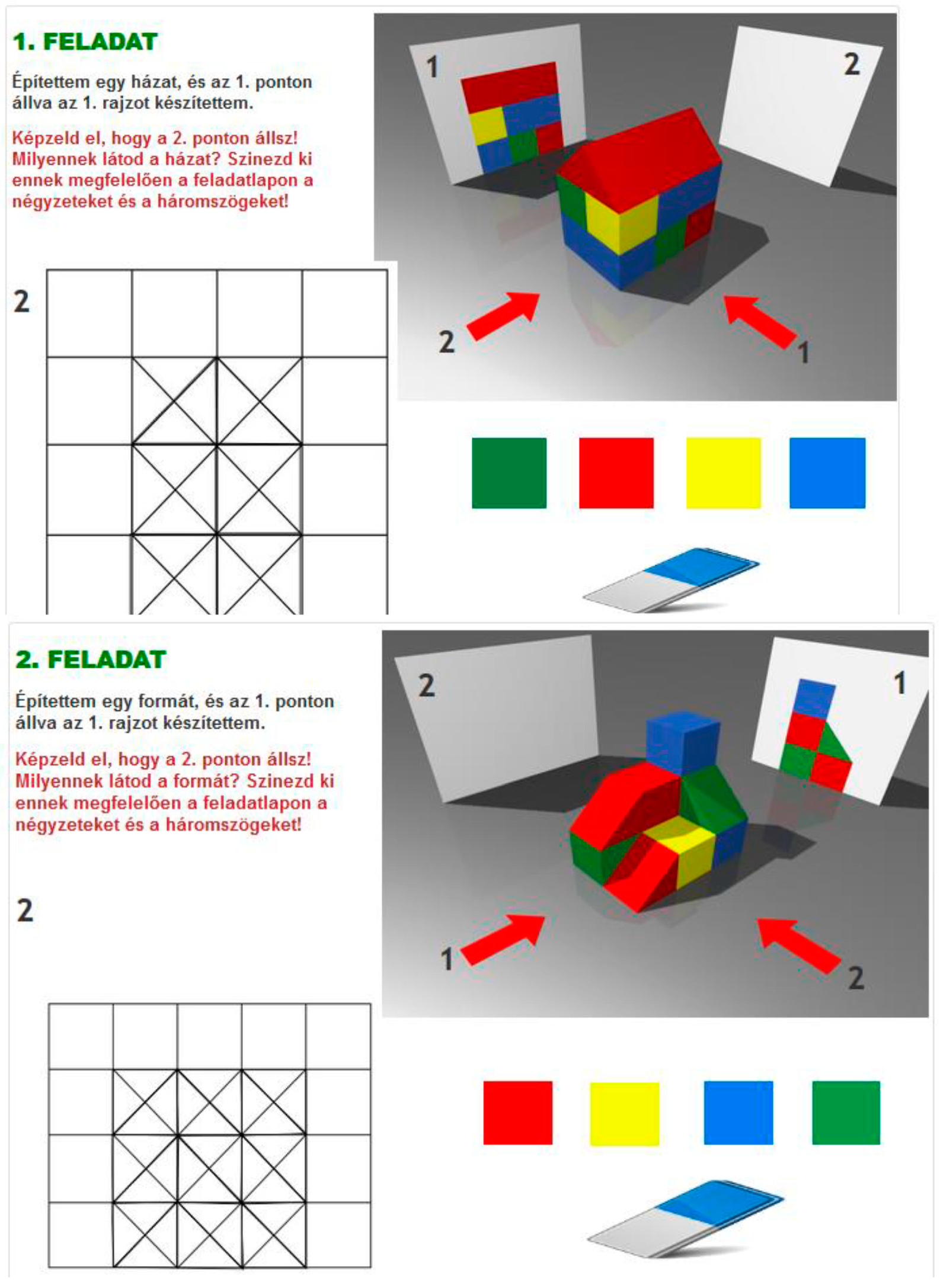
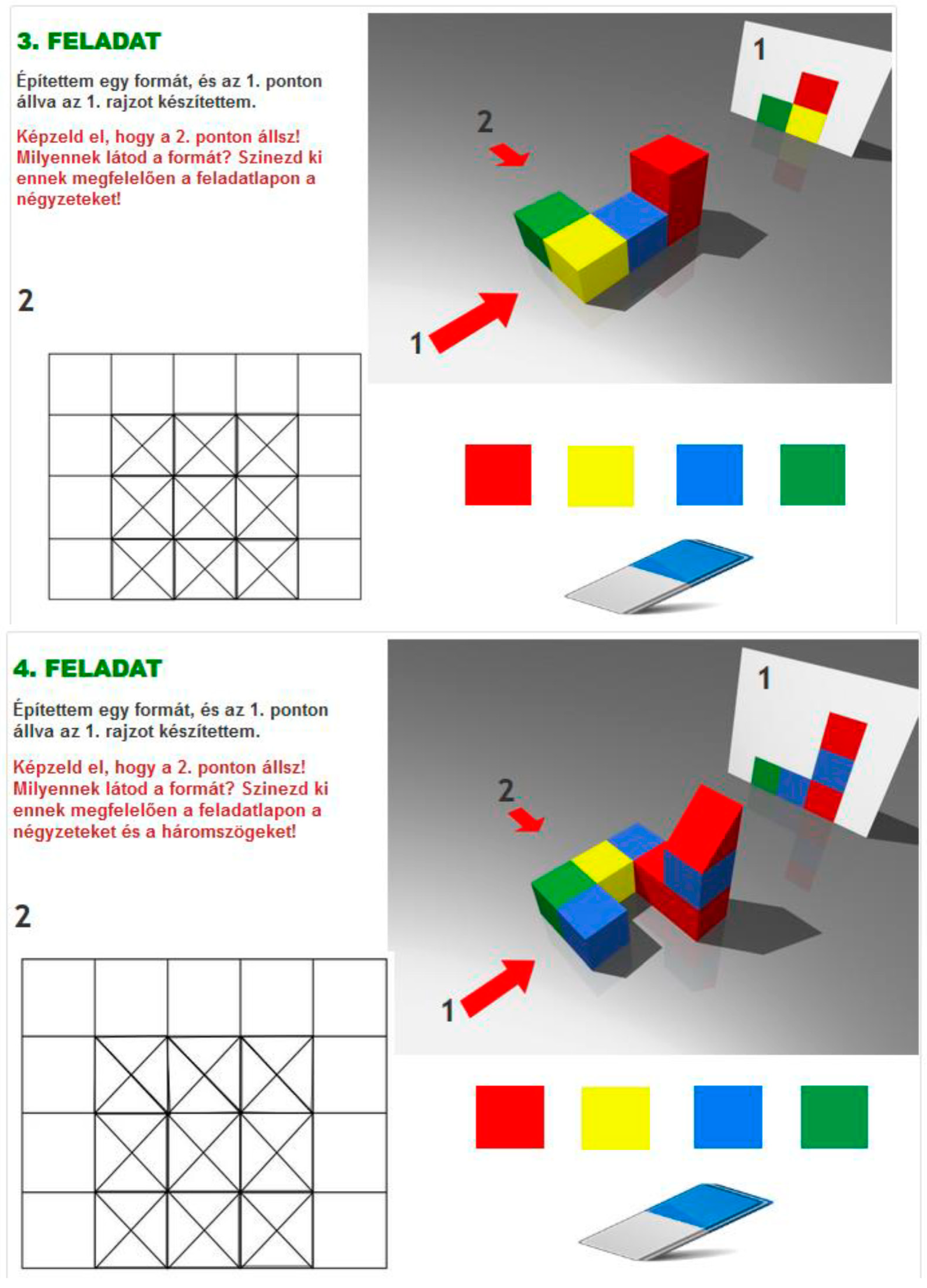
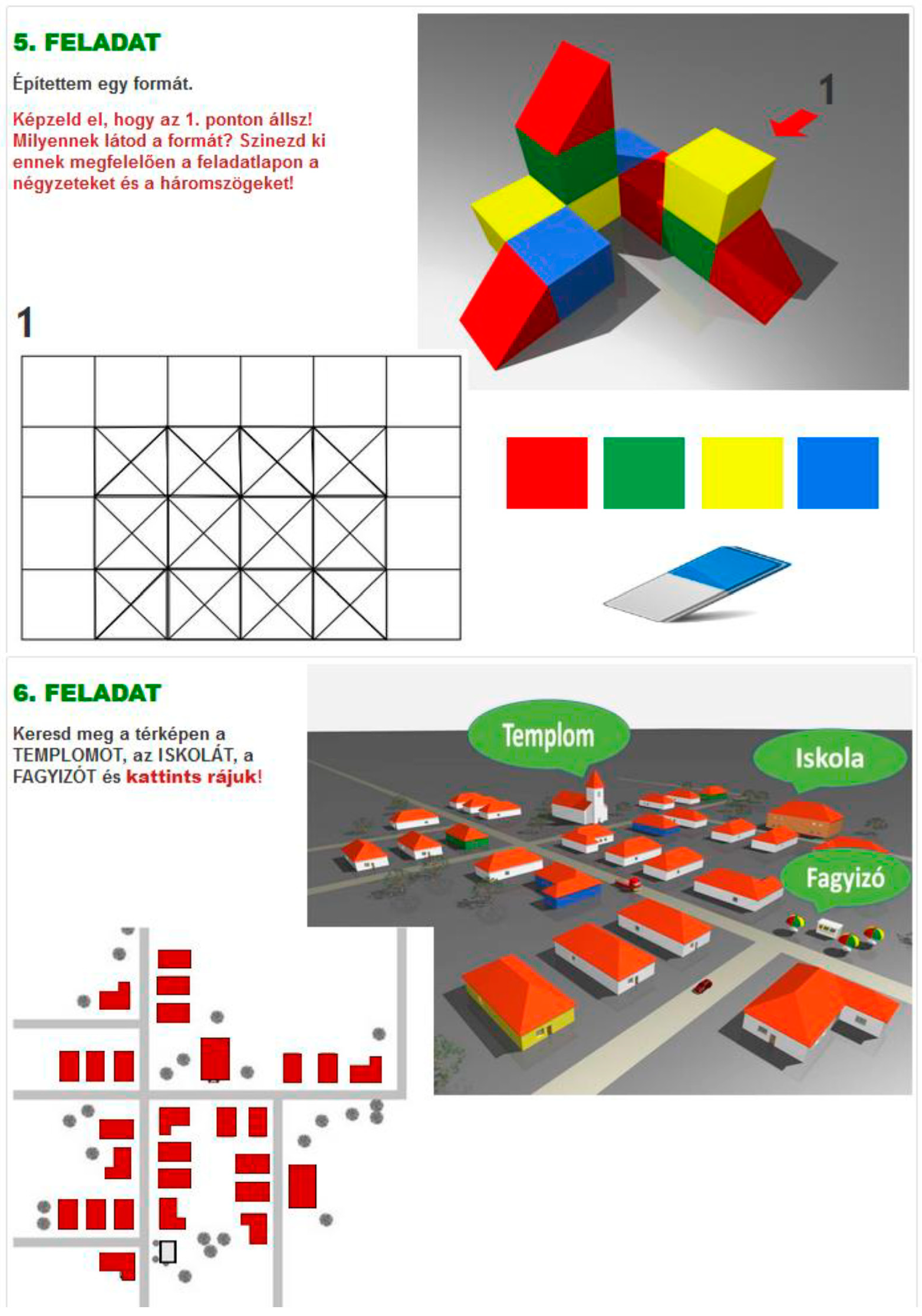
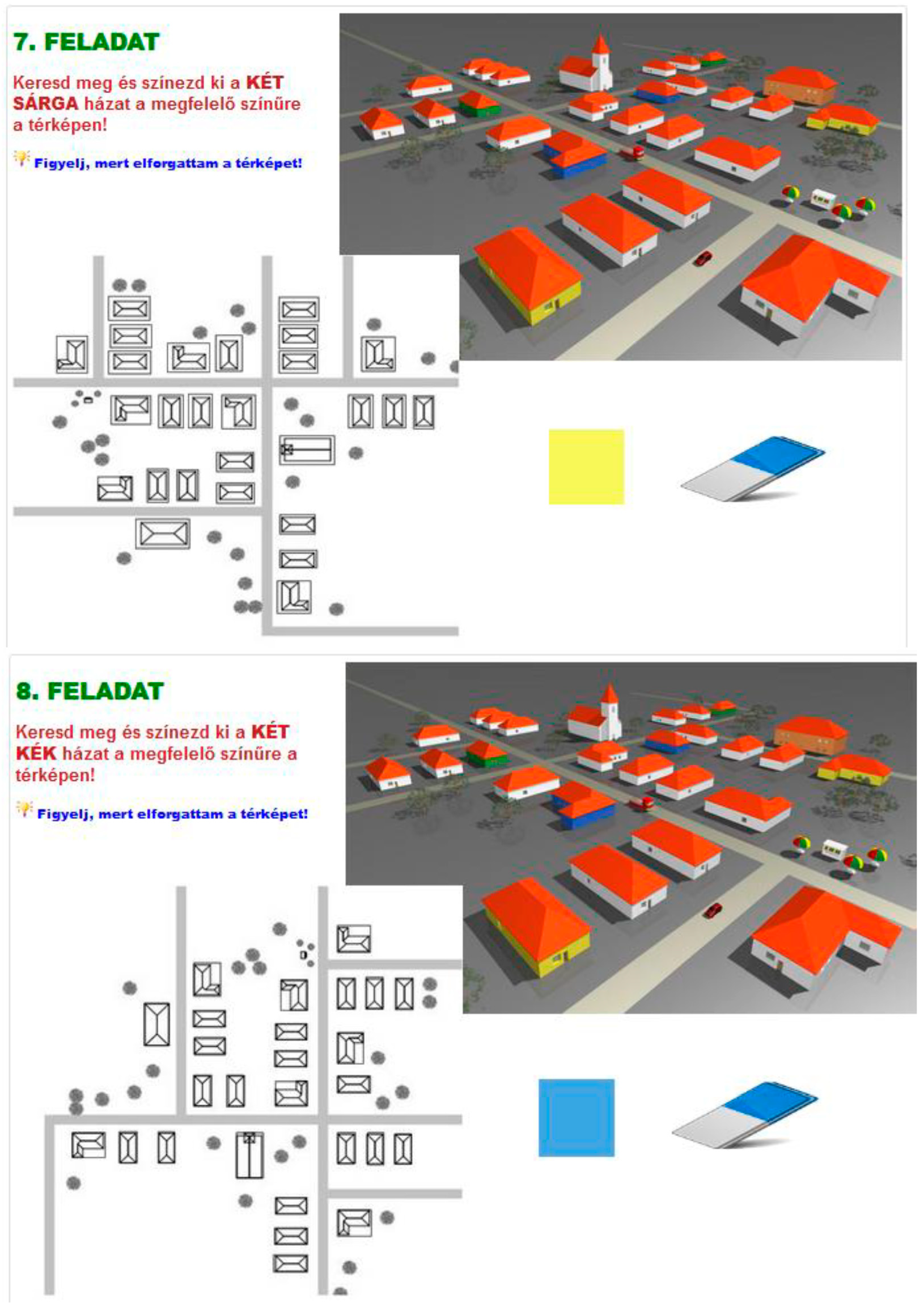

References
- Freudenthal, H. Mathematics as an Educational Task; Reidel: Dordrecht, The Netherlands, 1973. [Google Scholar]
- National Research Council. Mathematics Learning in Early Childhood: Paths toward Excellence and Equity; The National Academies Press: Washington, DC, USA, 2009. [Google Scholar] [CrossRef]
- Mohler, J.L. A Review of Spatial Ability Research. Eng. Des. Graph. J. 2008, 72, 19–30. [Google Scholar]
- Gutiérrez, A. Visualization in 3-dimensional geometry. In Search of a Framework, Proceedings of the 20th International Conference for the Psychology of Mathematics Education, Valencia, Spain, 8–12 July 1996; Puig, L., Gutiérrez, A., Eds.; University of Valencia: Valencia, Spain, 1996; Volume 1, pp. 3–19. [Google Scholar]
- Phillips, L.M.; Norris, S.R.; Macnab, J.S. Visualization in Mathematics, Reading and Science Education; Springer: New York, NY, USA, 2010; Volume 5. [Google Scholar]
- Vágová, R. Exploring the Interplay of Physical and Digital Manipulatives to Develop Students’ Visualisation in Solid Geometry; UKF Nitra: Nitra, Slovakia, 2021. [Google Scholar]
- Arcavi, A. The role of visual representations in the learning of mathematics. Educ. Stud. Math. 2003, 52, 215–241. [Google Scholar] [CrossRef]
- Rumanová, L.; Vallo, D.; Smiešková, E. Blueprint as a Motivation Factor for the Development of Spatial Ability in Teaching of Mathematics: An Action Research Study. TEM J. 2021, 10, 732–742. [Google Scholar] [CrossRef]
- Arana, A.; Moncosu, P. On the relationship between plane and solid geometry. Rev. Symb. Log. 2012, 5, 294–353. [Google Scholar] [CrossRef]
- Furinghetti, F.; Radford, L. Historical Conceptual Developments and the Teaching of Mathematics: From Phylogenesis and Ontogenesis Theory to Classroom Practice. In Handbook of International Research Mathematics Education; English, L.D., Ed.; Rutledge: New York, NY, USA, 2002. [Google Scholar]
- Hejný, M.; Benešová, M.; Bereková, H.; Bero, P.; Hrdina, L.; Repáš, V.; Vantuch, J. Teória Vyučovania matematiky 2; SPN: Bratislava, Slovakia, 1990. [Google Scholar]
- Zilkova, K.; Gucaga, J.; Kopacova, J. (Mis)Conceptions about Geometric Shapes in Pre-Service Primary Teachers. Acta Didact. Napoc. 2015, 8, 27–35. [Google Scholar]
- Bohning, G.; Althouse, J.K. Using Tangrams to Teach Geometry to Young Children. Early Child. Educ. J. 1997, 24, 239–242. [Google Scholar] [CrossRef]
- Lewin, K. Action research and minority problems. J. Soc. Issues 1946, 2, 34–46. [Google Scholar] [CrossRef]
- Cohen, L.; Manion, L.; Morrison, K. Research Methods in Education, 6th ed.; Routledge: London, UK; New York, NY, USA, 2007. [Google Scholar]
- McNiff, J. A Place for Learning, Sharing and Creating New Knowledge, Booklet. Available online: https://www.jeanmcniff.com/ar-booklet.asp (accessed on 17 July 2021).
- McNiff, J. Action Research: All You Need to Know, 1st ed.; SAGE Publication Ltd.: Los Angeles, CA, USA, 2017. [Google Scholar]
- Tripp, D. Action research: A methodological introduction. Educação e Pesquisa 2005, 31, 444–467. [Google Scholar]
- Atkinson, S. Rethinking the Principles and Practice of Action Research: The tensions for the teacher-researcher. Educ. Action Res. 1994, 2, 383–401. [Google Scholar] [CrossRef][Green Version]
- Mathematics, National Educational Program (in Slovak: Matematika, Štátny Vzdelávací Program ISCED 1). Available online: https://www.statpedu.sk/files/articles/dokumenty/statny-vzdelavaci-program/matematika_isced1.pdf (accessed on 18 July 2021).
- Babály, B.; Kárpáti, A. A téri képességek vizsgálata papír alapú és online tesztekkel. Magy. Pedagógia 2015, 115, 67–92. [Google Scholar] [CrossRef]
- Kárpáti, A.; Babály, B.; Budai, L. Developmental Assessment of Spatial Abilities through Interactive, Online 2D and Virtual 3D Task. Int. J. Arts Educ. 2014, 12, 94–124. [Google Scholar]
- Serin, H. Perspectives on the Teaching of Geometry: Teaching and Learning Methods. J. Educ. Train. 2018, 5, 1–7. [Google Scholar] [CrossRef]
- Sinclair, N.; Bussi, M.G.; de Villiers, M.; Jones, K.; Kortenkamp, U.; Leung, A.; Owens, K. Geometry Education, Including the Use of New Technologies: A Survey of Recent Research. In Proceedings of the 13th International Congress on Mathematical Education, Hamburg, Germany, 24–31 July 2016; Kaiser, G., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Fujita, T.; Jones, K.; Yamamoto, S. Geometrical Intuition and the Learning and Teaching of Geometry. In Proceedings of the 10th International Congress on Mathematical Education (ICME-10), Copenhagen, Denmark, 4–11 July 2004. [Google Scholar]
- Paivio, A. Mental Representations: A Dual Coding Approach; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Piaget’s Theory of Cognitive Development. Available online: https://en.wikipedia.org/wiki/Piaget%27s_theory_of_cognitive_development (accessed on 27 July 2021).
- Kollár, K.N.; Szabó, É. Pszichológia Pedagógusoknak; Orisis: Budapest, Hungary, 2004. [Google Scholar]
- Presmeg, N. Research on visualization in learning and teaching mathematics: Emergence from psychology. In Handbook of Research on the Psychology of Mathematics Education: Past, Present, and Future; Gutierrez, A., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2006; pp. 205–235. [Google Scholar]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kmetová, M.; Nagyová Lehocká, Z. Using Tangram as a Manipulative Tool for Transition between 2D and 3D Perception in Geometry. Mathematics 2021, 9, 2185. https://doi.org/10.3390/math9182185
Kmetová M, Nagyová Lehocká Z. Using Tangram as a Manipulative Tool for Transition between 2D and 3D Perception in Geometry. Mathematics. 2021; 9(18):2185. https://doi.org/10.3390/math9182185
Chicago/Turabian StyleKmetová, Mária, and Zuzana Nagyová Lehocká. 2021. "Using Tangram as a Manipulative Tool for Transition between 2D and 3D Perception in Geometry" Mathematics 9, no. 18: 2185. https://doi.org/10.3390/math9182185
APA StyleKmetová, M., & Nagyová Lehocká, Z. (2021). Using Tangram as a Manipulative Tool for Transition between 2D and 3D Perception in Geometry. Mathematics, 9(18), 2185. https://doi.org/10.3390/math9182185





