Abstract
The designed fractional order Stuxnet, the virus model, is analyzed to investigate the spread of the virus in the regime of isolated industrial networks environment by bridging the air-gap between the traditional and the critical control network infrastructures. Removable storage devices are commonly used to exploit the vulnerability of individual nodes, as well as the associated networks, by transferring data and viruses in the isolated industrial control system. A mathematical model of an arbitrary order system is constructed and analyzed numerically to depict the control mechanism. A local and global stability analysis of the system is performed on the equilibrium points derived for the value of = 1. To understand the depth of fractional model behavior, numerical simulations are carried out for the distinct order of the fractional derivative system, and the results show that fractional order models provide rich dynamics by means of fast transient and super-slow evolution of the model’s steady-state behavior, which are seldom perceived in integer-order counterparts.
1. Introduction
A small piece of software code or program in a computer system that works on a system without the consent of the user may cause damage or steal information for the exploitation of the desired targets. In strategic conflicting environments, as well as in the financial market, computer viruses can be used in a network operation as a digital weapon against the desired targets, e.g., a computer spyware program used as an information collection platform in the Syrian war [1], or Shamoon and Stuxnet viruses for cyber incidents [2]. The tools used for cyberwar vary from a tiny code that exhibits annoying messages on the console to a complicated routine that physically damages the system, such as Stuxnet [3]. Stuxnet was discovered at Natanz, Iran, a nuclear enrichment facility, in June 2010 [4]. The name of the Stuxnet virus was derived from two keywords in its source code, .stub and mrxnet.sys. The Stuxnet virus is a sophisticated piece of code that mainly targets the supervisory control and data acquisition systems (SCADA), exploits zero-day vulnerabilities/bugs to attack the targeted hosts, and uses advanced technology to hide from guard programs. The Stuxnet virus exploits different services, such as a print spooler (MS 10-061), the zero-day vulnerability of the windows system, network shares, file-sharing and server message block (SMB), etc. Stuxnet virus monitors the frequency of motors operating centrifuge machines before modification, which must be in the range of from 807 Hertz to 1210 Hertz. Stuxnet virus controls the running frequency of centrifuge machines for a short interval of time to 1410 Hertz and then decreases to 2 Hz and increases to 1064 Hertz. A change in the output frequency of the motors essentially sabotages the working of machines [5]. Due to the attack of the Stuxnet virus, approximately 1000 centrifuge machines were out of order, of a total of 5000 machines operating in the Iran nuclear facility at Natanz [6]. The purpose of the virus was not just to infect the computers, but to cause real-world physical damage.
A theoretical study of the Stuxnet’s malicious code behavior was conducted through the strength of epidemic modeling of virus spread [7,8,9]. The control scheme of these malicious codes is very challenging because they often hide, and may exploit zero-day vulnerabilities, gain administrative rights and execute code as an authenticated program. The development in technologies creates new issues regarding the safety and security of the critical infrastructure of the countries in the presence of these vulnerabilities and smart viruses. The desire to manufacture an automated process immensely increases software dependencies, which ultimately require lengthy and complex routines.
These complex codes are challenging to screen out completely using software testing mechanisms, and leftover vulnerabilities in these codes can compromise the whole system [10]. Therefore, the comprehensive and dynamic study of these codes is a promising domain for research communities to investigate.
The spread of the virus in a computer network is closely related to the spread of biological viruses in the population. Mathematical and statistical models are often based on concepts and methods borrowed from physics. Models play an important role in infection control by quickly predicting and understanding disease outbreaks. In recent decades, new infectious diseases have been observed, together with the development of eliminated technologies.
The ability to quickly measure the unfolding of outbreaks, communications, and movements is key to capturing the spread of a virus. The inherent complexity of such methods limits the study of these processes. However, developments in technology are helping to lift these limitations [11]. Classical approaches and linear thinking are unable to effectively mitigate the problem due to the lack of equilibrium and non-linear nature of the problems. A complex system, its counter-intuitive behavior, and other macro-level changes can be addressed by applying complex sciences. The usual models did not provide an in-depth picture of real system dynamics because these systems neglect feedback scenarios, cascade effects, and instabilities. To predict the global-scale spread of disease dynamics, several factors, such as demographic disparity, mobility scenarios which include air-flow system, commuter movement in the area, disease-specific information, and control mechanisms, should be acccounted for. There has long been work on the development of mathematical models for use in the analysis of infectious disease behavior. The mathematical model of Daniel Bernoulli against smallpox disease was published in 1766. Mathematical models of these types were designed to elaborate the behavior of an epidemic over the course of time, in which every single population of the virus is assumed to interact with the individual of other populations. The ability to monitor hidden outbreaks, as well as contact and communication, are key to the portrayal of disease-spreading [12]. It is known that immunizing a large fraction of the population or a computer network, the epidemic that spreads upon contact between infected nodes or individuals can be stopped.
Some diseases require 80–90% immunization (measles requires 95%), and the same is true for the computer, where 100% immunization from the Internet may stop viruses in connected networks [13]. Mathematical modeling of infectious disease or viruses in biology or in computer systems gives us a thorough understanding of the problem and helps us to devise a reliable, viable, and robust control strategy [14]. It was observed that the state of the various biological organisms at a certain time depends on its past states and fractional derivatives that also contains those characteristics. Thus, a fractional derivative is a natural approach to the solution of these biological systems. Mathematical modeling is used in numerous disciplines of science and engineering problems [15,16]. Kermack and McKendrick founded mathematical modeling at the beginning of twentieth century with a series of publications, and introduced a susceptible, infected and recovered epidemic model [17]. In this field, several other scientists, biologists, computer engineers and mathematicians have worked on epidemic modeling and published work in this area, such as time delay virus models [18], a fractional epidemiological model [19], antivirus strategy for computer virus model [20], modified susceptible, infected and susceptible models [21] and epidemic models with two control mechanisms, quarantine and immunity [22], and models that highlight the topological facets of the network [23]. Besides these, the role of fundamental concepts and underlying theories of fractional calculus was effectively applied in modeling complex systems in diversified fields with rich dynamics compared to its integer counterparts [24,25,26,27]. Considering these facts, the current study aims to exploit the rich heritage of fractional dynamics for the development of the fractional Stuxnet virus model by using the features of the Stuxnet model to illustrate the virus spread in SCADA systems [28]. In this study, a fractional-order mathematical model of the Stuxnet virus is presented to study the ultra-fast transient and slow evolutions of the virus spread dynamic and attack pattern on isolated critical infrastructures, managed by industrial control computers. The contribution of the proposed fractional Stuxnet virus model is briefly described as:
- A novel fractional-order Stuxnet virus model is proposed by exploiting the rich heritage of fractional calculus in an isolated and air-gapped network environment.
- Stability analysis of Stuxnet virus model for both local and global equilibrium points when disease-free, and endemic spread is performed.
- Correctness of the proposed Grunwald–Letnikov-based fractional numerical solver is ascertained, with close results to the state-of-the-art Runge–Kutta numerical solver for integer-order variants of the model.
- Numerical simulation with Grunwald–Letnikov-based fractional numerical solver for a distinct order of the fractional derivative terms in the system shows that fractional-order models offer rich characteristics by way of ultrafast transience and ultra-slow advancements of steady-state.
2. Fractional Calculus Fundamentals
2.1. Preliminaries
Fractional calculus is a branch of mathematics and a generalization of the calculus theory of integrals and derivatives of a real number or complex number power. The discussion of fractional calculus was started 300 years ago, and the idea of fractional calculus was first listed in the literature with a letter from Leibniz to L’Hostital in 1696. In this letter, a half-derivative term was introduced, i.e., the generalization of the derivative operator , where , representing the order of a fractional derivative. The history of the fractional derivative is as long as the classical differential operators in calculus, but the inherent strength of the fractional operator is relatively less exploited in engineering domains until the early 1980s. The physical interpretation of the fractional derivative outcomes is still ambiguous, and remained an open debate for clarity in the research community. However, the fractional derivative is an inspiring operator to describe the physics of many modeling phenomena, which are difficult to realize through integer-order derivatives. Recently, the kernel function of a fractional derivative is referred to as a memory function, and fractional-order derivative is proposed as a memory index [29,30] with different types of kernel [31,32,33,34,35,36]. The theory development of fractional calculus belonged to the efforts of several scientists, such as Letnikov, Liouville, Euler, and Riemann [37,38]. Different definitions of fractional order derivatives have existed; the most-used definitions are those of Riemann–Liouville (RL), Caputo (CP), and Grunwald–Letnikov (GL) [39]. The GL definition of fractional derivative is as follows:
The definition of Caputos fractional derivatives can be written as:
for and where is a gamma function.
The RL definition is given as:
For , while a and t are the bounds of the operation for , the Laplace transform method is normally used with CP, GL and-RL fractional derivatives under zero initial conditions, as: [40]
while the analytical expressions are represented by Mittag–Leffler (ML)-type functions [41] introduced by Agarwal and Humbert [42] and are given mathematically as:
where C represents the set of complex numbers and is a two-parameter-based ML function.
2.2. Grunwald–Letnikov-Based Numerical Solver for FDEs
Analytical solution to the fractional differential equations (FDEs) generally determined through the Laplace transform method (4), and these expressions are commonly represented by the ML function (5), while, for the numerical solutions, the most commonly used method is based on GL definition.
To introduce the numerical solver based on GL [43] for FDEs, let a general from of an FDE, along with its initial conditions, is given as follows:
where , using Equation (1), Ivo Petras [44] provided the final recursive expression of a GL-based solver is as follows:
simplifying above relation, we have
In case of discrete input grids between interval , where h represents the step size parameter, so and any grid points in the interval are represented as . Thus, in a discrete form, the above equation is written as:
In simple usage, the above term is written as:
where is defined as:
or equivalently with ,
GL numerical solver in the recursive form is written as:
A further elaboration of the Grunwald–Letnikov (GL)-based numerical solver can be seen in [45].
3. Model Formulation of Fractional Order Stuxnet Virus
The formulation of a fractional-order Stuxnet virus model (FO-SVM) is presented here. A detailed workflow of the proposed FO-SVM is shown in Figure 1. The entire FO-SVM is segmented into five classes: three for computer population, i.e., susceptible , infected , and damaged , and two for removable storage media, i.e., susceptible storage media and infected storage media . However, represents the total population, i.e., , and total removable devices , i.e., . In the rest of the article, the variables with respect to time t, , , , , , , and are denoted by S, I, M, , , N, and U, respectively. Let and represent the arrival of new computing nodes and removable storage media, respectively, damage rate caused to PLC’s due to virus infection is represented by , is the infectious contact rate of susceptible nodes with infected nodes during the network scan, and denotes the contact rate of infectious-removable storage media with susceptible computer nodes, and represent the natural removal (death) of computer nodes and removable devices from the network, respectively. The number of nodes in Internet protocol version 4 (IPv4) is , and the probability of finding susceptible nodes in IPv4 scheme is . Susceptible nodes can be infected at the rate or at , while the removable storage media could be infected at a rate of . Removable storage media is a common source of virus spread in critical industrial air-gapped networks, which are isolated from normal networks. The removable storage devices facilitate the flow of information to and from the networks that make them as an easy prey for intruders [46]. In this study, fractional-order virus model is used to explain the spread of the virus, especially Stuxnet [47,48] in industrial networks through removable storage media. A proposed flow chart diagram of the Stuxnet virus model is shown in Figure 2, and the fundamental mathematical equations of the model are given as:
where represents the order of the fractional derivative term . For the value of , the above-mentioned FO-SVM system provided in a set of Equation (9) will be converted into a first-order system. From the differential equations mentioned in (9), solving the equations by taking the value of = 1, we get
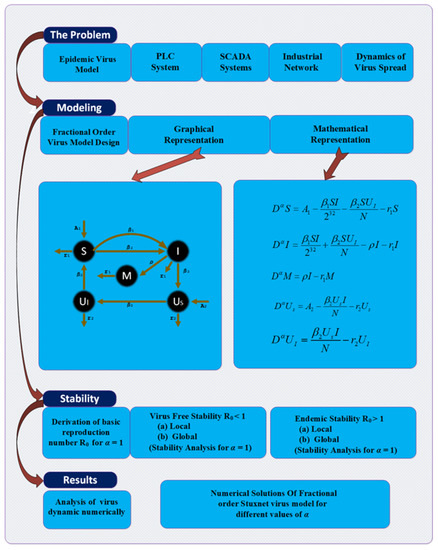
Figure 1.
FO-SVM model proposed graphical overview.
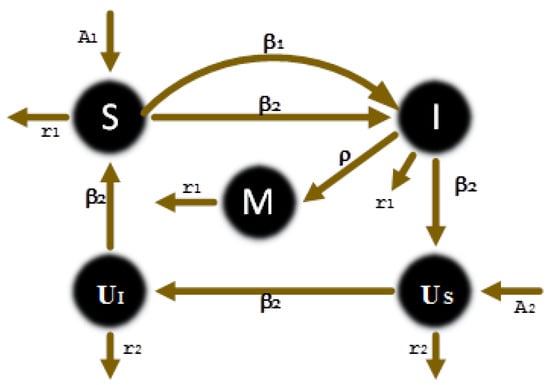
Figure 2.
FO-SVM model schematic flow diagram.
The change in population is given by and , and the values of these constants may be negative, positive or zero.
Solving the set of Equation (10), we get
4. Model Analysis
In this unit, stability analysis of the model is performed through the derivation of basic reproduction number, . The endemic and disease-free equilibrium points of the system are investigated for a local as well as global stability analysis.
4.1. Basic Reproduction Number ()
In epidemiology modeling, a basic reproduction number is defined as the advent of a new infection in an entirely susceptible population due to an infected individual, and is usually represented by . The value of determines the spread of infection; for infection will spread in the population, and for infection will soon end [51].
To simplify the derivation process, a reduced model (14) has been utilized for further investigation of . The calculation of is based on the value of = 1. The necessary condition of a disease epidemic is based on the increase in the infected individuals, with the supposition that, initially, the entire population is susceptible.
For the case of , we have
and, accordingly, in case of , we have
With the assumption that all the population is susceptible at the start, the above expressions may be written as:
Simplifying the above relations, we have
Accordingly,
Equation (20) represents the basic reproduction number derived for the model.
4.2. Equilibria Studies
In this subsection, we study the equilibrium points of FO-SVM model Equation (14). The FO-SVM model has virus-free equilibrium and endemic equilibrium points. In the endemic equilibrium point, the spread of infection is observed.
For equilibria studies, we have
equilibrium points of system (14) for virus-free and endemic are as: = (I, M, ) = (0, 0, 0) and = (, , ) for .
The analysis for the endemic equilibria of model (14) is written as:
Solving the equations in set (21), we obtain the expressions for the endemic equilibrium point (, , ) as:
where
It is evident from Equation (22) that the possibility of infection spread, i.e., , is only verified for the value of .
4.3. Disease Free Equilibrium
Theorem 1.
Disease-free equilibrium (DFE) point of a system is locally and asymptotically stable at , if .
Proof.
The DFE point of a system is locally asymptotically stable at = (I, M, ) = (0, 0, 0). The Jacobian matrix of function with components:
Thus, the Jacobian matrix at , DFE point of integer-order model (14) is given as:
The corresponding Eigen values of the above relation are
Simplifying the above expression to find the remaining Eigenvalues
and rearranging the above expression
and, for , Equation (9) can be written as:
Using the expression (31) in Section 4.3, make the coefficient positive for , which shows that system Section 4.3 eigenvalues are in a stable region; this confirms that the system is asymptotically stable for point when . If system is stable for the value of , it will be stable for the value of , as reported in [52]. This completes the proof. □
Theorem 2.
If , then point is globally asymptotically stable, and otherwise unstable.
Proof.
Considering the Lyapunov function mentioned below,
The function in is positive, for = () and .
For = 1, the derivative of Lyapunov function (32) is
For , this implies that and is the only invariant set of system (21). According to the LaSalle Invariance Principle, is proven to be globally asymptotically stable. Hence, equilibrium point is globally asymptotically stable for . Additionally, if the system is stable for the value of , then the system will be stable for , as described in [52]. □
4.4. Endemic Stability
The endemic stability of equilibrium point = (, , ) is investigated in this section for the values of and .
Theorem 3.
Endemic equilibrium point is locally asymptotically stable, if .
Proof.
The endemic equilibrium of system (14) is = (, , ), for the value of = 1, the Jacobian matrix at endemic point is mentioned below.
where .
For stability analysis, Hurwitz criteria may be used, as reported in [53,54] for system (36). Equating the Equation (36) coefficient with the general characteristics equation, we have
Determinants (, and ) of the Equation (36) are stated in Hurwitz as:
using the value of Equation (20) for as:
and
The above expressions remain positive, except for , , which, if positive for , is simply represented as:
Here, represent the positive terms in , while, for the remaining terms, represented with , we have
using the value of , and after simplification, the above expression becomes
as a result
The positivity of the expression for is already proved for the case ; therefore, .
Thus, all the values of , and are positive, so all the eigenvalues of the Equation (36) are negative, for . This proves that the endemic equilibrium point is locally asymptotically stable. The proof of theorem is completed. □
5. Simulation and Results
In this section, the results of numerical simulations for FO-SVM are presented to understand the dynamics of virus spread in a critical network infrastructure in the presence of removable storage connectivity, which may compromise the air-gap between the networks. Numerical experimentation is conducted for the designed FO-SVM as given in Equation (9) for a different variation in parameters and initial start-up scenarios, as given in Table 1 and Table 2, respectively. The dynamic behavior of the fractional order (FO) model is studied by varying the non-integer order derivative . Most FO differential systems lack exact analytical solutions, so the numerical solver based on Grunwald–Letnikov (GL) procedure, as described in Section 2 is exploited for an approximate solution to the model. The security firms, including Symantec, tracked 100,000 infected computers as of 29 September 2010, in the world. Additionally, available real data are used to validate the accuracy and convergence of the model for the Stuxnet virus spread. The virus infects approximately 100,000 users from 155 different countries, and 63% were only in Iran. Due to this attack, the number of hosts that lost functionality (hardware connected to these hosts was damaged due to sudden increase in frequency of up to 1410 Hz, which then decreased to 2 Hz and increased to 1064 Hz in spite of the normal working range of from 807 Hz to 1210 Hz) due to virus attack. A virus operates the machines connected with the hosts at an extreme range of frequencies dictated by Stuxnet and caused physical damage to 1500 centrifuge machines (approximately 1200 in Iran only). Approximately 3280 unique samples and variants of the Stuxnet virus were recorded by Symantec and other security corporations [3,6,55].

Table 1.
Values of parameters used in model simulation for different scenarios.

Table 2.
Starting values of variables used in the simulation of different scenarios.
In order to establish the working accuracy of GL-based numerical solvers, the results of the scheme are compared with state-of-the-art numerical solvers based on the Runge–Kutta (RK) method for the value of = 1. The results are determined for nine cases of integer order models (9) by a GL-based computing technique for inputs with step size h = 0.001 (time t represents months). Numerical solutions to the model for the same inputs are also calculated by the RK method for each variation. Figure 3 highlights the comparison of model behavior with Stuxnet virus real-world data. FO-SVM model results shown in Figure 3 are calculated using the RK method to assume the value of fractional order = 1.
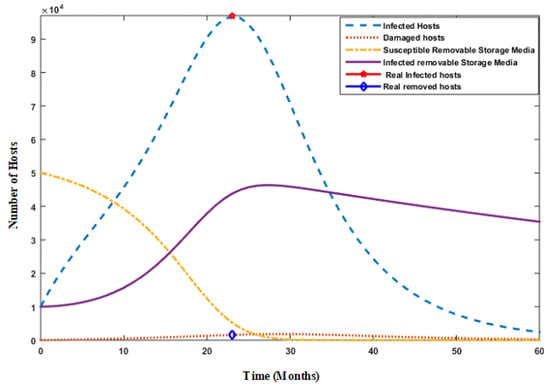
Figure 3.
Simulation of Stuxnet virus spread with available data of parameters = 0.042, = 0.042, = 0.366, = 0.6, = 0.00265, = 0.1126, = 0.0088, S = , I = 10,000, M = 10, = 50,000, = 10,000.
In Figure 3, the number of hosts versus time in months is plotted, which shows the effect of the Stuxnet attack on the number of hosts as time passes.The number of infected hosts is 96,760 (real infected host number was 100,000), and the number of damaged hosts is 1500 (real damaged host number was 1500) in 23 months time, which shows the model accuracy for real-world virus data, as shown in Figure 3, with red and blue dots, respectively. In this case, removable media are considered to be 60,000, and, after increasing the number of removable-storage media, infection in the host nodes also increases (96,760 after 23 months).
The number of infected removable-storage devices is 43,740 in 23 months, and in 24 months, the time number of infected devices increases to 44,920. An increase in the number of damaged hosts is observed after the increase in infected hosts in 24 months’ time. This highlights the role of removable-storage media in spreading the infection in isolated critical networks in the absence of any remedial strategy in the model. Stuxnet is an advanced, persistent threat (APT) type of malicious code that penetrates in the remote system in a quasi-autonomous fashion. Then, a 23-month decline in the number of infected hosts is observed due to the availability of remedial technique and other controlling mechanisms. However, the Stuxnet virus was carried by removable-storage media spreads in other·networks.
In Figure 4, the solutions to the RK method with GL solver is compared with an error analysis of susceptible hosts S: a and b for cases 2 to 4, c and d for cases 5 to 7, and e and f for cases 8 to 10. Comparisons of results from both the RK numerical solver and GL-based method (for fractional-order = 1) are presented for susceptible hosts S in nine cases. The error analysis, based on the absolute difference between the two approaches, is also plotted in Figure 4 to assess closeness. The results show a matching of both solutions of up to three decimal places of accuracy. The small errors in these plots show that the results of the GL method are in good agreement with the standard RK numerical technique, which establishes the working accuracy of the GL-based solver. In Figure 5, the solution of the RK method with the GL solver is compared in the case of infected hosts I and damaged hosts M: a and b for cases 1 to 3, c and d for cases 4 to 6, and e and f for cases 7 to 9. Figure 4 compares solutions for the RK method with GL solver in case of susceptible and infected removable-storage media: a and b for cases 1 to 3, c and d for cases 4 to 6, and e and f for cases 7 to 9. In Figure 5 and Figure 6, the solution of the RK method with a GL solver are compared and presented for infected nodes I, damaged node M, susceptible removable-storage media and infected removable-storage media , respectively, for nine model cases.
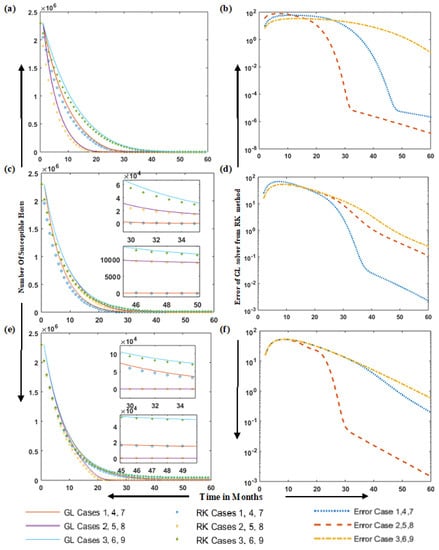
Figure 4.
Solution comparison of the RK method with GL solver and error analysis with susceptible S hosts: a and b for cases 2 to 4, c and d for cases 5 to 7, and e and f for cases 8 to 10. (a) Solution comparison of the RK method with GL solver for cases 2 to 4, (b) error analysis for cases 2 to 4, (c) Solution comparison of the RK method with GL solver for cases 5 to 7, (d) error analysis for cases 5 to 7, (e) Solution comparison of the RK method with GL solver for cases 8 to 10, (f) error analysis for cases 8 to 10.
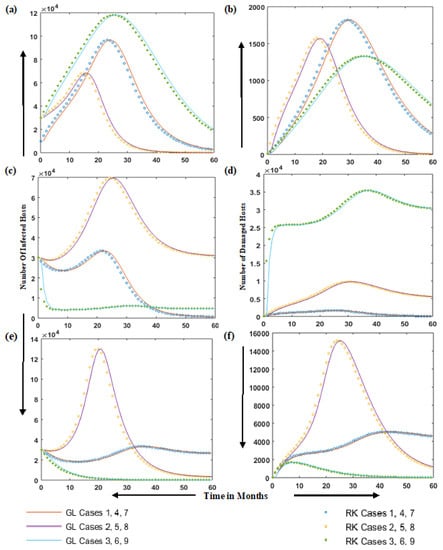
Figure 5.
Solution comparison of RK method with GL solver for infected hosts I and damaged hosts M; a and b for cases 1 to 3, c and d for cases 4 to 6 while e and f for cases 7 to 9. (a) Comparison of RK method with GL solver for infected hosts in cases 1 to 3, (b) Comparison of RK method with GL solver for damaged hosts in cases 1 to 3, (c) Comparison of RK method with GL solver for infected hosts in cases 4 to 6, (d) Comparison of RK method with GL solver for damaged hosts in cases 4 to 6, (e) Comparison of RK method with GL solver for infected hosts in cases 7 to 9, (f) Comparison of RK method with GL solver for damaged hosts in cases 7 to 9.
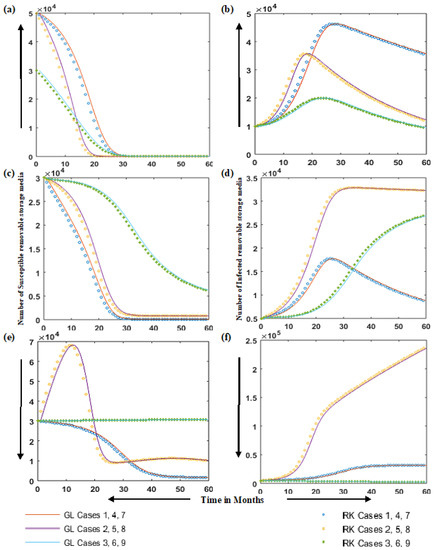
Figure 6.
Solution comparison RK method with GL solver for susceptible and infected-removable-storage media: a and b for cases 1 to 3, c and d for cases 4 to 6, and e and f for cases 7 to 9. (a) Comparison of RK method with GL solver for susceptible removable storage media in cases 1 to 3, (b) Comparison of RK method with GL solver for infected removable storage media in cases 1 to 3, (c) Comparison of RK method with GL solver for susceptible removable storage media in cases 4 to 6, (d) Comparison of RK method with GL solver for infected removable storage media in cases 4 to 6, (e) Comparison of RK method with GL solver for susceptible removable storage media in cases 7 to 9, (f) Comparison of RK method with GL solver for infected removable storage media in cases 7 to 9.
These nine cases also explain the virus spread behavior in different scenarios. Considering Figure 4, Figure 5 and Figure 6, and the different cases simulated, we have the following comments.
The effect of changing the infectious contact rate from 36.6% to 60% is highlighted in case 1 of Equation (9) (value of in Figure 3 is 36.6%). It is observed that the number of infected hosts in 24 months is 96,760, as shown in Figure 5a (in Figure 3, the number of infected hosts in 24 months is 96,270), which shows a slight increase in infected hosts due to . In case 2, the number of initially infected hosts is assumed to be 30,000. Increasing the contact rate of infectious removable media (in case 2) reduces the number of susceptible hosts rapidly as compared to case 1 (Figure 4a). However, the number of infected hosts is reduced (Figure 5a) due to an increase in the natural removal rate of hosts and removable storage and (hosts are removed to save them from the Stuxnet attack). In case 3, we reduce the damage rate and the quantity of initial susceptible removable-storage media, which reduces infected removable-storage media number (Figure 6b) and increases the infected hosts, as in Figure 5a). A decrease in damaged hosts is observed in case 3, despite the increase in the number of infected hosts.
In case 4, FO-SVM model dynamics are observed by increasing the arrival rate of new nodes and the arrival rate of new removable-storage devices, as mentioned in Table 1 and Table 2. The results show that increasing the arrival rate of new hosts and arrival rate of new removable-storage media will not spread the infection faster without the presence of a sufficient number of infected removable-storage devices, as shown in Figure 5c. In cases 5 and 6, we further increase the values of the arrival rate of new nodes as well as removable-storage devices for an in-depth behavior analysis of the model. Both cases have similar parameters, except case 6, which represents a higher damage rate (especially for zero-day vulnerability or for a new virus attack) that increases the number of damaged computers and reduces the number of infected computers (removed due to high damage rate) in the networks as compared to case 5. Case 5 shows the high number of infected nodes (Figure 5c) because the Stuxnet virus only destroys the machines with specific hardware (Siemens specific PLCs) and remains dormant till it finds the target. In case 6 (Figure 5c,d), the number of infected hosts decreases; however an increase in the number of damaged hosts is observed due to an increase in damage rate .
In case 7, the values of and of case 6 are swapped to observe the behavior of the model. In case 7, the value of = 0.745, as compared to 0.4 in case 6, and the value of = 0.4, as compared to 0.745 in case 6. These swaps are carried out to observe the devastation effect of infected removable storage media as compared to the effect of infected nodes in the model, because infected removable media have a greater devastation effect. Simulation results show that the number of damaged nodes in case 6 is 35,000, whereas, in case 7, it is 5000, due to a decrease in the value of infectious contact rate of removable storage media (Figure 5e).
However, by increasing value (removable-storage media’s infectious contact rate with susceptible computers) and (the arrival of removable-storage media) for case 8 will also increase the infection in the network. This outlines the importance of removable-storage media in spreading the virus in air-gapped networks (Figure 5e). In case 9, the contact rate of susceptible computer nodes with infectious removable-storage media is reduced, which results in a reduction in damaged nodes (Figure 5f) and infected nodes (Figure 5e), and an increase in the number of susceptible storage devices (Figure 6e). Case 9 further elaborates the scenario presented in case 8.
The derivative order = 1 is presented in Figure 4, Figure 5 and Figure 6. The effect of change in fractional order is presented in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. A detailed analysis of the FO-SVM model is conducted by changing the fractional order in the system (9), such that one may observe fast-changing as well as super-slow growth in the model dynamics. The fractional order solution of the FO-SVM model for different values of the fractional order is solved using a GL-based solver. The solutions are determined for nine cases of FO-SVM by a GL-based numerical procedure for different fractional orders, i.e., = [0.5, 0.75, 0.8, 0.85, 0.9, 0.95, 1], for the inputs with step size h = 0.001. Results for the dynamics of the FO-SVM model in terms of susceptible S, infected I, and damaged M computers are plotted in Figure 7, Figure 8 and Figure 9 for cases 1–3, 4–6, and 7–9, respectively. Susceptible removable-storage media and infected-removable-storage media are plotted in Figure 10 and Figure 11 for cases 1–4 and 5–9, respectively, for different values of the fractional order .
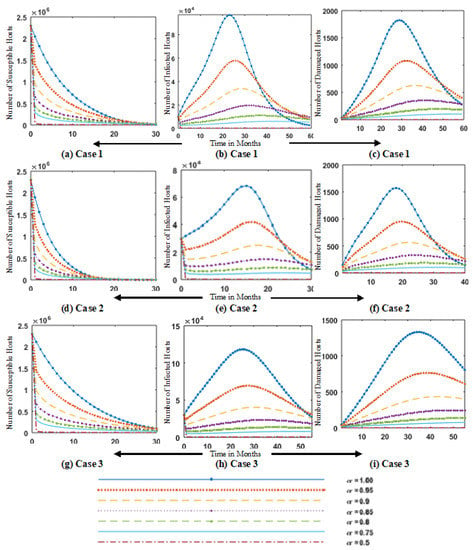
Figure 7.
Simulation of fractional order dynamics of FO-SVM model for different values of fractional order for cases 1 (a–c), 2 (b–f) and 3 (g–i) of susceptible S, infected I and damaged hosts M.
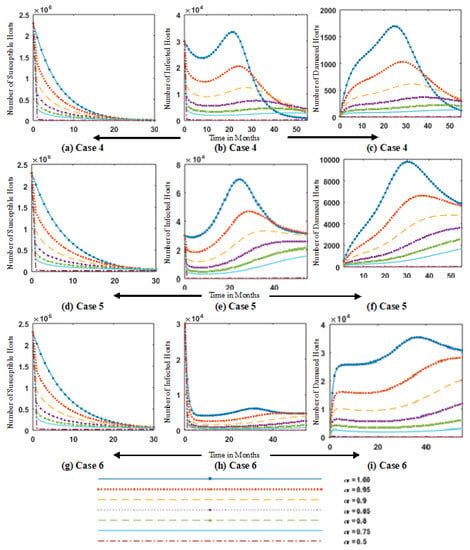
Figure 8.
Simulation of fractional order dynamics of FO-SVM model for different values of fractional order for cases 4 (a–c), 5 (b–f) and b (g–i) of susceptible S, infected I and damaged hosts M.
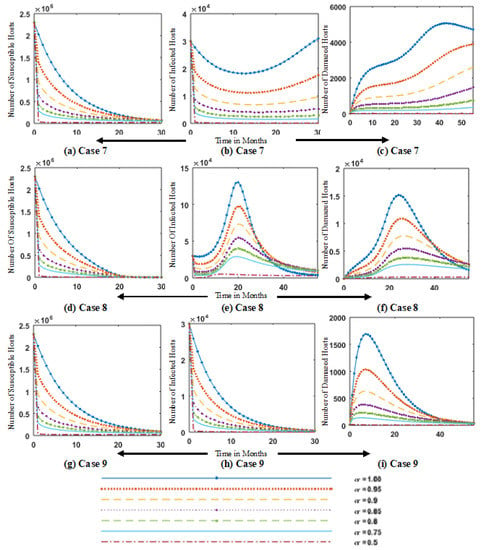
Figure 9.
Simulation of fractional order dynamics of FO-SVM model for different values of fractional order for cases 7 (a–c), 8 (b–f) and 9 (g–i) of susceptible S, infected I and damaged hosts M.
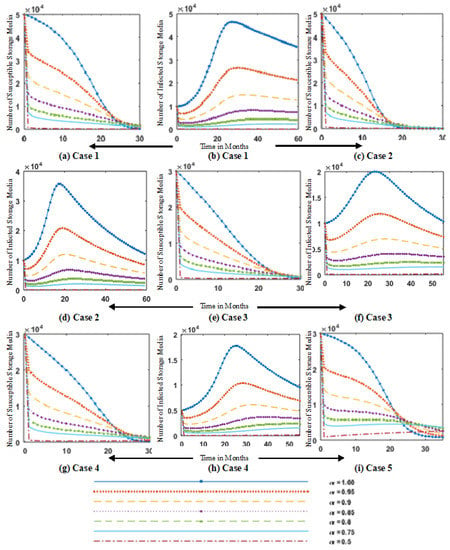
Figure 10.
Simulation of fractional order dynamics of FO-SVM model for different values of fractional order for cases 1 (a,b), 2 (c,d) and 3 (e,f), 4 (g,h) and 5 (i) of susceptible removable-storage media and infected-removable-storage media .
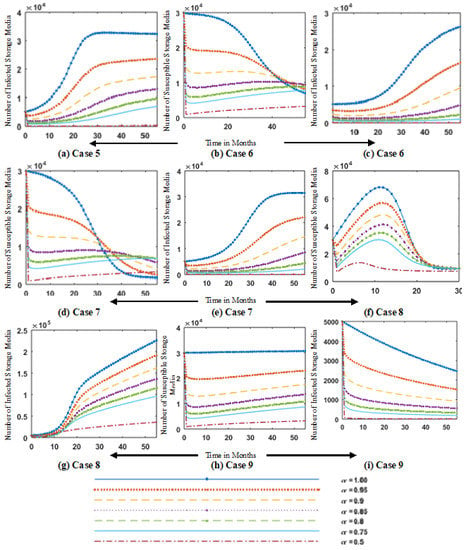
Figure 11.
Simulation of fractional order dynamics of FO-SVM model for different values of fractional order for cases 5 (a), 6 (b,c) and 7 (d,e), 8 (f,g) and 9 (h,i) of susceptible removable-storage media and infected-removable-storage media .
Figure 7 shows a simulation of fractional order, i.e., = [0.5, 0.75, 0.8, 0.85, 0.9, 0.95, 1] for the FO-SVM model for different values of fractional order for case 1–3 of susceptible S, infected I and damaged hosts M. In Figure 7, the number of susceptible, infected and damaged hosts is plotted versus time for cases 1–3 for different values of = [0.5, 0.75, 0.8, 0.85, 0.9, 0.95, 1]. A consistent pattern is observed in the evolution of curves with the value of . The value of infected hosts in case 1 with = 1 is 96,760, and for = 0.95, the value of infected hosts is approximately 56,000 for t = 24 months, as shown in Figure 7b. In Figure 7c, the number of damaged hosts (hosts that were connected with specific models of Siemens PLCs) for the value of = 0.95 are 1000 for t = 30. Adjusting the value of to 0.98 may adjust the number of damaged hosts to 1500, which matches the real published data of the Stuxnet virus. This illustrates the controllability feature of for tuning the model. Despite the rapid spreadability of the Stuxnet virus, it causes little or no harm to the systems that do not have specific hardware.
Figure 8 shows the simulation of fractional order dynamics of the FO-SVM model for different values of fractional order for cases 4–6, and Figure 9 depicts the simulation of fractional-order dynamics of the FO-SVM model for case 7–9. Figure 8 and Figure 9 highlight the results for variation in fractional order , which shows that variation in gives smooth variations in the dynamics of the model. For = 0.1, we have the slowest evolution. Simulation of fractional order dynamics of FO-SVM model for different values of fractional order for case 1–5 of susceptible removable-storage media and infected-removable-storage media are illustrated in Figure 10. Figure 11 shows the simulation of fractional order dynamics of FO-SVM model for different values of fractional order , for cases 5–9 of susceptible removable-storage media , and infected-removable-storage media . In Figure 10 and Figure 11, the number of susceptible storage media and infected storage media is plotted for case 1–9 against the time variation for different values of fractional order = [0.5, 0.75, 0.8, 0.85, 0.9, 0.95, 1]. It is observed that tuning the values of tunes the dynamics of transients, as shown in Figure 10a. The value of susceptible storage media for t = 1 and = 0.95 is 35,000, which is effectively reduced to 10,000 by a slight change in fractional order from 0.95 to 0.8. In contrast, a slow change is observed in the dynamics of the FO-SVM model for = 0.1. Increasing the fractional order increases the rate of change of the variables. Fractional-order virus models provide extra tunable parameters in the form of , which highlight more minute changes in the model dynamics.
6. Conclusions
A detailed analysis of the novel design of the fractional order Stuxnet virus model is presented, with richer dynamics for the transmission of virus spread in an isolated critical network through removable-storage media. The fractional-order Stuxnet-virus-based mathematical models are found to be at least as stable as integer-order models. The fractional order value of the proposed fractional Stuxnet virus model more effectively controls the solution reachability towards a steady state point. Additionally, the fractional order system of the Stuxnet virus model can tackle the different responses, including super-slow evolutions and very fast transients; these responses are found to have long memory characteristics in the system. Taking the value of = 0.98, one may adjust the number of damaged hosts to 1500 in case 1, which matches the damage caused by the Stuxnet virus. The transformation process of the classical model into a fractional model is very sensitive to the value of the order of differentiation , and can be converted to a simple SIR model if we choose the values of the infectious contact rate . A theoretical analysis of the model capturing the Stuxnet virus-spreading characteristics is determined by a mathematical derivation of the basic reproduction number for the value of = 1. Equilibrium points of the model are globally and asymptomatically stable for and , respectively.
In the future, one may exploit the strength of stochastic numerical solvers [56,57,58,59,60,61] based on fractional evolutionary and swarming techniques [62,63,64,65,66,67] for a detailed analysis of the designed fractional-order Stuxnet virus model. Additionally, new definitions of the fractional operator, such as Yang–Machado [35] and Yang–Abdel–Aty–Cattani [36] fractional derivatives looks promising for the development of new computing solvers for the numerical solution of the fractional-order Stuxnet virus model and other fractional-order systems with better theoretical justifications, a better applicability domain, proof of the accuracy, convergence, stability, and robustness.
Author Contributions
Conceptualization, Z.M. and M.A.Z.R.; methodology, Z.M. and M.A.Z.R.; software, Z.M.; validation, M.A.Z.R.; formal analysis, N.I.C. and M.A.Z.R.; investigation, Z.M.; writing—original draft preparation, Z.M.; writing—review and editing, N.I.C. and M.A.Z.R.; visualization, N.I.C. and M.A.Z.R.; project administration, K.M.C. and A.H.M.; funding acquisition, K.M.C. and A.H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rohde, M.; Aal, K.; Misaki, K.; Randall, D.; Weibert, A.; Wulf, V. Out of syria: Mobile media in use at the time of civil war. Int. J. Hum.-Comput. Interact. 2016, 32, 515–531. [Google Scholar] [CrossRef]
- Bronk, C.; Tikk-Ringas, E. The cyber attack on saudi aramco. Survival 2013, 55, 81–96. [Google Scholar] [CrossRef]
- Farwell, J.P.; Rohozinski, R. Stuxnet and the future of cyber war. Survival 2011, 53, 23–40. [Google Scholar] [CrossRef]
- Albright, D.; Brannan, P.; Walrond, C. Stuxnet malware and natanz: Update of isis December 22, 2010 report. Inst. Sci. Int. Secur. 2011, 15, 739883. [Google Scholar]
- Mueller, P.; Yadegari, B. The Stuxnet Worm. Département des Sciences de Linformatique, Université de lArizona. Available online: https://www2.cs.arizona.edu/˜collberg/Teaching/466-566/2012/Resources/presentations/topic9-final/report.pdf (accessed on 12 December 2017).
- Falliere, N.; Murchu, L.O.; Chien, E. W32. Stuxnet Dossier; White Paper; Symantec Corp., Security Response: Cupertino, CA, USA, 2011; Volume 5, p. 29. [Google Scholar]
- Shahrear, P.; Chakraborty, A.K.; Islam, M.A.; Habiba, U. Analysis of computer virus propagation based on compartmental model. Appl. Comput. Math. 2018, 7, 12–21. [Google Scholar]
- Khanh, N.H. Dynamical analysis and approximate iterative solutions of an antidotal computer virus model. Int. J. Appl. Comput. Math. 2017, 3, 829–841. [Google Scholar] [CrossRef]
- Latha, V.P.; Rihan, F.A.; Rakkiyappan, R.; Velmurugan, G. A fractional order model for ebola virus infection with delayed immune response on heterogeneous complex networks. J. Comput. Appl. Math. 2018, 339, 134–146. [Google Scholar] [CrossRef]
- Zhu, B.; Joseph, A.; Sastry, S. A taxonomy of cyber attacks on scada systems. In Proceedings of the 2011 IEEE International Conferences on Internet of Things, and Cyber, Physical and Social Computing, Dalian, China, 19–22 October 2011; pp. 380–388. [Google Scholar]
- Wang, Z.; Bauch, C.T.; Bhattacharyya, S.; d’Onofrio, A.; Manfredi, P.; Perc, M.; Perra, N.; Salathe, M.; Zhao, D. Statistical physics of vaccination. Phys. Rep. 2016, 664, 1–113. [Google Scholar] [CrossRef]
- Helbing, D.; Brockmann, D.; Chadefaux, T.; Donnay, K.; Blanke, U.; Woolley-Meza, O.; Moussaid, M.; Johansson, A.; Krause, J.; Schutte, S.; et al. Saving human lives: What complexity science and information systems can contribute. J. Stat. Phys. 2015, 158, 735–781. [Google Scholar] [CrossRef]
- Cohen, R.; Havlin, S.; Ben-Avraham, D. Efficient immunization strategies for computer networks and populations. Phys. Rev. Lett. 2003, 91, 247901. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Fu, C.; Liu, X.-Y.; Yang, J.; Zhu, T.; Han, L. Evolutionary virus immune strategy for temporal networks based on community vitality. Future Gener. Comput. Syst. 2017, 74, 276–290. [Google Scholar] [CrossRef]
- Yang, X.-J. General Fractional Derivatives: Theory, Methods and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar]
- Duarte Ortigueira, M.; Tenreiro Machado, J. Fractional derivatives: The perspective of system theory. Mathematics 2019, 7, 150. [Google Scholar] [CrossRef] [Green Version]
- Capasso, V.; Serio, G. A generalization of the kermack-mckendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Mishra, B.K.; Saini, D.K. Seirs epidemic model with delay for transmission of malicious objects in computer network. Appl. Math. Comput. 2007, 188, 1476–1482. [Google Scholar] [CrossRef]
- Kumar, S.; Ahmadian, A.; Kumar, R.; Kumar, D.; Singh, J.; Baleanu, D.; Salimi, M. An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets. Mathematics 2020, 8, 558. [Google Scholar] [CrossRef] [Green Version]
- Dong, T.; Wang, A.; Liao, X. Impact of discontinuous antivirus strategy in a computer virus model with the point to group. Appl. Math. Model. 2016, 40, 3400–3409. [Google Scholar] [CrossRef]
- Piqueira, J.R.C.; Araujo, V.O. A modified epidemiological model for computer viruses. Appl. Math. Comput. 2009, 213, 355–360. [Google Scholar] [CrossRef]
- Masood, Z.; Majeed, K.; Samar, R.; Raja, M.A.Z. Design of epidemic computer virus model with effect of quarantine in the presence of immunity. Fundam. Inform. 2018, 161, 249–273. [Google Scholar] [CrossRef]
- Calvert, K.L.; Doar, M.B.; Zegura, E.W. Modeling internet topology. IEEE Commun. Mag. 1997, 35, 160–163. [Google Scholar] [CrossRef]
- Sabatier, J.; Agrawal, O.P.; Machado, J.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007; Volume 4. [Google Scholar]
- Machado, J.T.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis, C.M.; Marcos, M.G.; Galhano, A.F. Some applications of fractional calculus in engineering. Math. Probl. Eng. 2010, 2010, 639801. [Google Scholar]
- Tenreiro Machado, J.A.; Mata, M.E.; Lopes, A.M. Fractional dynamics and pseudo-phase space of country economic processes. Mathematics 2020, 8, 81. [Google Scholar] [CrossRef] [Green Version]
- Masood, Z.; Samar, R.; Raja, M.A.Z. Design of fractional order epidemic model for future generation tiny hardware implants. Future Gener. Comput. Syst. 2020, 106, 43–54. [Google Scholar] [CrossRef]
- Masood, Z.; Samar, R.; Raja, M.A.Z. Design of a mathematical model for the stuxnet virus in a network of critical control infrastructure. Comput. Secur. 2019, 87, 101565. [Google Scholar] [CrossRef]
- Du, M.; Wang, Z.; Hu, H. Measuring memory with the order of fractional derivative. Sci. Rep. 2013, 3, 3431. [Google Scholar] [CrossRef]
- Heymans, N.; Podlubny, I. Physical interpretation of initial conditions for fractional differential equations with riemann-liouville fractional derivatives. Rheol. Acta 2006, 45, 765–771. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-J.; Feng, Y.-Y.; Cattani, C.; Inc, M. Fundamental solutions of anomalous diffusion equations with the decay exponential kernel. Math. Methods Appl. Sci. 2019, 42, 4054–4060. [Google Scholar] [CrossRef]
- Yang, X.-J. New rheological problems involving general fractional derivatives with nonsingular power-law kernels. Proc. Rom. Acad. Ser. A Math. Phys. Tech. Sci. Inf. Sci. 2018, 19, 45. [Google Scholar]
- Cao, Y.; Zhang, Y.; Wen, T.; Li, P. Research on dynamic nonlinear input prediction of fault diagnosis based on fractional differential operator equation in high-speed train control system. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013130. [Google Scholar] [CrossRef]
- Yang, X.-J.; Srivastava, H.M.; Torres, D.F.; Debbouche, A. General fractional-order anomalous diffusion with non-singular power-law kernel. Therm. Sci. 2017, 21, 1–9. [Google Scholar] [CrossRef]
- Yang, X.-J.; Machado, J.T. A new fractional operator of variable order: Application in the description of anomalous diffusion. Phys. A Stat. Mech. Its Appl. 2017, 481, 276–283. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.-J.; Abdel-Aty, M.; Cattani, C. A new general fractional order derivative with rabotnov fractional-exponential kernel applied to model the anomalous heat transfer. Therm. Sci. 2019, 23, 1677–1681. [Google Scholar] [CrossRef] [Green Version]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Machado, J.T.; Galhano, A.M.; Trujillo, J.J. On development of fractional calculus during the last fifty years. Scientometrics 2014, 98, 577–582. [Google Scholar] [CrossRef] [Green Version]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Petráš, I. A note on the fractional-order chuas system. Chaos Solitons Fractals 2008, 38, 140–147. [Google Scholar] [CrossRef]
- Haubold, H.J.; Mathai, A.M.; Saxena, R.K. Mittag-leffler functions and their applications. J. Appl. Math. 2011, 2011, 298628. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. The laplace transform method for linear differential equations of the fractional order. arXiv 1997, arXiv:funct-an/9710005. [Google Scholar]
- Cafagna, D. Fractional calculus: A mathematical tool from the past for present engineers [past and present]. IEEE Ind. Electron. Mag. 2007, 1, 35–40. [Google Scholar] [CrossRef]
- Petráš, I. Fractional derivatives, fractional integrals, and fractional differential equations in matlab. In Engineering Education and Research Using MATLAB; InTech: London, UK, 2011. [Google Scholar]
- Scherer, R.; Kalla, S.; Boyadjiev, L.; Al-Saqabi, B. Numerical treatment of fractional heat equations. Appl. Numer. Math. 2008, 58, 1212–1223. [Google Scholar] [CrossRef]
- Yang, L.-X.; Yang, X. The spread of computer viruses under the influence of removable storage devices. Appl. Math. Comput. 2012, 219, 3914–3922. [Google Scholar] [CrossRef]
- Langner, R. To Kill a Centrifuge: A Technical Analysis of What Stuxnet’s Creators Tried to Achieve; The Langner Group: Dover, DE, USA, 2013. [Google Scholar]
- Wueest, C. Targeted Attacks against the Energy Sector; Symantec Security Response: Mountain View, CA, USA, 2014. [Google Scholar]
- Markus, L. Ii. asymptotically autonomous differential systems. In Contributions to the Theory of Nonlinear Oscillations (AM-36); Princeton University Press: Princeton, NJ, USA, 2016; Volume 3, p. 17. [Google Scholar]
- Thieme, H.R. Asymptotically autonomous differential equations in the plane. Rocky Mt. J. Math. 1994, 24, 351–380. [Google Scholar] [CrossRef]
- den Driessche, P.V.; Watmough, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Petras, I. Stability of fractional-order systems with rational orders. arXiv 2008, arXiv:0811.4102. [Google Scholar]
- Gil, J.J.; Avello, A.; Rubio, A.; Florez, J. Stability analysis of a 1 dof haptic interface using the routh-hurwitz criterion. IEEE Trans. Control. Syst. Technol. 2004, 12, 583–588. [Google Scholar] [CrossRef]
- Rohn, J. Positive definiteness and stability of interval matrices. SIAM J. Matrix Anal. Appl. 1994, 15, 175–184. [Google Scholar] [CrossRef]
- Shakarian, P.; Shakarian, J.; Ruef, A. Introduction to Cyber-Warfare: A Multidisciplinary Approach; Newnes: Oxford, UK, 2013. [Google Scholar]
- Pinto, C.M.; Carvalho, A.R. A latency fractional order model for hiv dynamics. J. Comput. Appl. Math. 2017, 312, 240–256. [Google Scholar] [CrossRef]
- Chaharborj, S.S.; Chaharborj, S.; Mahmoudi, Y. Study of fractional order integro-differential equations by using chebyshev neural network. J. Math. Stat. 2017, 13, 1–13. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Mehmood, A.; Rehman, A.u.; Khan, A.; Zameer, A. Bioinspired computational heuristics for sisko fluid flow and heat transfer models. Appl. Soft Comput. 2018, 71, 622–648. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Shah, Z.; Manzar, M.A.; Ahmad, I.; Awais, M.; Baleanu, D. A new stochastic computing paradigm for nonlinear painlevé ii systems in applications of random matrix theory. Eur. Phys. J. Plus 2018, 133, 254. [Google Scholar] [CrossRef]
- Ahmad, I.; Ahmad, S.; Awais, M.; Ahmad, S.U.I.; Raja, M.A.Z. Neuroevolutionary computing paradigm for painlevé equation-ii in nonlinear optics. Eur. Phys. J. Plus 2018, 133, 184. [Google Scholar] [CrossRef]
- Raja, M.A.Z.; Manzar, M.A.; Samar, R. An efficient computational intelligence approach for solving fractional order riccati equations using ann and sqp. Appl. Math. Model. 2015, 39, 3075–3093. [Google Scholar] [CrossRef]
- Akbar, S.; Zaman, F.; Asif, M.; Rehman, A.U.; Raja, M.A.Z. Novel application of fo-dpso for 2-d parameter estimation of electromagnetic plane waves. Neural Comput. Appl. 2019, 31, 3681–3690. [Google Scholar] [CrossRef]
- Pires, E.S.; Machado, J.T.; Oliveira, P.d.; Cunha, J.B.; Mendes, L. Particle swarm optimization with fractional-order velocity. Nonlinear Dyn. 2010, 61, 295–301. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, Y.; Akhtar, R.; Khan, R.; Ullah, F.; Raja, M.A.Z.; Machado, J.T. Design of fractional evolutionary processing for reactive power planning with FACTS devices. Sci. Rep. 2021, 11, 593. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.W.; Muhammad, Y.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. A New Fractional Particle Swarm Optimization with Entropy Diversity Based Velocity for Reactive Power Planning. Entropy 2020, 22, 1112. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, Y.; Khan, R.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. Design of fractional swarm intelligent computing with entropy evolution for optimal power flow problems. IEEE Access 2020, 8, 111401–111419. [Google Scholar] [CrossRef]
- Escalante-Martínez, J.E.; Gómez-Aguilar, J.F.; Calderón-Ramón, C.; Aguilar-Meléndez, A.; Padilla-Longoria, P. Synchronized bioluminescence behavior of a set of fireflies involving fractional operators of liouville–caputo type. Int. J. Biomath. 2018, 11, 1850041. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).