Matrix Profile-Based Approach to Industrial Sensor Data Analysis Inside RDBMS
Abstract
:1. Introduction
2. Overview of Modern Time Series DBMSs
2.1. Classification of Time Series DBMSs
2.2. InfluxDB, Native Time Series DBMS
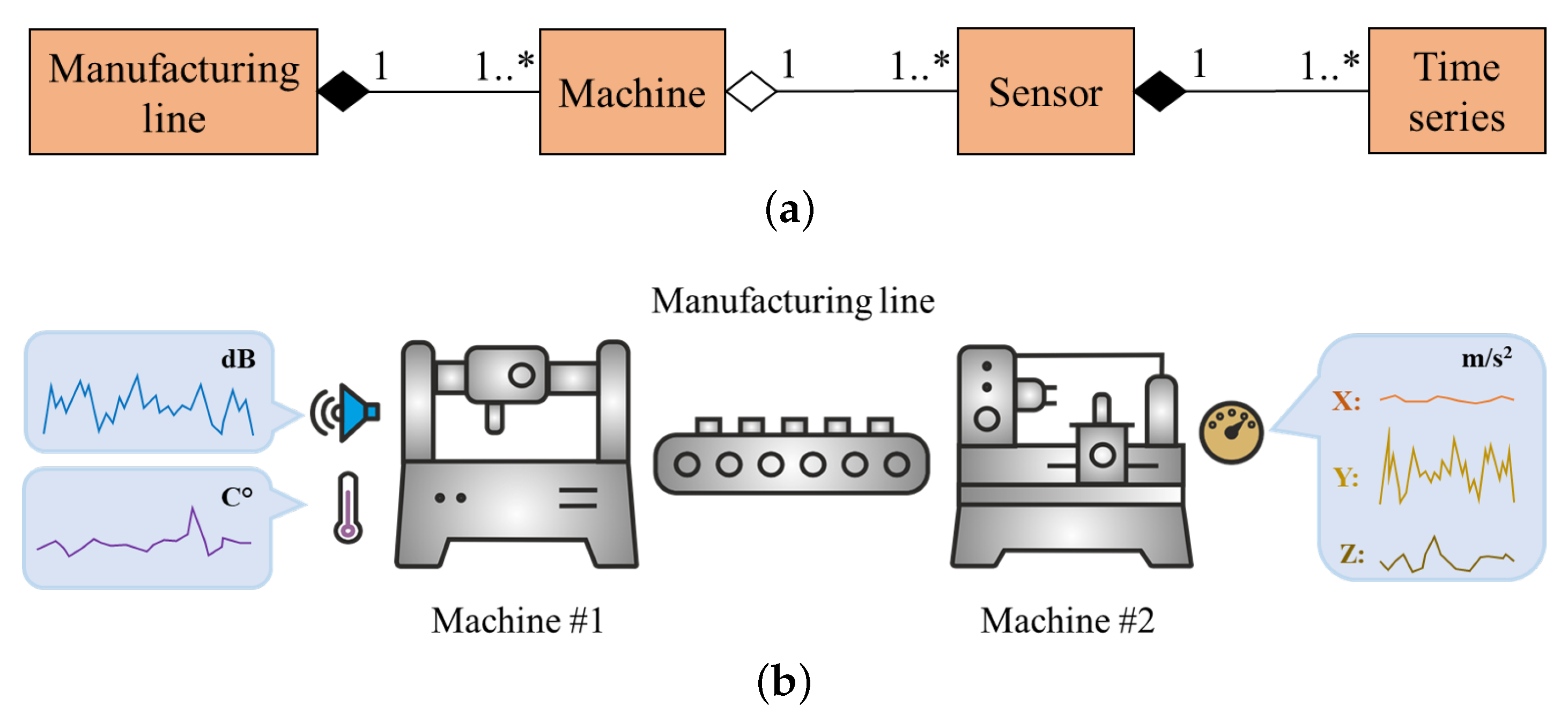
2.2.1. Organization of Data Storage
2.2.2. Query Language
2.3. OpenTSDB, NoSQL-Based Time Series DBMS
2.3.1. Organization of Data Storage
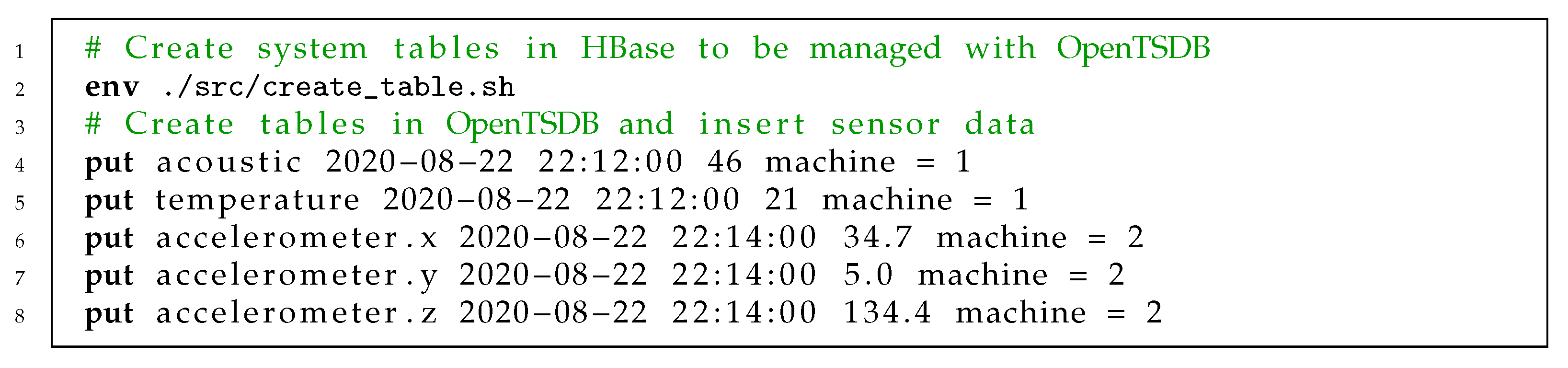
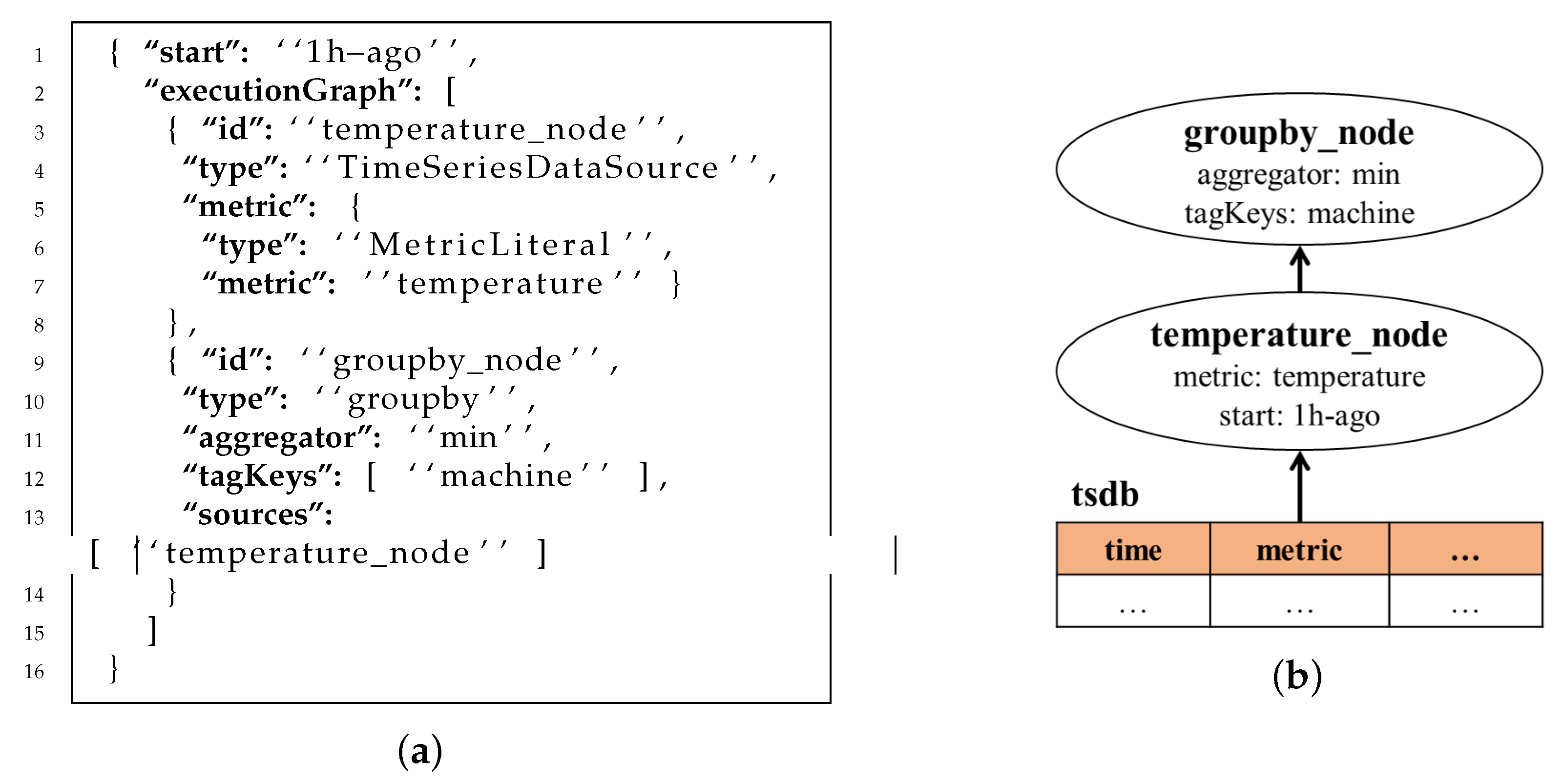
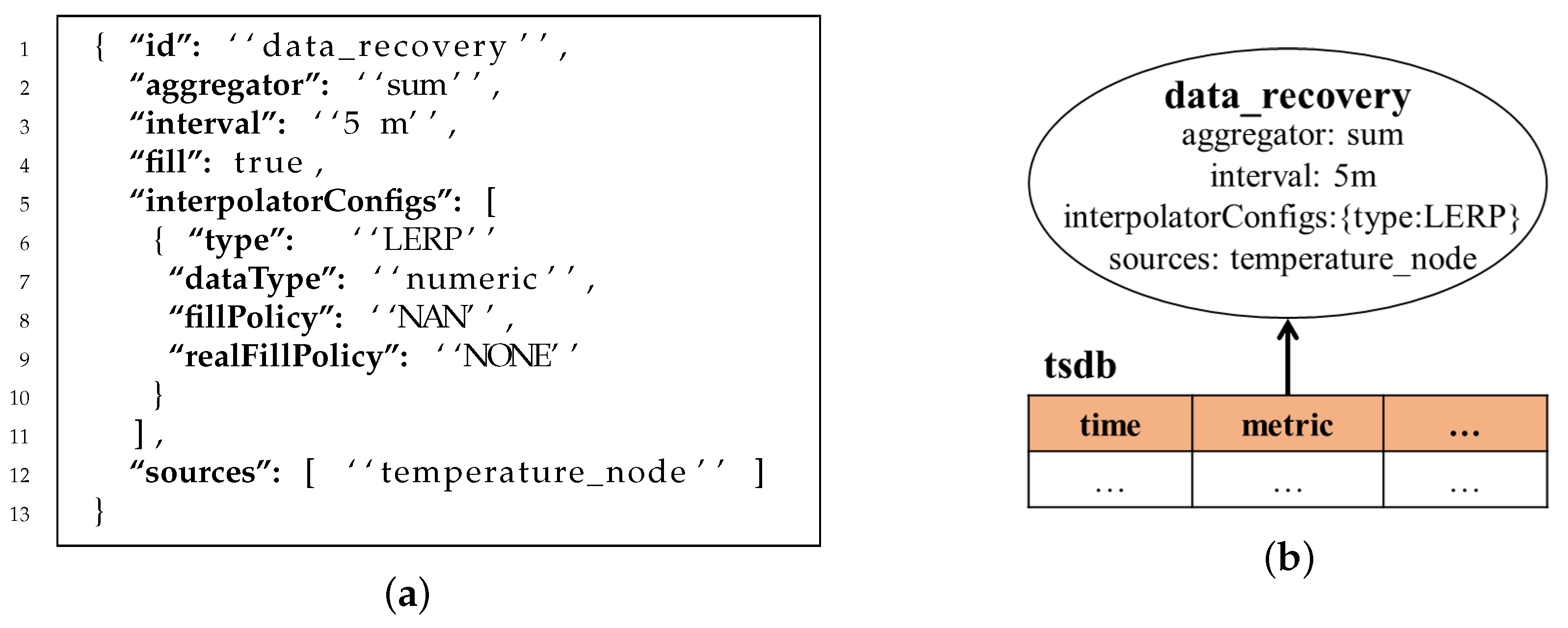
2.3.2. Query Language
2.4. TimescaleDB, Relational-Based Time Series DBMS
2.4.1. Organization of Data Storage
2.4.2. Query Language
3. Mining Sensor Data Inside RDBMS
3.1. Matrix Profile Concept
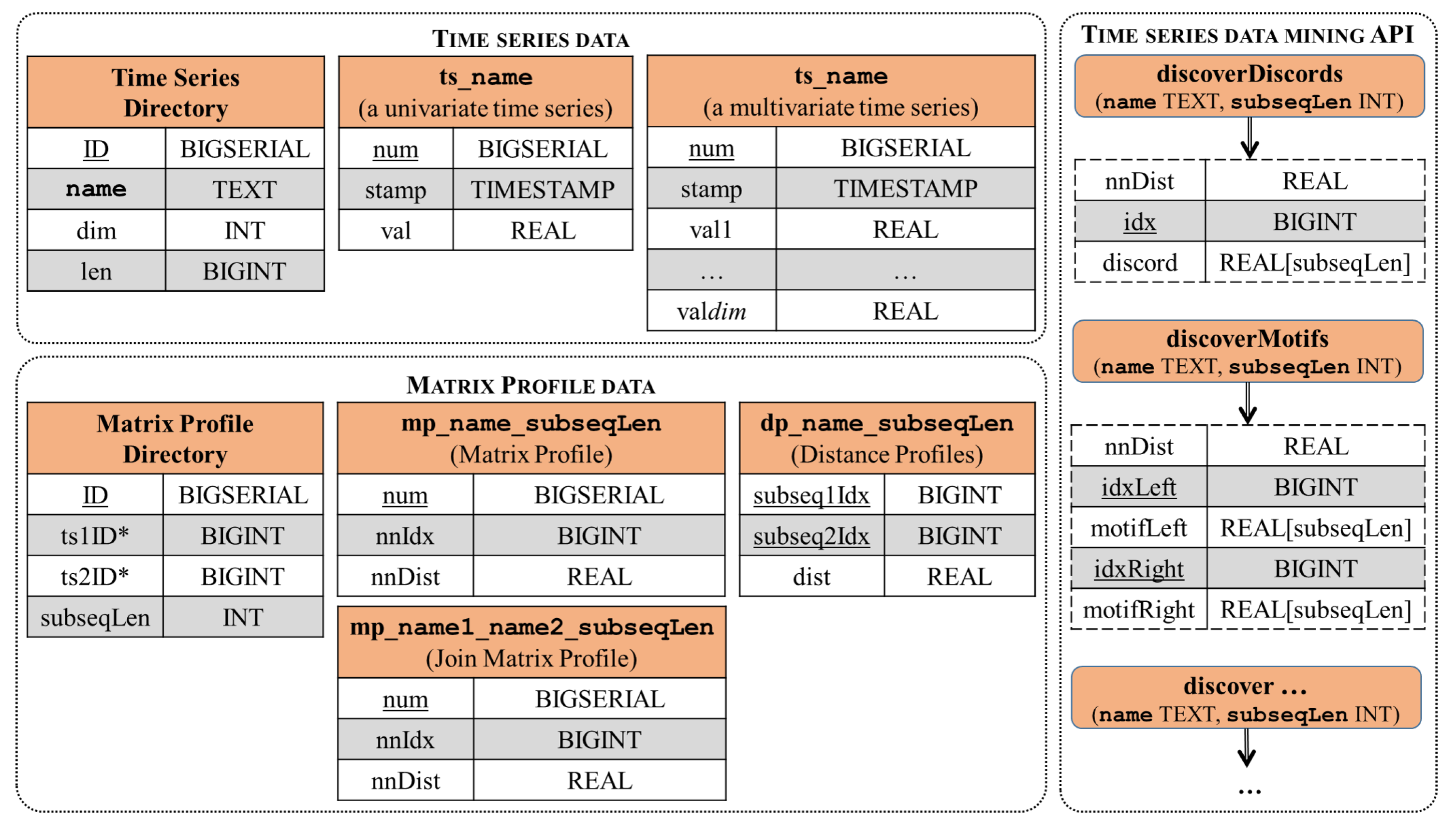
3.2. Embedding Matrix Profile Management into RDBMS
4. Experimental Case Studies
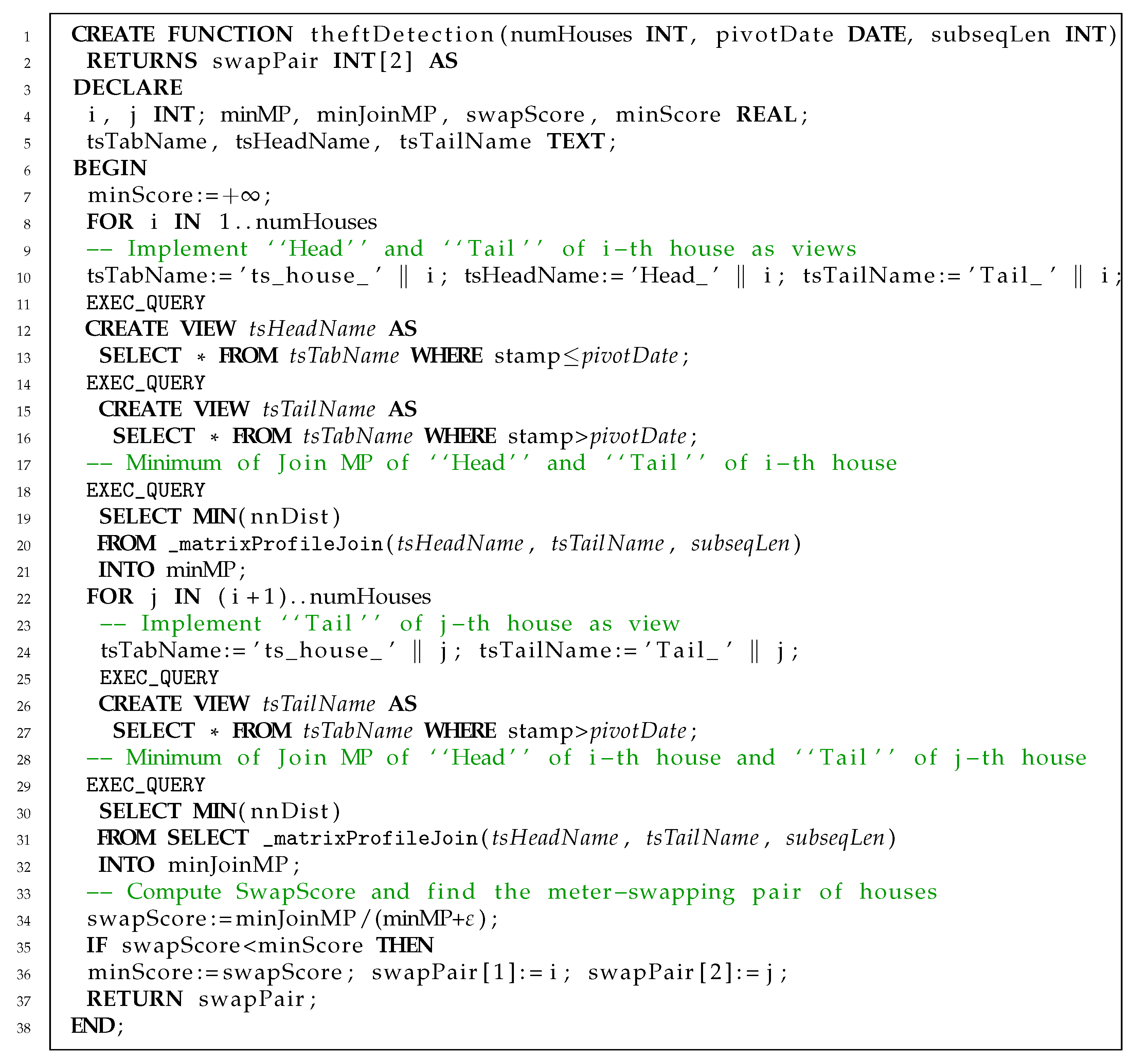
4.1. Electricity Theft Detection
4.2. Detection of Active Electricity Consumption
4.3. Tracking the Operational Status of an Industrial Machine
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, L.D.; Duan, L. Big Data for cyber physical systems in Industry 4.0: A survey. Enterp. Inf. Syst. 2019, 13, 148–169. [Google Scholar] [CrossRef]
- Kumar, S.; Tiwari, P.; Zymbler, M.L. Internet of Things is a revolutionary approach for future technology enhancement: A review. J. Big Data 2019, 6, 111. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, S.; Nikolskaya, K.; Radchenko, G.; Sokolinsky, L.; Zymbler, M. Digital twin of city: Concept overview. In Proceedings of the 2020 Global Smart Industry Conference, GloSIC 2020, Chelyabinsk, Russia, 17–19 November 2020; pp. 178–186. [Google Scholar] [CrossRef]
- Zymbler, M.; Kraeva, Y.; Latypova, E.; Kumar, S.; Shnayder, D.; Basalaev, A. Cleaning sensor data in smart heating control system. In Proceedings of the 2020 Global Smart Industry Conference, GloSIC 2020, Chelyabinsk, Russia, 17–19 November 2020; pp. 375–381. [Google Scholar] [CrossRef]
- Ordonez, C. Can we analyze big data inside a DBMS? In Proceedings of the 16th International Workshop on Data Warehousing and OLAP, DOLAP 2013, San Francisco, CA, USA, 28 October 2013; Song, I., Bellatreche, L., Cuzzocrea, A., Eds.; 2013; pp. 85–92. [Google Scholar] [CrossRef]
- Baralis, E.; Cerquitelli, T.; Chiusano, S. Index Support for Frequent Itemset Mining in a Relational DBMS. In Proceedings of the 21st International Conference on Data Engineering, ICDE 2005, Tokyo, Japan, 5–8 April 2005; Aberer, K., Franklin, M.J., Nishio, S., Eds.; 2005; pp. 754–765. [Google Scholar] [CrossRef]
- Sidló, C.I.; Lukács, A. Shaping SQL-Based Frequent Pattern Mining Algorithms. In Proceedings of the Knowledge Discovery in Inductive Databases, 4th International Workshop, (KDID 2005), Porto, Portugal, 3 October 2005; Revised Selected and Invited Papers; Lecture Notes in Computer Science. Bonchi, F., Boulicaut, J., Eds.; Springer: Berlin, Germany, 2005; Volume 3933, pp. 188–201. [Google Scholar] [CrossRef]
- Pelekis, N.; Tampakis, P.; Vodas, M.; Panagiotakis, C.; Theodoridis, Y. In-DBMS Sampling-based Sub-trajectory Clustering. In Proceedings of the 20th International Conference on Extending Database Technology, EDBT 2017, Venice, Italy, 21–24 March 2017; Markl, V., Orlando, S., Mitschang, B., Andritsos, P., Sattler, K., Breß, S., Eds.; 2017; pp. 632–643. [Google Scholar] [CrossRef]
- Zymbler, M.L.; Kraeva, Y.; Grents, A.; Perkova, A.; Kumar, S. An Approach to Fuzzy Clustering of Big Data Inside a Parallel Relational DBMS. In Proceedings of the Data Analytics and Management in Data Intensive Domains—21st International Conference, DAMDID/RCDL 2019, Kazan, Russia, 15–18 October 2019; Revised Selected Papers; Communications in Computer and Information Science. Elizarov, A.M., Novikov, B., Stupnikov, S.A., Eds.; Springer: Berlin, Germany, 2019; Volume 1223, pp. 211–223. [Google Scholar] [CrossRef]
- Pan, C.S.; Zymbler, M.L. Very Large Graph Partitioning by Means of Parallel DBMS. In Proceedings of the Advances in Databases and Information Systems—17th East European Conference, ADBIS 2013, Genoa, Italy, 1–4 September 2013; Catania, B., Guerrini, G., Pokorný, J., Eds.; Lecture Notes in Computer Science. Springer: Berlin, Germany, 2013; Volume 8133, pp. 388–399. [Google Scholar] [CrossRef]
- McCaffrey, J.D. A Hybrid System for Analyzing Very Large Graphs. In Proceedings of the 9th International Conference on Information Technology: New Generations (ITNG 2012), Las Vegas, NV, USA, 16–18 April 2012; Latifi, S., Ed.; pp. 253–257. [Google Scholar] [CrossRef]
- Hellerstein, J.M.; Ré, C.; Schoppmann, F.; Wang, D.Z.; Fratkin, E.; Gorajek, A.; Ng, K.S.; Welton, C.; Feng, X.; Li, K.; et al. The MADlib Analytics Library or MAD Skills, the SQL. Proc. VLDB Endow. 2012, 5, 1700–1711. [Google Scholar] [CrossRef]
- Feng, X.; Kumar, A.; Recht, B.; Ré, C. Towards a unified architecture for in-RDBMS analytics. In Proceedings of the ACM SIGMOD International Conference on Management of Data, SIGMOD 2012, Scottsdale, AZ, USA, 20–24 May 2012; pp. 325–336. [Google Scholar] [CrossRef] [Green Version]
- Mahajan, D.; Kim, J.K.; Sacks, J.; Ardalan, A.; Kumar, A.; Esmaeilzadeh, H. In-RDBMS Hardware Acceleration of Advanced Analytics. Proc. VLDB Endow. 2018, 11, 1317–1331. [Google Scholar] [CrossRef] [Green Version]
- Rechkalov, T.; Zymbler, M.L. Integrating DBMS and Parallel Data Mining Algorithms for Modern Many-Core Processors. In Proceedings of the Data Analytics and Management in Data Intensive Domains—XIX International Conference (DAMDID/RCDL 2017), Moscow, Russia, 10–13 October 2017; Revised Selected Papers; Communications in Computer and Information Science. Kalinichenko, L.A., Manolopoulos, Y., Malkov, O., Skvortsov, N.A., Stupnikov, S.A., Sukhomlin, V., Eds.; Springer: Berlin, Germany, 2017; Volume 822, pp. 230–245. [Google Scholar] [CrossRef]
- Yeh, C.M.; Zhu, Y.; Ulanova, L.; Begum, N.; Ding, Y.; Dau, H.A.; Zimmerman, Z.; Silva, D.F.; Mueen, A.; Keogh, E.J. Time series joins, motifs, discords and shapelets: A unifying view that exploits the matrix profile. Data Min. Knowl. Discov. 2018, 32, 83–123. [Google Scholar] [CrossRef]
- Bader, A.; Kopp, O.; Falkenthal, M. Survey and Comparison of Open Source Time Series Databases; Datenbanksysteme fur Business, Technologie und Web (BTW 2017), 17. Fachtagung des GI-Fachbereichs “Datenbanken und Informationssysteme” (DBIS), 6.–10. Marz 2017, Stuttgart, Germany, Workshopband; Mitschang, B., Ritter, N., Schwarz, H., Klettke, M., Thor, A., Kopp, O., Wieland, M., Eds.; Gesellschaft für Informatik e.V.: Bonn, Germany, 2017; pp. 249–268. [Google Scholar]
- Grzesik, P.; Mrozek, D. Comparative analysis of time series databases in the context of Edge computing for low power sensor networks. In Proceedings of the 20th International Conference on Computational Science (ICCS 2020), Amsterdam, The Netherlands, 3–5 June 2020; pp. 371–383. [Google Scholar] [CrossRef]
- Yang, F.; Tschetter, E.; Léauté, X.; Ray, N.; Merlino, G.; Ganguli, D. Druid: A real-time analytical data store. In Proceedings of the International Conference on Management of Data (SIGMOD 2014), Snowbird, UT, USA, 22–27 June 2014; Dyreson, C.E., Li, F., Ozsu, M.T., Eds.; ACM: New York, NY, USA, 2014; pp. 157–168. [Google Scholar] [CrossRef]
- Rhea, S.; Wang, E.; Wong, E.; Atkins, E.; Storer, N. LittleTable: A Time-Series Database and Its Uses. In Proceedings of the 2017 ACM International Conference on Management of Data (SIGMOD Conference 2017), Chicago, IL, USA, 14–19 May 2017; Salihoglu, S., Zhou, W., Chirkova, R., Yang, J., Suciu, D., Eds.; 2017; pp. 125–138. [Google Scholar] [CrossRef]
- Li, C.; Li, B.; Bhuiyan, M.Z.A.; Wang, L.; Si, J.; Wei, G.; Li, J. FluteDB: An efficient and scalable in-memory time series database for sensor-cloud. J. Parallel Distributed Comput. 2018, 122, 95–108. [Google Scholar] [CrossRef]
- MacDonald, A. PhilDB: The time series database with built-in change logging. PeerJ Comput. Sci. 2016, 2, e52. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Cao, Q.; Jiang, H. EdgeDB: An Efficient Time-Series Database for Edge Computing. IEEE Access 2019, 7, 142295–142307. [Google Scholar] [CrossRef]
- Lan, L.; Shi, R.; Wang, B.; Zhang, L.; Shi, J. A Lightweight Time Series Main-Memory Database for IoT Real-Time Services. In Proceedings of the Internet of Vehicles, Technologies and Services Toward Smart Cities—6th International Conference (IOV 2019), Kaohsiung, Taiwan, 18–21 November 2019; Lecture Notes in Computer Science. Hsu, C., Khemiri-Kallel, S., Lan, K., Zheng, Z., Eds.; Springer: Berlin, Germany, 2019; Volume 11894, pp. 220–236. [Google Scholar] [CrossRef]
- Pelkonen, T.; Franklin, S.; Cavallaro, P.; Huang, Q.; Meza, J.; Teller, J.; Veeraraghavan, K. Gorilla: A Fast, Scalable, In-Memory Time Series Database. Proc. VLDB Endow. 2015, 8, 1816–1827. [Google Scholar] [CrossRef]
- Matallah, H.; Belalem, G.; Bouamrane, K. Evaluation of NoSQL Databases: MongoDB, Cassandra, HBase, Redis, Couchbase, OrientDB. Int. J. Softw. Sci. Comput. Intell. 2020, 12, 71–91. [Google Scholar] [CrossRef]
- Andersen, M.P.; Culler, D.E. BTrDB: Optimizing Storage System Design for Timeseries Processing. In Proceedings of the 14th USENIX Conference on File and Storage Technologies (FAST 2016), Santa Clara, CA, USA, 22–25 February 2016; Brown, A.D., Popovici, F.I., Eds.; 2016; pp. 39–52. [Google Scholar]
- Shvachko, K.; Kuang, H.; Radia, S.; Chansler, R. The Hadoop Distributed File System. In Proceedings of the IEEE 26th Symposium on Mass Storage Systems and Technologies (MSST 2012), Lake Tahoe, NV, USA, 3–7 May 2010; Khatib, M.G., He, X., Factor, M., Eds.; 2010; pp. 1–10. [Google Scholar] [CrossRef]
- Sim, H.; Khan, A.; Vazhkudai, S.S.; Lim, S.; Butt, A.R.; Kim, Y. An Integrated Indexing and Search Service for Distributed File Systems. IEEE Trans. Parallel Distrib. Syst. 2020, 31, 2375–2391. [Google Scholar] [CrossRef]
- Idreos, S.; Groffen, F.; Nes, N.; Manegold, S.; Mullender, K.S.; Kersten, M.L. MonetDB: Two Decades of Research in Column-oriented Database Architectures. IEEE Data Eng. Bull. 2012, 35, 40–45. [Google Scholar]
- Deri, L.; Mainardi, S.; Fusco, F. tsdb: A Compressed Database for Time Series. In Proceedings of the Traffic Monitoring and Analysis—4th International Workshop (TMA 2012), Vienna, Austria, 12 March 2012; Lecture Notes in Computer Science. Pescapè, A., Salgarelli, L., Dimitropoulos, X.A., Eds.; Springer: Berlin, Germany, 2012; Volume 7189, pp. 143–156. [Google Scholar] [CrossRef] [Green Version]
- Seltzer, M.I. Berkeley DB: A Retrospective. IEEE Data Eng. Bull. 2007, 30, 21–28. [Google Scholar]
- Tsubouchi, Y.; Wakisaka, A.; Hamada, K.; Matsuki, M.; Abe, H.; Matsumoto, R. HeteroTSDB: An Extensible Time Series Database for Automatically Tiering on Heterogeneous Key-Value Stores. In Proceedings of the 43rd IEEE Annual Computer Software and Applications Conference (COMPSAC 2019), Milwaukee, WI, USA, 15–19 July 2019; Getov, V., Gaudiot, J., Yamai, N., Cimato, S., Chang, J.M., Teranishi, Y., Yang, J., Leong, H.V., Shahriar, H., Takemoto, M., et al., Eds.; 2019; Volume 1, pp. 264–269. [Google Scholar] [CrossRef]
- Sivasubramanian, S. Amazon dynamoDB: A seamlessly scalable non-relational database service. In Proceedings of the ACM SIGMOD International Conference on Management of Data (SIGMOD 2012), Scottsdale, AZ, USA, 20–24 May 2012; pp. 729–730. [Google Scholar] [CrossRef]
- Stonebraker, M.; Rowe, L.A.; Hirohama, M. The implementation of POSTGRES. In Making Databases Work: The Pragmatic Wisdom of Michael Stonebraker; Brodie, M.L., Ed.; ACM/Morgan & Claypool: San Rafael, CA, USA, 2019; pp. 519–559. [Google Scholar] [CrossRef] [Green Version]
- Arous, I.; Khayati, M.; Cudré-Mauroux, P.; Zhang, Y.; Kersten, M.L.; Stalinlov, S. RecovDB: Accurate and Efficient Missing Blocks Recovery for Large Time Series. In Proceedings of the 35th IEEE International Conference on Data Engineering (ICDE 2019), Macao, China, 8–11 April 2019; pp. 1976–1979. [Google Scholar] [CrossRef]
- Petre, I.; Boncea, R.; Radulescu, C. A time-series database analysis based on a multi-attribute maturity model. Stud. Inf. Control 2019, 2, 177–188. [Google Scholar] [CrossRef] [Green Version]
- O’Neil, P.E.; Cheng, E.; Gawlick, D.; O’Neil, E.J. The Log-Structured Merge-Tree (LSM-Tree). Acta Inf. 1996, 33, 351–385. [Google Scholar] [CrossRef]
- Holt, C. Forecasting seasonals and trends by exponentially weighted averages. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- Petersen, D.P.; Middleton, D. Linear interpolation, extrapolation, and prediction of random space-time fields with a limited domain of measurement. IEEE Trans. Inf. Theory 1965, 11, 18–30. [Google Scholar] [CrossRef]
- Agrawal, B.; Chakravorty, A.; Rong, C.; Wlodarczyk, T.W. R2Time: A Framework to Analyse Open TSDB Time-Series Data in HBase. In Proceedings of the IEEE 6th International Conference on Cloud Computing Technology and Science (CloudCom 2014), Singapore, 15–18 December 2014; pp. 970–975. [Google Scholar] [CrossRef]
- Gharghabi, S.; Ding, Y.; Yeh, C.M.; Kamgar, K.; Ulanova, L.; Keogh, E.J. Matrix Profile VIII: Domain Agnostic Online Semantic Segmentation at Superhuman Performance Levels. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM 2017), New Orleans, LA, USA, 18–21 November 2017; pp. 117–126. [Google Scholar] [CrossRef]
- Zhu, Y.; Imamura, M.; Nikovski, D.; Keogh, E.J. Matrix Profile VII: Time Series Chains: A New Primitive for Time Series Data Mining. In Proceedings of the 2017 IEEE International Conference on Data Mining, ICDM 2017, New Orleans, LA, USA, 18–21 November 2017; pp. 695–704. [Google Scholar] [CrossRef]
- Imani, S.; Madrid, F.; Ding, W.; Crouter, S.E.; Keogh, E.J. Matrix Profile XIII: Time Series Snippets: A New Primitive for Time Series Data Mining. In Proceedings of the 2018 IEEE International Conference on Big Knowledge, ICBK 2018, Singapore, 17–18 November 2018; Wu, X., Ong, Y., Aggarwal, C.C., Chen, H., Eds.; 2018; pp. 382–389. [Google Scholar] [CrossRef]
- Zhu, Y.; Gharghabi, S.; Silva, D.F.; Dau, H.A.; Yeh, C.M.; Senobari, N.S.; Almaslukh, A.; Kamgar, K.; Zimmerman, Z.; Funning, G.J.; et al. The Swiss army knife of time series data mining: Ten useful things you can do with the matrix profile and ten lines of code. Data Min. Knowl. Discov. 2020, 34, 949–979. [Google Scholar] [CrossRef]
- Shi, J.; Yu, N.; Keogh, E.; Chen, H.; Yamashita, K. Discovering and Labeling Power System Events in Synchrophasor Data with Matrix Profile. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; p. 19303617. [Google Scholar] [CrossRef]
- Nichiforov, C.; Stancu, I.; Stamatescu, I.; Stamatescu, G. Information Extraction Approach for Energy Time Series Modelling. In Proceedings of the 24th International Conference on System Theory, Control and Computing (ICSTCC 2020), Sinaia, Romania, 8–10 October 2020; Barbulescu, L., Ed.; 2020; pp. 886–891. [Google Scholar] [CrossRef]
- Lee, Y.Q.; Beh, W.L.; Ooi, B.Y. Tracking Operation Status of Machines through Vibration Analysis using Motif Discovery. J. Phys. Conf. Ser. 2020, 1529, 052005. [Google Scholar] [CrossRef]
- Pizoń, J.; Kulisz, M.; Lipski, J. Matrix profile implementation perspective in Industrial Internet of Things production maintenance application. J. Phys. Conf. Ser. 2021, 1736, 012036. [Google Scholar] [CrossRef]
- Yankov, D.; Keogh, E.J.; Rebbapragada, U. Disk aware discord discovery: Finding unusual time series in terabyte sized datasets. Knowl. Inf. Syst. 2008, 17, 241–262. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Zimmerman, Z.; Senobari, N.S.; Yeh, C.M.; Funning, G.J.; Mueen, A.; Brisk, P.; Keogh, E.J. Matrix Profile II: Exploiting a Novel Algorithm and GPUs to Break the One Hundred Million Barrier for Time Series Motifs and Joins. In Proceedings of the IEEE 16th International Conference on Data Mining (ICDM 2016), Barcelona, Spain, 12–15 December 2016; Bonchi, F., Domingo-Ferrer, J., Baeza-Yates, R., Zhou, Z., Wu, X., Eds.; 2016; pp. 739–748. [Google Scholar] [CrossRef] [Green Version]
- Benschoten, A.V.; Ouyang, A.; Bischoff, F.; Marrs, T. MPA: A novel cross-language API for time series analysis. J. Open Source Softw. 2020, 5, 2179. [Google Scholar] [CrossRef]
- Murray, D.; Liao, J.; Stankovic, L.; Stankovic, V.; Hauxwell-Baldwin, R.; Wilson, C.; Coleman, M.; Kane, T.; Firth, S. A data management platform for personalised real-time energy feedback. In Proceedings of the 8th International Conference on Energy Efficiency in Domestic Appliances and Lighting (EEDAL 2015), Lucerne, Switzerland, 26–28 August 2015; pp. 1–15. [Google Scholar] [CrossRef]
- Miller, C.; Meggers, F. The Building Data Genome Project: An open, public data set from non-residential building electrical meters. Energy Procedia 2017, 122, 439–444. [Google Scholar] [CrossRef]
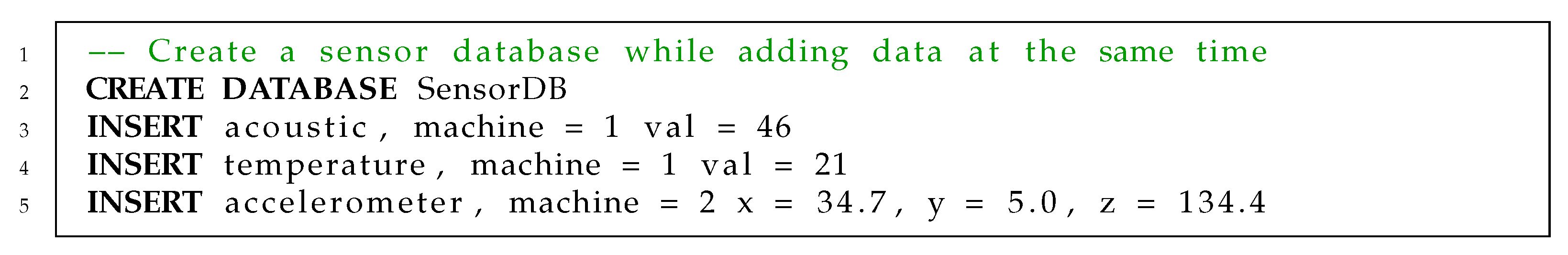





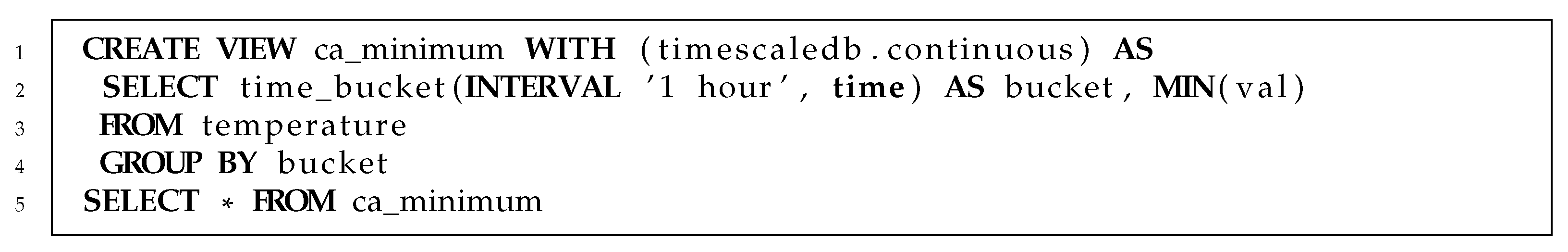


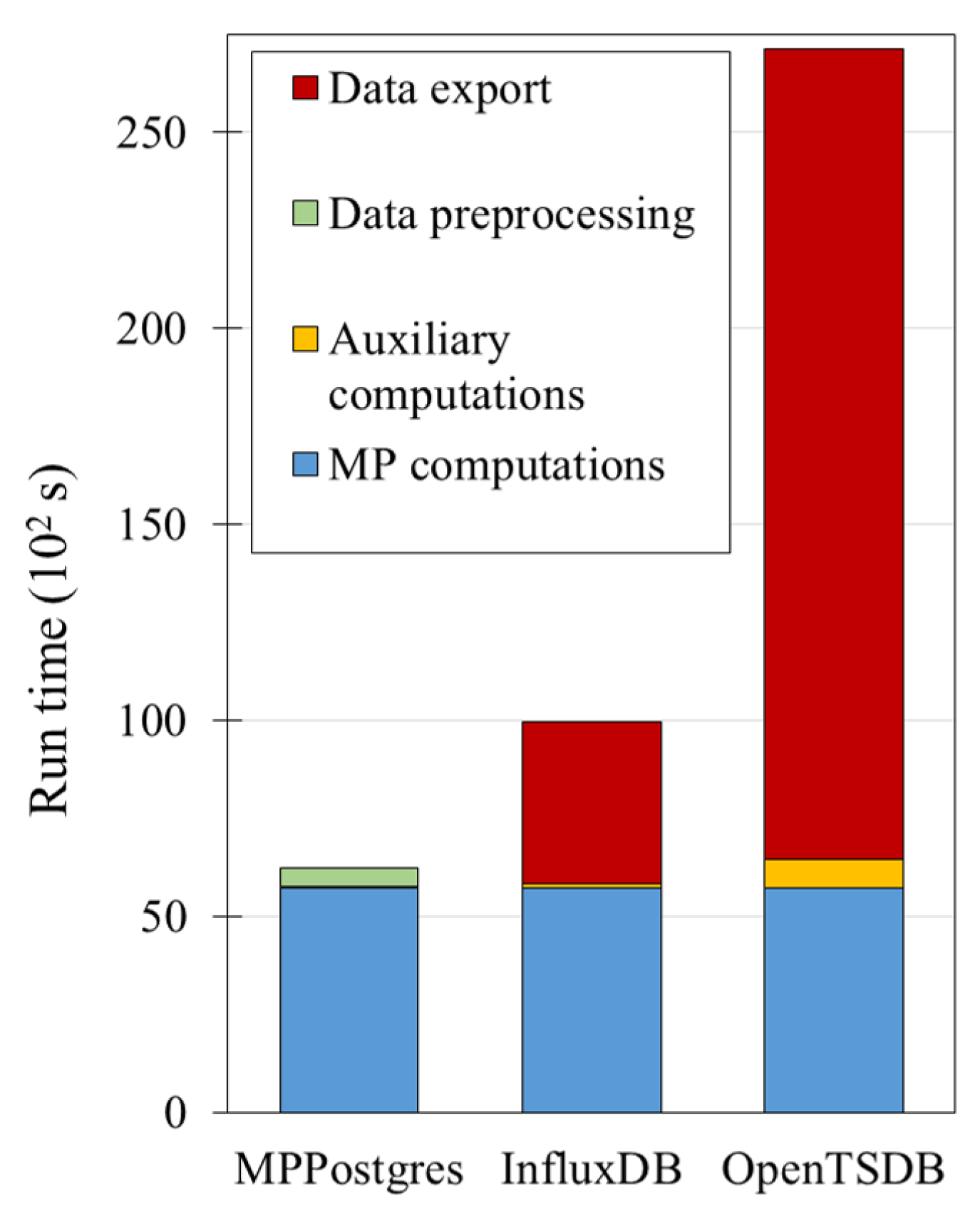

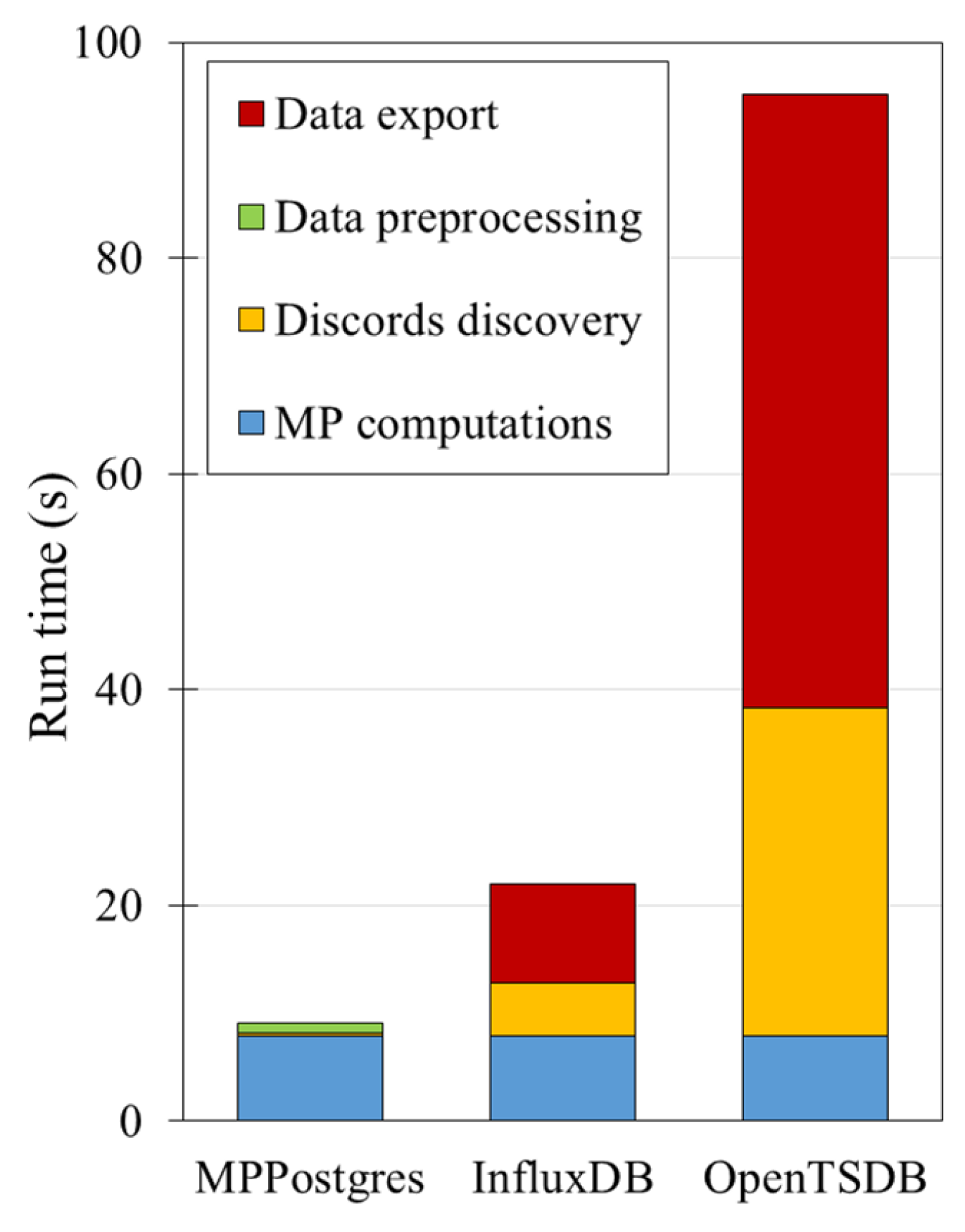

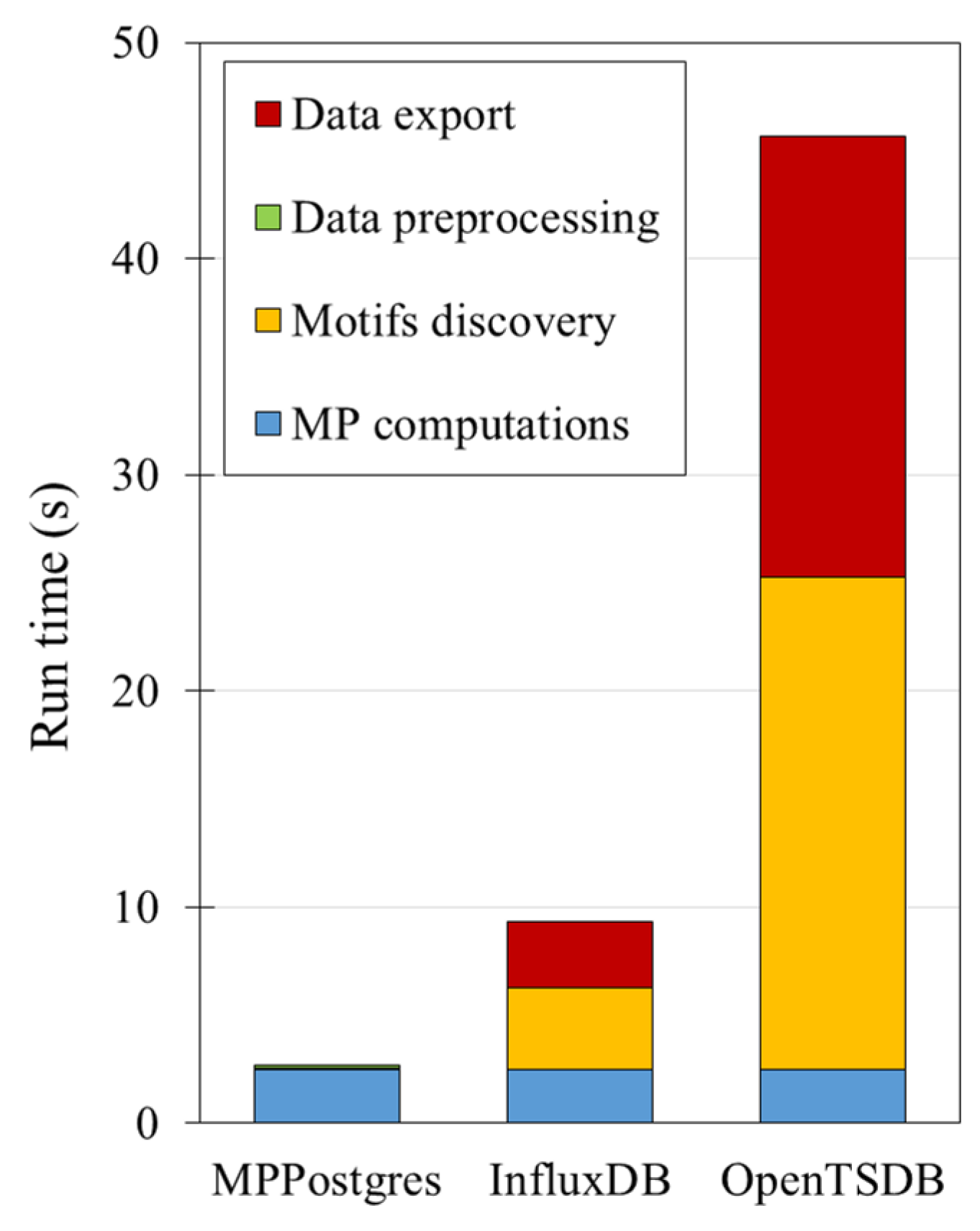
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zymbler, M.; Ivanova, E. Matrix Profile-Based Approach to Industrial Sensor Data Analysis Inside RDBMS. Mathematics 2021, 9, 2146. https://doi.org/10.3390/math9172146
Zymbler M, Ivanova E. Matrix Profile-Based Approach to Industrial Sensor Data Analysis Inside RDBMS. Mathematics. 2021; 9(17):2146. https://doi.org/10.3390/math9172146
Chicago/Turabian StyleZymbler, Mikhail, and Elena Ivanova. 2021. "Matrix Profile-Based Approach to Industrial Sensor Data Analysis Inside RDBMS" Mathematics 9, no. 17: 2146. https://doi.org/10.3390/math9172146
APA StyleZymbler, M., & Ivanova, E. (2021). Matrix Profile-Based Approach to Industrial Sensor Data Analysis Inside RDBMS. Mathematics, 9(17), 2146. https://doi.org/10.3390/math9172146






