1. Introduction—Motivation for Solution
Over its relatively short history, air transport has become an integral part of the globalized world. Not everyone, however, is aware that the undertaking of one regularly scheduled flight involves more than a year’s work of numerous people who are responsible for ensuring all activities happen according to plan. Planning air traffic requires creating many plans. The basic type of plan is the flight schedule. During the calendar year, the flight schedule is compiled for two consecutive planning periods. The creation of the flight schedule itself consists of three basic phases—the strategic phase, the tactical phase, and the operational phase.
During the strategic phase of the preparation of the flight schedule, which begins approximately one year before its taking effect, an anticipated set of destinations is created that the carrier is interested in serving. The destinations are assigned sequences of planned flights with estimated departure and arrival times and the types of aircraft under consideration to be used to operate routes to the destinations.
During the tactical phase, the flight schedule is adjusted depending on the partner companies and airport capacities. After the coordination of all interested parties, specific aircraft are assigned to the planned flights and the flight schedule is publicly published and published in sales and distribution systems.
The final operational phase takes place 3–6 months before the start of operations according to the planned flight schedule. In this phase, crews are also assigned to individual flights, thus completing the process of creating a flight schedule [
1].
Assembling the crews is a chapter all on its own in air traffic planning. However, it is very closely connected with the planning of the use of the aircraft fleet and the implementation of the flight schedule. The process of creating flight crews and their deployment consists of three steps—crew creation, crew pairing and crew rostering. In the first step, it is necessary to form permissible pairs from the set of all pilots available to the airline, which can form a crew. The creation of crews is limited by numerous restrictions, such as the composition of the crews themselves, whereas the crew, as a rule, is always made up of the captain and the first officer (FO). It is not possible for the crew to consist of two first officers. It is also not recommended that the crew consist of two captains, which could result in a threat to flight safety due to a clash of authorities. Another factor is seniority, i.e., the division of pilots depending on work experience with the employer. Seniority is mainly related to the knowledge of internal procedures and rules at the airline. Pilots are thus divided into two groups—experienced and inexperienced. The aim is to avoid having the crew made up of two pilots who are both designated as inexperienced. In addition to seniority as such, of course, experience in the form of the real flight hours of each pilot is also considered. The number of hours flown is calculated depending on the type of aircraft and depending on the position (captain vs. first officer). A limiting factor for the creation of crews is age. For safety reasons, it is not possible for the crew to consist of two pilots over the age of 60. During various training processes (e.g., when retraining for a new type of aircraft), pilots can be divided into two groups—instructor pilot and trainee pilot. The crew must always consist of a combination of the two. It is not possible for two pilots with training designation to sit side by side in the cockpit. Finally, the creation of crews and their subsequent assignment to flights depends on the destination, specifically on the category of the destination airport. Airports are divided into three categories according to the complexity of the procedures for approaches and departures—A, B, C and the crew must always consist of at least one pilot who has valid training for the relevant category of the airport. This composition is addressed in the conditions of B and C category airports because the category A concerns airports that are easy to approach and take off from, and therefore all pilots have the relevant classification. Personal and family reasons can be an important factor in assembling crews. To take these into account, the so-called Bidding process is used, with the help of which the requirements of pilots for the planning process are (can) be considered. Even pilots are only humans and there is a probability that two pilots can have an aversion to each other, which could have a negative impact on flight safety when putting together a joint crew. For the same reason, it is not recommended to create pilot crews composed of family members.
The second step of the crew formation process is crew pairing. This step involves the creation of short-term pilot plans, usually for a period of one month. This plan is made up of a sequence of flight segments starting and ending usually at the home airport. The duration of a sequence ranges from 1 to 5 days. The sequences of flight segments contain the individual flights to be served by the pilot during the interval. The objective of this step is to cover the set of all scheduled flights with a minimum number of crews.
The third step in the process of creating flight crews is crew rostering, sometimes called crew assignment. During this third step, additional activities such as training, education, study, or vacation requirements will be incorporated into the crew schedule.
In addition to the constraints mentioned above, human performance constraints, as defined in Regulation 1899/2006 of the European Parliament and of the Council (EU-OPS), Subpart Q [
2], may also affect the crew formation process. The above-mentioned regulation clearly states the limits on flight duty time and time on duty. The operator must ensure that:
the crew member’s total hours of service did not exceed 190 h over 28 consecutive days,
the crew member’s total hours of service did not exceed 60 h over 7 consecutive days,
the total flying time on which the crew member is deployed does not exceed 900 h in a calendar year,
the total flying time on which the crew member is deployed does not exceed 100 h over 28 consecutive days.
The regulations stipulate that the base daily flight duty time of a crew member is 13 h. In staffing pilots for duty, the regulations recommend that the distribution of flight performance over time should be as even as possible.
Even with the best preparation of a flight schedule, it is unavoidable that during the validity of the flight schedule various traffic anomalies will occur which will disrupt the scheduled operations. These disruptions may result in delays, diversion to another airport or even cancellation of one or more flights. The causes of disruptions to regularly scheduled operations may be varied.
Unfavorable weather conditions. Unfavorable weather conditions can significantly affect the flight. In the event of unfavorable conditions at the departure airport, it is necessary to wait for suitable conditions, which may delay or even result in the cancellation of the flight. Any waiting will incur additional financial costs associated with the operation of the aircraft itself. In addition, it also consumes the time on duty available to the crews. In the winter, when repeated de-icing of the aircraft may be required, costs can rise dramatically. If weather conditions, such as storms, affect a flight in progress, this again results in additional financial costs being incurred due to the extension of the flight.
Volcanic activity in a way, also complements weather conditions. In fact, volcanic ash is present mainly at altitudes of around 10,000–15,000 m above sea level, where it is dispersed over large areas due to atmospheric flow, which can extend up to 3500 km from the eruption site [
3]. Aircraft may need to fly around the affected area, which increases costs due to longer flight times. At the same time, such an extended flight uses up more of the pilots’ allowed time on duty than originally planned. If the aircraft is within range of volcanic ash fallout, the flight itself may also be cancelled.
A technical fault on an aircraft and the need for its subsequent rectification may not only delay or cancel a flight, but also put the aircraft out of service for a certain amount of time. Depending on the severity of the defect and the resulting time required to rectify it, the airline has several solution options. If the aircraft can be repaired in a short time, only a delay will occur. If the repair is more complicated, the flight will have to be rescheduled for the next day and operated after the repair or another aircraft will be deployed to operate the flight. A bigger problem arises when the technical fault occurs outside the home airport. The airline is then forced to rely on local airport technicians or may send its own maintenance technicians to the destination, which leads to increased costs. If repair of the technical defect is postponed to subsequent days, additional costs related to the accommodation of passengers and crew must again be considered.
A shortfall of fuel may cause unscheduled stopovers or extended stays at only one of the flight’s terminal airports, which may also lead to delays. In the effort to minimize operating costs, a method referred to in the professional literature as tankering is now used to determine the optimum fuel quantity. This method optimizes fuel management, which can be significantly disrupted by, for example, extended flight times due to adverse weather conditions.
Passenger health or safety problems are other factors that can significantly affect the course of the flight and at the same time disrupt the planned flight schedule. In the event of a serious medical problem of a passenger or a threat to the safety of the flight by a passenger, pilots have the right to land at any airport if it is safe to do so. Unplanned stopovers, of course, entail financial costs, delays, and consequent flight schedule disruptions.
Health complications of crew members, unlike the health complications of passengers, are a significantly more serious problem, which, from the airline’s point of view, must be immediately, responsively resolved, because flight safety is directly endangered. Crew health complications can also include fatigue, which can occur for crews due to a demanding schedule or due to transitions between time zones [
4].
Air traffic control flight diversion is a situation that can occur in Europe, for example, during the summer scheduling period when there is increased traffic density in the airspace and some routes may reach their maximum capacity. For this reason, air traffic controllers may decide to divert some flights away from the main flight paths. Diversions may also occur in emergency situations when an aircraft is in difficulty and surrounding flights need to be diverted.
Another type of contingency is the closure of part of the airspace, which at the same time is not an exceptional event. The closure of part of the airspace may be due to military operations (however, only local airspace (TRA, TSA) is affected), but in some cases the entire airspace is also closed, such as in February 2019, when Pakistan closed the entire airspace over its territory [
5]. In some extreme cases, a situation may arise when a country’s airspace is closed to a particular type of aircraft, as happened in March 2019, when the Boeing B-737 MAX was restricted from entering the airspace of individual nations [
6]. Some aircraft of the given type then had to land outside their final destinations and passengers were subsequently picked up by aircraft of a different type.
Other emergencies that can significantly disrupt flight plans may be strikes by airline staff, air traffic controllers, airport staff or handling staff.
Delays for other reasons (accumulation of delays) are mainly caused by traffic at take-off and landing airports. These problems at airports usually occur during peak periods, when there is an accumulation of delays that cascade to other flights.
The situations described above make it clear that crew scheduling is a very extensive problem, with many restrictions that must be satisfied, making it a very complex task. Today, it is virtually impossible to imagine crew scheduling in the context of large airlines without the possibility of using IT, yet there are still airlines operating in the market where this was common practice still not long ago. Until the 1970s, everything was planned manually based on the experience of the employees. It took a team of eight planners several weeks to create a crew work schedule. However, a breakthrough occurred in the 1970s when IBM developed the first crew scheduling software. In the 1990s, most major airlines started using IT for crew scheduling. At the same time, there was a major development in the mathematical approaches that were used for scheduling purposes. Depending on computing power, they were able to create crew turnarounds numbering up to 7000 pilots within 14 h. Regardless of the solution, these software solutions can save an airline a lot of money. This effect is particularly evident in situations where there is an emergency that needs to be dealt with quickly, as any instability in the flight schedule can lead to large financial losses. Despite all the progress, there are still a relatively large number of small airlines that deal with the prompt rescheduling of crews in the event of an emergency manually without the use of IT. This is mainly for financial reasons. These are the relatively high acquisition costs of the software and hardware itself, as well as the costs of training personnel to work with these systems. Another problem is the interconnection of the software enabling crew planning with existing systems that the airline already uses in its operations. It is therefore often necessary to spend additional funds to create interfaces for cooperation between the systems. Therefore, many airlines prefer to incur financial losses due to imperfect handling of operational emergencies at the expense of investing in software support [
7].
Staffing solutions for emergency situations depend primarily on the cause that requires crew replacement and then on the location of the emergency.
Essentially, only two causes for a crew not being able to continue can be:
If the crew has exhausted the permitted daily time on duty, it is possible for them to resume duty after a specified period of rest. However, if a crew member has health complications, his or her early return to duty is not expected. These facts must then be considered when dealing with an emergency.
The locations in which an emergency arises can also be divided into two groups:
In the first instance, the airline’s operational control center has the possibility of choosing one of the solution options:
Deploying a stand-by crew,
Deploying a crew originally scheduled for another flight,
Deploying pilots fulfilling other than their direct flight obligations at the airport (on duty),
Deploying pilots currently on personal leave.
Most airlines maintain stand-by crews to minimize the impact of emergencies. The stand-by mode can be implemented in two forms—either the pilots are available directly at the airport or they are within driving distance of the airport. Both methods have their advantages and disadvantages. The advantage of placing a backup crew directly at the airport is its immediate availability. The disadvantage is that if the pilot performs reserve duty at the airport, then the time spent by performing this standby duty is included in the time allowed on duty, which limits the possibilities of using that pilot. Conversely, if the pilot is on standby within driving distance of the airport, then the pilot’s time is not counted as on duty. Time begins to count towards the time allowed on duty only at the time of the pilot’s transfer to work in the event of an emergency. On the other hand, it is necessary to consider a certain loss of time associated with the transfer of the pilot to the airport and his or her preparation for the flight.
Another way to replace the crew affected by an emergency is to replace it with the crew of another flight. The airline’s aim is to minimize delays, so in some situations it may be more advantageous to deploy a crew that is the most available at the current time, i.e., a crew waiting for another flight at the airport. Subsequently, upon arrival, the backup crew (considering a situation where stand-by is performed outside the airport) will replace the crew originally waiting at the airport. A limitation of this situation may be that the assigned crew may already have exhausted part of their time on duty as a result of the previous flight.
In extreme cases, to mitigate the consequences of an emergency, the airline may use pilots who are performing non-flight tasks related to their performance of duty at the airport. These are, for example, various trainings. The pilots are at the airport and are therefore theoretically available, even if they do not have scheduled flight duty. Similarly, it is possible to contact a pilot who is taking personal time off. In both cases, however, the pilot may refuse an unplanned duty deployment because he or she is not obliged to perform actions beyond his or her long-term plan submitted by the airline.
In the event of an emergency away from the airport, the operations centers are markedly limited and are as follows:
Transport of the reserve crew to the airport of departure of the delayed flight,
Deployment of a crew from another flight,
Reassignment of the crew after the compulsory rest period.
Resolving an emergency away from the base is always a complicated problem. The first option that presents itself is to send a backup crew. This entails great time and financial costs associated with the transfer of the crew to the airport of departure of the flight affected by the emergency. Depending on the distance of the airport and the possibilities of transporting the crew, the crew can be transported by another air connection, a train connection or the pilots may be transported by individual car transport. It is important, however, that the time for the transfer to the airport of departure is included in the pilots’ time on duty.
Another way to solve the problem of crew replacement is to deploy another crew that has another flight scheduled in the same destination. As in the base situation, it is important that delays are not passed on to other flights due to crew rerouting. The backup crew will board the originally scheduled flight, which will reach its destination later than planned. Additionally, the airline must also solve the problem of further use of the crew from the delayed flight, which will be available at the destination (whether it will take mandatory rest or will be deployed to another flight at a later time).
The final option is to re-deploy the crew. This option is only permissible in a situation where the crew is in good health and the only reason they cannot continue is that they have exhausted the daily on duty time limit. This solution is applied in a situation where the airline does not have another reserve crew available or in a situation where the transport of the reserve crew would exceed the time the original crew needs to rest to continue the service. This applies to situations where an emergency occurs in one of the more distant destinations from the base. In such situations, the crew and passengers are accommodated in alternative accommodation and the flight is subsequently undertaken only after the expiration of the statutory rest period of the crew.
All the above operational measures carry with them additional costs, which the airline must expend to eliminate the consequences of emergencies.
As the description of the above-mentioned emergency situations, which may disrupt the scheduled operation of individual flights, shows, delays as such do not only generate time loss for passengers, but above all significant financial costs for the airline. Of course, the airline does not always have to cover these costs from its own resources. It depends on the actual cause of the incident. If it was the fault of the airline, such as a technical fault due to lack of maintenance, then all costs arising from the subsequent emergency must be paid by the airline. If the emergency is not caused by the airline and could not have been foreseen by the airline, the airline is not obliged to compensate passengers financially. However, it should also be noted that the airline is always obliged to provide care for passengers affected by the occurrence of the extraordinary event causing the delay. If the cause is not attributable to the airline, the airline shall recover the additional costs from the originator of the incident, or the costs shall be covered by the airline’s insurance.
The extent of the additional operating costs incurred depends on the situation that arises. In the event of a delay on the ground, it is important to remember that the aircraft is still in operation and is only waiting to depart. This means that it is necessary to ensure the functionality of all systems on board, such as hydraulic, air or pneumatic systems. Therefore, a power source is required, which may be an engine start, an auxiliary power unit (APU) or a connected ground source. Running engines or APUs consume fuel at a certain cost. The connection of a ground source is burdened with a rental fee. If the aircraft is parked on the apron for more than a certain amount of time, the airline must subsequently pay certain charges to the airport for the occupation of that space. During extended parking periods, the aircraft must be under the constant supervision of airport ground staff and additional handling requirements may arise, such as repeated de-icing of the aircraft during the winter months. These costs may also include the cost of repeated buses to pick up or drop off passengers at the aircraft. These costs are of course eliminated when the airport is equipped with boarding bridges. If the delay is due to a technical fault, additional costs may be incurred to repair the aircraft. If the aircraft cannot be repaired at the check-in point (stand), then it must be moved to a designated repair point, which is again a chargeable service.
If a delay occurs during the flight itself, when the flight must be diverted from the original route, it is necessary, above all, to count on increased fuel costs.
In both cases, it is important to remember that regardless of the emergency situation, the aircrew is still on duty. Although the crew is on duty during the delay, it does not generate any profit for the airline by waiting for the situation to be resolved. Consequently, a proportion of the crew’s salary corresponding to the length of the delay can be considered as having been expended without purpose and can therefore be regarded as additional costs incurred in connection with the incident. If the delay exceeds a certain value and the crew is in danger of exceeding the permitted daily duty time, another crew must be substituted. In such case, the cost of transporting another crew to the place of departure must be added to the additional costs. If a situation arises when the crew cannot be replaced, the flight must be rescheduled until the crew is able to fly again after sufficient rest. In such case, the airline must consider the cost of crew accommodation and travel allowances (meals, etc.).
In extreme cases, in the event of a flight delay, cancellation or re-routing due to a technical defect, the airline must consider the cost of sending a replacement aircraft.
The second group of additional costs that an airline must consider in the event of an emergency concerns the costs associated with passenger compensation. Each airline is obliged to take care of passengers on its flights in case of any problems. For example, the airline is obliged to provide passengers with refreshments to the extent adequate to the duration of the delay. In a situation where it is necessary for passengers to be accommodated, the airline must arrange their accommodation, transport them from the airport to the place of accommodation and back. In addition to providing the above services, passengers are also entitled to financial compensation for the delay.
Passengers’ claims for financial compensation for delays are governed by Regulation No 261/2004 of the European Parliament and of the Council [
8], which lays down common rules on compensation and assistance to air passengers in the event of denied boarding and of cancellation or long delay of flights. The level of this compensation depends on the length of the flight and the scope of the delay. The passenger is entitled to compensation if the operating airline has reasonable grounds to expect that, from scheduled departure time, the flight will be delayed by:
Two hours or more in the case of flights of 1500 km or less, or
Three hours or more in the case of all flights within the European Community longer than 1500 km and all other flights between 1500 and 3500 km, or
Four hours or more in the case of all flights not falling under (a) or (b).
The Regulation entered into force on 17 February 2005 and applies to all passengers departing from an airport located in the territory of a State to which the Treaty applies and to passengers departing from an airport located in the territory of a third country to an airport located in the territory of a Member State to which the Treaty applies, unless they have already received compensation or redress, and have not received assistance in that third country and the operating air carrier is a Community carrier [
8]. The costs associated with compensations resulting from flight delays are shown in
Table 1.
The paper is thematically related to the publication [
9]. It extends the mathematical model published in this paper in a fundamental way. While the previous mathematical model involves pre-formed crews, the model in this paper allows these crews to be formed from individual pilots while maintaining the requirements for interpersonal relationships.
5. Calculation Experiments with the Proposed Model
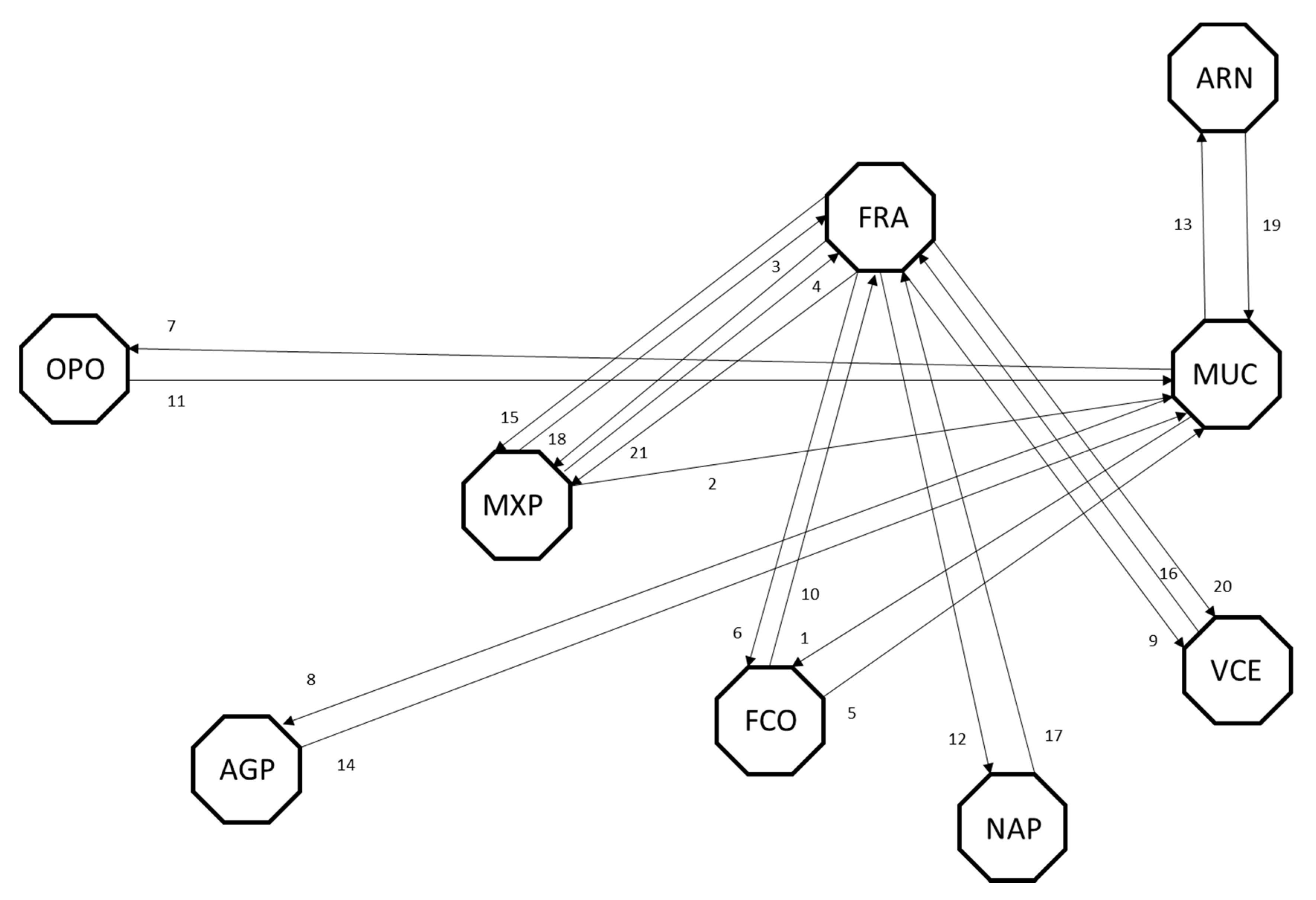
For experimental verification of the functionality of the proposed model, a real network of a European airline operating a homogeneous fleet was selected. The fleet consists of Embraer E195 aircraft. Within this network, traffic was monitored over a period of 24 h. The airline served nine destinations within the selected day, of which two destinations were the selected airline’s hubs. These hubs were the airports in Frankfurt am Main (FRA) and Munich (MUC). Other destinations served by the airline that day were Milan (MXP), Venice (VCE), Rome (FCO), Naples (NAP), Porto (OPO), Malaga (AGP) and Stockholm (ARN). A total of 21 flights were operated during the day. The scheme of flights to be operated is shown in
Figure 1. Data were obtained from the Flightradar24 server [
47].
The airline has 22 pilots available to operate flights. Of these, 10 pilots are in the position of captain and 12 pilots in the position of first officer. Based on professional qualities and interpersonal relationships, it is possible to create 37 crew combinations. The procedure for creating crews was described in
Section 5. These possible combinations of crews are listed in
Table 4, where the rows represent the set of captains (10 pilots) and the columns represent the set of first officers (12 pilots). In a situation where the symbol x appears in the table, it means that the respective pair of pilots cannot create a crew. If there is a number in the table, it is the serial number of the possible crew. For example, crew number 13 consists of captain number 4 and first officer number 3.
As described above, the model automatically ensures that multiple crews consisting of one pilot are not deployed. This prevents, for example, crews 13 and 14 from being deployed at the same time because they have the same captain.
For the purposes of experimental verification of the model’s functionality, an emergency will be simulated during the flight day. These contingencies will be the delay of flight 11 from Porto (OPO) to Munich (MUC) and adverse weather at Frankfurt Airport (FRA). These events will split the flight set into two subsets. The first subset consists of flights 1–10. The second subset consists of flights 11–21. The experiment will be divided into two parts:
In the first part of the computational experiment, the process of planning crew routes using a suitably modified model will be carried out. The result of the first part of the computational experiment will be information regarding the distribution of pilots or crews within the operated network at the time of the emergency.
Based on the information regarding the current location and the current time on duty, the second part of the experiment will allow the design of an optimal crew turn-around plan for operating the remaining 11 flights (flights 11–21) that may be affected by the emergency. From this plan, it will be easy to determine the allocation of crews to the flights already served, and at which destination they should terminate their service.
The information on this original plan will then serve as a benchmark in the third part, in the operational rescheduling of the crews with the aim of restoring its original form as much as possible. Thus, the model will behave in the calculation to deploy crews to operate flights during the rescheduling so that, to the maximum extent possible, they operate the flights that were in the original crew pairing plan.
The calculations of all parts of the experiment were performed in the Xpress-IVE optimization software. The models in this software were created in the MOSEL programming language. The software was installed on a personal computer running the Windows 10 operating system, using an Intel i5-5200U processor with a frequency of 2.2 GHz and 8 GB of RAM.
To make it possible to obtain information on the specific crew positions at the time of the emergency, it is necessary to establish a crew routing plan for all flights to be operated on a given day. This can be achieved by applying existing approaches or using a model (1)–(20), in which only a partial modification will take place of the objective function—the addition of one constraint and the omission of some input values that are unnecessary for this type of calculation. The objective function for creating crew routes without delays will be in the form:
This objective function contains two optimization criteria. The first criterion is the number of assigned crews and the second criterion is the cost of moving crews and pilots to operate individual flights. The number of crew assignments is multiplied by a large enough constant in the objective function to allow the results to easily distinguish between the number of crew assignments and the cost of assigning them to individual flights.
As this calculation will create a completely new pairing plan, logically there is no previous state or standard to follow and it is therefore not necessary to include matrix in the input data to describe the original state of the system.
The final modification to be made in the model will be the replacement of the group of constraints (16) with the group of constraints (22) in the form:
The stated group of constraints will not allow delay of any kind on any flight.
In the initial crew pairings, individual pilots were placed at the following airports—see
Table 5.
Most pilots did not yet log any activity related to the performance of duty on that day. The exception is the three crews who were completing their night flights. These were crews No. 6 (Captain No. 2, FO No. 1), 24 (Captain No. 7, FO No. 9) and 31 (Captain No. 9, FO No. 5). Depending on the pilots who took part in the flights, the current sum of the time of on duty (
time for the day will also be reflected in all potential crews in which the mentioned pilots may appear–see
Table 10.
Other input information for the model are data from matrices and . The element of matrix expresses costs incurred from the unproductive transfer of the crew k to operate the flight after operation of the flight and the element of matrix expresses the time required for the unproductive transfer of the crew to operate the flight after operating flight .
The results of the experiment showed that seven crews will be needed to operate the planned set of flights. These crews are crew numbers 6, 12, 13, 19, 24, 31 and 35. The schedule of routes of these crews and their daily time on duty after completing these flights are described in
Table 11.
Figure 2 schematically shows the routes of individual crews and the subsequent location of pilots after the end of the scheduled set of flights. After completing their daily duty, the pilots will be deployed at four airports—Frankfurt am Main, Munich, Milan and Venice. Captains’ numbers are shown in bold, FO numbers are indicated in italics. The route plan and the final placement of the pilots will be the input to create a matrix
, which will be used in the next part of the experiment to consider the original crew pairing plan.
The second part of the experiment is devoted to the verification of the functionality of the proposed model (1)–(20), i.e., the contingency rescheduling of crew routes. The input values depend on the moment of occurrence of the emergency. It is definitely necessary to identify from the original plan the positions of pilots and their running time on duty up to the actual time of occurrence of the delay. Furthermore, it is necessary to introduce a matrix into the model, the elements of which create a penalty in a situation where pilots operate flights in a different way than specified in the original pairing plan.
Emergencies will be simulated on three flights. On flight number 11 from Porto, and on flights 12 and 15, which are operated from Frankfurt n. M. airport, the estimated delay time for the arrival of flight 11 will be set at 50 min. According to the original plan, crew No. 31 is deployed for this flight. The estimated time of delay in the arrival of each flight from Frankfurt am Main will be 220 min. Crew No. 12 is deployed on flight 12 and crew No. 6 is deployed on flight 15. The occurrence of an emergency will be modeled by introducing predefined values of variables
, see constraints 23, 24 and 25.
The input values will correspond to the moment when the airline’s operations center receives information on the occurrence of an emergency. In this case, it will be the time 825, corresponding to the planned start of flight No. 11. Depending on the determination of this moment, it is necessary to adjust the input values. The rescheduling process will only apply to unhandled flights. These are therefore flights 11–21. Depending on the current position of the crews, it will also be necessary to adjust the matrices
and
and also the values of the constant
, which determine the daily time on duty for each crew, and hence for the pilots. As already mentioned, the input values will be supplemented by a matrix
, to minimize the deviations of the newly created crew routes from the original plan. The input values for the constants
and
are taken from
Table 7. The input values for the constants
,
and
are taken from
Table 9. The values of the constant
are shown in
Table 12. Please note that matrices
,
and
will not be presented in this paper due to their scope—they are available in the external files—see the Data Availability Statement.
Table 13 provides information on the current deployment of pilot crews within the network at the time of the emergency (time 825 min). The pilots are deployed in a total of five destinations, with pilots 5 and 11, forming crew No. 19, not yet physically present in Venice, but operating flight No. 9 to this destination. Likewise, pilots 4 and 3, forming crew No. 13, are on their way to Frankfurt am Main. Pilots who are not physically at the airport at the time of the emergency are indicated in italics in the table.
The results of the optimization calculation with the proposed model (1)–(20) showed that in the event all three emergencies arise, the number of active crews will increase to nine. This increase is caused by two factors, which are exhaustion of the maximum time of daily in-flight duty allowed for the crews operating delayed flights as well as efforts to minimize the costs incurred in reimbursing passengers due to flight delays.
The routes of active crews after operational re-planning are shown in
Table 14.
The above crew pairing plan also shows evidence that the model works with crews as a pair of pilots that can be divided during the day. Such a case occurred with crews No. 13 and No. 26. FO No. 3, originally assigned to crew 13, which terminated its activities after completing Flight No. 10 in Frankfurt n. M. at time 925, is subsequently deployed to Flight No. 18 as part of crew No. 26. This flight is operated from Milan with a departure time of 1105. The time to move between these airports is determined in the matrix and corresponds to a value of 170 min. The time between the arrival of flight No. 10 and the departure of flight No. 18 is 180 min. A transfer time of 170 min is therefore permissible for such transfer. In total, nine captains and eight FOs will be involved in the operation after rescheduling.
Figure 3 schematically shows the rescheduled crew pairings. The numbers at the peaks show the final position of the pilots after completing the operation of all scheduled flights. The locations of the captains are shown in bold and the FO locations are indicated in italics.
The resulting placement differs in part from the original plan. The difference is mainly in the location of the pilots of crew No. 12 (Captain No. 3 and FO No. 10) at the airport in Naples, because originally, it was not planned to end their activities here. This location is related to the delay of flight No. 12 From Frankfurt n. M. to Naples. Due to the long delay (220 min), the crew could not operate the connecting flight No. 17, which had a scheduled departure already 45 min after the arrival of flight No. 12. Therefore, a new crew was chosen to operate Flight No. 17, namely crew No. 21 (consisting of Captain No. 6 and FO No. 6). In other cases, these are only pilots located in a different way than originally planned, but while maintaining the airports, where they were deployed in the original plan of crew routes.
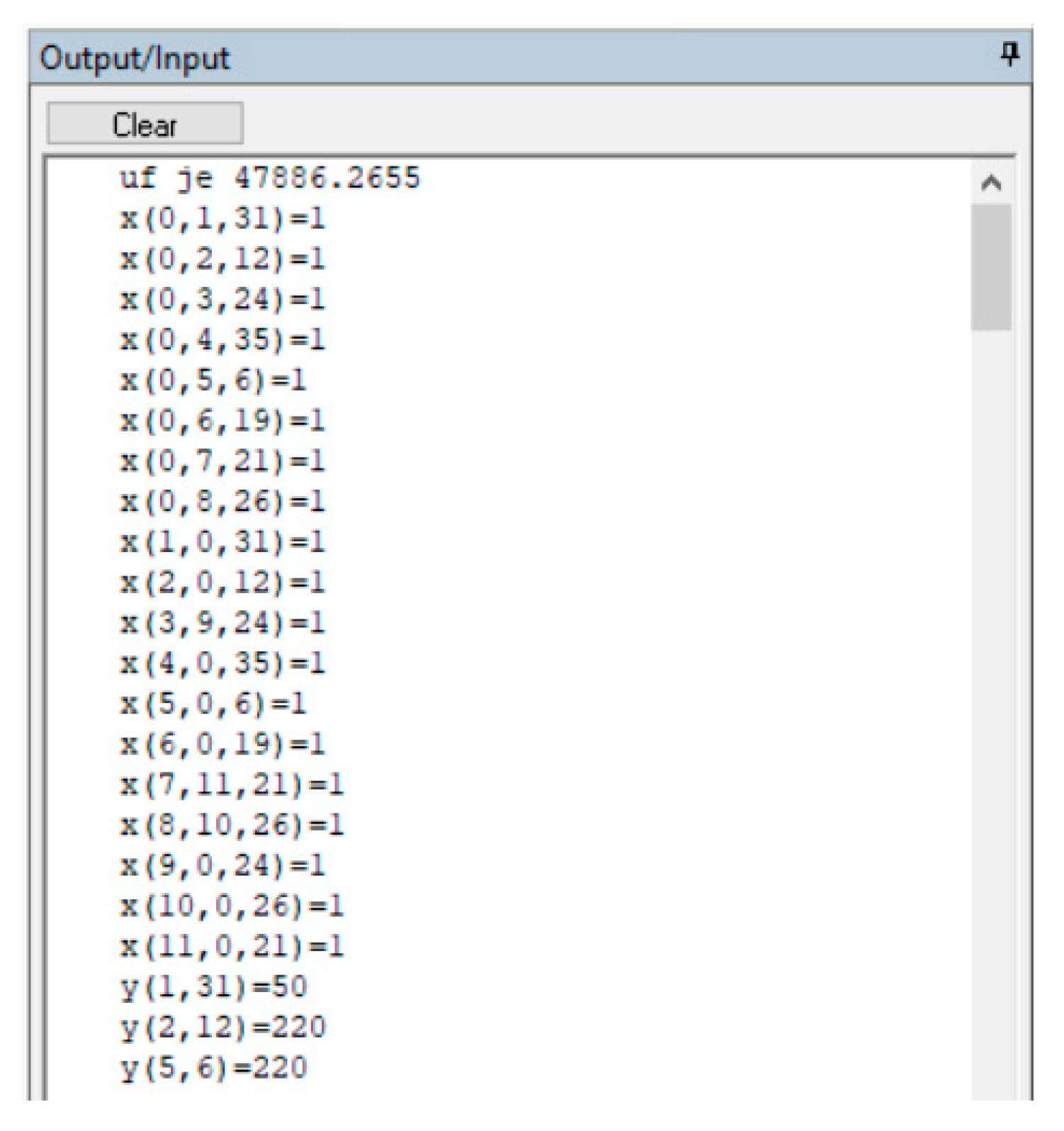
Figure 4 shows the output of the Xpress-IVE program, where it can be seen that the value of the total optimization criterion is 47 886.2655. The values after the decimal point are not important for the interpretation of the results, because in the calculation they only serve to ensure that the range of the beginning and end of the on-duty time of individual crews is minimal. It is therefore necessary to deal in more detail only with the value 47,886, which is the sum of the results of three partial optimization criteria.
The primary criterion is costs for non-productive transfers of crews, expressed in the objective function by the following formula:
In this case, two non-productive transfers took place, and their costs added up to 370 monetary units.
Another criterion that affects the value of the objective function is the cost of compensating passengers for the occurrence of a delay. The minimum delay value at which passengers can claim compensation has been exceeded for two flights. These are the already mentioned flights flying from Frankfurt am Main. Here, the total cost of compensation was calculated at 47,500 monetary units. In the optimization criterion, this criterion is expressed by the following term:
The final term affecting the value of the optimization criterion, are penalties related to non-compliance with the original schedule of crew rotations. In the optimization criterion, this criterion is expressed by the following formula:
In this case, eight transfers were penalized, and the total value of the penalty was 16 monetary units.
By adding up the values of all the above-listed expressions, a value of 47, 886 was achieved, which corresponds to the value of the optimization criterion.
Another positive aspect of the proposed rescheduling is that the delays caused by the proposed solution were not passed on to other flights or crews. This is also evidenced by the Xpress-IVE output shown in
Figure 4, where it can be seen that the variable takes on non-zero values only in situations that were deliberately set in the model.
The optimality of the found solution is confirmed in the Xpress-IVE report in
Figure 5 in the Status line. The rounded value of the objective function can again be seen in the Best solution item. The computation time, indicated in the Time line, was 7.5 s.