Abstract
Relay synchronization in multi-layer networks implies inter-layer synchronization between two indirectly connected layers through a relay layer. In this work, we study the relay synchronization in a three-layer multiplex network by introducing degree-based weighting mechanisms. The mechanism of within-layer connectivity may be hubs-repelling or hubs-attracting whenever low-degree or high-degree nodes receive strong influence. We adjust the remote layers to hubs-attracting coupling, whereas the relay layer may be unweighted, hubs-repelling, or hubs-attracting network. We establish that relay synchronization is improved when the relay layer is hubs-repelling compared to the other cases. We determine analytically necessary stability conditions of relay synchronization state using the master stability function approach. Finally, we explore the relation between synchronization and the topological property of the relay layer. We find that a higher clustering coefficient hinders synchronizability, and vice versa. We also look into the intra-layer synchronization in the proposed weighted triplex network and establish that intra-layer synchronization occurs in a wider range when relay layer is hubs-attracting.
1. Introduction
Over the last few decades, the study of complex networks has been a topic of great interest due to its application in diverse scientific fields [1,2]. Recent advances in network science revealed that many systems in nature could be represented by multi-layer networks [3,4], where elements are interconnected through various links between more than one layer. Such a framework is well known for illustrating many real-world systems, such as social networks [5], transportation networks [6], power-grid networks [7], ecological networks [8], and neuronal networks of the brain [9,10]. A particular subclass of multi-layer networks are multiplex networks where each layer contains the same number of nodes, and one-to-one inter-layer connections between the replica nodes from neighboring layers are allowed.
Due to the interactions of dynamical units within and between the layers, many emergent phenomena occur in the multiplex network. Synchronization [11,12,13,14,15] is one among them. Different types of synchronization scenarios have been observed in multiplex framework, such as intra-layer synchronization [16,17], inter-layer synchronization [18,19,20], cluster synchronization [21,22], explosive synchronization [23,24,25], and chimera states [26,27,28].
Relay synchronization in a multiplex network has received much attention from researchers in the past few years. This synchronization phenomenon occurs between two distant layers, not directly connected but only through a relay layer. First reported in a star-like network [29,30], this type of synchronization has also been detected in laser systems [31], circuits of chaotic oscillators [32], and between remote pairs of nodes within the network [33]. Besides, it is of great importance in the human brain networks, where the thalamus [34] acts as a relay between distant cortical areas. Recently, relay synchronization has been illustrated in multi-layer and multiplex frameworks with different intra-layer topologies, such as Erdős-Rényi and scale-free [35]. In Reference [36], random inhomogeneities of the small-world type have been introduced in the network layers to scrutinize the robustness of relay synchronization. Continuous and discrete-time systems have been used as individual units to induce spatiotemporal structures in triplex networks [37,38]. However, in the above cases, the network topology of both the relay and remote layers are represented by unweighted networks. Although weighted networks, where coupling weights are heterogeneous, are present in many real-world networks, such as the network of scientific collaborations [39], structural and functional networks of the brain [40], transportation networks [41], epidemic spreading [42], ecological networks [43], etc., we would like to emphasize that the recent progress in this direction has been achieved considering weighted mono-layer networks [44,45,46,47,48] and weighted duplex networks [49,50,51]. However, the effect of weighted networks upon synchronization in the multiplex network with more than two layers is less studied. So, the lack of works on the synchronization in weighted multi-layer networks encouraged us to unveil the effect of weighted networks upon the relay synchronization in a multiplex network.
In this regard, we would like to highlight the very recent works by Estrada et al. [52,53], in which the authors have introduced two opposite approaches to explore the degree-biased mechanisms on the network dynamics based on the generalization of the graph Laplacian operator. The Laplacians are defined so that the pairwise weights of connectivity matrix are introduced as a ratio of degrees of two coupled nodes. As a result, an unweighted graph is transformed into a weighted directed one following two distinct methods. One forces the network to obey high-degree nodes, and the other is biased towards the low-degree nodes. In the first case, referred as hubs-attracting Laplacian [52], a high-degree unit receives weaker influence from its low-degree neighbor than from a high-degree one. Opposed to the above, the low-degree units produce more potent effects in the second case, illustrated by the hubs-repelling Laplacian [53]. These findings have motivated us to dig into the comparison between the weighted directed networks generated by different degree-based weighting mechanisms to achieve synchronization in a relay multiplex network.
In this letter, we consider a three-layer multiplex (triplex) network with intra-layer coupling set up by a random Erdős-Rényi (ER) topology with individual nodes as chaotic Rössler oscillator. The intra-layer connectivity is set up in such a way that the corresponding Laplacian matrices are equal to either hubs-attracting or the hubs-repelling Laplacian matrices. In particular, we set the remote layers to be hubs-attracting and consider three configurations of relay layer: hubs-attracting, hubs-repelling, and unweighted network. Further, we estimate the onset of relay synchronization for all three configurations. Our study shows that the relay synchronization is improved when the relay layer is hubs-repelling compared to the other two cases. Using analytical tools, we demonstrate the necessary conditions for the synchronized state. We also explain the enhancing behavior in terms of clustering coefficient analysis of the relay layer. Apart from this, we also examine the emergence of intra-layer synchrony for all three configurations.
2. Mathematical Model
We consider a triplex network, schematically presented in Figure 1. The layers are denoted by , where indicates remote layers and corresponds to the relay layer. Each layer contains nodes following m-dimensional identical dynamical systems. The nodes are mutually connected with their corresponding replica nodes from the neighboring layers. The states of the kth layer are represented by the vectors , where and . The dynamics of the ith node in each layer is governed by the system of ordinary differential equations:
where , , and represent the autonomous evolution of the uncoupled oscillator, intra-layer, and inter-layer coupling matrices, respectively. In the current study, we suggest that the autonomous evolution of each node in the triplex network (1) obeys the dynamics of chaotic Rössler oscillators, for which is given by
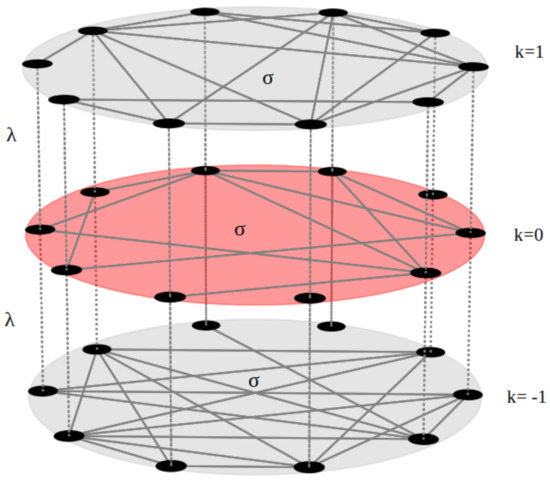
Figure 1.
Schematic diagram of a general triplex relay network. The intra-layer coupling with strength is presented with solid lines, and inter-layer coupling with strength is depicted with dashed lines. The two outer layers , shown in gray, are connected through the middle layer , colored in red.
In system (2), the control parameters are fixed and set equal for all oscillators as , which provide chaotic dynamics. The intra-layer coupling matrix G for all the layers is taken as linear diffusive coupling through x-variable, i.e, , where denotes the transpose of a matrix. The inter-layer coupling is considered to be through all the state variables. Thus, the inter-layer coupling matrix H is an identity matrix. Strengths of intra-layer and inter-layer coupling are introduced as and , respectively. Laplacian matrix of the layer is defined as . These matrices are constructed from the weighted matrices , where the element is obtained by the element-wise scaling of unweighted adjacency matrix with the ratios of interacting units degrees . The element if the and nodes are connected with each other and otherwise, and .
The parameter determines if the layer remains unweighted network (U, ) or converted into weighted directed graph (). For , matrix specifies that the high-degree nodes produce strong influence on their low-degree neighbors, and vice versa. For , defines the opposite mechanism, the low-degree units have a strong impact on their high-degree neighbors, and vice versa. The Laplacian obtained for , respectively, corresponds to hubs-repelling [53] and hubs-attracting [52] Laplacian matrices, and associated networks are called hubs-repelling and hubs-attracting networks.
Here, the connection topology of each layer is given by Erdős-Rényi (ER) random graph with the edge connectivity probability . We transform the network of each layer to a directed weighted graph by introducing the mechanism of hubs-attracting (A) and hubs-repelling (R) Laplacian. The remote layers are transformed to the hubs-attracting network, and the middle (relay) layer could be transformed to one of three configurations: Hubs-repelling (R, ), unweighted (U, ), and Hubs-attracting (A, ). We classify the layer stacks regarding the weighting sequence of each layer. For instance, the triplex network with remote layers Hubs-attracting and middle layer Hubs-repelling will be denoted as ARA. Consequently, the triplex networks with middle layers unweighted and Hubs-attracting will be denoted as AUA and AAA, respectively. We will scrutinize the relay synchronization for all three configurations: AAA, AUA, and ARA in the next section.
3. Results
3.1. Valuation of Relay Synchronization Error
To analyze the relay synchronization in our networks, we employ the synchronization error as:
where denotes the Euclidean norm, determines the transient of the numerical simulation, and T is a sufficiently large positive number. To measure the synchronization errors, the time interval is taken over units after an initial transient of units, i.e., and . In all our simulations, we consider the threshold value of synchronization error to be for synchrony.
The triplex network (1) is solved numerically using the Runge–Kutta–Fehlberg algorithm with integration step and fixed random initial conditions chosen from the interval [−1, 1]. For each result, 20 network realizations with random initial conditions are considered.
We first scrutinize synchronization error for a fixed value of intra-layer coupling strength by varying inter-layer coupling . Figure 2 displays three curves for three different configurations: AAA, AUA, and ARA, respectively. For the AAA configuration, red dotted line, the synchrony is achieved at the critical coupling . For the AUA configuration, black dotted curve, the critical value shifts towards a slightly lower value of . At the same time, for the ARA case, blue dotted curve, the critical value of synchronization decreases further – the synchrony is reached at . Thus, one can conclude that, for a fixed value of intra-layer coupling, the relay synchronization enhances as the value of decreases from 1 to within the relay layer, and the remote layers are fixed to be hubs-attracting (A) network.
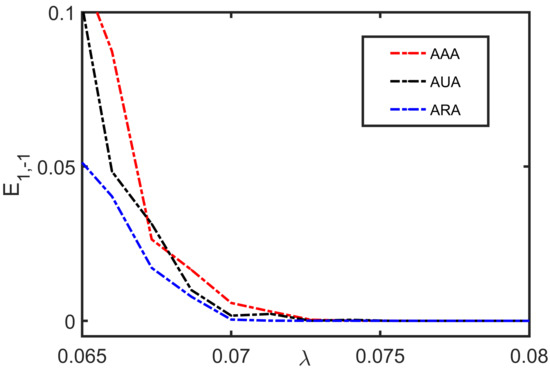
Figure 2.
Synchronization error between the outer layers as a function of inter-layer coupling strength for the fixed value of intra-layer coupling . Red, black, and blue dashed curves represent the synchronization errors for AAA, AUA, and ARA configurations.
Therefore, without introducing parameter mismatch in the relay layer or introducing a time delay between the layers, changing the weighting mechanism between the middle (relay) layer nodes may effectively improve the relay synchronization in multiplex networks.
3.2. Stability Analysis of Relay Synchronization
Thereafter, we analytically derive the conditions for stability of the relay synchronization using Master Stability Function [54] approach. The synchronization solution is given by, .
Let be the vector describing the difference between the dynamics of the mirror layers. Considering to be a small perturbation of synchronous solution, we have linearized Equation (1) as:
where J is the Jacobian operator, and represents the synchronous state satisfying
In the above equation, is the state variable of the node in the relay layer, which satisfies the equation of motion
In the variational Equation (5), the state variable evolves transverse to the synchronization manifold. Therefore, the Lyapunov exponents of Equation (5) depict the stability of the synchronization manifold. The maximum Lyapunov exponent (MLE) as a function of the parameters , gives a necessary condition for the stability of the inter-layer synchronization solution. For a stable solution, perturbation along all the transverse directions must die out, i.e., the values of MLE should be negative. Solving the linearized Equation (5) along with the non-linear Equations (6) and (7) gives the MLEs transverse to the synchronization manifold. In Figure 3, we have plotted the MLEs for the same parameter values as in Figure 1 to validate the stability condition. It clearly shows that the MLE passes zero-level at the exact value of where becomes less than 10 for each of the three configurations considered. Therefore, the analytical stability condition suitably agreed with our numerical results.
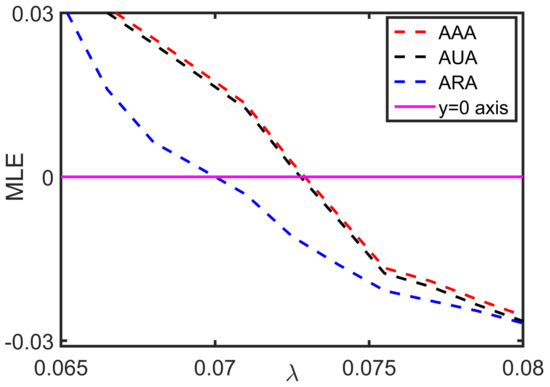
Figure 3.
Maximum Lyapunov Exponents (MLEs) as a function of supporting the results presneted in Figure 1. Red, black, and blue dashed curves display MLEs for AAA, AUA, and ARA configurations, respectively. Purple horizontal line indicates zero-level.
3.3. Delineation of Relay Synchronization in Parameter Space
To better understand the enhancement in the relay synchronization, we have plotted the variation of synchronization error in the -plane for all the three network configurations. The results depicted in Figure 4 show that the region of synchronization increases in ARA (Figure 4c) configuration compared to the other configurations, AAA (Figure 4a) and AUA (Figure 4b). Thus, rigorously plotting the synchronization error, we can perceive the synchronization scenario for all three configurations. It reaffirms our statement about an enhancement of relay synchronization in ARA configuration of the multiplex network as compared to AAA and AUA configurations.
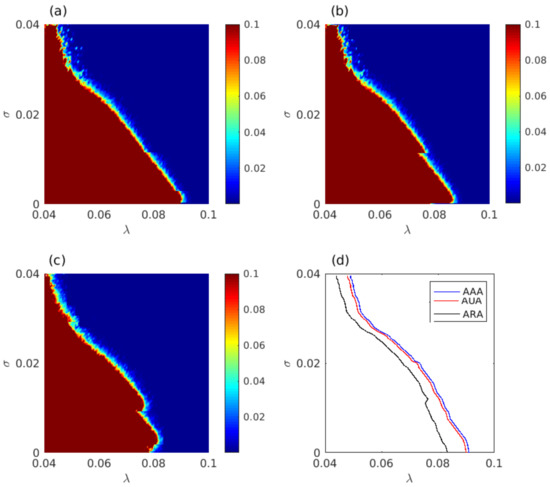
Figure 4.
Variation of synchronization error in the )-plane for (a) AAA, (b) AUA, and (c) ARA configurations. The color bar denotes the variation of the synchronization error where the deep red and blue correspond to the desynchronized and synchronized domains, respectively. The subplot (d) displays the boundaries of synchronization in the )-plane for all considered configurations of the triplex relay network.
3.4. Structural Analysis
Apart from quantifying the synchronization error and linear stability analysis, for a profound understanding of enhancement in the relay synchronization, we also go through the structural analysis of the middle (relay) layer for all three cases. With increasing from −1 to 1, we analyze the average clustering coefficient, , where is a local clustering coefficient, within the relay layer. As for non-zero , the network becomes a weighted directed network, and we follow the formula for local clustering coefficient for weighted directed network proposed in Reference [55]:
where and are the in-degree and input strength of ith node, respectively. Here, we have taken only the in-component of clustering coefficient, as the hubs-attracting network’s input strength corresponds to the hubs-repelling network’s output strength, and vice versa. In Figure 5, we plotted the average clustering coefficient for different values of within the relay layer. The largest value (CC = 0.0649) of clustering coefficient corresponds to when the relay layer is Hubs-attracting, and for , when relay layer is Hubs repelling, the value of clustering coefficient is lowest (CC = 0.0630). It is a well-known fact that the clustering coefficient plays a crucial role in synchronization. Larger values of clustering coefficient hinder the synchronization, and smaller values determine the improvement [56]. Due to large clustering, the network splits into dynamical clusters that follow different trajectories and, as a result, impedes synchronization. Hence, the result depicted in Figure 5 can reasonably explain improving the relay synchronization with ARA configuration.
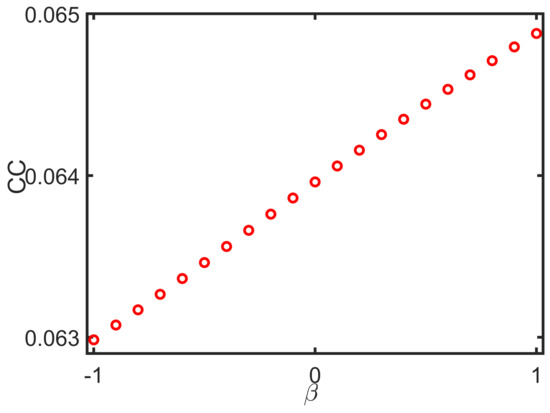
Figure 5.
Average clustering coefficient for increasing value of within the relay layer.
3.5. Emergence of Intra-Layer Synchronization State
Now, we investigate the intra-layer synchronization in the multiplex network (1). For intra-layer synchronization, each individual layer evolves on the same time evolution, which occurs when each individual oscillator in each layer of the multiplex network is appropriately coupled [17,57]. To quantify the intra-layer synchronization state, we introduce the synchronization error as,
where
is the synchronization error of each layer k. indicates the emergence of intra-layer synchronization in the triplex network.
We have plotted the intra-layer synchronization error in Figure 6 by varying the intra-layer coupling strength for the three configurations: AAA (red dotted line), AUA (black dotted line) and ARA (blue dotted line), respectively. From the figure, we can elucidate that, for all the three cases, the triplex network shows two transitions—one from desynchrony to synchrony and other one from synchrony to desynchrony state. So, the intra-layer synchronization appears in a bounded range of intra-layer coupling strength . For AAA configuration, the first transition occurs at intra-layer coupling and the second transition takes place at . For AUA configuration, the intra-layer synchronization occurs in the range of intra-layer coupling strength. The range shrinks further for the ARA configuration for which synchronization occurs in . One point of note is that the intra-layer synchronization occurred simultaneously [58], and desynchronization to synchronization also occurred at the same value of intra-layer coupling strength .
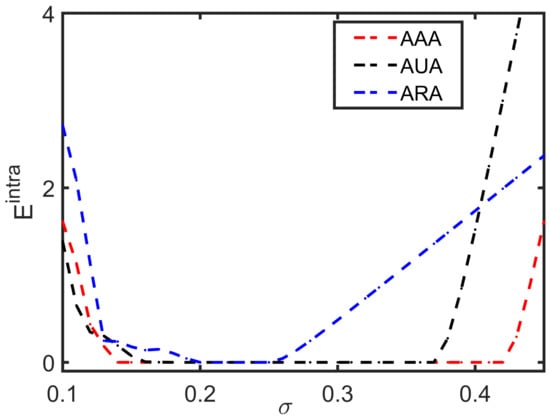
Figure 6.
Intra-layer synchronization error as a function of intra-layer coupling strength for the fixed value of inter-layer coupling strength . Red, black, and blue dashed curves represent the synchronization errors for AAA, AUA, and ARA configurations.
Therefore, intra-layer synchronization for the multiplex network emerges in a bounded range of coupling strength. The range is wider for AAA configuration compared to AUA and ARA configurations.
4. Discussion and Conclusions
In summary, we have explicitly addressed the emergence of relay synchronization in weighted triplex networks of chaotic non-linear oscillators. We constructed within-layer connection topologies following the Erdős-Rényi algorithm for nodes. The pairwise intra-layer interactions are scaled such that the influence produced by the ith node on the jth node is proportional to the ratio of their degrees . Values of the exponent determine changes of the edges’ weights according to one of the triplex configurations: hubs-repelling (), hubs-attracting (), and unweighted network ().
The current study evidences an enhancement in the relay synchronization if the middle layer exhibits hubs-repelling interactions compared to hubs-attracting and original unweighted couplings. We have supported numerical findings by analytical treatment of the synchronized state stability conducted via master stability function. Moreover, we have also scrutinized the topological properties of the intra-layer connection within the relay layers, which helps in understanding that, in the case of hubs-repelling interactions, the middle layer exhibits a lower clustering coefficient. The latter contributes to a more efficient relay synchronization in a considered triplex network. Lastly, we investigated the intra-layer synchronization for the multiplex network which emerges in a bounded range of intra-layer coupling strength and the range of synchrony expands if the relay layer is hubs-attracting compared to unweighted and hubs-repelling couplings.
We expect that our investigation considering such mechanisms of network weighting as hubs-attracting and hubs-repelling will open the door for a new perception of various collective behaviors emerging in a multi-layer network.
Author Contributions
M.S.A.: Conceptualization, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing—original draft. D.G. & N.F.: Conceptualization, Methodology, Writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data needed to evaluate the conclusions in the paper are present in the paper itself. Additional data related to this paper may be requested to the corresponding authors.
Acknowledgments
This work has been supported by the Department of Science and Technology, Government of India (Project no. INT/RUS/RFBR/360) and the Russian Foundation for Basic Research (Grant No. 19-52-45026).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–94. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwanga, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; del Genio, C.I.; Gómez-Gardeñes, J.; Romance, M.; Sendixnxa-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1. [Google Scholar] [CrossRef] [Green Version]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203. [Google Scholar] [CrossRef] [Green Version]
- Szell, M.; Lambiotte, R.; Thurner, S. Multirelational organization of large-scale social networks in an online world. Proc. Natl. Acad. Sci. USA 2010, 107, 13636–13641. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cardillo, A.; Zanin, M.; Gómez-Gardeñes, J.; Romance, M.; del Amo García, A.; Boccaletti, S. Modeling the multi-layer nature of the European Air Transport Network: Resilience and passengers re-scheduling under random failures. Eur. Phys. J. Spec. Top. 2013, 215, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Brummitt, C.D.; D’Souza, R.M.; Leicht, E.A. Suppressing cascades of load in interdependent networks. Proc. Natl. Acad. Sci. USA 2012, 109, E680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pilosof, S.; Porter, M.A.; Pascual, M.; Kéfi, S. The multilayer nature of ecological networks. Nat. Ecol. Evol. 2017, 1, 0101. [Google Scholar] [CrossRef] [Green Version]
- Majhi, S.; Bera, B.K.; Ghosh, D.; Perc, M. Chimera states in neuronal networks: A review. Phys. Life Rev. 2019, 28, 100–121. [Google Scholar] [CrossRef] [PubMed]
- Frolov, N.; Maksimenko, V.; Hramov, A. Revealing a multiplex brain network through the analysis of recurrences. Chaos 2020, 30, 121108. [Google Scholar] [CrossRef] [PubMed]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Osipov, G.V.; Kurths, J.; Zhou, C. Synchronization in Oscillatory Networks; Springer: Berlin, Germany, 2007. [Google Scholar]
- Gunasekaran, N.; Zhai, G.; Yu, Q. Sampled-data synchronization of delayed multi-agent networks and its application to coupled circuit. Neurocomputing 2020, 413, 499–511. [Google Scholar] [CrossRef]
- Anbuvithya, R.; Sri, S.D.; Vadivel, R.; Gunasekaran, N.; Hammachukiattikul, P. Extended dissipativity and non-fragile synchronization for recurrent neural networks with multiple time-varying delays via sampled-data control. IEEE Access 2021, 9, 31454–31466. [Google Scholar] [CrossRef]
- Vadivel, R.; Hammachukiattikul, P.; Gunasekaran, N.; Saravanakumar, R.; Dutta, H. Strict dissipativity synchronization for delayed static neural networks: An event-triggered scheme. Chaos Solitons Fractals 2021, 150, 111212. [Google Scholar] [CrossRef]
- Gambuzza, L.V.; Frasca, M.; Gómez-Gardeñes, J. Intra-layer synchronization in multiplex networks. Europhys. Lett. 2015, 110, 20010. [Google Scholar] [CrossRef] [Green Version]
- Rakshit, S.; Bera, B.K.; Bollt, E.M.; Ghosh, D. Intralayer Synchronization in Evolving Multiplex Hypernetworks: Analytical Approach. SIAM J. Appl. Dyn. Syst. 2020, 19, 918–963. [Google Scholar] [CrossRef]
- Sevilla-Escoboza, R.; Sendiña-Nadal, I.; Leyva, I.; Gutiérrez, R.; Buldú, J.M.; Boccaletti, S. Inter-layer synchronization in multiplex networks of identical layers. Chaos 2016, 26, 065304. [Google Scholar] [CrossRef]
- Leyva, I.; Sevilla-Escoboza, R.; Sendiña-Nadal, I.; Gutiérrez, R.; Buldú, J.M.; Boccaletti, S. Inter-layer synchronization in non-identical multi-layer networks. Sci. Rep. 2017, 7, 45475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pitsik, E.; Makarov, V.; Kirsanov, D.; Frolov, N.; Goremyko, M.; Li, X.; Wang, Z.; Hramov, A.; Boccaletti, S. Inter-layer competition in adaptive multiplex network. New J. Phys. 2018, 20, 075004. [Google Scholar] [CrossRef] [Green Version]
- Della Rossa, F.; Pecora, L.; Blaha, K.; Shirin, A.; Klickstein, I.; Sorrentino, F. Symmetries and cluster synchronization in multilayer networks. Nat. Commun. 2020, 11, 3179. [Google Scholar] [CrossRef]
- Jalan, S.; Singh, A. Cluster synchronization in multiplex networks. Europhys. Lett. 2016, 113, 30002. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Boccaletti, S.; Guan, S.; Liu, Z. Explosive Synchronization in Adaptive and Multilayer Networks. Phys. Rev. Lett. 2015, 114, 038701. [Google Scholar] [CrossRef]
- Kumar, A.; Jalan, S.; Kachhvah, A.D. Interlayer adaptation-induced explosive synchronization in multiplex networks. Phys. Rev. Res. 2020, 2, 023259. [Google Scholar] [CrossRef]
- Frolov, N.; Rakshit, S.; Maksimenko, V.; Kirsanov, D.; Ghosh, D.; Hramov, A. Coexistence of interdependence and competition in adaptive multilayer network. Chaos Solitons Fractals 2021, 147, 110955. [Google Scholar] [CrossRef]
- Maksimenko, V.A.; Makarov, V.V.; Bera, B.K.; Ghosh, D.; Dana, S.K.; Goremyko, M.V.; Frolov, N.S.; Koronovskii, A.A.; Hramov, A.E. Excitation and suppression of chimera states by multiplexing. Phys. Rev. E 2016, 94, 052205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Majhi, S.; Perc, M.; Ghosh, D. Chimera states in uncoupled neurons induced by a multilayer structure. Sci. Rep. 2016, 6, 39033. [Google Scholar] [CrossRef] [Green Version]
- Frolov, N.S.; Maksimenko, V.A.; Makarov, V.V.; Kirsanov, D.V.; Hramov, A.E.; Kurths, J. Macroscopic chimeralike behavior in a multiplex network. Phys. Rev. E 2018, 98, 022320. [Google Scholar] [CrossRef] [PubMed]
- Kuptsov, P.V.; Kuptsova, A.V. Variety of regimes of starlike networks of Henon maps. Phys. Rev. E 2015, 92, 042912. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bergner, A.; Frasca, M.; Sciuto, G.; Buscarino, A.; Ngamga, E.J.; Fortuna, L.; Kurths, J. Remote synchronization in star networks. Phys. Rev. E 2012, 85, 026208. [Google Scholar] [CrossRef] [Green Version]
- Fischer, I.; Vicente, R.; Buldú, J.M.; Peil, M.; Mirasso, C.R.; Torrent, M.C.; García-Ojalvo, J. Zero-lag long-range synchronization via dynamical relaying. Phys. Rev. Lett. 2006, 97, 123902. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, R.; Ghosh, D.; Padmanaban, E.; Ramaswamy, R.; Pecora, L.M.; Dana, S.K. Enhancing synchrony in chaotic oscillators by dynamic relaying. Phys. Rev. E 2012, 85, 027201. [Google Scholar] [CrossRef] [Green Version]
- Gambuzza, L.V.; Frasca, M.; Fortuna, L.; Boccaletti, S. Inhomogeneity induces relay synchronization in complex networks. Phys. Rev. E 2016, 93, 042203. [Google Scholar] [CrossRef]
- Guillery, R.; Sherman, S.M. Thalamic relay functions and their role in corticocortical communication: Generalizations from the visual system. Neuron 2020, 33, 163–175. [Google Scholar] [CrossRef] [Green Version]
- Leyva, I.; Sendiña-Nadal, I.; Sevilla-Escoboza, R.; Vera-Avila, V.P.; Chholak, P.; Boccaletti, S. Relay synchronization in multiplex networks. Sci. Rep. 2018, 8, 8629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drauschke, F.; Sawicki, J.; Berner, R.; Omelchenko, I.; Schöll, E. Effect of topology upon relay synchronization in triplex neuronal networks. Chaos 2020, 30, 051104. [Google Scholar] [CrossRef]
- Sawicki, J.; Omelchenko, I.; Zakharova, A.; Schöll, E. Delay controls chimera relay synchronization in multiplex networks. Phys. Rev. E 2018, 98, 062224. [Google Scholar] [CrossRef] [Green Version]
- Rybalova, E.; Strelkova, G.; Schöll, E.; Anishchenko, V. Relay and complete synchronization in heterogeneous multiplex networks of chaotic maps. Chaos 2020, 30, 061104. [Google Scholar] [CrossRef]
- Newman, M.E.J. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys. Rev. E 2001, 64, 016132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buzsaki, G.; Geisler, C.; Henze, D.A.; Wang, X.J. Interneuron Diversity series: Circuit complexity and axon wiring economy of cortical interneurons. Trends Neurosci. 2004, 27, 186–193. [Google Scholar] [CrossRef]
- Barrat, A.; Barthélemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747. [Google Scholar] [CrossRef] [Green Version]
- Kamp, C.; Moslonka-Lefebvre, M.; Alizon, S. Epidemic Spread on Weighted Networks. PLoS Comput. Biol. 2013, 9, e1003352. [Google Scholar] [CrossRef] [PubMed]
- McCann, K.; Hastings, A.; Huxel, G.R. Weak trophic interactions and the balance of nature. Nature 1998, 395, 794. [Google Scholar] [CrossRef]
- Motter, A.E.; Zhou, C.; Kurths, J. Network synchronization, diffusion, and the paradox of heterogeneity. Phys. Rev. E 2005, 71, 016116. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Kurths, J. Dynamical Weights and Enhanced Synchronization in Adaptive Complex Networks. Phys. Rev. Lett. 2006, 96, 164102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, C.; Motter, A.E.; Kurths, J. Universality in the Synchronization of Weighted Random Networks. Phys. Rev. Lett. 2006, 96, 034101. [Google Scholar] [CrossRef] [Green Version]
- Chavez, M.; Hwang, D.U.; Amann, A.; Boccaletti, S. Synchronizing weighted complex networks. Chaos 2006, 16, 015106. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.B.; Wang, X.F.; Li, X.; Fang, J.Q. Synchronization in weighted complex networks: Heterogeneity and synchronizability. Phys. A 2006, 370, 381–389. [Google Scholar] [CrossRef]
- Li, Y.; Wu, X.; Lu, J.; Lü, J. Synchronizability of duplex networks. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 206–210. [Google Scholar] [CrossRef]
- Kempton, L.; Herrmann, G.; di Bernardo, M. Self-organization of weighted networks for optimal synchronizability. IEEE Trans. Control Netw. Syst. 2018, 5, 1541–1550. [Google Scholar] [CrossRef] [Green Version]
- Anwar, M.S.; Kundu, S.; Ghosh, D. Enhancing synchrony in asymmetrically weighted multiplex networks. Chaos Solitons Fractals 2021, 142, 110476. [Google Scholar] [CrossRef]
- Gambuzza, L.V.; Frasca, M.; Estrada, E. Hubs-attracting Laplacian and Related Synchronization on Networks. SIAM J. Appl. Dyn. Syst. 2020, 19, 1057–1079. [Google Scholar] [CrossRef]
- Estrada, E. ‘Hubs-repelling’ Laplacian and related diffusion on graphs/networks. Linear Algebra Appl. 2020, 596, 256–280. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Master Stability Functions for Synchronized Coupled Systems. Phys. Rev. Lett. 1998, 80, 2109. [Google Scholar] [CrossRef]
- Clemente, G.P.; Grassi, R. Directed clustering in weighted networks: A new perspective. Chaos Solitons Fractals 2018, 107, 26–38. [Google Scholar] [CrossRef] [Green Version]
- Arenas, A.; Díaz-Guilera, A.; Kurths, J.; Moreno, Y.; Zhou, C. Synchronization in complex networks. Phys. Rep. 2008, 469, 93–153. [Google Scholar] [CrossRef] [Green Version]
- Rakshit, S.; Majhi, S.; Bera, B.K.; Sinha, S.; Ghosh, D. Time-varying multiplex network: Intralayer and interlayer synchronization. Phys. Rev. 2017, 96, 062308. [Google Scholar] [CrossRef] [PubMed]
- Bera, B.K.; Rakshit, S.; Ghosh, D. Intralayer synchronization in neuronal multiplex network. Eur. Phys. J. Spec. Top. 2019, 228, 2441–2454. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).