Weighted Fractional-Order Transform Based on Periodic Matrix

Abstract

Tao et al. proposed the definition of the linear summation of fractional-order matrices based on the theory of Yeh and Pei. This definition was further extended and applied to image encryption. In this paper, we propose a reformulation of the definitions of Yeh et al. and Tao et al. and analyze them theoretically. The results show that many weighted terms are invalid. Therefore, we use the proposed reformulation to prove that the effective weighted terms depend on the period of the matrix. This also shows that the image encryption methods based on the weighted fractional-order transform will lead to the security risk of key invalidation. Finally, our hypothesis is verified by the unified theoretical framework of multiple-parameter discrete fractional-order transforms.

1. Introduction

Fractional Fourier transform (FRFT) is widely used in quantum mechanics, optics, pattern recognition, time-frequency representation, signal processing, information security and other fields [1,2,3,4,5,6,7,8,9,10,11,12]. Therefore, discrete fractional Fourier transforms, mainly including weighted-type FRFTs [13,14], eigendecomposition-type FRFTs [15,16] and sampling-type FRFTs [17,18,19], have been proposed. In 2003, Yeh and Pei proposed a new computation method of the discrete FRFT [20]. This method is similar to Shih’s weighted FRFT [13], with the difference being that the fractional power of the discrete Fourier transform (DFT) is used in the definition of Yeh and Pei. Then, Tao et al. presented the linear summation of fractional-order matrices based on the method proposed by Yeh and Pei. Therefore, the fractional power for any diagonalizable periodic matrix is defined, which provides a new idea for information processing [21]. Recently, Kang et al. extended the definition of Tao et al., proposed a computation method for the multiple-parameter discrete FRFT, and further extended the method to multiple parameter discrete fractional cosine, sine, Hartley, and Hadamard transforms. These definitions can be applied to signal processing and image encryption [22]. In this paper, our analysis results show that there are only four effective weighted terms in the definition of Yeh and Pei, which will lead to the security risk of key invalidation when applied to image encryption. Furthermore, our results also show that the effective weighting term in the definition of Tao et al. is related to the period of the matrix. Such extension methods based on that definition are applied to image encryption, which will lead to the security risk of key invalidation.

The remainder of this paper is organized as follows. Preliminary knowledge is described in Section 2. Section 3 analyzes the definition of Yeh et al. Section 4 analyzes the definition of Tao et al. Effective weighted terms and security are discussed in Section 5. Finally, conclusions are presented in Section 6.

2. Preliminaries

Tao et al. proposed the idea of the linear summation of fractional-order matrices [21]. If a matrix $L$ satisfies $L^P=I$, then $L$ is a periodic matrix with period P. Assume matrix $L$ is a matrix satisfying $L^P=I$ and its eigendecomposition form is $L=VD{V}^H$. Let $b=P/M$ and $L^b=L^{P/M}=V{D}^{P/M}{V}^H$. Then, $L^{\alpha }$ can be computed as

$$L^{\alpha }={\displaystyle \sum _{n=0}^{M-1}{C}_{n,\alpha /b}{L}^{nb}}.$$

(1)

In fact, the computation method of the discrete fractional Fourier transform (DFRFT) of Yeh and Pei [20] can be regarded as a special case of the definition of Tao et al. Consider DFRFT matrices $I$, $F^b$, $F^{2b}$,…, $F^{\left(M-1\right)b}$, where $b=4/M$. Denote the sum of these DFRFT matrices as

$$F^{\alpha }={\displaystyle \sum _{n=0}^{M-1}{C}_{n,\alpha }{F}^{nb}},$$

(2)

with coefficients

$$C_{n,\alpha }=\frac{1}{M}\frac{1-e^{2\pi i\left(n-\alpha \right)}}{1-e^{\left(2\pi i/M\right)\left(n-\alpha \right)}},$$

(3)

where $n=0,1,2,\cdots ,M-1$. Tao et al. discussed the correlation between the signal length and the period of the matrix to present $C_{n,\alpha }$ and $C_{n,\alpha /b}$. Because the fractional-order $\alpha$ is a real number, there is no essential difference between the two. Moreover, Shih’s research also shows that the signal length is independent of the period of the matrix [13].

However, our analysis shows that the effective weighting term of such a definition depends on the period of the matrix. Next, we will reanalyze the definitions of Yeh et al. and Tao et al.

3. Theoretical Analysis of the Definition of Yeh et al.

Equation (3) is the sum of geometric progression, and its common ratio is $e^{2\pi i\left(n-\alpha \right)/M}$. Then, Equation (3) can also be expressed as

$$\begin{array}{ll}{C}_{n,\alpha }& =\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{e}^{2\pi i\left(n-\alpha \right)k/M}}\\ & =\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{e}^{\left(-2\pi i\alpha k/M\right)}{e}^{\left(2\pi ink/M\right)}}\\ & =IDFT{\left[e^{\left(-2\pi i\alpha k/M\right)}\right]}_{k=0,1,2,\cdots \cdots ,M-1}\end{array}$$

(4)

where $n=0,1,\cdots ,M-1$; and Equation (4) can be further expressed as

$$\left(\begin{array}{c}{C}_{0,\alpha }\\ C_{1,\alpha }\\ ⋮\\ C_{M-1,\alpha }\end{array}\right)=\frac{1}{M}\left(\begin{array}{cccc}{w}^{0\times 0}& w^{0\times 1}& \cdots & w^{0\times (M-1)}\\ w^{1\times 0}& w^{1\times 1}& \cdots & w^{1\times (M-1)}\\ ⋮& ⋮& \ddots & ⋮\\ w^{(M-1)\times 0}& w^{(M-1)\times 1}& \cdots & w^{(M-1)\times (M-1)}\end{array}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i\alpha 0/M\right)}\\ e^{\left(-2\pi i\alpha 1/M\right)}\\ ⋮\\ e^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\end{array}\right),$$

(5)

where $w=\exp \left(2\pi i/M\right)$. Then, the definition (Equation (2)) of Yeh and Pei can be expressed as

$$\begin{array}{ll}{F}^{\alpha }& ={\displaystyle \sum _{n=0}^{M-1}{C}_{n,\alpha }{F}^{4n/M}}\\ & =\left(F^0,F^{4/M},\cdots ,F^{4\left(M-1\right)/M}\right)\left(\begin{array}{c}{C}_{0,\alpha }\\ C_{1,\alpha }\\ ⋮\\ C_{M-1,\alpha }\end{array}\right)\\ & =\frac{1}{M}\left(F^0,F^{4/M},\cdots ,F^{4\left(M-1\right)/M}\right)\left(\begin{array}{cccc}{w}^{0\times 0}& w^{0\times 1}& \cdots & w^{0\times (M-1)}\\ w^{1\times 0}& w^{1\times 1}& \cdots & w^{1\times (M-1)}\\ ⋮& ⋮& \ddots & ⋮\\ w^{(M-1)\times 0}& w^{(M-1)\times 1}& \cdots & w^{(M-1)\times (M-1)}\end{array}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i\alpha 0/M\right)}\\ e^{\left(-2\pi i\alpha 1/M\right)}\\ ⋮\\ e^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\end{array}\right).\end{array}$$

(6)

Here, we let

$$\{\begin{array}{l}{W}_0=w^{0\times 0}{F}^0+w^{1\times 0}{F}^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times 0}{F}^{\frac{4\left(M-1\right)}{M}}\\ W_1=w^{0\times 1}{F}^0+w^{1\times 1}{F}^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times 1}{F}^{\frac{4\left(M-1\right)}{M}}\\ W_2=w^{0\times 2}{F}^0+w^{1\times 2}{F}^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times 2}{F}^{\frac{4\left(M-1\right)}{M}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ W_{M-1}=w^{0\times \left(M-1\right)}{F}^0+w^{1\times \left(M-1\right)}{F}^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times \left(M-1\right)}{F}^{\frac{4\left(M-1\right)}{M}}\end{array}$$

(7)

Definition 1.

A new reformulation of the definition of Yeh and Pei as

$$\begin{array}{ll}{F}^{\alpha }& =\frac{1}{M}\left(W_0,W_1,\cdots ,W_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i\alpha 0/M\right)}\\ e^{\left(-2\pi i\alpha 1/M\right)}\\ ⋮\\ e^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{W}_k{e}^{\left(-2\pi i\alpha k/M\right)}}.\end{array}$$

(8)

In ref. [20], $I$, $F^b$, $F^{2b}$,…, $F^{\left(M-1\right)b}$ are the DFRFT; and the DFRFT has diversity. For Equation (7), we use the eigendecomposition type and the weighted type FRFT for verification.

3.1. Eigendecomposition Type FRFT

Proposition 1.

Eigendecomposition type FRFT is used as the basis function, there are only four effective weighting terms for the definition of Yeh and Pei.

Proof. 

At present, the discrete definition [16] closest to the continuous FRFT is

$$F^{\alpha }\left(m,n\right)={\displaystyle \sum _{k=0}^{N-1}{v}_k\left(m\right)e^{-i\frac{\pi }{2}k\alpha }{v}_k\left(n\right)},$$

(9)

where $v_k\left(n\right)$ is an arbitrary orthonormal eigenvector set of the $N\times N$ DFT. Equation (9) can be written as

$$F^{\alpha }=V{D}^{\alpha }{V}^H,$$

(10)

where $V=\left(v_0,v_1,\cdots ,v_{N-1}\right)$, $v_k$ is the kth-order DFT Hermite eigenvector, and $D^{\alpha }$ is a diagonal matrix defined as

$$D^{\alpha }=\mathrm{diag}\left(1,e^{-i\frac{\pi }{2}\alpha },\cdots ,e^{-i\frac{\pi }{2}\left(N-2\right)\alpha },e^{-i\frac{\pi }{2}\left(N-1\right)\alpha }\right),for N odd,$$

(11)

and

$$D^{\alpha }=\mathrm{diag}\left(1,e^{-i\frac{\pi }{2}\alpha },\cdots ,e^{-i\frac{\pi }{2}\left(N-2\right)\alpha },e^{-i\frac{\pi }{2}\left(N\right)\alpha }\right),for N even.$$

(12)

We only prove that N is odd (when N is even, the proof process is the same). In [23,24], the eigenvalues of the DFT can be expressed as ${\lambda }_n=e^{n\pi i/2}$. Then, the possible values of the eigenvalue are ${\lambda }_n=\left\{1,-1,i,-i\right\}$. Therefore,

$$D^{\alpha }=\mathrm{diag}\left({\left(1\right)}^{\alpha },{\left(-i\right)}^{\alpha },{\left(-1\right)}^{\alpha },{\left(i\right)}^{\alpha },{\left(1\right)}^{\alpha },{\left(-i\right)}^{\alpha },{\left(-1\right)}^{\alpha },{\left(i\right)}^{\alpha },\cdots \cdots ,{\left(1 or-1\right)}^{\alpha }\right).$$

(13)

Thus, Equation (7) can be written as

$$W_k=w^{0\times k}\times I+w^{1\times k}\times F^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times F^{\frac{4\left(M-1\right)}{M}},$$

(14)

where $w=\exp \left(2\pi i/M\right)$ and $k=0,1,\cdots ,M-1$. When the eigendecomposition type FRFT is used, Equation (15) is obtained as

$$\begin{array}{ll}{W}_k& =w^{0\times k}\times F^0+w^{1\times k}\times F^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times F^{\frac{4\left(M-1\right)}{M}}\\ & =w^{0\times k}V{D}^0{V}^H+w^{1\times k}V{D}^{\frac{4}{M}}{V}^H+\cdots +w^{\left(M-1\right)\times k}V{D}^{\frac{4\left(M-1\right)}{M}}{V}^H\\ & =w^{0\times k}V\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& {\left(-i\right)}^0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\left(1 or-1\right)}^0\end{array}\right)V^H+w^{1\times k}V\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& {\left(-i\right)}^{\frac{4}{M}}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\left(1 or-1\right)}^{\frac{4}{M}}\end{array}\right)V^H+\cdots +w^{\left(M-1\right)\times k}V\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& {\left(-i\right)}^{\frac{4\left(M-1\right)}{M}}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\left(1 or-1\right)}^{\frac{4\left(M-1\right)}{M}}\end{array}\right)V^H.\end{array}$$

(15)

Therefore, we obtain Equation (16) as

$$W_k=V\left(\begin{array}{cccc}{S}^{\left(1\right)}\left(k\right)& 0& \cdots & 0\\ 0& S^{\left(-i\right)}\left(k\right)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & S^{\left(1 or-1\right)}\left(k\right)\end{array}\right)V^H.$$

(16)

From Equation (16), the diagonal matrix only contains $S^{\left(1\right)}\left(k\right)$, $S^{\left(i\right)}\left(k\right)$, $S^{\left(-1\right)}\left(k\right)$, and $S^{\left(-i\right)}\left(k\right)$. The multiplicities of the DFT eigenvalues are shown in Table 1. Therefore,

$$\begin{array}{ll}{\lambda }_n& =\left\{1,i,-1,-i\right\}\\ & =\left\{e^{4n\pi i/2},e^{\left(4n+1\right)\pi i/2},e^{\left(4n+2\right)\pi i/2},e^{\left(4n+3\right)\pi i/2}\right\}\\ & =\left\{e^{2n\pi i}{e}^{0\pi i/2},e^{2n\pi i}{e}^{\pi i/2},e^{2n\pi i}{e}^{2\pi i/2},e^{2n\pi i}{e}^{3\pi i/2}\right\}\\ & =\left\{e^{0\pi i/2},e^{\pi i/2},e^{2\pi i/2},e^{3\pi i/2}\right\}.\end{array}$$

(17)

Table 1. Multiplicities of the DFT eigenvalues.

N	1	−1	−i	i
4n	n + 1	n	n	n − 1
4n + 1	n + 1	n	n	n
4n + 2	n + 1	n + 1	n	n
4n + 3	n + 1	n + 1	n + 1	n

When the eigenvalue is 1, $S^{\left(1\right)}\left(k\right)$ can be expressed as

$$\begin{array}{ll}{S}^{(1)}\left(k\right)& =w^{0\times k}{1}^0+w^{1\times k}{1}^{4/M}+\cdots +w^{\left(M-1\right)\times k}{1}^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1k/M}+e^{2\pi i2k/M}+\cdots +e^{2\pi i\left(M-1\right)k/M}\\ & =\frac{1-{\left(e^{2\pi ik/M}\right)}^M}{1-e^{2\pi ik/M}}.\end{array}$$

(18)

Therefore, we obtain

$$S^{\left(1\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=0\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(19)

When the eigenvalue is i, $S^{\left(i\right)}\left(k\right)$ can be expressed as

$$\begin{array}{ll}{S}^{\left(i\right)}\left(k\right)& =w^{0\times k}{\left(i\right)}^0+w^{1\times k}{\left(i\right)}^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\left(i\right)}^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1\left(k+1\right)/M}+e^{2\pi i2\left(k+1\right)/M}+\cdots +e^{-2\pi i\left(M-1\right)\left(k+1\right)/M}\\ & =\frac{1-{\left(e^{2\pi i\left(k+1\right)/M}\right)}^M}{1-e^{2\pi i\left(k+1\right)/M}}.\end{array}$$

(20)

Therefore,

$$S^{\left(i\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=M-1\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(21)

When the eigenvalue is −1, $S^{\left(-1\right)}\left(k\right)$ can be expressed as

$$\begin{array}{ll}{S}^{\left(-1\right)}\left(k\right)& =w^{0\times k}{\left(-1\right)}^0+w^{1\times k}{\left(-1\right)}^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\left(-1\right)}^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1\left(k+2\right)/M}+e^{2\pi i2\left(k+2\right)/M}+\cdots +e^{2\pi i\left(M-1\right)\left(k+2\right)/M}\\ & =\frac{1-{\left(e^{2\pi i\left(k+2\right)/M}\right)}^M}{1-e^{2\pi i\left(k+2\right)/M}}.\end{array}$$

(22)

Then, we can obtain

$$S^{\left(-1\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=M-2\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(23)

When the eigenvalue is −i, $S^{\left(-i\right)}\left(k\right)$ can be expressed as

$$\begin{array}{ll}{S}^{\left(-i\right)}\left(k\right)& =w^{0\times k}{\left(-i\right)}^0+w^{1\times k}{\left(-i\right)}^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\left(-i\right)}^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1\left(k+3\right)/M}+e^{2\pi i2\left(k+3\right)/M}+\cdots +e^{2\pi i\left(M-1\right)\left(k+3\right)/M}\\ & =\frac{1-{\left(e^{2\pi i\left(k+3\right)/M}\right)}^M}{1-e^{2\pi i\left(k+3\right)/M}}.\end{array}$$

(24)

Therefore,

$$S^{\left(-i\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=M-3\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(25)

From Equations (19), (21), (23) and (25), Equation (16) can be written as

$$W_k=\{\begin{array}{ll}{W}_k,& for k=0,M-3,M-2,M-1\\ 0,& for k=1,2,\cdots ,M-4.\end{array}$$

(26)

Thus, Equation (8) is expressed as

$$\begin{array}{ll}{F}^{\alpha }& =\frac{1}{M}\left(W_0,W_1,\cdots ,W_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i\alpha 0/M\right)}\\ e^{\left(-2\pi i\alpha 1/M\right)}\\ ⋮\\ e^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}\left(W_0,0,\cdots ,0,W_{M-3},W_{M-2},W_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i\alpha 0/M\right)}\\ e^{\left(-2\pi i\alpha 1/M\right)}\\ ⋮\\ e^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}\left(W_0{e}^{\left(-2\pi i\alpha 0/M\right)}+W_{M-3}{e}^{\left(-2\pi i\alpha \left(M-3\right)/M\right)}+W_{M-2}{e}^{\left(-2\pi i\alpha \left(M-2\right)/M\right)}+W_{M-1}{e}^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\right).\end{array}$$

(27)

□

Remark 1.

From Equation (27), it is not difficult to find that when$I$,$F^b$,$F^{2b}$, …,$F^{\left(M-1\right)b}$are eigendecomposition-type FRFTs, there are only four effective weighting terms defined by Yeh and Pei.

3.2. Weighted Type FRFT

Proposition 2.

Weighted type FRFT is used as the basis function, there are only four effective weighting terms for the definition of Yeh and Pei.

Proof. 

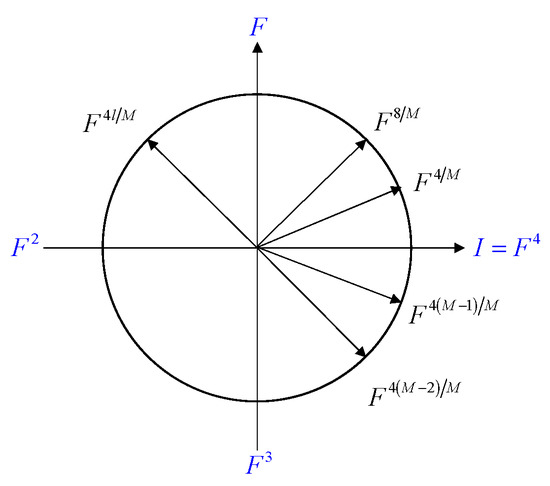
In ref. [20], $I$, $F^b$, $F^{2b}$,…, $F^{\left(M-1\right)b}$ ($b=4/M$) are the DFRFTs, which can be explained as shown in Figure 1. Therefore, the definition of Yeh and Pei is more accurate as the generalized form of Shih’s FRFT [13]. For Equation (7), we introduce the weighted fractional Fourier transform (WFRFT).

Figure 1. Time-frequency denotation.

Shih proposed the WFRFT [13]. Shih’s WFRFT with a period of 4 is also called the 4-weighted type fractional Fourier transform (4-WFRFT), which is defined as

$$F_4^{\alpha }\left[f\left(t\right)\right]={\displaystyle \sum _{l=0}^3{A}_l^{\alpha }{f}_l\left(t\right)},$$

(28)

with

$$A_l^{\alpha }=\cos \left(\frac{(\alpha -l)\pi }{4}\right)\cos \left(\frac{2(\alpha -l)\pi }{4}\right)\exp \left(\frac{3(\alpha -l)i\pi }{4}\right),$$

(29)

where $f_l\left(t\right)=F^l\left[f\left(t\right)\right]$ and $l=0,1,2,3$ (F denotes the Fourier transform). Equation (29) can also be expressed as

$$\begin{array}{ll}{F}_4^{\alpha }\left[f\left(t\right)\right]& =\left(A_0^{\alpha }\cdot I+A_1^{\alpha }\cdot F+A_2^{\alpha }\cdot F^2+A_3^{\alpha }\cdot F^3\right)f\left(t\right)\\ & =\left(I,F,F^2,F^3\right)\left(\begin{array}{c}{A}_0^{\alpha }\\ A_1^{\alpha }\\ A_2^{\alpha }\\ A_3^{\alpha }\end{array}\right)f\left(t\right).\end{array}$$

(30)

According to the definition of the weighting coefficient $A_l^{\alpha }$ [13], Equation (30) can be expressed as

$$F_4^{\alpha }\left[f\left(t\right)\right]=\frac{1}{4}\left(I,F,F^2,F^3\right)\left(\begin{array}{cccc}1& 1& 1& 1\\ 1& -i& -1& i\\ 1& -1& 1& -1\\ 1& i& -1& -i\end{array}\right)\left(\begin{array}{l}{B}_0^{\alpha }\\ B_1^{\alpha }\\ B_2^{\alpha }\\ B_3^{\alpha }\end{array}\right)f\left(t\right),$$

(31)

where $B_k^{\alpha }=\exp \left(\frac{2\pi ik\alpha }{4}\right)$ and $k=0,1,2,3$. Here, we let

$$\{\begin{array}{l}{P}_0=I+F+F^2+F^3\\ P_1=I-F*i-F^2+F^3*i\\ P_2=I-F+F^2-F^3\\ P_3=I+F*i-F^2-F^3*i.\end{array}$$

(32)

Therefore, Shih’s WFRFT can be represented as

$$F_4^{\alpha }\left[f\left(t\right)\right]=\frac{1}{4}\left(P_0,P_1,P_2,P_3\right)\left(\begin{array}{l}{B}_0^{\alpha }\\ B_1^{\alpha }\\ B_2^{\alpha }\\ B_3^{\alpha }\end{array}\right)f\left(t\right).$$

(33)

From Equations (7) and (33), we can obtain

$$\begin{array}{ll}{W}_k& =w^{0\times k}\times F_4^0+w^{1\times k}\times F_4^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times F_4^{\frac{4\left(M-1\right)}{M}}\\ & =\frac{1}{4}\left(P_0,P_1,P_2,P_3\right)\left(w^{0\times k}\times \left(\begin{array}{l}{B}_0^0\\ B_1^0\\ B_2^0\\ B_3^0\end{array}\right)+w^{1\times k}\times \left(\begin{array}{l}{B}_0^{\frac{4}{M}}\\ B_1^{\frac{4}{M}}\\ B_2^{\frac{4}{M}}\\ B_3^{\frac{4}{M}}\end{array}\right)+\cdots +w^{\left(M-1\right)\times k}\times \left(\begin{array}{l}{B}_0^{\frac{4\left(M-1\right)}{M}}\\ B_1^{\frac{4\left(M-1\right)}{M}}\\ B_2^{\frac{4\left(M-1\right)}{M}}\\ B_3^{\frac{4\left(M-1\right)}{M}}\end{array}\right)\right)\\ & =\frac{1}{4}\left(P_0,P_1,P_2,P_3\right)\left(\begin{array}{c}{w}^{0\times k}\times B_0^0+w^{1\times k}\times B_0^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times B_0^{\frac{4\left(M-1\right)}{M}}\\ w^{0\times k}\times B_1^0+w^{1\times k}\times B_1^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times B_1^{\frac{4\left(M-1\right)}{M}}\\ w^{0\times k}\times B_2^0+w^{1\times k}\times B_2^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times B_2^{\frac{4\left(M-1\right)}{M}}\\ w^{0\times k}\times B_3^0+w^{1\times k}\times B_3^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times B_3^{\frac{4\left(M-1\right)}{M}}\end{array}\right),\end{array}$$

(34)

where $k=0,1,\cdots ,M-1$ and $w=\exp \left(2\pi i/M\right)$. Therefore, Equation (35) is obtained as

$$\begin{array}{ll}{W}_k& =\frac{1}{4}\left(P_0,P_1,P_2,P_3\right)\left(\begin{array}{c}1+\exp \left(\frac{2\pi i1k}{M}\right)+\exp \left(\frac{2\pi i2k}{M}\right)+\cdots +\exp \left(\frac{2\pi i\left(M-1\right)k}{M}\right)\\ 1+\exp \left(\frac{2\pi i1\left(k+1\right)}{M}\right)+\exp \left(\frac{2\pi i2\left(k+1\right)}{M}\right)+\cdots +\exp \left(\frac{2\pi i\left(M-1\right)\left(k+1\right)}{M}\right)\\ 1+\exp \left(\frac{2\pi i1\left(k+2\right)}{M}\right)+\exp \left(\frac{2\pi i2\left(k+2\right)}{M}\right)+\cdots +\exp \left(\frac{2\pi i\left(M-1\right)\left(k+2\right)}{M}\right)\\ 1+\exp \left(\frac{2\pi i1\left(k+3\right)}{M}\right)+\exp \left(\frac{2\pi i2\left(k+3\right)}{M}\right)+\cdots +\exp \left(\frac{2\pi i\left(M-1\right)\left(k+3\right)}{M}\right)\end{array}\right)\\ & =\frac{1}{4}\left(P_0,P_1,P_2,P_3\right)\left(\begin{array}{c}{J}_0\left(k\right)\\ J_1\left(k\right)\\ J_2\left(k\right)\\ J_3\left(k\right)\end{array}\right).\end{array}$$

(35)

According to Equations (18), (20), (22) and (24), for $k=0,1,\cdots ,M-1$, we can easily determine

$$J_0\left(k\right)=\{\begin{array}{ll}M,& if k=0\\ 0,& otherwise\end{array}$$

(36)

$$J_1\left(k\right)=\{\begin{array}{ll}M,& if k=M-1\\ 0,& otherwise\end{array}$$

(37)

$$J_2\left(k\right)=\{\begin{array}{ll}M,& if k=M-2\\ 0,& otherwise\end{array}$$

(38)

and

$$J_3\left(k\right)=\{\begin{array}{ll}M,& if k=M-3\\ 0,& otherwise\end{array}$$

(39)

Thus, Equation (35) is simplified as

$$W_k=\{\begin{array}{ll}\frac{M}{4}{P}_k,& for k=0,M-3,M-2,M-1\\ 0,& for k=1,2,\cdots ,M-4.\end{array}$$

(40)

Therefore, Equation (8) can be expressed as

$$\begin{array}{ll}{F}^{\alpha }& =\frac{1}{M}\left(W_0,W_1,\cdots ,W_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i\alpha 0/M\right)}\\ e^{\left(-2\pi i\alpha 1/M\right)}\\ ⋮\\ e^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{4}\left(P_0,0,\cdots ,0,P_{M-3},P_{M-2},P_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i\alpha 0/M\right)}\\ e^{\left(-2\pi i\alpha 1/M\right)}\\ ⋮\\ e^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{4}\left(P_0{e}^{\left(-2\pi i\alpha 0/M\right)}+P_{M-3}{e}^{\left(-2\pi i\alpha \left(M-3\right)/M\right)}+P_{M-2}{e}^{\left(-2\pi i\alpha \left(M-2\right)/M\right)}+P_{M-1}{e}^{\left(-2\pi i\alpha \left(M-1\right)/M\right)}\right).\end{array}$$

(41)

From Equation (41), the result shows once again that there are only four effective weighted terms for the definition of Yeh and Pei.

□

Remark 2.

From Equation (41), the result shows once again that there are only four effective weighted terms for the definition of Yeh and Pei.

4. Theoretical Analysis of the Definition of Tao et al.

Tao et al. proposed the definition of the fractional power of the periodic matrix, which can be expressed as

$$L^{\alpha }={\displaystyle \sum _{n=0}^{M-1}{C}_{n,\alpha /b}{L}^{nb}},$$

(42)

where $b=P/M$ ($P$ is the period of the matrix). Then,

$$C_{n,\alpha /b}=IDFT{\left[e^{\left(-2\pi i(\alpha /b)k/M\right)}\right]}_{k=0,1,2,\cdots \cdots ,M-1}$$

(43)

Therefore, Equation (42) can be expressed as

$$\begin{array}{ll}{L}^{\alpha }& ={\displaystyle \sum _{n=0}^{M-1}{C}_{n,\alpha /b}{L}^{nP/M}}\\ & =\left(L^0,L^{P/M},\cdots ,L^{P\left(M-1\right)/M}\right)\left(\begin{array}{c}{C}_{0,\alpha /b}\\ C_{1,\alpha /b}\\ ⋮\\ C_{M-1,\alpha /b}\end{array}\right)\\ & =\frac{1}{M}\left(L^0,L^{P/M},\cdots ,L^{P\left(M-1\right)/M}\right)\left(\begin{array}{cccc}{w}^{0\times 0}& w^{0\times 1}& \cdots & w^{0\times (M-1)}\\ w^{1\times 0}& w^{1\times 1}& \cdots & w^{1\times (M-1)}\\ ⋮& ⋮& \ddots & ⋮\\ w^{(M-1)\times 0}& w^{(M-1)\times 1}& \cdots & w^{(M-1)\times (M-1)}\end{array}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i(\alpha /b)0/M\right)}\\ e^{\left(-2\pi i(\alpha /b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\end{array}\right).\end{array}$$

(44)

Here, we let

$$\{\begin{array}{l}{G}_0=w^{0\times 0}{L}^0+w^{1\times 0}{L}^{\frac{P}{M}}+\cdots +w^{\left(M-1\right)\times 0}{L}^{\frac{P\left(M-1\right)}{M}}\\ G_1=w^{0\times 1}{L}^0+w^{1\times 1}{L}^{\frac{P}{M}}+\cdots +w^{\left(M-1\right)\times 1}{L}^{\frac{P\left(M-1\right)}{M}}\\ G_2=w^{0\times 2}{L}^0+w^{1\times 2}{L}^{\frac{P}{M}}+\cdots +w^{\left(M-1\right)\times 2}{L}^{\frac{P\left(M-1\right)}{M}}\\ ⋮\\ G_{M-1}=w^{0\times \left(M-1\right)}{L}^0+w^{1\times \left(M-1\right)}{L}^{\frac{P}{M}}+\cdots +w^{\left(M-1\right)\times \left(M-1\right)}{L}^{\frac{P\left(M-1\right)}{M}}\end{array}$$

(45)

Definition 2.

A new reformulation of the definition of Tao et al.

$$\begin{array}{ll}{L}^{\alpha }& =\frac{1}{M}\left(G_0,G_1,\cdots ,G_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i(\alpha /b)0/M\right)}\\ e^{\left(-2\pi i(\alpha /b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k{e}^{-2\pi i(\alpha /b)k/M}}.\end{array}$$

(46)

We know that Tao et al. define the fractional power of the periodic matrix. Next, we will analyze the DFT and the discrete Hartley transform as examples.

4.1. DFT as Periodic Matrix

Proposition 3.

DFT is used as the periodic matrix, there are only four effective weighting terms for the definition of Tao et al.

Proof. 

The calculation of the fractional power of the matrix is applied to the eigenvalues, so eigenvalue decomposition of the matrix is required. Therefore, the eigendecomposition of the matrix can be expressed as

$$F=VD{V}^H,$$

(47)

where F is the matrix of the DFT, V is the eigenvector, and D is the eigenvalue.

In refs. [23,24], the eigenvalues of the DFT can be expressed as ${\lambda }_n=e^{n\pi i/2}$. Then, the possible values of the eigenvalue are ${\lambda }_r=\left\{1,-1,i,-i\right\}$ and $r=1,2,\cdots ,n$. In this way, the eigenvalue matrix D can be expressed as

$$D=\left(\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_n\end{array}\right).$$

(48)

Then, the fractional power operation of matrix F can be expressed as

$$F^{4l/M}=V{D}^{4l/M}{V}^H.$$

(49)

For L = F, Equation (45) can be expressed as

$$\begin{array}{ll}{G}_k& =w^{0\times k}I+w^{1\times k}\times F^{\frac{4}{M}}+\cdots +w^{\left(M-1\right)\times k}\times F^{\frac{4\left(M-1\right)}{M}}\\ & =w^{0\times k}V{D}^0{V}^H+w^{1\times k}V{D}^{4/M}{V}^H+\cdots +w^{\left(M-1\right)\times k}V{D}^{4\left(M-1\right)/M}{V}^H.\end{array}$$

(50)

Therefore, we can obtain

$$\begin{array}{ll}{G}_k& =V\left(w^{0\times k}\times D^0+w^{1\times k}\times D^{4/M}+\cdots +w^{\left(M-1\right)\times k}\times D^{4\left(M-1\right)/M}\right)V^H\\ & =V\left(\begin{array}{cccc}{w}^{0\times k}{\lambda }_1^0+w^{1\times k}{\lambda }_1^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_1^{4\left(M-1\right)/M}& 0& \cdots & 0\\ 0& w^{0\times k}{\lambda }_2^0+w^{1\times k}{\lambda }_2^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_2^{4\left(M-1\right)/M}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & w^{0\times k}{\lambda }_n^0+w^{1\times k}{\lambda }_n^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_n^{4\left(M-1\right)/M}\end{array}\right)V^H.\end{array}$$

(51)

Here, let

$$\{\begin{array}{c}{Q}_1\left(k\right)=w^{0\times k}{\lambda }_1^0+w^{1\times k}{\lambda }_1^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_1^{4\left(M-1\right)/M}\\ Q_2\left(k\right)=w^{0\times k}{\lambda }_2^0+w^{1\times k}{\lambda }_2^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_2^{4\left(M-1\right)/M}\\ ⋮\\ Q_n\left(k\right)=w^{0\times k}{\lambda }_n^0+w^{1\times k}{\lambda }_n^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_n^{4\left(M-1\right)/M}.\end{array}$$

(52)

Then, Equation (51) can be expressed as

$$G_k=V\left(\begin{array}{cccc}{Q}_1\left(k\right)& 0& \cdots & 0\\ 0& Q_2\left(k\right)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& Q_n\left(k\right)\end{array}\right)V^H.$$

(53)

The multiplicities of the DFT eigenvalues are shown in Table 1. Therefore, from Equation (17), we obtain

$$\begin{array}{ll}{\lambda }_r& =\left\{1,i,-1,-i\right\}\\ & =\left\{e^{0\pi i/2},e^{\pi i/2},e^{2\pi i/2},e^{3\pi i/2}\right\}.\end{array}$$

(54)

For the sake of simplicity, Equation (52) can be expressed as

$$Q_r\left(k\right)=w^{0\times k}{\lambda }_r^0+w^{1\times k}{\lambda }_r^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_r^{4\left(M-1\right)/M};$$

(55)

$$r=1,2,\cdots ,n.$$

When the eigenvalues ${\lambda }_r=e^{0\pi i/2}=1$ and $w=e^{2\pi i/M}$, $Q_r^{\left(1\right)}\left(k\right)$ can be expressed using Equation (55) as

$$\begin{array}{ll}{Q}_r^{\left(1\right)}\left(k\right)& =w^{0\times k}{\lambda }_r^0+w^{1\times k}{\lambda }_r^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_r^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1k/M}+e^{2\pi i2k/M}+\cdots +e^{2\pi i\left(M-1\right)k/M}\\ & =\frac{1-{\left(e^{2\pi ik/M}\right)}^M}{1-e^{2\pi ik/M}}.\end{array}$$

(56)

Therefore, we obtain

$$Q_r^{\left(1\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=0\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(57)

When the eigenvalue ${\lambda }_r=e^{\pi i/2}=i$, $Q_r^{\left(i\right)}\left(k\right)$, can be expressed using Equation (55) as

$$\begin{array}{ll}{Q}_r^{\left(i\right)}\left(k\right)& =w^{0\times k}{\lambda }_r^0+w^{1\times k}{\lambda }_r^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_r^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1\left(k+1\right)/M}+e^{2\pi i2\left(k+1\right)/M}+\cdots +e^{2\pi i\left(M-1\right)\left(k+1\right)/M}\\ & =\frac{1-{\left(e^{2\pi i\left(k+1\right)/M}\right)}^M}{1-e^{2\pi i\left(k+1\right)/M}}.\end{array}$$

(58)

Therefore,

$$Q_r^{\left(i\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=M-1\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(59)

When the eigenvalue ${\lambda }_r=e^{2\pi i/2}=-1$, $Q_r^{\left(-1\right)}\left(k\right)$ can be expressed using Equation (55) as

$$\begin{array}{ll}{Q}_r^{\left(-1\right)}\left(k\right)& =w^{0\times k}{\lambda }_r^0+w^{1\times k}{\lambda }_r^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_r^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1\left(k+2\right)/M}+e^{2\pi i2\left(k+2\right)/M}+\cdots +e^{2\pi i\left(M-1\right)\left(k+2\right)/M}\\ & =\frac{1-{\left(e^{2\pi i\left(k+2\right)/M}\right)}^M}{1-e^{2\pi i\left(k+2\right)/M}}.\end{array}$$

(60)

Then, we can obtain

$$Q_r^{\left(-1\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=M-2\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(61)

When the eigenvalue ${\lambda }_r=e^{3\pi i/2}=-i$, $Q_r^{\left(-i\right)}\left(k\right)$ can be expressed using Equation (55) as

$$\begin{array}{ll}{Q}_r^{\left(-i\right)}\left(k\right)& =w^{0\times k}{\lambda }_r^0+w^{1\times k}{\lambda }_r^{4/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_r^{4\left(M-1\right)/M}\\ & =1+e^{2\pi i1\left(k+3\right)/M}+e^{2\pi i2\left(k+3\right)/M}+\cdots +e^{2\pi i\left(M-1\right)\left(k+3\right)/M}\\ & =\frac{1-{\left(e^{2\pi i\left(k+3\right)/M}\right)}^M}{1-e^{2\pi i\left(k+3\right)/M}}.\end{array}$$

(62)

Therefore,

$$Q_r^{\left(-i\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=M-3\\ 0,& otherwise\end{array};\hspace{1em}k=0,1,\cdots ,M-1$$

(63)

Using Equations (57), (59), (61) and (63), we can formulate Equation (45) as

$$G_k=\{\begin{array}{ll}{G}_k,& for k=0,M-3,M-2,M-1\\ 0,& for k=1,2,\cdots ,M-4.\end{array}$$

(64)

In this way, the definition of Tao et al. can be expressed as

$$\begin{array}{ll}{L}^{\alpha }& =\frac{1}{M}\left(G_0,G_1,\cdots ,G_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i(\alpha /b)0/M\right)}\\ e^{\left(-2\pi i(\alpha /b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}\left(G_0,G_1,\cdots ,G_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i(\alpha /b)0/M\right)}\\ e^{\left(-2\pi i(\alpha /b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}\left(G_0,0,\cdots ,0,G_{M-3},G_{M-2},G_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i(\alpha /b)0/M\right)}\\ e^{\left(-2\pi i(\alpha /b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}\left(G_0{e}^{\left(-2\pi i(\alpha /b)0/M\right)}+G_{M-3}{e}^{\left(-2\pi i(\alpha /b)\left(M-3\right)/M\right)}+G_{M-2}{e}^{\left(-2\pi i(\alpha /b)\left(M-2\right)/M\right)}+G_{M-1}{e}^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\right).\end{array}$$

(65)

□

Remark 3.

The DFT matrix has a period of 4, and the definition of Tao et al. has only four effective weighting terms, as shown in Equation (65).

4.2. Discrete Hartley Transform as Periodic Matrix

Proposition 4.

Discrete Hartley transform is used as the periodic matrix, there are only four effective weighting terms for the definition of Tao et al.

Proof. 

We use the discrete Hartley transform as an example to verify the definition of Tao et al. The discrete Hartley transform [25] can be expressed as

$$H=\frac{1}{\sqrt{N}}\left[\cos \left(\frac{2\pi mn}{N}\right)+\sin \left(\frac{2\pi mn}{N}\right)\right].$$

(66)

The Hartley matrix has a period of 2, L = H and Equation (45) can be expressed as

$$\begin{array}{ll}{G}_k& =w^{0\times k}{L}^0+w^{1\times k}{L}^{\frac{P}{M}}+\cdots +w^{\left(M-1\right)\times k}{L}^{\frac{P\left(M-1\right)}{M}}\\ & =w^{0\times k}{H}^0+w^{1\times k}{H}^{\frac{2}{M}}+\cdots +w^{\left(M-1\right)\times k}{H}^{\frac{2\left(M-1\right)}{M}}.\end{array}$$

(67)

where $k=0,1,\cdots ,M-1$ and $w=\exp \left(2\pi i/M\right)$. The fractional power of the Hartley matrix can be expressed as

$$H^{2l/M}=V{D}^{2l/M}{V}^H,$$

(68)

where $l=0,1,\cdots ,M-1$; $D$ is the eigenvalue matrix and $V$ is the eigenvector. Therefore, Equation (67) can be expressed as

$$\begin{array}{ll}{G}_k& =V\left(w^{0\times k}\times D^0+w^{1\times k}\times D^{2/M}+\cdots +w^{\left(M-1\right)\times k}\times D^{2\left(M-1\right)/M}\right)V^H\\ & =V\left(\begin{array}{cccc}{w}^{0\times k}{\lambda }_1^0+w^{1\times k}{\lambda }_1^{2/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_1^{2\left(M-1\right)/M}& 0& \cdots & 0\\ 0& w^{0\times k}{\lambda }_2^0+w^{1\times k}{\lambda }_2^{2/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_2^{2\left(M-1\right)/M}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & w^{0\times k}{\lambda }_n^0+w^{1\times k}{\lambda }_n^{2/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_n^{2\left(M-1\right)/M}\end{array}\right)V^H.\end{array}$$

(69)

The eigenvalues of the Hartley matrix are {1, −1} [25], and the weighted sum of the diagonal matrix of Equation (69) can be expressed as

$$E^{\left(1\right)}\left(k\right)=w^{0\times k}{\left(1\right)}^0+w^{1\times k}{\left(1\right)}^{2/M}+\cdots +w^{\left(M-1\right)\times k}{\left(1\right)}^{2\left(M-1\right)/M},$$

(70)

or

$$E^{\left(-1\right)}\left(k\right)=w^{0\times k}{\left(-1\right)}^0+w^{1\times k}{\left(-1\right)}^{2/M}+\cdots +w^{\left(M-1\right)\times k}{\left(-1\right)}^{2\left(M-1\right)/M},$$

(71)

where $k=0,1,\cdots ,M-1$. From Equation (70), we can obtain

$$E^{\left(1\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=0\\ 0,& otherwise\end{array}$$

(72)

and from Equation (71), we can obtain

$$E^{\left(-1\right)}\left(k\right)=\{\begin{array}{ll}M,& if k=M-1\\ 0,& otherwise\end{array}$$

(73)

Then, Equation (67) is determined as

$$G_k=\{\begin{array}{ll}{G}_k,& for k=0,M-1\\ 0,& for k=1,2,3,\cdots ,M-2.\end{array}$$

(74)

From Equation (46), the definition of Tao et al. can be expressed as

$$\begin{array}{ll}{L}^{\alpha }& =\frac{1}{M}\left(G_0,G_1,\cdots ,G_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i(\alpha /b)0/M\right)}\\ e^{\left(-2\pi i(\alpha /b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}\left(G_0,0,\cdots ,0,G_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i(\alpha /b)0/M\right)}\\ e^{\left(-2\pi i(\alpha /b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}\left(G_0{e}^{\left(-2\pi i(\alpha /b)0/M\right)}+G_{M-1}{e}^{\left(-2\pi i(\alpha /b)\left(M-1\right)/M\right)}\right).\end{array}$$

(75)

□

Remark 4.

The Hartley matrix has a period of 2, so there are only two effective weighted terms for the definition of Tao et al. Therefore, from Equations (65) and (75), we judge that the effective weighting term defined by Tao et al. is related to the period of the matrix. InSection 5, we will prove and explain the security risk of key invalidation when this definition is applied to image encryption.

5. Discussion

5.1. Effective Weighted Terms Analysis

The definition of Tao et al. is the general form of the definition of Yeh et al. Tao et al. proposed that the fractional power of any periodic diagonalizable matrix can be expressed as Equation (42). However, our analysis in Section 4 shows that some weighting terms defined by Tao et al. are invalid, such as the weighted sum of the fractional powers of the DFT, which has only four effective weighted terms from Equation (65). We use the fractional power of the discrete Hartley transform to verify that the effective weighting terms are only two terms from Equation (75). Therefore, we judge that the effective weighting terms in the definition of Tao et al. are related to the period of the matrix.

Theorem 1.

The effective weighting terms of the Weighted fractional-order transform depend on the period of the matrix.

Assumption 1.

The$N\times N$matrix$L$is a periodic matrix satisfying$L^P=I$and its eigendecomposition form be$L=VD{V}^H$.

Assumption 2.

The eigenvalues of the periodic matrix$L$satisfy${\lambda }^P=1$, and these P eigenvalues can be expressed as$\lambda =\left\{e^{2\pi i0/P},e^{2\pi i1/P},\cdots ,e^{2\pi i\left(P-1\right)/P}\right\}$.

Proof. 

The eigenvalue can be expressed as

$${\lambda }_h=e^{2\pi ih/P},$$

(76)

where $h=0,1,\cdots ,P-1.$ Therefore, Equation (45) can be expressed as

$$\begin{array}{ll}{G}_k& =w^{0\times k}{L}^0+w^{1\times k}\times L^{\frac{P}{M}}+\cdots +w^{\left(M-1\right)\times k}\times L^{\frac{P\left(M-1\right)}{M}}\\ & =w^{0\times k}V{D}^0{V}^H+w^{1\times k}V{D}^{P/M}{V}^H+\cdots +w^{\left(M-1\right)\times k}V{D}^{P\left(M-1\right)/M}{V}^H.\end{array}$$

(77)

Equation (77) can be further expressed as

$$\begin{array}{ll}{G}_k& =V\left(w^{0\times k}\times D^0+w^{1\times k}\times D^{P/M}+\cdots +w^{\left(M-1\right)\times k}\times D^{P\left(M-1\right)/M}\right)V^H\\ & =V\left(\begin{array}{cccc}{w}^{0\times k}{\lambda }_1^0+w^{1\times k}{\lambda }_1^{P/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_1^{P\left(M-1\right)/M}& 0& \cdots & 0\\ 0& w^{0\times k}{\lambda }_2^0+w^{1\times k}{\lambda }_2^{P/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_2^{P\left(M-1\right)/M}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & w^{0\times k}{\lambda }_n^0+w^{1\times k}{\lambda }_n^{P/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_n^{P\left(M-1\right)/M}\end{array}\right)V^H.\end{array}$$

(78)

where the eigenvalues ${\lambda }_n\in \left\{e^{2\pi i0/P},e^{2\pi i1/P},\cdots ,e^{2\pi i\left(P-1\right)/P}\right\}$. Therefore, the weighted sum of the diagonal matrix in Equation (77) can be expressed as

$$D_h\left(k\right)=w^{0\times k}{\lambda }_h^0+w^{1\times k}{\lambda }_h^{P/M}+\cdots +w^{\left(M-1\right)\times k}{\lambda }_h^{P\left(M-1\right)/M},$$

(79)

where ${\lambda }_h=e^{2\pi ih/P}$ with $h=0,1,\cdots ,P-1$. Then, we obtain

$$\begin{array}{ll}{D}_h\left(k\right)& ={\displaystyle \sum _{l=0}^{M-1}{w}^{lk}{\lambda }_h^{Pl/M}}\\ & ={\displaystyle \sum _{l=0}^{M-1}{e}^{2\pi ilk/M}{e}^{2\pi ilh/M}}\\ & ={\displaystyle \sum _{l=0}^{M-1}{e}^{2\pi il\left(k+h\right)/M}},\end{array}$$

(80)

where $k=0,1,\cdots ,M-1$. For $P<M$, Equation (80) can be written as

$$D_h\left(k\right)=\{\begin{array}{ll}M,& for k\equiv \left(M-h\right)\mathrm{mod}M\\ 0,& for k\cancel{\equiv }\left(M-h\right)\mathrm{mod}M\end{array}$$

(81)

Then, Equation (77) is expressed as

$$G_k=\{\begin{array}{ll}{G}_k,& if k=0,M-P+1,M-P+2,\cdots ,M-1\\ 0,& otherwise\end{array}$$

(82)

□

Remark 5.

Equation (46) has only P effective weighting terms. Therefore, the effective weighting terms depend on the period of the matrix. This explains our analysis in Section 4.1 and Section 4.2. Since the DFT has a period of 4, it explains that there are only four effective weighting terms in Section 3.

5.2. Security Analysis

Kang et al. extended the definitions of Yeh et al. and Tao et al., and proposed a unified framework for multiple-parameter discrete fractional-order transforms (MPDFRT) [22]. This undoubtedly provides ideas for the further application of the weighted fractional-order transform based on the periodic matrix, especially for the security of image encryption [26]. However, with the help of our research in Section 5.1, the results indicate that the theoretical framework of Kang et al. cannot provide better security.

Therefore, we refer to the theoretical framework of II MPDFRT, and assume that L is a periodic matrix satisfying $L^P=I$ and the type II MPDFRT operator is defined as

$$L_{\mathrm{II}}^{\overline{\alpha }}={\displaystyle \sum _{n=0}^{M-1}{C}_{n,\overline{\alpha }/b}{L}^{nb}},$$

(83)

where $b=P/M$. In Equation (83), the vector parameter $\overline{\alpha }=\left\{{\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_{N-1}\right\}$; if ${\alpha }_0={\alpha }_1=\cdots ={\alpha }_{N-1}=\alpha$, then Equation (42) is obtained. It is not difficult to find that the definition of Kang et al. is an extended form of the definition of Tao et al., and its weighted term $C_{n,\overline{\alpha }/b}$ can be expressed as

$$\begin{array}{ll}{C}_{n,\overline{\alpha }/b}& =\frac{1}{M}\frac{1-e^{2\pi i\left(n-\overline{\alpha }/b\right)}}{1-e^{\left(2\pi i/M\right)\left(n-\overline{\alpha }/b\right)}}\\ & =IDFT{\left[e^{\left(-2\pi i({\alpha }_k/b)k/M\right)}\right]}_{k=0,1,2,\cdots \cdots ,M-1}\end{array}$$

(84)

where $n=0,1,2,\cdots ,M-1$. Equation (84) can be further expressed as

$$\left(\begin{array}{c}{C}_{0,\overline{\alpha }/b}\\ C_{1,\overline{\alpha }/b}\\ ⋮\\ C_{M-1,\overline{\alpha }/b}\end{array}\right)=\frac{1}{M}\left(\begin{array}{cccc}{w}^{0\times 0}& w^{0\times 1}& \cdots & w^{0\times (M-1)}\\ w^{1\times 0}& w^{1\times 1}& \cdots & w^{1\times (M-1)}\\ ⋮& ⋮& \ddots & ⋮\\ w^{(M-1)\times 0}& w^{(M-1)\times 1}& \cdots & w^{(M-1)\times (M-1)}\end{array}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i({\alpha }_0/b)0/M\right)}\\ e^{\left(-2\pi i({\alpha }_1/b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i({\alpha }_{M-1}/b)\left(M-1\right)/M\right)}\end{array}\right).$$

(85)

where $w=\exp \left(2\pi i/M\right)$. Thus, Equation (83) can be expressed as

$$\begin{array}{ll}{L}_{\mathrm{II}}^{\overline{\alpha }}& ={\displaystyle \sum _{n=0}^{M-1}{C}_{n,\overline{\alpha }/b}{L}^{nP/M}}\\ & =\left(L^0,L^{P/M},\cdots ,L^{P\left(M-1\right)/M}\right)\left(\begin{array}{c}{C}_{0,\overline{\alpha }/b}\\ C_{1,\overline{\alpha }/b}\\ ⋮\\ C_{M-1,\overline{\alpha }/b}\end{array}\right)\\ & =\frac{1}{M}\left(L^0,L^{P/M},\cdots ,L^{P\left(M-1\right)/M}\right)\left(\begin{array}{cccc}{w}^{0\times 0}& w^{0\times 1}& \cdots & w^{0\times (M-1)}\\ w^{1\times 0}& w^{1\times 1}& \cdots & w^{1\times (M-1)}\\ ⋮& ⋮& \ddots & ⋮\\ w^{(M-1)\times 0}& w^{(M-1)\times 1}& \cdots & w^{(M-1)\times (M-1)}\end{array}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i({\alpha }_0/b)0/M\right)}\\ e^{\left(-2\pi i({\alpha }_1/b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i({\alpha }_{M-1}/b)\left(M-1\right)/M\right)}\end{array}\right).\end{array}$$

(86)

From Equation (45), we can obtain

$$G_k=w^{0\times k}{L}^0+w^{1\times k}{L}^{\frac{P}{M}}+\cdots +w^{\left(M-1\right)\times k}{L}^{\frac{P\left(M-1\right)}{M}}.$$

(87)

where $k=0,1,\cdots ,M-1$.

Definition 3.

A new reformulation of the definition of Kang et al.

$$\begin{array}{ll}{L}_{\mathrm{II}}^{\overline{\alpha }}& =\frac{1}{M}\left(G_0,G_1,\cdots ,G_{M-1}\right)\left(\begin{array}{c}{e}^{\left(-2\pi i({\alpha }_0/b)0/M\right)}\\ e^{\left(-2\pi i({\alpha }_1/b)1/M\right)}\\ ⋮\\ e^{\left(-2\pi i({\alpha }_{M-1}/b)\left(M-1\right)/M\right)}\end{array}\right)\\ & =\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k{e}^{-2\pi i({\alpha }_k/b)k/M}}.\end{array}$$

(88)

where$G_k$is the same as Equation (82). Thus, Equation (88) has only P effective weighting terms. Because$b=P/M$, Equation (88) can be further expressed as

$$\begin{array}{ll}{L}_{\mathrm{II}}^{\overline{\alpha }}& =\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k{e}^{-2\pi i{\alpha }_{k}k/P}}\\ & =\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k{X}_k}.\end{array}$$

(89)

where$X_k=e^{-2\pi i{\alpha }_{k}k/P}$.

The theoretical framework of II MPDFRT is proposed in [22]; these transforms include multiple-parameter discrete fractional-order Fourier transforms (MPDFRFT), multiple-parameter discrete fractional-order cosine transforms (MPDFRCT), multiple-parameter discrete fractional-order sine transforms (MPDFRST), multiple-parameter discrete fractional-order Hartley transforms (MPDFRHT), and multiple-parameter discrete fractional-order Hadamard transforms (MPDFRHaT). In our study, these definitions can be easily defined by Equation (89).

(a)

MPDFRFT

The MPDFRFT is proposed in Ref. [22]. According to our reformulation process, the MPDFRFT can be redefined. Here, $L=F$ ($F$ denotes the Fourier matrix, and $F^4=I$), and period $P=4$, we let

$$X_k=\exp \left[-j\left(\pi /2\right){\alpha }_{k}k\right].$$

(90)

Therefore, the MPDFRFT is redefined as

$$F^{\overline{\alpha }}=\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k^F{X}_k}.$$

(91)

For Equation (87), when L = F, $G_k^F$ is obtained.

(b)

MPDFRCT

The MPDFRCT is proposed in ref. [22]. Ref. [27] presents four types of discrete cosine transform (DCT) kernel matrices, where the DCT-I ($C_N^{{\rm I}}=\sqrt{\frac{2}{N-1}}\left[k_m{k}_n\cos \left(\frac{mn\pi }{N-1}\right)\right]$) kernel is a symmetric-structured periodic matrix with period 2. Here $m,n=0,1,\cdots ,N-1$, and $k_m$ and $k_n$ are defined as

$$k_m=\{\begin{array}{ll}\frac{1}{\sqrt{2}},& m=0 and m=N\\ 1,& other.\end{array},$$

(92)

we let

$$X_k=\exp \left(-j\pi {\alpha }_{k}k\right).$$

(93)

Then, the MPDFRCT is redefined:

$$C^{\overline{\alpha }}=\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k^C{X}_k}.$$

(94)

For Equation (87), when $L=C_N^{\mathrm{I}}$, $G_k^C$ is obtained.

(c)

MPDFRST

Like the DCT, the discrete sine transform (DST) has four definitions [27]. The DST-I ($S_N^{\mathrm{I}}=\sqrt{\frac{2}{N+1}}\left[\sin \left(\frac{mn\pi }{N+1}\right)\right]$) kernel is a symmetric-structured periodic matrix with period 2. Therefore, $L=S_N^{\mathrm{I}}$ with period 2. $X_k$ is the same as Equation (93), so the MPDFRST is redefined as

$$S^{\overline{\alpha }}=\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k^S{X}_k}.$$

(95)

For Equation (87), when $L=S_N^{\mathrm{I}}$, $G_k^S$ is obtained.

(d)

MPDFRHT

MPDFRHT is defined in ref. [22], where the discrete Hartley transform (DHT) [25] is

$$H=\frac{1}{\sqrt{N}}\left[\cos \left(\frac{2\pi mn}{N}\right)+\sin \left(\frac{2\pi mn}{N}\right)\right].$$

(96)

Here, $L=H$ with period 2. Here, $X_k$ is the same as Equation (93), and the MPDFRHT is redefined as

$$H^{\overline{\alpha }}=\frac{1}{M}{\displaystyle \sum _{k=0}^{M-1}{G}_k^H{X}_k}.$$

(97)

For Equation (87), when $L=H$, $G_k^H$ is obtained.

(e)

MPDFRHaT

A Hadamard matrix is a symmetric matrix whose elements are the real numbers 1 and −1. The rows (and columns) of a Hadamard matrix are mutually orthogonal [28]. The normalized Hadamard matrices of order $2^n$, denoted by $H{a}_n$, can be defined recursively:

$$H{a}_1=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right], H{a}_{n+1}=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}H{a}_n& H{a}_n\\ H{a}_n& H{a}_n\end{array}\right]; n\ge 1$$

(98)

We make $L=H{a}_n$ with period 2, and $X_k$ is the same as Equation (93), therefore the MPDFRHaT is redefined:

$$H{a}^{\overline{\alpha }}=\frac{1}{N}{\displaystyle \sum _{k=0}^{N-1}{G}_k^{Ha}{X}_k}.$$

(99)

For Equation (87), when $L=Ha$, $G_k^{Ha}$ is obtained.

Remark 6.

The transforms a–e involved here are proposed in [22]. However, definitions a–e are easy to present with the help of our reformulation. In our new reformulation, the effective weighting terms depend on the period of the matrix. For example, the base matrix L = F of MPDFRFT with period 4, so there are only four effective weighting terms. The parameter $\overline{\alpha }=\left({\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_{M-1}\right)$ is the main key of the system. From Equation (91), it is not difficult to find that the valid keys are only $\left({\alpha }_0,{\alpha }_{M-3},{\alpha }_{M-2},{\alpha }_{M-1}\right)$. Furthermore, when $k=0$, ${\alpha }_0$ is also invalid, and only $\left({\alpha }_{M-3},{\alpha }_{M-2},{\alpha }_{M-1}\right)$ are valid. MPDFRCT, MPDFRST, MPDFRHT and MPDFRHaT have the base matrix with period 2, which has only two effective weighting terms. It is not difficult to find that the valid keys are only $\left({\alpha }_0,{\alpha }_{M-1}\right)$. Furthermore, when $k=0$, ${\alpha }_0$ is also invalid, and only ${\alpha }_{M-1}$ are valid.

Therefore, we take MPDFRHaT as an example for numerical verification analysis, and the code is shown in the Appendix A. M is a positive integer greater than or equal to 4. For example, if M = 6, there are 6 weighting terms and the vector parameters $\overline{\alpha }=\left({\alpha }_0,{\alpha }_1,\cdots ,{\alpha }_5\right)$. The size of the image is selected as 256 × 256, so N = 256.

The image encryption/decryption based on MPDFRHaT is shown in Figure 2, and Figure 2a is the original image (plaintext). We set the encryption keys as:

$$\left(M;{\alpha }_0,{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5\right)=\left(6;\sqrt{31},\sqrt{5},\sqrt{13},\sqrt{33},\sqrt{27},\sqrt{2}\right)$$

the encrypted image (ciphertext) is shown in Figure 2b, and the plaintext is encrypted into a noise image. Therefore, the decryption keys are

$$\left(M;-{\alpha }_0,-{\alpha }_1,-{\alpha }_2,-{\alpha }_3,-{\alpha }_4,-{\alpha }_5\right)=\left(6;-\sqrt{31},-\sqrt{5},-\sqrt{13},-\sqrt{33},-\sqrt{27},-\sqrt{2}\right)$$

the decrypted image is shown in Figure 2c. The image is restored losslessly, because decryption process is equivalent to the inverse transformation of MPDFRHaT. To verify the validity of the keys, the wrong decryption keys are selected,

$$\left(M;-{\alpha }_0,-{\alpha }_1,-{\alpha }_2,-{\alpha }_3,-{\alpha }_4,-{\alpha }_5\right)=\left(6;-\sqrt{8},-\sqrt{28},-\sqrt{33},-\sqrt{17},-\sqrt{10},-\sqrt{2}\right)$$

where the keys ${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ and ${\alpha }_4$ are wrong. The decrypted result is shown in Figure 2d, and the original image is well restored. This verifies our above analysis results. Because the weighted terms with the keys (${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ and ${\alpha }_4$) are invalid, these keys are also invalid. This shows that the keys (${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ and ${\alpha }_4$) have no effect on the encryption/decryption process, regardless of the value. The wrong decryption key is selected again,

$$\left(M;-{\alpha }_0,-{\alpha }_1,-{\alpha }_2,-{\alpha }_3,-{\alpha }_4,-{\alpha }_5\right)=\left(6;-\sqrt{31},-\sqrt{5},-\sqrt{13},-\sqrt{33},-\sqrt{27},-\sqrt{11}\right)$$

where the key ${\alpha }_5$ is wrong. The decryption result is shown in Figure 2e, and no information about the original image is obtained. This indicates that the key ${\alpha }_5$ is valid.

Figure 2. Encryption/decryption based on the MPDFRHaT: (a) plaintext, (b) ciphertext, (c) decrypted image with the correct keys, (d) decrypted image with the wrong keys (${\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$ and ${\alpha }_4$), (e) decrypted image with the wrong key ${\alpha }_5$.

A numerical simulation also verified that many keys are invalid for the image encryption based on MPDFRHaT, which again supports our hypothesis. This security risk comes from the periodicity of the basis matrix. Strictly speaking, the period of the matrix determines the number of weighted terms of the weighted fractional-order transform. This discovery provides an important reference for future research.

6. Conclusions

In this paper, we propose a reformulation of the definition of Yeh et al., and the eigendecomposition type FRFT and the weighted type FRFT are verified. The results show that there are only four effective weighting terms. Furthermore, we determine that the definition of Tao et al. is an extended definition for that of Yeh et al., and propose a reformulation of the former. The fractional power of the DFT and the fractional power of the discrete Hartley transform are verified, and the results show that the effective weighting terms are defined as four terms and two terms, respectively. We perform a further analysis, and the results show that the effective weighting terms depend on the period of the matrix, which will lead to the security risk of key invalidation. Therefore, we propose a reformulation of the unified framework for MPDFRT, and determine that many keys are invalid for image encryption. Finally, we take MPDFRHaT as an example to verify that there is only one valid key, with other keys being invalid. Our observations prove once again that the effective weighting terms of the weighted fractional-order transform based on the periodic matrix depend on the period of the matrix, which will lead to the security risk of key invalidation for image encryption.