Adaptive Proportional Integral Robust Control of an Uncertain Robotic Manipulator Based on Deep Deterministic Policy Gradient
Abstract
:1. Introduction
- Considering the uncertainty and time-varying disturbance of the dynamic model of the n-link robot manipulator system and the influence of friction resistance, the adaptive robust term is used to compensate for the uncertainty of the system. An adaptive PIR control method based on the DDPG is proposed, which has good adaptability and high-precision trajectory tracking ability for the uncertainty of the n-link robot manipulator system.
- A reward function combining a Gaussian function and the Euclidean distance is proposed, which can ensure the reinforcement learning agent learns efficiently and stably and can effectively avoid a convergence of the deep neural network to the local optimal problem.
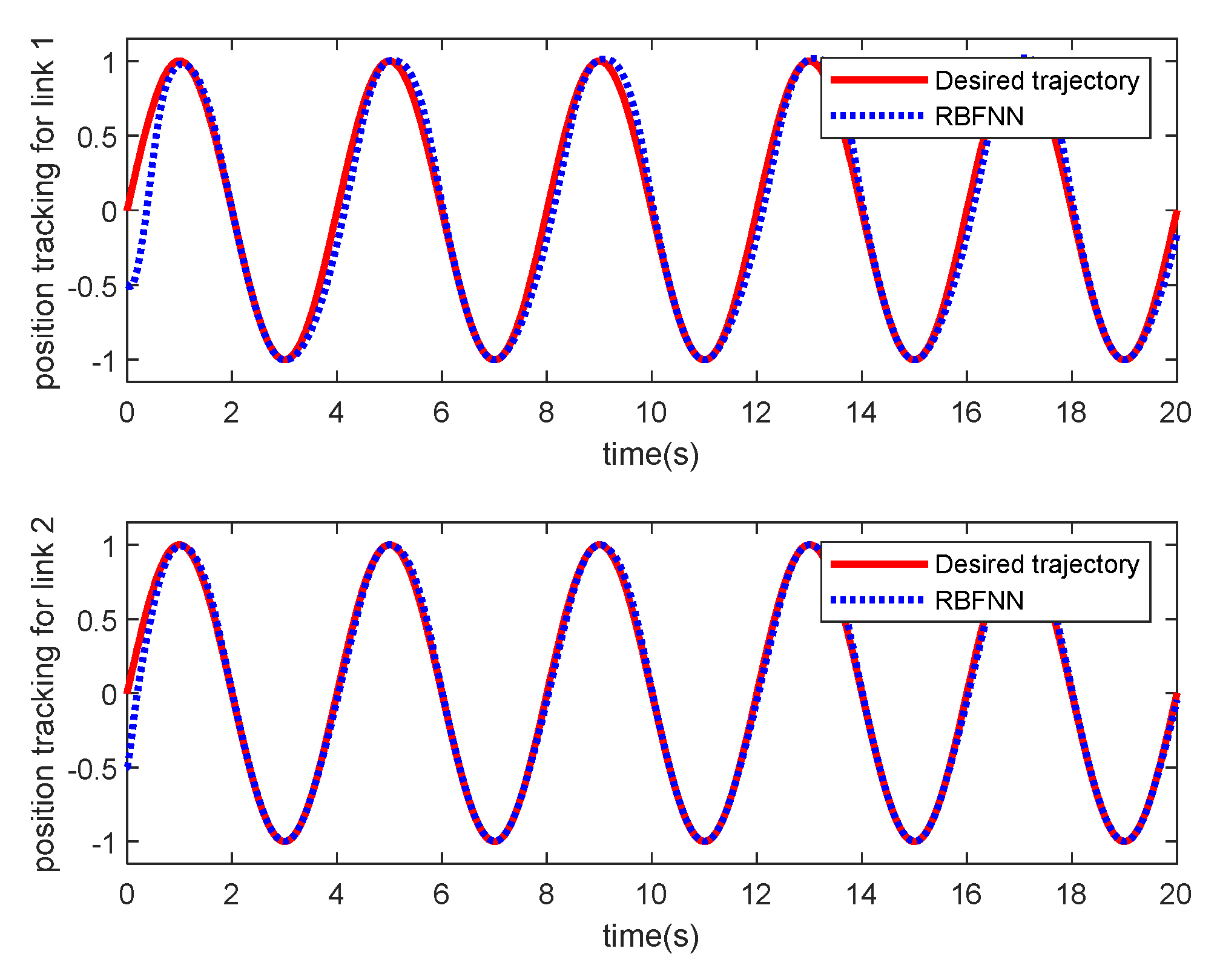
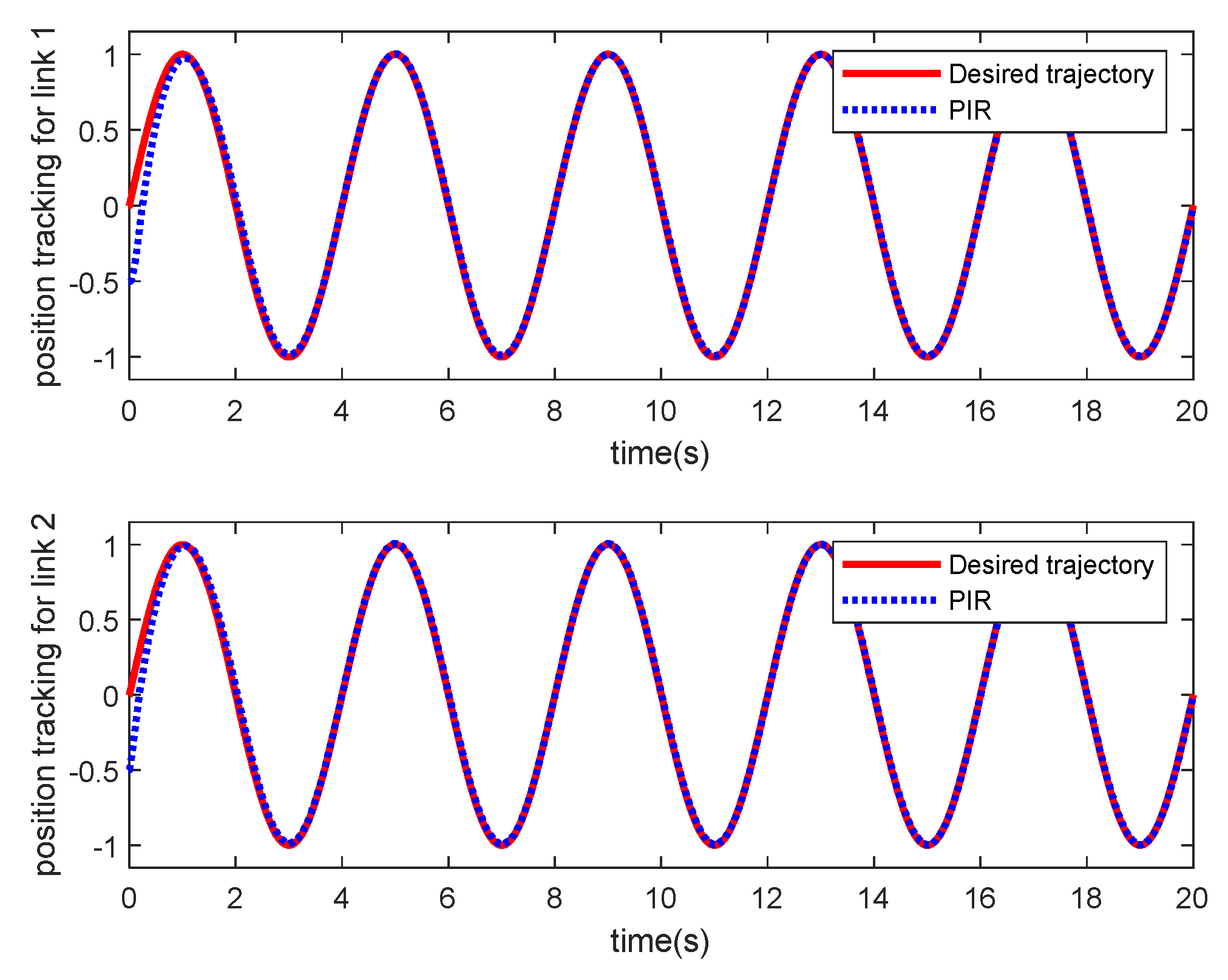
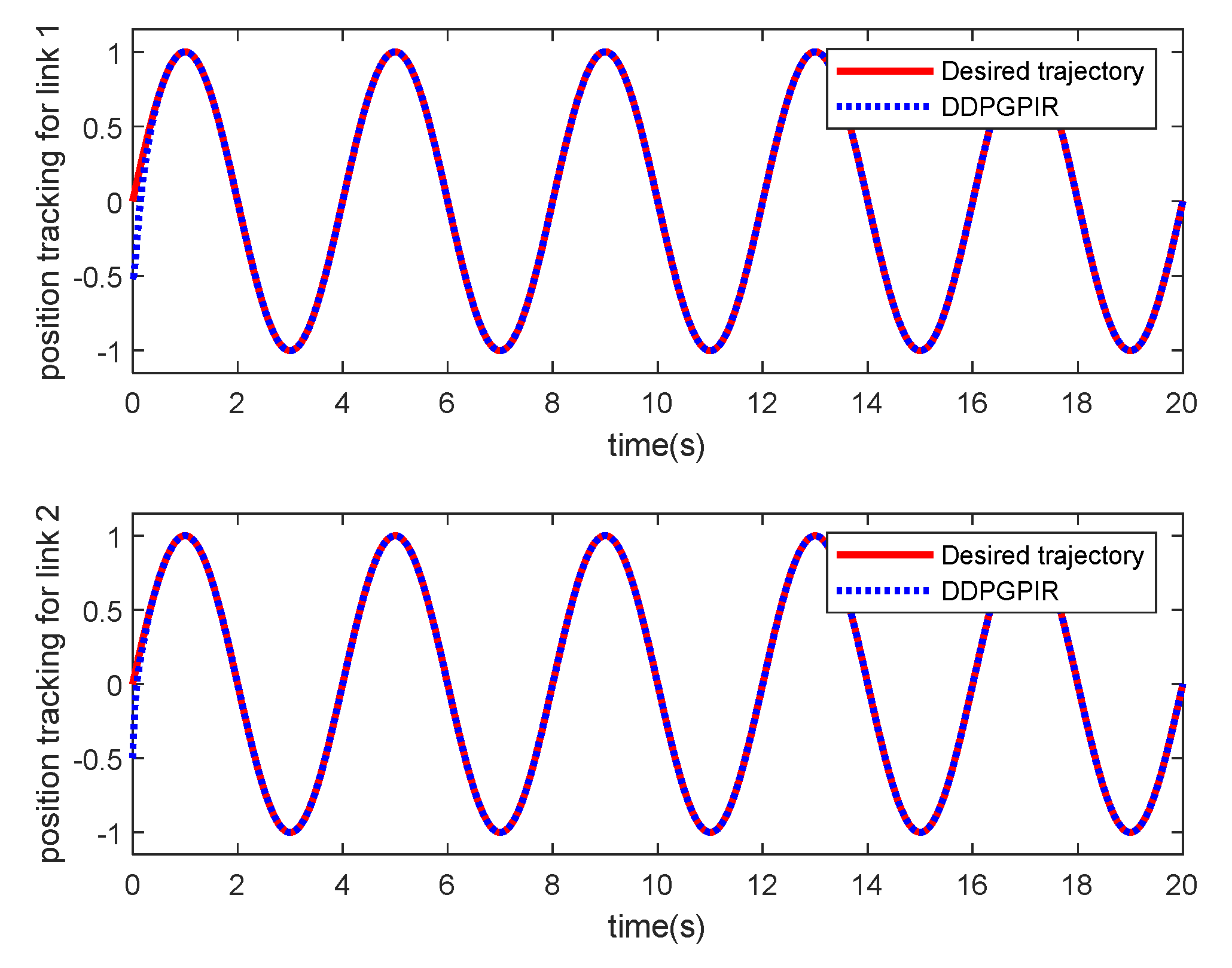
- Taking a two-link robotic manipulator as an example, the simulation results show that the proposed method is effective compared with an adaptive control based on radial basis function neural network (RBFNN) approximation and PIR control with fixed parameters.
2. Dynamic Model of the n-Link Robot Manipulator
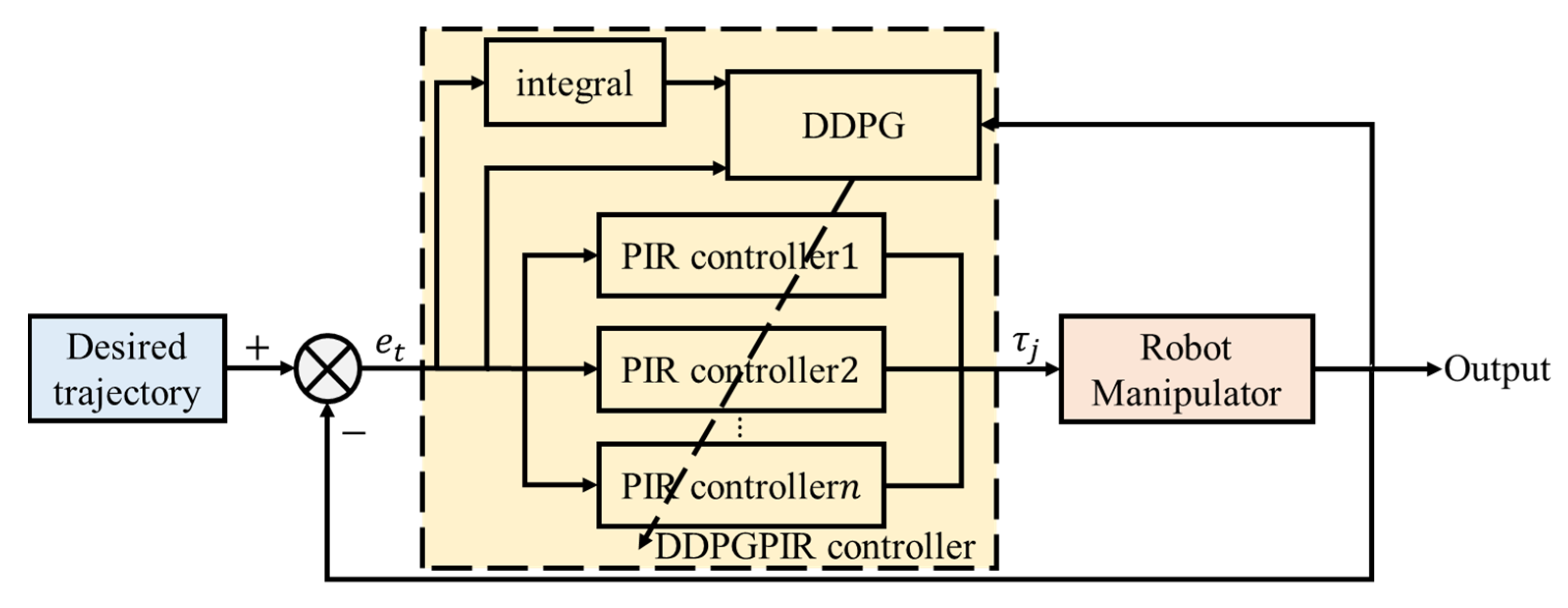
3. DDPGPIR Control Design
3.1. PIR Control Design
3.2. Reinforcement Learning and Policy Gradient Method
3.3. DDPG Adaptive PIR Control
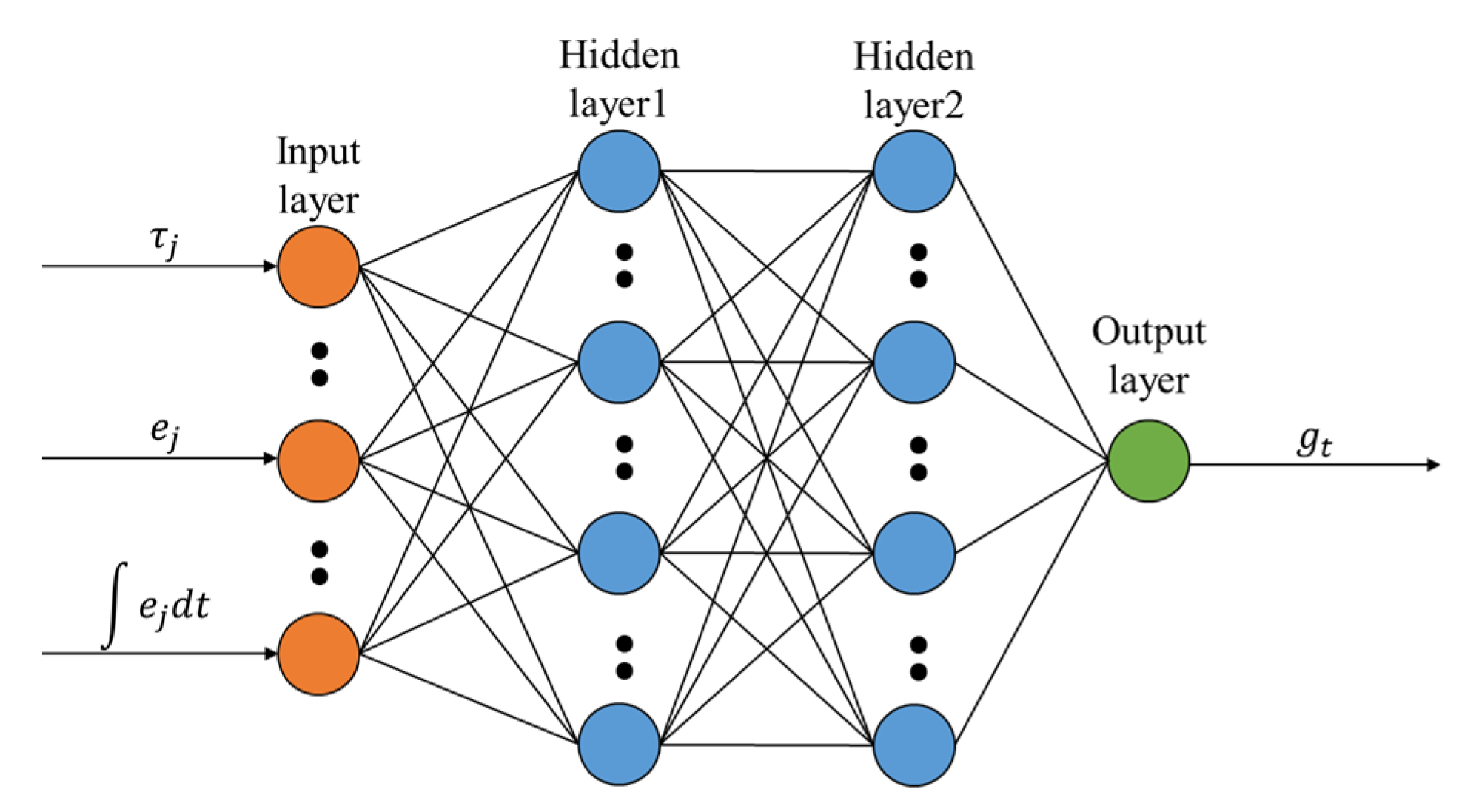
3.4. Network Design of DDPGPIR
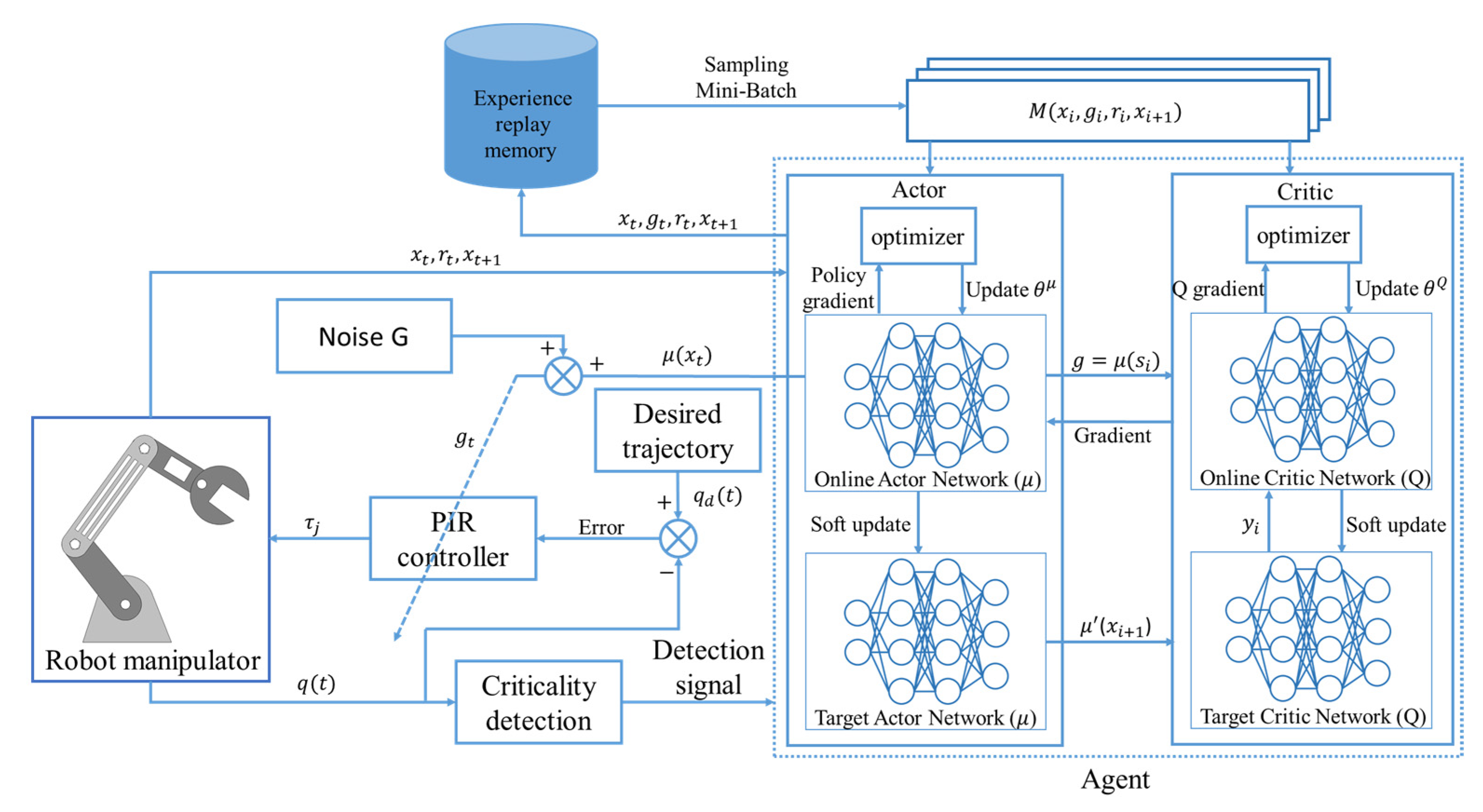
3.5. Learning Process of DDPGPIR
| Algorithm 1. DDPGPIR Algorithm. |
| Initialize the critic network and the actor network |
| Initialize the target network and with the same weights |
| Initialize replay memory |
| Initialize Gaussian noise |
| for episode = do |
| Receive initial observation state |
| for do |
| select action |
| select execution action |
| if |
| reject and add a negative number to |
| else: |
| execute and get observed reward and observe new state |
| store transition in |
| sample mini-batch of transitions from |
| set |
| update critic according to Equations and |
| update actor according to Equation |
| update the target networks according to Equation |
| end for |
| end for |
3.6. Reward Function
4. Experiment and Results
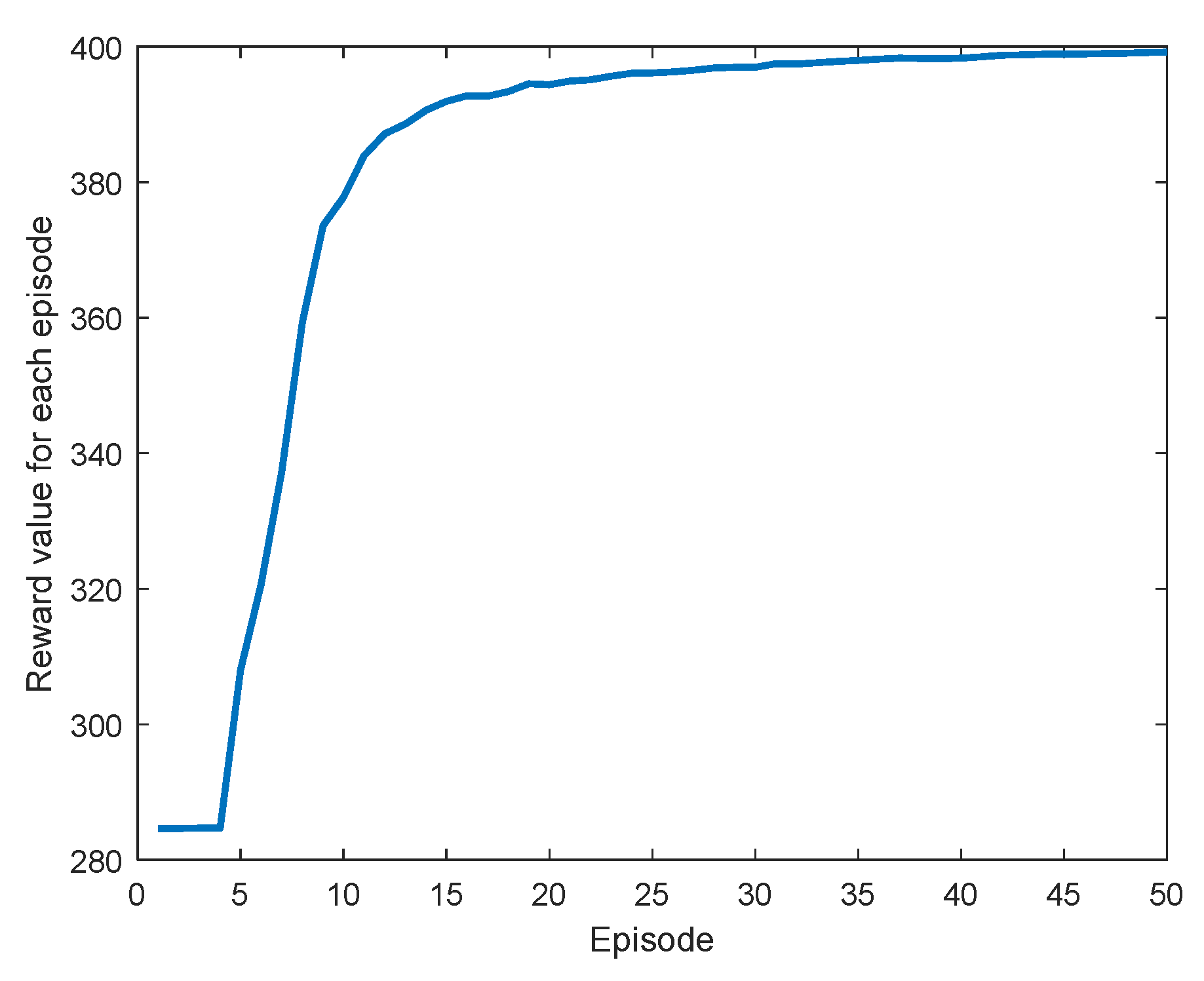
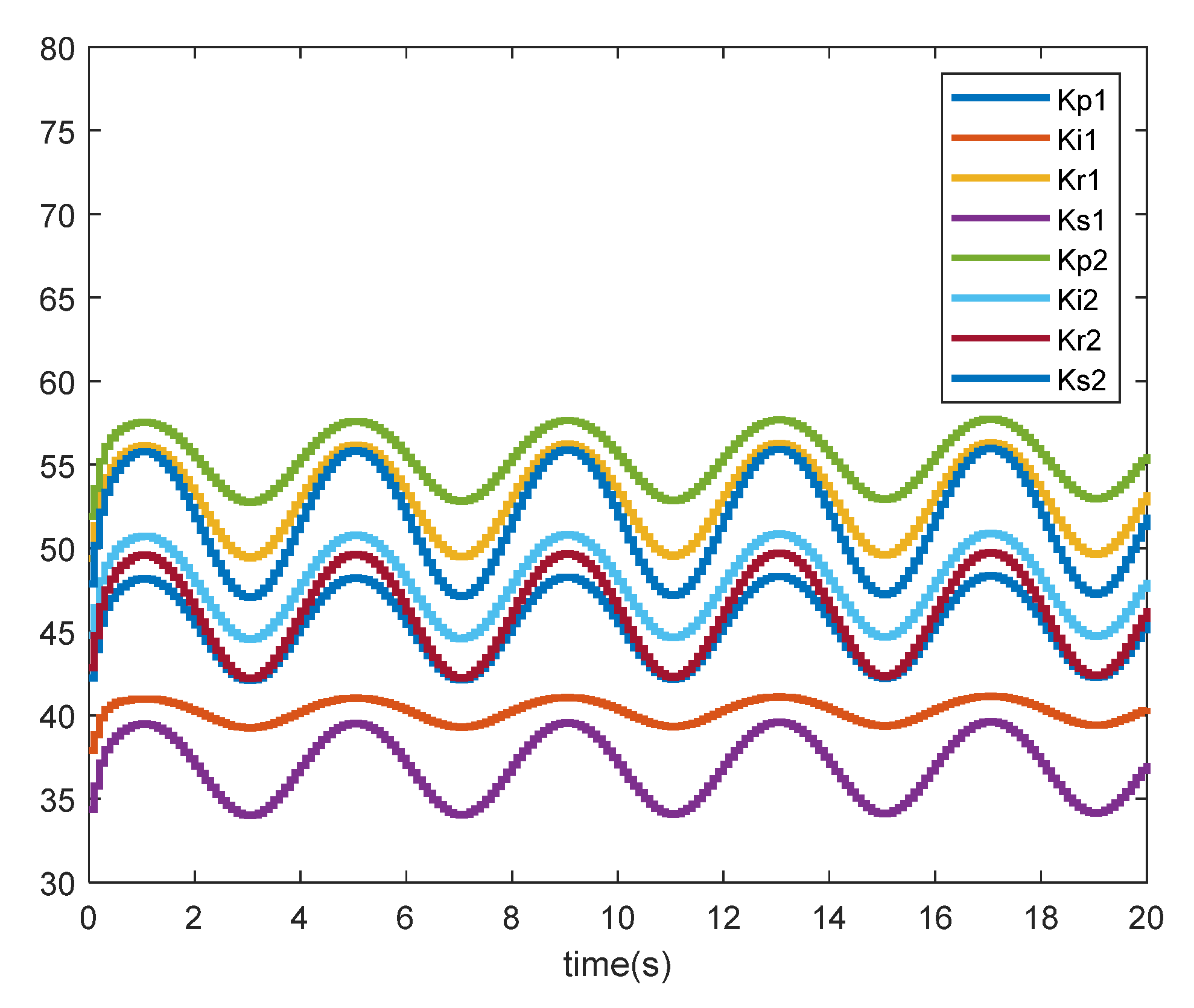
4.1. Learning Results for DDPGPIR
4.2. Control Effect Comparison of the Controller
4.3. Control Performance Index Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Feng, Z.; Hu, G.; Sun, Y.; Soon, J. An overview of collaborative robotic manipulation in multi-robot systems. Annu. Rev. Control. 2020, 49, 113–127. [Google Scholar] [CrossRef]
- Wang, Z.; Cui, W. For safe and compliant interaction: An outlook of soft underwater manipulators. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2020, 235, 3–14. [Google Scholar] [CrossRef]
- Kuo, C.-H.; Dai, J.S.; Dasgupta, P. Kinematic design considerations for minimally invasive surgical robots: An overview. Int. J. Med Robot. Comput. Assist. Surg. 2012, 8, 127–145. [Google Scholar] [CrossRef]
- Albu-Schaffer, A.; Bertleff, W.; Rebele, B.; Schafer, B.; Landzettel, K.; Hirzinger, G. ROKVISS—Robotics component verification on ISS—Current experimental results on parameter identification. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–16 May 2006; pp. 3879–3885. [Google Scholar]
- Sage, H.G.; De Mathelin, M.F.; Ostertag, E. Robust control of robot manipulators: A survey. Int. J. Control. 1999, 72, 1498–1522. [Google Scholar] [CrossRef]
- Pan, H.; Xin, M. Nonlinear robust and optimal control of robot manipulators. Nonlinear Dyn. 2013, 76, 237–254. [Google Scholar] [CrossRef]
- Loucif, F.; Kechida, S.; Sebbagh, A. Whale optimizer algorithm to tune PID controller for the trajectory tracking control of robot manipulator. J. Braz. Soc. Mech. Sci. Eng. 2019, 42, 1. [Google Scholar] [CrossRef]
- Elkhateeb, N.A.; Badr, R.I. Novel PID Tracking Controller for 2DOF Robotic Manipulator System Based on Artificial Bee Colony Algorithm. Electr. Control. Commun. Eng. 2017, 13, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Ardeshiri, R.R.; Khooban, M.H.; Noshadi, A.; Vafamand, N.; Rakhshan, M. Robotic manipulator control based on an optimal fractional-order fuzzy PID approach: SiL real-time simulation. Soft Comput. 2019, 24, 3849–3860. [Google Scholar] [CrossRef]
- Ardeshiri, R.R.; Kashani, H.N.; Ahrabi, A.R. Design and simulation of self-tuning fractional order fuzzy PID controller for robotic manipulator. Int. J. Autom. Control. 2019, 13, 595. [Google Scholar] [CrossRef]
- Shah, D.; Chatterjee, S.; Bharati, K.; Chatterjee, S. Tuning of Fractional-Order PID Controller—A Review. In Frontiers in Computer, Communication and Electrical Engineering; Taylor & Francis Group: London, UK, 2016; pp. 323–329. [Google Scholar]
- Kong, L.; Zhang, S.; Yu, X. Approximate optimal control for an uncertain robot based on adaptive dynamic programming. Neurocomputing 2020, 423, 308–317. [Google Scholar] [CrossRef]
- Kong, L.; He, W.; Dong, Y.; Cheng, L.; Yang, C.; Li, Z. Asymmetric Bounded Neural Control for an Uncertain Robot by State Feedback and Output Feedback. IEEE Trans. Syst. Man Cybern. Syst. 2019, 51, 1735–1746. [Google Scholar] [CrossRef] [Green Version]
- Wang, S. Adaptive Fuzzy Sliding Mode and Robust Tracking Control for Manipulators with Uncertain Dynamics. Complexity 2020, 2020, 1492615. [Google Scholar] [CrossRef]
- Yang, C.; Jiang, Y.; Na, J.; Li, Z.; Cheng, L.; Su, C.-Y. Finite-Time Convergence Adaptive Fuzzy Control for Dual-Arm Robot with Unknown Kinematics and Dynamics. IEEE Trans. Fuzzy Syst. 2018, 27, 574–588. [Google Scholar] [CrossRef]
- Rouhani, E.; Erfanian, A. A Finite-time Adaptive Fuzzy Terminal Sliding Mode Control for Uncertain Nonlinear Systems. Int. J. Control. Autom. Syst. 2018, 16, 1938–1950. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, J.; Liu, Y. Adaptive neural network force tracking impedance control for uncertain robotic manipulator based on nonlinear velocity observer. Neurocomputing 2018, 331, 263–280. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Neural Adaptive Backstepping Control of a Robotic Manipulator with Prescribed Performance Constraint. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 3572–3583. [Google Scholar] [CrossRef] [PubMed]
- Gosavi, A. Reinforcement Learning: A Tutorial Survey and Recent Advances. INFORMS J. Comput. 2009, 21, 178–192. [Google Scholar] [CrossRef] [Green Version]
- Khan, S.G.; Herrmann, G.; Lewis, F.L.; Pipe, T.; Melhuish, C. Reinforcement learning and optimal adaptive control: An overview and implementation examples. Annu. Rev. Control. 2012, 36, 42–59. [Google Scholar] [CrossRef]
- Liu, C.; Xu, X.; Hu, D. Multiobjective Reinforcement Learning: A Comprehensive Overview. IEEE Trans. Syst. Man Cybern. Syst. 2014, 45, 385–398. [Google Scholar] [CrossRef]
- Kukker, A.; Sharma, R. Stochastic Genetic Algorithm-Assisted Fuzzy Q-Learning for Robotic Manipulators. Arab. J. Sci. Eng. 2021, 1–13. [Google Scholar] [CrossRef]
- Runa; Sharma, R.; IEEE. A Lyapunov theory based Adaptive Fuzzy Learning Control for Robotic Manipulator. In Proceedings of the International Conference on Recent Developments in Control, Automation and Power Engineering, Noida, India, 12–13 March 2015; pp. 247–252. [Google Scholar]
- Kim, W.; Kim, T.; Kim, H.J.; Kim, S.; IEEE. Three-link Planar Arm Control Using Reinforcement Learning. In Proceedings of the 2017 14th International Conference on Ubiquitous Robots and Ambient Intelligence, Jeju, Korea, 28 June–1 July 2017; pp. 424–428. [Google Scholar]
- Du, T.; Cox, M.T.; Perlis, D.; Shamwell, J.; Oates, T.; IEEE. From Robots to Reinforcement Learning. In Proceedings of the 25th International Conference on Tools with Artificial Intelligence, Herndon, VA, USA, 4–6 November 2013; pp. 540–545. [Google Scholar]
- Agostinelli, F.; Hocquet, G.; Singh, S.; Baldi, P. From Reinforcement Learning to Deep Reinforcement Learning: An Overview. In Braverman Readings in Machine Learning: Key Ideas from Inception to Current State; Rozonoer, L., Mirkin, B., Muchnik, I., Eds.; Springer: Cham, Switzerland, 2018; Volume 11100, pp. 298–328. [Google Scholar]
- Wang, H.-N.; Liu, N.; Zhang, Y.-Y.; Feng, D.-W.; Huang, F.; Li, D.-S.; Zhang, Y.-M. Deep reinforcement learning: A survey. Front. Inf. Technol. Electron. Eng. 2020, 21, 1726–1744. [Google Scholar] [CrossRef]
- Mousavi, S.S.; Schukat, M.; Howley, E. Deep Reinforcement Learning: An Overview. In Proceedings of the Sai Intelligent Systems Conference, London, UK, 21–22 September 2016; Volume 16, pp. 426–440. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D.; Continuous Control with Deep Rein-Forcement Learning. Comput. Sci. 2015. Available online: https://arxiv.org/abs/1509.02971 (accessed on 18 July 2021).
- Shi, X.; Li, Y.; Sun, B.; Xu, H.; Yang, C.; Zhu, H. Optimizing zinc electrowinning processes with current switching via Deep Deterministic Policy Gradient learning. Neurocomputing 2019, 380, 190–200. [Google Scholar] [CrossRef]
- Sun, M.; Zhao, W.; Song, G.; Nie, Z.; Han, X.; Liu, Y. DDPG-Based Decision-Making Strategy of Adaptive Cruising for Heavy Vehicles Considering Stability. IEEE Access 2020, 8, 59225–59246. [Google Scholar] [CrossRef]
- Zhao, H.; Zhao, J.; Qiu, J.; Liang, G.; Dong, Z.Y. Cooperative Wind Farm Control with Deep Reinforcement Learning and Knowledge-Assisted Learning. IEEE Trans. Ind. Inform. 2020, 16, 6912–6921. [Google Scholar] [CrossRef]
- Özyer, B. Adaptive fast sliding neural control for robot manipulator. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 3154–3167. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, S.; Fu, Q.; Xue, C.; Sun, W. Fuzzy Logic Control of an Uncertain Manipulator with Full-State Constraints and Disturbance Observer. IEEE Access 2020, 8, 24284–24295. [Google Scholar] [CrossRef]
- Nohooji, H.R. Constrained neural adaptive PID control for robot manipulators. J. Frankl. Inst. 2020, 357, 3907–3923. [Google Scholar] [CrossRef]
- Ge, S.S.; Lee, T.H.; Harris, C.J. Adaptive Neural Network Control of Robotic Manipulator; World Scientific: London, UK, 1998. [Google Scholar]
- Zhang, D.; Wei, B. A review on model reference adaptive control of robotic manipulators. Annu. Rev. Control. 2017, 43, 188–198. [Google Scholar] [CrossRef]
- Liu, J.; Dong, X.; Yang, Y.; Chen, H. Trajectory Tracking Control for Uncertain Robot Manipulators with Repetitive Motions in Task Space. Math. Probl. Eng. 2021, 2021, 8838927. [Google Scholar] [CrossRef]
- Xu, W.; Cai, C.; Zou, Y. Neural-network-based robot time-varying force control with uncertain manipulator–environment system. Trans. Inst. Meas. Control 2014, 36, 999–1009. [Google Scholar] [CrossRef]
- Yu, L.; Fei, S.; Huang, J.; Gao, Y. Trajectory Switching Control of Robotic Manipulators Based on RBF Neural Networks. Circuits Syst. Signal Process. 2013, 33, 1119–1133. [Google Scholar] [CrossRef]
- Wang, L.; Chai, T.; Yang, C. Neural-Network-Based Contouring Control for Robotic Manipulators in Operational Space. IEEE Trans. Control. Syst. Technol. 2011, 20, 1073–1080. [Google Scholar] [CrossRef]
- Wang, N.; Wang, D. Adaptive manipulator control based on RBF network approximation. In Proceedings of the 2017 Chinese Automation Congress, Jinan, China, 20–22 October 2017; pp. 2625–2630. [Google Scholar]

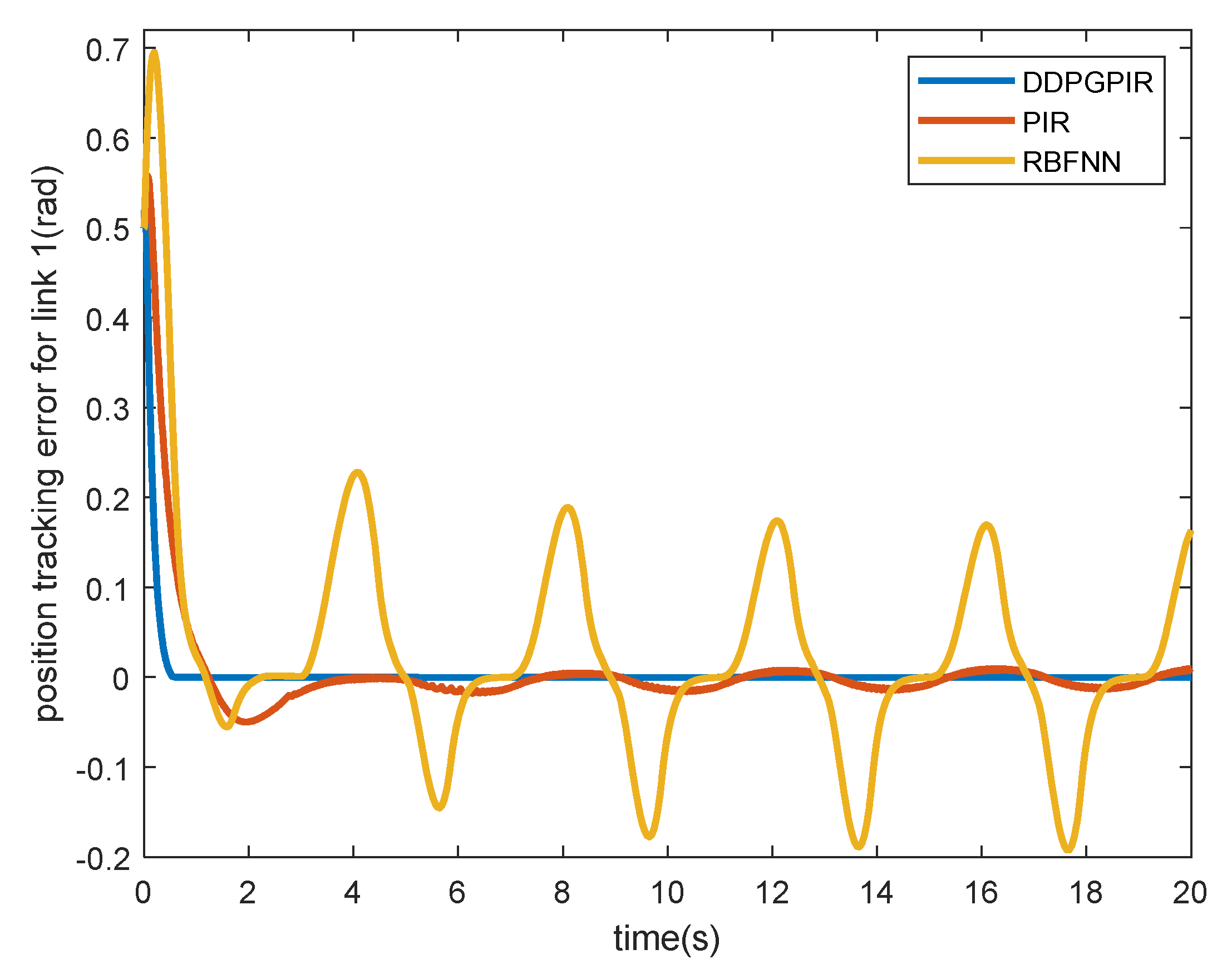
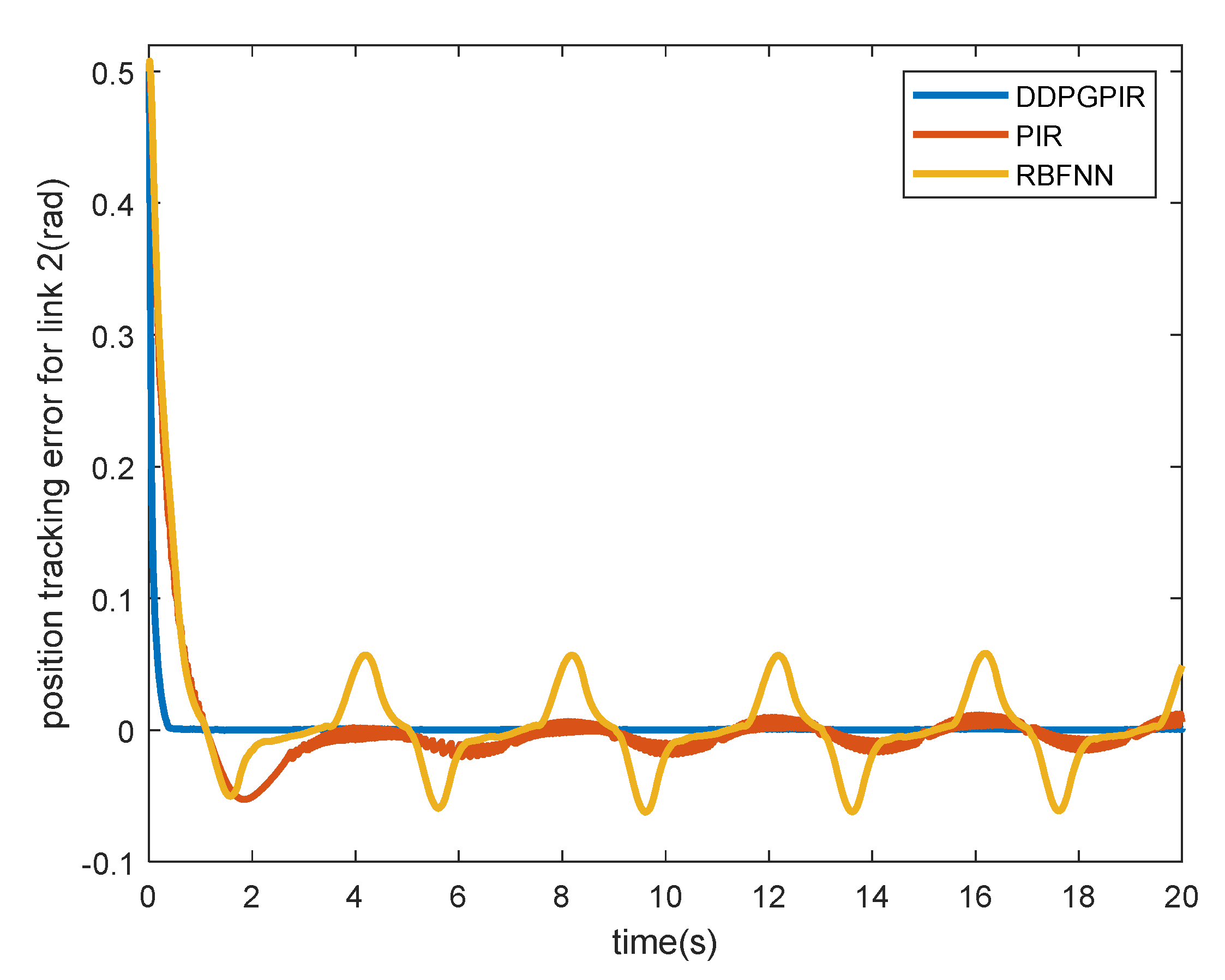
| Controller | Indicator | Joint 1 | Joint 2 |
|---|---|---|---|
| RBFNN | IAE | 1.5978 | 0.5440 |
| ITAE | 13.4532 | 3.9454 | |
| PIR | IAE | 0.4217 | 0.3476 |
| ITAE | 1.6596 | 1.5451 | |
| DDPGPIR | IAE | 0.0866 | 0.0410 |
| ITAE | 0.0285 | 0.0848 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, P.; Huang, W.; Xiao, J.; Zhou, F.; Hu, W. Adaptive Proportional Integral Robust Control of an Uncertain Robotic Manipulator Based on Deep Deterministic Policy Gradient. Mathematics 2021, 9, 2055. https://doi.org/10.3390/math9172055
Lu P, Huang W, Xiao J, Zhou F, Hu W. Adaptive Proportional Integral Robust Control of an Uncertain Robotic Manipulator Based on Deep Deterministic Policy Gradient. Mathematics. 2021; 9(17):2055. https://doi.org/10.3390/math9172055
Chicago/Turabian StyleLu, Puwei, Wenkai Huang, Junlong Xiao, Fobao Zhou, and Wei Hu. 2021. "Adaptive Proportional Integral Robust Control of an Uncertain Robotic Manipulator Based on Deep Deterministic Policy Gradient" Mathematics 9, no. 17: 2055. https://doi.org/10.3390/math9172055
APA StyleLu, P., Huang, W., Xiao, J., Zhou, F., & Hu, W. (2021). Adaptive Proportional Integral Robust Control of an Uncertain Robotic Manipulator Based on Deep Deterministic Policy Gradient. Mathematics, 9(17), 2055. https://doi.org/10.3390/math9172055






