Abstract
Improving the performance of the convolution operation has become a key target for High Performance Computing (HPC) developers due to its prevalence in deep learning applied mainly to video processing. The improvement is being pushed by algorithmic and implementation innovations. Algorithmically, the convolution can be solved as it is mathematically enunciated, but other methods allow to transform it into a Fast Fourier Transform (FFT) or a GEneral Matrix Multiplication (GEMM). In this latter group, the Winograd algorithm is a state-of-the-art variant that is specially suitable for smaller convolutions. In this paper, we present openCNN, an optimized CUDA C++ implementation of the Winograd convolution algorithm. Our approach achieves speedups of up to on Turing RTX 2080Ti and up to on Ampere RTX 3090 with respect to Winograd convolution in cuDNN 8.2.0. OpenCNN is released as open-source software.
1. Introduction
The use of GPUs in machine learning is generating a tremendous innovation boost, specially in areas like computer vision [1]. There are several problems that the community is trying to solve using computer vision approaches [2,3,4]. Despite these proposals having different targets, they usually share a key aspect, the architecture of the neural network used under the hood—Convolutional Neural Networks (CNNs). CNNs have achieved state-of-the-art accuracy in many areas related to computer vision, being able to pinpoint the expected result and to overcome human precision in many cases. As their name suggests, the convolution operation is the core of this type of networks.
CNNs architectures are continuously growing in depth and width, hence, their training and inference are causing the computational cost to increase [5]. For this reason, trying to optimize the performance of the convolution operation is the target of recent research works. In those terms, the Winograd’s algorithm has demonstrated a great performance in convolutional operations, especially for filters, achieving a theoretical arithmetic complexity reduction of . The main hardware-vendor libraries provide implementations carefully tuned for their devices, such as NVIDIA cuDNN [6], ARM Compute Library [7], Intel oneDNN [8], previously called MKL-DNN, or AMD MIOpen [9]. In Nvidia GPUs, cuDNN is clearly the reference to beat in terms of performance, Nvidia GPUs being also a reference architecture for this type of workload. However, some considerations must be taken into account:
- Some libraries such as cuDNN contain important sections of machine assembly code;
- Nvidia engineers hand-tune their libraries at Shader ASSembly (SASS) level to optimize the performance on their devices at a very low level;
- These implementations are not usually open-source, so it is not possible to tune the performance of these implementations for special use-cases.
For these reasons, recent research works [10,11] have cracked the Instruction Set Architecture (ISA) of different generations of Nvidia GPUs providing an intermediate SASS assembler, which enables the direct generation of machine code. While these third-party implementations usually outperform cuDNN, SASS programming is hard and the resulting code is restricted to a specific architecture. Taking into account that in large AutoML processes it is quite common to use hybrid or mixed devices to train neural networks (NNs), these solutions will be unaffordable. An example of this is Neon [12], a deep learning framework that achieves high performance on Maxwell and Pascal GPUs, but fails in newer architectures such as Turing because some kernels were hand-crafted in SASS. Nowadays, this project is discontinued. Another consequence of this situation is that it is not easy to find CUDA-level implementations, as it is really difficult to outperform SASS codes. Furthermore, third-party assembly-level implementations of the convolution, particularly of the Winograd algorithm, are not publicly available, thus the difficulty is even greater.
An analysis of the design of recent Winograd implementations detected deficiencies that can lead to important performance drops [10]. A performance-competitive only-CUDA implementation of the Winograd algorithm can be the base for a performance-portable implementation and it makes it easier to tune low-level implementation details between different platforms without requiring the generation of new specific SASS code, and eventually having to crack the ISA of a new platform.
This paper makes the following contributions:
- An only-CUDA implementation of the single-precision Winograd algorithm for kernels is introduced. The code was released as open-source software under the name openCNN and it can be found at https://github.com/UDC-GAC/openCNN, accessed on 28 July 2021.
- Its performance has been evaluated on NVIDIA Turing RTX 2080Ti and NVIDIA Ampere RTX 3090 and compared to the state-of-the-art Winograd implementation in cuDNN 8.2.0, achieving a speedup up to on RTX2080Ti and on RTX 3090 in ResNet [13].
- Moreover, the performance of our openCNN implementation has been compared with different convolution algorithms available in cuDNN. The average speedups achieved are (w.r.t. FFT), (FFT Tiling), (GEMM), (Implicit GEMM), (Precomputed implicit GEMM) and (Winograd Non-Fused version) on Turing NVIDIA RTX 2080Ti. Equivalently, on Ampere NVIDIA RTX 3090 the speedups obtained are (w.r.t. FFT), (FFT Tiling), (GEMM), (Implicit GEMM), (Precomputed implicit GEMM) and (Winograd Non-Fused version).
This paper uses the implementation proposed in [10] as a reference, making the following contributions with respect to that work:
- Our implementation is fully written in CUDA and can be easily tuned and ported to different NVIDIA hardware platforms. However, the implementation described in [10] contains important fragments of architecture-specific assembly code which is restricted to a particular GPU architecture and ISA encoding.
- The implementation of the reference paper uses assembly code to improve the performance of key hotspots of the method, some of them containing costly memory movements. In our paper, these hotspots are encoded in CUDA, using microbenchmarking to find the most efficient way to implement them. The paper also discusses different alternative methods to implement those important sections of the code. As a consequence of all this, our implementation achieves speedups up to on NVIDIA Turing RTX 2080Ti and up to on NVIDIA Ampere RTX 3090 over the CUDA implementation of [10]. A direct comparison with [10] is not possible as its full code is not publicly available.
- Unlike the study in [10], the full code of our paper is released as open-source software.
The rest of the paper is organized as follows: Section 2 introduces the fundamentals of the Winograd algorithm. Section 3 presents a high-level analysis of the Winograd algorithm oriented to its implementation and reveals the baseline code details. In Section 4, the set of optimizations applied to the baseline implementation is described. The experimental results are reported in Section 5, while Section 6 summarizes the related work and Section 7 concludes the paper.
2. The Winograd Convolution Algorithm
The minimal filtering algorithm for convolution was promoted initially in [14] by Shmuel Winograd and later rescued for its application in convolutional neural networks in [15]. The algorithm has the status of a state-of-the-art implementation of the convolution operator, and its popularity resides in its reduction of the number of operations required with respect to the direct method. For this, it takes advantage of the inherent overlapping present in the direct method.
The general (direct) 2D batched convolution can be expressed as:
where is the input data element, is a filter element and is an output tile. Each subindex represents:
- h: input image height;
- w: input image width;
- r: filter height;
- s: filter width;
- n: number of input images;
- c: number of channels;
- k: number of filters.
Let us illustrate the aforementioned overlapping of this method through an example.
Figure 1 shows the convolution operation of a single channel input matrix and a filter with stride 1. The direct convolution slides the filter along the input image performing separated Hadamard products [16] which are then reduced with a sum. If this processing is divided into tiles, the convolution generates a matrix of values per tile. The right side of the figure focuses on the processing of the first of these tiles, the top leftmost one, showing that all the elements of the highlighted tile of the input image, except a, d, m and p, are used in several Hadamard multiplications.
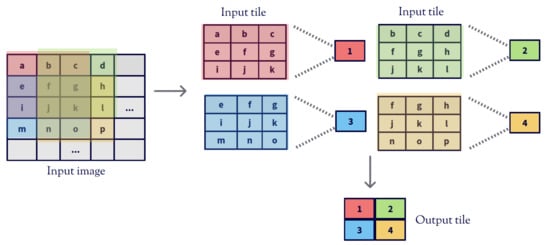
Figure 1.
Traditional convolution.
Winograd exploits this overlapping by creating an intermediate representation of the input tile and the filter that generates the same result as the direct method but requiring fewer operations and, thus, instructions. The mathematical rationale of this approach is now illustrated for the one-dimensional case. Let us consider the convolution of a vector K and a filter w, where ∗ is the convolution operation:
Using stride 1, the resulting O vector would be calculated as:
thus involving six multiplications and four additions.
In this case, Winograd’s method proposes computing O as:
where:
which requires four multiplications and eight additions. However, the filter weights remain constant for the entire input image, so and can be precomputed, which reduces the total number of additions to four. By substitution we can check that this method provides the same result as the direct one.
This idea can be extended to different numbers of dimensions and input sizes. The formulation of the method depends on two factors: the output tile size m and the filter size r. These two values condition the value of the input tile size which can be calculated as:
In the general case, the Winograd algorithm solves the convolution between a filter g and an input tile d using the following formula:
where ⊙ is a Hadamard (element-wise) product. The contents of matrices B, G and A are constant for a given combination of m and r. For instance, for , the contents of these matrices are:
The fact that the contents of these matrices change for every possible value of is not a big deal for deep learning applications, as the shape of the inner layers of convolutional networks is very regular. For instance, having filters of elements is common in modern networks, and the value of the output tile can be fixed to favor the performance of the implementation. The generic algorithm used to build these matrices for each combination of m and r can be found in [17].
In the two dimensional case (Figure 2), the value of is calculated as:
and the convolution formula is adapted as:
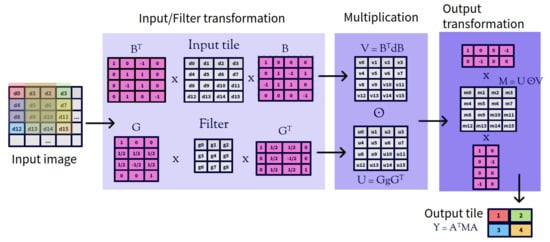
Figure 2.
Winograd’s convolution in two dimensional case.
The three-dimensional case is quite similar, as it consists of applying the base Winograd algorithm independently to all the C input channels and then reducing the results into a single matrix using an element-wise addition, resulting in the expression:
3. Implementation of the Winograd Algorithm
This section provides further details of the implementation of the Winograd algorithm. At the top level, the algorithm starts with an input matrix, which is divided into tiles of elements. Then, these tiles are processed separately. In fact, the processing of different tiles can take place in parallel and this is an important source of parallelism. The processing of each tile is done using the formulas introduced in the previous section, making space for the following sequence of four steps, where and are the row and column of the tile, respectively :
- Filter transformation: the original filter g is operated with matrix G using the following expression ;
- Input transformation: the input tile is operated with matrix B using the following expression ;
- Multiplication: the outputs of the two previous steps are multiplied using a Hadamard product;
- Output transformation: the result of the previous step is operated using the following expression .
Let us recall that the contents of matrices G, B and A are constant for each tile size . The value of has a big influence on the performance of the algorithm. The larger it is, the higher the arithmetic reduction ratio, but also the worse the precision of the calculation. Thus, it is necessary to find a trade-off between precision and performance when choosing the value of . Many previous implementations of the algorithm use as standard.
This paper uses the implementation proposed in [10] as a starting point. In the remaining, it will be called the reference implementation. Its authors combine several low-level optimizations with the usage of Shader ASSembly (SASS) code to achieve state-of-the-art performance on GPUs. Our aim is to generate a CUDA-only C++ implementation and to optimize it as much as possible. In addition, our implementation (https://github.com/UDC-GAC/openCNN, accessed on 28 July 2021) is open-source and competitive in several hardware platforms.
Our code was written from scratch, as the reference implementation is not freely available. Algorithm 1 shows an enriched version of the pseudocode introduced in the original paper, which contains additional details such as software pipelining, barrier synchronization and data prefetch.
| Algorithm 1: Pseudocode of the Winograd’s algorithm implementation for . SMEM stands for Shared MEMory while GMEM stands for Global MEMory. |
 |
GPUs have a small amount of fast memory (i.e., shared memory and registers) available. The reference implementation uses cache blocking for maximizing data reuse, hence, filters, input tiles and channels are assigned to each thread block in each iteration, which means that and block sizes are used for input and filter, respectively.
The reference implementation uses a cache block size of , , unlike other recent implementations like cuDNN [6] and Neon [12] that use , . The reason is that several recent CNN architectures like VGG or ResNet have a number of filters multiple of 64 and this block size increases the arithmetic intensity by 33%, while it reduces the number of input data loads and transformation steps. Furthermore, it makes the resulting code more robust to L2 cache misses.
The filter transformation step is implemented following the FX variant [15,18] (Figure 3), i.e., in a kernel separate from the main loop. The filter is usually much smaller than the input, thus its transformation takes a negligible time. The implementation details of this filter transformation are not included in the pseudocode. To put this into perspective, in this step of the reference implementation, each thread block loads filter tiles in each iteration. As each thread block has threads, each thread of the block loads two tiles (Line 4 in Algorithm 1).
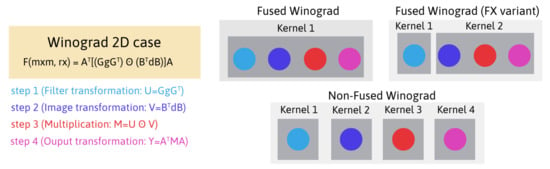
Figure 3.
Implementation alternatives of Winograd’s algorithm.
The Input Transformation step is implemented in the CUDA kernel of the main loop (Line 15 in Algorithm 1). In each iteration of the algorithm, each thread block loads input tiles to shared memory and transforms them. As each block has 256 threads, each thread loads and transforms a single input tile (Line 3 in Algorithm 1).
The following step of the algorithm is the element-wise (Hadamard) matrix multiplication (EWMM) (Line 28 in Algorithm 1). At this point we should remember Equation (5), where, after calculating the Hadamard product independently for all the channels, they have to be reduced using an element-wise addition. The reference implementation takes advantage of the fact that the accumulation on each tile can be performed concurrently. Thus, we can turn the element-wise multiplication into a 16-batched matrix multiplication. Letting each thread compute two matrix multiplications, the computation intensity increases, hiding better the shared memory latency. As a result, each warp computes of GEMMs.
A key aspect for performance of the batched matrix multiply step is to map input and filter tiles to the threads of a warp avoiding bank conflicts. The reference implementation uses the Lane ID arrangement shown in Figure 4, which requires transposing the data first. The data transposing buffer is arranged as for input tiles and for filter tiles (Line 1, 2 in Algorithm 1), 16 being the number of elements of an tile. Each lane loads four consecutive elements from shared memory (LDS, LoaD from Shared memory instruction), enabling the usage of 128-bit instructions (). For example loads input data at locations 8, 9, 10, 11 and 24, 25, 26, 27, and filter data at locations 0, 1, 2, 3 and 32, 33, 34, 35, across channels. As a result, elements of input data and of filter data are stored into registers.
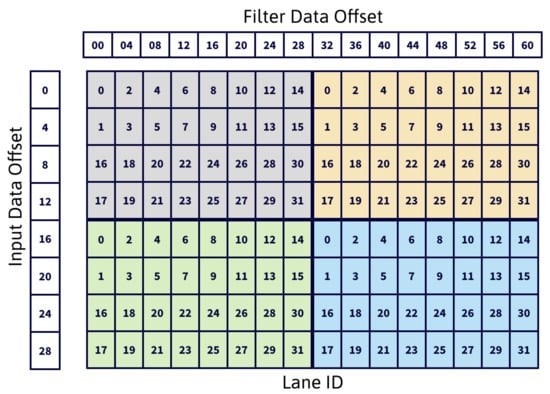
Figure 4.
Lane ID arrangement for the data transposing buffer.
Finally, the last step of the algorithm corresponds to the output transformation and storage. In this step, the pre-transform output data (result of the multiplication step) are transposed back to return to the initial matrix organization. Specifically, each thread block has 128 KB of information stored in registers that have to be written to global memory in several rounds. Every round transposes and transforms an output tile (Line 39 in Algorithm 1) of 32 KB. The proposed layout is shown on the right side of Figure 5. The padding defined between elements for avoiding bank conflicts implies that 8 additional KB of shared memory are needed in every round. As a consequence, this process is performed in 4 rounds of 32 KB because in Turing GPUs the shared memory can be configured up to 64 KB [19] and every round needs KB. The left side of Figure 5 highlights in red the data transposed in the first round. The 32 KB correspond to 4 bytes/element × 32 (elements to transform in a round) × 4 (filters per position in data transposing buffer, Figure 4) × 4 (input elements per position in data transposing buffer, Figure 4) × 8 (warps within each block of threads) × 2 (output tiles per thread).
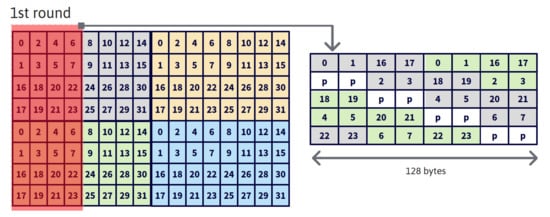
Figure 5.
Lane ID arrangement for output transform buffer (right side, being p the padding elements) and pre-transform output data transposed in the first round (left side).
4. Optimization of the Method
The layout proposed by the reference implementation for the output transform buffer (right side of Figure 5) in the output transform step leads to thread divergence, as it uses a quarter of each half-warp per round (e.g., lanes 0–7 and 16–23 in round 1). The reference implementation uses this layout for several reasons: (1) it matches the initial data organization and thus it ensures result correctness; (2) it generates stores of 32 continuous output elements to shared memory and avoids bank conflicts; and (3) the total buffer size of 40 KB fits in the available shared memory on Turing GPUs, 64 KB [19].
The 64 KB of shared memory of Turing architectures is organized in 32 banks and data are distributed cyclically among the banks in 32-bit words. Additionally, each bank can transfer 32 bits per clock cycle [20]. The theoretical peak memory throughput can be calculated by multiplying the Load Store Unit (LSU) count per Streaming Multiprocessor (SM) (, 16 in Turing) by the number of bytes that each LSU can load per cycle per instruction (4 bytes in Turing) which gives 64 bytes/cycle in Turing [21].
The theoretical peak shared memory performance is achieved if the 32 threads of a warp read/write 32-bit words on separated memory banks simultaneously. Shared memory instructions of more than 32 bits per thread (64- or 128-bit) are broken down into 128-byte (32 banks × 32 bits/bank) memory operations by the memory controller. Thus, if the word size is 64 or 128 bits, then two or four transactions per instruction will be needed, respectively.
It has been demonstrated [11] that, in Kepler architectures, 64-bit loads perform better for shared memory while texture cached 128-bit load instructions perform better for global memory. We wanted to make our own study of the performance of load and store instructions from/to shared memory in our testing environment since the performance of these instructions is crucial in the output transformation step.
There are some works that try to measure the performance of shared memory loads and stores in Turing [21,22]. In [22], the authors prove that benchmarking those instructions using code written in CUDA or PTX is not fair since the compiler can apply its own optimizations, thus they recommend doing the test directly using SASS code.
The repository associated to our paper contains a reproduction of these experiments (https://github.com/UDC-GAC/openCNN/tree/main/bench/smem, accessed on 28 July 2021), that has been used to validate their conclusions on our testing environment. The test are written directly in Turingas SASS code [10].
Table 1a,b contains the results of our experiment and show that their conclusions also apply to our testing environment. The tests have been performed using an NVIDIA RTX 2080Ti GPU with Turing architecture and the CUDA 11.2 Toolkit. The results show that memory throughput improves using wider memory words. For example, 128-bit memory instructions have 20% higher throughput than 64-bit ones (remember the peak limit of 64 bytes/cycle). However, this advantage vanishes if using wider instructions imply using just half of the threads of a warp for storing the information as it happens in the proposal of Figure 5. To test this, we measured the CPI and throughput of a SASS code with the same divergence patterns as Figure 5 and the result is that the CPI is 10 clocks and the throughput 25.60 (51.21/2) bytes/cycle. That means that despite halving the number of memory transactions required, the number of clock cycles per instruction remains the same, therefore, the throughput is divided by two. However, if STS.64 stores are used, the throughput, 42.61, is larger, which means that using narrower instructions and avoiding thread divergence can significantly improve memory performance.

Table 1.
LoaD from Shared memory (LDS) and STore to Shared memory (STS) instructions metrics.
4.1. Alternative Output Buffer Layouts
The previous analysis indicates that there is an important performance drop in the output transformation step of Winograd due to the way data are written from registers to shared memory when transposing the pre-transform output data. Notice that 16-tile elements are placed across different thread registers, which are private. Thus, the results must be merged into Shared MEMory (SMEM) first, where all the threads in the block can share their results. The implementation proposed in this paper solves this performance problem at CUDA-source code level. Let us remark that the output transformation step is composed by three tasks that are: (1) transposition of the pre-transform output data from registers to shared memory, (2) output data transformation from shared memory to registers and (3) transformed data storage from registers to global memory. Each of these tasks is covered separately in the rest of this section.
4.1.1. (1) Output Data Transposition
The first task transposes the pre-transform output data, stored in registers, into shared memory. Our implementation uses a new layout for the output transform buffer. The layout is shown in Figure 6, whose cell numbers indicate the lane ID and padding locations. Notice that this figure follows the same representation convention as the right side of Figure 5 and it replaces it in our implementation. Furthermore, this one uses float2 instead of float4 data types, and it partially keeps the original data layout order (left part in yellow/green and red/dark blue), but it appends a second half buffer containing some elements that would be transposed in a second round (right part in gray/cyan and magenta/orange). Since a shorter data type, float2, is now used, the initial layout, based on float4, has been organized into two different buffers, each one with one half of the associated elements. Thus, in this layout, half of the float4 elements are located in the upper matrix while the other half are in the lower one. This layout uses twice more threads in each round than the original proposal and it avoids thread divergence as well as bank-conflicts. As we are doubling the amount of information written in each round (two rounds are represented in Figure 6), we have to divide by two the number of filters in each of those rounds. Consequently, the final size of this buffer layout is 4 bytes/element × 64 (elements to transform in a round) × 2 (half of the filters per position in the data transposing buffer, Figure 4) × 4 (input elements per position in the data transposing buffer, Figure 4) × 8 (warps within each block of threads) × 2 (output tiles per thread) = 32 KB.
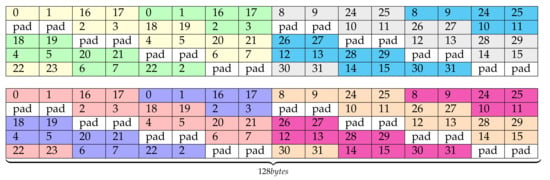
Figure 6.
optSTS64 layout.
The amount of padding can be reduced with the new layout proposal shown in Figure 7. This layout merges the left and right halves of the previous matrix layout proposal while keeping the order of the elements and avoiding bank conflicts. The color pattern of this figure does not match the one of the previous figure, so it should not be interpreted the same way. This new layout locates contiguously the analogous rows of the two halves (e.g., row n of matrices 0 and 1, which are always in the same memory bank). This allows to remove some padding, which may not be a big concern in Turing architectures but it can make a difference in older platforms. In the following, this proposal will be called optSTS64, and it is one of the alternative optimizations that will be compared in the experiments section.
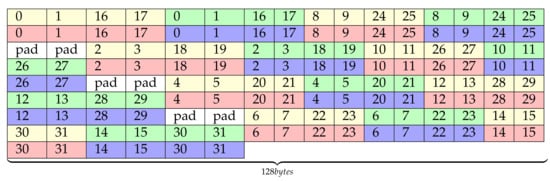
Figure 7.
Final optSTS64 layout.
In the previous layout proposal, the padding introduced in the layout for avoiding bank conflicts can be replaced with useful data. To do this while keeping the layout properties, the padding must be replaced with the last cells of a segment of consecutive 128 bytes. For example, lane 26 and 27 are moved up to the padding position from row fourth to third. This movement of data generates a ripple effect of lane reorganization that flushes padding from the buffer. Figure 8 shows the result of this lane rearrangement. In the remaining we will refer to this proposal as optSTS64 compact.
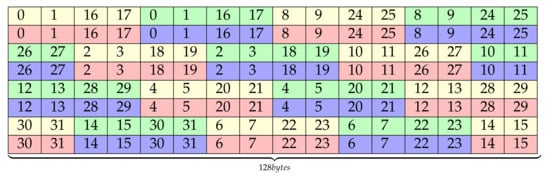
Figure 8.
optSTS64 compact layout.
The optSTS64 compact layout enables a more efficient memory usage and a reduction of the total number of rounds needed to transpose the data, transferring 32 KB of useful data to shared memory in every round. Considering that there are 64 KB of shared memory in Turing GPUs, it is possible to double the amount of information transposed on each round.
The problem of writing 64 KB of data to SMEM in each round, unlike the 40 KB of the original proposal, is that it is more difficult to overlap memory accesses with computation. However, the extra 32 KB available using the optSTS64 compact layout can be used as a virtual double memory buffer. Thus, data storage can be pipelined with transformation as it was done in the main loop with the input and filter transformation and GEMM. This approach still requires four rounds to finish the data transposition and transformation but memory accesses are overlapped with computation, thus reducing the effect of memory latency.
4.1.2. (2) Output Data Transformation
The transformation step of the output begins just after the results have been transposed into the shared memory. Each warp of threads reads and transforms a set of two consecutive rows of the previous layout (notice that, despite their being stored separately they are actually a float4 datatype broken into two float2 elements), that is 256 B in total.
Figure 9 shows how our implementation reads the previously transposed data, ensuring coalesced and bank conflict-free shared memory accesses. Within each cell, two laneIds are represented since each one contains a float2 value but LDS.32 instructions are used for loading data. For simplicity, we have just depicted the first two rows of the optSTS64 layout taking into account that the other rows will be processed by other warps in the same way. There exist several possible ways to read these data, but we have to take into account how they will be stored later in Global Memory (GMEM), so the next major concerns must be considered:

Figure 9.
Data reading order from shared memory to registers.
- The red/yellow vectors will not be consecutive to the green/blue ones. Remember that in Figure 6, two buffers had been appended side-by-side that were not contiguous in memory according to the initial layout, in Figure 4. That enabled the full warp utilization in the transposition step, but the initial organization must be taken into account at this point to ensure result correctness.
- Float4 data types were divided into two float2 elements. For this reason, the final order in GMEM within each group of elements (yellow/red or blue/green) is as Figure 10 depicts. After the first column the flow has been simplified for clarity, but it would be as it is depicted here for the first four elements.
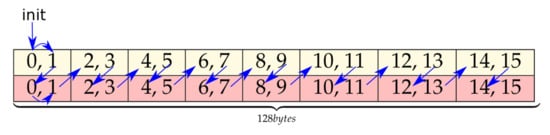 Figure 10. Order of the elements after replacing float4 elements by two float2 elements.
Figure 10. Order of the elements after replacing float4 elements by two float2 elements. - Each thread computes two output tiles, so the wider instruction that can be used to store the results to GMEM is STG.64.
As a result of the previous considerations, each half-warp must be associated to one of the analogous two vectors as Figure 9 shows, avoiding bank conflicts and ensuring future GMEM 128-bit coalesced accesses, since memory instructions will be broken down into two separate transactions. Furthermore, using STG.64 instructions requires previously shuffling the results as Figure 11 represents. This way, data can be read from SMEM using 32-bit instructions (Figure 9), but later each thread will have two consecutive values to store to GMEM, enabling the usage of STG.64.
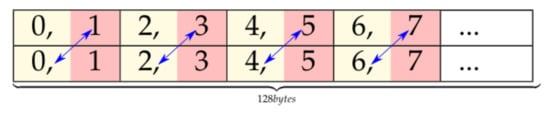
Figure 11.
Virtual elements shuffle.
Nevertheless, the shuffle instruction introduces an overhead that can be avoided if the swap is performed during the Outer-Product step. Considering that the datatype used in that stage is float4, the values of the ‘y’ and ‘z’ coordinates can be swapped with no performance degradation (Figure 12).

Figure 12.
Final data reading order from shared memory to registers after the shuffle of elements.
The previous considerations can be applied to the optSTS64 compact layout, the only difference being that the indexes of the wrapped-around elements within each warp must be recomputed.
Another possibility is to replace the 32-bit loads from shared memory by 64-bit ones. One way to do so is depicted in Figure 13. Some sources in the bibliography define a half-warp as a group of 16 consecutive threads. Thus, this access pattern leads to shared memory bank conflicts when loading data. Furthermore, no great performance improvement is expected from changing 32-bit to 64-bit instructions when loading data from shared memory. Returning to Table 1b, going from 32- to 64-bit loads only means a 5.6% of higher throughput, which is a small improvement in the total computation time. This alternative has been discarded after checking the previous concerns empirically.

Figure 13.
Data reading order from shared memory to registers with LDS.64 instructions.
4.1.3. (3) Output Data Storage
Finally, the results can be written to global memory following the order in Figure 14. This order is followed in our two candidate implementations optSTS64 and optSTS64 compact. As it relies on STG.64 stores, the memory operations must be broken into 128-byte transactions, one for each half-warp.

Figure 14.
Layout STG.64 from registers to global memory (fully coalesced).
5. Experimental Results
This section evaluates our CUDA C++ Winograd minimal filtering implementation. The CUDA 11.2 Toolkit has been used on two platforms: NVIDIA Turing RTX 2080Ti and NVIDIA Ampere RTX 3090 GPUs. The dataset used consists of all the layers of the ResNet architecture (Table 2). ResNet is a powerful CNN model used in many computer vision (CV) problems [13]. Its recent incorporation in the standard machine learning benchmarks [23] supports the importance of this NN since it is considered a milestone in deep learning. ResNet represents a backbone model applied very frequently to CV tasks such as object detection. Time measurement is done using CUDA events [24] and calculated using the average value of 50 executions. The performance of our implementation is compared to that of a CUDA-only C++ implementation of [10] and cuDNN 8.2.0 (23 April 2021) Winograd implementation (CUDNN_CONVOLUTION_FWD_ALGO_WINOGRAD) with the NCHW data layout.

Table 2.
ResNet layers.
The performance is expressed in FLOPS, which are calculated following Equation (6). The filter transformation time is negligible compared to the execution time, so it is ignored in the FLOPs calculation, but it is included in time measurement.
Figure 15 compares the performance of our implementation with a CUDA-only C++ implementation of [10] and cuDNN’s Winograd convolution. Four batch sizes are tested: 32, 64, 96, 128. All the possible combinations of layers and batch sizes are named as ConvmNn, n being the batch size and m the layer number, so that greater values of m are associated to deeper layers in the network. The results show that our approach is better than cuDNN as we go deeper in the network, the reason being that since our approach uses larger blocks ( vs. ), then it can hide better the input data over-fetching when K, the number of filters, increases. We can also see that the difference between our implementation and [10] decreases with the number of channels because the waste of time of the output transposition is better overlapped with computation. We must notice that the outer loop of Algorithm 1 is with respect to C. This way, since each thread block always writes 128 KB of output data, when C increases, the number of computations increases accordingly, and the time wasted on transposing the results can be hidden more easily.
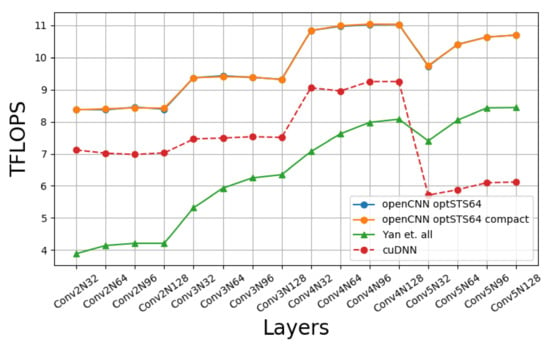
Figure 15.
Winograd’s openCNN performance on Turing RTX 2080Ti.
Something remarkable is that the optSTS64 compact layout does not achieve a better performance than optSTS64. The advantage of using the optSTS64 compact layout is that it allows to build a double buffer for interleaving data transposition with data transformation and the storage to global memory. A profiling analysis of the machine assembly code generated by the compiler shows that memory instructions were overlapped with arithmetic instructions as we had expected, namely, each STS.64 with 2 FADDs. However, this does not generate a significant performance gain. In [10], the scheduling of load/store instructions is changed to increase the distance between memory instructions, improving the performance notably. We speculate that the optSTS64 compact layout could have achieved a much better performance if assembly-level optimizations were applied, but the generation of platform-specific assembly code is out of the scope of this paper.
Table 3 shows the speedups of openCNN with respect to cuDNN and the method in [10]. The peak speed up with respect to cuDNN is ×, and the average speedup is . Since ours is a CUDA C++ level implementation while cuDNN code is directly written in SASS, we consider that these results are very positive.As for the CUDA version of [10], the maximum and averages of speedup achieved are × and , respectively. The higher speedups are related to the first layers, precisely where the SASS implementation of [10] achieved the lower speedups with respect to cuDNN [10]. We hope that these optimizations can also be applied to SASS-level implementations, improving their performance.

Table 3.
SpeedUp. 1.34× on average over cuDNN and 1.58x over the [10] CUDA C++ implementation on Turing RTX 2080Ti.
Figure 16 contains a roofline model representation showing the effect of applying the previous optimizations on the three main tasks of the output transformation. The model compares the Fused Winograd convolution using optSTS64 layout (blue dot) to the cuDNN implementation (orange dot). Our implementation significantly increases the arithmetic intensity with respect to cuDNN because it uses a more aggressive cache-block size strategy as described in Section 3.
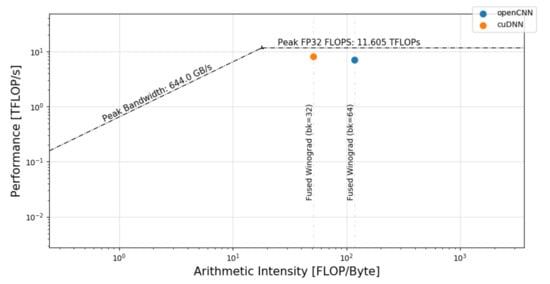
Figure 16.
Roofline model of cuDNN and openCNN on the Fused Winograd convolution.
Figure 17 shows the speedups of openCNN with respect to different cuDNN convolution implementations. The average speedups achieved with respect to the algorithms listed from top to bottom in the figure are: ×, , , , and . The results are favorable in most layers, the exception being the non-fused version of Winograd when K > 128. However, this is agnostic to the algorithm implementation, since in mathematical terms, there exists a break point with respect to the Non-Fused version of F() when the K value is above this threshold. Nevertheless, since the Non-Fused version implements each Winograd step in a different kernel, it needs to store the intermediate results in global memory, hence it must allocate a significant amount of memory as workspace and data loading can turn into a bottleneck. Moreover, the speedup over the GEMM-based convolution (IMPLICIT PRECOMP GEMM) goes up to , which is close to the theoretical multiplication reduction.
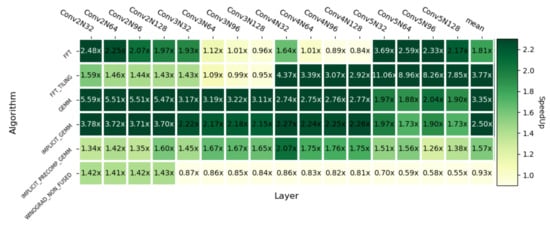
Figure 17.
Heatmap with respect to other cuDNN convolution algorithms on Turing RTX 2080Ti.
As described at the beginning of this section, the performance of our approach has also been measured on the Ampere architecture, namely on a NVIDIA RTX 3090 GPU. The aim of this experiment is to prove that, contrary to SASS code, our implementation can be ported to other architectures with little or no performance loss. Figure 18 depicts the results obtained. We can see that the proportions are maintained with respect to the results in Turing. However, this GPU provides much higher FP32 performance, and thus the FLOPS increase significantly.
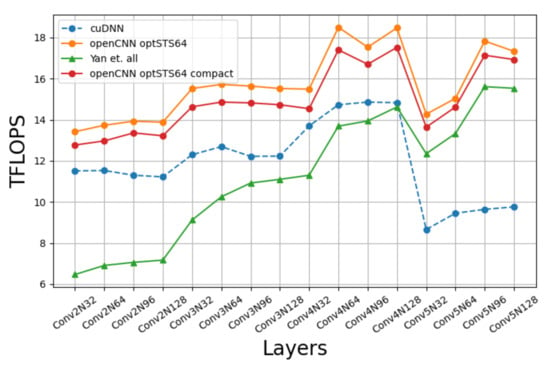
Figure 18.
Winograd openCNN performance on Ampere RTX 3090.
Table 4 shows the speedUp over cuDNN and the [10] CUDA implementation. In this case, the peak speedup with respect to cuDNN is and the average speedup is , both being higher than in Turing (Table 3).

Table 4.
SpeedUp. 1.34× on average over cuDNN and 1.49× over the [10] CUDA C++ implementation on Ampere RTX 3090.
Finally, returning to the comparison with different cuDNN convolution algorithms, Figure 19 represents the same information as Figure 17, but for the Ampere RTX 3090 GPU. We can see that the results are also positive despite changing the GPU architecture.
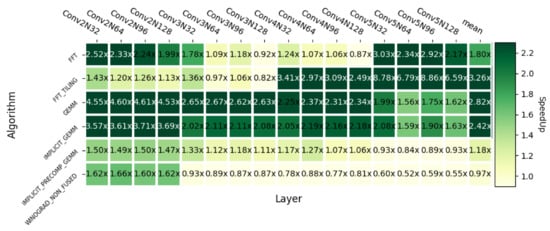
Figure 19.
Heatmap with respect to other cuDNN convolution algorithms on Ampere RTX 3090.
6. Related Work
There are some other works that focus on the optimization of the Winograd convolution algorithm in GPUs [15], CPUs [18] and FPGAs [25]. Regarding GPU approaches, the study in [10] tries to crack the ISA encoding in order to generate it directly from a machine assembly code (SASS) written by the programmer. This topic is not new, since many other projects followed a similar approach for older architectures like Kepler [11] and Maxwell/Pascal [26]. This strategy opens the possibility of hand-tuning low-level parameters like warp load-balancing or load/store instruction scheduling. Although [10] demonstrates that this approach can achieve a good performance on the Winograd convolution in comparison to cuDNN, it lacks generality with respect to other architectures, especially older ones.
Other works try to accelerate the Winograd convolution in a different way, by reusing computations rather than applying traditional optimizations [27]. This novel technique is called deep reuse. Another recent but sophisticated approach [28] divides the Winograd algorithm in subcomputations and establishes the data movement lower bounds to finally define the optimal I/O dataflow that maximizes data re-reuse. Furthermore, they propose an auto-tuning technique to dynamically find the optimal parameter configuration. We have noticed that none of the aforementioned projects have released their source code, making it difficult to reproduce this research and to compare with the performance of other approaches.
Another strategy is to try to accelerate CNNs through different convolution algorithms like FFT [29], GEMM-based [30] or direct convolution [31]. FFT is a competitive approach compared to Winograd when the filter size is large. However, in current CNN architectures, small filters are more popular [15]. A collection of CUDA C++ templates for Linear Algebra Subroutines is developed in [30]. As a result, in [30] there exists an open-source GEMM-based convolution implementation. However, Winograd implementations are approaching the theoretical multiplication reduction compared to GEMM-based solutions and thus, as we have seen in Section 5, Winograd is currently the reference to beat, free implementations being the key to continue improving its performance.
7. Conclusions
We have presented an open-source CUDA-only implementation of the Winograd convolution which is competitive in modern Nvidia GPU architectures such as Turing and Ampere. This implementation is based on the optimization ideas of a previous implementation of the algorithm, which combined CUDA and SASS code to achieve state-of-the-art performance. Unlike this reference implementation, ours is open-source and it is completely written in CUDA C++, which makes it more portable in terms of other platforms.
The design process of our proposal used microbenchmarking to fine-tune the performance of different hotspots detected in the reference implementation. Our openCNN approach achieves speedups up to with respect to cuDNN on Turing RTX 2080Ti and up to on Ampere RTX 3090. The code of this proposal has been released with the name openCNN as open-source software at https://github.com/UDC-GAC/openCNN, accessed on 28 July 2021.
As future work, we plan to generate a version of our code, the performance of which can be easily ported between different architectures through iterative parameter tuning.
Author Contributions
Conceptualization, R.L.C.; methodology, R.L.C., D.A. and B.B.F.; software, R.L.C.; validation, R.L.C.; formal analysis, R.L.C.; investigation, R.L.C., D.A. and B.B.F.; resources, D.A. and B.B.F.; data curation, R.L.C.; writing—original draft preparation, R.L.C. and D.A.; writing—review and editing, R.L.C., D.A. and B.B.F.; visualization, R.L.C.; supervision, D.A. and B.B.F.; project administration, D.A. and B.B.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ministry of Science and Innovation of Spain (PID2019-104184RB-I00, AEI/FEDER/EU, 10.13039/501100011033) and the predoctoral grant of Roberto L. Castro (FPU19/03974). and by the Xunta de Galicia co-founded by the European Regional Development Fund (ERDF) under the Consolidation Programme of Competitive Reference Groups (ED431C 2021/30). CITIC, Centro de Investigación de Galicia ref. ED431G 2019/01, receives financial support from Consellería de Educación, Universidade e Formación Profesional, Xunta de Galicia, through the ERDF (80%) and Secretaría Xeral de Universidades (20%).
Data Availability Statement
The source code was released as open-source software under the name openCNN and it can be found at https://github.com/UDC-GAC/openCNN, accessed on 28 July 2021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. Adv. Neural Inf. Process. Syst. 2015, 28, 91–99. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Hestness, J.; Narang, S.; Ardalani, N.; Diamos, G.F.; Jun, H.; Kianinejad, H.; Patwary, M.M.A.; Yang, Y.; Zhou, Y. Deep Learning Scaling is Predictable, Empirically. arXiv 2017, arXiv:1712.00409. [Google Scholar]
- Chetlur, S.; Woolley, C.; Vandermersch, P.; Cohen, J.; Tran, J.; Catanzaro, B.; Shelhamer, E. cuDNN: Efficient Primitives for Deep Learning. arXiv 2014, arXiv:1410.0759. [Google Scholar]
- ARM. Compute Library. Available online: https://github.com/ARM-software/ComputeLibrary (accessed on 28 June 2021).
- Intel. oneDNN. Available online: https://github.com/oneapi-src/oneDNN (accessed on 7 July 2021).
- Khan, J.; Fultz, P.; Tamazov, A.; Lowell, D.; Liu, C.; Melesse, M.; Nandhimandalam, M.; Nasyrov, K.; Perminov, I.; Shah, T.; et al. MIOpen: An open source library for deep learning primitives. arXiv 2019, arXiv:1910.00078. [Google Scholar]
- Yan, D.; Wang, W.; Chu, X. Optimizing Batched Winograd Convolution on GPUs. In Proceedings of the 25th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, San Diego, CA, USA, 22–26 February 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 32–44. [Google Scholar]
- Zhang, X.; Tan, G.; Xue, S.; Li, J.; Zhou, K.; Chen, M. Understanding the GPU Microarchitecture to Achieve Bare-Metal Performance Tuning. In Proceedings of the 22nd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Austin, TX, USA, 4–8 February 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 31–43. [Google Scholar]
- Nervana Systems. Neon. Available online: https://github.com/NervanaSystems/neon (accessed on 25 June 2021).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Winograd, S. Arithmetic Complexity of Computations; Siam: Philadelphia, PA, USA, 1980; Volume 33. [Google Scholar]
- Lavin, A.; Gray, S. Fast algorithms for convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4013–4021. [Google Scholar]
- Horn, R.A. The hadamard product. Proc. Symp. Appl. Math. 1990, 40, 87–169. [Google Scholar]
- Barabasz, B.; Gregg, D. Winograd Convolution for DNNs: Beyond Linear Polynomials. In AI*IA 2019–Advances in Artificial Intelligence; Alviano, M., Greco, G., Scarcello, F., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 307–320. [Google Scholar]
- Jia, Z.; Zlateski, A.; Durand, F.; Li, K. Optimizing N-dimensional, winograd-based convolution for manycore CPUs. ACM SIGPLAN Not. 2018, 53, 109–123. [Google Scholar] [CrossRef]
- NVIDIA. NVIDIA Turing GPU Architecture. 2018. Available online: https://images.nvidia.com/aem-dam/en-zz/Solutions/design-visualization/technologies/turing-architecture/NVIDIA-Turing-Architecture-Whitepaper.pdf (accessed on 18 June 2021).
- NVIDIA. CUDA C++ Programming Guide. Available online: https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#shared-memory-7-x (accessed on 24 June 2021).
- Jia, Z.; Maggioni, M.; Smith, J.; Scarpazza, D.P. Dissecting the NVidia Turing T4 GPU via Microbenchmarking. arXiv 2019, arXiv:1903.07486. [Google Scholar]
- Yan, D.; Wang, W.; Chu, X. Demystifying Tensor Cores to Optimize Half-Precision Matrix Multiply. In Proceedings of the 2020 IEEE International Parallel and Distributed Processing Symposium (IPDPS), New Orleans, LA, USA, 18–22 May 2020; pp. 634–643. [Google Scholar]
- MLPerf Org. Available online: https://mlcommons.org/en/ (accessed on 13 August 2021).
- NVIDIA. How to Implement Performance Metrics in CUDA C/C++. 2019. Available online: https://developer.nvidia.com/blog/how-implement-performance-metrics-cuda-cc/ (accessed on 21 June 2021).
- Huang, Y.; Shen, J.; Wang, Z.; Wen, M.; Zhang, C. A high-efficiency FPGA-based accelerator for convolutional neural networks using Winograd algorithm. J. Phys. Conf. Ser. 2018, 1026, 012019. [Google Scholar] [CrossRef]
- Gray, S. Maxas. Available online: https://github.com/NervanaSystems/maxas (accessed on 29 June 2021).
- Wu, R.; Zhang, F.; Zheng, Z.; Du, X.; Shen, X. Exploring deep reuse in winograd CNN inference. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Seoul, Korea, 27 February–3 March 2021; pp. 483–484. [Google Scholar]
- Zhang, X.; Xiao, J.; Tan, G. I/O lower bounds for auto-tuning of convolutions in CNNs. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Seoul, Korea, 27 February–3 March 2021; pp. 247–261. [Google Scholar]
- Mathieu, M.; Henaff, M.; LeCun, Y. Fast training of convolutional networks through FFTS. In Proceedings of the 2nd International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- NVIDIA. Cutlass. Available online: https://github.com/NVIDIA/cutlass (accessed on 14 July 2021).
- Georganas, E.; Avancha, S.; Banerjee, K.; Kalamkar, D.; Henry, G.; Pabst, H.; Heinecke, A. Anatomy of High-Performance Deep Learning Convolutions on SIMD Architectures. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis, Dallas, TX, USA, 11–16 November 2018; IEEE Press: New York, NY, USA, 2018. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).