1. Introduction
In this paper, we introduce a new second-order hydrodynamic traffic model that generalizes the existing second-order models. The key feature of the new model is the notion of the relative velocity of the congestion (compression wave) propagation. This quantity can be obtained empirically from traffic detector measurements. Moreover, knowledge of the congestion relative velocity obviates the need for the fundamental diagram. We test the proposed model through numerical experiments using typical traffic detector data from the Performance Measurement System (PeMS) ([
1]), on the I-580 freeway in California, USA.
An extensive development of gas dynamics (generalized conservation laws, stable differencing schemes) occurred in the 1950s, when the first macroscopic (hydrodynamic) models were developed. In those models, traffic flow was likened to a flow of “motivated” compressible liquid. For instance, the Lighthill–Whitham–Richards (LWR) model ([
2,
3]) describes the traffic flow through the law of conservation of vehicles. This model postulates the unique dependence of traffic flow on traffic density, which is called a fundamental diagram, and assumes a unique relationship between traffic speed
and density
:
. Here,
denotes vehicle density—the number of vehicles per unit length of the road at time
t around the position
x; and
denotes mean traffic speed at time t around the position
x. The function
is non-increasing:
. We denote the flow (i.e., the number of vehicles passing a reference point in unit time) as
. The function is referred to as the fundamental diagram (although sometimes this name is reserved for
). The vehicle conservation law in the LWR model is expressed in the differential form of a continuity equation with zero right-hand side:
Later, the class of macroscopic models has expanded to systems of non-linear hyperbolic second-order PDEs, where the unique dependence of traffic density and speed is no longer assumed ([
4,
5,
6,
7,
8,
9,
10,
11,
12]). These models differ in the way that they describe the dependency of traffic flow (or velocity) on density. Here, we will discuss some popular second-order models and show how they can be generalized using the relative velocity of the congestion.
We start with the Payne–Whitham model ([
4,
13]) with zero right-hand side to simplify the subsequent calculations:
where
is the so-called traffic ‘sound speed’, and generalize it for the arbitrary form of the relative velocity of the congestion,
:
With
defined in (
3), model (
2) can be rewritten ([
8]):
which generalizes (
2). The proposed model (
4) can also be written in the conservative form:
The work ([
8]) also proposed the model (
4) in anisotropic form, defined by system:
where the relative velocity of the congestion propagation is expressed through the derivative of the equilibrium speed:
Note that system (
6) is almost identical to the system proposed in ([
7]) when its second equation is in a non-conservative form. The difference is in the form of
. In ([
7]), the smooth function
is used instead of the equilibrium speed
:
From the physical standpoint, the use of the equilibrium speed
in (
7) instead of an arbitrary smooth increasing function
is more justified (see ([
8])), as the function
is generally not smooth in points of transition between different traffic phases.
A system similar to (
6), but with an additional relaxation term
in the right-hand side, was introduced in ([
10,
11]):
where the equilibrium speed is expressed as
in ([
10,
11]); and as
in ([
11]).
The rest of the paper is organized as follows.
Section 2 has two parts: in
Section 2.1 the relative velocity of congestion propagation is expressed using the model variables, traffic velocity
v and density
;
Section 2.2 proposes the generalized second-order model and shows, using the relative velocity of the congestion (compression wave) propagation, that the existing second-order models are special cases of the proposed one.
Section 3 presents the discretized numerical method for model simulation.
Section 4 discusses the simulation results, which support the proposition that different second-order models with the same expression for the relative velocity of the congestion behave similarly.
Section 5 concludes the paper.
3. Computational Method
The second-order model (
15) is of a hyperbolic type. A variety of finite-difference methods for solving such systems exist. By introducing vectors
and
, the system (
15) can be written in the vector form:
with the Jacobian:
In (
22),
is a diagonal matrix of eigenvalues of the Jacobian
A;
is the matrix of left eigenvectors of
A; and
is the inverse of
.
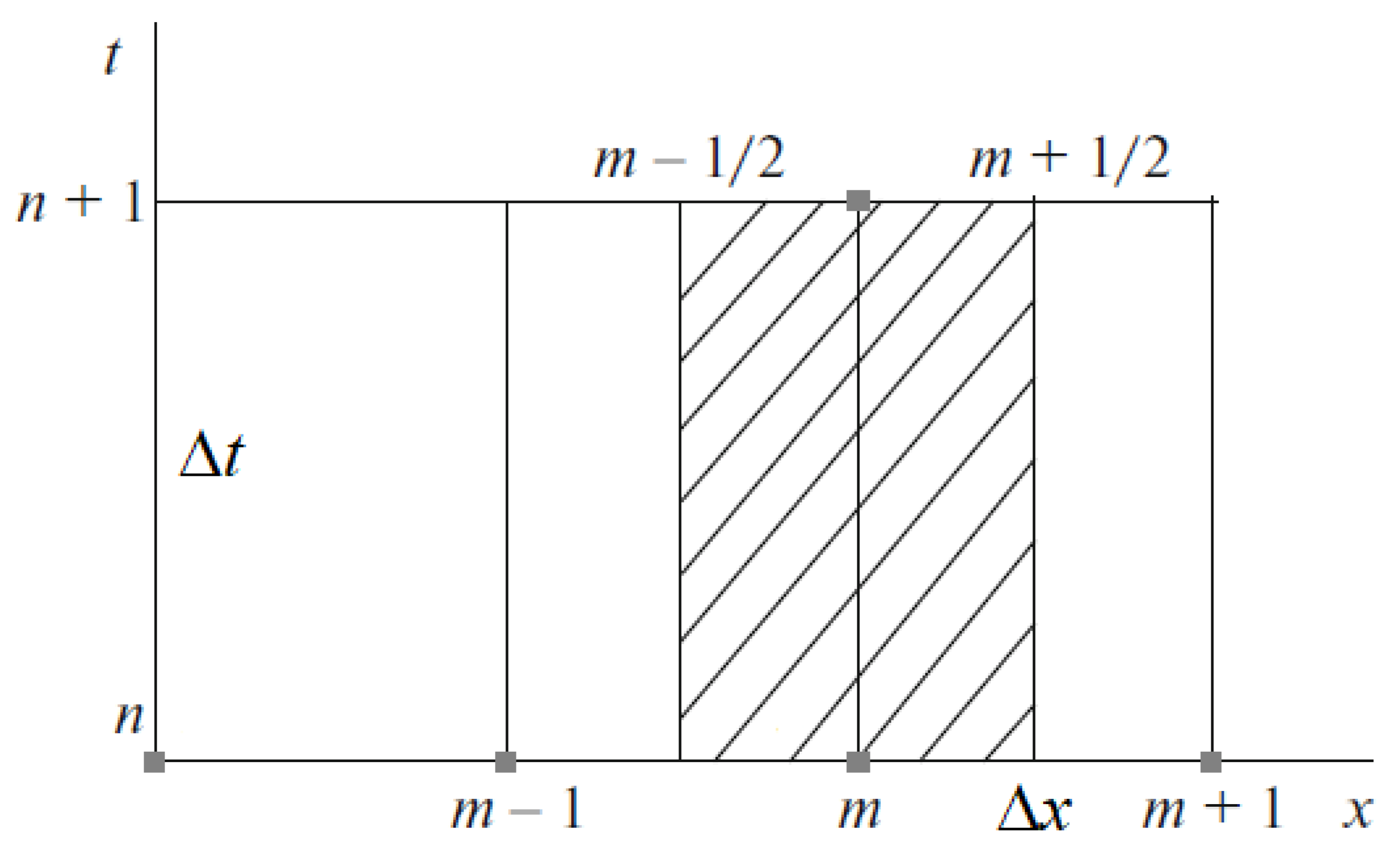
Next, we write a finite-difference approximation on the grid shown in
Figure 1 by making the values of the equation variables constant at the edges of the grid:
Here, is the grid node index along the x-axis, , is the grid node index along the t-axis, and are numerical integration steps bounded via the Courant condition: .
For system (
15), the whole family of difference schemes can be expressed as follows (Kholodov and Tsybulin, 2018):
The choice of the approximation method for
in (
23) is crucial for obtaining the scheme with the desired properties. When choosing a difference scheme, we presume that the solution for the model equations at every road segment is defined by the change in computed values in its boundary points. In this case, we can choose the conservative monotonic characteristic method of the first-order approximation ([
16]) with the following expressions for
:
These could also be more complex expressions, which allow for the building of higher-order (hence, higher-accuracy) difference schemes for a given stencil. Variable values in the neighboring nodes
in (
24) can be computed using a simple linear interpolation without loss of accuracy.
To obtain the characteristic form of compatibility equations, equivalent to the system (
21) along the characteristics
, we multiply the system (
21) from the left by the eigenvector matrix
(i.e., we compose 2 linearly independent combinations of the original equations) and bring it to the characteristic form:
Then, in the scalar form, this yields:
Each of the two equations (
26) is an ordinary differential equation along the characteristic
.
We usually need to numerically integrate the compatibility conditions (
26) at boundary points along the characteristics entering the integration area. For example, at the beginning of the freeway segment at boundary point
with negative eigenvalue
, we use:
together with the boundary condition for traffic velocity
.
At the end of the freeway segment, we do the same for the positive
:
for both compatibility equations, because
is always positive.
We should reiterate that the relative velocity of the congestion,
in (
22)–(
28) can be defined using equilibrium velocity
as was done in ([
8]). The function for equilibrium velocity
(fundamental diagram) can be empirically set using historic traffic detector data for each road segment. We propose the new approach without using equilibrium velocity or any form of a fundamental diagram
. We approximate the value of the relative velocity of the congestion propagation,
, using traffic density and velocity observed by traffic detection at the current time instant:
This approach enables our model (
15) to instantly adjust to the changing road situation at runtime.
4. Numerical Results
To verify the proposed model, we carried out numerical experiments using traffic detector data for a segment of the I-580 freeway in California, USA, obtained from PeMS ([
1]). We used two loop detectors, denoted
and
, separated by
km segment of the 4-lane freeway with no entrances or exits, as shown in
Figure 2.
The data of the stationary traffic detectors
and
were used to construct the corresponding fundamental diagrams for equilibrium velocity
. According to the three-phase traffic theory ([
17]), the following traffic phases are distinguished:
For each phase, we define separate functions and , stitching them together at the transition points:
Free flow:
Synchronized flow:
Wide moving jam:
For the traffic detectors showcased in
Figure 2, we have the following coefficients and parameters, aggregated over four lanes of I-580:
detectors : veh./m, , , veh./m, , , , m/s, veh./m;
detectors # 2: veh./m, , , veh./m, , , , m/s, veh./m;
For the separate lane of the I-580 freeway, the following parameters are different. For example, in the first lane:
detectors : veh./m, , , veh./m, , , , m/s, veh./m;
detectors : veh./m, , , veh./m, , , , m/s, veh./m;
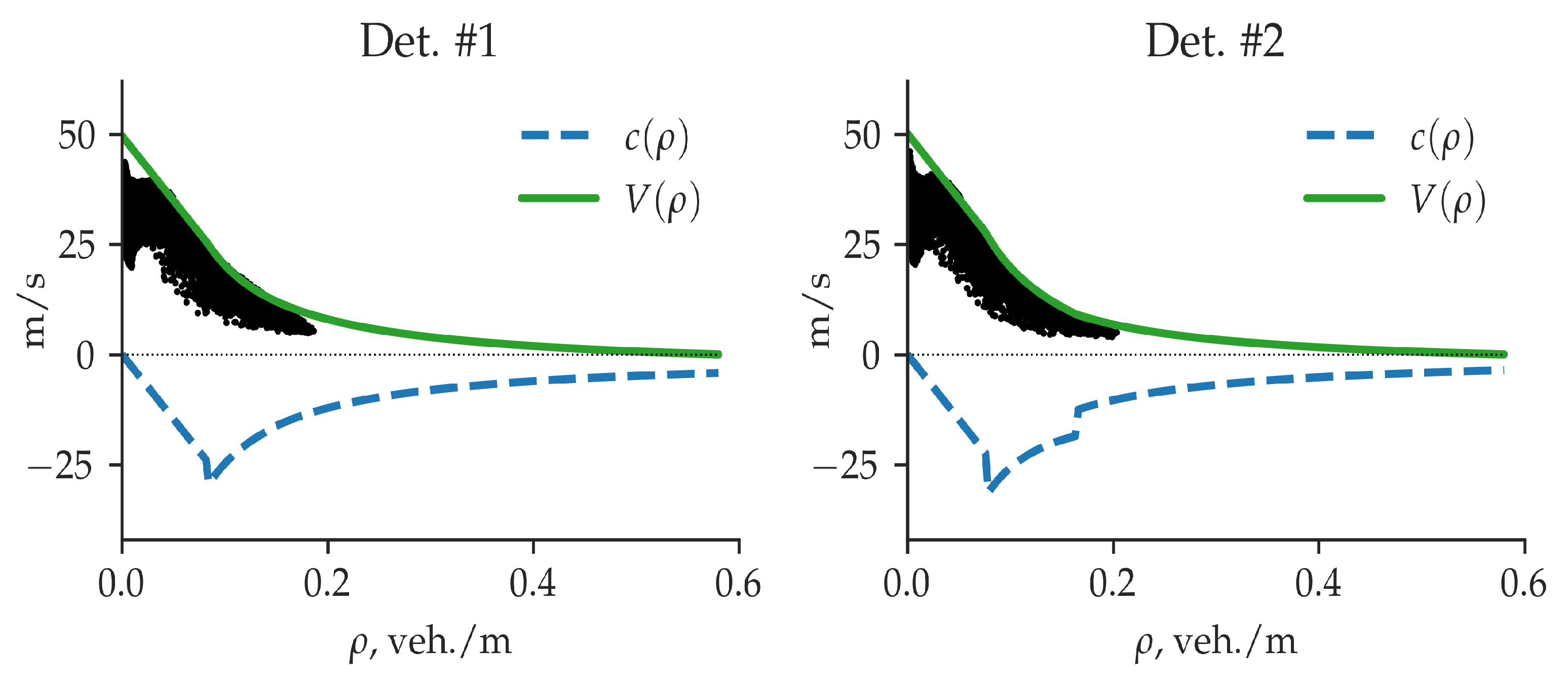
The equilibrium velocity
— solid green line and the relative velocity of the congestion propagation
— dashed blue line are shown as the functions of density for both detectors, together with the historic data for the one-year period in
Figure 3 for the first lane and in
Figure 4 aggregated over all four lanes.
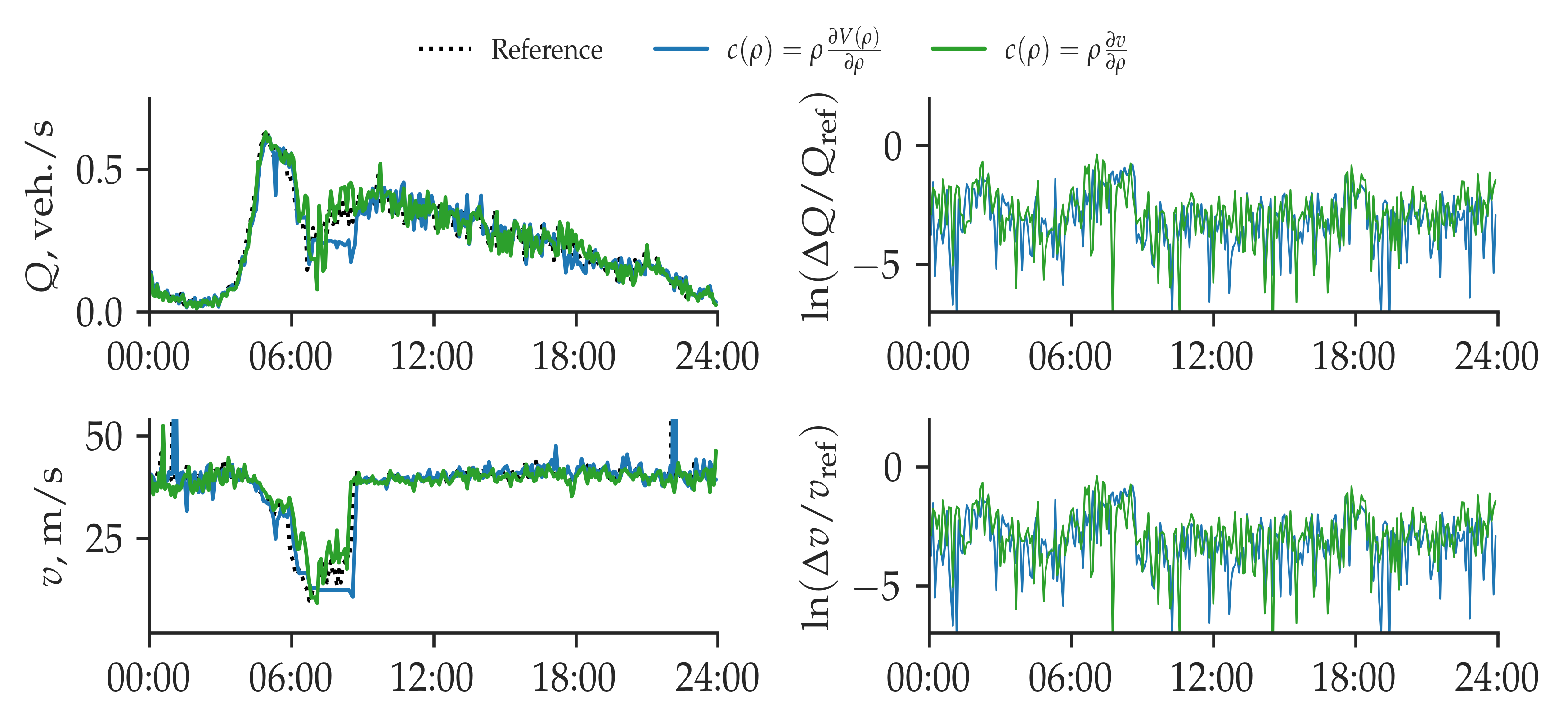
Data (traffic flow and velocity, with 30-second temporal resolution) from detector
were used as the initial and left boundary conditions, and data from the downstream detector
were used for verification of the model output. We simulated a 24-h interval for a single weekday for all lanes of I-580. The results are shown in
Figure 5 for the first lane and in
Figure 6 aggregated over four lanes in different subplots: top left, traffic flows; top right, flow relative error in logarithmic scale; bottom left—traffic velocities; bottom right — velocity relative error in the logarithmic scale.
The simulation results obtained with a different expression for the relative velocity of the congestion propagation are shown in different colors: proposed macroscopic second-order model, where we approximate the value of relative velocity of the congestion,
, using instantaneous measurements of traffic density and speed (
29), is shown in green; the same model (
15), with equilibrium velocity
as an empirical function of density obtained from the historic detector data, is shown in blue. The reference results (data of detector
) are depicted by a grey dashed line.
The simulation shows a good but not exact match with the results obtained using the same second-order macroscopic model (15) with a different form of the relative velocity of the congestion propagation, . We also see that both approaches have a good match with the reference results.
The root mean square error (RMSE) of velocity for the results of compared models and the detector
measurements in
Figure 5 is
m/s for the model (
15) with
; and
m/s, if
. For the flow, RMSE is
veh./s, if
; and
veh./s, if
. For the results in
Figure 6, velocity RMSE is
m/s, if
; and
m/s, if
. The flow RMSE is
veh./s if and
veh./s, respectively.
The difference in the results between these two approaches come from the time structure. In the first case, we have the continuous empirical function , with values dependent only on traffic density at each time instant. In the second case, we have a discrete function , with values dependent both on traffic density and velocity. An instant error generally occurs in detector measurements, which is smoothed out in the first case, when we use the fundamental diagram.