Abstract
In this paper, we consider the application of several gradient methods to the traffic assignment problem: we search equilibria in the stable dynamics model (Nesterov and De Palma, 2003) and the Beckmann model. Unlike the celebrated Frank–Wolfe algorithm widely used for the Beckmann model, these gradients methods solve the dual problem and then reconstruct a solution to the primal one. We deal with the universal gradient method, the universal method of similar triangles, and the method of weighted dual averages and estimate their complexity for the problem. Due to the primal-dual nature of these methods, we use a duality gap in a stopping criterion. In particular, we present a novel way to reconstruct admissible flows in the stable dynamics model, which provides us with a computable duality gap.
1. Introduction
The Beckmann model for searching static traffic equilibria in road networks is among the most widely used models by transportation planners [1,2]. The equilibria found are practical for evaluating the network efficiency and distribution of business centers and residential areas, and establishing urban development plans, etc. This model introduces a cost function on every link of a transportation network, which defines a dependence of the travel cost on the flow along the link. In practice, the BPR functions are usually employed [3]:
where are free flow times, and are road capacities of a given network’s link e. We take these functions with parameters and .
Nesterov and de Palma [4] proposed an alternative model called the stable dynamics model, which takes an intermediate place between static and dynamic network assignment models. Namely, its equilibrium can be interpreted as the stationary regime of some dynamic process. Its key assumption is that we no longer introduce a complex dependence of the travel cost on the flow (as in the standard static models) but only pose capacity constraints, i.e., the flow value on each link imposes the feasible set of travel times
Unlike in the Beckmann model, there is no one-to-one correspondence between equilibrium travel times and flows on the links of the network. We can illustrate the difference on a simple example of two parallel routes (Figure 1).
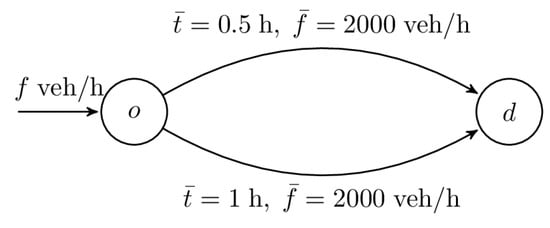
Figure 1.
Parallel routes.
Let the input flow take values 1000, 2000, and 3000 veh/h. For the stable dynamics model, in the first and second cases, all drivers choose the upper route; the equilibrium travel time simply equals the upper route’s free flow time (0.5 h) in the first case and varies from 0.5 to 1 h (according to the model) in the second. In the third case, the input flow exceeds the upper route’s capacity, so the upper route’s flow is 2000 veh/h, the lower one is 1000 veh/h, and the equilibrium travel time is 1 h. All these equilibria can be interpreted as stationary regimes of some dynamic processes, e.g., the last case can be viewed as the result of the queue at the beginning of the upper route (since this route’s capacity is smaller than the input flow) created by drivers who wanted to take this route until the waiting time plus the route’s travel time reached the lower route’s travel time [4]. In the Beckmann model, equilibria are as follows: for all three cases, only the upper route is used, and the equilibrium travel times are approximately 0.5, 0.6, and 0.9 h, respectively. Chudak, Dos Santos Eleuterio, and Nesterov [5] conducted a detailed comparison—for large and small networks—of equilibria in these two models.
In the Beckmann model, searching equilibria reduces to minimization of a potential function. One of the most popular and effective approaches to solve this problem numerically is the famous Frank–Wolfe method [6,7] as well as its numerous modifications [8,9,10,11].
In the case of the stable dynamics model, one cannot directly apply the Frank–Wolfe method. However, an equilibrium can be found as a solution of a pair of primal and dual optimization problems. The same holds also for the Beckmann model, so in both cases we can apply primal-dual (sub)gradient methods.
In this work, we compare several primal-dual gradient methods for searching equilibria in both the Beckmann and the stable dynamics models, namely, the universal gradient method (UGM) [12], the universal method of similar triangles (UMST) [13], and the method of weighted dual averages (WDA) [14]. The main advantage of the above universal methods is an automatic adjustment to a local (Hölder) smoothness of a minimized function, which is especially important since the dual problems we are dealing with are essentially non-smooth. Due to the primal-dual nature of these methods, one can use an adaptive stopping criterion guaranteeing required accuracy.
The main contributions of this paper include the following:
- We propose a novel way to reconstruct admissible flows (i.e., meeting the capacity constraints and induced by flows on the paths) in the stable dynamics model and a novel computable duality gap, which can be used in a stopping criterion.
- We provide theoretical upper bounds on the complexity of searching equilibria by the considered algorithms: UMST, UGD, and WDA.
- We conducted numerical experiments comparing these algorithms on the Anaheim transportation network—the source code is available for use and can be found in [15].
The paper is organized as follows. In Section 2, we give a problem statement and define equilibria in the Beckmann and the stable dynamics models and corresponding optimization problems. Section 3 is devoted to the complexity analysis of UGM, UMST, and WDA. We show that the number of iterations required to obtain an -solution of primal and dual problems is for UGM and UMST. In Section 4, results of experiments on the Anaheim transportation network are presented. Finally, some conclusions are drawn in Section 5.
2. Problem Statement
Let the urban road network be represented by a directed graph , where vertices V correspond to intersections or centroids [16] and edges E correspond to roads, respectively. Suppose we are given the travel demands: namely, let (veh/h) be a trip rate for an origin–destination pair w from the set . Here, is the set of all possible origins of trips, and is the set of destination nodes. For OD pair denote by the set of all simple paths from i to j. Respectively, is the set of all possible routes for all OD pairs. Agents traveling from node i to node j are distributed among paths from , i.e., for any there is a flow along the path p, and . Flows from vertices from the set O to vertices from the set D create the traffic in the entire network G, which can be represented by an element of
Note that the dimension of X can be extremely large: e.g., for Manhattan network . To describe a state of the network, we do not need to know an entire vector x but only flows on arcs:
where . Let us introduce a matrix such that for , , so in vector notation we have . To describe an equilibrium we use both path- and link-based notations or .
- Beckmann model.
One of the key ideas behind the Beckmann model is that the cost (e.g., travel time, gas expenses) of passing a link e is the same for all agents and depends solely on the flow along it. In what follows, we denote this cost for a given flow by . Another essential point is a behavioral assumption on agents called the first Wardrop’s principle: we suppose that each of them knows the state of the whole network and chooses a path p minimizing the total cost
The cost functions are supposed to be continuous, non-decreasing, and non-negative. Then , where , is an equilibrium state, i.e., it satisfies conditions
if and only if is a minimum of the potential function:
and [1].
Another way to find an equilibrium numerically is by solving a dual problem. According to Theorem 4 from [4], we can construct it in the following way:
where
is the conjugate function of , . Finally, we obtain the dual problem, the solution of which is :
When we search for the solution to this problem numerically, on every step of an applied method, we can reconstruct primal variable f from the current dual variable t: (see Section 3.1). Then we can use the duality gap, which is always nonnegative, for the estimation of the method’s accuracy:
It vanishes only at the equilibrium .
- Stable dynamics model [4].
An equilibrium state of the stable dynamics model satisfies the next conditions:
where is defined earlier by (2). The above formula can be reformulated in terms of an optimization problem:
Here, we add underlined constant terms to show that the pair is an equilibrium if and only if it is a solution of the saddle-point problem
where its primal problem is
and its dual problem is
In contrast with the Beckmann model, the equilibrium state in the stable dynamics model is defined by pair (in particular, it differs from the system optimum in the model only by the time value).
3. Numerical Methods
We have the following objective functions
- The stable dynamics model:
- The Beckmann model:
In both cases, it has the form
The optimization problem (4) is convex, non-smooth, and composite. We use all these properties to identify the best optimization method to solve the considered problem.
3.1. Subgradient
In our research, we consider first-order methods, i.e., they require a subgradient of , the properties and effective computation of which we discuss in this section.
To get the subdifferential , let us re-write in the following way:
where the vector encodes a path p. Obviously, the shortest path may not be unique. Using the rules of subgradient calculus [17] we get the following expression:
i.e., the subdifferential is a sum of convex hulls of binary vectors that encode the shortest length paths. An important consequence is that for any and , , the following bound holds:
where H is the diameter of the graph G.
Note that any element from the set has the form , where is a flow distribution on links induced by concentrated on the shortest paths for given times t (and vice versa: any such f corresponds to a subgradient of ).
In practice, the calculation of flows f is the most expensive part, since we have to find the shortest paths for all pairs . We use the following Algorithm 1. We use Dijkstra’s Algorithm [18] to find the shortest paths in line 3, which runs in time; finding the traversal order with topological sort (Section 22.4 in [19]) and further flows aggregation have linear performance . Hence, the total complexity of Algorithm 1 is . When the transportation network is an (almost) planar graph or another sparse graph, and the complexity is . Moreover, flows reconstruction for every source can be computed in parallel, and Dijkstra’s algorithm can also be parallelized and has efficient implementations [20,21].
| Algorithm 1 Flows reconstruction. |
Input: times t
|
3.2. Reconstruction of Admissible Flows in SD Model
For given times t considered, Algorithm 1 reconstructs feasible flows f, i.e., for some . These flows meet all the constraints in the Beckmann model, but they can violate the capacity constraints in the stable dynamics model. In the latter case, an additional step is required to obtain admissible flows from f. Note that we could instead find flows that meet capacity constraints first (Theorem 8 from [4]), but to reconstruct feasible flows from them is a more complex problem.
Suppose we are given some flows such that
Then for any we can construct admissible flows in the following way: let , then
In practice, we propose the following procedure to find admissible flows g: run some optimization method (e.g., UGM) for a small number of iterations for the same problem but with decreased capacities: instead of ; if obtained feasible flows satisfy , then take ; otherwise, run it again with capacities and check , etc.
- Stopping criterion.
The stopping criterion we use for the stable dynamics model is based on a duality gap
where , are estimates of an equilibrium after N iterations of the applied method. Note that here the duality gap with is not applicable.
3.3. Universal Gradient Method
The method for solving non-smooth problems with smooth techniques was proposed by Nesterov [12] and was called the universal gradient method. The pseudocode of UGM for the considered problem (4) is provided in Algorithm 2. Here, the euclidean prox-structure is used. Note that we did not specify the stopping criterion as it can be different for different models.
| Algorithm 2 Universal gradient method. |
Input:, accuracy
|
Now let us define
where are the estimates of the local Lipschitz constant in UGM and UMST methods.
Convergence of the UGM was proved in [12] and is summarized in the following lemma and theorem. Appendix A is the proofs for UGM.
Lemma 1.
After N iterations of UGM for the stable dynamics model, it holds that
where , , and are defined by (8), and is the distance from the starting point to a solution.
Theorem 1.
Now we provide results on the rate of convergence for the Beckmann model. The stopping criterion in this case is the following:
Lemma 2.
3.4. Universal Method of Similar Triangles
Let us introduce the following notations:
Flows are reconstructed in the following way:
Lemma 3.
After N iterations of UMST for the stable dynamics model, it holds that
where is defined by (18) and is the distance from the starting point to a solution.
Theorem 3.
Theorem 4.
Let , where M comes from (5). Then, after at most
iterations of UMST for the Beckmann model, it holds that . Moreover, the stopping criterion (14) with is fulfilled after at most
iterations, where is defined by (17). Appendix B is the proofs for UMST.
3.5. Method of Weighted Dual Averages
Convergence of the WDA method was proved in [14] and is summarized in the following theorem. Appendix C is the proofs for WAD.
Theorem 5.
Non-composite WDA-method satisfies the following bounds
- For the stable dynamics model:
- For the Beckmann model if :
4. Numerical Experiments
This section presents numerical results for the algorithms described above, namely, composite variants of UMST and UGM, both composite and non-composite WDA-method, on the Anaheim network [5,22]. The network consists of 38 zones, 416 nodes, and 916 links. Experiments and the source code in Python 3 [23] can be found in [15]. We used Dijkstra’s algorithm for finding the shortest paths in the network from the graph-tool library [24], where it is implemented in C++. We also used the Numpy library [25] for all vector operations.
- Stable dynamics model.
Parameters of the network are adjusted to the Beckmann model, so we have to increase the capacities to ensure the existence of an equilibrium for the stable dynamics model. In our experiments, the capacities are multiplied by . In Figure 2, we plot the number of (inner) iterations of the algorithms required to fulfill the stopping criterion (7) against . We consider the number of inner iterations for Algorithms 3 and 2 since the complexity of an inner iteration in this case is similar to the complexity of an iteration of the other algorithms. Note that according to ([12], formula (2.23)) the number of inner iterations of UGM or UMST at step k is bounded as
so asymptotic rates from Theorems 1–4 are still valid.
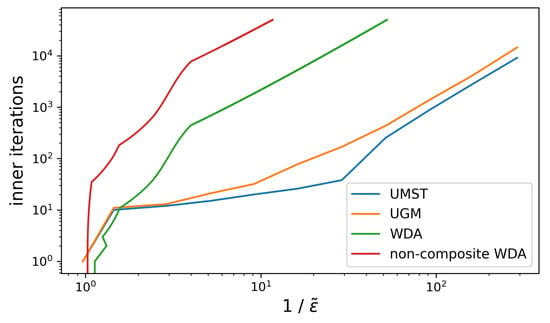
Figure 2.
Convergence rates of UMST, UGM, composite and non-composite WDA-methods for the stable dynamics model with the stopping criterion (7). Here, is the relative accuracy , where is the duality gap at the start point.
As we can see, the best results are shown by UMST, followed by UGM having similar performance. Both composite and non-composite WDA-method in Algorithm 4 are much slower.
| Algorithm 3 Universal Method of Similar Triangles. |
Input:, accuracy
|
| Algorithm 4 Method of Weighted Dual Averages. |
Input: accuracy , constant
|
- Beckmann model.
For the Beckmann model, we also compare our methods with the Frank–Wolfe algorithm (Algorithm 5), of which the theoretical convergence rate for a convex objective (with Lipschitz-continuous gradient) is [7,26].
Figure 3 shows the convergence rates of the methods for the Beckmann model. The Frank–Wolfe method demonstrates the best results and is followed by UMST. Unlike the stable dynamics case, the composite WDA-method is faster than UGM. However, the non-composite WDA-method has the worst performance again.
| Algorithm 5 Frank–Wolfe algorithm. |
Input: accuracy
|
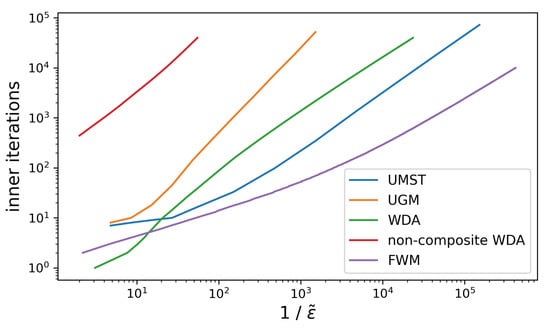
Figure 3.
Convergence rates of UMST, UGM, composite and non-composite WDA-methods, and the Frank–Wolfe method for the Beckmann model with the stopping criterion (14). Here, is the relative accuracy , where is the duality gap at the start point.
5. Conclusions
We considered several primal-dual subgradient methods for finding equilibria in the stable dynamics and the Beckmann models. We suggested a way to reconstruct admissible flows in the stable dynamics model, which provides us with a novel computable duality gap. Complexity bounds for UMST and UGM were presented in terms of the iterations number required to achieve a desired accuracy in the dual function value or the duality gap. Finally, we conducted numerical experiments comparing convergence of the considered algorithms on the Anaheim transportation network: UMST is the best one for optimization of the dual problems in both models. Furthermore, using the duality gap as a stopping criterion, we compared these methods with the Frank–Wolfe algorithm for the Beckmann model, which, as expected, remains the most suitable approach in this case (but it is not applicable for the stable dynamics model).
The reader may be interested in another related topic—searching stochastic traffic equilibria. In [27,28], we (with our colleagues) studied the application of the UMST for finding Nash–Wardrop stochastic equilibria in the Beckmann model. In this case, a driver selects a route randomly according to Gibbs’ distribution taking into account current time costs on the links of the network. It leads to iteration complexity , where is a stochasticity parameter (when , the model boils down to the ordinary Beckmann model). However, the great decrease in the number of iterations comes along with a more expensive calculation of the objective function’s gradient.
Author Contributions
Conceptualization, A.G.; formal analysis, M.K. and A.G.; software, M.K.; supervision, A.G; validation, M.K. and A.G.; writing—original draft, M.K.; Writing—review and editing, M.K. and A.G. All authors have read and agreed to the published version of the manuscript.
Funding
The research of M. Kubentayeva was supported by the Russian Science Foundation (project 18-71-10108). The research of A. Gasnikov was partially supported by RFBR, project number 18-29-03071 mk, and was partially supported by the Ministry of Science and Higher Education of the Russian Federation (Goszadaniye) No. 075-00337-20-03.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank Yu. Nesterov for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Proofs for UGM
Proof of Lemma 1.
Equation (9) follows immediately if one substitutes . Now let us estimate the first term on the r.h.s.
Here, we used . Therefore,
Now, notice that since the flow is induced by some traffic distribution , we have
hence
This yields
and thus
□
Proof of Theorem 1.
Theorem 1 in [12] ensures that for all , thus . Then the first bound (12) follows immediately from (9).
Now, let us prove the second bound. First, suppose for all . Then , thus by (10) for
Otherwise, if , one has , where , hence (9) and (10) yield
Finally, according to (11)
Combining all bounds together we obtain
and substituting , we conclude that the stopping criterion (7) is fulfilled. □
Proof of Lemma 2.
First of all, note that
and maximum is attained at point . As in the proof of Theorem 1, the inequality (A1) holds in Beckmann’s model case. Then, the first term in the r.h.s. can be estimated as follows
and we finally get an upper bound on the duality gap:
At the same time, substituting one obtains
□
Proof of Theorem 2.
By construction, for all , thus . According to Theorem 1 in [12] ; thus, the statement follows immediately from Lemma 2. □
Appendix B. Proofs for UMST
Proof of Lemma 3.
According to the inequality (30) in [13]
Note that the above inequality has the same form as (A1), if one replaces with , with , with , and with . Then the claim follows by the same reasoning as in the proof of Lemma 1. □
Proof of Theorem 3.
Due to (5) one has
From Young’s inequality we get that
If , then the stopping condition for inner iterations is fulfilled. Therefore, at the end of the k-th iteration either or .
Now we are going to prove by induction that , which is equivalent to , for all . For it follows from and . In the case where equation immediately yields . If , then by the induction hypothesis and monotonicity of the sequence we obtain
Therefore,
Arguing in the same way as in the proof of Theorem 1, we obtain that
and
After substitution or the claim follows. □
Proof of Theorem 4.
Repeating the proof of Theorem 2, we obtain that
Then, we conclude applying (A3). □
Appendix C. Proof for WDA
Proof of Theorem 5.
According to Equation (3.5) from [14],
whenever for all k.
In case of the stable dynamics model ; thus, we can take .
For the Beckmann model
Theorem 3 in [14] yields that for all k, thus . Then, using one obtains
thus we can take
□
References
- Beckmann, M.J.; McGuire, C.B.; Winsten, C.B. Studies in the Economics of Transportation; Yale University Press: New Haven, CT, USA, 1956. [Google Scholar]
- Patriksson, M. The Traffic Assignment Problem: Models and Methods; Courier Dover Publications: Mineola, NY, USA, 2015. [Google Scholar]
- US Bureau of Public Roads. Traffic Assignment Manual; Department of Commerce, Urban Planning Division: Washington, DC, USA, 1964.
- Nesterov, Y.; De Palma, A. Stationary dynamic solutions in congested transportation networks: Summary and perspectives. Netw. Spat. Econ. 2003, 3, 371–395. [Google Scholar] [CrossRef]
- Chudak, F.A.; Dos Santos Eleuterio, V.; Nesterov, Y. Static traffic assignment problem: A comparison between Beckmann (1956) and Nesterov & de Palma (1998) models. In Proceedings of the 7th Swiss Transport Research Conference, Ascona, Switzerland, 12–14 September 2007. [Google Scholar]
- Frank, M.; Wolfe, P. An algorithm for quadratic programming. Nav. Res. Logist. Q. 1956, 3, 95–110. [Google Scholar] [CrossRef]
- Jaggi, M. Revisiting Frank–Wolfe: Projection-free sparse convex optimization. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 427–435. [Google Scholar]
- Fukushima, M. A modified Frank–Wolfe algorithm for solving the traffic assignment problem. Transp. Res. Part B Methodol. 1984, 18, 169–177. [Google Scholar] [CrossRef]
- LeBlanc, L.J.; Helgason, R.V.; Boyce, D.E. Improved efficiency of the Frank–Wolfe algorithm for convex network programs. Transp. Sci. 1985, 19, 445–462. [Google Scholar] [CrossRef]
- Arezki, Y.; Van Vliet, D. A full analytical implementation of the PARTAN/Frank–Wolfe algorithm for equilibrium assignment. Transp. Sci. 1990, 24, 58–62. [Google Scholar] [CrossRef]
- Chen, A.; Jayakrishnan, R.; Tsai, W. Faster Frank–Wolfe Traffic Assignment with New Flow Update Scheme. J. Transp. Eng. ASCE 2002, 128. [Google Scholar] [CrossRef]
- Nesterov, Y. Universal gradient methods for convex optimization problems. Math. Program. 2015, 152, 381–404. [Google Scholar] [CrossRef]
- Gasnikov, A.V.; Nesterov, Y.E. Universal method for stochastic composite optimization problems. Comput. Math. Math. Phys. 2018, 58, 48–64. [Google Scholar] [CrossRef]
- Nesterov, Y. Primal-dual subgradient methods for convex problems. Math. Program. 2009, 120, 221–259. [Google Scholar] [CrossRef]
- Kubentayeva, M. TransportNet. 2021. Available online: https://github.com/MeruzaKub/TransportNet (accessed on 30 April 2021).
- Sheffi, Y. Urban Transportation Networks; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985; Volume 6. [Google Scholar]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Crauser, A.; Mehlhorn, K.; Meyer, U.; Sanders, P. A parallelization of Dijkstra’s shortest path algorithm. In International Symposium on Mathematical Foundations of Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; pp. 722–731. [Google Scholar]
- Yin, C.; Wang, H. Developed Dijkstra shortest path search algorithm and simulation. In Proceedings of the 2010 International Conference on Computer Design and Applications, Qinhuangdao, China, 25–27 June 2010; Volume 1, pp. V1–V116. [Google Scholar]
- Transportation Networks for Research Core Team. Transportation Networks for Research. 2021. Available online: https://github.com/bstabler/TransportationNetworks (accessed on 30 April 2021).
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Peixoto, T.P. The graph-tool python library. Figshare 2014. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Negiar, G.; Askari, A.; Jaggi, M. Linearly Convergent Frank-Wolfe with Backtracking Line-Search. In Proceedings of the 23rd International Conference on Artificial Intelligence and Statistics, Palermo, Italy, 3–5 June 2020. [Google Scholar]
- Gasnikov, A.V.; Kubentayeva, M.B. Searching stochastic equilibria in transport networks by universal primal-dual gradient method. Comput. Res. Model. 2018, 10, 335–345. [Google Scholar] [CrossRef]
- Baimurzina, D.R.; Gasnikov, A.V.; Gasnikova, E.V.; Dvurechensky, P.E.; Ershov, E.I.; Kubentaeva, M.B.; Lagunovskaya, A.A. Universal method of searching for equilibria and stochastic equilibria in transportation networks. Comput. Math. Math. Phys. 2019, 59, 19–33. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).