Two Gaussian Bridge Processes for Mapping Continuous Trait Evolution along Phylogenetic Trees
Abstract
1. Introduction
2. Methods
2.1. Bridge Process
2.1.1. The Brownian Bridge
2.1.2. The OU Bridge
2.2. Bridge Process along Phylogenetic Tree
3. Result
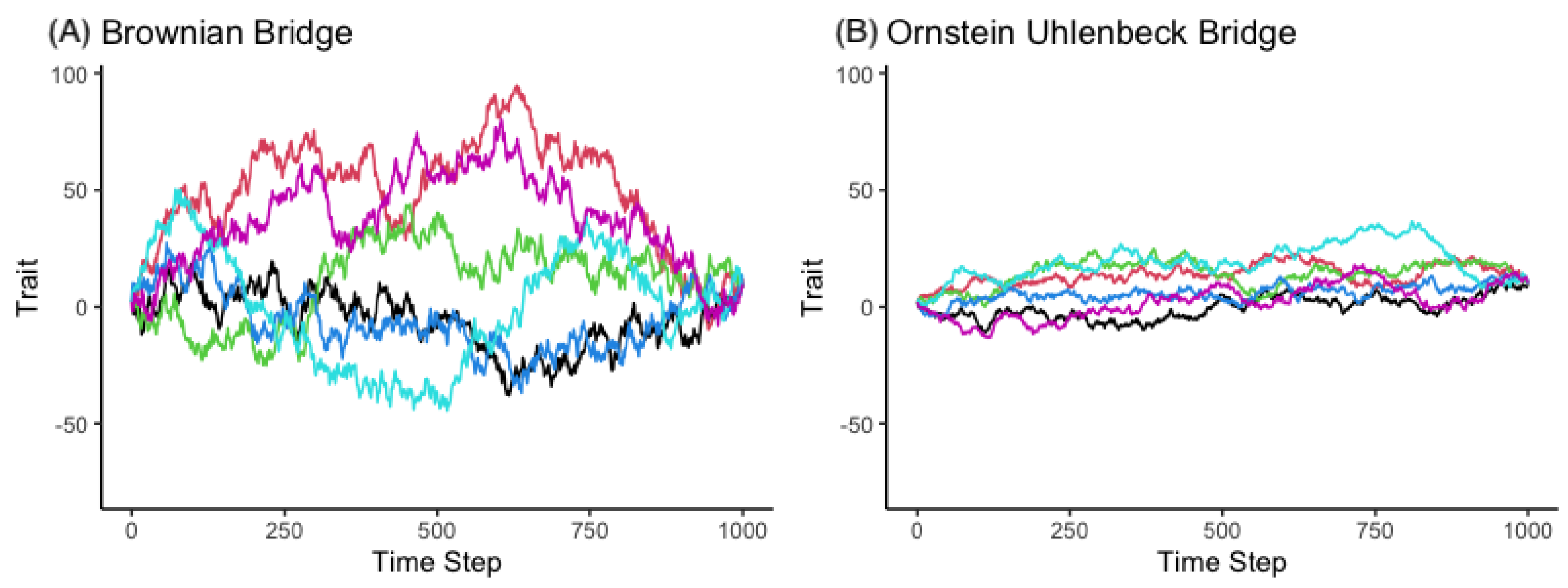
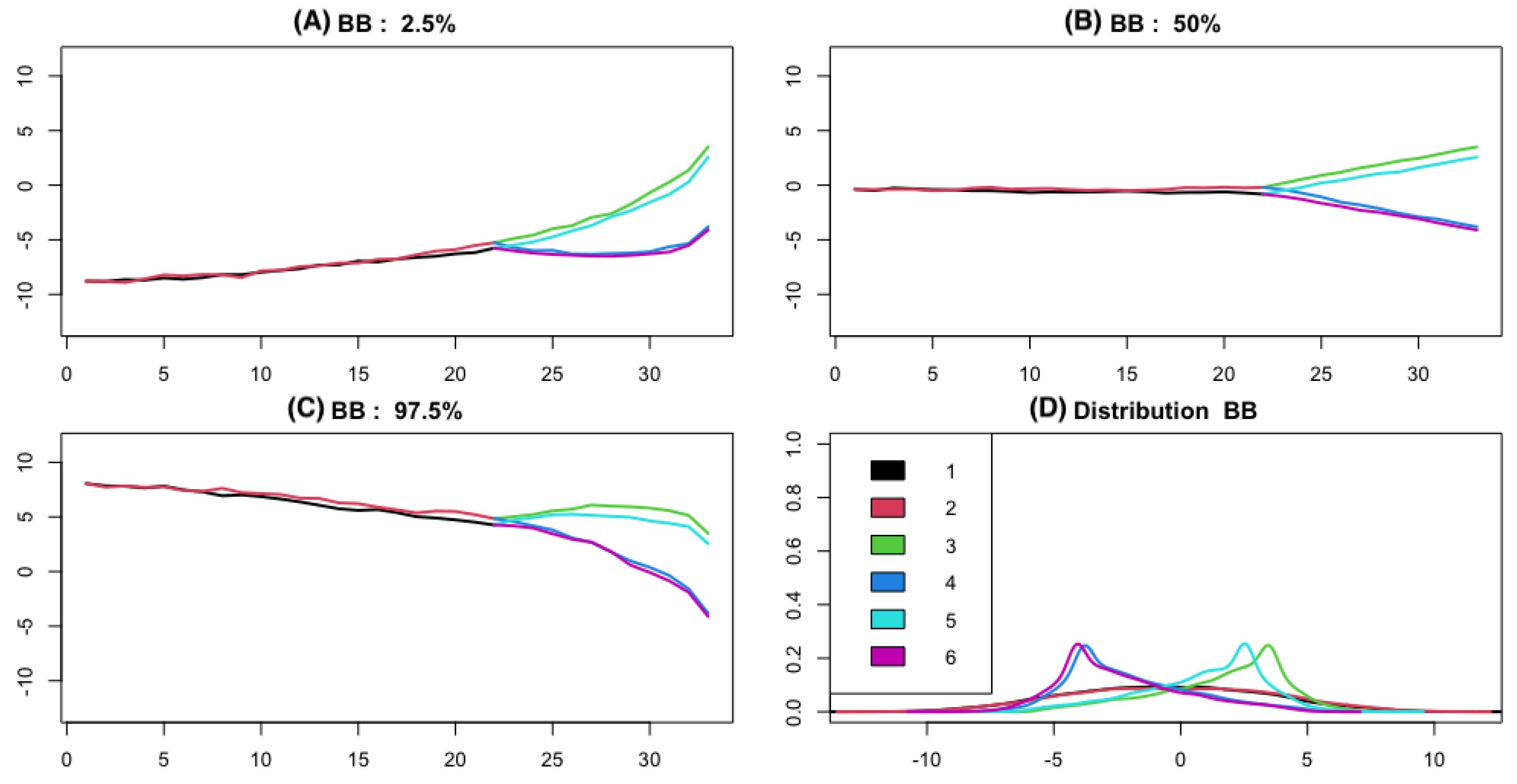
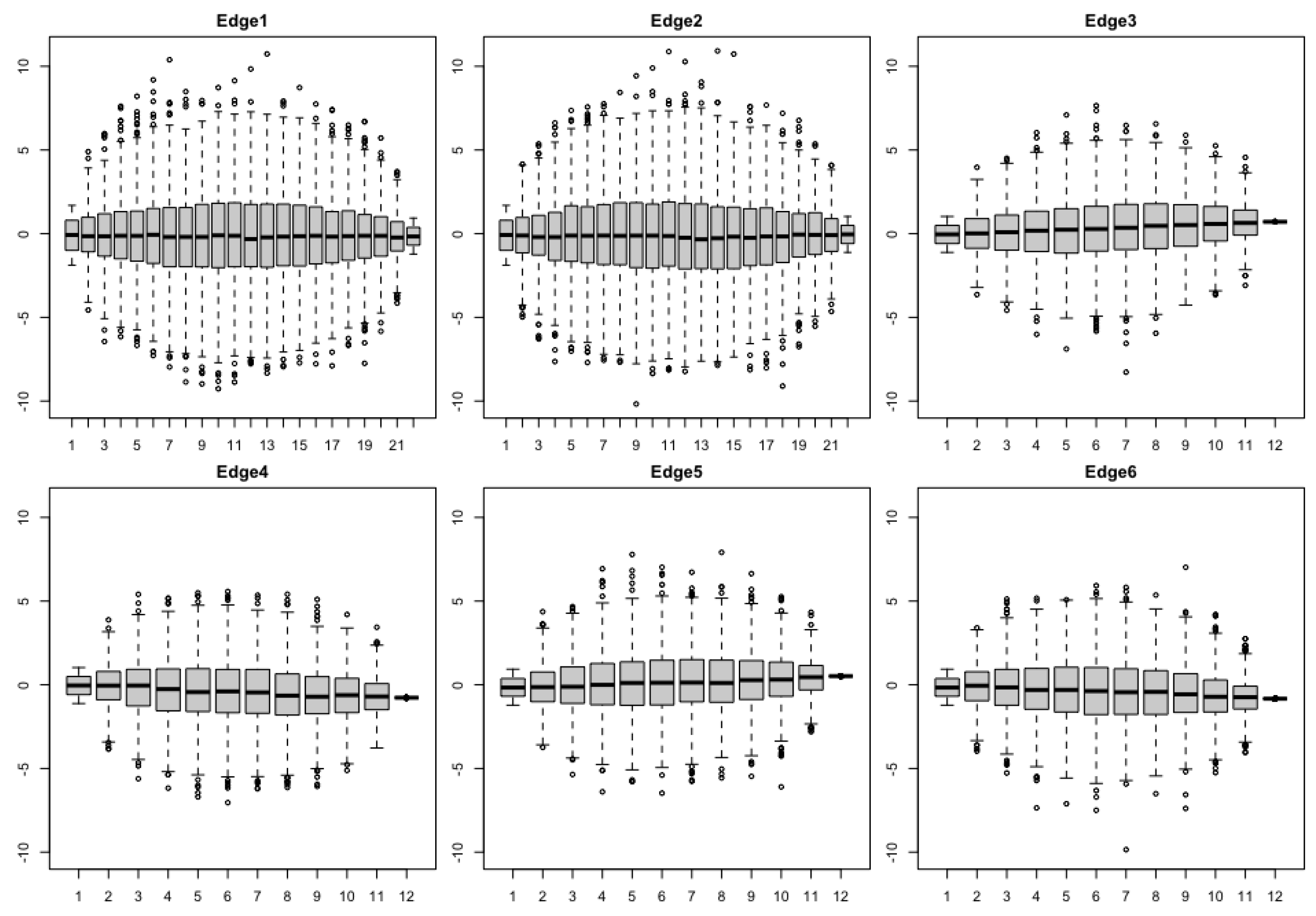
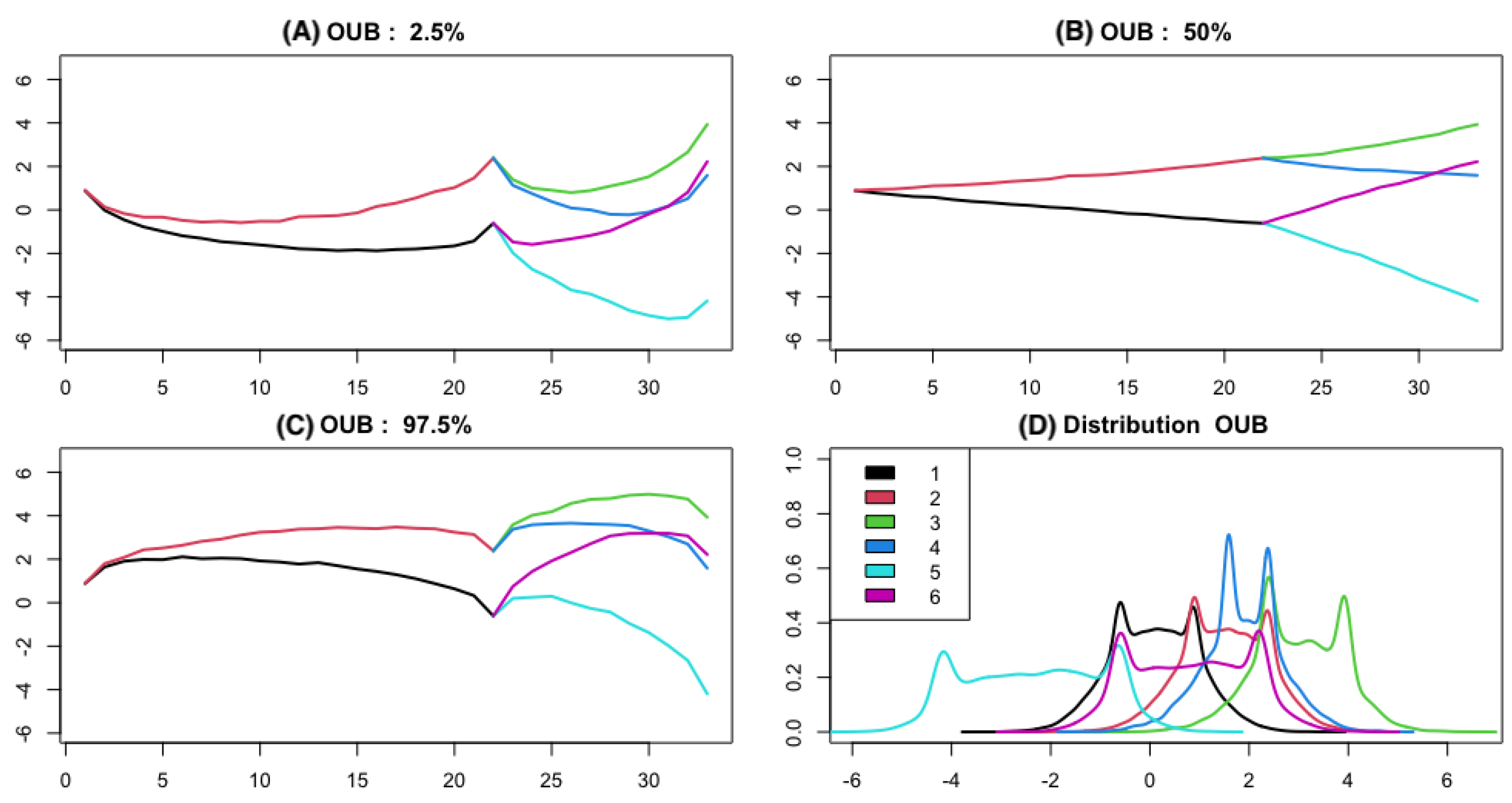
3.1. Simulation
3.1.1. The Brownian Bridge Model
3.1.2. The OU Bridge Model
3.2. Empirical Study by Traitgram
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Results for Simulation
- Results: http://www.tonyjhwueng.info/bridgepcm/simwrap.html (accessed date: 20 August 2021).
Appendix A.2. R Scripts and Data Files
- Figure 1: http://www.tonyjhwueng.info/bridgepcm/bboub100.html (accessed date: 20 August 2021).
- Figure 2: http://www.tonyjhwueng.info/bridgepcm/plotbridgetreebboub.html (accessed date: 20 August 2021).
- Figure 3 and Figure 5: http://www.tonyjhwueng.info/bridgepcm/bboubalg.html (accessed date: 20 August 2021).
- Figure 4 and Figure 6: http://www.tonyjhwueng.info/bridgepcm/boxplot4traits.html (accessed date: 20 August 2021).
- Figure 7, Figure 8 and Figure 9: http://www.tonyjhwueng.info/bridgepcm/contMapbridge.html (accessed date: 20 August 2021).
- Table 1 and Table 2: http://www.tonyjhwueng.info/bridgepcm/simbboubtable.html (accessed date: 20 August 2021).
References
- Hall, B.; Hallgrimsson, B. Strickberger’s Evolution; Jones & Bartlett Learning: Burlington, MA, USA, 2008. [Google Scholar]
- Butler, M.; King, A. Phylogenetic comparative analysis: A modeling approach for adaptive evolution. Am. Nat. 2004, 164, 683–695. [Google Scholar] [CrossRef]
- Beaulieu, J.; Jhwueng, D.C.; Boettiger, C.; O’Meara, B. Modeling stabilizing selection: Expanding the Ornstein-Uhlenbeck model of adaptive evolution. Evolution 2012, 66, 2369–2383. [Google Scholar] [CrossRef]
- Freckleton, R.P. Fast likelihood calculations for comparative analyses. Methods Ecol. Evol. 2012, 3, 940–947. [Google Scholar] [CrossRef]
- Felsenstein, J. Phylogeny and the comparative method. Am. Nat. 1985, 125, 1–15. [Google Scholar] [CrossRef]
- O’Meara, B.; Ané, C.; Sanderson, M.; Wainwright, P. Testing different rates of continuous trait evolution using likelihood. Evolution 2006, 60, 922–933. [Google Scholar] [CrossRef] [PubMed]
- Hansen, T.F.; Martins, E.P. Translating between microevolutionary process and macroevolutionary patterns: The correlation structure of interspecific data. Evolution 1996, 50, 1404–1417. [Google Scholar] [CrossRef]
- Martins, E.P. Estimation of ancestral states of continuous characters: A computer simulation study. Syst. Biol. 1999, 48, 642–650. [Google Scholar] [CrossRef]
- Felsenstein, J. Inferring Phylogenies; Sinauer Associates: Sunderland, MA, USA, 2004; Volume 2. [Google Scholar]
- Cornwell, W.; Nakagawa, S. Phylogenetic comparative methods. Curr. Biol. 2017, 27, R333–R336. [Google Scholar] [CrossRef]
- De Mendoza, R.S.; Gómez, R.O.; Tambussi, C.P. The lacrimal/ectethmoid region of waterfowl (Aves, Anseriformes): Phylogenetic signal and major evolutionary patterns. J. Morphol. 2020, 281, 1486–1500. [Google Scholar] [CrossRef]
- Hansen, T.F.; Pienaar, J.; Orzack, S.H. A comparative method for studying adaptation to a randomly evolving environment. Evolution 2008, 62, 1965–1977. [Google Scholar] [CrossRef]
- Revell, L.J.; Harmon, L.J.; Collar, D.C. Phylogenetic signal, evolutionary process, and rate. Syst. Biol. 2008, 57, 591–601. [Google Scholar] [CrossRef]
- Revell, L.J. Ancestral character estimation under the threshold model from quantitative genetics. Evolution 2014, 68, 743–759. [Google Scholar] [CrossRef] [PubMed]
- Blomberg, S.P.; Garland, T.; Ives, A.R. Testing for phylogenetic signal in comparative data: Behavioral traits are more labile. Evolution 2003, 57, 717–745. [Google Scholar] [CrossRef] [PubMed]
- Revell, L.J. Phylogenetic signal and linear regression on species data. Methods Ecol. Evol. 2010, 1, 319–329. [Google Scholar] [CrossRef]
- Weiblen, G. Correlated evolution in fig pollination. Syst. Biol. 2004, 53, 128–139. [Google Scholar] [CrossRef]
- Revell, L.J.; Collar, D.C. Phylogenetic analysis of the evolutionary correlation using likelihood. Evol. Int. J. Org. Evol. 2009, 63, 1090–1100. [Google Scholar] [CrossRef]
- Revell, L.J. Two new graphical methods for mapping trait evolution on phylogenies. Methods Ecol. Evol. 2013, 4, 754–759. [Google Scholar] [CrossRef]
- Szavits-Nossan, J.; Evans, M.R. Inequivalence of nonequilibrium path ensembles: The example of stochastic bridges. J. Stat. Mech. Theory Exp. 2015, 2015, P12008. [Google Scholar] [CrossRef]
- Buchin, K.; Sijben, S.; Arseneau, T.; Willems, E.P. Detecting movement patterns using Brownian bridges. In Proceedings of the 20th International Conference on Advances in Geographic Information Systems, ACM, Redondo Beach, CA, USA, 6–9 November 2012; pp. 119–128. [Google Scholar]
- Boyce, W.E.; Di Prima, R.C.; Meade, D.B. Elementary Differential Equations and Boundary Value Problems; Wiley: New York, NY, USA, 1992; Volume 9. [Google Scholar]
- Platen, E.; Bruti-Liberati, N. Numerical Solution of Stochastic Differential Equations with Jumps in Finance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010; Volume 64. [Google Scholar]
- Joy, J.B.; Liang, R.H.; Mc Closkey, R.M.; Nguyen, T.; Poon, A.F. Ancestral reconstruction. PLoS Comput. Biol. 2016, 12, e1004763. [Google Scholar] [CrossRef]
- Schluter, D.; Price, T.; Mooers, A.Ø.; Ludwig, D. Likelihood of ancestor states in adaptive radiation. Evolution 1997, 51, 1699–1711. [Google Scholar] [CrossRef] [PubMed]
- Pagel, M. Detecting character correlation on phylogenies: A general method for the comparative analysis of discrete characters. Proc. R. Soc. Lond. B 2000, 255, 37–45. [Google Scholar]
- Harmon, L.J.; Weir, J.T.; Brock, C.D.; Glor, R.E.; Challenger, W. GEIGER: Investigating evolutionary radiations. Bioinformatics 2008, 24, 129–131. [Google Scholar] [CrossRef]
- Clavel, J.; Escarguel, G.; Merceron, G. mvMORPH: An R package for fitting multivariate evolutionary models to morphometric data. Methods Ecol. Evol. 2015, 6, 1311–1319. [Google Scholar] [CrossRef]
- Jhwueng, D.C. Assessing the goodness of fit of phylogenetic comparative methods: A meta-analysis and simulation study. PLoS ONE 2013, 8, e67001. [Google Scholar] [CrossRef] [PubMed]
- Boucher, F.C.; Démery, V. Inferring bounded evolution in phenotypic characters from phylogenetic comparative data. Syst. Biol. 2016, 65, 651–661. [Google Scholar] [CrossRef] [PubMed]
- Morris, J. Traversing binary trees simply and cheaply. Inf. Process. Lett. 1979, 9, 197–200. [Google Scholar] [CrossRef]
- Paradis, E.; Schliep, K. ape 5.0: An environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 2018, 35, 526–528. [Google Scholar] [CrossRef]
- Klaassen, M.; Nolet, B.A. Stoichiometry of endothermy: Shifting the quest from nitrogen to carbon. Ecol. Lett. 2008, 11, 785–792. [Google Scholar] [CrossRef]
- Kumar, S.; Stecher, G.; Suleski, M.; Hedges, S.B. TimeTree: A Resource for Timelines, Timetrees, and Divergence Times. Mol. Biol. Evol. 2017, 34, 1812–1819. [Google Scholar] [CrossRef]
- Castiglione, S.; Serio, C.; Mondanaro, A.; Melchionna, M.; Carotenuto, F.; Di Febbraro, M.; Profico, A.; Tamagnini, D.; Raia, P. Ancestral State Estimation with Phylogenetic Ridge Regression. Evol. Biol. 2020, 47, 220–232. [Google Scholar] [CrossRef]
- Blomberg, S.P.; Rathnayake, S.I.; Moreau, C.M. Beyond Brownian motion and the Ornstein-Uhlenbeck process: Stochastic diffusion models for the evolution of quantitative characters. Am. Nat. 2020, 195, 145–165. [Google Scholar] [CrossRef] [PubMed]
- Jhwueng, D.C. Modeling rate of adaptive trait evolution using Cox–Ingersoll–Ross Process: An approximate Bayesian computation approach. Comput. Stat. Data Anal. 2020, 145, 106924. [Google Scholar] [CrossRef]

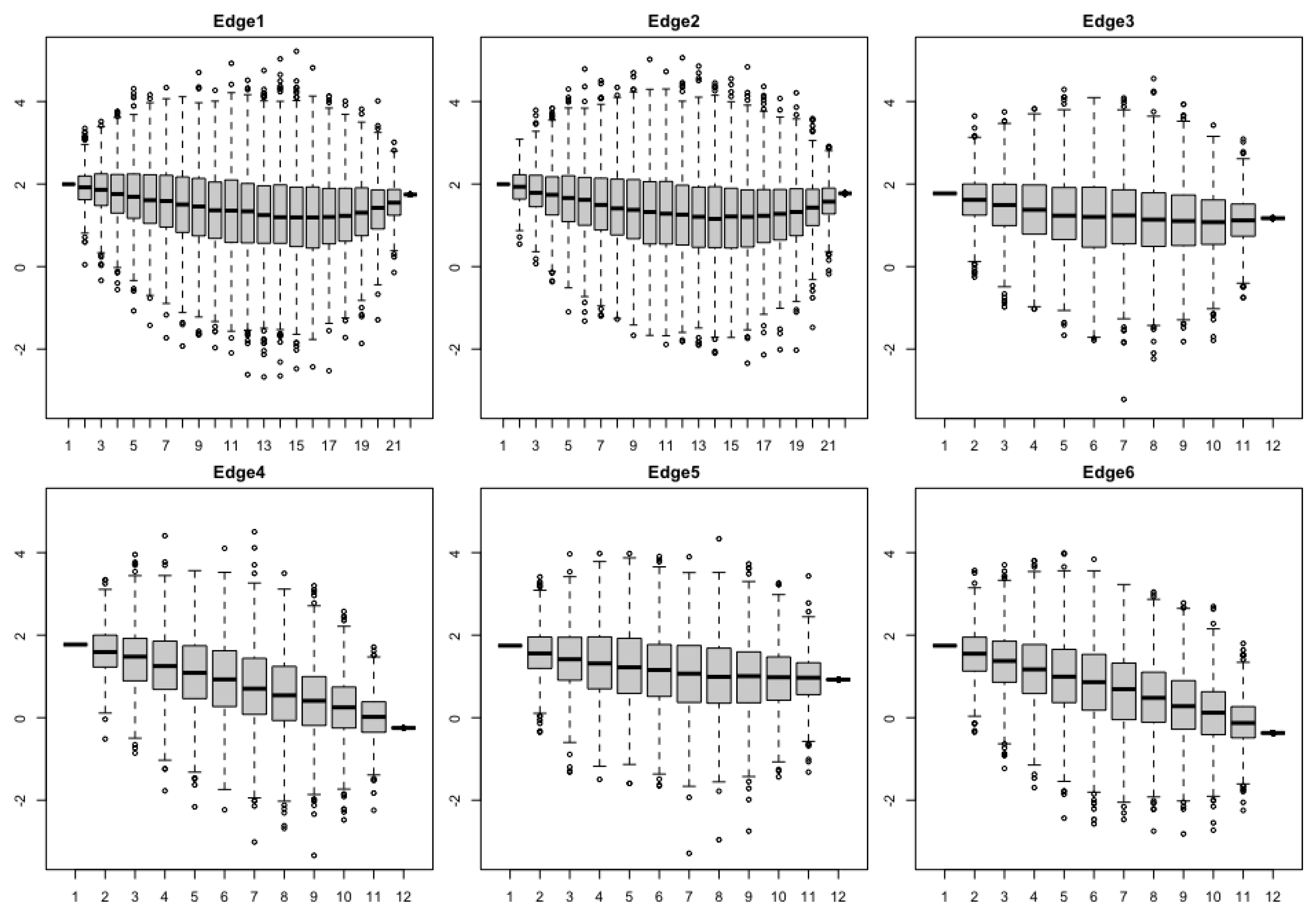
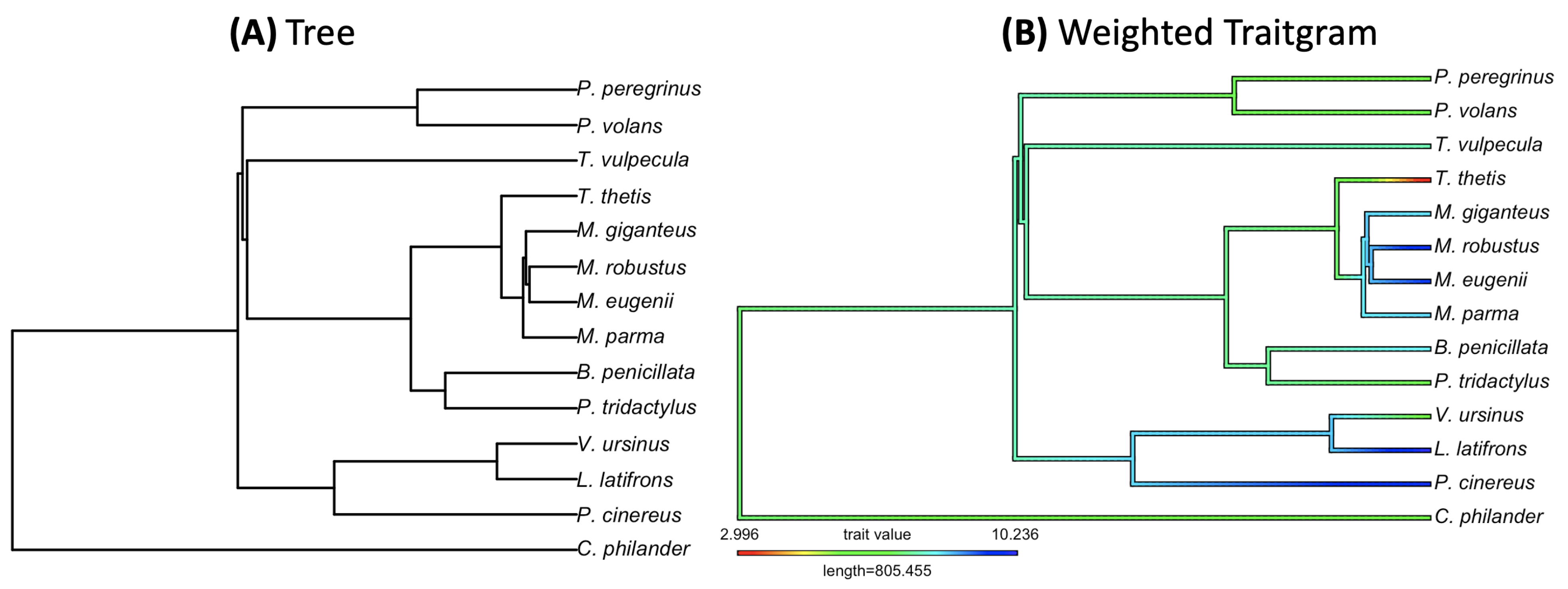
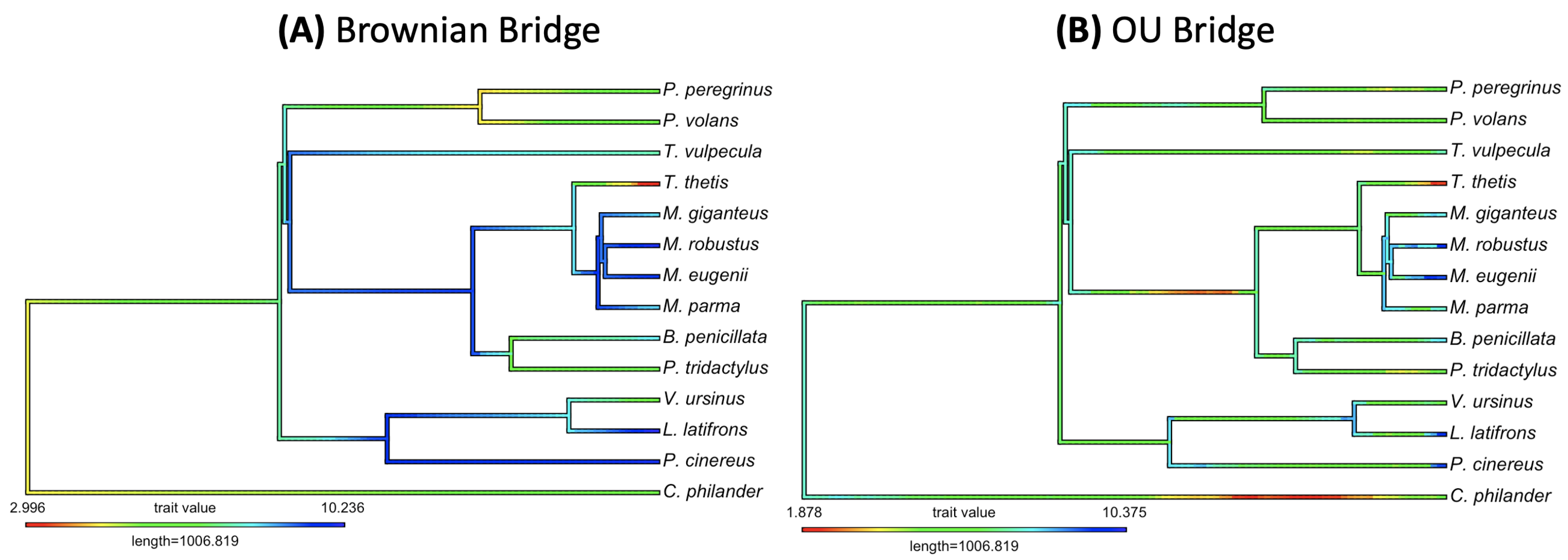
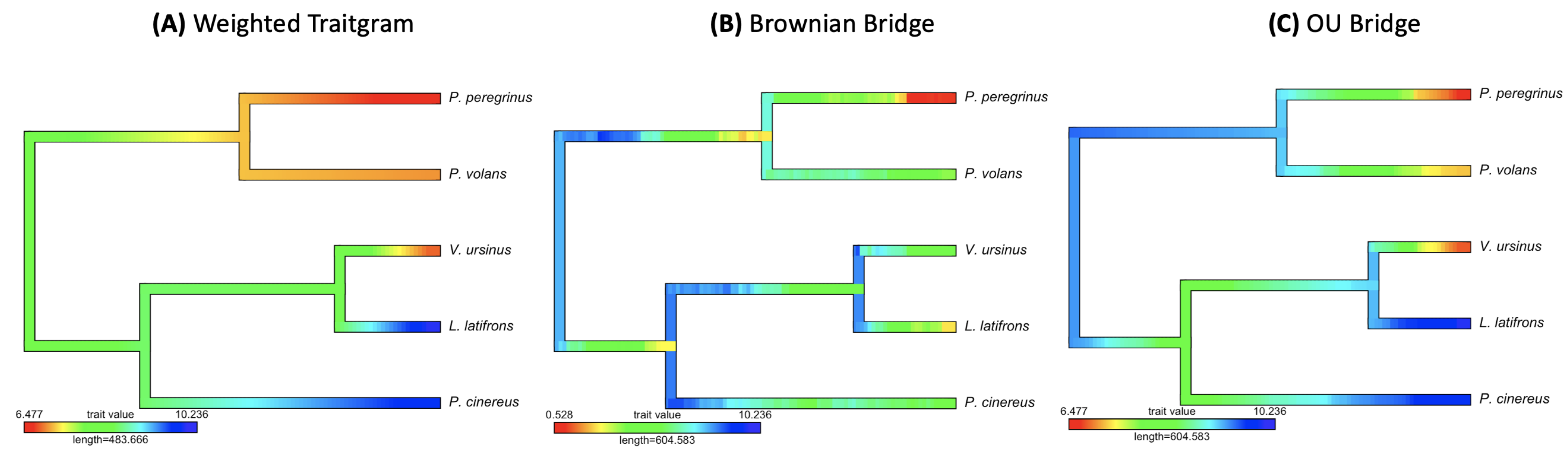
| Min | 1st Qu. | Median | Mean | 3rd Qu. | Max. | sd | skewness | kurtosis | |
|---|---|---|---|---|---|---|---|---|---|
| br1 | −12.842 | −3.382 | −0.580 | −0.584 | 2.216 | 11.676 | 3.846 | 0.008 | 2.522 |
| br2 | −12.106 | −3.245 | −0.349 | −0.345 | 2.615 | 10.770 | 3.945 | −0.020 | 2.417 |
| br3 | −6.202 | 0.097 | 2.208 | 1.646 | 3.506 | 8.484 | 2.500 | −0.695 | 2.929 |
| br4 | −9.297 | −3.812 | −2.541 | −2.018 | −0.454 | 6.123 | 2.466 | 0.662 | 2.985 |
| br5 | −8.042 | −0.601 | 1.361 | 0.898 | 2.560 | 8.592 | 2.421 | −0.628 | 3.029 |
| br6 | −9.762 | −4.107 | −2.878 | −2.362 | −0.899 | 6.092 | 2.443 | 0.700 | 3.030 |
| full | −12.842 | −3.204 | −0.474 | −0.462 | 2.293 | 11.676 | 3.467 | 0.004 | 2.469 |
| Min | 1st Qu. | Median | Mean | 3rd Qu. | Max. | sd | skewness | kurtosis | |
|---|---|---|---|---|---|---|---|---|---|
| br1 | −1.816 | 1.074 | 1.599 | 1.623 | 2.282 | 5.063 | 0.856 | −0.004 | 3.005 |
| br2 | −2.699 | 0.029 | 0.539 | 0.555 | 1.140 | 4.071 | 0.843 | 0.036 | 3.194 |
| br3 | −2.617 | 0.083 | 0.877 | 0.878 | 1.679 | 4.165 | 0.925 | −0.028 | 2.623 |
| br4 | −4.150 | −1.856 | −0.986 | −0.977 | −0.084 | 2.472 | 1.009 | 0.017 | 2.310 |
| br5 | −1.359 | 1.927 | 2.349 | 2.358 | 2.750 | 5.396 | 0.751 | −0.124 | 4.078 |
| br6 | −0.653 | 1.935 | 2.354 | 2.367 | 2.772 | 6.497 | 0.758 | −0.068 | 3.884 |
| full | −4.150 | 0.182 | 1.207 | 1.124 | 2.194 | 6.497 | 1.364 | −0.447 | 2.981 |
| Species | Body Mass (kg) | |
|---|---|---|
| 1 | Pseudocheirus peregrinus | 0.65 |
| 2 | Petauroides volans | 1.10 |
| 3 | Trichosurus vulpecula | 2.20 |
| 4 | Thylogale thetis | 4.30 |
| 5 | Macropus giganteus | 24.45 |
| 6 | Macropus robustus | 13.90 |
| 7 | Macropus eugenii | 4.62 |
| 8 | Macropus parma | 3.80 |
| 9 | Bettongia penicillata | 1.10 |
| 10 | Potorous tridactylus | 0.90 |
| 11 | Vombatus ursinus | 27.90 |
| 12 | Lasiorhinus latifrons | 23.10 |
| 13 | Phascolarctos cinereus | 6.70 |
| 14 | Caluromys philander | 0.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jhwueng, D.-C. Two Gaussian Bridge Processes for Mapping Continuous Trait Evolution along Phylogenetic Trees. Mathematics 2021, 9, 1998. https://doi.org/10.3390/math9161998
Jhwueng D-C. Two Gaussian Bridge Processes for Mapping Continuous Trait Evolution along Phylogenetic Trees. Mathematics. 2021; 9(16):1998. https://doi.org/10.3390/math9161998
Chicago/Turabian StyleJhwueng, Dwueng-Chwuan. 2021. "Two Gaussian Bridge Processes for Mapping Continuous Trait Evolution along Phylogenetic Trees" Mathematics 9, no. 16: 1998. https://doi.org/10.3390/math9161998
APA StyleJhwueng, D.-C. (2021). Two Gaussian Bridge Processes for Mapping Continuous Trait Evolution along Phylogenetic Trees. Mathematics, 9(16), 1998. https://doi.org/10.3390/math9161998






