Stable Optical Solitons for the Higher-Order Non-Kerr NLSE via the Modified Simple Equation Method

Abstract

This paper studies the propagation of the short pulse optics model governed by the higher-order nonlinear Schrödinger equation (NLSE) with non-Kerr nonlinearity. Exact one-soliton solutions are derived for a generalized case of the NLSE with the aid of software symbolic computations. The modified Kudryashov simple equation method (MSEM) is employed for this purpose under some parametric constraints. The computational work shows the difference, effectiveness, reliability, and power of the considered scheme. This method can treat several complex higher-order NLSEs that arise in mathematical physics. Graphical illustrations of some obtained solitons are presented.

1. Introduction

The nonlinear Schrödinger-type equations (NLSEs) are essential to describe the optical soliton propagation in a variety of branches of fiber communication sciences, e.g., nonlinear optics [1,2]. Additionally, these models have successfully addressed the ultrashort pulses of the wave dynamics, which will increase the power of high-bit-rate transmission systems [3,4]. Consequently, understanding the dynamics of the soliton can lead to an extensive improvement in technology and industry. Therefore, there has been significant progress in the development of diverse schemes for treating NLSEs and nonlinear partial differential equations (NPDEs) in the general case. For approximate schemes, we cite the Adomian decomposition method [5,6], collocation method [7], homotopy perturbation method [8], homotopy analysis method [9], reduced differential transform method [10,11], q-homotopy analysis method [12], variational iteration method [13], reproducing kernel Hilbert space method [14], iterative Shehu transform method [15], and residual power series method [16,17]. While constructing an exact analytic solution is of more importance since this can provide the best understanding of the model’s nature to be processed in an efficient way, researchers have developed various powerful tools to analyze NPDEs. Furthermore, these can be utilized to estimate the boundary data that are used in numeric and semi-analytic methods. Such techniques include the Kudryashov method and its modifications [18,19,20], functional variable method [19], generalized Riccati equation mapping method [21], Jacobi elliptic function method [21,22], sine-Gordon expansion method [23], Hirota method [24], subequation method [25], soliton ansatz method [26], $G^{\prime }/G$-expansion method [27], new extended direct algebraic method [28], extended trial function method [29], new generalized exponential rational function method [30], integral dispersion equation method [31,32], modified extended tanh-function method [33], simple equation method [34,35], and modified simple equation methods [36] (see also the references that appear therein).

In the present work, we aim to analytically process the higher-order NLSE with derivative non-Kerr nonlinearity given by:

$$S_x-i(a_1{S}_{tt}+a_2{|S|}^{2}S)-a_3{S}_{ttt}-a_4{({|S|}^{2}S)}_t-a_{5}S{({|S|}^2)}_t-i{a}_6{|S|}^{4}S-a_7{({|S|}^{4}S)}_t-a_{8}S{({|S|}^4)}_t=0,$$

(1)

where $i=\sqrt{-1},$ t is the normalized time with the frame of reference moving along the fiber at the group velocity, x is the normalized distance along the fiber, the real parameters $a_j,(j=1,2,\cdots ,5)$ are respectively related to group velocity dispersion (GVD), self-phase modulation (SPM), third-order dispersion (TOD), self-steepening and self-frequency shift due to stimulated Raman scattering (SRS), and $a_j,(j=6,7,8)$ symbolize the quintic non-Kerr nonlinear terms. The non-Kerr terms are crucial when one increases the intensity of the incident light power to produce shorter (femtosecond) pulses. The unknown function $S(x,t)$ represents the slowly varying complex envelope of the electric field. Equation (1) illustrates the propagation in the pulse beyond the ultra-short range in the systems of optical communication [37].

Recently, this model has been well analyzed by many researchers to construct different types of exact solitary wave solutions. These attempts include the hyperbolic ansatz algorithm [37], $exp(-\phi (\xi ))$-expansion and extended simple equation methods [38], generalized auxiliary equation method and Adomain decomposition method [39], mapping method, auxiliary equation method, and expansion methods [40]. With unity $a_1, a_2$, and $a_3$, Equation (1) was processed to induce diverse bright–dark and Lorentzian-type solutions [41]. The basic idea of these methods, as well as for most traveling-wave schemes, is the assumption that the solution depends on some special functions. Such functions satisfy some ordinary differential equation, with a known general solution, which is referred to as the simplest equation. Here, we employ the modified simple equation method (MSEM), with a different procedure, to look for some bright and dark optical solitons in a number of cases.

The remaining article is ordered as follows: Descriptions of the modified simple equation algorithm to process the general $(1+1)$-dimensional NPDE is given in Section 2. In Section 3, we consider an analytical treatment of the NLSE (1). Applications to our model by the MSEM are included in Section 4. A discussion and conclusions, with the numerical depiction of some derived one-solitons, are included in Section 5.

2. Methodology

In the current part, the major steps of the MSEM are described. As a generic example, consider the dimensionless nonlinear evolution equation (NLEE) of the form:

$$P\left(v,v_t,v_x,v_{tt},v_{xx},v_{xt},\dots \right)=0,$$

(2)

where P is a polynomial in $v\left(x,t\right)$ and its partial derivatives, which involves the highest-order derivative and nonlinear terms:

Step 1:

Define the wave variable $\xi =x\pm \alpha t$, where $v\left(x,t\right)=v\left(\xi \right)$ and $\alpha$ is the wave speed, to reduce the NLEE (2) into a nonlinear ordinary differential equation (NODE) for $v\left(\xi \right)$ as:

$$F\left(v,v^{\prime },v^{″},v^{‴},\dots \right)=0,$$

(3)

where $v^{\prime },v^{″}$, etc., denote the derivatives of v with respect to $\xi$, and F is a polynomial in v and its total derivatives. Integrate Equation (3) as many times as is applicable;

Step 2:

The MSEM [36] expresses the solution of Equation (3) by making an ansatz for $v\left(\xi \right)$ as:

$$v\left(\xi \right)=\sum _{i=0}^N{A}_i{\left(\frac{{\varphi }^{\prime }\left(\xi \right)}{\varphi \left(\xi \right)}\right)}^i,A_N\ne 0,$$

(4)

where the $A_i$’s are the parameters to be calculated and N is a positive integer that can be determined by considering the homogeneous balance between the highest-order derivative and the linear term of highest order in the resulting equation of Equation (3). $\varphi \left(\xi \right)$ is an unspecified function to be determined subsequently;

Step 3:

Substitute Equation (4) into Equation (3), with the already determined value of N, which results in a polynomial of ${\varphi }^{-i}$ and ${\varphi }^{(i)}$, $i>0$. Gathering the items with the same power of ${\varphi }^{-i}$ and equating to zero yield a system of equations in the $A_i$’s, $\varphi$, and its derivatives;

Step 4:

Solve the obtained system in the previous step to obtain the values of the $A_i$’s and $\varphi$. Substitute the results into Equation (4) to completely determine the exact solutions of Equation (2).

The MSEM and its various extensions are successfully implemented to tackle a wide range of NLEEs and systems. For the most recent related works, we mention the Ito integrodifferential equation [42], fiber Bragg grating model [43], weakly nonlocal Schrödinger equation with parabolic nonlinearity [44], modified Camassa–Holm equation [45], Lakshmanan–Porsezian–Daniel model [46], van der Waals p-system [47], Kundu–Mukherjee–Naskar model [48], modified Fornberg–Whitham equation [49], Kundu–Eckhaus equation and derivative nonlinear Schrodinger equation [50], Landau–Ginzburg–Higgs equation, and Cahn–Allen equation [51].

3. Mathematical Analysis

An analytic processing of Equation (1), as the starting steps, to completely solve this model by the MSEM is discussed in this section. For simplicity, and in parallel with the works of Khater et al. [39] and Elsayed [40], the following assumption:

$$S={\epsilon }_{1}V,x={\epsilon }_2\chi ,t={\epsilon }_3\tau .$$

(5)

transforms Equation (1) to:

$$V_{\chi }-i(V_{\tau \tau }+{|V|}^{2}V)-V_{\tau \tau \tau }-{\alpha }_1{({|V|}^{2}V)}_{\tau }-{\alpha }_2{({|V|}^2)}_{\tau }V-i{\alpha }_3{|V|}^{4}V-{\alpha }_4{({|V|}^{4}V)}_{\tau }-{\alpha }_5{({|V|}^4)}_{\tau }V=0,$$

(6)

where:

$$\begin{array}{c}{\alpha }_1=\frac{{\epsilon }_1^2{\epsilon }_2{a}_4}{{\epsilon }_3}=\frac{a_4{a}_1}{a_3{a}_2},{\alpha }_2=\frac{{\epsilon }_1^2{\epsilon }_2{a}_5}{{\epsilon }_3}=\frac{a_5{a}_1}{a_3{a}_2},{\alpha }_3={\epsilon }_1^4{\epsilon }_2{a}_0=\frac{a_1^3{a}_0}{a_3^2{a}_2^2},\hfill \\ {\alpha }_4=\frac{{\epsilon }_1^4{\epsilon }_2{a}_7}{{\epsilon }_3}=\frac{a_7{a}_1^4}{a_3^3{a}_2^2},{\alpha }_5=\frac{{\epsilon }_1^4{\epsilon }_2{a}_8}{{\epsilon }_3}=\frac{a_8{a}_1^4}{a_3^3{a}_2^2},\hfill \\ {\epsilon }_1=\sqrt{\frac{a_1^3}{a_3^2{a}_2^2}},{\epsilon }_2=\frac{a_3^2}{a_1^3},{\epsilon }_3=\frac{a_3}{a_1}.\hfill \end{array}$$

(7)

By considering the following wave transformation:

$$V(\chi ,\tau )=V(\vartheta )e^{i\eta },$$

(8)

where:

$$\vartheta =s\chi +\tau ,\eta =k\chi -\Omega \tau ,$$

(9)

separating the real and imaginary parts of the obtained transformed equation by the aid of the Mathematica software package, and comparing the coefficients of $V, V^3, V^5$, we obtain:

$$\frac{\left(s-2\Omega +3{\Omega }^3\right)\left(1-3\Omega \right)}{k+{\Omega }^2-{\Omega }^3}=\frac{\left(3{\alpha }_1+{\alpha }_2\right)\left(1-3\Omega \right)}{3\left(1-{\alpha }_1\right)}=\frac{\left(5{\alpha }_4+4{\alpha }_5\right)\left(1-3\Omega \right)}{5\left({\alpha }_3-\Omega {\alpha }_4\right)}.$$

(10)

Subject to real scalars $a,b$, and c defined by:

$$a=s-2\Omega +3{\Omega }^2,b=\frac{1}{6}\left(3{\alpha }_1+2{\alpha }_2\right),c=\frac{1}{15}\left(5{\alpha }_4+4{\alpha }_5\right),$$

(11)

the real part of Equation (6), along with Equations (8) and (9), should be converted to the nonlinear higher-order ordinary differential equation:

$$V^{″}-aV+2b{V}^3+3c{V}^5=0.$$

(12)

4. Optical Solitons

To handle the underlying model by the MSEM, the balancing procedure between the terms $V^{″}$ and $V^5$ yields $N=\frac{1}{2}.$ Therefore, the solution of Equation (12) is transformed as follows:

$$V(\vartheta )=U^{\frac{1}{2}}(\vartheta ).$$

(13)

Inserting Equation (13) into Equation (12) yields:

$$2U{U}^{″}-{(U^{\prime })}^2-4a{U}^2+8b{U}^3+12c{U}^4=0.$$

(14)

Applying the balance procedure between the terms $U{U}^{″}$ and $U^4$ gives $N=1.$ The MSEM assumes that the solution of Equation (14) has the form:

$$U(\vartheta )=A_0+A_1\frac{{\Phi }^{\prime }}{\Phi },$$

(15)

where $\Phi (\vartheta )$ is an unknown function to be found afterward and $A_0$ and $A_1$ are arbitrary constants such that $A_1\ne 0.$ One can easily attain that the first- and second-order derivatives of $U(\vartheta )$ as:

$$U^{\prime }=A_1\left(\frac{{\Phi }^{″}}{\Phi }-{\left(\frac{{\Phi }^{\prime }}{\Phi }\right)}^2\right),$$

(16)

$$U^{″}=A_1\left(\frac{{\Phi }^{″}}{\Phi }-3\frac{{\Phi }^{\prime }{\Phi }^{″}}{{\Phi }^2}+2{\left(\frac{{\Phi }^{\prime }}{\Phi }\right)}^3\right).$$

(17)

Inserting Equations (15)–(17) into Equation (14) and collecting different powers of ${\Phi }^{-i}(\vartheta )$ where $i=0,1,2,3,4$ and equating them to zero, a set of equations is achieved as:

$$12c{A_0}^4+8b{A_0}^3-4a{A_0}^2=0,$$

(18)

$$\left(48c{A}_1{A_0}^3+24b{A}_1{A_0}^2-8a{A}_1{A}_0\right){\Phi }^{\prime }+2A_1{A}_0{\Phi }^{‴}=0,$$

(19)

$$\left(72c{A_1}^2{A_0}^2+24b{A_1}^2{A}_0^2-4a{A_1}^2\right){\left({\Phi }^{\prime }\right)}^2+2{A_1}^2{\Phi }^{‴}{\Phi }^{\prime }-{A_1}^2{\left({\Phi }^{″}\right)}^2-6A_1{A}_0{\Phi }^{″}{\Phi }^{\prime }=0,$$

(20)

$$\left(48c{A}_0{A_1}^3+8b{A_1}^3+4A_0{A}_1\right){\left({\Phi }^{\prime }\right)}^3-4{A_1}^2{\left({\Phi }^{\prime }\right)}^2{\Phi }^{″}=0,$$

(21)

$$\left(12c{A_1}^4+3{A_1}^2\right){\left({\Phi }^{\prime }\right)}^4=0.$$

(22)

From Equations (18) and (22), we have:

$$A_0=0,\frac{-b\mp \sqrt{3ac+b^2}}{3c},A_1=\mp \frac{1}{2\sqrt{-c}}.$$

(23)

Provided that $c\ne 0,$ from Equations (19) and (21), we obtain:

$${\Phi }^{\prime }=\frac{A_1}{12c{A}_0{A_1}^2+2b{A_1}^2+A_0}{\Phi }^{″}=\frac{1}{-24c{A_0}^2-12b{A}_0+4a}{\Phi }^{‴}.$$

(24)

Consequently:

$$\frac{{\Phi }^{‴}}{{\Phi }^{″}}=\frac{-24c{A_0}^2{A}_1-12b{A}_0{A}_1+4a{A}_1}{12c{A}_0{A_1}^2+2b{A_1}^2+A_0}.$$

(25)

Upon integration, we obtain:

$${\Phi }^{″}(\vartheta )=c_{1}exp\left(\frac{-24c{A_0}^2{A}_1-12b{A}_0{A}_1+4a{A}_1}{12c{A}_0{A_1}^2+2b{A_1}^2+A_0}\vartheta \right).$$

(26)

From Equation (24), we have:

$${\Phi }^{\prime }(\vartheta )=\frac{A_1{c}_1}{12c{A}_0{A_1}^2+2b{A_1}^2+A_0}exp\left(\frac{-24c{A_0}^2{A}_1-12b{A}_0{A}_1+4a{A}_1}{12c{A}_0{A_1}^2+2b{A_1}^2+A_0}\vartheta \right).$$

(27)

Upon integration, we obtain:

$$\Phi (\vartheta )=c_2+\frac{c_1}{-24c{A_0}^2-12b{A}_0+4a}exp\left(\frac{-24c{A_0}^2{A}_1-12b{A}_0{A}_1+4a{A}_1}{12c{A}_0{A_1}^2+2b{A_1}^2+A_0}\vartheta \right),$$

(28)

where $c_1$ and $c_2$ are the constants of integration. Using Equation (20) along with Equations (19) and (21) yields:

$$a=\frac{4{\left(6c{A}_0+b\right)}^2{A_1}^4+\left(72c{A_0}^2+16b{A}_0\right){A_1}^2+7{A_0}^2}{4{A_1}^2}.$$

(29)

Accordingly, the following cases are achieved as follows:

Case 1. If $A_0=0$ and $A_1=\mp \frac{1}{2\sqrt{-c}},$ this leads to $a=-\frac{b^2}{4c}.$ The exact solution of Equation (14) is achieved as:

$$U(\vartheta )=\frac{b{c}_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)}{2c\left(\frac{b^2{c}_2}{c}-c_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)\right)}.$$

(30)

Consequently, we obtain:

$$V(\vartheta )={\left(\frac{b{c}_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)}{2c\left(\frac{b^2{c}_2}{c}-c_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)\right)}\right)}^{\frac{1}{2}}.$$

(31)

One can randomly choose the arbitrary parameters $c_1$ and $c_2.$ By setting $c_1=-\frac{b^2{c}_2}{c},$ we obtain:

$$V(\vartheta )={\left(\frac{-b}{4c}\left(1\mp tanh\left(\frac{b\vartheta }{2\sqrt{-c}}+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}},$$

(32)

where ${\vartheta }_0$ is an arbitrary constant. Consequently, the solitary wave solutions of Equation (1) are obtained as:

$$S_1(x,t)={\epsilon }_1{\left(\frac{-b}{4c}\left(1+tanh\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)},$$

(33)

and:

$$S_2(x,t)={\epsilon }_1{\left(\frac{-b}{4c}\left(1-tanh\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)}.$$

(34)

Similarly, by setting $c_1=\frac{b^2{c}_2}{c},$ we obtain:

$$V(\vartheta )={\left(\frac{-b}{4c}\left(1\mp coth\left(\frac{b\vartheta }{2\sqrt{-c}}+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}},$$

(35)

where ${\vartheta }_0$ is an arbitrary constant. Consequently, the solitary wave solution of Equation (1) is obtained as:

$$S_3(x,t)={\epsilon }_1{\left(\frac{-b}{4c}\left(1+coth\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)},$$

(36)

and:

$$S_4(x,t)={\epsilon }_1{\left(\frac{-b}{4c}\left(1-coth\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)};$$

(37)

Case 2. If $A_0=\frac{-b\mp \sqrt{3ac+b^2}}{3c}$ and $A_1=\mp \frac{1}{2\sqrt{-c}}$, this leads to $a=-\frac{b^2}{4c}$. The exact solution of Equation (14) is achieved as:

$$U(\vartheta )=\frac{-b}{2c}-\frac{b{c}_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)}{2c\left(\frac{b^2{c}_2}{c}-c_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)\right)}.$$

(38)

Consequently, we obtain:

$$V(\vartheta )={\left(\frac{-b}{2c}-\frac{b{c}_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)}{2c\left(\frac{b^2{c}_2}{c}-c_{1}exp\left(\frac{b}{\sqrt{-c}}\vartheta \right)\right)}\right)}^{\frac{1}{2}}.$$

(39)

One can randomly choose the arbitrary parameters $c_1$ and $c_2$. By setting $c_1=-\frac{b^2{c}_2}{c},$ we obtain:

$$V(\vartheta )={\left(\frac{-b}{2c}+\frac{b}{4c}\left(1\mp tanh\left(\frac{b\vartheta }{2\sqrt{-c}}+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}.$$

(40)

where ${\vartheta }_0$ is an arbitrary constant. Consequently, the solitary wave solutions of Equation (1) are obtained as:

$$S_5(x,t)={\epsilon }_1{\left(\frac{-b}{2c}+\frac{b}{4c}\left(1+tanh\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)},$$

(41)

and:

$$S_6(x,t)={\epsilon }_1{\left(\frac{-b}{2c}+\frac{b}{4c}\left(1-tanh\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)}.$$

(42)

Similarly, by setting $c_1=\frac{b^2{c}_2}{c},$ we obtain:

$$V(\vartheta )={\left(\frac{-b}{2c}+\frac{b}{4c}\left(1\mp coth\left(\frac{b\vartheta }{2\sqrt{-c}}+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}},$$

(43)

where ${\vartheta }_0$ is an arbitrary constant. Consequently, the solitary wave solution of Equation (1) is obtained as:

$$S_7(x,t)={\epsilon }_1{\left(\frac{-b}{2c}+\frac{b}{4c}\left(1+coth\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)},$$

(44)

and:

$$S_8(x,t)={\epsilon }_1{\left(\frac{-b}{2c}+\frac{b}{4c}\left(1-coth\left(\frac{b}{2\sqrt{-c}}\left(\frac{s}{{\epsilon }_2}x+\frac{1}{{\epsilon }_3}t\right)+{\vartheta }_0\right)\right)\right)}^{\frac{1}{2}}{e}^{i\left(\frac{k}{{\epsilon }_2}x-\frac{\Omega }{{\epsilon }_3}t\right)}.$$

(45)

Remark 1.

It should be emphasized that $exp(x)=e^x.$

5. Discussion and Conclusions

The modified simple equation algorithm was successfully examined to the higher-order nonlinear Schrodinger partial differential equation with non-Kerr nonlinearity subject to constraint relations among the parameters. The mentioned scheme was based on converting the case study model into a nonlinear ordinary differential equation (NODE) by some complex wave transform assumption. The obtained NODE could be processed by an ansatz depending on a rational expression of the parametric function and its first derivative with assumed scalars to be determined. Applying such an ansatz would result in a system of algebraic-differential equations, unlike most of the well-known methods. By solving this mixed system and making a backward substitution, we derived exact analytic solutions. The modified scheme works without the need to use some simple ordinary differential equation with known solutions. The method depends on the skills of treating the ODEs.

The ultra-short pulse propagation model governed by the considered equation describes the dynamics of light pulses. We confirmed that the non-Kerr terms induce diverse types of dark, bright, and dark-in-bright optical one-solitons subject to constraint relations among the parameters. The higher-order terms are important to compensate the nonlinear absorption during propagation in highly nonlinear material and play a significant role in the postsoliton compression to obtain highly stable compressed optical pulse. These short pulses are useful to increase the capacity of carrying information to make ultra-fast communication.

The detailed analysis of Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 is as follows. In the form of kink, kink-like, singular kink, periodic, and singular periodic soliton solutions, a numerical simulation of the absolute, real, and imaginary parts of some obtained solutions is depicted for special values of the parameters in Figure 1, Figure 3, Figure 5 and Figure 7. The corresponding two-dimensional density of the wave behavior is also shown in Figure 2, Figure 4, Figure 6 and Figure 8 respectively. Many other structures can be obtained by choosing free parameters. In comparison to the other applied methods [38,39,40], the gained solutions are included while applying the MSEM. One can easily conclude that the modified technique is inclusive, efficient, and direct and reduces the size of the computations. The validity of the derived solutions is guaranteed by putting them back into the original equation.

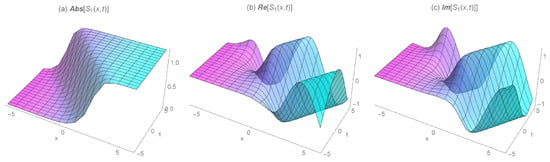
Figure 1. The 3D wave profiles for the absolute, real, and imaginary values of the dark (kink) soliton solution for $b=0.9$, $c=-0.3$, $s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1={\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$

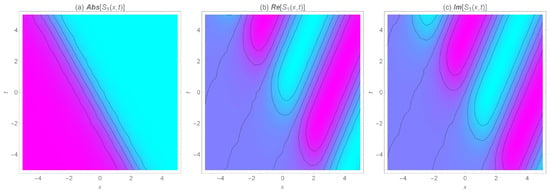
Figure 2. The 2D density of the wave surfaces for the absolute, real, and imaginary values of the dark (kink) soliton solution for $b=0.9,c=-0.3,s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1=1,{\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$

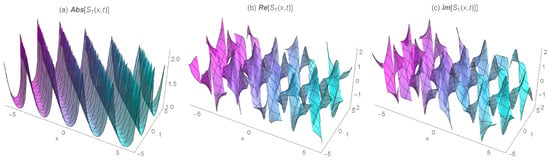
Figure 3. The 3D wave profiles for the absolute, real, and imaginary values of the periodic soliton solution for $b=0.9,c=0.3,$$s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1={\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$

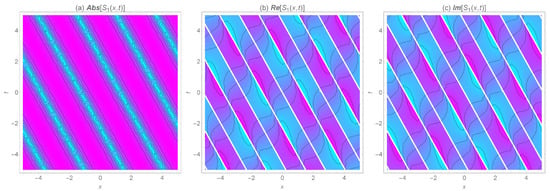
Figure 4. The 2D density of the wave surfaces for the absolute, real, and imaginary values of the periodic soliton solution for $b=0.9$, $4c=-0.3$, $s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1=1,{\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$

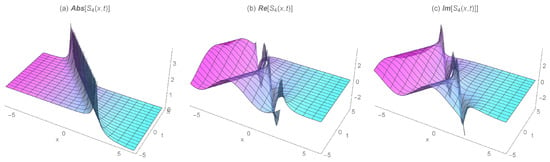
Figure 5. The 3D wave profiles for the absolute, real, and imaginary values of the singular kink-like soliton solution for $b=0.9,$$c=-0.3,s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1=1,{\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$

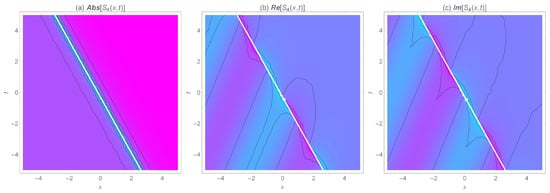
Figure 6. The 2D density of the wave surfaces for the absolute, real, and imaginary values of the singular kink soliton solution for $b=0.9,c=-0.3,s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1=1,{\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$

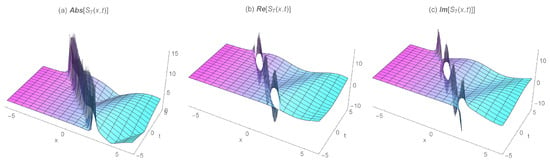
Figure 7. The 3D wave profiles for the absolute, real, and imaginary values of the singular kink soliton solution for $b=0.9,c=-0.3,$$s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1=1,{\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$

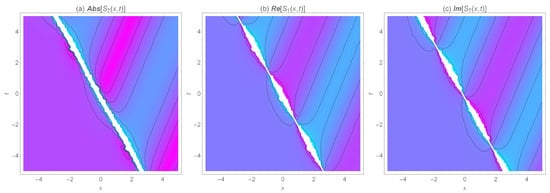
Figure 8. The 2D density of the wave surfaces for the absolute, real, and imaginary values of the singular kink-like soliton solution for $b=0.9,c=-0.3,s=1.5,k=1,{\vartheta }_0=0.2,{\epsilon }_1=1,{\epsilon }_2=1,{\epsilon }_3=1.2,\Omega =0.5.$