Approximate Iterative Method for Initial Value Problem of Impulsive Fractional Differential Equations with Generalized Proportional Fractional Derivatives
Abstract
:1. Introduction
2. Main Results
2.1. Statement of the Problem
2.2. Explicit Solution of the Impulsive Linear Fractional Equation
2.3. Mild Lower/Upper Solutions
2.4. Monotone-Iterative Technique
- 1.
- The functions are a mild lower solution and a mild upper solution of the PIVP (1), respectively, such that for ;
- 2.
- The function and there exist constants such that, for any , if then the inequalityholds;
- 3.
- The functions and there exist constants , such that, for any , if then the inequalitieshold.
- [a]
- The sequences and are defined by andand
- [b]
- For any the functions and are mild lower and mild upper solutions of PIVP (1), respectively;
- [c]
- The sequence is increasing, i.e., , for ;
- [d]
- The sequence is decreasing , i.e., , for , ;
- [e]
- The inequalityholds.
- [f]
- For any , the sequences and converge uniformly on to and , respectively, whereand for
- [g]
- The functions and are mild solutions of the PIVP (1) on and , where
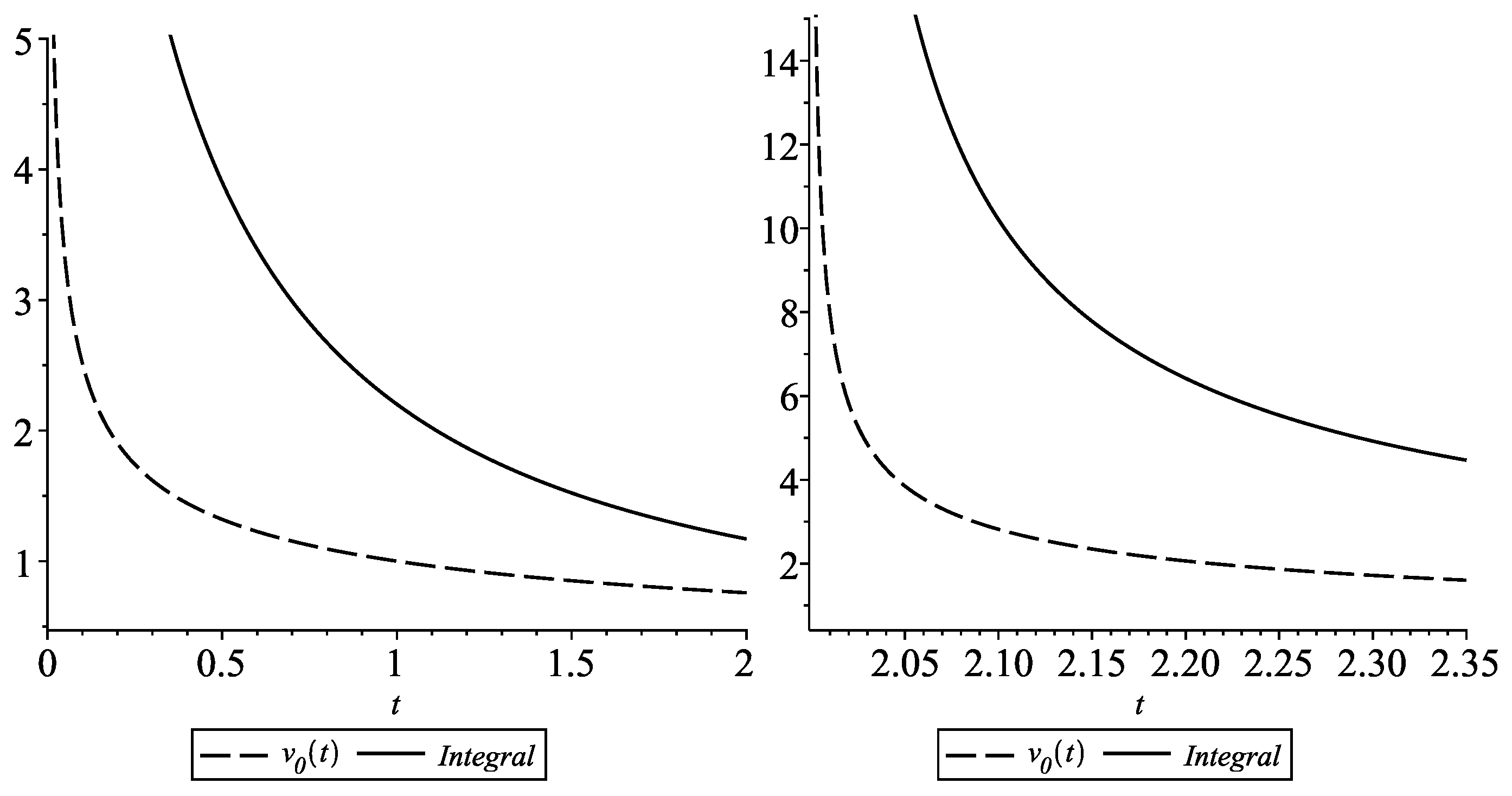
2.5. Example
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Abbas, M.I. Non-instantaneous impulsive fractional integro-differential equations with proportional fractional derivatives with respect to another function. Math. Meth. Appl. Sci. 2021, 44, 10432–10447. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier B.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Srivastava, H.M.; Saad, K.M. Some new models of the time-fractional gas dynamic equation. Adv. Math. Models Appl. 2018, 3, 5–17. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Application of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany; Higher Education Press: Beijing, China, 2010. [Google Scholar]
- Shammakh, W.; Alzumi, H.Z. Existence results for nonlinear fractional boundary value problem involving generalized proportional derivative. Adv. Differ. Equ. 2019, 2019, 94. [Google Scholar] [CrossRef] [Green Version]
- Jarad, F.; Abdeljawad, T.; Alzabut, J. Generalized fractional derivatives generated by a class of local proportional derivatives. Eur. Phys. J. Spec. Top. 2017, 226, 3457–3471. [Google Scholar] [CrossRef]
- Abbas, M.I. Controllability and Hyers-Ulam stability results of initial value problems for fractional differential equations via generalized proportional-Caputo fractional derivative. Miskolc Math. Notes 2021, 22, 1–12. [Google Scholar] [CrossRef]
- Abbas, M.I.; Ragusa, M.A. On the hybrid fractional differential equations with fractional proportional derivatives of a function with respect to a certain function. Symmetry 2021, 13, 264. [Google Scholar] [CrossRef]
- Abbas, M.I. Existence results and the Ulam Stability for fractional differential equations with hybrid proportional-Caputo derivatives. J. Nonlinear Func. Anal. 2020, 2020, 48. [Google Scholar] [CrossRef]
- Boucenna, D.; Baleanu, D.; Makhlouf, A.; Nagy, A.M. Analysis and numerical solution of the generalized proportional fractional Cauchy problem. Appl. Num. Math. 2021, 167, 173–186. [Google Scholar] [CrossRef]
- Hristova, S.; Abbas, M.I. Explicit solutions of initial value problems for fractional generalized proportional differential equations with and without impulses. Symmetry 2021, 13, 996. [Google Scholar] [CrossRef]
- Benchohra, M.; Henderson, J.; Ntouyas, S.K. Impulsive Differential Equations and Inclusions; Hindawi Publishing Corporation: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Lakshmikantham, V.; Bainov, D.D.; Simeonov, P.S. Theory of Impulsive Differential Equations; World Scientific: Singapore, 1989. [Google Scholar]
- Samoilenko, A.M.; Perestyuk, N.A. Impulsive Differential Equations; World Scientific: River Edge, NJ, USA, 1995. [Google Scholar]
- Song, Q.; Yang, X.; Li, C.; Huang, T.; Chen, X. Stability analysis of nonlinear fractional-order systems with variable-time impulses. J. Frankl. Inst. 2017, 354, 2959–2978. [Google Scholar] [CrossRef]
- Stamov, T.; Stamova, I. Design of impulsive controllers and impulsive control strategy for the Mittag–Leffler stability behavior of fractional gene regulatory networks. Neurocomputing 2021, 424, 54–62. [Google Scholar] [CrossRef]
- Wang, J.R.; Feckan, M.; Zhou, Y. On the new concept of solutions and existence results for impulsive fractional evolution equations. Dyn. Partial Differ. Equ. 2011, 8, 345–361. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agarwal, R.P.; Hristova, S.; O’Regan, D.; Almeida, R. Approximate Iterative Method for Initial Value Problem of Impulsive Fractional Differential Equations with Generalized Proportional Fractional Derivatives. Mathematics 2021, 9, 1979. https://doi.org/10.3390/math9161979
Agarwal RP, Hristova S, O’Regan D, Almeida R. Approximate Iterative Method for Initial Value Problem of Impulsive Fractional Differential Equations with Generalized Proportional Fractional Derivatives. Mathematics. 2021; 9(16):1979. https://doi.org/10.3390/math9161979
Chicago/Turabian StyleAgarwal, Ravi P., Snezhana Hristova, Donal O’Regan, and Ricardo Almeida. 2021. "Approximate Iterative Method for Initial Value Problem of Impulsive Fractional Differential Equations with Generalized Proportional Fractional Derivatives" Mathematics 9, no. 16: 1979. https://doi.org/10.3390/math9161979
APA StyleAgarwal, R. P., Hristova, S., O’Regan, D., & Almeida, R. (2021). Approximate Iterative Method for Initial Value Problem of Impulsive Fractional Differential Equations with Generalized Proportional Fractional Derivatives. Mathematics, 9(16), 1979. https://doi.org/10.3390/math9161979








