Approximate Iterative Method for Initial Value Problem of Impulsive Fractional Differential Equations with Generalized Proportional Fractional Derivatives

Abstract

The main aim of the paper is to present an algorithm to solve approximately initial value problems for a scalar non-linear fractional differential equation with generalized proportional fractional derivative on a finite interval. The main condition is connected with the one sided Lipschitz condition of the right hand side part of the given equation. An iterative scheme, based on appropriately defined mild lower and mild upper solutions, is provided. Two monotone sequences, increasing and decreasing ones, are constructed and their convergence to mild solutions of the given problem is established. In the case of uniqueness, both limits coincide with the unique solution of the given problem. The approximate method is based on the application of the method of lower and upper solutions combined with the monotone-iterative technique.

1. Introduction

Fractional differential equations are effective in both theoretical and applied mathematics and arise in models of medicine, engineering, biochemistry, thermal and mechanical systems, acoustics and modeling of materials, etc. There are different forms of fractional derivatives and consequently numerous fractional derivatives have appeared (see, for example, [1,2,3,4,5,6] and the references cited therein). Jarad et al. [7] introduced a new generalized proportional derivative which is well-behaved and has several advantages over classical derivatives and generalizes known derivatives in the literature. For recent contributions relevant to fractional differential equations via generalized proportional derivatives, see e.g., [8,9,10,11,12]. We note that initial value problems for Riemann–Liouville fractional differential equations differ from the Caputo fractional ones and requires a separate study.

The theory of impulsive differential equations has undergone rapid development over the years (see, for example, the monographs by Benchohra et al. [13], Lakshmikantham et al. [14], Samoilenko and Perestyuk [15], and the references therein). Impulses were also considered for fractional-order differential systems, and the theory of impulsive fractional differential systems was presented in the literature, mainly for fractional derivatives of Caputo type (see for example, [16,17,18]).

Note that most fractional differential equations have no explicit solutions, so developing approximate methods is usually required. In this paper, a new algorithm for approximate solving an initial value problem for scalar non-linear fractional differential equations with generalized proportional fractional derivative is proposed. This method is based on the application of the method of lower and upper solutions and the monotone-iterative technique. Two monotone sequences, increasing and decreasing ones, are constructed and their convergence to mild solutions of the given problem is established. In the case of uniqueness, both limits coincide with the unique solution of the given problem.

2. Main Results

2.1. Statement of the Problem

Let ${\left\{t_i\right\}}_{i=1}^{m+1}$ be a sequence of points with

$$0=t_0<\cdots <t_i<t_{i+1}<\cdots <t_{m+1}=T,i=1,2,\dots ,m.$$

Consider the following fractional differential equation with the generalized proportional fractional derivative with fractional initial and impulsive conditions (PIVP):

$$\begin{array}{cc}& \left({}_{t_i}^R{\mathcal{D}}^{\alpha ,\rho }u\right)\left(t\right)=\psi \left(t,u\left(t\right)\right),t\in (t_i,t_{i+1}],i=0,1,2,\dots ,m,\hfill \\ & \underset{t\to t_i+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_i)}{(t-t_i)}^{1-\alpha }u\left(t\right)\right)=\frac{{\Psi }_i\left(u(t_i-0)\right){\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},i=1,2,\dots ,m,\hfill \\ & \underset{t\to 0+}{lim}\left(e^{\frac{1-\rho }{\rho }t}{t}^{1-\alpha }u\left(t\right)\right)=\frac{u_0{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},\hfill \end{array}$$

(1)

where $u:[0,T]\to \mathbb{R}$ is a function, $\rho \in (0,1],\alpha \in (0,1)$ are two reals, $u_0$ is a real constant, and $\psi :[0,T]\times \mathbb{R}\to \mathbb{R}$ and ${\Psi }_i:\mathbb{R}\to \mathbb{R},i=1,2,\dots ,m$ are two functions. We recall that the generalized proportional fractional integral and the generalized proportional fractional derivative of a function $\upsilon :[a,b]\to \mathbb{R}$ are defined, respectively, by (see [7])

$$\left({}_a{\mathcal{I}}^{\alpha ,\rho }\upsilon \right)\left(t\right)=\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_a^t{e}^{\frac{\rho -1}{\rho }\left(t-s\right)}{\left(t-s\right)}^{\alpha -1}\upsilon \left(s\right)ds,t\in (a,b],$$

and

$$\left({}_a^R{\mathcal{D}}^{\alpha ,\rho }v\right)\left(t\right)=\frac{1}{{\rho }^{1-\alpha }\Gamma (1-\alpha )}{\mathcal{D}}^{1,\rho }\left({\int }_a^t{e}^{\frac{\rho -1}{\rho }\left(t-s\right)}{\left(t-s\right)}^{-\alpha }\upsilon \left(s\right)ds\right),t\in (a,b],$$

where $\left({\mathcal{D}}^{1,\rho }\upsilon \right)\left(t\right)=\left({\mathcal{D}}^{\rho }\upsilon \right)\left(t\right)=(1-\rho )\upsilon \left(t\right)+\rho {\upsilon }^{\prime }\left(t\right)$.

Remark 1.

Note that the generalized proportional fractional derivative of Riemann–Liouville fractional type leads to an appropriate definition of the impulsive conditions similar to the initial condition (see the last two equations in problem (1). Additionally, we consider the case when the lower limit of the fractional derivative is changed at any impulsive point.

Observe that a solution of the PIVP (1) can have singularities at the points $t_i$, for $i=0,1,2,\dots ,m$.

Let

$$C_{1-\alpha ,\rho }\left([a,b]\right)=\left\{u:[a,b]\to \mathbb{R}:u(·)\in C\left((a,b]\right),\underset{t\to a+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-a)}{(t-a)}^{1-\alpha }u\left(t\right)\right)<\infty \right\}$$

and

$$\begin{array}{cc}\hfill P{C}_{1-\alpha ,\rho }\left([0,T]\right)& =\left\{u:[0,T]\to \mathbb{R}:u\in C_{1-\alpha ,\rho }\left([t_i,t_{i+1}]\right)\mathrm{for} \mathrm{all}i=0,1,2,\dots ,m\right\}\hfill \end{array}$$

equipped with the norms

$${\left|x\right|}_{C_{1-\alpha ,\rho }[a,b]}=\underset{t\in [a,b]}{max}\left|e^{\frac{1-\rho }{\rho }(t-a)}{(t-a)}^{1-\alpha }x\left(t\right)\right|$$

and

$${\left|x\right|}_{P{C}_{1-\alpha ,\rho }[a,b]}=\underset{i=0,1,2,\dots ,m}{max}{\left|x\right|}_{C_{1-\alpha ,\rho }[t_i,t_{i+1}]},$$

respectively. Note that $C_{1-\alpha ,\rho }\left([a,b]\right)$ is a Banach space. If

$$u_n\in C_{1-\alpha ,\rho }\left([a,b]\right),n=1,2,\dots \mathrm{and}={|u_n-u|}_{C_{1-\alpha ,\rho }[a,b]}\to 0$$

then $u\in C_{1-\alpha ,\rho }\left([a,b]\right)$.

2.2. Explicit Solution of the Impulsive Linear Fractional Equation

Consider the linear scalar impulsive fractional equation with the generalized proportional fractional derivative and the initial value condition (IVP)

$$\begin{array}{cc}& \left({}_{t_i}^R{\mathcal{D}}^{\alpha ,\rho }u\right)\left(t\right)=\lambda u\left(t\right)+f\left(t\right),t\in (t_i,t_{i+1}],\hfill \\ & \underset{t\to t_i+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_i)}{(t-t_i)}^{1-\alpha }u\left(t\right)\right)=\frac{P_k\left(u(t_i-0)\right){\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)}i=1,2,\dots ,m,\hfill \\ & \underset{t\to 0+}{lim}\left(e^{\frac{1-\rho }{\rho }t}{t}^{1-\alpha }u\left(t\right)\right)=\frac{u_0{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)}\hfill \end{array}$$

(2)

where $\lambda$ is a real constant, and $f\in C\left(\right[0,T\left]\right)$, $P_k:R\to R,k=0,1,2,\dots ,m$ are given functions. We recall the following result (see (Theorem 2) in [12]):

Lemma 1.

The IVP (3) has a unique solution $u\in P{C}_{1-\alpha ,\rho }[0,T]$ given by

$$\begin{array}{cc}\hfill u\left(t\right)=& P_k\left(u(t_k-0)\right)e^{\frac{\rho -1}{\rho }(t-t_k)}{E}_{\alpha ,\alpha }\left(\lambda {\left(\frac{t-t_k}{\rho }\right)}^{\alpha }\right){\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}\hfill \\ & +\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(\rho -1)\left(\frac{t-s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(\lambda {\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)f\left(s\right)ds,\hfill \end{array}$$

(3)

for $t\in (t_k,t_{k+1}]$, $k=0,1,2,\dots ,m,$ where $P_0\left(u(t_0-0)\right)\equiv u_0$.

Consider the special case when $P_k\left(u\right)={\mu }_{k}u+{\gamma }_k,k=1,2,\dots ,m,$ i.e., consider the IVP

$$\begin{array}{cc}& \left({}_{t_i}^R{\mathcal{D}}^{\alpha ,\rho }u\right)\left(t\right)=\lambda u\left(t\right)+f\left(t\right),t\in (t_i,t_{i+1}],\hfill \\ & \underset{t\to t_i+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_i)}{(t-t_i)}^{1-\alpha }u\left(t\right)\right)=\frac{[{\mu }_{i}u(t_i-0)+{\gamma }_i]{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},i=1,2,\dots ,m,\hfill \\ & \underset{t\to 0+}{lim}\left(e^{\frac{1-\rho }{\rho }t}{t}^{1-\alpha }u\left(t\right)\right)=\frac{u_0{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},\hfill \end{array}$$

(4)

with ${\mu }_k,{\gamma }_k\in R,k=1,2,\dots ,m$.

As a special case of Lemma 1 we obtain the following explicit form of the solution of (4):

Lemma 2.

The IVP (4) has a unique solution $u\in P{C}_{1-\alpha ,\rho }[0,T]$ given by

$$\begin{array}{c}\hfill u\left(t\right)=\left\{\begin{array}{c}{u}_0{A}_0\left(t\right)+I_0^f\left(t\right),fort\in (0,t_1],\hfill \\ \\ {\mu }_k{A}_k\left(t\right)\left[u_0\prod _{j=0}^{k-1}\left({\mu }_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{k-1}{I}_j^f\left(t_{j+1}\right)\prod _{p=j+1}^{k-j-1}\left({\mu }_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ +A_k\left(t\right)\sum _{j=1}^k{\gamma }_j\prod _{p=j}^{k-1}\left({\mu }_{p+1}{A}_p\left(t_{p+1}\right)\right)+I_k^f\left(t\right),\hfill \\ fort\in (t_k,t_{k+1}],k=1,2,\dots ,m,\hfill \end{array}\right.\end{array}$$

(5)

where ${\mu }_0=1,{\gamma }_0=0$, and for $t\in (t_k,t_{k+1}],k=0,1,2,\dots ,m$,

$$\begin{array}{cc}& I_k^f\left(t\right)=\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(\rho -1)\left(\frac{t-s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(\lambda {\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)f\left(s\right)ds,\hfill \end{array}$$

(6)

and

$$A_k\left(t\right)=e^{\frac{\rho -1}{\rho }(t-t_k)}{E}_{\alpha ,\alpha }\left(\lambda {\left(\frac{t-t_k}{\rho }\right)}^{\alpha }\right){\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}>0.$$

(7)

Remark 2.

According to Lemma 1, the solution $u(·)$ of the linear problem (4) satisfies

$$\begin{array}{c}\hfill u\left(t\right)=\left\{\begin{array}{c}{u}_0{A}_0\left(t\right)+I_0^f\left(t\right),t\in (0,t_1]\hfill \\ \left({\mu }_{k}u(t_k-0)+{\gamma }_k\right)A_k\left(t\right)+I_k^f\left(t\right),t\in (t_k,t_{k+1}],k=1,2,\dots ,m.\hfill \end{array}\right.\end{array}$$

(8)

Proof. 

We will use an induction argument. First, let $t\in (0,t_1]$. By (6) and Lemma 1 with $k=0$ we get

$$u\left(t\right)=u_0{A}_0\left(t\right)+I_0^f\left(t\right)=u_0\left({\mu }_0{A}_0\left(t\right)\right)+I_0^f\left(t\right).$$

Let $t\in (t_1,t_2]$. By (6) and Lemma 1 with $k=1$ we obtain

$$\begin{array}{cc}\hfill u\left(t\right)& =[{\mu }_{1}u(t_1-0)+{\gamma }_1]A_1\left(t\right)+I_1^f\left(t\right)\hfill \\ & =u_0\left({\mu }_1{A}_1\left(t\right)\right)\left({\mu }_0{A}_0\left(t_1\right)\right)+I_0^f\left(t_1\right)\left({\mu }_1{A}_1\left(t\right)\right)+{\gamma }_1{A}_1\left(t\right)+I_1^f\left(t\right)\hfill \end{array}$$

(9)

Let $t\in (t_2,t_3]$. By (6) and Lemma 1 with $k=2$ we get

$$\begin{array}{cc}\hfill u\left(t\right)& =[{\mu }_{2}u(t_2-0)+{\gamma }_2]A_2\left(t\right)+I_2^f\left(t\right)\hfill \\ & ={\mu }_2[{\mu }_1{u}_0{A}_0\left(t_1\right)A_1\left(t_2\right)+I_0^f\left(t_1\right)\left({\mu }_1{A}_1\left(t_2\right)\right)+{\gamma }_1{A}_1\left(t_2\right)+I_1^f\left(t_2\right)]A_2\left(t\right)\hfill \\ & +{\gamma }_1{A}_2\left(t\right)+I_2^f\left(t\right)\hfill \\ & =u_0\left({\mu }_1{A}_1\left(t_2\right)\right)\left({\mu }_0{A}_0\left(t_1\right)\right)\left({\mu }_2{A}_2\left(t\right)\right)+I_0^f\left(t_1\right)\left({\mu }_1{A}_1\left(t_2\right)\right){\mu }_2{A}_2\left(t\right)\hfill \\ & +I_1^f\left(t_2\right)\left({\mu }_2{A}_2\left(t\right)\right)+{\gamma }_1{A}_1\left(t_2\right)\left({\mu }_2{A}_2\left(t\right)\right)+{\gamma }_2{A}_2\left(t\right)+I_2^f\left(t\right)\hfill \\ & ={\mu }_2{A}_2\left(t\right)\left[u_0\prod _{j=0}^{2-1}\left({\mu }_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{2-1}{I}_j^f\left(t_{j+1}\right)\prod _{p=j+1}^{2-j-1}\left({\mu }_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ & +A_2\left(t\right)\sum _{j=1}^2{\gamma }_j\prod _{p=j}^{2-1}\left({\mu }_{p+1}{A}_p\left(t_{p+1}\right)\right)+I_2^f\left(t\right).\hfill \end{array}$$

(10)

Let $t\in (t_3,t_4]$. Then

$$\begin{array}{cc}\hfill u\left(t\right)& =[{\mu }_{3}u(t_3-0)+{\gamma }_3]A_3\left(t\right)+I_3^f\left(t\right)\hfill \\ & =\left({\mu }_3{A}_3\left(t\right)\right)[u_0\left({\mu }_1{A}_1\left(t_2\right)\right)\left({\mu }_0{A}_0\left(t_1\right)\right)\left({\mu }_2{A}_2\left(t_3\right)\right)+I_0^f\left(t_1\right)\left({\mu }_1{A}_1\left(t_2\right)\right){\mu }_2{A}_2\left(t_3\right)\hfill \\ & +I_1^f\left(t_2\right)\left({\mu }_2{A}_2\left(t_3\right)\right)+{\gamma }_1{A}_1\left(t_2\right)\left({\mu }_2{A}_2\left(t_3\right)\right)+{\gamma }_2{A}_2\left(t_3\right)+I_2^f\left(t_3\right)]\hfill \\ & +{\gamma }_3{A}_3\left(t\right)+I_3^f\left(t\right)\hfill \\ & ={\mu }_3{A}_3\left(t\right)\left[u_0\prod _{j=0}^{3-1}\left({\mu }_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{3-1}{I}_j^f\left(t_{j+1}\right)\prod _{p=j+1}^{3-j-1}\left({\mu }_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ & +A_3\left(t\right)\sum _{j=1}^3{\gamma }_j\prod _{p=j}^{3-1}\left({\mu }_{p+1}{A}_p\left(t_{p+1}\right)\right)+I_3^f\left(t\right).\hfill \end{array}$$

(11)

□

2.3. Mild Lower/Upper Solutions

Let $L_i,M_i,i=1,2,\dots ,m$ be positive constants (to be determined later). Then PIVP (1) can be equivalently written in the form

$$\begin{array}{cc}& \left({}_0^R{\mathcal{D}}^{\alpha ,\rho }u\right)\left(t\right)=-L_{i}u\left(t\right)+F\left(t,u\left(t\right)\right),t\in (t_i,t_{i+1}],i=0,1,2,\dots ,m,\hfill \\ & \underset{t\to t_i+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_i)}{(t-t_i)}^{1-\alpha }u\left(t\right)\right)=\frac{[M_{i}u(t_i-0)+G_i\left(u(t_i-0)\right)]{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},\hfill \\ & i=1,2,\dots ,m,\hfill \\ & \underset{t\to 0+}{lim}\left(e^{\frac{1-\rho }{\rho }t}{t}^{1-\alpha }u\left(t\right)\right)=\frac{u_0{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},\hfill \end{array}$$

(12)

where

$$F\left(t,u\right)=\psi \left(t,u\right)+L_{i}u,u\in \mathbb{R},t\in (t_i,t_{i+1}],i=0,1,2,\dots ,m,$$

(13)

and

$$G_i\left(x\right)={\Psi }_i\left(x\right)-M_{i}x,x\in \mathbb{R},i=1,2,\dots ,m.$$

(14)

The solution $x\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ of PIVP (12), based on Lemma 2 with $\lambda =-L$, $f\left(t\right)=F(t,x\left(t\right)),{\mu }_i=M_i,$ and ${\gamma }_i=G_i\left(x(t_i-0)\right),i=1,2,\dots ,m,$ has the form

$$\begin{array}{c}\hfill x\left(t\right)=\left\{\begin{array}{c}{u}_0{A}_0\left(t\right)+I_0(t,x),t\in (0,t_1]\hfill \\ \\ M_k{A}_k\left(t\right)[u_0\prod _{j=0}^{k-1}\left(M_j{A}_j\left(t_{j+1}\right)\right)\hfill \\ +\sum _{j=0}^{k-1}{I}_j(t_{j+1},x)\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)]\hfill \\ +A_k\left(t\right)\sum _{j=1}^k({\Psi }_j\left(x(t_j-0)\right)-M_j\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)+I_k(t,x),\hfill \\ t\in (t_k,t_{k+1}],k=1,2,\dots ,m,\hfill \end{array}\right.\end{array}$$

(15)

where for $t\in (t_k,t_{k+1}]$ and $k=0,1,2,\dots ,m$,

$$A_k\left(t\right)=e^{\frac{\rho -1}{\rho }(t-t_k)}\left(-L_k{\left(\frac{t-t_k}{\rho }\right)}^{\alpha }\right){\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}>0,$$

(16)

and

$$I_k(t,x)=\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(\rho -1)\left(\frac{t-s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\left(\psi \left(s,x\left(s\right)\right)+L_{k}x\left(s\right)\right)ds.$$

(17)

Remark 3.

According to Lemma 1, the solution $x\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ of PIVP (12) satisfies

$$\begin{array}{cc}\hfill x\left(t\right)=& [M_{k}x(t_k-0)+G_k\left(x(t_k-0)\right)]A_k\left(t\right)+I_k(t,x),\hfill \end{array}$$

(18)

for $t\in (t_k,t_{k+1}]$, $x\in C_{1-\alpha ,\rho }([t_k,t_{k+1}]$, and $k=1,2,\dots ,m$.

Based on (15) we will define mild lower/upper solutions of (1).

Definition 1.

We say that function $x\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ is a mild solution of PIVP (1) if it satisfies

$$\begin{array}{c}\hfill x\left(t\right)=\left\{\begin{array}{c}{u}_0{A}_0\left(t\right)+I_0(t,x)fort\in (0,t_1],\hfill \\ \\ M_k{A}_k\left(t\right)\left[u_0\prod _{j=0}^{k-1}\left(M_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{k-1}{I}_j(t_{j+1},x)\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ +A_k\left(t\right)\sum _{j=1}^k\left({\Psi }_j\left(x(t_j-0)\right)-M_x(t_j-0)\right)\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)\hfill \\ +I_k(t,x)fort\in (t_k,t_{k+1}],k=1,2,\dots ,m,\hfill \end{array}\right.\end{array}$$

(19)

where $A_k\left(t\right),I_k(t,x),t\in (t_k,t_{k+1}],k=0,1,2,\dots ,m$ are defined by (16) and (17), respectively.

Proposition 1.

The mild solution $x\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ of PIVP (1) satisfies the equalities

$$\underset{t\to t_k+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_k)}{(t-t_k)}^{1-\alpha }x\left(t\right)\right)=\frac{{\Psi }_k\left(x(t_k-0)\right){\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},k=1,2,\dots ,m.$$

Proof. 

The claim follows from Remark 3, Definition 1, (14), the two following equalities

$$e^{\frac{1-\rho }{\rho }(t-t_k)}{(t-t_k)}^{1-\alpha }{A}_k\left(t\right)=E_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-t_k}{\rho }\right)}^{\alpha }\right){\rho }^{1-\alpha },t\in (t_k,t_{k+1}],k=1,2,\dots ,m,$$

$$E_{\alpha ,\alpha }\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)},$$

and from

$$\begin{array}{c}{e}^{\frac{1-\rho }{\rho }(t-t_k)}{(t-t_k)}^{1-\alpha }{I}_k(t,x)\hfill \\ \hspace{1em}\hspace{1em}=\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{e}^{\frac{1-\rho }{\rho }(s-t_k)}{\left(\frac{t-t_k}{t-s}\right)}^{1-\alpha }{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\left(\psi \left(s,x\left(s\right)\right)+L_{k}x\left(s\right)\right).\hfill \end{array}$$

□

Definition 2.

We say that function $x\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ is a mild lower (a mild upper) solution of the PIVP (1) if it satisfies the integral inequalities

$$\begin{array}{c}\hfill x\left(t\right)\le (\ge )\left\{\begin{array}{c}{u}_0{A}_0\left(t\right)+I_0(t,x)fort\in (0,t_1],\hfill \\ \\ M_k{A}_k\left(t\right)\left[u_0\prod _{j=0}^{k-1}\left(M_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{k-1}{I}_j(t_{j+1},x)\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ +A_k\left(t\right)\sum _{j=1}^k\left({\Psi }_j\left(x(t_j-0)\right)-M_{j}x(t_j-0)\right)\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)\hfill \\ +I_k(t,x)fort\in (t_k,t_{k+1}],k=1,2,\dots ,m.\hfill \end{array}\right.\end{array}$$

(20)

2.4. Monotone-Iterative Technique

For any function $v\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ we define the operator

$$\begin{array}{c}\hfill \Omega \left(v\right)\left(t\right)=\left\{\begin{array}{c}{u}_0{A}_0\left(t\right)+I_0(t,v),t\in (0,t_1],\hfill \\ \\ M_k{A}_k\left(t\right)[u_0\sum _{j=0}^{k-1}\left(M_j{A}_j\left(t_{j+1}\right)\right)\hfill \\ +\sum _{j=0}^{k-1}{I}_j(t_{j+1},v)\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)]\hfill \\ +A_k\left(t\right)\sum _{j=1}^k\left({\Psi }_j\left(v(t_j-0)\right)-M_{j}v(t_j-0)\right)\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)\hfill \\ +I_k(t,v),t\in (t_k,t_{k+1}],k=1,2,\dots ,m,\hfill \end{array}\right.\end{array}$$

(21)

with $A_k\left(t\right),I_k(t,x),t\in (t_k,t_{k+1}],k=0,1,2,\dots ,m$, the functions F and G defined by (13), (14), (16), (17), respectively.

Remark 4.

Note that, from Proposition 1 and (14), it follows that the function $x\left(t\right)=\Omega \left(v\right)\left(t\right)$ satisfies the equalities

$$\begin{array}{cc}& \underset{t\to 0+}{lim}\left(e^{\frac{1-\rho }{\rho }t}{t}^{1-\alpha }x\left(t\right)\right)=\frac{u_0{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},\hfill \\ & \underset{t\to t_i+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_i)}{(t-t_i)}^{1-\alpha }x\left(t\right)\right)=\frac{[M_{i}x(t_i-0)+G_i\left(v(t_i-0)\right)]{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)}\hfill \\ & =\frac{[M_i(x(t_i-0)-v(t_i-0))+{\Psi }_i\left(v(t_i-0)\right)]{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},i=1,2,\dots ,m.\hfill \end{array}$$

(22)

Theorem 1.

Let the following conditions be fulfilled:

1. 

The functions $v,w\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ are a mild lower solution and a mild upper solution of the PIVP (1), respectively, such that $v\left(t\right)\le w\left(t\right)$ for $t\in (0,T]$;

2. 

The function $\psi \in C({\cup }_{k=0}^m(t_k,t_{k+1}]\times \mathbb{R},\mathbb{R})$ and there exist constants $L_k>0$ such that, for any $t\in (t_k,t_{k+1}],k=0,1,2,\dots ,x,y\in \mathbb{R}$, if $v\left(t\right)\le x\le y\le w\left(t\right)$ then the inequality

$$\psi (t,x)-\psi (t,y)\le L_k(x-y)$$

holds;

3. 

The functions ${\Psi }_k\in C(\mathbb{R},\mathbb{R}),k=1,2,\dots ,m,$ and there exist constants $M_k>0$, such that, for any $x,y\in \mathbb{R}$, if $v\left(t_k\right)\le x\le y\le w\left(t_k\right)$ then the inequalities

$${\Psi }_k\left(x\right)-{\Psi }_k\left(y\right)\le M_k(x-y)$$

hold.

Then, there exist two sequences of functions ${\left\{v^{\left(n\right)}(·)\right\}}_{n=0}^{\infty }$ and ${\left\{w^{\left(n\right)}(·)\right\}}_{n=0}^{\infty }$, with $v^{\left(n\right)},w^{\left(n\right)}\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$, such that:

 [a] 

The sequences ${\left\{v^{\left(k\right)}\left(t\right)\right\}}_{k=0}^{\infty }$ and ${\left\{w^{\left(k\right)}\left(t\right)\right\}}_{k=0}^{\infty }$ are defined by $v^{\left(0\right)}\left(t\right)=v\left(t\right),w^{\left(0\right)}\left(t\right)=w\left(t\right)$ and

$$\begin{array}{cc}& v^{(n+1)}\left(t\right)=\Omega \left(v^{\left(n\right)}\right)\left(t\right)fort\in (0,T],n\ge 0,\hfill \end{array}$$

(23)

and

$$\begin{array}{cc}& w^{(n+1)}\left(t\right)=\Omega \left(w^{\left(n\right)}\right)\left(t\right)fort\in (0,T],n\ge 0.\hfill \end{array}$$

(24)

 [b] 

For any $j=0,1,2,\dots$ the functions $v^{\left(j\right)}(·)$ and $w^{\left(j\right)}(·)$ are mild lower and mild upper solutions of PIVP (1), respectively;

 [c] 

The sequence ${\left\{v^{\left(j\right)}(·)\right\}}_{j=0}^{\infty }$ is increasing, i.e., $v^{(j-1)}\left(t\right)\le v^{\left(j\right)}\left(t\right)$, for $t\in (0,T],$$j=1,2,\dots$;

 [d] 

The sequence ${\left\{w^{\left(j\right)}(·)\right\}}_{j=0}^{\infty }$ is decreasing , i.e., $w^{(j-1)}\left(t\right)\ge w^{\left(j\right)}\left(t\right)$, for $t\in (0,T]$, $j=1,2,\dots$;

 [e] 

The inequality

$$v^{\left(k\right)}\left(t\right)\le w^{\left(k\right)}\left(t\right),fort\in (0,T],k=1,2,\dots$$

(25)

holds.

 [f] 

For any $k=0,1,2,\dots ,m$, the sequences $\left\{{\tilde{V}}_k^{\left(n\right)}(·)\right\}{\}}_{n=1}^{\infty }$ and $\left\{{\tilde{W}}_k(·)\right\}{\}}_{n=1}^{\infty }$ converge uniformly on $[t_k,t_{k+1}],k=0,1,2,\dots ,m$ to ${\tilde{V}}_k\in C_{1-\alpha ,\rho }\left([t_k,t_{k+1}]\right)$ and ${\tilde{W}}_k\in C_{1-\alpha ,\rho }\left([t_k,t_{k+1}]\right)$, respectively, where

$${\tilde{V}}_0^{\left(n\right)}\left(t\right)=\left\{\begin{array}{cc}\frac{u_0}{\Gamma \left(\alpha \right)},\hfill & t=0,\hfill \\ e^{\frac{1-\rho }{\rho }t}{\left(\frac{t}{\rho }\right)}^{1-\alpha }{v}^{\left(n\right)}\left(t\right),\hfill & t\in (0,t_1],\hfill \end{array}\right.$$

$${\tilde{W}}_0^{\left(n\right)}\left(t\right)=\left\{\begin{array}{cc}\frac{u_0}{\Gamma \left(\alpha \right)},\hfill & t=0,\hfill \\ e^{\frac{1-\rho }{\rho }t}{\left(\frac{t}{\rho }\right)}^{1-\alpha }{w}^{\left(n\right)}\left(t\right),\hfill & t\in (0,t_1],\hfill \end{array}\right.$$

and for $k=1,2,\dots ,m,$

$${\tilde{V}}_k^{\left(n\right)}\left(t\right)=\left\{\begin{array}{cc}\frac{M_k(v^{\left(n\right)}(t_k-0)-v^{(n-1)}(t_k-0))+{\Psi }_k\left(v^{(n-1)}(t_k-0)\right)}{\Gamma \left(\alpha \right)},\hfill & t=t_k,\hfill \\ e^{\frac{1-\rho }{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{1-\alpha }{v}^{\left(n\right)}\left(t\right),\hfill & t\in (t_k,t_{k+1}],\hfill \end{array}\right.$$

$${\tilde{W}}_k^{\left(n\right)}\left(t\right)=\left\{\begin{array}{cc}\frac{M_k(w^{\left(n\right)}(t_k-0)-w^{(n-1)}(t_k-0))+{\Psi }_k\left(w^{(n-1)}(t_k-0)\right)}{\Gamma \left(\alpha \right)},\hfill & t=t_k,\hfill \\ e^{\frac{1-\rho }{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{1-\alpha }{w}^{\left(n\right)}\left(t\right),\hfill & t\in (t_k,t_{k+1}].\hfill \end{array}\right.$$

 [g] 

The functions $V\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ and $W\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ are mild solutions of the PIVP (1) on $[0,T]$ and $V\left(t\right)\le W\left(t\right),t\in [0,T]$, where

$$\begin{array}{cc}& V\left(t\right)=e^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}{\tilde{V}}_k\left(t\right),\hfill \\ & W\left(t\right)=e^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}{\tilde{W}}_k\left(t\right),t\in (t_k,t_{k+1}],k=0,1,2,\dots ,m.\hfill \end{array}$$

Proof. 

Define

$$v^{\left(0\right)}\left(t\right)=v\left(t\right),w^{\left(0\right)}\left(t\right)=w\left(t\right),$$

and for $n\ge 0$,

$$v^{(n+1)}\left(t\right)=\Omega \left(v^{\left(n\right)}\right)\left(t\right),w^{(n+1)}\left(t\right)=\Omega \left(w^{\left(n\right)}\right)\left(t\right).$$

From Remark 4 it follows that, for all $k=1,2,\dots ,m$, the equalities

$$\begin{array}{cc}& \underset{t\to t_k+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_k)}{(t-t_k)}^{1-\alpha }{v}^{(n+1)}\left(t\right)\right)\hfill \\ & =\frac{[M_k(v^{(n+1)}(t_k-0)-v^{\left(n\right)}(t_k-0))+{\Psi }_i\left(v^{\left(n\right)}(t_k-0)\right)]{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},\hfill \\ & \underset{t\to t_k+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_k)}{(t-t_k)}^{1-\alpha }{w}^{(n+1)}\left(t\right)\right)\hfill \\ & =\frac{[M_k(w^{(n+1)}(t_k-0)-w^{\left(n\right)}(t_k-0))+{\Psi }_i\left(w^{\left(n\right)}(t_k-0)\right)]{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)},n=0,1,2,\dots \hfill \end{array}$$

(26)

hold. According to Remark 3, the functions $v^{(n+1)}(·),w^{(n+1)}(·)$ satisfy

$$\begin{array}{cc}& v^{(n+1)}\left(t\right)=u_0{A}_0\left(t\right)+I_0(t,v^{\left(n\right)}),w^{(n+1)}\left(t\right)=u_0{A}_0\left(t\right)+I_0(t,w^{\left(n\right)}),t\in (0,t_1],\hfill \end{array}$$

(27)

and also

$$\begin{array}{cc}& v^{(n+1)}\left(t\right)=[M_k{v}^{(n+1)}(t_k-0)+G_k\left(v^{\left(n\right)}(t_k-0)\right)]A_k\left(t\right)+I_k(t,v^{\left(n\right)}),\hfill \\ & w^{(n+1)}\left(t\right)=[M_k{w}^{(n+1)}(t_k-0)+G_k\left(w^{\left(n\right)}(t_k-0)\right)]A_k\left(t\right)+I_k(t,w^{\left(n\right)}),\hfill \\ & t\in (t_k,t_{k+1}],k=1,2,\dots ,m.\hfill \end{array}$$

(28)

We use induction to prove properties of the sequences of successive approximations. First, let $n=1$. The function $v(·)$ is a mild lower solution of PIVP (1). Therefore, for $t\in (0,T]$, it satisfies the inequalities

$$\begin{array}{cc}\hfill v^{\left(0\right)}\left(t\right)& =v\left(t\right)\le u_0{A}_0\left(t\right)+I_0(t,v^{\left(0\right)})=v^{\left(1\right)}\left(t\right),t\in (0,t_1],\hfill \\ \hfill v^{\left(0\right)}\left(t\right)& =v\left(t\right)\le M_k{A}_k\left(t\right)\left[u_0\prod _{j=0}^{k-1}\left(M_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{k-1}{I}_j(t_{j+1},v)\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ & +A_k\left(t\right)\sum _{j=1}^k\left({\Psi }_j\left(v(t_j-0)\right)-M_{j}v(t_j-0)\right)\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)+I_k(t,v),\hfill \\ & =v^{\left(1\right)}\left(t\right),t\in (t_k,t_{k+1}],k=1,2,\dots ,m.\hfill \end{array}$$

(29)

From inequality (29) it follows that $v^{\left(0\right)}\left(t\right)\le v^{\left(1\right)}\left(t\right),t\in (0,T]$. Then, from condition (A1) and equality (17), we get

$$\begin{array}{cc}& I_k\left(t,v^{\left(0\right)}\right)\hfill \\ & =\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(\rho -1)\left(\frac{t-s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\left(\psi \left(t,v^{\left(0\right)}\left(s\right)\right)+L_k{v}^{\left(0\right)}\left(s\right)\right)ds,\hfill \\ & =\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(\rho -1)\left(\frac{t-s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\left(\psi \left(t,v^{\left(1\right)}\left(s\right)\right)+L_k{v}^{\left(1\right)}\left(s\right)\right)ds,\hfill \\ & +\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(\rho -1)\left(\frac{t-s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)(\psi \left(t,v^{\left(0\right)}\left(s\right)\right)-\psi \left(t,v^{\left(1\right)}\left(s\right)\right)\hfill \\ & +L_k{v}^{\left(0\right)}\left(s\right)+L{v}^{\left(1\right)}\left(s\right))ds\le I_k\left(t,v^{\left(1\right)}\right),k=0,1,2,\dots ,m.\hfill \end{array}$$

(30)

From the definition of the operator $\Omega$, conditions (A1) and (A2) with

$$x=v^{\left(0\right)}\left(t\right)\le y=v^{\left(1\right)}\left(t\right),$$

inequality (30) and the inequality

$$\begin{array}{cc}& {\Psi }_j\left(v^{\left(0\right)}(t_j-0)\right)-{\Psi }_j\left(v^{\left(1\right)}(t_j-0)\right)-M_j(v^{\left(0\right)}(t_j-0)-v^{\left(1\right)}(t_j-0))\le 0,\hfill \end{array}$$

(31)

for $j=1,2,\dots ,m$, we obtain

$$\begin{array}{cc}& v^{\left(1\right)}\left(t\right)=u_0{A}_0\left(t\right)+I_0(t,v^{\left(0\right)})\le u_0{A}_0\left(t\right)+I_0(t,v^{\left(1\right)}),t\in (0,t_1],\hfill \\ & v^{\left(1\right)}\left(t\right)=M_k{A}_k\left(t\right)\left[u_0\prod _{j=0}^{k-1}\left(M_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{k-1}{I}_j(t_{j+1},v^{\left(0\right)})\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ & +A_k\left(t\right)\sum _{j=1}^k\left({\Psi }_j\left(v^{\left(0\right)}(t_j-0)\right)-M_j{v}^{\left(0\right)}(t_j-0)\right)\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)+I_k(t,v^{\left(0\right)})\hfill \\ & \le M_k{A}_k\left(t\right)\left[u_0\sum _{j=0}^{k-1}\left(M_j{A}_j\left(t_{j+1}\right)\right)+\sum _{j=0}^{k-1}{I}_j(t_{j+1},v^{\left(1\right)})\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ & +A_k\left(t\right)\sum _{j=1}^k\left({\Psi }_j\left(v^{\left(1\right)}(t_j-0)\right)-M_j{v}^{\left(1\right)}(t_j-0)\right)\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)+I_k(t,v^{\left(1\right)}),\hfill \\ & t\in (t_k,t_{k+1}],k=1,2,\dots ,m.\hfill \end{array}$$

(32)

Therefore, function $v^{\left(1\right)}\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ is a mild lower solution of PIVP (1).

From the definition of functions $v^{\left(i\right)}(·),i=1,2$, conditions (A1), (A2) with

$$x=v^{\left(0\right)}\left(t\right)\le y=v^{\left(1\right)}\left(t\right),$$

inequalities (30) and (31), we obtain for $t\in (t_k,t_{k+1}],k=0,1,2,\dots ,m,$

$$\begin{array}{cc}\hfill v^{\left(1\right)}\left(t\right)& \le u_0{A}_0\left(t\right)+I_0(t,v^{\left(1\right)})=v^{\left(2\right)}\left(t\right),t\in (0,t_1],\hfill \\ \hfill v^{\left(1\right)}\left(t\right)& \le v^{\left(2\right)}\left(t\right)+A_k\left(t\right)\sum _{j=1}^k({\Psi }_j\left(v^{\left(0\right)}(t_j-0)\right)-{\Psi }_j\left(v^{\left(1\right)}(t_j-0)\right)\hfill \\ & -M_j(v^{\left(0\right)}(t_j-0)-v^{\left(1\right)}(t_j-0)))\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)\hfill \\ & \le v^{\left(2\right)}\left(t\right),t\in (t_k,t_{k+1}],k=1,2,\dots ,m.\hfill \end{array}$$

(33)

Inductively we can prove that the functions $v^{\left(n\right)}(·),n=1,2,\dots ,$ are mild lower solutions of PIVP (1) and that

$$v^{\left(n\right)}\left(t\right)\le v^{(n+1)}\left(t\right),t\in (t_k,t_{k+1}],k=0,1,2\dots ,m,n=0,1,2,\dots .$$

Similarly, we have $w^{\left(0\right)}\left(t\right)\ge w^{\left(1\right)}\left(t\right)$ and the functions $w^{\left(n\right)}(·),n=1,2,\dots ,$ are mild upper solutions of PIVP (1) and

$$w^{\left(n\right)}\left(t\right)\ge w^{(n+1)}\left(t\right),t\in (t_k,t_{k+1}],k=0,1,2\dots ,m,n=0,1,2,\dots .$$

From condition 1 it follows that $v^{\left(0\right)}\left(t\right)\le w^{\left(0\right)}\left(t\right)$, for $t\in [0,T]$. Similar to the inequality (30), we could prove that the inequality

$$I_k\left(t,v^{\left(0\right)}\right)\le I_k\left(t,w^{\left(0\right)}\right),t\in (t_k,t_{k+1}],k=0,1,2,\dots ,m$$

holds. Therefore, from the definition of the operator $\Omega$, conditions (A1), (A2) with $x=v^{\left(0\right)}\left(t\right)\le y=w^{\left(0\right)}\left(t\right)$, we get

$$\begin{array}{cc}& v^{\left(1\right)}\left(t\right)-w^{\left(1\right)}\left(t\right)\hfill \\ & =M_k{A}_k\left(t\right)\left[\sum _{j=0}^{k-1}\left(I_j(t_{j+1},v^{\left(0\right)})-I_j(t_{j+1},w^{\left(0\right)})\right)\prod _{p=j+1}^{k-j-1}\left(M_p{A}_p\left(t_{p+1}\right)\right)\right]\hfill \\ & +A_k\left(t\right)\sum _{j=1}^k({\Psi }_j\left(v^{\left(0\right)}(t_j-0)\right)-{\Psi }_j\left(w^{\left(0\right)}(t_j-0)\right)\hfill \\ & -M_j{v}^{\left(0\right)}(t_j-0)+M_j{w}^{\left(0\right)}(t_j-0))\prod _{p=j}^{k-1}\left(M_{p+1}{A}_p\left(t_{p+1}\right)\right)\hfill \\ & +I_k(t,v^{\left(0\right)})-I_k(t,w^{\left(0\right)})\le 0,t\in (t_k,t_{k+1}],k=1,2,\dots ,m.\hfill \end{array}$$

(34)

In a similar way we can prove the inequality (25). Therefore, claims [b]-[e] are established. We now prove the convergence, i.e., claim [f]. For that, consider the interval $[0,t_1]$. Define the sequence ${\left\{V_0^{\left(n\right)}\left(t\right)\right\}}_1^{\infty }$ by

$$V_0^{\left(n\right)}\left(t\right)=e^{\frac{1-\rho }{\rho }t}{\left(\frac{t}{\rho }\right)}^{1-\alpha }{v}^{\left(n\right)}\left(t\right),(0,t_1].$$

From the definition of the functions $v^{\left(n\right)}(·)$ we get that

$$\underset{t\to 0+}{lim}{V}_0^{\left(n\right)}\left(t\right)={\rho }^{\alpha -1}\underset{t\to 0+}{lim}\left(e^{\frac{1-\rho }{\rho }t}{t}^{1-\alpha }{v}^{\left(n\right)}\left(t\right)\right)={\rho }^{\alpha -1}\frac{u_0{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)}.$$

Thus, we define $V_0^{\left(n\right)}\left(0\right)=\frac{u_0}{\Gamma \left(\alpha \right)},n=1,2,\dots .$ Multiplying the equalities (23) by $e^{\frac{1-\rho }{\rho }t}{\left(\frac{t}{\rho }\right)}^{1-\alpha }$, we obtain on $(0,t_1]$:

$$\begin{array}{cc}& V_0^{\left(n\right)}\left(t\right)=u_0{E}_{\alpha ,\alpha }\left(-L_0{\left(\frac{t}{\rho }\right)}^{\alpha }\right)\hfill \\ & +\frac{{\left(\frac{t}{\rho }\right)}^{1-\alpha }}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}{e}^{(1-\rho )\left(\frac{s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_0{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\left[\psi \left(s,e^{\frac{\rho -1}{\rho }s}{\left(\frac{s}{\rho }\right)}^{\alpha -1}{V}_0^{\left(n\right)}\left(s\right)\right)\right.\hfill \\ & \left.+L_0{e}^{\frac{\rho -1}{\rho }s}{\left(\frac{s}{\rho }\right)}^{\alpha -1}{V}_0^{\left(n\right)}\left(s\right)\right]ds.\hfill \end{array}$$

(35)

According to claims [c]-[e], the sequence ${\left\{V_0^{\left(n\right)}(·)\right\}}_{n=0}^{\infty }$ is monotonic and bounded on $[0,t_1]$. Also, this sequence is equicontinuous on $[0,t_1]$. Therefore, it is uniformly convergent on $[0,t_1]$. Let ${\tilde{V}}_0\left(t\right)={lim}_{n\to \infty }{V}_0^{\left(n\right)}\left(t\right),t\in [0,t_1].$ According to the claims [c]-[e], the inequalities

$$\begin{array}{cc}& V_0^{\left(n\right)}\left(t\right)\le {\tilde{V}}_0\left(t\right),t\in [0,t_1],n=1,2,\dots ,\hfill \end{array}$$

(36)

hold. Take the limit as $n\to \infty$ in (35), use the continuity of the function $\psi$ and we obtain the Volterra fractional integral equation

$$\begin{array}{cc}& {\tilde{V}}_0\left(t\right)=u_0{E}_{\alpha ,\alpha }\left(-L_0{\left(\frac{t}{\rho }\right)}^{\alpha }\right)\hfill \\ & +\frac{{\left(\frac{t}{\rho }\right)}^{1-\alpha }}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}{e}^{(1-\rho )\left(\frac{s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_0{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\left[\psi \left(s,e^{\frac{\rho -1}{\rho }s}{\left(\frac{s}{\rho }\right)}^{\alpha -1}{\tilde{V}}_0\left(s\right)\right)\right.\hfill \\ & \left.+L_0{e}^{\frac{\rho -1}{\rho }s}{\left(\frac{s}{\rho }\right)}^{\alpha -1}{\tilde{V}}_0\left(s\right)\right]ds,\mathrm{for}t\in (0,t_1].\hfill \end{array}$$

(37)

Denote

$$V_0\left(t\right)=e^{\frac{\rho -1}{\rho }t}{\left(\frac{t}{\rho }\right)}^{\alpha -1}{\tilde{V}}_0\left(t\right)\in C_{1-\alpha ,\rho }\left([0,t_1]\right).$$

Therefore, the equalities

$$\underset{t\to 0+}{lim}\left(e^{\frac{1-\rho }{\rho }t}{t}^{1-\alpha }{V}_0\left(t\right)\right)={\rho }^{1-\alpha }\underset{t\to 0+}{lim}{\tilde{V}}_0\left(t\right)=\frac{u_0{\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)}$$

and

$$\begin{array}{cc}& V_0\left(t\right)=u_0{E}_{\alpha ,\alpha }\left(-L_0{\left(\frac{t}{\rho }\right)}^{\alpha }\right)e^{\frac{\rho -1}{\rho }t}{\left(\frac{t}{\rho }\right)}^{\alpha -1}\hfill \\ & +\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }\left(-L_0{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\left[\psi (s,V_0\left(s\right))+L_0{V}_0\left(s\right)\right]ds,t\in (0,t_1].\hfill \end{array}$$

(38)

hold.

We will now use an induction argument. Consider the interval $[t_k,t_{k+1}]$, where $k\in \{1,\dots ,m\},$ is a fixed integer. Define the sequence ${\left\{V_k^{\left(n\right)}(·)\right\}}_{n=1}^{\infty }$ by

$$V_k^{\left(n\right)}\left(t\right)=e^{\frac{1-\rho }{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{1-\alpha }{v}^{\left(n\right)}\left(t\right)$$

on $(t_k,t_{k+1}].$ From the definition of the functions $v^{\left(n\right)}(·)$, Remark 4 and equalities (26), we get

$$\begin{array}{cc}\hfill \underset{t\to t_k+}{lim}{V}_k^{\left(n\right)}\left(t\right)& ={\rho }^{\alpha -1}\underset{t\to t_k+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_k)}{(t-t_k)}^{1-\alpha }{v}^{\left(n\right)}\left(t\right)\right)\hfill \\ & =\frac{M_k(v^{\left(n\right)}(t_k-0)-v^{(n-1)}(t_k-0))+{\Psi }_k\left(v^{(n-1)}(t_k-0)\right)}{\Gamma \left(\alpha \right)}.\hfill \end{array}$$

(39)

Thus, we define

$$V_k^{\left(n\right)}\left(t_k\right)=\frac{M_k(v^{\left(n\right)}(t_k-0)-v^{(n-1)}(t_k-0))+{\Psi }_k\left(v^{(n-1)}(t_k-0)\right)}{\Gamma \left(\alpha \right)},n=1,2,\dots .$$

Multiply the equalities (28) by $e^{\frac{1-\rho }{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{1-\alpha }$, and we obtain on $(t_k,t_{k+1}]$:

$$\begin{array}{cc}\hfill V_k^{\left(n\right)}\left(t\right)& =e^{\frac{1-\rho }{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{1-\alpha }{v}^{\left(n\right)}\left(t\right)\hfill \\ & =\left[M_k{e}^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}{V}_k^{\left(n\right)}(t_k-0)\right.\hfill \\ & \left.+G_k\left(e^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}{V}_k^{(n-1)}(t_k-0)\right)\right]E_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-t_k}{\rho }\right)}^{\alpha }\right)\hfill \\ & +\frac{{\left(\frac{t-t_k}{\rho }\right)}^{1-\alpha }}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(1-\rho )\left(\frac{s-t_k}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\hfill \\ & \times \left[\psi \left(s,e^{\frac{\rho -1}{\rho }(s-t_k)}{\left(\frac{s-t_k}{\rho }\right)}^{\alpha -1}{V}_k^{(n-1)}\left(s\right)\right)\right.\hfill \\ & \left.+L_k{e}^{\frac{\rho -1}{\rho }(s-t_k)}{\left(\frac{s-t_k}{\rho }\right)}^{\alpha -1}{V}_k^{(n-1)}\left(s\right)\right]ds.\hfill \end{array}$$

(40)

According to claims [c]-[e], the sequence ${\left\{V_k^{\left(n\right)}(·)\right\}}_{n=0}^{\infty }$ is monotonic and bounded on $[t_k,t_{k+1}]$. This sequence is equicontinuous on $[t_k,t_{k+1}]$. Therefore, it is uniformly convergent on $[t_k,t_{k+1}]$. Let

$${\tilde{V}}_k\left(t\right)=\underset{n\to \infty }{lim}{V}_k^{\left(n\right)}\left(t\right),t\in [t_k,t_{k+1}].$$

According to the claims [c]-[e], the inequalities

$$V_k^{\left(n\right)}\left(t\right)\le {\tilde{V}}_k\left(t\right),t\in [t_k,t_{k+1}],n=1,2,\dots ,$$

hold. Take the limit as $n\to \infty$ in (40), use the continuity of the function $\psi$, the definition (14) of the function $G_k$, and we obtain the Volterra fractional integral equation

$$\begin{array}{cc}\hfill {\tilde{V}}_k\left(t\right)& ={\Psi }_k\left(e^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}{\tilde{V}}_k(t_k-0)\right)E_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-t_k}{\rho }\right)}^{\alpha }\right)\hfill \\ & +\frac{{\left(\frac{t-t_k}{\rho }\right)}^{1-\alpha }}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(1-\rho )\left(\frac{s-t_k}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\hfill \\ & \times \left[\psi \left(s,e^{\frac{\rho -1}{\rho }(s-t_k)}{\left(\frac{s-t_k}{\rho }\right)}^{\alpha -1}{\tilde{V}}_k\left(s\right)\right)\right.\hfill \\ & \left.+L_k{e}^{\frac{\rho -1}{\rho }(s-t_k)}{\left(\frac{s-t_k}{\rho }\right)}^{\alpha -1}{\tilde{V}}_k\left(s\right)\right]ds,t\in [t_k,t_{k+1}],\hfill \end{array}$$

(41)

and

$$\underset{t\to t_k+}{lim}{\tilde{V}}_k\left(t\right)=\frac{{\Psi }_i\left(e^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}{\tilde{V}}_k(t_k-0)\right)}{\Gamma \left(\alpha \right)}.$$

Denote

$$V_k\left(t\right)=e^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}{\tilde{V}}_k\left(t\right)\in C_{1-\alpha ,\rho }\left([t_k,t_{k+1}]\right).$$

Therefore, the equalities

$$\underset{t\to t_k+}{lim}\left(e^{\frac{1-\rho }{\rho }(t-t_k)}{(t-t_k)}^{1-\alpha }{V}_k\left(t\right)\right)={\rho }^{1-\alpha }\underset{t\to t_k+}{lim}{\tilde{V}}_k\left(t\right)=\frac{{\Psi }_i\left(V_k(t_k-0)\right){\rho }^{1-\alpha }}{\Gamma \left(\alpha \right)}$$

and

$$\begin{array}{cc}\hfill V_k\left(t\right)& ={\Psi }_k\left(V_k(t_k-0)\right)E_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-t_k}{\rho }\right)}^{\alpha }\right)e^{\frac{\rho -1}{\rho }(t-t_k)}{\left(\frac{t-t_k}{\rho }\right)}^{\alpha -1}\hfill \\ & +\frac{1}{{\rho }^{\alpha }\Gamma \left(\alpha \right)}{\int }_{t_k}^t{(t-s)}^{\alpha -1}{e}^{(\rho -1)\left(\frac{t-s}{\rho }\right)}{E}_{\alpha ,\alpha }\left(-L_k{\left(\frac{t-s}{\rho }\right)}^{\alpha }\right)\hfill \\ & \times \left[\psi (s,V_k\left(s\right))+L_k{V}_k\left(s\right)\right]ds,t\in [t_k,t_{k+1}]\hfill \end{array}$$

(42)

hold. Define the function $V\left(t\right)=V_k\left(t\right)$ for $t\in (t_k,t_{k+1}],k=1,2,\dots ,m.$ Then, function $V\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$ is a mild solution of the PIVP (1) on $[0,T]$, i.e., the functions $V(·)$ and $W(·)$ satisfy the initial value problem in (1).

Similarly, we can construct a sequence ${\left\{W_k^{\left(n\right)}(·)\right\}}_{n=1}^{\infty },k=0,1,2,\dots ,m$ and the limit functions ${\tilde{W}}_k(·),k=0,1,2,\dots ,m$ such that ${\tilde{W}}_k\left(t\right)\le W_k^{\left(n\right)}\left(t\right),t\in [t_k,t_{k+1}],n=1,2,\dots ,$ and ${\tilde{V}}_k\left(t\right)\le {\tilde{W}}_k\left(t\right)$. Then similarly, we define $W\in P{C}_{1-\alpha ,\rho }\left([0,T]\right)$, which is a mild solution of PIVP (1) and $V\left(t\right)\le W\left(t\right),t\in [0,T]$. □

2.5. Example

Consider the PIVP

$$\begin{array}{cc}& \left({}_0^R{\mathcal{D}}^{0.3,0.5}x\right)\left(t\right)=\frac{x^2\left(t\right)}{t+1}\mathrm{for}t\in (0,2]\cup (2,2.35],\hfill \\ & \underset{t\to 2+}{lim}\left(e^{\frac{1-0.5}{0.5}(t-2)}{(t-2)}^{1-0.3}y\left(t\right)\right)=0,\hfill \\ & \underset{t\to 0+}{lim}\left(e^{\frac{1-0.5}{0.5}t}{t}^{1-0.3}y\left(t\right)\right)=0,\hfill \end{array}$$

(43)

with $\psi (t,x)=\frac{x^2}{t+1}$, $\alpha =0.3,\rho =0.5$.

Consider the function

$$v_0\left(t\right)=\left\{\begin{array}{cc}{t}^{-0.4},\hfill & t\in (0,2],\hfill \\ {(t-2)}^{-0.45},\hfill & t\in (2,2.35].\hfill \end{array}\right.$$

Let $t\in [0,2]$ and $v_0\left(t\right)=t^{-0.4}\le x\le y$. Then,

$$\frac{1}{t+1}(x+y)\ge 2\frac{1}{t+1}{t}^{-0.4}\ge \frac{2}{3}{2}^{-0.4}$$

and

$$\frac{x^2}{t+1}-\frac{y^2}{t+1}=\frac{1}{t+1}(x+y)(x-y)\le \frac{2}{3}{2}^{-0.4}(x-y),$$

Therefore, we could choose the constant $L_0=\frac{2}{3}{2}^{-0.4}$. Then the inequality

$$\begin{array}{cc}\hfill t^{-0.4}& \le \frac{1}{0.5^{0.3}\Gamma \left(0.3\right)}{\int }_0^t{(t-s)}^{-0.7}{e}^{-t+s}{E}_{0.3,0.3}\left(-\frac{2}{3}{2}^{-0.4}{(t-s)}^{0.3}\right)\hfill \\ & \times \left(\frac{s^{-0.8}}{s+1}+\frac{2}{3}{2}^{-0.4}{s}^{-0.4}\right)ds\hfill \end{array}$$

(44)

holds (see Figure 1, left).

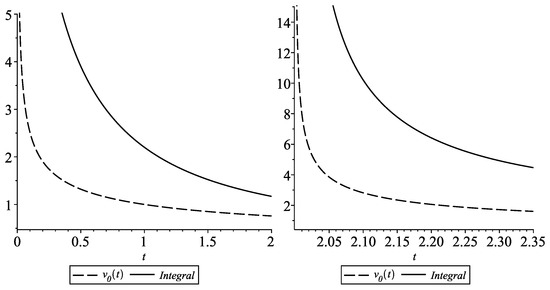
Figure 1. Graphs of $v_0\left(t\right)=t^{-0.4}$ and the integral in (44) with $t\in (0,2]$ (left) and of $v_0\left(t\right)={(t-2)}^{-0.45}$ and the integral (45) with $t\in (2,2.35]$ (right).

Let $t\in (2,2.35]$ and $v_0\left(t\right)={(t-2)}^{-0.45}\le x\le y$. Then,

$$\frac{1}{t+1}(x+y)\ge 2\frac{1}{t+1}{(t-2)}^{-0.4}\ge \frac{2}{3.35}0.{35}^{-0.45}$$

and

$$\frac{x^2}{t+1}-\frac{y^2}{t+1}=\frac{1}{t+1}(x+y)(x-y)\le \frac{2}{3.35}0.{35}^{-0.45}(x-y),$$

i.e., $L_1=\frac{2}{3.35}0.{35}^{-0.45}$. Then the inequality

$$\begin{array}{cc}\hfill {(t-2)}^{-0.45}\le & \frac{1}{0.5^{0.3}\Gamma \left(0.3\right)}{\int }_2^t{(t-s)}^{-0.7}{e}^{-t+s}{E}_{0.3,0.3}\left(-\frac{2}{3.35}0.{35}^{-0.45}{(t-s)}^{0.3}\right)\hfill \\ & \times \left(\frac{{(s-2)}^{-0.9}}{s+1}+\frac{2}{3.35}0.{35}^{-0.45}{(s-2)}^{-0.45}\right)ds\hfill \end{array}$$

holds (see Figure 1, right).

From inequalities (44) and (45) it follows that the function $v_0\left(t\right)$ is a mild lower solution of PIVP (43) on $[0,2.35]$ (see Definition 2).

Now, apply the suggested iterative scheme given by Formulas (23) and (24) with the operator $\Omega$ defined by Equation (21) to obtain for $n=0,1,2,3,\dots$ the successive approximations by

$$\begin{array}{c}\hfill v_{n+1}\left(t\right)=\left\{\begin{array}{c}\frac{1}{0.5^{0.3}\Gamma \left(0.3\right)}{\int }_0^t{(t-s)}^{-0.7}{e}^{-t+s}{E}_{0.3,0.3}\left(-\frac{2}{32^{-0.4}}\frac{{(t-s)}^{0.3}}{0.5}\right)\left(\frac{v_n^2\left(s\right)}{s+1}+\frac{2}{32^{0.4}}{v}_n\left(s\right)\right)ds\hfill \\ fort\in (0,2]\hfill \\ \frac{1}{0.5^{0.3}\Gamma \left(0.3\right)}{\int }_0^t{(t-s)}^{-0.7}{e}^{-t+s}{E}_{0.3,0.3}\left(-\frac{2}{3.35}0.{35}^{-0.45}\frac{{(t-s)}^{0.3}}{0.5}\right)\hfill \\ \times \left(\frac{v_n^2\left(s\right)}{s+1}\frac{2}{3.35}0.{35}^{-0.45}{v}_n\left(s\right)\right)ds\mathrm{for}t\in (2,2.35].\hfill \end{array}\right.\end{array}$$

According to Theorem 1 the sequence of successive approximations $\left\{v_{n+1}\left(t\right)\right\}$ is an increasing one and it is convergent to a mild solution of PIVP (43) on $[0,2.35]$.

3. Conclusions

Recently many different types of fractional derivatives are defined and applied to model more adequate real world phenomena. One of the last introduced fractional derivatives is the so called generalized proportional fractional derivative, which is a generalization of the classical Caputo and Riemann–Liouville fractional ones. The main difficulties in the application of these derivatives to differential equations is that it is very difficult to obtain exact solutions even in the scalar case. As a result we require some algorithm to solve the corresponding initial value problems approximately. In this paper an approximate method for solving an initial value problem for a scalar non-linear fractional differential equation with generalized proportional fractional derivative of Riemann–Liouville type on a finite interval is proposed. We study the case when some impulsive perturbations with negligible small action time are applied to the equation. In connection with these impulses we set up in appropriate way both the impulsive and the initial conditions. Additionally, we consider the case when the lower limit of the fractional derivative is hanged at any impulsive time. The suggested approximate scheme is based on the method of lower and upper solutions combined with the monotone-iterative technique. Mild lower and mild upper solutions are defined in an appropriate way. Two monotone sequences, increasing and decreasing ones, are constructed and their convergence to mild solutions of the given problem is established. In the case of uniqueness, both limits coincide with the unique solution of the given problem. To the best of our knowledge it is the first approximate scheme suggested to the initial value problem of this type of fractional differential equation.