Fast Terminal Sliding Control of Underactuated Robotic Systems Based on Disturbance Observer with Experimental Validation
Abstract
:1. Introduction
- (a)
- Design of a disturbance observer-based FTSMC technique for stabilization of underactuated systems with exterior perturbations.
- (b)
- Satisfaction of the stabilization of the state trajectories based on Barbalat’s lemma.
- (c)
- Finite time convergence of disturbance approximation error to zero using the disturbance observer law.
- (d)
- Confirmation of the proposed method by using the illustrative simulations and experimental assessments on the practical cart-inverted pole.
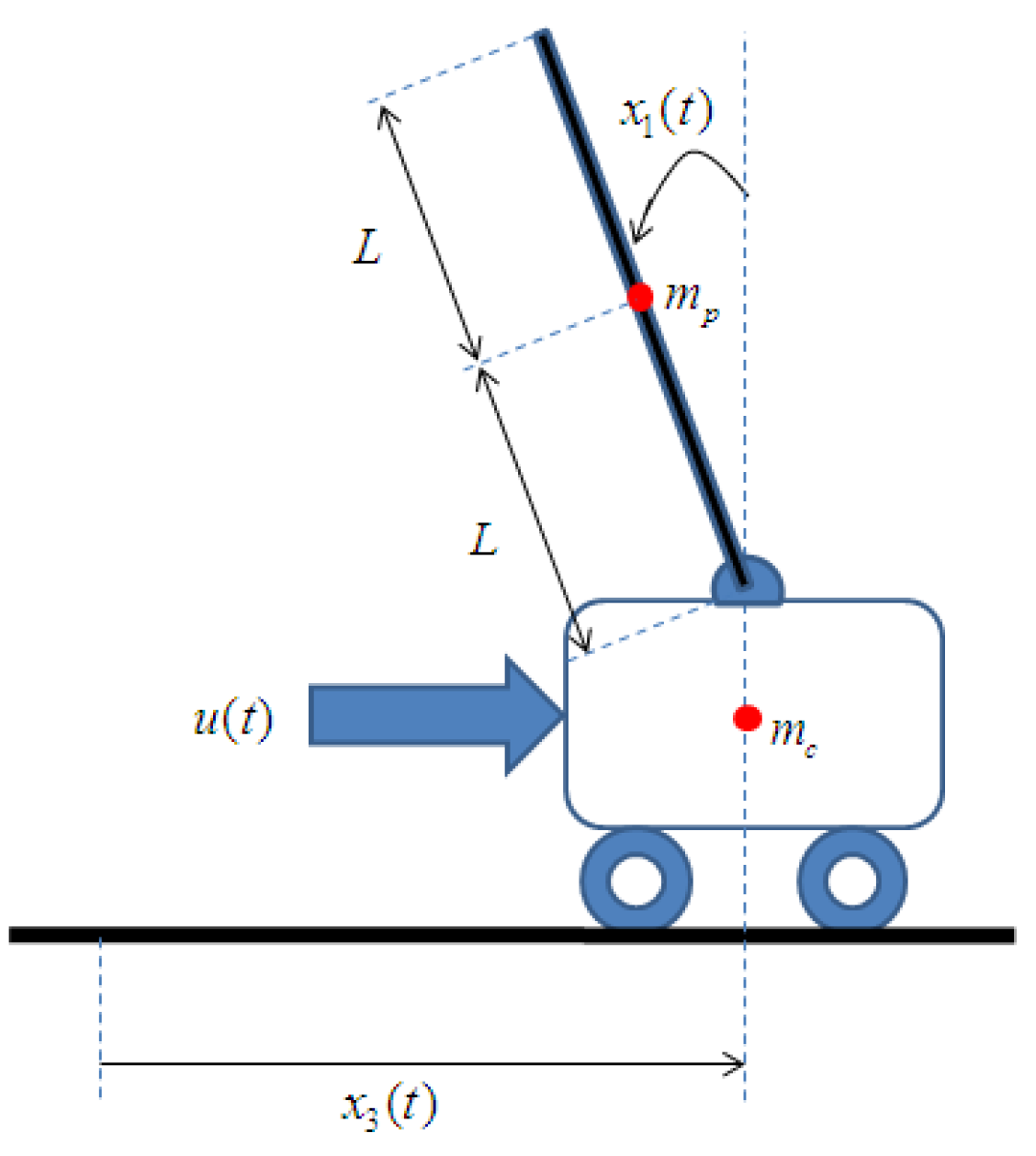
2. Problem Definition
3. Main Results
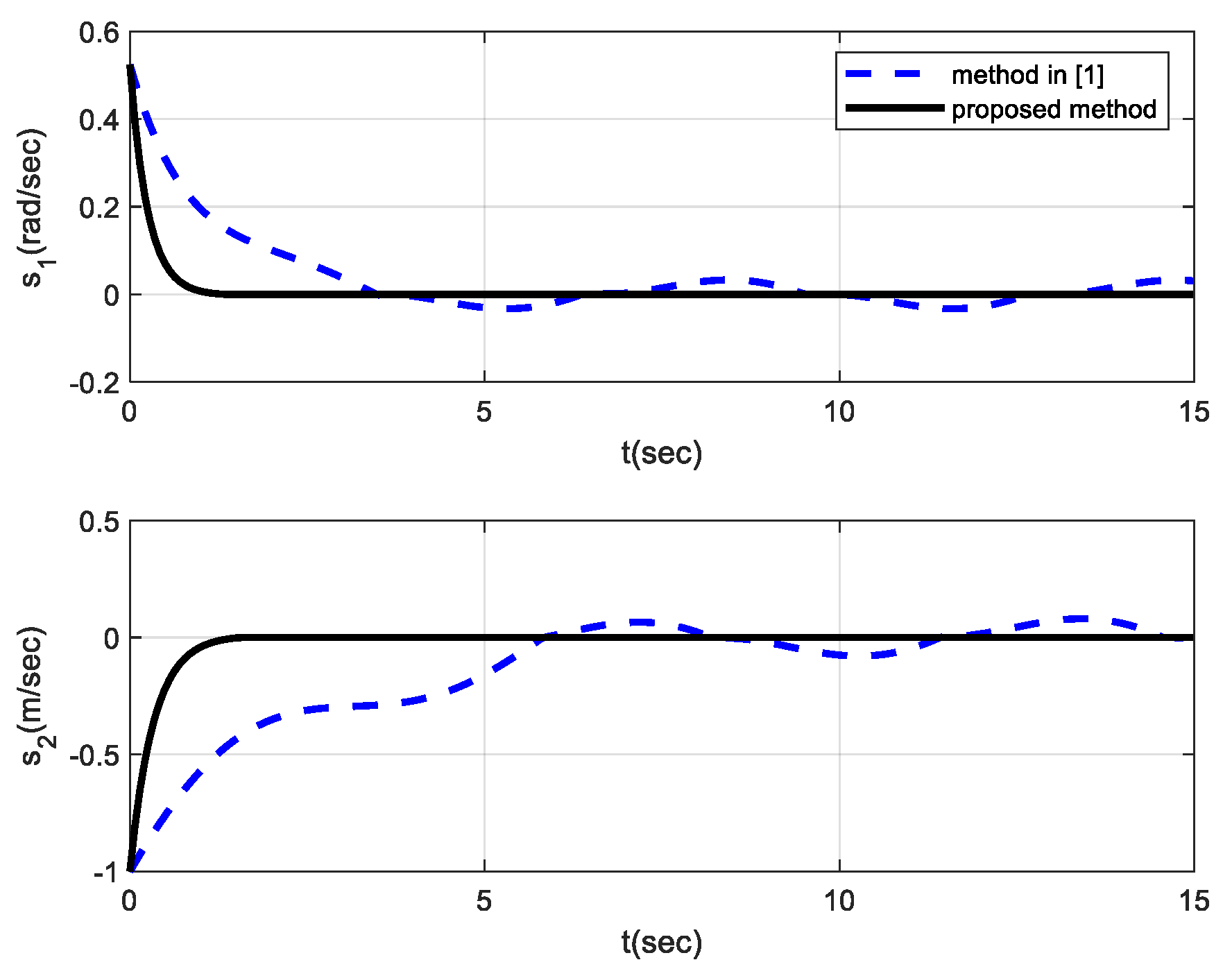
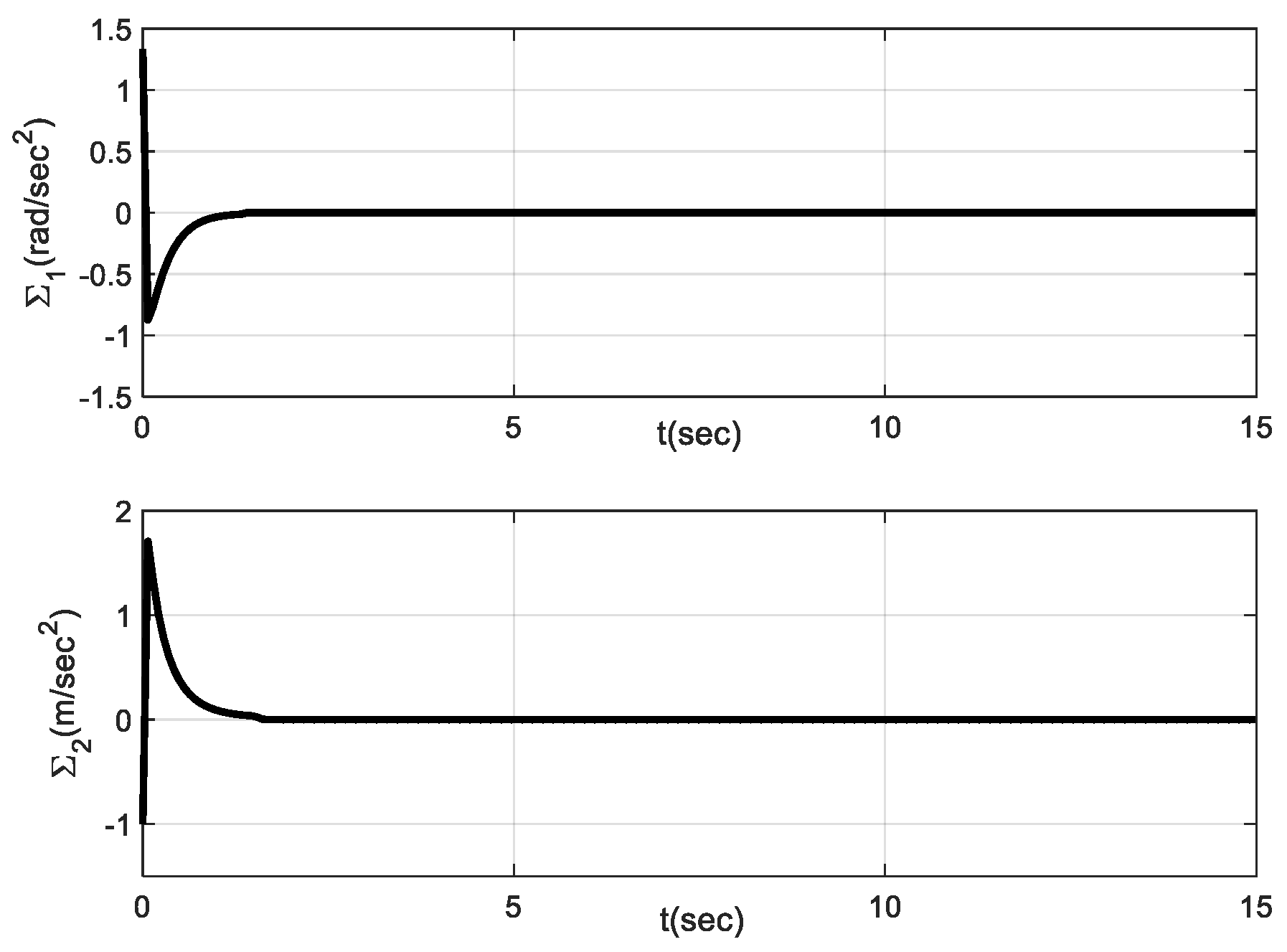
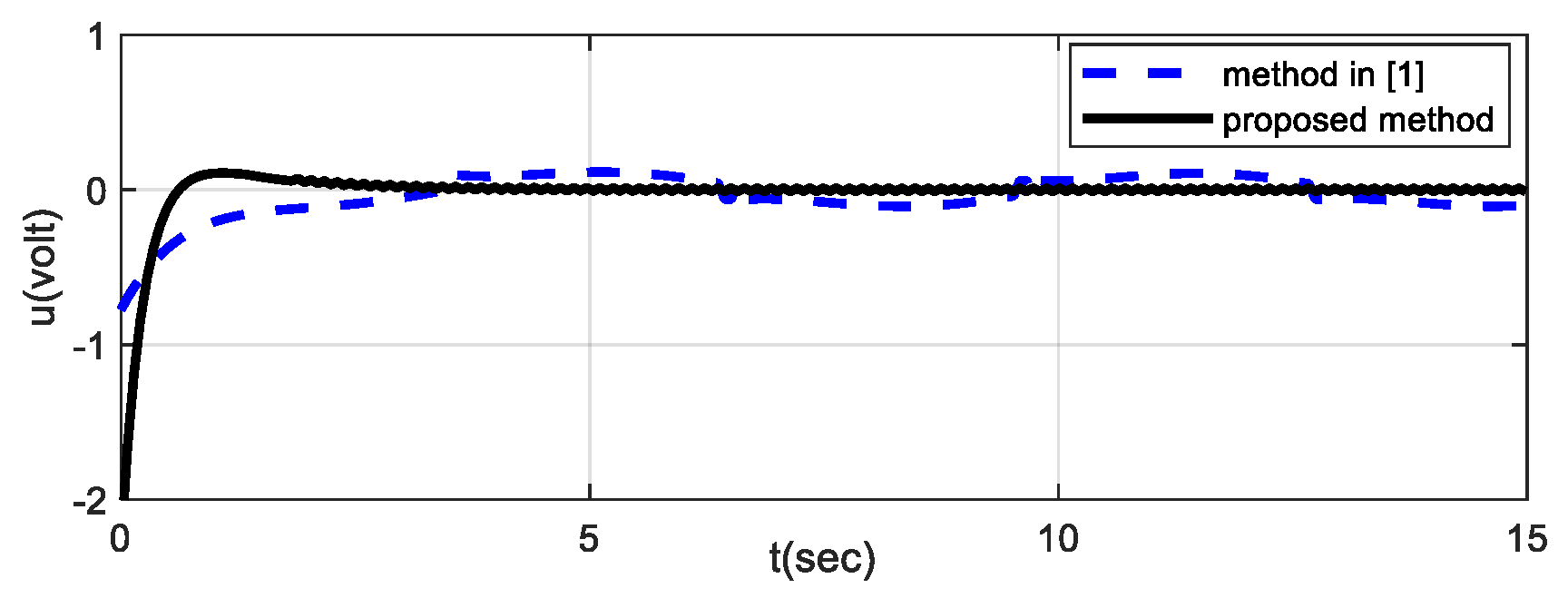
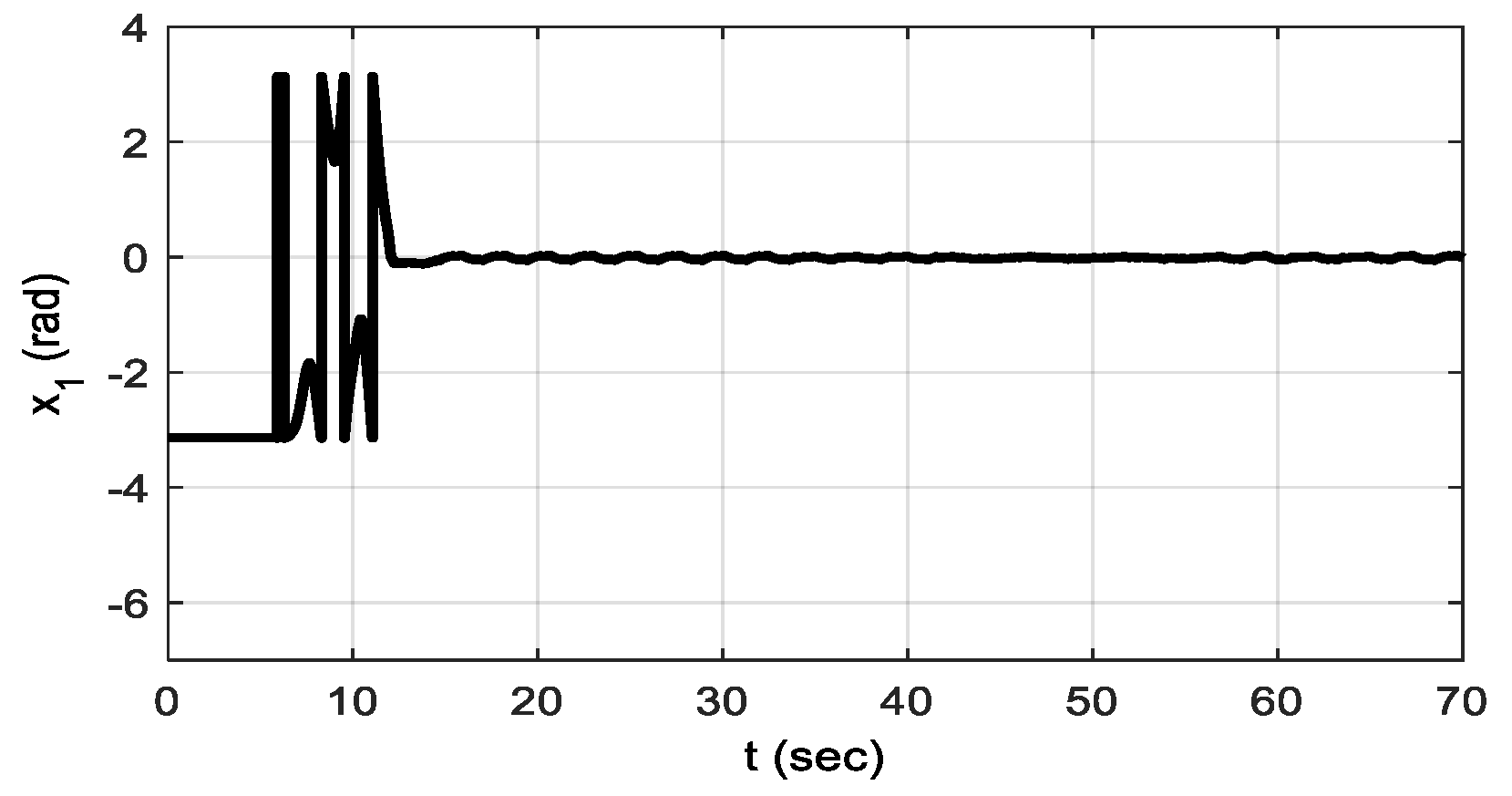
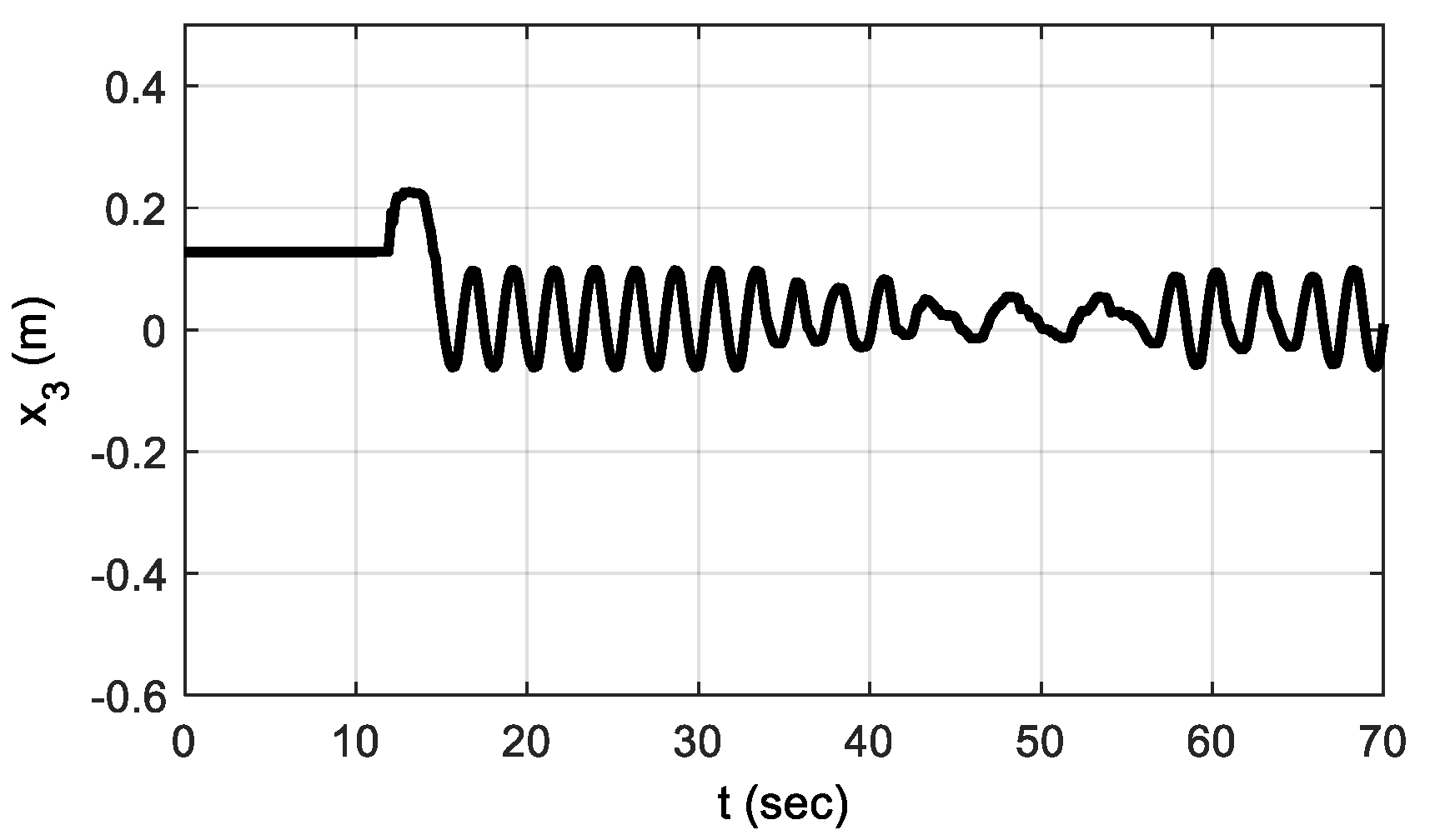
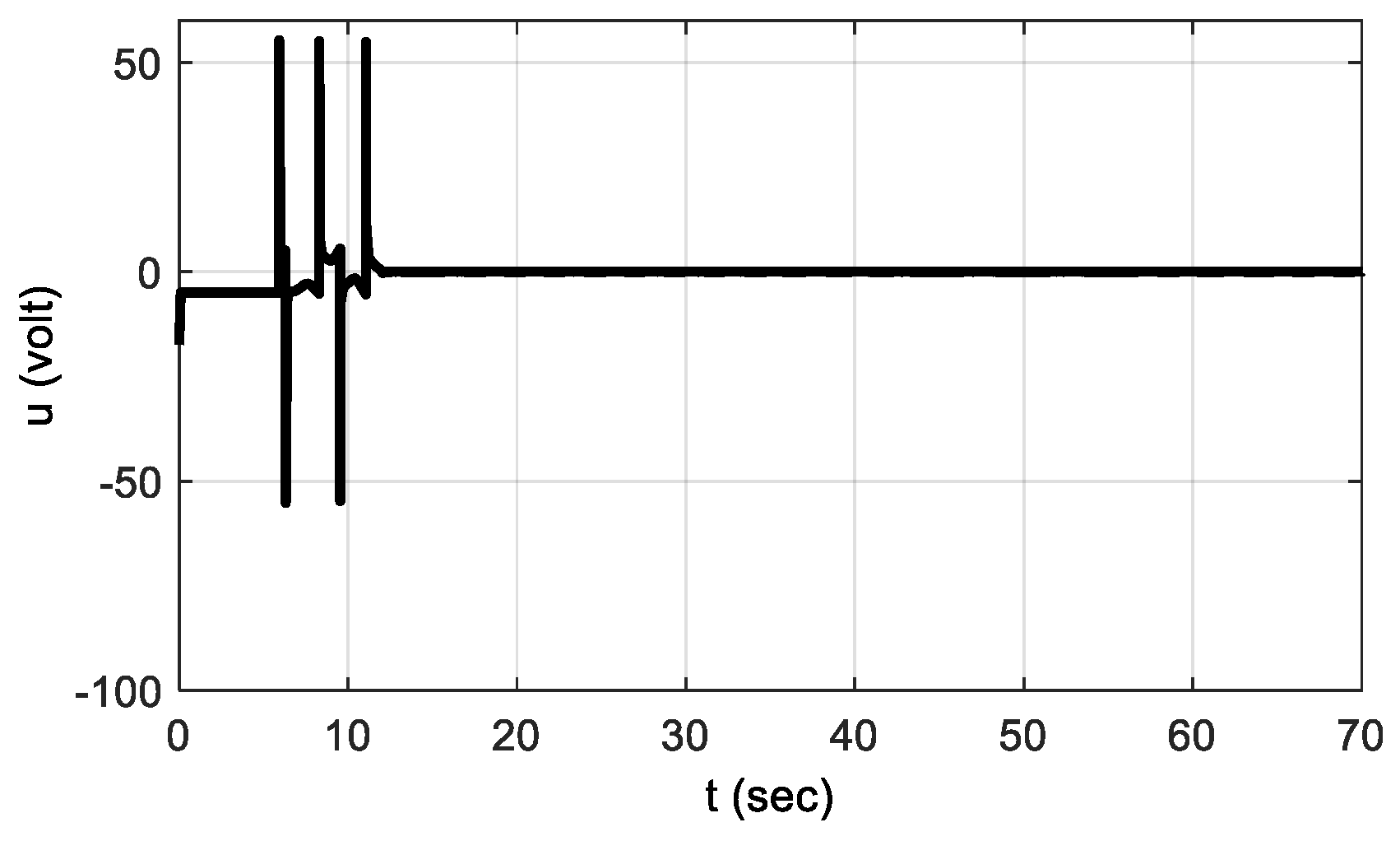
4. Simulation and Experimental Outcomes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, H.; Zhang, G.; Ouyang, H.; Mei, L. Novel fixed-time nonsingular fast terminal sliding mode control for second-order uncertain systems based on adaptive disturbance observer. IEEE Access 2020, 8, 126615–126627. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoo, S.J. Nonlinear-Observer-Based Design Approach for Adaptive Event-Driven Tracking of Uncertain Underactuated Underwater Vehicles. Mathematics 2021, 9, 1144. [Google Scholar] [CrossRef]
- Rehman, F.U.; Mehmood, N.; Din, S.U.; Mufti, M.R.; Afzal, H. Adaptive Sliding Mode Based Stabilization Control for the Class of Underactuated Mechanical Systems. IEEE Access 2021, 9, 26607–26615. [Google Scholar] [CrossRef]
- Viswanathan, S.P.; Sanyal, A.K.; Samiei, E. Integrated Guidance and Feedback Control of Underactuated Robotics System in SE (3). J. Intell. Robot. Syst. 2018, 89, 251–263. [Google Scholar] [CrossRef]
- Idá, E.; Briot, S.; Carricato, M. Natural Oscillations of Underactuated Cable-Driven Parallel Robots. IEEE Access 2021, 9, 71660–71672. [Google Scholar] [CrossRef]
- Xin, X.; Liu, Y. A set-point control for a two-link underactuated robot with a flexible elbow joint. J. Dyn. Syst. Meas. Control 2013, 135, 051016. [Google Scholar] [CrossRef]
- Weng, Y.; Wang, N.; Soares, C.G. Data-driven sideslip observer-based adaptive sliding-mode path-following control of underactuated marine vessels. Ocean. Eng. 2020, 197, 106910. [Google Scholar] [CrossRef]
- Hamed, K.A.; Buss, B.G.; Grizzle, J.W. Continuous-time controllers for stabilizing periodic orbits of hybrid systems: Application to an underactuated 3D bipedal robot. In Proceedings of the IEEE 53rd Annual Conference on Decision and Control (CDC), Los Angeles, CA, USA, 15–17 December 2014; pp. 1507–1513. [Google Scholar]
- Disyadej, T.; Kwanmuang, S.; Muneesawang, P.; Promjan, J.; Poochinapan, K. Smart Transmission Line Maintenance and Inspection using Mobile Robots. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 493–500. [Google Scholar] [CrossRef]
- Roy, B.; Asada, H. Nonlinear Feedback Control of a Gravity-Assisted Underactuated Manipulator With Application to Aircraft Assembly. IEEE Trans. Robot. 2009, 25, 1125–1133. [Google Scholar] [CrossRef]
- Muñoz-Mansilla, R.; Chaos, D.; Díaz, J.; Aranda, J. Application of quantitative feedback theory techniques for the control of a non-holonomic underactuated hovercraft. IET Control Theory Appl. 2012, 6, 2188–2197. [Google Scholar] [CrossRef]
- Berkemeier, M.D.; Fearing, R.S. Control experiments on an underactuated robot with application to legged locomotion. In Proceedings of the IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 149–154. [Google Scholar]
- Lu, B.; Fang, Y.; Sun, N. Sliding mode control for underactuated overhead cranes suffering from both matched and unmatched disturbances. Mechatronics 2017, 47, 116–125. [Google Scholar] [CrossRef]
- Alamir, M.; Boyer, F. Fast Generation of Attractive Trajectories for an Under-Actuated Satellite Application to Feedback Control Design. Optim. Eng. 2003, 4, 215–230. [Google Scholar] [CrossRef]
- Zeng, W.; Wang, Q. Learning from adaptive neural network control of an underactuated rigid spacecraft. Neurocomputing 2015, 168, 690–697. [Google Scholar] [CrossRef]
- Riachy, S.; Orlov, Y.; Floquet, T.; Santiesteban, R.; Richard, J.P. Second-order sliding mode control of underactuated mechanical systems I: Local stabilization with application to an inverted pendulum. Int. J. Robust Nonlinear Control 2008, 18, 529–543. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Mottershead, J.E. Robust passivity-based continuous sliding-mode control for under-actuated nonlinear wing sections. Aerosp. Sci. Technol. 2017, 60, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Bi, F.; Wei, Y.; Zhang, J.; Cao, W. Position-tracking control of underactuated autonomous underwater vehicles in the presence of unknown ocean currents. IET Control Theory Appl. 2010, 4, 2369–2380. [Google Scholar] [CrossRef]
- Yoo, S.J.; Park, B.S. Guaranteed performance design for distributed bounded containment control of networked uncertain underactuated surface vessels. J. Frankl. Inst. 2017, 354, 1584–1602. [Google Scholar] [CrossRef]
- Yih, C.-C. Robust Flight Control of an Underactuated Quadrotor via Sliding Modes. In Applications of Sliding Mode Control; Springer: Singapore, 2017; pp. 87–104. [Google Scholar]
- Zhang, Y.; Chen, Z.; Zhang, X.; Sun, Q.; Sun, M. A novel control scheme for quadrotor UAV based upon active disturbance rejection control. Aerosp. Sci. Technol. 2018, 79, 601–609. [Google Scholar] [CrossRef]
- Rsetam, K.A.; Cao, Z.; Man, Z. Cascaded Extended State Observer Based Sliding Mode Control for Underactuated Flexible Joint Robot. IEEE Trans. Ind. Electron. 2019, 67, 10822–10832. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, L.; Wu, Y. Disturbance-observer-based antiswing control of underactuated crane systems via terminal sliding mode. IET Control Theory Appl. 2018, 12, 2588–2594. [Google Scholar] [CrossRef]
- De Plinval, H.; Morin, P.; Mouyon, P. Stabilization of a class of underactuated vehicles with uncertain position measurements and application to visual servoing. Automatica 2017, 77, 155–169. [Google Scholar] [CrossRef] [Green Version]
- Belzile, B.; Birglen, L. Stiffness Analysis of Underactuated Fingers and Its Application to Proprioceptive Tactile Sensing. IEEE/ASME Trans. Mechatron. 2016, 21, 2672–2681. [Google Scholar] [CrossRef]
- Hua, M.-D.; Hamel, T.; Morin, P.; Samson, C. A control approach for thrust-propelled underactuated vehicles and its application to VTOL drones. IEEE Trans. Autom. Control 2009, 54, 1837–1853. [Google Scholar]
- Khan, Q.; Akmeliawati, R.; Bhatti, A.I.; Khan, M.A. Robust stabilization of underactuated nonlinear systems: A fast terminal sliding mode approach. ISA Trans. 2017, 66, 241–248. [Google Scholar] [CrossRef]
- Shin, S.-Y.; Lee, J.-J. Fuzzy sliding mode control for an under-actuated system with mismatched uncertainties. Artif. Life Robot. 2010, 15, 355–358. [Google Scholar] [CrossRef]
- Ravichandran, M.T.; Mahindrakar, A.D. Robust stabilization of a class of underactuated mechanical systems using time scaling and Lyapunov redesign. IEEE Trans. Ind. Electron. 2011, 58, 4299–4313. [Google Scholar] [CrossRef]
- Sadeghian, H.; Ott, C.; Garofalo, G.; Cheng, G. Passivity-based control of underactuated biped robots within hybrid zero dynamics approach. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4096–4101. [Google Scholar]
- Colombo, L.; De Diego, D.M.; Zuccalli, M. Optimal control of underactuated mechanical systems: A geometric approach. J. Math. Phys. 2010, 51, 083519. [Google Scholar] [CrossRef] [Green Version]
- Chhabra, R.; Emami, M.R. A unified approach to input-output linearization and concurrent control of underactuated open-chain multi-body systems with holonomic and nonholonomic constraints. J. Dyn. Control Syst. 2016, 22, 129–168. [Google Scholar] [CrossRef]
- Azimi, M.M.; Koofigar, H.R. Adaptive fuzzy backstepping controller design for uncertain underactuated robotic systems. Nonlinear Dyn. 2015, 79, 1457–1468. [Google Scholar] [CrossRef]
- Rudra, S.; Barai, R.K.; Maitra, M. Design of nonlinear state feedback control law for underactuated two-link planar robot: A block backstepping approach. In Proceedings of the Conference on Advances in Robotics, New York, NY, USA, 4–6 July 2013; pp. 1–6. [Google Scholar]
- Sun, N.; Fang, Y.; Chen, H. A new antiswing control method for underactuated cranes with unmodeled uncertainties: Theoretical design and hardware experiments. IEEE Trans. Ind. Electron. 2015, 62, 453–465. [Google Scholar] [CrossRef]
- Hasan, A.T. Under-actuated robot manipulator positioning control using artificial neural network inversion technique. Adv. Artif. Intell. 2012, 2012, 7. [Google Scholar] [CrossRef]
- Moussaoui, S.; Boulkroune, A. Stable Adaptive Fuzzy Sliding-Mode Controller for a Class of Underactuated Dynamic Systems. In Recent Advances in Electrical Engineering and Control Applications; Springer: Cham, Switzerland, 2017; pp. 114–124. [Google Scholar]
- Seifried, R. Two approaches for feedforward control and optimal design of underactuated multibody systems. Multibody Syst. Dyn. 2012, 27, 75–93. [Google Scholar] [CrossRef]
- Rascón, R.; Alvarez, J.; Aguilar, L.T. Discontinuous H∞ control of underactuated mechanical systems with friction and backlash. Int. J. Control Autom. Syst. 2016, 14, 1213–1222. [Google Scholar] [CrossRef]
- Sun, N.; Fang, Y.; Zhang, X. An increased coupling-based control method for underactuated crane systems: Theoretical design and experimental implementation. Nonlinear Dyn. 2012, 70, 1135–1146. [Google Scholar] [CrossRef]
- Schnelle, F.; Eberhard, P. Adaptive Model Predictive Control Design for Underactuated Multibody Systems with Uncertain Parameters. In ROMANSY 21-Robot Design, Dynamics and Control; Springer: New York, NY, USA, 2016; pp. 145–152. [Google Scholar]
- Khan, Q.; Akmeliawati, R. Robust control of underactuated systems: Higher order integral sliding mode approach. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Din, S.; Khan, Q.; Rehman, F.; Akmeliawanti, R. A Comparative Experimental Study of Robust Sliding Mode Control Strategies for Underactuated Systems. IEEE Access 2017, 5, 10068–10080. [Google Scholar] [CrossRef]
- Alhato, M.M.; Ibrahim, M.N.; Rezk, H.; Bouallègue, S. An Enhanced DC-Link Voltage Response for Wind-Driven Doubly Fed Induction Generator Using Adaptive Fuzzy Extended State Observer and Sliding Mode Control. Mathematics 2021, 9, 963. [Google Scholar] [CrossRef]
- Mouktonglang, T.; Worapun, P. A Comparison of Robust Criteria for Vehicle Routing Problem with Soft Time Windows. Int. J. Math. Math. Sci. 2019, 2019. [Google Scholar] [CrossRef]
- Majumder, K.; Patre, B. Adaptive sliding mode control for asymptotic stabilization of underactuated mechanical systems via higher-order nonlinear disturbance observer. J. Vib. Control 2019, 25, 2340–2350. [Google Scholar] [CrossRef]
- Xi, X.; Mobayen, S.; Ren, H.; Jafari, S. Robust finite-time synchronization of a class of chaotic systems via adaptive global sliding mode control. J. Vib. Control 2018, 24, 3842–3854. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.-J. A Backstepping Global Fast Terminal Sliding Mode Control for Trajectory Tracking Control of Industrial Robotic Manipulators. IEEE Access 2021, 9, 31921–31931. [Google Scholar] [CrossRef]
- Khoo, S.; Xie, L.; Zhao, S.; Man, Z. Multi-surface sliding control for fast finite-time leader-follower consensus with high order SISO uncertain nonlinear agents. Int. J. Robust Nonlinear Control 2013, 24, 2388–2404. [Google Scholar] [CrossRef]
- Mondal, S.; Mahanta, C. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty. ISA Trans. 2013, 52, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Bilgin, N.; Salamci, M.U. Sliding Mode Control Design For Nonlinear Systems without Reaching Phase and Its Applications to a Flexible Spacecraft. In Proceedings of the ASME 2014 12th Biennial Conference on Engineering Systems Design and Analysis, Copenhagen, Denmark, 25–27 June 2014; p. V002T007A005. [Google Scholar]
- Mobayen, S. A novel global sliding mode control based on exponential reaching law for a class of underactuated systems with external disturbances. J. Comput. Nonlinear Dyn. 2016, 11, 021011. [Google Scholar] [CrossRef]
- Liu, J.; Laghrouche, S.; Wack, M. Observer-based higher order sliding mode control of power factor in three-phase AC/DC converter for hybrid electric vehicle applications. Int. J. Control 2014, 87, 1117–1130. [Google Scholar] [CrossRef]
- Sam, Y.M.; Osman, J.H.; Ghani, M.R.A. A class of proportional-integral sliding mode control with application to active suspension system. Syst. Control Lett. 2004, 51, 217–223. [Google Scholar] [CrossRef]
- Plestan, F.; Shtessel, Y.; Bregeault, V.; Poznyak, A. Sliding mode control with gain adaptation—Application to an electropneumatic actuator. Control Eng. Pract. 2013, 21, 679–688. [Google Scholar] [CrossRef]
- González, I.; Salazar, S.; Lozano, R. Chattering-free sliding mode altitude control for a quad-rotor aircraft: Real-time application. J. Intell. Robot. Syst. 2014, 73, 137–155. [Google Scholar] [CrossRef]
- Baek, J.; Jin, M.; Han, S. A new adaptive sliding-mode control scheme for application to robot manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Wang, Z. Adaptive smooth second-order sliding mode control method with application to missile guidance. Trans. Inst. Meas. Control 2017, 39, 848–860. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Trajectory tracking sliding mode control of underactuated AUVs. Nonlinear Dyn. 2016, 84, 1079–1091. [Google Scholar] [CrossRef] [Green Version]
- Nasir, M.T.; El-Ferik, S. Adaptive sliding-mode cluster space control of a non-holonomic multi-robot system with applications. IET Control Theory Appl. 2017, 11, 1264–1273. [Google Scholar] [CrossRef]
- Huang, J.; Ri, S.; Fukuda, T.; Wang, Y. A disturbance observer based sliding mode control for a class of underactuated robotic system with mismatched uncertainties. IEEE Trans. Autom. Control 2018, 64, 2480–2487. [Google Scholar] [CrossRef]
- Asl, R.M.; Hagh, Y.S.; Palm, R. Robust control by adaptive non-singular terminal sliding mode. Eng. Appl. Artif. Intell. 2017, 59, 205–217. [Google Scholar]
- Patnaik, R.; Dash, P.; Mahapatra, K. Adaptive terminal sliding mode power control of DFIG based wind energy conversion system for stability enhancement. Int. Trans. Electr. Energy Syst. 2016, 26, 750–782. [Google Scholar] [CrossRef]
- Xiong, J.; Gan, Q.; Ren, W. Boundedness of discretised non-linear systems under fast terminal sliding mode control. IET Control Theory Appl. 2016, 10, 2100–2109. [Google Scholar] [CrossRef] [Green Version]
- Asl, S.B.F.; Moosapour, S.S. Adaptive backstepping fast terminal sliding mode controller design for ducted fan engine of thrust-vectored aircraft. Aerosp. Sci. Technol. 2017, 71, 521–529. [Google Scholar]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]
- Yu, S.; Guo, G.; Ma, Z.; Du, J. Global fast terminal sliding mode control for robotic manipulators. Int. J. Model. Identif. Control 2006, 1, 72–79. [Google Scholar] [CrossRef]
- Li, S.-B.; Li, K.-Q.; Wang, J.-Q.; Yang, B. Nonsingular fast terminal-sliding-mode control method and its application on vehicular following system. Control Theory Appl. 2010, 27, 543–550. [Google Scholar]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Fei, J.; Yan, W. Adaptive control of MEMS gyroscope using global fast terminal sliding mode control and fuzzy-neural-network. Nonlinear Dyn. 2014, 78, 103–116. [Google Scholar] [CrossRef]
- Li, H.; Dou, L.; Su, Z. Adaptive nonsingular fast terminal sliding mode control for electromechanical actuator. Int. J. Syst. Sci. 2013, 44, 401–415. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Ma, J.; Zheng, Z.; Geng, L. Fast nonsingular integral terminal sliding mode control for nonlinear dynamical systems. In Proceedings of the IEEE 53rd Annual Conference on Decision and Control (CDC), Los Angeles, CA, USA, 15–17 December 2014; pp. 4739–4746. [Google Scholar]
- Lee, S.H.; Park, J.B.; Choi, Y.H. Finite time control of nonlinear underactuated systems using terminal sliding surface. In Proceedings of the IEEE International Symposium on Industrial Electronics, Seoul, Korea, 5–8 July 2009; pp. 626–631. [Google Scholar]
- Zhu, Q.; Yu, R.; Liu, Z. A discontinuous control law of an underactuated surface vessel based on fast terminal sliding mode. In Proceedings of the 8th World Congress on Intelligent Control and Automation (WCICA), Jinan, China, 6–9 July 2010; pp. 1168–1173. [Google Scholar]
- Tian, Z.; Wu, H. Hierarchical terminal sliding mode control for underactuated space robots. In Proceedings of the International Conference on Machine Vision and Human-Machine Interface (MVHI), Kaifeng, China, 24–25 April 2010; pp. 195–198. [Google Scholar]
- Wang, X.; Li, S. Finite-time trajectory tracking control of under-actuated autonomous surface vessels based on non-singular terminal sliding mode. Aust. J. Electr. Electron. Eng. 2012, 9, 235–246. [Google Scholar] [CrossRef]
- Zheng, E.; Xiong, J. Quad-rotor unmanned helicopter control via novel robust terminal sliding mode controller and under-actuated system sliding mode controller. Opt. Int. J. Light Electron Opt. 2014, 125, 2817–2825. [Google Scholar] [CrossRef]
- Khan, Q.; Bhatti, A.I.; Akmeliawati, R. Robust stabilization of underactuated systems via fast terminal sliding mode. In Proceedings of the 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; pp. 1–6. [Google Scholar]
- Liu, G.; Xu, G.; Chen, Y.; Zhang, W.; Wang, G.; Li, F. A Novel Terminal Sliding Mode Control for the Navigation of An Under-actuated UUV. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–21 July 2016. [Google Scholar]
- Yan, Z.-P.; Yu, H.-M.; Li, B.-Y. Bottom-following control for an underactuated unmanned undersea vehicle using integral-terminal sliding mode control. J. Cent. South Univ. 2015, 22, 4193–4204. [Google Scholar] [CrossRef]
- Huang, X.; Yan, Y.; Zhou, Y.; Hao, D. Fast terminal sliding mode control of underactuated spacecraft formation reconfiguration. J. Aerosp. Eng. 2016, 29, 04016020. [Google Scholar] [CrossRef]
- Hongbin, W.; Zelin, Y.; Zhen, Z. Rbf-based terminal sliding mode control for a class of underactuated mechanical system. In Proceedings of the Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 664–667. [Google Scholar]
- Yan, Z.-P.; Yu, H.-M.; Hou, S.-P. Diving control of underactuated unmanned undersea vehicle using integral-fast terminal sliding mode control. J. Cent. South Univ. 2016, 23, 1085–1094. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles. Ocean. Eng. 2017, 129, 613–625. [Google Scholar] [CrossRef]
- Bhave, M.; Janardhanan, S.; Dewan, L. Configuration control of planar underactuated robotic manipulator using terminal sliding mode. IFAC-PapersOnLine 2016, 49, 148–153. [Google Scholar] [CrossRef]
- Vaghei, Y.; Farshidianfar, A. Trajectory tracking of under-actuated nonlinear dynamic robots: Adaptive fuzzy hierarchical terminal sliding-mode control. J. Artif. Intell. Data Min. 2016, 4, 93–102. [Google Scholar]
- Wang, Y.; Li, T.; Chen, C.P. Adaptive Terminal Sliding Mode Control for Formations of Underactuated Vessels. In Proceedings of the International Conference on Cognitive Systems and Signal Processing, Beijing, China, 19–23 November 2016; pp. 27–35. [Google Scholar]
- Shikai, W.; Hongzhang, J.; Lingwei, M. Trajectory tracking for underactuated UUV using terminal sliding mode control. In Proceedings of the Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; pp. 6833–6837. [Google Scholar]
- Bayramoglu, H.; Komurcugil, H. Time-varying sliding-coefficient-based decoupled terminal sliding-mode control for a class of fourth-order systems. ISA Trans. 2014, 53, 1044–1053. [Google Scholar] [CrossRef] [PubMed]
- Moulay, E.; Perruquetti, W. Finite time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 2006, 323, 1430–1443. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.L. Dynamic output feedback integral sliding mode control design for uncertain systems. Int. J. Robust Nonlinear Control 2012, 22, 841–857. [Google Scholar] [CrossRef]
- Wang, W.; Yi, J.; Zhao, D.; Liu, D. Design of a stable sliding-mode controller for a class of second-order underactuated systems. IEE Proc. Control Theory Appl. 2004, 151, 683–690. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojsiraphisal, T.; Mobayen, S.; Asad, J.H.; Vu, M.T.; Chang, A.; Puangmalai, J. Fast Terminal Sliding Control of Underactuated Robotic Systems Based on Disturbance Observer with Experimental Validation. Mathematics 2021, 9, 1935. https://doi.org/10.3390/math9161935
Rojsiraphisal T, Mobayen S, Asad JH, Vu MT, Chang A, Puangmalai J. Fast Terminal Sliding Control of Underactuated Robotic Systems Based on Disturbance Observer with Experimental Validation. Mathematics. 2021; 9(16):1935. https://doi.org/10.3390/math9161935
Chicago/Turabian StyleRojsiraphisal, Thaned, Saleh Mobayen, Jihad H. Asad, Mai The Vu, Arthur Chang, and Jirapong Puangmalai. 2021. "Fast Terminal Sliding Control of Underactuated Robotic Systems Based on Disturbance Observer with Experimental Validation" Mathematics 9, no. 16: 1935. https://doi.org/10.3390/math9161935
APA StyleRojsiraphisal, T., Mobayen, S., Asad, J. H., Vu, M. T., Chang, A., & Puangmalai, J. (2021). Fast Terminal Sliding Control of Underactuated Robotic Systems Based on Disturbance Observer with Experimental Validation. Mathematics, 9(16), 1935. https://doi.org/10.3390/math9161935








