Statistical Machine Learning in Model Predictive Control of Nonlinear Processes
Abstract
:1. Introduction
2. Preliminaries
2.1. Notation
2.2. Class of Systems
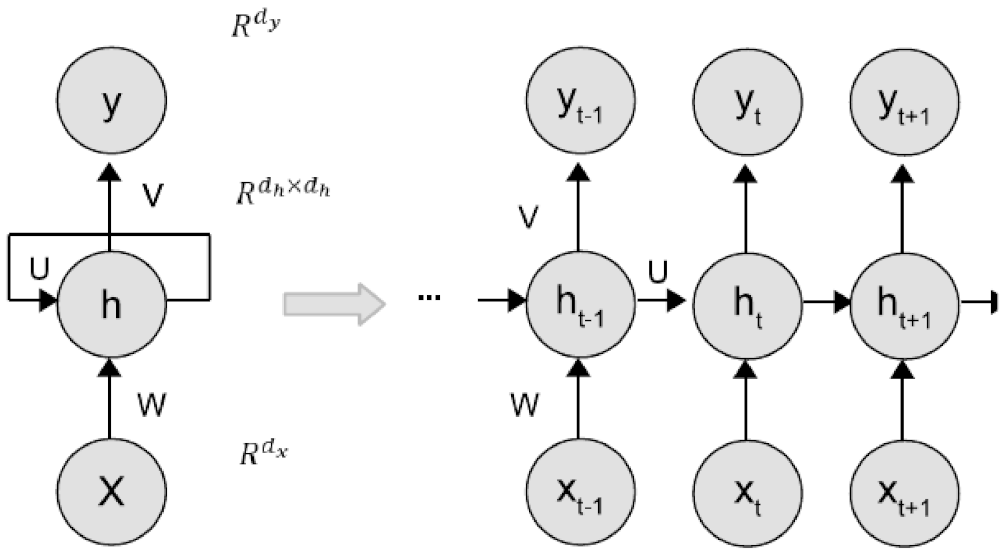
2.3. Recurrent Neural Network Model
3. RNN Generalization Error
3.1. Preliminaries
3.2. Rademacher Complexity Bound
4. RNN-Based MPC with Probabilistic Stability Analysis
4.1. Lyapunov-Based Control Using RNN Models
4.2. Stabilization of Nonlinear System under Lyapunov-Based Controller
4.3. Lyapunov-Based MPC Using RNN Models for Nonlinear Systems
5. Application to a Chemical Process Example
5.1. RNN Generalization Performance
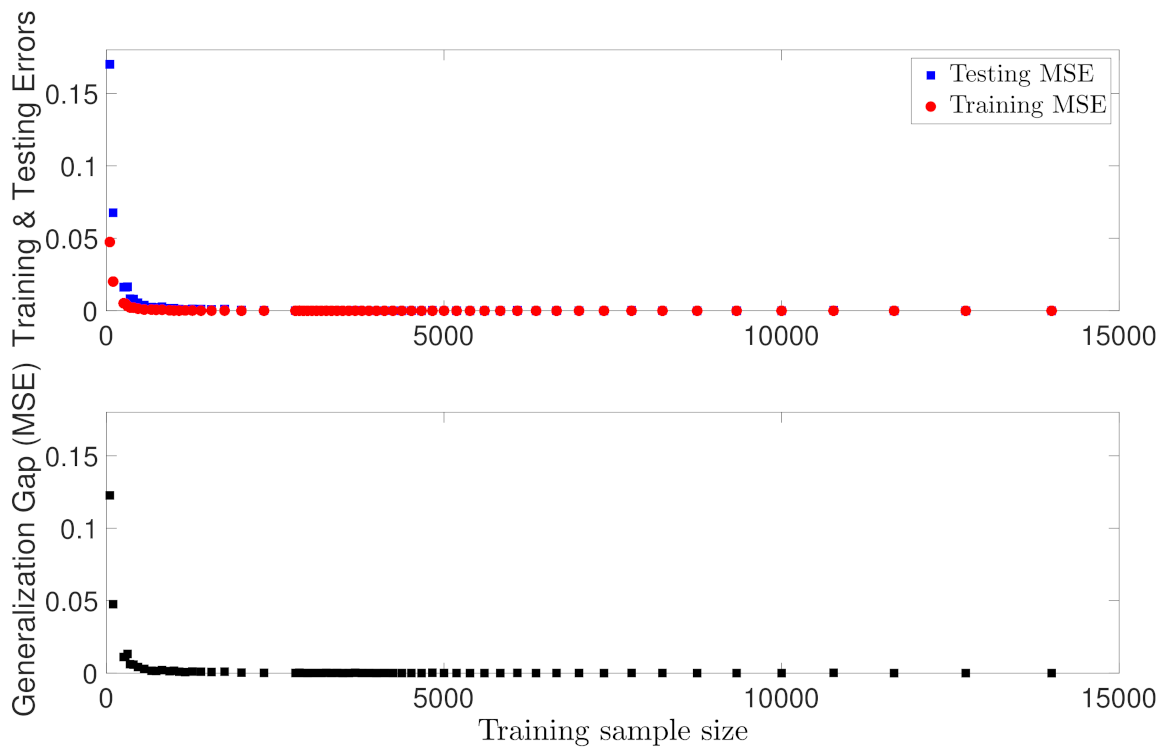
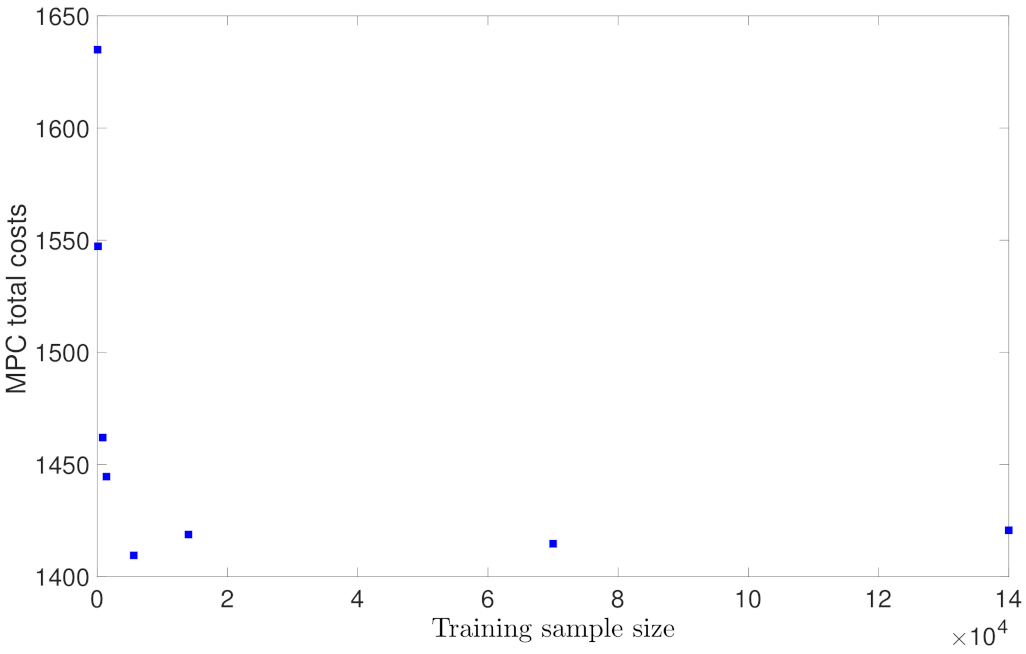
5.1.1. Case Study 1: Data Sample Size
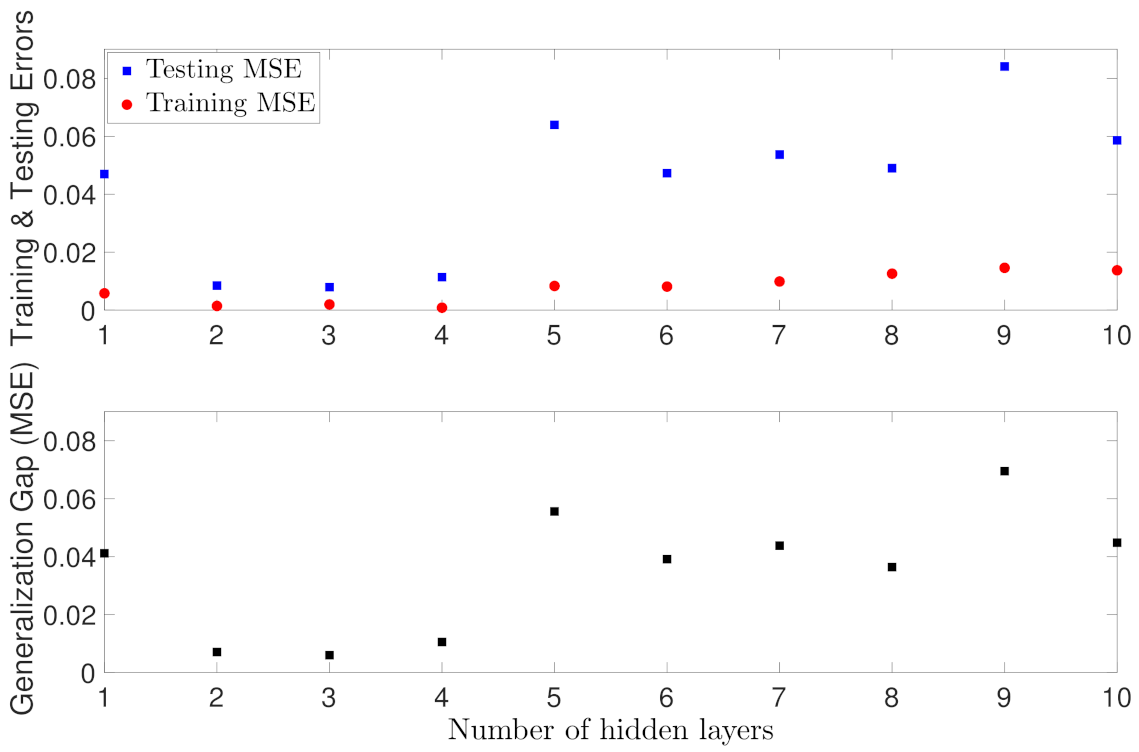
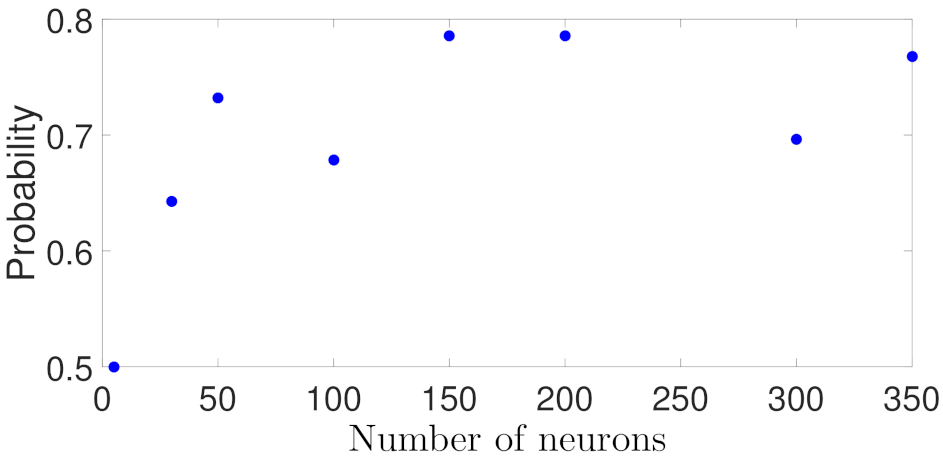
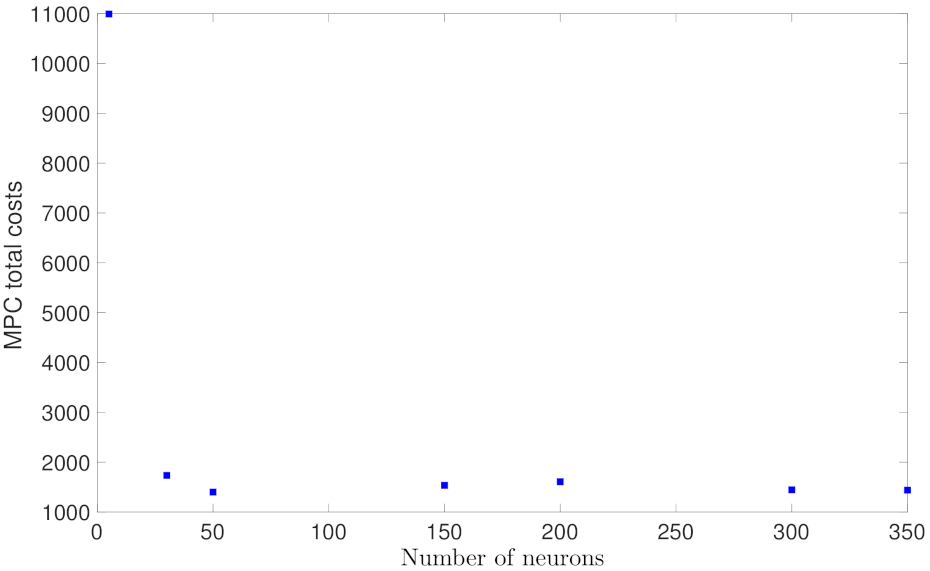
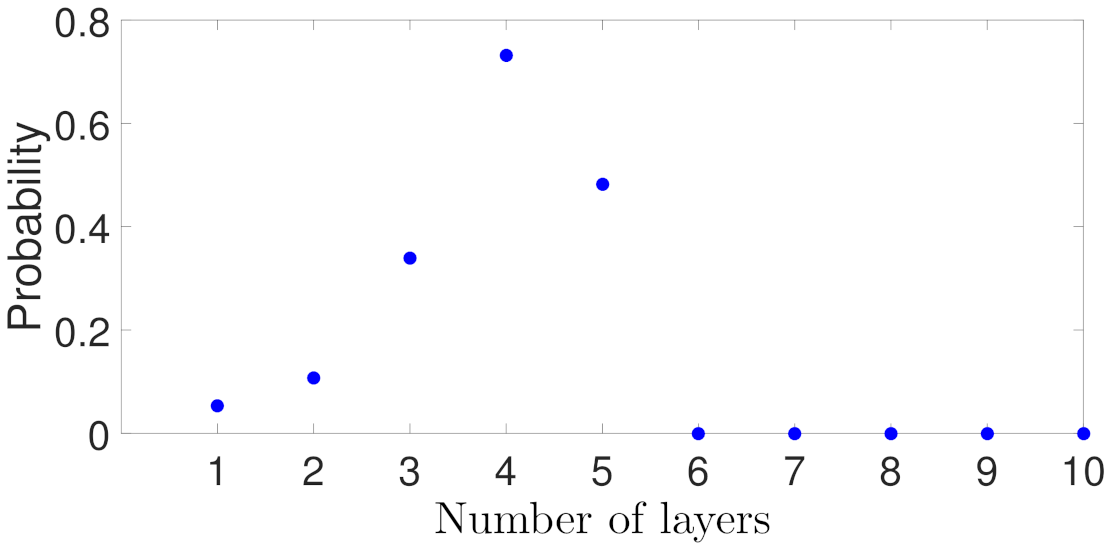
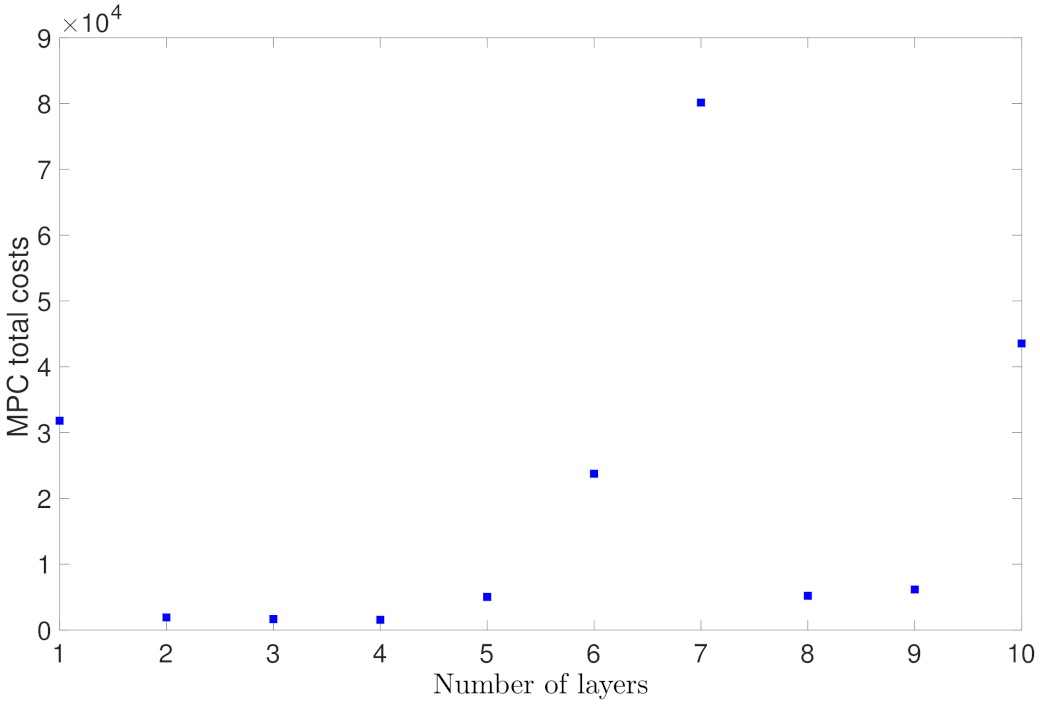
5.1.2. Case Study 2: RNN Depth and Width
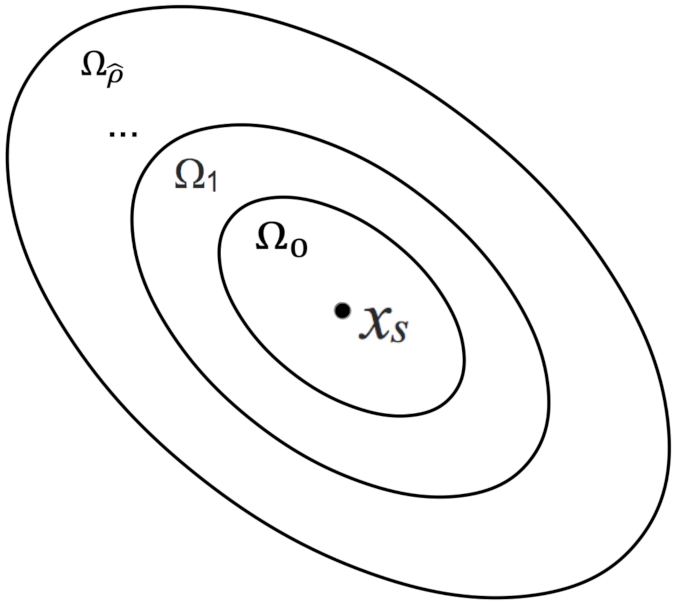
5.1.3. Case Study 3: Different Regions in
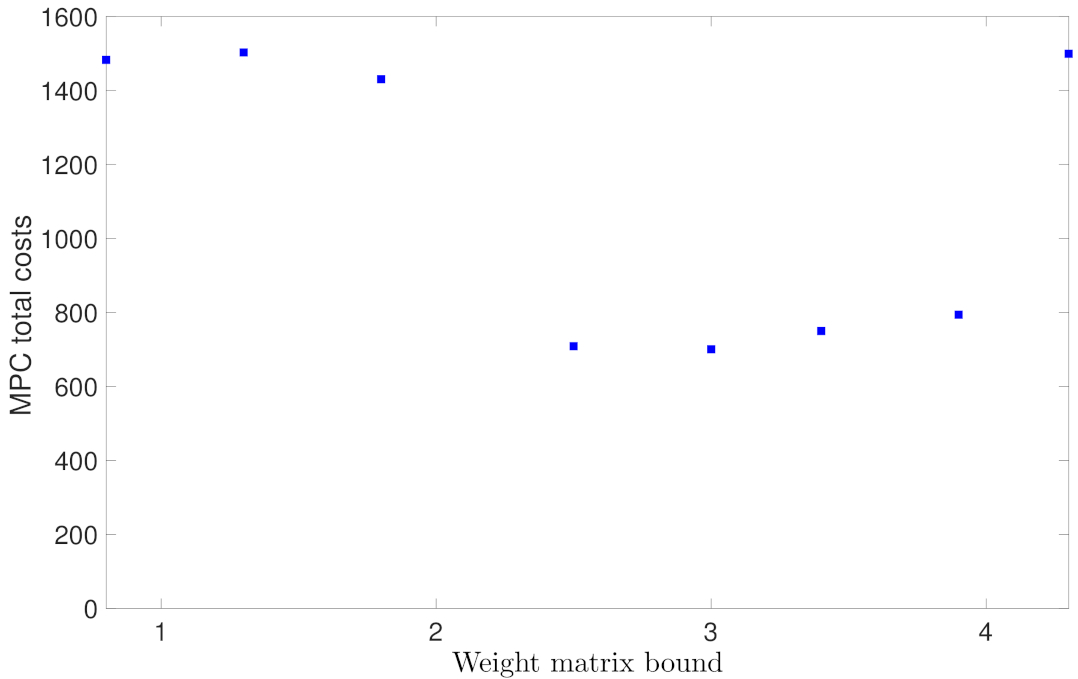
5.1.4. Case Study 4: Weight Matrix Bound
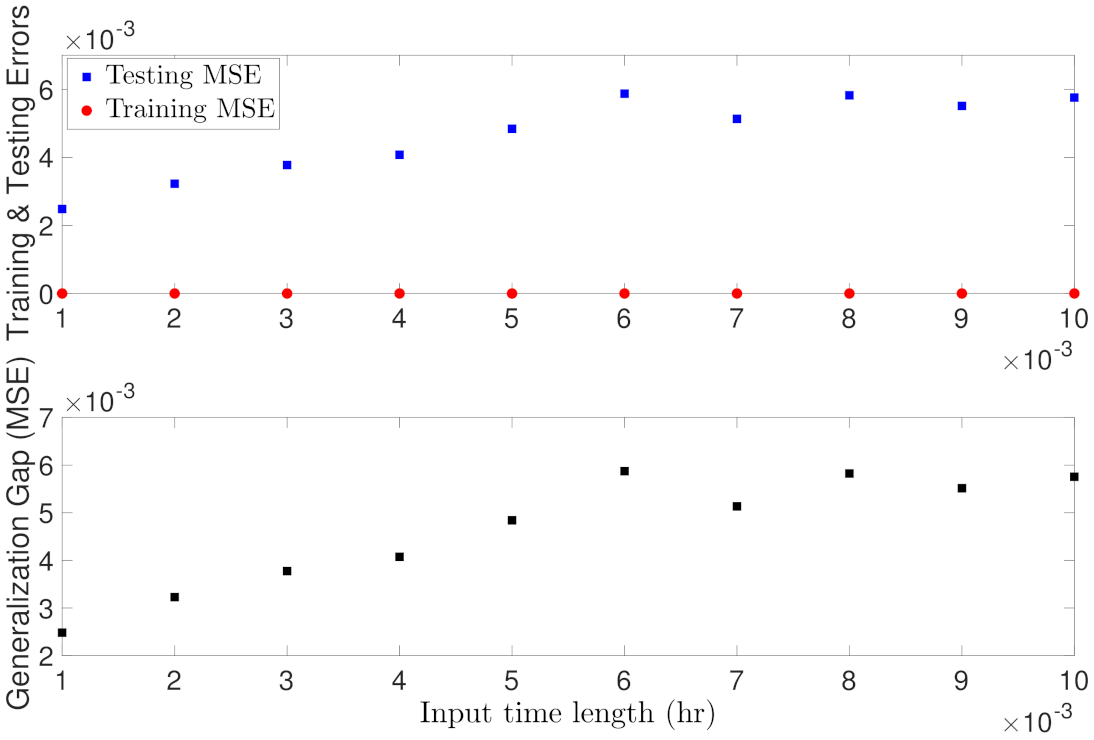
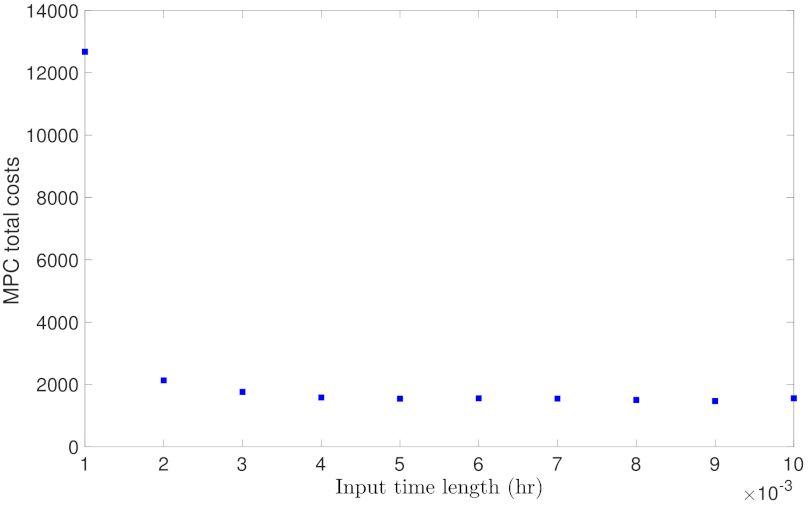
5.1.5. Case Study 5: RNN Input Length
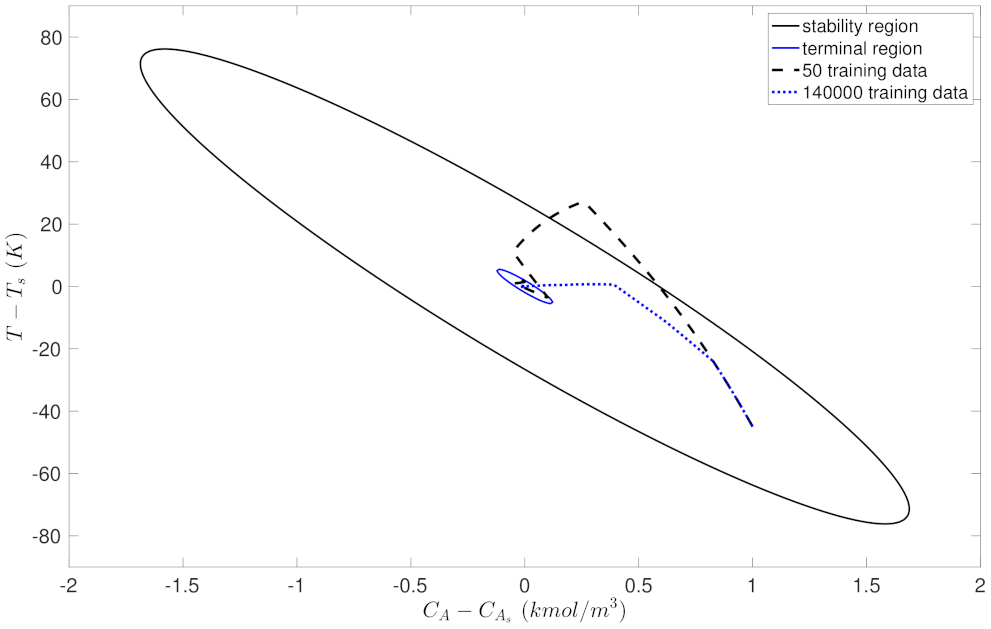
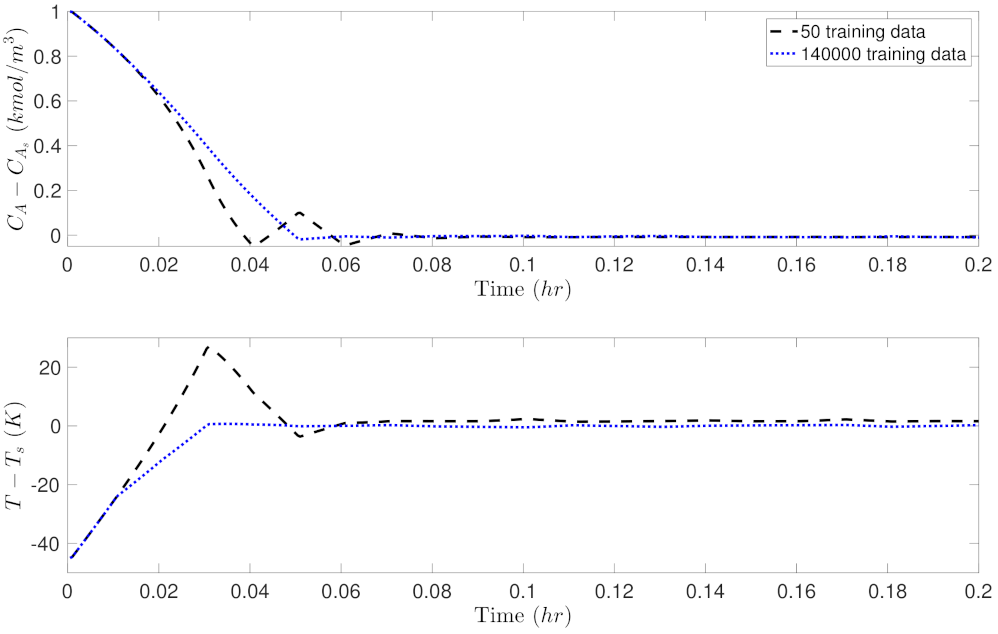
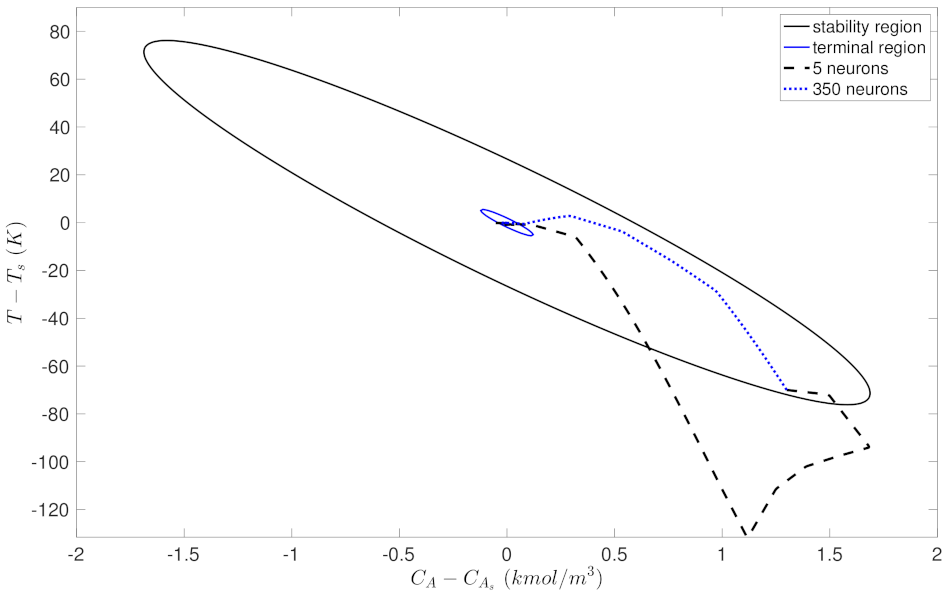
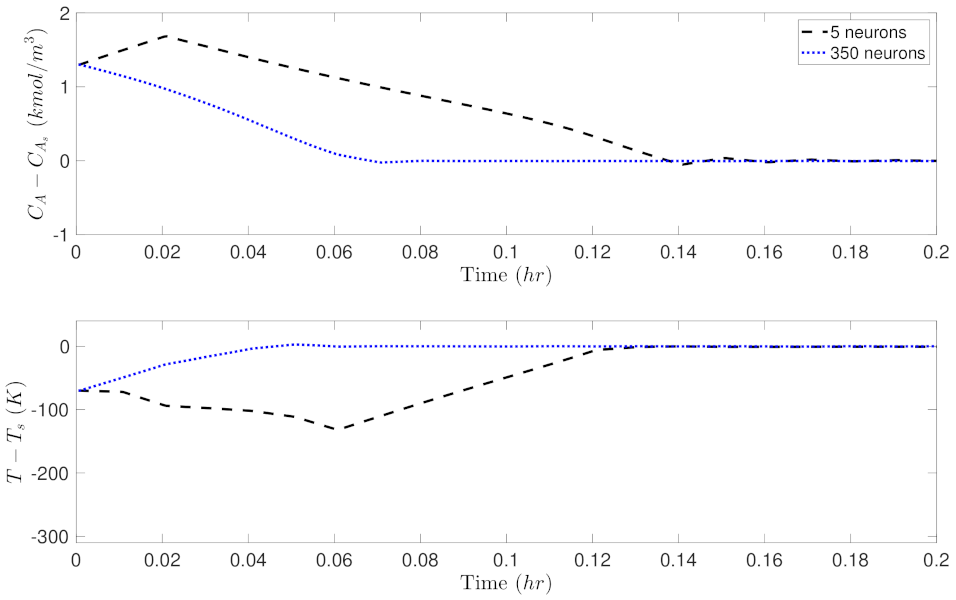
5.2. Closed-Loop Performance Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cozad, A.; Sahinidis, N.V.; Miller, D.C. A combined first-principles and data-driven approach to model building. Comput. Chem. Eng. 2015, 73, 116–127. [Google Scholar] [CrossRef]
- Wilson, Z.T.; Sahinidis, N.V. The ALAMO approach to machine learning. Comput. Chem. Eng. 2017, 106, 785–795. [Google Scholar] [CrossRef] [Green Version]
- Ali, J.M.; Hussain, M.A.; Tade, M.O.; Zhang, J. Artificial Intelligence techniques applied as estimator in chemical process systems–A literature survey. Expert Syst. Appl. 2015, 42, 5915–5931. [Google Scholar]
- Han, H.; Wu, X.; Qiao, J. Real-time model predictive control using a self-organizing neural network. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1425–1436. [Google Scholar] [PubMed]
- Wang, T.; Gao, H.; Qiu, J. A combined adaptive neural network and nonlinear model predictive control for multirate networked industrial process control. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 416–425. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y. A new concept using LSTM Neural Networks for dynamic system identification. In Proceedings of the American Control Conference 2017, Seattle, WA, USA, 24–26 May 2017; pp. 5324–5329. [Google Scholar]
- Wong, W.; Chee, E.; Li, J.; Wang, X. Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing. Mathematics 2018, 6, 242. [Google Scholar] [CrossRef] [Green Version]
- Shahnazari, H.; Mhaskar, P.; House, J.M.; Salsbury, T.I. Modeling and fault diagnosis design for HVAC systems using recurrent neural networks. Comput. Chem. Eng. 2019, 126, 189–203. [Google Scholar] [CrossRef]
- Wu, Z.; Tran, A.; Rincon, D.; Christofides, P.D. Machine Learning-Based Predictive Control of Nonlinear Processes. Part I: Theory. AIChE J. 2019, 65, e16729. [Google Scholar] [CrossRef]
- Wu, Z.; Tran, A.; Rincon, D.; Christofides, P.D. Machine Learning-Based Predictive Control of Nonlinear Processes. Part II: Computational Implementation. AIChE J. 2019, 65, e16734. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, J. Nonlinear model predictive control using a recurrent neural network. In Proceedings of the IEEE International Joint Conference on Neural Networks 2008, Hong Kong, China, 1–8 June 2008; pp. 2296–2301. [Google Scholar]
- Pan, Y.; Wang, J. Model predictive control of unknown nonlinear dynamical systems based on recurrent neural networks. IEEE Trans. Ind. Electron. 2011, 59, 3089–3101. [Google Scholar] [CrossRef]
- Xu, J.; Li, C.; He, X.; Huang, T. Recurrent neural network for solving model predictive control problem in application of four-tank benchmark. Neurocomputing 2016, 190, 172–178. [Google Scholar] [CrossRef]
- Hoskins, J.; Himmelblau, D. Process control via artificial neural networks and reinforcement learning. Comput. Chem. Eng. 1992, 16, 241–251. [Google Scholar] [CrossRef]
- Vepa, R. A review of techniques for machine learning of real-time control strategies. Intell. Syst. Eng. 1993, 2, 77–90. [Google Scholar] [CrossRef]
- Hussain, M. Review of the applications of neural networks in chemical process control—Simulation and online implementation. Artif. Intell. Eng. 1999, 13, 55–68. [Google Scholar] [CrossRef]
- Hewing, L.; Wabersich, K.; Menner, M.; Zeilinger, M. Learning-based model predictive control: Toward safe learning in control. Annu. Rev. Control Robot. Auton. Syst. 2020, 3, 269–296. [Google Scholar] [CrossRef]
- Venkatasubramanian, V. The promise of artificial intelligence in chemical engineering: Is it here, finally? AIChE J. 2019, 65, 466–478. [Google Scholar] [CrossRef]
- Mittal, M.; Gallieri, M.; Quaglino, A.; Salehian, S.; Koutník, J. Neural lyapunov model predictive control. arXiv 2020, arXiv:2002.10451. [Google Scholar]
- Limon, D.; Calliess, J.; Maciejowski, J. Learning-based nonlinear model predictive control. IFAC-PapersOnLine 2017, 50, 7769–7776. [Google Scholar] [CrossRef]
- Aswani, A.; Gonzalez, H.; Sastry, S.; Tomlin, C. Provably safe and robust learning-based model predictive control. Automatica 2013, 49, 1216–1226. [Google Scholar] [CrossRef] [Green Version]
- Valiant, L.G. A theory of the learnable. Commun. ACM 1984, 27, 1134–1142. [Google Scholar] [CrossRef] [Green Version]
- Lygeros, J.; Margellos, K.; Prandini, M. Compression learning for chance constrained stochastic MPC. IFAC-PapersOnLine 2015, 48, 286–293. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, D.; Spanos, C. Learning optimization friendly comfort model for HVAC model predictive control. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; pp. 430–439. [Google Scholar]
- Bartlett, P.; Foster, D.J.; Telgarsky, M. Spectrally-normalized margin bounds for neural networks. arXiv 2017, arXiv:1706.08498. [Google Scholar]
- Zhang, Y.; Lee, J.; Wainwright, M.; Jordan, M.I. On the learnability of fully-connected neural networks. In Proceedings of the Artificial Intelligence and Statistics PMLR 2017, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 83–91. [Google Scholar]
- Golowich, N.; Rakhlin, A.; Shamir, O. Size-independent sample complexity of neural networks. In Proceedings of the Conference On Learning Theory PMLR 2018, Stockholm, Sweden, 5–9 July 2018; pp. 297–299. [Google Scholar]
- Cao, Y.; Gu, Q. Tight sample complexity of learning one-hidden-layer convolutional neural networks. arXiv 2019, arXiv:1911.05059. [Google Scholar]
- Chen, M.; Li, X.; Zhao, T. On generalization bounds of a family of recurrent neural networks. arXiv 2019, arXiv:1910.12947. [Google Scholar]
- Cao, Y.; Gu, Q. Generalization bounds of stochastic gradient descent for wide and deep neural networks. arXiv 2019, arXiv:1905.13210. [Google Scholar]
- Zou, D.; Gu, Q. An improved analysis of training over-parameterized deep neural networks. arXiv 2019, arXiv:1906.04688. [Google Scholar]
- Akpinar, N.; Kratzwald, B.; Feuerriegel, S. Sample complexity bounds for recurrent neural networks with application to combinatorial graph problems. arXiv 2019, arXiv:1901.10289. [Google Scholar]
- Reid, M. Generalization bounds. In Encyclopedia of Machine Learning; Springer: Boston, MA, USA, 2010; pp. 447–454. [Google Scholar] [CrossRef]
- Hanson, J.; Raginsky, M.; Sontag, E. Learning Recurrent Neural Net Models of Nonlinear Systems. arXiv 2020, arXiv:2011.09573. [Google Scholar]
- Sammut, C.; Webb, G.I. Encyclopedia of Machine Learning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Maurer, A. A vector-contraction inequality for rademacher complexities. In Lecture Notes in Computer Science, Proceedings of the International Conference on Algorithmic Learning Theory, Bari, Italy, 19–21 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 3–17. [Google Scholar]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Ledoux, M.; Talagrand, M. Probability in Banach Spaces: Isoperimetry and Processes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wu, Z.; Rincon, D.; Christofides, P.D. Process structure-based recurrent neural network modeling for model predictive control of nonlinear processes. J. Process Control 2020, 89, 74–84. [Google Scholar] [CrossRef]
- Keras. Available online: https://keras.io (accessed on 1 August 2015).
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Rincon, D.; Gu, Q.; Christofides, P.D. Statistical Machine Learning in Model Predictive Control of Nonlinear Processes. Mathematics 2021, 9, 1912. https://doi.org/10.3390/math9161912
Wu Z, Rincon D, Gu Q, Christofides PD. Statistical Machine Learning in Model Predictive Control of Nonlinear Processes. Mathematics. 2021; 9(16):1912. https://doi.org/10.3390/math9161912
Chicago/Turabian StyleWu, Zhe, David Rincon, Quanquan Gu, and Panagiotis D. Christofides. 2021. "Statistical Machine Learning in Model Predictive Control of Nonlinear Processes" Mathematics 9, no. 16: 1912. https://doi.org/10.3390/math9161912
APA StyleWu, Z., Rincon, D., Gu, Q., & Christofides, P. D. (2021). Statistical Machine Learning in Model Predictive Control of Nonlinear Processes. Mathematics, 9(16), 1912. https://doi.org/10.3390/math9161912





