Time-Inhomogeneous Feller-Type Diffusion Process in Population Dynamics
Abstract
:1. Introduction and Background
Plan of the Paper
2. Diffusion Approximation of Birth-Death Process with Immigration
3. Moment Generating Function and Transition PDF in Special Cases
3.1. Moment Generating Function, Conditional Mean and Conditional Variance
3.2. Absence of Immigration
3.3. Proportional Case
3.4. Time-Homogeneous Feller Process
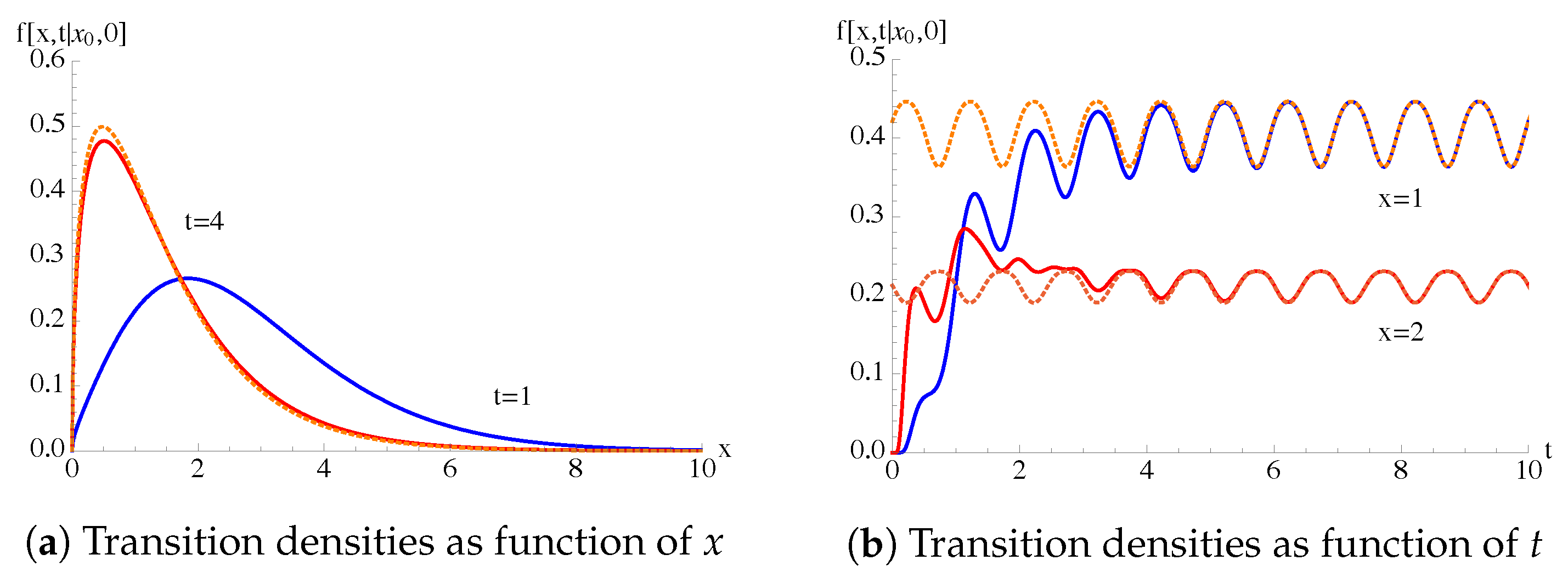
4. Transition PDF and Conditional Moments in the General Case
- (1)
- we determine the transition pdf for and ;
- (2)
- we calculate the transition density for , and as a convolution between and the transition pdf , given in (18), of the Feller-type process in the absence of immigration.
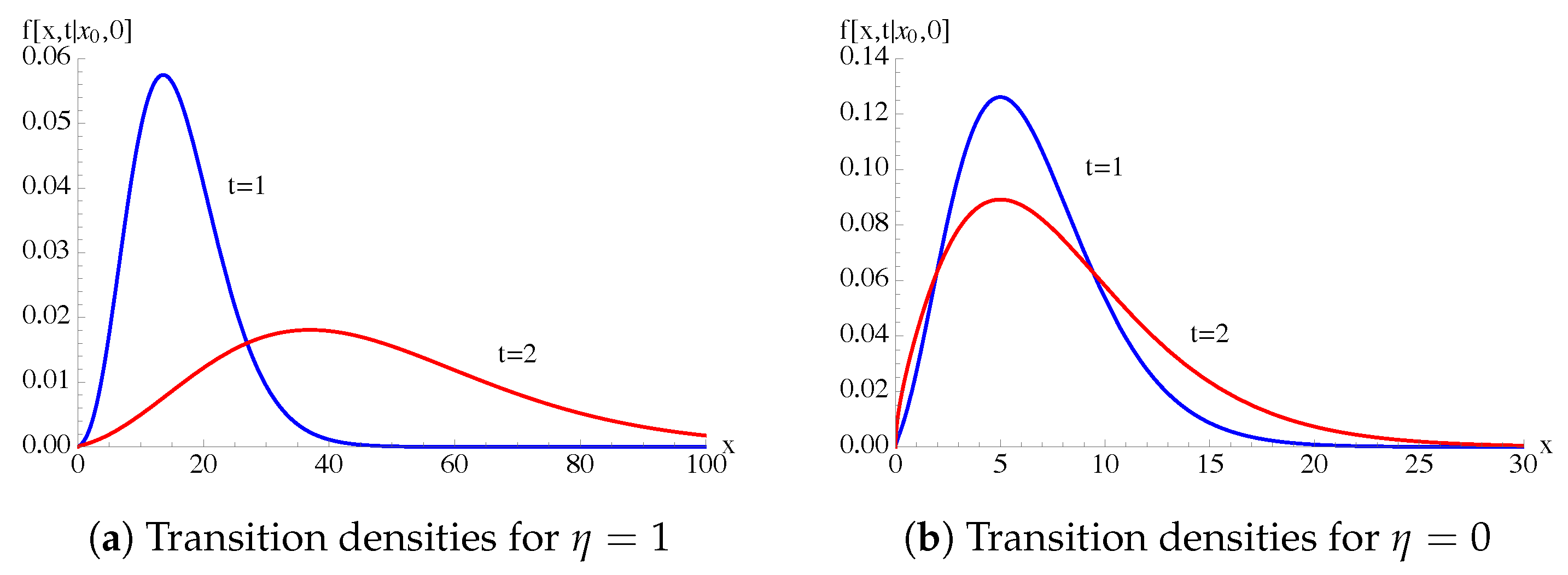
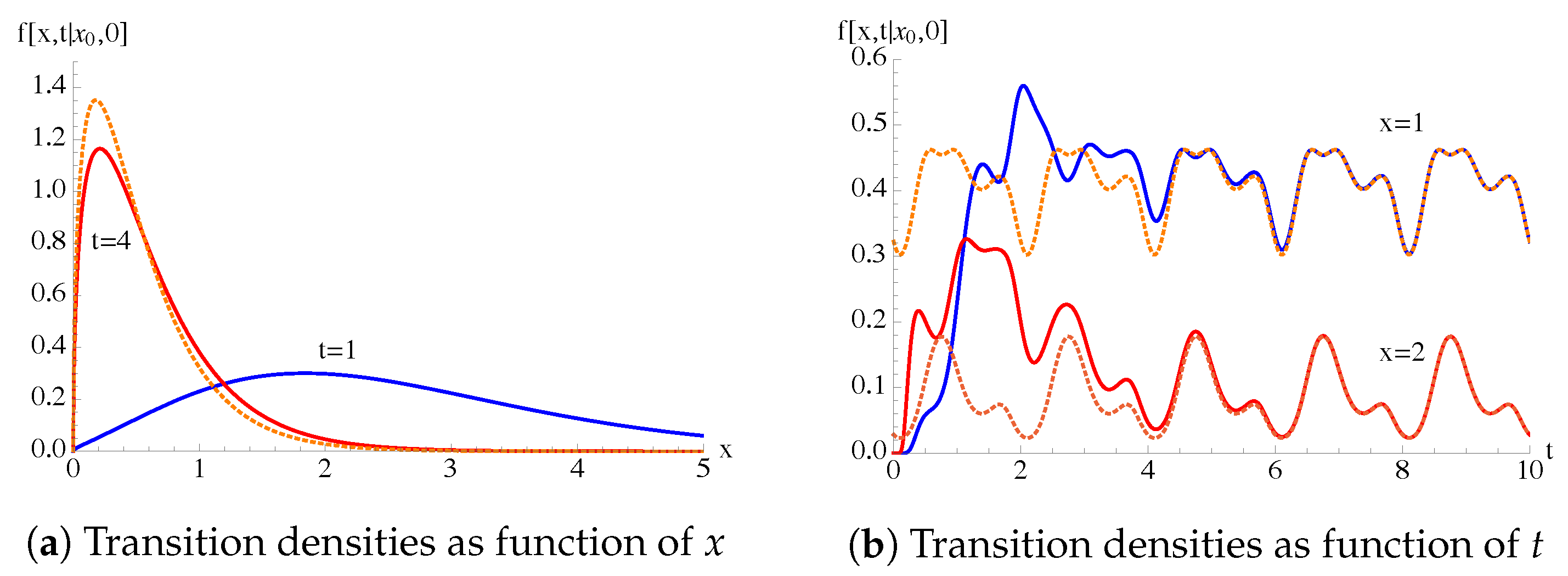
4.1. General Case:
4.2. General Case:
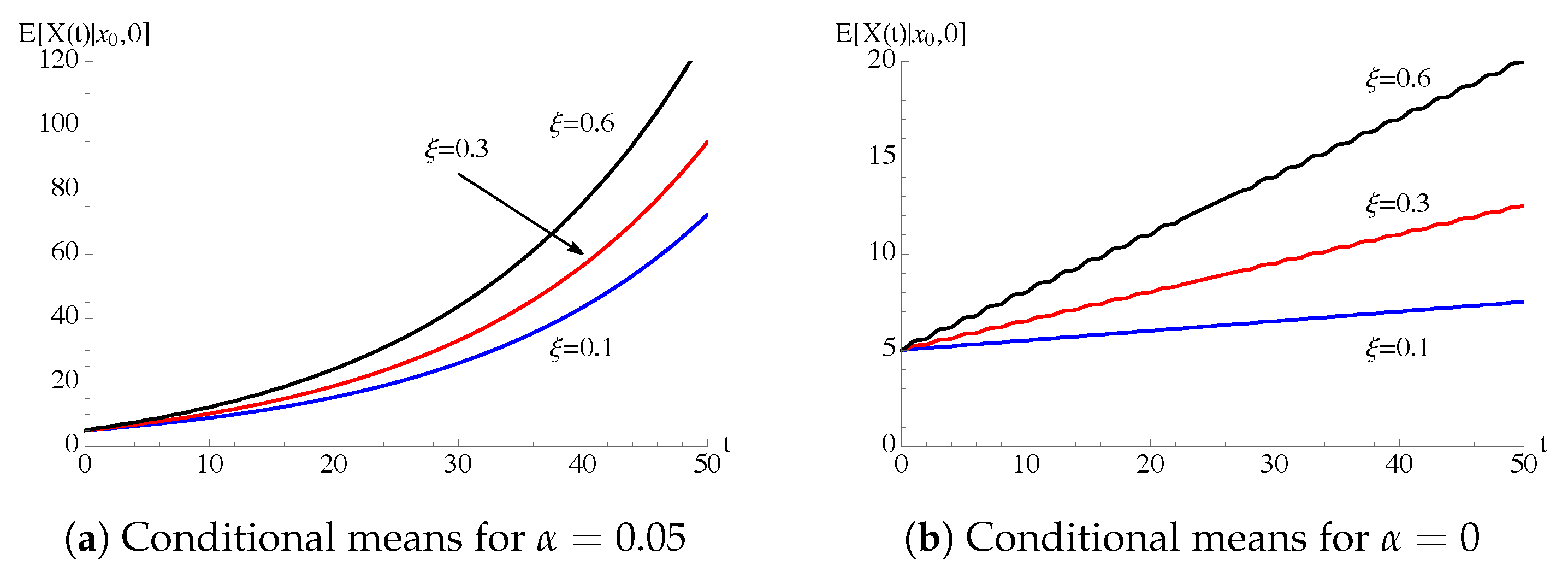
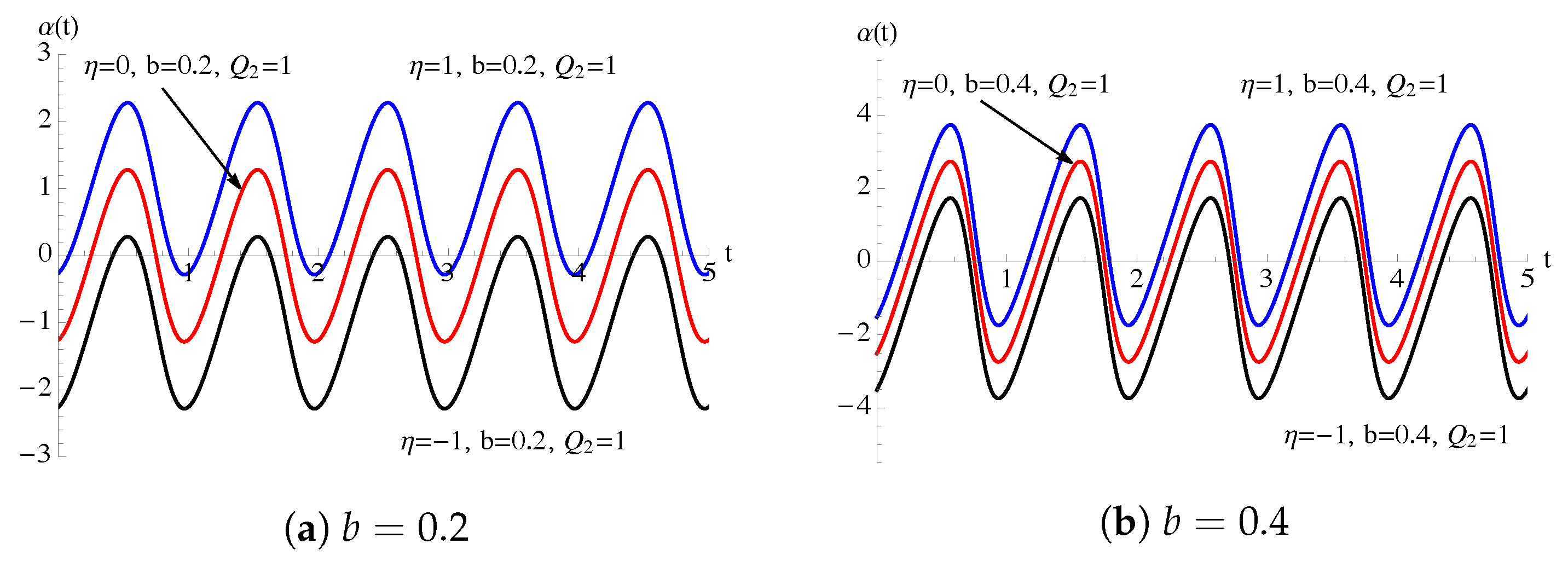
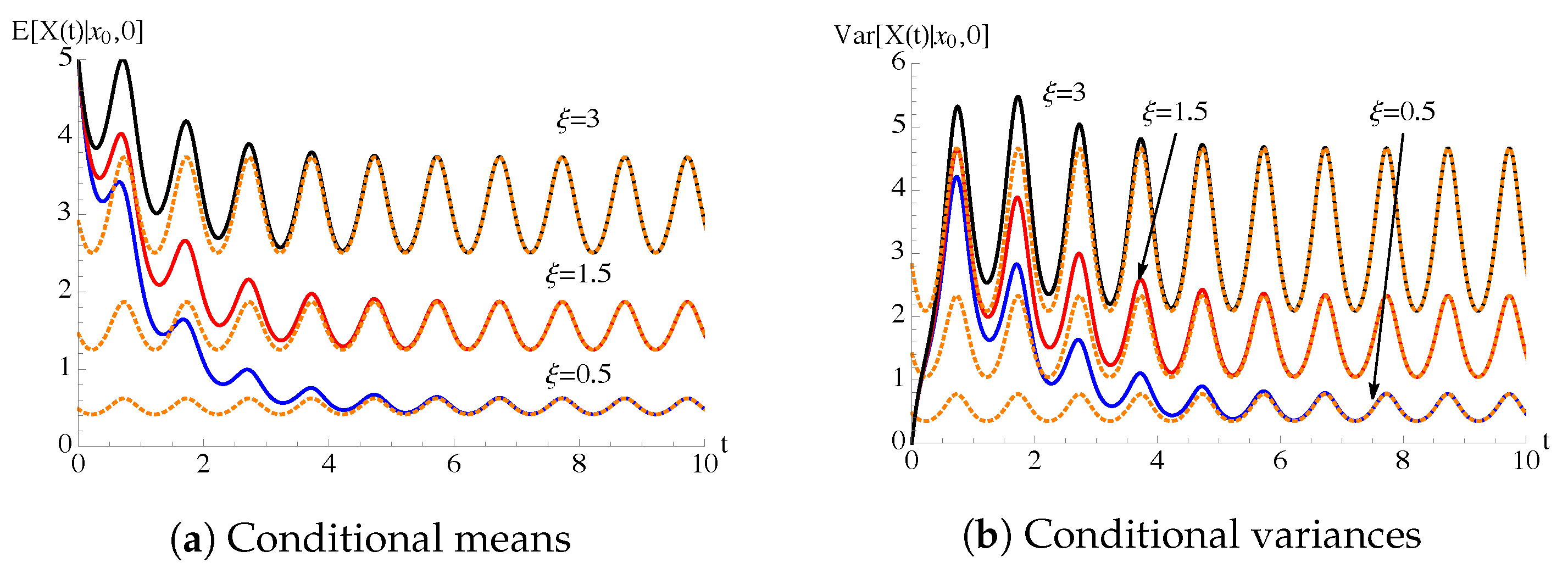
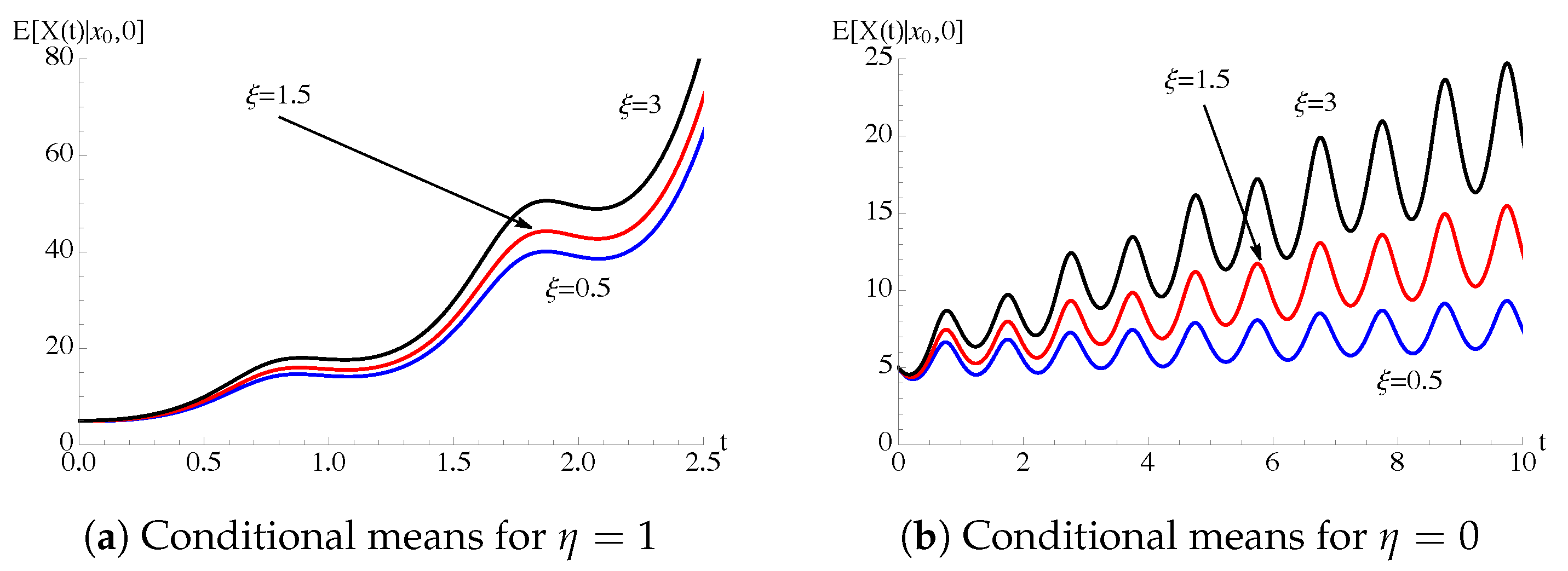
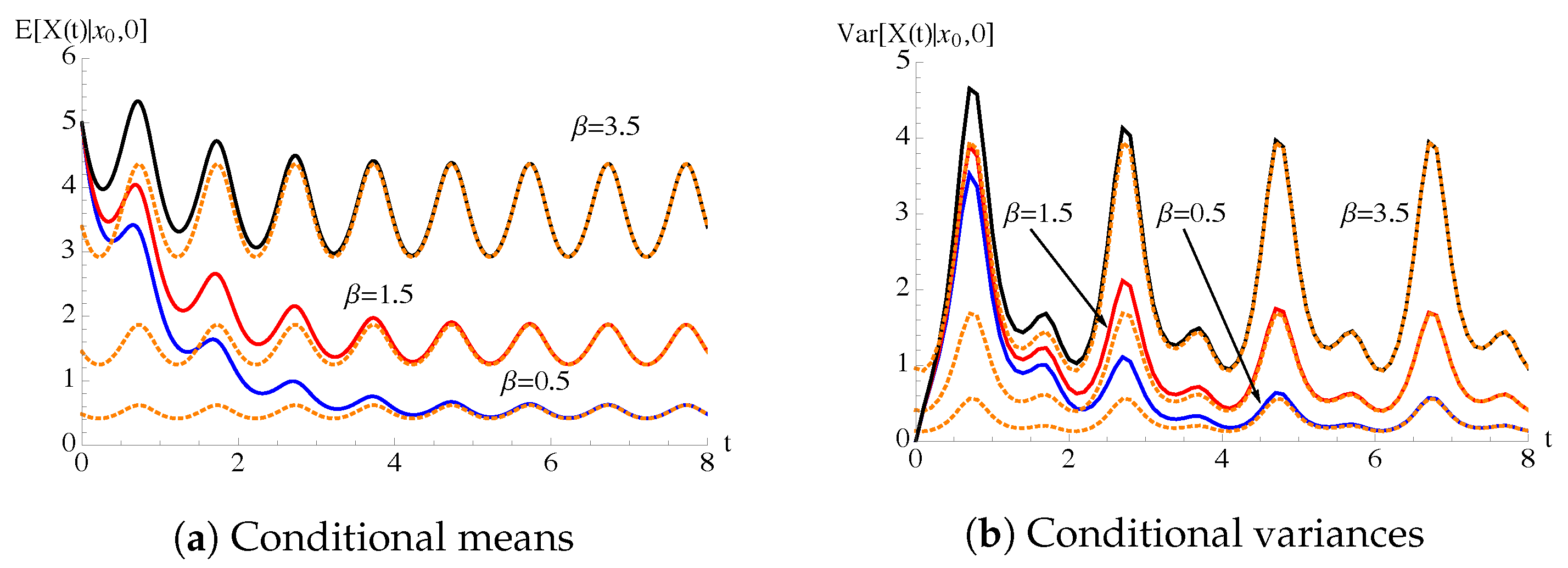
5. Periodic Intensity Functions
5.1. Periodic Immigration Intensity Function
5.2. Periodic Growth Intensity Function
5.3. Periodic Immigration and Growth Intensity Functions
5.4. Periodic Immigration, Growth and Noise Intensity Functions
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Proposition 1
Appendix B. Proof of Proposition 2
Appendix C. Proof of Proposition 3
Appendix D. Proof of Proposition 4
Appendix E. Proof of Proposition 5
Appendix F. Proof of Proposition 7
References
- Bharucha-Reid, A.T. Elements of the Theory of Markov Processes and Their Applications; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- Cox, D.R.; Miller, H.D. The Theory of Stochastic Processes; Chapman & Hall/CRC: Boca Raton, FL, USA, 1996. [Google Scholar]
- Ricciardi, L.M. Diffusion Processes and Related Topics in Biology; Springer: Berlin, Germany, 1977. [Google Scholar]
- Ricciardi, L.M. Stochastic Population Theory: Diffusion Processes. In Mathematical Ecology; Hallam, T.G., Levin, S.A., Eds.; Springer: Berlin, Germany, 1986; Volume 17, pp. 191–238. [Google Scholar]
- Tuckwell, H.C. Introduction to Theoretical Neurobiology: Volume 2, Nonlinear and Stochastic Theories; Cambridge University Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods: For Physics, Chemistry and the Natural Sciences; Springer: Berlin, Germany, 1985. [Google Scholar]
- Feller, W. Diffusion processes in genetics. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability; Statistical Laboratory of the University of California: Berkeley, CA, USA, 1951; pp. 227–246. [Google Scholar]
- Ricciardi, L.M.; Di Crescenzo, A.; Giorno, V.; Nobile, A.G. An outline of theoretical and algorithmic approaches to first passage time problems with applications to biological modeling. Math. Jpn. 1999, 50, 247–322. [Google Scholar]
- Pugliese, A.; Milner, F. A structured population model with diffusion in structure space. J. Math. Biol. 2018, 77, 2079–2102. [Google Scholar] [CrossRef] [Green Version]
- Masoliver, J.; Perelló, J. First-passage and escape problems in the Feller process. Phys. Rev. E 2012, 86, 041116. [Google Scholar] [CrossRef] [Green Version]
- Masoliver, J. Nonstationary Feller process with time-varying coefficients. Phys. Rev. E 2016, 93, 012122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Crescenzo, A.; Nobile, A.G. Diffusion approximation to a queueing system with time-dependent arrival and service rates. Queueing Syst. 1995, 19, 41–62. [Google Scholar] [CrossRef]
- Sacerdote, L. On the solution of the Fokker-Planck equation for a Feller process. Adv. Appl. Prob. 1990, 22, 101–110. [Google Scholar] [CrossRef]
- Ditlevsen, S.; Lánský, P. Estimation of the input parameters in the Feller neuronal model. Phys. Rev. E 2006, 73, 061910. [Google Scholar] [CrossRef] [PubMed]
- Buonocore, A.; Giorno, V.; Nobile, A.G.; Ricciardi, L.M. A neuronal modeling paradigm in the presence of refractoriness. BioSystems 2002, 67, 35–43. [Google Scholar] [CrossRef]
- Giorno, V.; Lánský, P.; Nobile, A.G.; Ricciardi, L.M. Diffusion approximation and first-passage-time problem for a model neuron. III. A birth-and-death process approach. Biol. Cyber. 1988, 58, 387–404. [Google Scholar] [CrossRef] [Green Version]
- Nobile, A.G.; Pirozzi, E. On time non-homogeneous Feller-type diffusion process in neuronal modeling. In Computer Aided Systems Theory—Eurocast 2015; Moreno-Díaz, R., Pichler, F., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9520, pp. 183–191. [Google Scholar]
- D’Onofrio, G.; Lánský, P.; Pirozzi, E. On two diffusion neuronal models with multiplicative noise: The mean first-passage time properties. Chaos 2018, 28, 043103. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, H. Skew CIR process, conditional characteristic function, moments and bond pricing. Appl. Math. Comput. 2018, 329, 230–238. [Google Scholar] [CrossRef]
- Cox, J.C.; Ingersoll, J.E., Jr.; Ross, S.A. A theory of the term structure of interest rates. Econometrica 1985, 53, 385–407. [Google Scholar] [CrossRef]
- Maghsoodi, Y. Solution of the extended CIR term structure and bond option valuation. Math. Financ. 1996, 6, 89–109. [Google Scholar] [CrossRef]
- Peng, Q.; Schellhorn, H. On the distribution of extended CIR model. Stat. Probab. Lett. 2018, 142, 23–29. [Google Scholar] [CrossRef]
- Linetsky, V. Computing hitting time densities for CIR and OU diffusions. Applications to mean-reverting models. J. Comput. Financ. 2004, 7, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Di Nardo, E.; D’Onofrio, G. A cumulant approach for the first-passage-time problem of the Feller square-root process. Appl. Math. Comput. 2021, 391, 125707. [Google Scholar]
- Lavigne, F.; Roques, L. Extinction times of an inhomogeneous Feller diffusion process: A PDF approach. Expo. Math. 2021, 39, 137–142. [Google Scholar] [CrossRef]
- Giorno, V.; Nobile, A.G. Time-inhomogeneous Feller-type diffusion process with absorbing boundary condition. J. Stat. Phys. 2021, 183, 1–27. [Google Scholar]
- Bhattacharya, R.N.; Waymire, E.C. Stochastic Processes with Applications; Classics in Applied Mathematics; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Giorno, V.; Nobile, A.G. Bell polynomial approach for time-inhomogeneous linear birth-death process with immigration. Mathematics 2020, 8, 1123. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Giorno, V.; Krishna Kumar, B.; Nobile, A.G. A double-ended queue with catastrophes and repairs, and a jump-diffusion approximation. Methodol. Comput. Appl. Probab. 2012, 14, 937–954. [Google Scholar] [CrossRef] [Green Version]
- Di Crescenzo, A.; Giorno, V.; Krishna Kumar, B.; Nobile, A.G. A time-non-homogeneous double-ended queue with failures and repairs and its continuous approximation. Mathematics 2018, 6, 81. [Google Scholar] [CrossRef] [Green Version]
- Dharmaraja, S.; Di Crescenzo, A.; Giorno, V.; Nobile, A.G. A continuous-time Ehrenfest model with catastrophes and its jump-diffusion approximation. J. Stat. Phys. 2015, 161, 326–345. [Google Scholar] [CrossRef]
- Gan, X.; Waxman, D. Singular solution of the Feller diffusion equation via a spectral decomposition. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 2015, 91, 012123. [Google Scholar] [CrossRef]
- Abramowitz, I.A.; Stegun, M. Handbook of Mathematical Functions; Dover Publications, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Feller, W. Two singular diffusion problems. Ann. Math. 1951, 54, 173–182. [Google Scholar] [CrossRef]
- Feller, W. The parabolic differen tial equations and the associated semi-groups of transformations. Ann. Math. 1952, 55, 468–518. [Google Scholar] [CrossRef]
- Karlin, S.; Taylor, H.W. A Second Course in Stochastic Processes; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Giorno, V.; Nobile, A.G.; Ricciardi, L.M.; Sacerdote, L. Some remarks on the Rayleigh process. J. Appl. Prob. 1986, 23, 398–408. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products; Academic Press Inc.: Cambridge, MA, USA, 2014. [Google Scholar]
- Erdèlyi, A.; Magnus, W.; Oberthettinger, F.; Tricomi, F.G. Higher Trascendental Functions; Mc Graw-Hill: New York, NY, USA, 1953; Volume II. [Google Scholar]
- Coleman, B.D.; Hsieh, Y.-H.; Knowles, G.P. On the optimal choice of r for a population in a periodic environment. Math. Biosci. 1979, 46, 71–85. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Williams, W.E. Partial Differential Equations; Clarendon Press: Oxford, UK, 1980. [Google Scholar]
- Erdèlyi, A.; Magnus, W.; Oberthettinger, F.; Tricomi, F.G. Tables of Integral Transforms; Mc Graw-Hill: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions; D. Reidel Publishing Company: Dordrecht, The Netherlands; Boston, MA, USA, 1974. [Google Scholar]







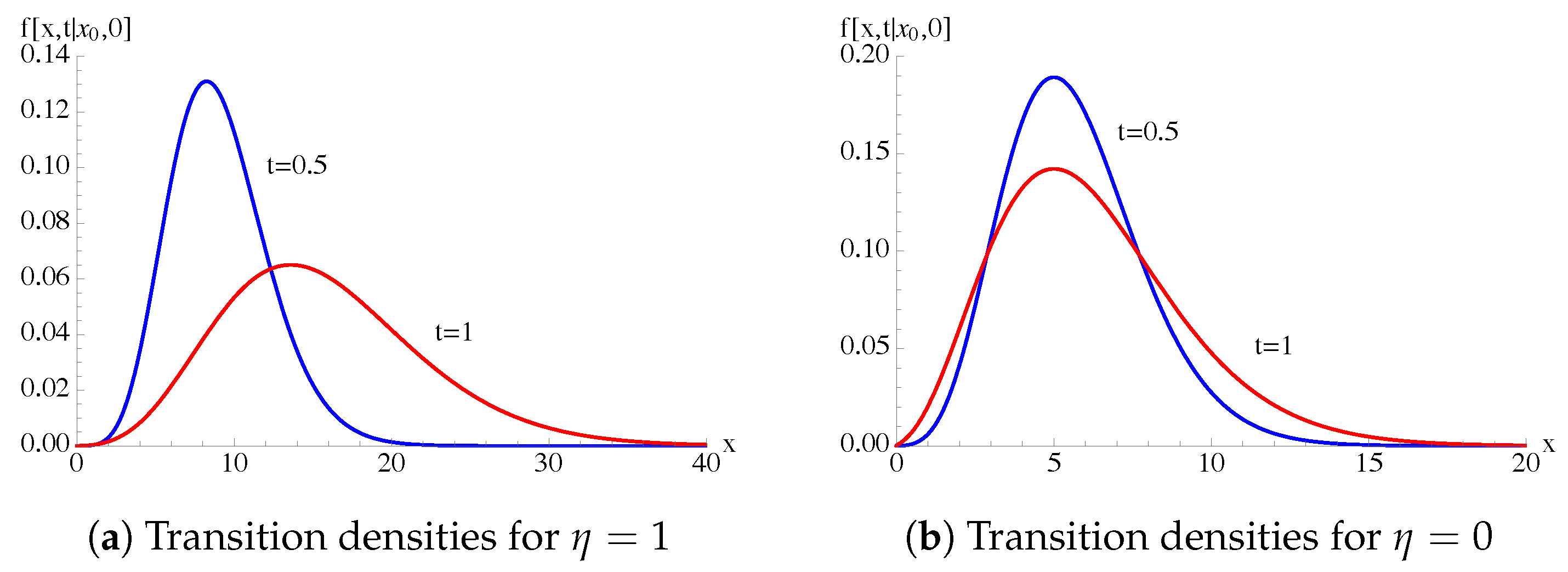


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giorno, V.; Nobile, A.G. Time-Inhomogeneous Feller-Type Diffusion Process in Population Dynamics. Mathematics 2021, 9, 1879. https://doi.org/10.3390/math9161879
Giorno V, Nobile AG. Time-Inhomogeneous Feller-Type Diffusion Process in Population Dynamics. Mathematics. 2021; 9(16):1879. https://doi.org/10.3390/math9161879
Chicago/Turabian StyleGiorno, Virginia, and Amelia G. Nobile. 2021. "Time-Inhomogeneous Feller-Type Diffusion Process in Population Dynamics" Mathematics 9, no. 16: 1879. https://doi.org/10.3390/math9161879
APA StyleGiorno, V., & Nobile, A. G. (2021). Time-Inhomogeneous Feller-Type Diffusion Process in Population Dynamics. Mathematics, 9(16), 1879. https://doi.org/10.3390/math9161879





